Resolving molecular contributions of ion channel noise to interspike interval variability through stochastic shielding

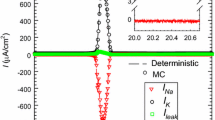
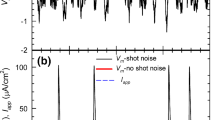
Abstract

Molecular fluctuations can lead to macroscopically observable effects. The random gating of ion channels in the membrane of a nerve cell provides an important example. The contributions of independent noise sources to the variability of action potential timing have not previously been studied at the level of molecular transitions within a conductance-based model ion-state graph. Here we study a stochastic Langevin model for the Hodgkin–Huxley (HH) system based on a detailed representation of the underlying channel state Markov process, the “$14\times 28$D model” introduced in (Pu and Thomas in Neural Computation 32(10):1775–1835, 2020). We show how to resolve the individual contributions that each transition in the ion channel graph makes to the variance of the interspike interval (ISI). We extend the mean return time (MRT) phase reduction developed in (Cao et al. in SIAM J Appl Math 80(1):422–447, 2020) to the second moment of the return time from an MRT isochron to itself. Because fixed-voltage spike detection triggers do not correspond to MRT isochrons, the inter-phase interval (IPI) variance only approximates the ISI variance. We find the IPI variance and ISI variance agree to within a few percent when both can be computed. Moreover, we prove rigorously, and show numerically, that our expression for the IPI variance is accurate in the small noise (large system size) regime; our theory is exact in the limit of small noise. By selectively including the noise associated with only those few transitions responsible for most of the ISI variance, our analysis extends the stochastic shielding (SS) paradigm (Schmandt and Galán in Phys Rev Lett 109(11):118101, 2012) from the stationary voltage clamp case to the current clamp case. We show numerically that the SS approximation has a high degree of accuracy even for larger, physiologically relevant noise levels. Finally, we demonstrate that the ISI variance is not an unambiguously defined quantity, but depends on the choice of voltage level set as the spike detection threshold. We find a small but significant increase in ISI variance, the higher the spike detection voltage, both for simulated stochastic HH data and for voltage traces recorded in in vitro experiments. In contrast, the IPI variance is invariant with respect to the choice of isochron used as a trigger for counting “spikes.”

Appendices

Model parameters, common symbols and notations

Table 2 Parameters used for simulations in this paper

Subunit kinetics for Hodgkin and Huxley parameters are given by

$$\begin{aligned}&\alpha _m(V)= \frac{0.1*(25-V)}{ \exp (2.5-0.1V)-1} \end{aligned}$$

(107)

$$\begin{aligned}&\beta _m(V)= 4*\exp (-V/18) \end{aligned}$$

(108)

$$\begin{aligned}&\alpha _h(V)= 0.07*\exp (-V/20) \end{aligned}$$

(109)

$$\begin{aligned}&\beta _h(V)= \frac{1}{ \exp (3-0.1V)+1} \end{aligned}$$

(110)

$$\begin{aligned}&\alpha _n(V)= \frac{0.01* (10-V)}{\exp (1-0.1V)-1} \end{aligned}$$

(111)

$$\begin{aligned}&\beta _n(V)= 0.125\exp (-V/80) \end{aligned}$$

(112)

$$\begin{aligned}&A_K(V) =\begin{bmatrix} D_1(1)&{} \beta _n(V) &{} 0 &{} 0 &{} 0\\ 4\alpha _n(V)&{} D_1(2)&{} 2\beta _n(V) &{} 0&{} 0\\ 0&{} 3\alpha _n(V)&{} D_1(3)&{} 3\beta _n(V)&{} 0\\ 0&{} 0&{} 2\alpha _n(V)&{} D_1(4)&{} 4\beta _n(V)\\ 0&{} 0&{} 0&{} \alpha _n(V)&{} D_1(5) \end{bmatrix},\nonumber \\&A_\text {Na}\nonumber \\&\quad =\begin{bmatrix} D_2(1) &{} \beta _m&{}0 &{}0 &{}\beta _h&{}0&{}0&{}0\\ 3\alpha _m&{}D_2(2)&{}2\beta _m&{}0&{}0&{}\beta _h&{}0&{}0\\ 0&{}2\alpha _m&{}D_2(3) &{}3\beta _m&{}0&{}0&{}\beta _h&{}0 \\ 0&{}0&{}\alpha _m&{}D_2(4)&{}0&{}0&{}0&{}\beta _h \\ \alpha _h&{}0&{}0&{}0&{}D_2(5)&{}\beta _m&{}0&{}0\\ 0&{}\alpha _h&{}0&{}0&{}3\alpha _m&{}D_2(6)&{}2\beta _m&{}0\\ 0&{}0&{}\alpha _h&{}0&{}0&{}2\alpha _m&{}D_2(7)&{}3\beta _m\\ 0&{}0&{}0&{}\alpha _h&{}0&{}0&{}\alpha _m&{}D_2(8)\\ \end{bmatrix},\nonumber \\ \end{aligned}$$

(113)

where the diagonal elements

$$\begin{aligned} D_k(i)=-\sum _{j\ne i}A_\text {ion}(j,i),\quad k\in \{1,2\} \quad \text {ion}\in \{\text {Na},\text {K}\}. \end{aligned}$$

Table 3 Table of common symbols and notations

Diffusion matrix of the 14D model

Define the state vector for $\hbox {Na}^+$ and $\hbox {K}^+$ channels as

$$\begin{aligned}&{\mathbf {M}}=[m_{00},m_{10},m_{20},m_{30},m_{01},m_{11},m_{21},m_{31}]^\intercal , \end{aligned}$$

and ${\mathbf {N}}=[n_0,n_1,n_2,n_3,n_4]^\intercal$, respectively.

The matrices $S_\text {K}$ and $S_\text {Na}$ are given by

and

where $S^{(i:j)}_\text {Na}$ is the $\hbox {i}^{th}$-$\hbox {j}^{th}$ column of $S_\text {Na}$.

Note that each of the 8 columns of $S_\text {K}$ corresponds to the flux vector along a single directed edge in the $\hbox {K}^+$ channel transition graph. Similarly, each of the 20 columns of $S_\text {Na}$ corresponds to the flux vector along a directed edge in the $\hbox {Na}^+$ graph (cf. Fig. 2). Factors $M_\text {ref}=6000$ and $N_\text {ref}=1800$ represent the reference number of $\hbox {K}^+$ and $\hbox {Na}^+$ channels from Goldwyn and Shea-Brown’s model (Goldwyn and Shea-Brown 2011).

Proof of Lemma 1

For the reader’s convenience, we restate

Lemma  1For a conductance-based model of the form (3), and for any fixed applied current $I_\text {app}$, there exist upper and lower bounds $v_\text {max}$ and $v_\text {min}$ such that trajectories with initial voltage condition $v\in [v_\mathrm{min},v_\mathrm{max}]$ remain within this interval for all times $t>0$, with probability 1, regardless of the initial channel state, provided the gating variables satisfy $0\le M_{ij}\le 1$ and $0\le N_i\le 1$.

Proof

Let $V_1={\text {min}}_{\mathrm{ion}}\{V_\mathrm{ion}\}\wedge V_\mathrm{leak}$, and $V_2={\text {max}}_{\mathrm{ion}}\{V_\mathrm{ion}\}\vee V_\mathrm{leak}$, where $\text {ion}\in \{\text {Na}^+, \text {K}^+\}$. Note that by assumption, for both the $\hbox {Na}^+$  and $\hbox {K}^+$ channel, $0\le {M_{31}} \le 1$, $0\le {N_4} \le 1$. Moreover, $g_i>0,\ g_\mathrm{leak}>0$; therefore, when $V\le V_1$

$$\begin{aligned} \frac{\hbox {d}V}{\hbox {d}t}&=\frac{1}{C}\left\{ I_\text {app}(t)-{\bar{g}}_\text {Na}{M_{31}}\left( V-V_\text {Na}\right) \nonumber \right. \\&\left. -{\bar{g}}_\text {K}{N_4}\left( V-V_\text {K}\right) -g_\text {leak}(V-V_\text {leak})\right\} \end{aligned}$$

(114)

$$\begin{aligned}&\ge \frac{1}{C}\left\{ I_\text {app}(t)-{\bar{g}}_\text {Na}{M_{31}}\left( V-V_1\right) \nonumber \right. \\&\left. -{\bar{g}}_\text {K}{N_4}\left( V-V_1\right) -g_\text {leak}(V-V_1)\right\} \end{aligned}$$

(115)

$$\begin{aligned}&\ge \frac{1}{C}\left\{ I_\text {app}(t)-{{\bar{g}}_\text {Na}\times 0\times }\left( V-V_1\right) \nonumber \right. \\&\quad \left. -{{\bar{g}}_\text {K}\times 0\times }\left( V-V_1\right) -g_\text {leak}(V-V_1)\right\} \end{aligned}$$

(116)

$$\begin{aligned}&=\frac{1}{C}\left\{ I_\text {app}(t)-g_\text {leak}(V-V_1)\right\} . \end{aligned}$$

(117)

Inequality (115) holds with probability 1 because $V_1 ={\text {min}}_{i\in {\mathcal {I}}} \wedge V_\text {leak}$, and inequality (116) follows because $V-V_1\le 0$, $g_i>0$ and ${M_{31}}\ge 0$, ${N_4}\ge 0$. Let $V_\text {min}:=\text {min}\left\{ \frac{I_-}{g_\text {leak}} +V_1,V_1\right\}$. When $V<V_\text {min}$, $\frac{\hbox {d}V}{\hbox {d}t}>0$. Therefore, V will not decrease beyond $V_\text {min}$.

Similarly, when $V\ge V_2$

$$\begin{aligned} \frac{\hbox {d}V}{\hbox {d}t}&=\frac{1}{C}\left\{ I_\text {app}(t)-{\bar{g}}_\text {Na}{M_{31}}\left( V-V_\text {Na}\right) \nonumber \right. \\&\quad \left. -{\bar{g}}_\text {K}{N_4}\left( V-V_\text {K}\right) -g_\text {leak}(V-V_\text {leak})\right\} \end{aligned}$$

(118)

$$\begin{aligned}&\le \frac{1}{C}\left\{ I_\text {app}(t)-{\bar{g}}_\text {Na}{M_{31}}\left( V-V_2\right) \nonumber \right. \\&\left. \quad -{\bar{g}}_\text {K}{N_4}\left( V-V_2\right) -g_\text {leak}(V-V_2)\right\} \end{aligned}$$

(119)

$$\begin{aligned}&\le \frac{1}{C}\left\{ I_\text {app}(t)-{{\bar{g}}_\text {Na}\times 0\times }\left( V-V_2\right) \nonumber \right. \\&\left. \quad -{{\bar{g}}_\text {K}\times 0\times }\left( V-V_2\right) -g_\text {leak}(V-V_2)\right\} \end{aligned}$$

(120)

$$\begin{aligned}&=\frac{1}{C}\left\{ I_\text {app}(t)-g_\text {leak}(V-V_2)\right\} . \end{aligned}$$

(121)

Inequality (119) and inequality (120) hold because $V_2={\text {max}}_{i\in {\mathcal {I}}}\{V_i\}\vee V_\text {leak},$ $V-V_2\ge 0$, $g_i>0$ and ${M_{31}}\ge 0$, ${N_4}\ge 0$. Let $V_\text {max}=\text {max}\left\{ \frac{I_\text {app}}{g_\text {leak}}+V_2, V_2 \right\}$. When $V>V_\text {max},$ $\frac{\hbox {d}V}{\hbox {d}t}<0$. Therefore, V will not go beyond $V_\text {max}$.

We conclude that if V takes an initial condition in the interval $[V_\text {min},V_\text {max}],$ and if $0\le M_{ij},N_i\le 1$ for all time, then V(t) remains within this interval for all $t\ge 0$. Thus, we complete the proof of Lemma 1. $\square$

Experimental methods

Whole-cell current clamp recordings of Purkinje cells from in vitro cerebellar slice preparations taken from wild type and leaner mice were performed in the laboratory of Dr. David Friel (Case Western Reserve University School of Medicine), as described in Ovsepian and Friel (2008). Experimental procedures conformed to guidelines approved by the Institutional Animal Care and Use Committee at Case Western Reserve University. Voltage signals were sampled at a frequency of 20kHz, filtered at 5–10 kHz, digitized at a resolution of 32/mV and analyzed using custom software written in IgorPro and MATLAB.

Comparison of our main theorem with the related literature

1.1 Comparison with Giacomin et al. (2018)

Giacomin et al. (2018) considered a one-parameter family of strong solutions of the (Ito) stochastic differential equation

$$\begin{aligned} \hbox {d}X_t^\varepsilon =F(X_t^\varepsilon )\,\hbox {d}t+\varepsilon G(X_t^\varepsilon )\,\hbox {d}B_t, \end{aligned}$$

(122)

where the parameter $\varepsilon > 0$, $F(\cdot )$ is a locally Lipschitz vector field on ${\mathbb {R}}^d$, $G(\cdot )$ is a locally Lipschitz function on ${\mathbb {R}}^d$ with values in the $d\times m$ matrices and $B_\cdot$ is a standard m dimensional Brownian motion. Note that in our formulation of the Langevin system (3), we use $\sqrt{\epsilon }$ where Giacomin et al. use $\varepsilon$. Consequently, our expressions involving $GG^\intercal$ scale as $\epsilon$, whereas the analogous expressions scale as $\varepsilon ^2$ in Giacomin et al. (2018).

If the deterministic asymptotic phase is $\theta (x)$, then evaluated along a trajectory $\theta (X^\varepsilon _t)$ the phase obeys Ito’s formula:

$$\begin{aligned} \hbox {d}\theta (x)= & {} \left[ F_i(x)\partial _i\theta (x)\nonumber \right. \\&\left. +\frac{\varepsilon ^2}{2}{\mathcal {D}}_{ij}(x)\partial ^2_{ij}\theta (x)\right] \hbox {d}t\nonumber \\&+\varepsilon (\partial _i\theta (x))G_{ik}(x)\,\hbox {d}W_k(t), \end{aligned}$$

(123)

where ${\mathcal {D}}=GG^\intercal$ and we use Einstein’s summation convention. Given their definition of the asymptotic phase function and their Theorem 2.1 on page 1024, $F_i(x)\partial _i\theta (x)=1$. As a result of their Theorem 2.3 (page 1026 in Giacomin et al. 2018), if $\varepsilon$ is small, then over long times, we can establish that (since $X^\varepsilon _t$ stays “close to” the deterministic limit cycle solution $q_t=X^0_t$ for times on the order of $t/\varepsilon ^2$) approximately

$$\begin{aligned}&d\tilde{\theta }\approx \left( 1+\varepsilon ^2 b\right) \,dt+\varepsilon \sigma \, dW_t \end{aligned}$$

(124)

for some constants $\sigma$ and b that one may calculate in terms of F and G for any particular system. The notation ${\tilde{\theta }}$ refers to the “lift” of $\theta$ from the circle $\theta \in {\mathbb {S}}_T\equiv [0,T)$ to ${\tilde{\theta }}\in {\mathbb {R}}$, i.e., the integral of (124) without the jumps induced by taking $\theta$ mod the period T. For small noise $\varepsilon$, integrating up to time t, we have (provided t is $o(\varepsilon ^{-2})$, and setting $x_0\equiv X_0^\varepsilon$),

$$\begin{aligned} {\tilde{\theta }}(X^\varepsilon _t)\approx \theta (x_0)+t(1+\varepsilon ^2 b)+\varepsilon \sigma \,W_t, \end{aligned}$$

(125)

where $W_t$ is now a 1D standard Brownian motion (with $\approx$ signifying convergence in distribution, after rescaling time). Upon rescaling time, the authors establish that

$$\begin{aligned} {\tilde{\theta }}(X_{t/\varepsilon ^{2}}^\varepsilon )\approx \theta (x_0)+\frac{t}{\varepsilon ^2}+tb+\sigma \, W_t. \end{aligned}$$

(126)

Therefore, the accumulated variance of ${\tilde{\theta }}(X^\varepsilon _t)$ during one (deterministic) period T is

$$\begin{aligned} {\mathbb {V}}({\tilde{\theta }}(t+T)-{\tilde{\theta }}(t))&\approx {\mathbb {V}}\left( T+\varepsilon ^2bT+\varepsilon \sigma (W_{t+T}-W_t)\right) \end{aligned}$$

(127)

$$\begin{aligned}&=\varepsilon ^2\sigma ^2T \end{aligned}$$

(128)

$$\begin{aligned}&=\varepsilon ^2\int _0^T (D\theta (q_s)G(q_s)G^t(q_s)D\theta ^t(q_s))\,\hbox {d}s. \end{aligned}$$

(129)

Equation (128) holds because the variance of the Wiener process increment over time T is exactly T and because the limit cycle period T is a deterministic quantity.⁷ Equation (129) holds by virtue of the authors’ formula, Eq. (2.20) on page 1026 in Giacomin et al. (2018).

Finally, we note that, for a conductance-based channel noise model of the type we consider in this paper, the expression $D\theta (q_s)G(q_s)G^t(q_s)D\theta ^t(q_s)$ in Giacomin et al. (2018) corresponds exactly with our expression $\sum _{ij}({\mathcal {G}}{\mathcal {G}}^\intercal )_{ij}\partial _{i}T_0\partial _{j}T_0$ and $\sum _{k=1}^{28}\alpha _k(v){\mathbf {X}}_{i(k)} \left( \zeta _k^\intercal {\tilde{{\mathbf {Z}}}}\right) ^2,$ as in our Theorem 1 and Corollary 1. To see the correspondence, note that $D\theta (q_s)$, the gradient of the phase function evaluated along the limit cycle is none other than the infinitesimal phase response curve and is identical to the gradient of the zero-noise timing function $\nabla T_0$; the rest follows from the structure of ${\mathcal {G}}$ as shown in the proof of our main theorem.

1.2 Comparison with Aminzare et al. (2019)

In Aminzare et al. (2019), the authors consider the scaled Langevin model (Eq. (10) on page 4718)

$$\begin{aligned} \hbox {d}x={\mathbf {F}}(x)\hbox {d}t+\sigma B(x)\hbox {d}{\mathbf {W}}(t). \end{aligned}$$

(130)

The authors consider the special case in which $B(x)=\text {diag}(\beta _1,\ldots ,\beta _n)$. Our corresponding matrix ${\mathcal {G}}$ is not diagonal, due to the biophysical origin of channel noise, so direct comparison of our results is somewhat limited. Nevertheless, the authors consider the moments of the stochastic period, defined as the time to complete one oscillation, and arrive at an expression for the variance of the stochastic period that we can compare with the result of our theorem 1. In particular, in Proposition 3 on page 4721 in Aminzare et al. (2019), the authors calculate the first and second moments of the stochastic return time T for system (130) with $B(x)=\text {diag}(\beta _1,\ldots ,\beta _n)$ as

$$\begin{aligned} {\mathbb {E}}[T]=\frac{2\pi }{\omega }-\frac{\sigma ^2}{\omega ^2}\int _0^{2\pi }\varPi (\alpha )\,\hbox {d}\alpha +o(\sigma ^2), \end{aligned}$$

(131)

and

$$\begin{aligned} {\mathbb {E}}[T^2]= & {} \frac{4\pi ^2}{\omega ^2}-\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }(2\pi -\alpha )\varPi (\alpha )\,\hbox {d}\alpha \nonumber \\&+\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }\zeta (\alpha )\,\hbox {d}\alpha \nonumber \\&-\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }\int _\xi ^{2\pi }\varPi (\alpha )\,\hbox {d}\alpha \, \hbox {d}\xi +o(\sigma ^2), \end{aligned}$$

(132)

where

$$\begin{aligned} \varPi (\theta _0)= & {} \frac{1}{2}\sum _{i=1}^n\beta ^2_iH_{ii}(\theta _0),\quad \text {and }\nonumber \\ \zeta (\theta _0)= & {} \frac{1}{2}\sum _{i=1}^n\beta ^2_iZ_{i}(\theta _0)^2, \end{aligned}$$

(133)

$H(\theta )$ is the “second-order” PRC (the Hessian of the asymptotic phase function) and $Z(\theta )$ is the infinitesimal phase response curve. Note that because (Aminzare et al. 2019) scales phase from 0 to $2\pi$, their expression $\zeta (\theta _0)$ has units of radians/time. In contrast, our infinitesimal phase response curve ${\mathbf {Z}}(t)$ has units of time; we may convert by multiplying by $T_0/2\pi$ (Sect. 2.4). Although ${\mathcal {G}}$ is not diagonal for conductance-based neural oscillators driven by channel noise (cf. Eq. (3)), we can still express the term $\zeta (\theta _0)$ as

$$\begin{aligned} \zeta (\theta _0)= & {} 2\pi ^2\sum _{ij}({\mathcal {G}}{\mathcal {G}}^\intercal )_{ij}\partial _{i}T_0\partial _{j}T_0\nonumber \\= & {} 2\pi ^2\sum _{k=1}^{28}\alpha _k(v){\mathbf {X}}_{i(k)} \left( \zeta _k^\intercal {\tilde{{\mathbf {Z}}}}\right) ^2. \end{aligned}$$

(134)

Given the first and second moments of the time period in Aminzare et al. (2019), the variance is given by

$$\begin{aligned} {\mathbb {V}}[T]&={\mathbb {E}}[T^2]-\left( {\mathbb {E}}[T]\right) ^2 \end{aligned}$$

(135)

$$\begin{aligned}&=\frac{4\pi ^2}{\omega ^2}-\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }(2\pi -\alpha )\varPi (\alpha )\hbox {d}\alpha \nonumber \\&\quad +\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }\zeta (\alpha )\hbox {d}\alpha -\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }\int _\xi ^{2\pi }\varPi (\alpha )\hbox {d}\alpha \hbox {d}\xi \nonumber \\&\quad - \frac{4\pi ^2}{\omega ^2}+\frac{4\pi \sigma ^2}{\omega ^2}\nonumber \\&\quad \int _0^{2\pi }\varPi (\alpha )\hbox {d}\alpha + o(\sigma ^2)\ \end{aligned}$$

(136)

$$\begin{aligned}&=-\frac{4\pi \sigma ^2}{\omega ^3}\int _0^{2\pi }\varPi (\alpha )\hbox {d}\alpha +\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }\alpha \varPi (\alpha )\hbox {d}\alpha \nonumber \\&\quad +\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }\zeta (\alpha )\hbox {d}\alpha \nonumber \\&\quad -\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }\int _\xi ^{2\pi }\varPi (\alpha )\hbox {d}\alpha \hbox {d}\xi \nonumber \\&\quad +\frac{4\pi \sigma ^2}{\omega ^2}\int _0^{2\pi }\varPi (\alpha )\hbox {d}\alpha + o(\sigma ^2) \end{aligned}$$

(137)

$$\begin{aligned}&\quad =\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }\alpha \varPi (\alpha )\hbox {d}\alpha +\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }\zeta (\alpha )\hbox {d}\alpha \nonumber \\&\quad -\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }\int _\xi ^{2\pi }\varPi (\alpha )\hbox {d}\alpha \hbox {d}\xi . \end{aligned}$$

(138)

By Tonelli’s Theorem (Saks 1937),

$$\begin{aligned}&\int _0^{2\pi }\int _\xi ^{2\pi }\varPi (\alpha )\hbox {d}\alpha \hbox {d}\xi \end{aligned}$$

(139)

$$\begin{aligned}&\quad =\int \limits _{\begin{array}{c} \xi \le \alpha \le 2\pi \\ (\alpha ,\xi )\in [0,2\pi ]\times [0,2\pi ] \end{array}}\varPi (\alpha )d(\alpha ,\xi ) \end{aligned}$$

(140)

$$\begin{aligned}&\quad =\int _0^{2\pi }\int _0^{\alpha }\varPi (\alpha )\hbox {d}\xi \hbox {d}\alpha \end{aligned}$$

(141)

$$\begin{aligned}&\quad =\int _0^{2\pi }\left( \int _0^{\alpha }\varPi (\alpha )\hbox {d}\xi \right) \hbox {d}\alpha \end{aligned}$$

(142)

$$\begin{aligned}&\quad =\int _0^{2\pi }\alpha \varPi (\alpha )\hbox {d}\alpha . \end{aligned}$$

(143)

Therefore, Eq. (138) reduces to

$$\begin{aligned} {\mathbb {V}}[T]&=\frac{2\sigma ^2}{\omega ^3}\int _0^{2\pi }\zeta (\alpha )\hbox {d}\alpha \end{aligned}$$

(144)

$$\begin{aligned}&=\frac{2\sigma ^2}{\omega ^3}\times \frac{\omega ^2}{2\pi }\times 2\pi ^2\int _0^{T} \sum _{k=1}^{28}\alpha _k(v){\mathbf {X}}_{i(k)} \left( \zeta _k^\intercal {\tilde{{\mathbf {Z}}}}\right) ^2\hbox {d}t \end{aligned}$$

(145)

$$\begin{aligned}&=\sigma ^2T\sum _{k=1}^{28}\int _0^{T}\alpha _k(v){\mathbf {X}}_{i(k)} \left( \zeta _k^\intercal {\tilde{{\mathbf {Z}}}}\right) ^2\hbox {d}t \end{aligned}$$

(146)

which is consistent with our main result, because $\sigma ^2=\epsilon$, $\omega =2\pi /T$, and $\hbox {d}\alpha \sim \omega \,\hbox {d}t$.