Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-23T23:09:26.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectrality of Moran Sierpinski-type measures on ${\mathbb R}^2$

Part of: Nontrigonometric harmonic analysis Harmonic analysis in one variable Classical measure theory

Published online by Cambridge University Press:  18 January 2021

Min-Min Zhang
Min-Min Zhang*
Affiliation:
Department of Mathematics and Statistics, Central China Normal University, Wuhan430079, P.R.China.
*
e-mail:zhangminmin0907@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 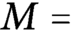$M=$ diag 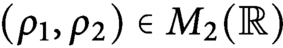$(\rho _1,\rho _2)\in M_{2}({\mathbb R})$ be an expanding matrix and Let 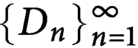$\{D_n\}_{n=1}^{\infty }$ be a sequence of digit sets with 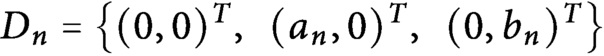$D_n=\left \{(0, 0)^T,\,\,\,(a_n, 0 )^T, \,\,\, (0, b_n )^T \right \}$ , where 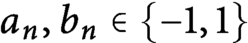$a_n, b_n\in \{-1,1\}$ . The associated Borel probability measure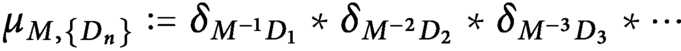

$$ \begin{align*} \mu_{M,\{D_n\}}:=\delta_{M^{-1}D_1}\ast \delta_{M^{-2}D_2}\ast \delta_{M^{-3}D_3}\ast \cdots \end{align*} $$
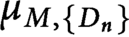is called a Moran Sierpinski-type measure. In this paper, we show that $\mu _{M, \{D_n\}}$ is a spectral measure if and only if 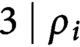$3\mid \rho _i$ for each 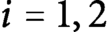$i=1, 2$ . The special case is the Sierpinski-type measure with 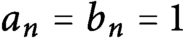$a_n=b_n=1$ for all 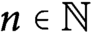$n\in {\mathbb N}$ , which is proved by Dai et al. [Appl. Comput. Harmon. Anal. (2020), https://doi.org/10.1016/j.acha.2019.12.001].

Keywords

Moran measuresFourier transformspectral measureconvolutionsorthogonal

MSC classification

Primary: 28A80: Fractals
Secondary: 42A85: Convolution, factorization 42C05: Orthogonal functions and polynomials, general theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 4 , December 2021 , pp. 1024 - 1040
Check for updates
Copyright
© Canadian Mathematical Bulletin 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

An, L. X., Fu, X. Y., and Lai, C. K., On Spectral Cantor-Moran measures and a variant of Bourgain’s sum of sine problem. Adv. Math. 349(2019), 84–12. https://doi.org/10.1016/j.aim.2019.04.014 CrossRefGoogle Scholar
An, L. X., He, L., and He, X. G., Spectrality and non-spectrality of the Riesz product measures with three elements in digit sets. J. Funct. Anal. 277(2019), 255–278. https://doi.org/10.1016/j.jfa.2018.10.017 CrossRefGoogle Scholar
An, L. X. and He, X. G., A class of spectral Moran measures. J. Funct. Anal. 266(2014), 343–354. https://doi.org/10.1016/j.jfa.2013.08.031 CrossRefGoogle Scholar
Dai, X. R., When does a Bernoulli convolution admit a spectrum? Adv. Math. 231(2012), 1681–1693. https://doi.org/10.1016/j.aim.2012.06.026 CrossRefGoogle Scholar
Dai, X. R., He, X. G., and Lai, C. K., Spectral property of Cantor measures with consecutive digits. Adv. Math. 242(2013), 187–208. https://doi.org/10.1016/j.aim.2013.04.016 CrossRefGoogle Scholar
Dai, X. R., He, X. G., and Lau, K. S., On spectral N-Bernoulli measures. Adv. Math. 259(2014), 511–531. https://doi.org/10.1016/j.aim.2014.03.026 CrossRefGoogle Scholar
Dai, X. R. and Sun, Q. Y., Spectral measures with arbitrary Hausdorff dimensions. J. Funct. Anal. 268(2015), 2464–2477. https://doi.org/10.1016/j.jfa.2015.01.005 CrossRefGoogle Scholar
Deng, Q. R., Spectrality of one dimensional self-similar measures with consecutive digits. J. Math. Anal. Appl. 409(2014), 331–346. http://dx.doi.org/10.1016/j.jmaa.2013.07.046 CrossRefGoogle Scholar
Deng, Q. R. and Lau, K. S., Sierpinski-type spectral self-similar measures. J. Funct. Anal. 269(2015), 1310–1326. http://dx.doi.org/10.1016/j.jfa.2015.06.013 CrossRefGoogle Scholar
Dutkay, D., Han, D. G., and Sun, Q. Y., Divergence of the mock and scrambled Fourier series on fractal measures. Trans. Amer. Math. Soc. 366(2014), 2191–2208. https://doi.org/10.1090/s0002-9947-2013-060217 CrossRefGoogle Scholar
Dutkay, D., Haussermann, J., and Lai, C. K., Hadamard triples generate self-affine spectral measures. Trans. Amer. Math. Soc. 371(2019), 1439–1481. https://doi.org/10.1090/tran/7325 CrossRefGoogle Scholar
Dutkay, D. and Lai, C. K., Spectral measures generated by arbitrary and random convolutions. J. Math. Pures Appl. 107(2017), 183–204. https://doi.org/10.1016/j.matpur.2016.06.003 CrossRefGoogle Scholar
Dutkay, D. E., Han, D. G., Sun, Q. Y., and Weber, E., On the Beurling dimension of exponential frames. Adv. Math. 226(2011), 285–297. https://doi.org/10.1016/j.aim.2010.06.017 CrossRefGoogle Scholar
Dutkay, D. E. and Jorgensen, P., Wavelets on fractals. Rev. Mat. Iberoam. 22(2006), 131–180. https://doi.org/10.4171/rmi/452 CrossRefGoogle Scholar
Dutkay, D. E. and Jorgensen, P., Analysis of orthogonality and of orbits in affine iterated function systems. Math. Z. 256(2007), 801–823. https://doi.org/10.1007/s00209-007-0104-9 CrossRefGoogle Scholar
Fan, A. H., Fan, S. L., Liao, L. M., and Shi, R. X., Fuglede’s conjecture holds in $\ {\mathbb{Q}}_p$ . Math. Ann. 375(2019), 315–341. https://doi.org/10.1007/s00288-019-01867-8 CrossRefGoogle Scholar
Dai, X. R., Fu, X. Y., and Yan, Z. H., Spectrality of self-affine Sierpinski-type measures on $\ {\mathbb{R}}^2$ . Appl. Comput. Harmon. Anal. (2020). https://doi.org/10.1016/j.acha.2019.12.001 Google Scholar
Fu, Y. S., He, X. G., and Wen, Z. Y., Spectra of Bernoulli convolutions and random convolutions. J. Math. Pures Appl. 116(2018), 105–131. https://doi.org/10.1016/j.matpur.2018.06.002 CrossRefGoogle Scholar
Fu, Y. S. and Wen, Z. X., Spectrality of infinite convolutions with three-element digit sets. Monatsh. Math. 183(2017), 465–485. https://doi.org/10.1007/s00605-017-1026-1 CrossRefGoogle Scholar
Fuglede, B., Commuting self-adjoint partial differential operators and a group theoretic problem. J. Funct. Anal. 16(1974), 101–121. https://doi.org/10.1016/0022-1236(74)90072-x CrossRefGoogle Scholar
Greenfeld, R. and Lev, N., Fuglede’s spectral set conjecture for convex polytopes. Anal. PDE 10(2017), 1497–1538. https://doi.org/10.2140/apde.2017.10.1497 CrossRefGoogle Scholar
He, L. and He, X. G., On the Fourier orthonormal basis of Cantor-Moran measure. J. Funct. Anal. 272(2017), 1980–2004. https://doi.org/10.1016/j.jfa.2016.09.021 CrossRefGoogle Scholar
Hu, T. Y. and Lau, K. S., Spectral property of the Bernoulli convolutions. Adv. Math. 219(2008), 554–567. https://doi.org/10.1016/j.aim.2008.05.004 CrossRefGoogle Scholar
Jorgensen, P. and Pedersen, S., Dense analytic subspaces in fractal $\ {L}^2-$ spaces. J. Anal. Math. 75(1998), 185–228. https://doi.org/10.1007/bf02788699 CrossRefGoogle Scholar
Kolountzakis, M. and Matolcsi, M., Tiles with no spectra. Forum Math. 18(2006), 519–528. https://doi.org/10.1515/forum.2006.026 CrossRefGoogle Scholar
Laba, I. and Wang, Y., On spectral Cantor measures. J. Funct. Anal. 193(2002), 409–420. https://doi.org/10.1006/jfan.2001.3941 CrossRefGoogle Scholar
Liu, Y. M. and Wang, Y., The uniformity of non-uniform Gabor bases. Adv. Comput. Math. 18(2003), 345–355. https://doi.org/10.1023/A:1021350103925 CrossRefGoogle Scholar
Strichartz, R., Mock Fourier series and transforms associated with certain Cantor measures. J. Anal. Math. 81(2000), 209–238. https://doi.org/10.1007/bf02788990 CrossRefGoogle Scholar
Strichartz, R., Convergence of Mock Fourier series. J. Anal. Math. 99(2006), 333–353. https://doi.org/10.1007/bf02789451 CrossRefGoogle Scholar
Tao, T., Fuglede’s conjecture is false in 5 and higher dimensions. Math. Res. Lett. 11(2004), 251–258. https://doi.org/10.4310/mrl.2004.v11.n2.a8 CrossRefGoogle Scholar
Wang, Z. M., On the spectra of a class of self-affine measures on $\ {\mathbb{R}}^2$ . J. Funct. Anal. (2020). https://doi.org/10.1016/j.jfa.2020.108685 CrossRefGoogle Scholar