Site-Monotonicity Properties for Reflection Positive Measures with Applications to Quantum Spin Systems

Abstract

We consider a general statistical mechanics model on a product of local spaces and prove that, if the corresponding measure is reflection positive, then several site-monotonicity properties for the two-point function hold. As an application, we derive site-monotonicity properties for the spin–spin correlation of the quantum Heisenberg antiferromagnet and XY model, we prove that spin-spin correlations are point-wise uniformly positive on vertices with all odd coordinates—improving previous positivity results which hold for the Cesàro sum. We also derive site-monotonicity properties for the probability that a loop connects two vertices in various random loop models, including the loop representation of the spin O(N) model, the double-dimer model, the loop O(N) model and lattice permutations, thus extending the previous results of Lees and Taggi (2019).

1 Introduction

We consider a general probabilistic model on the torus ${\mathbb {T}}_L={\mathbb {Z}}^d/L{\mathbb {Z}}^d$, whose realisations live in a product of local spaces. Each local space is associated to one of the vertices of ${\mathbb {T}}_L$ and elements of the local spaces interact with each other via a linear functional acting on a real algebra of observables. This general setting includes various important models in statistical mechanics, for example the spin O(N) model, the quantum Heisenberg anti-ferromagnet and XY model, the dimer and the double-dimer model, lattice permutations, and the loop O(N) model. We prove that, if the linear functional acting on functions of our state space is reflection positive, then several site-monotonicity properties for the two-point function hold. This generalises the monotonicity and positivity results of [13] to a very general system. This general result has the following implications.

Firstly, in their seminal paper [6], Fröhlich, Simon and Spencer introduced a method for proving the non-decay of correlations of the two-point function of several statistical mechanics models in dimension $d > 2$. This method was further developed in [7] and used in many other works (we additionally refer to [4] for an overview). More precisely, this method is used to prove that the Cesàro sum of the two-point function is uniformly positive. Our general monotonicity result shows that, when this method works, a stronger result can often be obtained. Namely not only is the Cesàro sum of the two-point function uniformly positive in the system size, but the two-point function is also uniformly positive point-wise. This result was derived by Lees and Taggi [13] in the special case of the spin O(N) model and here it is generalised to an abstract statistical mechanics setting.

As an example of a new application we consider quantum spin systems including the Heisenberg antiferromagnet and XY model, which were not covered by the framework of [13]. Quantum spin systems are important class of statistical mechanics models whose realisation space is the tensor product of local Hilbert spaces.

It is already known [5, 7,8,9, 16] that the Gibbs states of this model are reflection positive in the presence of anti-ferromagnetic interactions and that, in dimension $d > 2$, the Cesàro sum of the two-point function is uniformly positive for large enough values of the inverse temperature parameter and system size. Our result implies that, when the spin or dimension is large enough, the spin-spin correlation is point-wise uniformly positive for vertices with all odd coordinates, extending the existing results. We fully expect that this uniform positivity should extend to all vertices, not just ‘odd’ vertices. In addition this method can be applied to other cases where the Cesàro sum of two-point functions is known to be positive, such as in [11, 12, 15].

Our third main result involves a general class of random loop soup models, which we refer to as the random path model. This class includes the loop representation of the spin O(N) model [1, 13], the double-dimer model [10], lattice permutations [2, 3, 15], and the loop O(N) model [14]. In [13], site-monotonicity properties for the two-point function—which is defined as the ratio of partition functions with a walk connecting two-points in a system of loops and the partition function with only loops—were derived. Here we extend the result to a general class of two-point functions, including the probability that two fixed vertices have a loop passing through both of them.

2 Model and Main Result

Consider the torus ${\mathbb {T}}_L={\mathbb {Z}}^d/L{\mathbb {Z}}^d$ with $d\ge 2$ and $L\in 2{\mathbb {N}}$.

Denote by $o=(0,\dots ,0)$ the origin of the torus. For each $x\in {\mathbb {T}}_L$ let $\Sigma _x$ be a Polish space of local states (for example ${\mathbb {S}}^{N-1}$, ${\mathbb {C}}^{2S+1}$, $\{-1,+1\}, \ldots$). Further let $\otimes$ be some associative product between the $\Sigma _x$’s (for example the cartesian product or the tensor product). Our state space is

$$\begin{aligned} {\mathcal S }=\otimes _{x\in {\mathbb {T}}_L} \Sigma _x. \end{aligned}$$

(2.1)

We denote elements of ${\mathcal S }$ by $w=(w_x)_{x\in {\mathbb {T}}_L}$ where $w_x\in \Sigma _x$. Let ${\mathcal A }_L$ be a real, finite dimensional, algebra of functions on ${\mathcal S }$ with unit. For example if $\Sigma _x={\mathbb {S}}^{N-1}$ (as in the case of the spin O(N) model) then we could take $\otimes$ to be the cartesian product and ${\mathcal A }_L$ to be the algebra of functions ${\mathcal S }\rightarrow {\mathbb {R}}$ that are measurable with respect to the Haar measure on ${\mathcal S }$. If $\Sigma _x={\mathbb {C}}^{2S+1}$ (as in the case of spin-S quantum systems) then we take $\otimes$ to be the tensor product and ${\mathcal A }_L$ the set of Hermitian matrices acting on ${\mathcal S }$. Further, let $\langle \cdot \rangle$ be a linear functional on ${\mathcal A }_L$ such $\langle 1\rangle =1$. Our key requirement is that $\langle \cdot \rangle$ is reflection positive, which we describe briefly.

2.1 Reflection Positivity

Consider a plane $R=\{z\in {\mathbb {R}}^d\, :\, z_i =m\}$ (where $z_i=$ is the ith coordinate of z) for some $m\in \tfrac{1}{2}{\mathbb {Z}}\cap [0,L)$ and some $i\in \{1,\ldots , d\}$. Let $\vartheta :{\mathbb {T}}_L\rightarrow {\mathbb {T}}_L$ be the reflection operator that reflects vertices of ${\mathbb {T}}_L$ in the plane R (although it is worth noting that R corresponds to a pair of plane in ${\mathbb {T}}_L$). More precisely, for any $x=(x_1,\ldots ,x_d)\in {\mathbb {T}}_L$

$$\begin{aligned} (\vartheta x)_k:={\left\{ \begin{array}{ll} x_ k &{} \text {if }k\ne i, \\ 2m-x_k\mod L &{} \text {if }k=i. \end{array}\right. } \end{aligned}$$

(2.2)

If $m\in \tfrac{1}{2}{\mathbb {Z}}\setminus {\mathbb {Z}}$ we call such a reflection a reflection through edges, if $m\in {\mathbb {Z}}$ we call such a reflection a reflection through vertices. We denote by ${\mathbb {T}}_L^+,{\mathbb {T}}_L^-$ the partition of ${\mathbb {T}}_L$ into two halves with the property that $\vartheta ({\mathbb {T}}_L^{\pm })={\mathbb {T}}_L^{\mp }$.

We say a function $A\in {\mathcal A }_L$ has domain $D\subset {\mathbb {T}}_L$ if for any $w_1,w_2\in {\mathcal S }$ that agree on D we have $A(w_1)=A(w_2)$. Consider the algebras ${\mathcal A }_L^+,{\mathcal A }_L^-\subset {\mathcal A }_L$, of functions with domain ${\mathbb {T}}_L^+,{\mathbb {T}}_L^-$ respectively. The reflection $\vartheta$ acts on elements $w\in {\mathcal S }$ as $(\vartheta w)_x=w_{\vartheta x}$ and for $A\in {\mathcal A }^+_L$ it acts as $\vartheta A(w)=A(\vartheta w)$.

We say that $\langle \cdot \rangle$ is reflection positive with respect to $\vartheta$ if, for any $A,B\in {\mathcal A }^+_L$,

• 1. $\langle A\vartheta B\rangle =\langle B\vartheta A\rangle$,

• 2. $\langle A\vartheta A\rangle \ge 0$.

A consequence of this is the Cauchy–Schwarz inequality

$$\begin{aligned} \langle A\vartheta B\rangle ^2\le \langle A\vartheta A\rangle \langle B\vartheta B\rangle . \end{aligned}$$

(2.3)

We say $\langle \cdot \rangle$ is reflection positive for reflections through edges resp. vertices if, for any reflection $\vartheta$ through edges resp. vertices, $\langle \cdot \rangle$ is reflection positive with respect to $\vartheta$.

2.2 Main Results

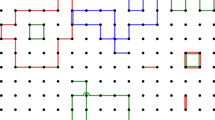
For $j\in \{1,2\}$ let $F^j_o\in {\mathcal A }_L$ be functions with domain $\{o\}$. Fix an arbitrary vertex $x \in {\mathbb {T}}_L$ and let $o=t_0$, $t_1, \ldots , t_k = x$ be a self-avoiding nearest-neighbour path from o to t, and for any $i \in \{1, \ldots , k\}$, let $\Theta _i$ be the reflection with respect to the plane through the edge $\{ t_{i-1}, t_{i} \}$ such that $\Theta _it_{i-1}=t_i$. Define

$$\begin{aligned} (F^j_o)^{[x]} : = \Theta _k \circ \Theta _{k-1} \, \ldots \, \circ \Theta _1 \, ( F^j_o ). \end{aligned}$$

Observe that the function $(F^j_o)^{[x]}$ does not depend on the chosen path (see Fig. 1 for an illustration). For a lighter notation denote by $F^j_x=(F^j_o)^{[x]}$ the function obtained from $F^j_o$ by applying a sequence of reflections that send o to x.

Fig. 1

An example of a sequence of reflections sending a function with domain o to a function with domain x

We define the two-point function,

$$\begin{aligned} G_L(x,y) : = \Big \langle \, F^2_x \, \, F^2_{y} \, \, \big ( \prod _{z \in {\mathbb {T}}_L \setminus \{ x,y\} }F^1_z \big ) \Big \rangle , \end{aligned}$$

omitting the dependence on the functions $F_o^j$ in the notation. For spin system examples we would usually take $F^2_o$ to be the spin at o and $F^1_o=1$, meaning that $G_L(x,y)$ is a spin–spin correlation. We say that the two-point function is translation invariant if, for any $A,B\subset {\mathbb {T}}_L$ and $z\in {\mathbb {T}}_L$

$$\begin{aligned} \big \langle \prod _{x\in A}F^1_x \prod _{x\in B} F^2_x\big \rangle =\big \langle \prod _{x\in A+z}F^1_x \prod _{x\in B+z} F^2_x\big \rangle , \end{aligned}$$

(2.4)

where the sum is with respect to addition on ${\mathbb {T}}_L$. As a consequence, for any $x, y, z \in {\mathbb {T}}_L$,

$$\begin{aligned} G_L(x,y) = G_L(x + z, y + z), \quad \quad G_L(o,x) = G_L(-x, o). \end{aligned}$$

(2.5)

Our first theorem states several site-monotinicity properties for the two-point function.

Theorem 2.1

Consider the torus ${\mathbb {T}}_L={\mathbb {Z}}^d/L{\mathbb {Z}}^d$ for $d\ge 2$ and $L\in 2{\mathbb {N}}$.

Take $i\in \{1,\ldots ,d\}$. Suppose that $\langle \cdot \rangle$ is reflection positive for reflections through edges and that the two-point function is translation invariant. For any $z=(z_1,\dots ,z_d)$,

$$\begin{aligned} G_L(o,z)&\le G_L(o, z_i \varvec{e}_i)&\text{ if } z_i \text { odd,} \end{aligned}$$

(2.6)

$$\begin{aligned} G_L(o,z)&\le \frac{1}{2} \Big ( G_L \big (o, \varvec{e}_i (z_i - 1) \Big ) + G_L \big (o, \varvec{e}_i (z_i + 1) \big ) \Big )&\text{ if } z_i \text { even.} \end{aligned}$$

(2.7)

Further, for $y\in {\mathbb {T}}_L$ such that $y_i=0$ (possibly $y=o$) the function

$$\begin{aligned} G_L \big (o, y + n \varvec{e}_i \big ) + G_L \big (o, n \varvec{e}_i \big ) \end{aligned}$$

(2.8)

is a non-increasing function of $n\in (0,L/2)\cap \big (2{\mathbb {N}}+1\big )$. If, in addition, $\langle \cdot \rangle$ is reflection positive for reflections through vertices then (2.6) also holds for $z_i$ even and (2.8) holds for any $n\in (0,L/2]$.

Our next theorem is a consequence of Theorem 2.1 and consists of the following statements. Suppose that the two-point function is uniformly bounded from above by a constant M, (i) Whenever the Cesàro sum of the two-point function is uniformly positive, the two-point function is point-wise uniformly positive on cartesian axes. (ii)–(iii) If the uniformly positive lower bound to the Cesàro sum is close enough to M, then the two-point function is point-wise uniformly positive not only on the cartesian axes, but also at any site in a box centred at the origin whose side length is of order O(L). Applications of the theorem are discussed in Sect. 3.

Theorem 2.2

Consider the torus ${\mathbb {T}}_L={\mathbb {T}}^d/L{\mathbb {Z}}^d$ for $d\ge 2$ and $L\in 2{\mathbb {N}}$.

Take $i\in \{1,\ldots ,d\}$. Suppose that $\langle \cdot \rangle$ is reflection positive for reflections through edges and that the two-point function is translation invariant. Moreover, suppose that for some $C_1>0$ we have

$$\begin{aligned} \liminf _{\begin{array}{c} L\rightarrow \infty \\ L\text { even} \end{array}}\frac{1}{|{\mathbb {T}}_L|}\sum _{x\in {\mathbb {T}}_L} G_L(o,x) \, \ge \, C_1>0, \end{aligned}$$

(2.9)

and that for some $M\in (0,\infty )$ we have that,

$$\begin{aligned} \forall L \in 2 {\mathbb {N}} \quad \forall x, y \in {\mathbb {T}}_L \quad G_L(x,y) \le M. \end{aligned}$$

(2.10)

Then, the following properties hold,

• (i) For any $\varphi \in (0, \frac{C_1}{2})$ there exists $\varepsilon > 0$ such that for any integer $n \in (- \varepsilon \, L, \varepsilon L )$ and any $i\in \{1,\dots ,d\}$,

  $$\begin{aligned} G_L(o, n\varvec{e}_i ) \ge \varphi . \end{aligned}$$

• (ii) For $\varepsilon \in (0,\tfrac{1}{2})$ and $L \in 2 {\mathbb {N}}$ sufficiently large, for any $x\in {\mathbb {T}}_L$ such that $|x_i|\in (0,\varepsilon L)\cap (2{\mathbb {N}}+1)$ for every $i\in \{1,\ldots ,d\}$,

  $$\begin{aligned} G_L(o,x) \ge M-\big (\tfrac{1}{4}-\tfrac{1}{2}\varepsilon \big )^{-d}(M-C_1). \end{aligned}$$

• (iii) If $\langle \cdot \rangle$ is also reflection positive for reflections through vertices then for any $\varepsilon \in (0,\tfrac{1}{2})$ and $L \in 2 {\mathbb {N}}$ sufficiently large, for all $x\in {\mathbb {T}}_L$ such that $|x_i| \in (0, \varepsilon L)$ for every $i\in \{1,\ldots ,d\}$,

  $$\begin{aligned} G_L(o,x)\ge M-\big (\tfrac{1}{2}-\varepsilon \big )^{-d}(M-C_1). \end{aligned}$$

Remark 2.3

• (i) For many statistical mechanics models one has that there exists some positive $c > 0$ such that, if x and y are nearest neighbours, then $G_L(o,x) \ge G_L(o,y) \, \, c$. When such a property is fulfilled, the properties of point-wise positivity of the two-point function stated in (i) and (ii) can be extended to vertices which are not necessarily odd.

• (ii) If we do not care about the size of the box around o where we can show that two-point functions are uniformly bounded then we can simple look at the limit $\varepsilon \rightarrow 0$. In this case the bound in (ii) becomes $M-4^d(M-C_1)$ and the bound in (iii) becomes $M-2^d(M-C_1)$.

• (iii) In many cases M and $C_1$ will agree to leading order, meaning that the term $M-C_1$ can be made small (for example by taking higher dimension or larger spin value). This is due to the nature of the infrared bound method that provides (2.9).

3 Applications

3.1 The Quantum Heisenberg Model

For $S\in \tfrac{1}{2}{\mathbb {N}}$ we define $\Sigma _x={\mathbb {C}}^{2S+1}$ and $\otimes$ to be the tensor product, hence ${\mathcal S }=\otimes _{x\in {\mathbb {T}}_L}{\mathbb {C}}^{2S+1}$. Let $S^1,S^2,S^3$ denote the spin-S operators on ${\mathbb {C}}^{2S+1}$. They are hermitian matrices defined by

$$\begin{aligned}&[S^1,S^2]=iS^3,\qquad [S^2,S^3]=iS^1,\qquad [S^3,S^2]=iS^2, \end{aligned}$$

(3.1)

$$\begin{aligned}&(S^1)^2+(S^2)^2+(S^3)^2=S(S+1)\mathbb {1}, \end{aligned}$$

(3.2)

where $\mathbb {1}$ is the identity matrix. Each spin matrix has spectrum $\{-S,-S+1,\dots ,S\}$. We denote by $S^i_x=S^i\otimes \mathbb {1}_{{\mathbb {T}}_L\setminus \{x\}}$ the operator on ${\mathcal S }$ that acts as $S^i$ on $\Sigma _x$ and as $\mathbb {1}$ on each $\Sigma _y$, $y\ne x$. For $u\in [-1,1]$ consider the hamiltonian

$$\begin{aligned} H_u=-2\sum _{\{x,y\}\in {\mathcal E }_L}\left( S^1_xS^1_y+uS^2_xS^2_y+S^3_xS^3_y\right) . \end{aligned}$$

(3.3)

The case $u=1$ gives the Heisenberg ferromagnet, $u=-\,1$ is unitarily equivalent to the Heisenberg antiferromagnet on bipartite graphs, (such as we have) and $u=0$ is the quantum XY model. For $\beta \ge 0$ corresponding to the inverse temperature our linear operator is given by the usual Gibbs state at inverse temperature $\beta$. More precisely, for operator A on ${\mathcal S }$ the expectation of A in the Gibbs state is

$$\begin{aligned} \langle A\rangle =\frac{1}{Z_{u}(\beta )}{{\text {Tr}}}\,A e^{-\beta H_u}, \qquad Z_u(\beta )={{\text {Tr}}}\,e^{-\beta H_u}. \end{aligned}$$

(3.4)

Take

$$\begin{aligned} F^1_x=\mathbb {1}_x\quad \text { and } \quad F^2_x=S^3_x. \end{aligned}$$

(3.5)

For $u\le 0$ we have reflection positivity for reflections through edges [6, 9, 17]. The following theorem is a direct consequence of Theorem 2.1.

Theorem 3.1

Let $\beta \ge 0$, $L\in 2{\mathbb {N}}$, $S\in \tfrac{1}{2}{\mathbb {N}}$, $d\ge 2$ and $u\le 0$. For any $z\in {\mathbb {T}}_L\setminus \{o\}$,

$$\begin{aligned} \langle S^3_oS^3_z\rangle \le {\left\{ \begin{array}{ll}\langle S^3_oS^3_{z_i\varvec{e}_i}\rangle &{} \text {if }z_i\in 2{\mathbb {N}}+1, \\ \tfrac{1}{2} \left( \langle S^3_oS^3_{(z_i+1)\varvec{e}_i}\rangle + \langle S^3_oS^3_{(z_i-1)\varvec{e}_i}\rangle \right) &{} \text {if }z_i\in 2{\mathbb {N}}\setminus \{o\}. \end{array}\right. } \end{aligned}$$

(3.6)

Further for $y\in {\mathbb {T}}_L$ such that $y_i=0$ (for example $y=o$) the function

$$\begin{aligned} \langle S^3_oS^3_{y+n\varvec{e}_i}\rangle + \langle S^3_oS^3_{n\varvec{e}_i}\rangle , \end{aligned}$$

(3.7)

is a non-increasing function of n for odd $n\in (0,L/2)$.

We now turn our attention to the consequence of Theorem 2.2. It is known from the famous result of Dyson, Lieb and Simon [5] and various extensions of this result [8, 9, 17] that for $d\ge 3$ and $S\in \tfrac{1}{2} {\mathbb {N}}$ there are constants $c_1,c_2>0$ such that for $L\in 2{\mathbb {N}}$ sufficiently large

$$\begin{aligned} \frac{1}{|{\mathbb {T}}_L|}\sum _{x\in {\mathbb {T}}_L}\langle S^3_oS^3_x\rangle \ge c_1-\frac{c_2}{\beta }. \end{aligned}$$

(3.8)

Our next theorem extends such a result by showing that the two-point function is point-wise uniformly positive on vertices whose coordinates are all odd.

Theorem 3.2

Suppose that $d\ge 3$ and $u\le 0$.

• (i) For any $\varphi \in (0, \frac{c_1}{2})$ there exists $\beta$ large enough and $\epsilon > 0$ such that, for any $L \in 2 {\mathbb {N}}$, any odd integer $n\in (-\varepsilon L,\varepsilon L)$ and any $i\in \{1,\ldots ,d\}$,

  $$\begin{aligned} \langle S_o^3S_{n\varvec{e}_i}^3\rangle \ge \varphi . \end{aligned}$$

  (3.9)

• (ii) There exists an explicit $Q(d, u) \in (0 , \infty )$ such that if $S > Q(d, u)$ and $\beta$ is large enough, then there exists $\varphi , \varepsilon > 0$ such that, for any $L \in 2 {\mathbb {N}}$ and $y \in {\mathbb {T}}_L$ such that $\Vert y \Vert _{\infty } \le \varepsilon L$ and, for each $i\in \{1,\ldots ,d\}$, $y_i\in 2{\mathbb {N}}+1$,

  $$\begin{aligned} \langle S_o^3S_{y}^3\rangle \ge \varphi . \end{aligned}$$

  (3.10)

In particular, Q(3, 0) can be taken equal to 79 and $Q(3,-1)$ can be taken equal to 90. If we could find a constant $c>0$ as in Remark 2.3 (i) then we could extend (3.10) to all vertices y such that $\Vert y\Vert _{\infty }\le \varepsilon L$.

Proof

The first claim follows from (3.8), and from an immediate application of the claim (i) in Theorem 2.2. We now prove the claim (ii). We start from (3.8), we have $M=S(S+1)/3$. From [17] obtain an explicit expression for $c_1$ in the limit $\beta \rightarrow \infty$,

$$\begin{aligned} c_1=\frac{S(S+1)}{3}-\frac{1}{\sqrt{2}}\frac{1}{|{\mathbb {T}}_L|}\sum _{k\in {\mathbb {T}}_L^*\setminus \{o\}}\sqrt{\frac{\varepsilon _u(k)}{\varepsilon (k)}}, \end{aligned}$$

(3.11)

where ${\mathbb {T}}_L^*$ is the Fourier dual lattice, $\varepsilon (k)=2\sum _{i=1}^d(1-\cos (k_i))$ and $\varepsilon _u(k)=\sum _{i=1}^d\big [(1-u\cos (k_i))\langle S^1_oS^1_{e_i}\rangle + (u-\cos (k_i))\langle S^2_oS^2_{e_i}\rangle \big ]$. Now it is easy to check that $\varepsilon _u(k)\le \tfrac{S(S+1)}{3}(1-u)\sum _{i=1}^d(1+|\cos (k_i)|)$ and in the special case $u=-1$ we can show $\varepsilon _{-1}(k)\le \tfrac{S(S+1)}{3}\varepsilon (k+\varvec{\pi })$. This gives, for $u=-1$

$$\begin{aligned} c_1\ge \frac{S(S+1)}{3}-\frac{1}{\sqrt{2}}\sqrt{\frac{S(S+1)}{3}}J_{d,L}, \end{aligned}$$

(3.12)

where

$$\begin{aligned} J_{d,L}=\frac{1}{|{\mathbb {T}}_L|}\sum _{k\in {\mathbb {T}}_L^*\setminus \{o\}}\sqrt{\frac{\varepsilon (k+\varvec{\pi })}{\varepsilon (k)}}, \end{aligned}$$

(3.13)

satisfies $\lim _{d\rightarrow \infty }\lim _{L\rightarrow \infty }J_{d,L}=1$. Further $\lim _{L\rightarrow \infty }J_{d,L}$ is a decreasing function of d and $\lim _{L\rightarrow \infty }J_{3,L}=1.15672\ldots$. Using these bounds, the inequality (ii) of Theorem 2.2 shows that there is some $\varphi >0$ such that for any $x\in {\mathbb {T}}_L$ with $|x\cdot \varvec{e}_i|\in (0,\varepsilon L)\cap 2{\mathbb {N}}+1$ for every $i\in \{1,\dots ,d\}$ we have $\langle S_o^3S_x^3\rangle \ge \varphi$ once $\beta$ is sufficiently large if

$$\begin{aligned} S^2+S-\sqrt{\tfrac{3}{2}}\sqrt{S(S+1}J_{d,L}\big (\tfrac{1}{4}-\tfrac{1}{2}\varepsilon \big )^{-d}>0, \end{aligned}$$

(3.14)

which is fulfilled for any large enough S (for $d=3$, $S\ge 90$ suffices). Performing a similar calculation for $u=0$ with the bound above we find for $d=3$, that $S\ge 109$ suffices. However, by using the bounds in [8] for the XY model ($u=0$) it can be shown that for $d=3$, $S\ge 79$ suffices. Similar bounds can be found for intermediate values of u. This completes the proof. $\square$

Remark 3.3

It is likely that the values of Q(d, u) could be improved somewhat, but the case of $S=1/2$, $d=3$ (for example) is unlikely to be within reach of any currently known bounds on M or $C_1$.

3.2 The Random Path Model

The Random Path Model (RPM) was introduced in [13]. It can be viewed as a random loop model with an arbitrary number of coloured loops and walks, with loops and walks possibly sharing the same edge and, at every vertex, a pairing function which pairs pairs of links touching that vertex or leaving them unpaired. It was shown in [13] that, for different choices of the parameters of the RPM, we can obtain many interesting models such as the loop O(N) model, the spin O(N) model, the dimer and double-dimer model and random lattice permutations. Here we introduce the RPM in a more general setting than in [13]. Such a generalisation consists of allowing pairings of links with different colours and allows us to derive site monotonicity properties for a more general class of two-point functions, for example, for the probability that a loop connects two distinct vertices of the torus.

Let $\mathcal {E}_L$ be the set of edges connecting nearest neighbour vertices of the torus. Let $m=(m_e)_{e\in {\mathcal E }_L}\in {\mathbb {N}}^{{\mathcal E }_L}$ be an assignment of a number of links on each edge of ${\mathcal E }_L$ and, for $N\in N_{>0}$, let $c(m)\in \times _{e\in {\mathcal E }_L}\big (\{1,\dots ,N\}^{m_e}\big )$ be a function, which we call a colouring, that for each $e\in {\mathcal E }_L$ assigns the $m_e$ links on e with a colour in $\{1,\dots ,N\}$. Lastly we define $\pi (m,c(m))=(\pi _x(m,c(m)))_{x\in {\mathbb {T}}_L}$ consisting of a collection of partitions of links. $\pi _x(m,c(m))$ is a partition of the links incident to x into sets with at most two links each. If, for some $x\in {\mathbb {T}}_L$, two links are in the same element of the partition at x then we say the links are paired at x and call this element a pairing. If a link is not paired to any other link at x then we say x is unpaired at x. Links can be paired or unpaired at both end points of their corresponding edge. We denote by ${\mathcal W }_L$ the set of all such triples $(m,c(m),\pi (m,c(m))$ and refer to elements $w=(m(w),c(w),\pi (w))\in {\mathcal W }_L$ as configurations. Configurations can be interpreted as a collection of multicoloured loops and walks on $({\mathbb {T}}_L,{\mathcal E }_L)$.

Now for $x\in {\mathbb {T}}_L$ and $i\in \{1,\dots ,N\}$ let $u^i_x$ be the number of unpaired links of colour i at x, let $K_x$ be the number of pairings at x between two differently coloured links, and let $n_x$ be the number of elements of $\pi _x$. If $K_x=0$ we define $v^i_x$ to be the number of pairings at x between links with colour i, otherwise we define $v^i_x=0$. Finally let $t_x$ be the number of pairings at x between links on the same edge (this is required to recover, for example, the loop O(N) model from the RPM).

Let $U:{\mathbb {N}}^{2N+3}\rightarrow {\mathbb {R}}$ and $\beta \ge 0$. We define our measure $\mu _{L,N,\beta ,U}$ on ${\mathcal W }_L$ as

$$\begin{aligned} \mu _{L,N,\beta ,U}(w)=\prod _{e\in {\mathcal E }_L}\frac{\beta ^{m_e(w)}}{m_e(w)!}\prod _{x\in {\mathbb {T}}_L}U_x(w)\qquad \forall w\in {\mathcal W }_L, \end{aligned}$$

(3.15)

where $U_x(w)=U(u^1_x,\dots ,u^N_x,v^1_x,\dots ,v^N_x,K_x,n_x,t_x)$. We refer to U as a vertex weight function. For $f:{\mathcal W }_L\rightarrow {\mathbb {R}}$ we use the same notation for the expectation of f, $\mu _{L,N,\beta ,U}(f):=\sum _{w\in {\mathcal W }_L}f(w)\mu _{L,N,\beta ,U}(w)$.

The measure $\mu _{L, N, \beta , U }$ was proven to be reflection positive for reflections through edges in [13, Proposition 3.2]. The same result holds for the more general random path model defined in this note, since allowing pairing of links with different colour does not modify the proof.

It can be shown that the random path model fits the general framework introduced in the present note, by considering local state spaces for $x\in {\mathbb {T}}_L$ that consist of a specification of the number of coloured links on each edge incident to x (an element of ${\mathbb {N}}^{2dN}$) together with a function that maps ${\mathbb {N}}^{2dN}$ to partitions of $\sqcup _{m\ge 0}\{1,\dots ,m\}$. The measure is then supported on configurations whose functions partition the correct value of m (the value corresponding to the total number of incident links) at each $x\in {\mathbb {T}}_L$ and which, for each $e\in {\mathcal E }_L$ specify the same link numbers on e for both end points of e.

Suppose that $U_x(w)=0$ whenever $K_x\ne 0$, then $\mu _{L,N,\beta ,U}$ is supported on configurations of monochromatic loops and walks. From this we can recover the RPM introduced in [13] which reduces to the specific examples mentioned above if we further specify U in an appropriate way. In this case we could take

$$\begin{aligned} \langle \cdot \rangle =\frac{1}{Z^{loop}_{L,N,\beta ,U}}\mu _{L,N,\beta ,U}(\cdot ), \end{aligned}$$

(3.16)

where $Z^{loop}_{L,N,\beta ,U}$ is the total measure under $\mu _{L,N,\beta ,U}$ of configurations with only loops. We then take

$$\begin{aligned} F^1_x=\mathbb {1}_{u^1_x=0}\qquad \text { and } F^2_x=\mathbb {1}_{u^1_x=1}, \end{aligned}$$

(3.17)

and find that $G_L(x,y)$ corresponds to the two-point function introduced in [13], when U is chosen appropriately this is equal to the spin–spin correlation of the spin O(N) model. From this we can recover Theorems 2.4, 2.6 and 2.8 in [13] .

Now suppose that $N > 1$, that $U_x$ allows links of different colours to be paired, and that it is 0 if $\sum _i u^i_x\ne 0$ (meaning the model only has loops and no walks). Our linear functional $\langle \cdot \rangle$ could then be given by

$$\begin{aligned} \langle \cdot \rangle =\frac{1}{Z^{mono}_{L,N,\beta ,U}}\mu _{L,N,\beta ,U}(\cdot ), \end{aligned}$$

(3.18)

where $Z^{mono}_{L,N,\beta ,U}$ is the total measure under $\mu _{L,N,\beta ,U}$ of configurations with $\sum _xK_x=0$ and only loops. Now we take

$$\begin{aligned} F^1_x=\mathbb {1}_{K_x=0}\quad \text { and }\quad F^2_x=\mathbb {1}_{K_x=1}. \end{aligned}$$

(3.19)

We have that $G_L(x,y)=2\left( {\begin{array}{c}N\\ 2\end{array}}\right) {\mathbb {P}}(x\leftrightarrow y)$ where the probability is in the system with only monochromatic loops with colours in $\{1,\ldots ,N\}$ and there are no walks. The event $x\leftrightarrow y$ is the event that there is a loop that passes through x and y.

Theorem 2.1 leads then to the following theorem.

Theorem 3.4

Let ${\mathbb {P}}( x \leftrightarrow y )$ be the probability that a loop passes through x and y in the random path model with only monochromatic loops and no open paths. For any $z=(z_1,\ldots ,z_d)$,

$$\begin{aligned} {\mathbb {P}}(o\leftrightarrow z)&\le {\mathbb {P}}(o\leftrightarrow z_i\varvec{e}_i) \qquad \qquad \qquad \qquad \qquad \quad \,\,&\text { if } z_i\in 2{\mathbb {Z}}+1, \end{aligned}$$

(3.20)

$$\begin{aligned} {\mathbb {P}}(o\leftrightarrow z)&\le \tfrac{1}{2}{\mathbb {P}}(o\leftrightarrow (z_i-1)\varvec{e}_i)+\tfrac{1}{2} {\mathbb {P}}(o\leftrightarrow (z_i+1)\varvec{e}_i) \,&\text { if } z_i\in 2{\mathbb {Z}}\setminus \{0\}, \end{aligned}$$

(3.21)

and that for $y\in {\mathbb {T}}_L$ such that $y_i=0$

$$\begin{aligned} {\mathbb {P}}(o\leftrightarrow y+n\varvec{e}_i)+{\mathbb {P}}(o\leftrightarrow n\varvec{e}_i), \end{aligned}$$

(3.22)

is a non-increasing function of n for all odd $n\in (0,L/2)$.

Note that ${\mathbb {P}}( x \leftrightarrow y )$ equals the probability that a loop connects x and y in the loop O(N) model, in the double dimer model, in lattice permutations or in the loop representation of the spin O(N) model under an appropriate choice of U [13]. Further, it has been proven [1] that, when U is chosen appropriately, such a probability equals the following correlation, ${\mathbb {P}}( x \leftrightarrow y ) = \left\langle S_x^1 S_x^2 S_y^1 S_y^2 \right\rangle$, in the spin O(N) model with $N> 1$, hence our theorem provides monotonicity properties for such a four-spin correlation function.

4 Proof of Theorem 2.1

Suppose that $\langle \cdot \rangle$ is reflection positive with respect to the reflection $\vartheta$. Let $Q\subset {\mathbb {T}}_L$ and define $Q^{\pm }:=(Q\cap {\mathbb {T}}_L^{\pm })\cup \vartheta (Q\cap {\mathbb {T}}_L^{\pm })$. The key to the proof is the following lemma.

Lemma 4.1

For $Q\subset {\mathbb {T}}_L$ such that $|Q^+|=|Q^-|$

$$\begin{aligned} \sum _{\begin{array}{c} x,y\in Q\\ x\ne y \end{array}}G_L(x,y)\le \frac{1}{2} \sum _{\begin{array}{c} x,y\in Q^+\\ x\ne y \end{array}}G_L(x,y)+\frac{1}{2}\sum _{\begin{array}{c} x,y\in Q^-\\ x\ne y \end{array}}G_L(x,y). \end{aligned}$$

(4.1)

Proof

For $0<\eta \ll 1$ we consider the following functions

$$\begin{aligned} A=\prod _{x\in Q\cap {\mathbb {T}}_L^+}(1+\eta F^2_x\prod _{z\in {\mathbb {T}}^+_L\setminus \{x\}}F^1_z),\qquad B=\prod _{x\in Q\cap {\mathbb {T}}_L^-}(1+\eta F^2_{\vartheta x}\prod _{z\in {\mathbb {T}}^-_L\setminus \{ x\}}F^1_{\vartheta z}). \end{aligned}$$

(4.2)

Now for simplicity of notation we write ${\mathbb {T}}_L(x)$ for ${\mathbb {T}}_L^+\setminus \{x\}$ if $x\in {\mathbb {T}}_L^+$ and ${\mathbb {T}}_L^-\setminus \{x\}$ if $x\in {\mathbb {T}}_L^-$. A simple calculation gives

$$\begin{aligned} \begin{aligned} \langle A\vartheta B\rangle&=\left\langle \prod _{x\in Q}\big (1+\eta F^2_x\prod _{z\in {\mathbb {T}}_L(x)}F^1_z\big )\right\rangle \\&=1+\eta \sum _{x\in Q}\left\langle F^2_x\prod _{z\in {\mathbb {T}}_L(x)}F^1_z\right\rangle +\eta ^2\sum _{\begin{array}{c} x,y\in Q\\ x\ne y \end{array}}\left\langle F^2_xF^2_y\prod _{z\in {\mathbb {T}}_L(x)}F^1_z\prod _{z\in {\mathbb {T}}_L(y)}F^1_z\right\rangle +O(\eta ^3), \end{aligned} \end{aligned}$$

(4.3)

and analogously

$$\begin{aligned} \langle A\vartheta A\rangle&=1+\eta \sum _{x\in Q^+}\left\langle F^2_x\prod _{z\in {\mathbb {T}}_L(x)}F^1_z\right\rangle +\eta ^2\sum _{\begin{array}{c} x,y\in Q^+\\ x\ne y \end{array}}\left\langle F^2_xF^2_y\prod _{z\in {\mathbb {T}}_L(x)}F^1_z\prod _{z\in {\mathbb {T}}_L(y)}F^1_z\right\rangle +O(\eta ^3), \end{aligned}$$

(4.4)

$$\begin{aligned} \langle B\vartheta B\rangle&=1+\eta \sum _{x\in Q^-}\left\langle F^2_x\prod _{z\in {\mathbb {T}}_L(x)}F^1_z\right\rangle +\eta ^2\sum _{\begin{array}{c} x,y\in Q^-\\ x\ne y \end{array}}\left\langle F^2_xF^2_y\prod _{z\in {\mathbb {T}}_L(x)}F^1_z\prod _{z\in {\mathbb {T}}_L(y)}F^1_z\right\rangle +O(\eta ^3). \end{aligned}$$

(4.5)

Now suppose that $x,y\in Q\cap {\mathbb {T}}_L^+$, then $x,y,\vartheta x,\vartheta y\in Q^+$ and we further note that

$$\begin{aligned} \left\langle F^2_xF^2_y\prod _{z\in {\mathbb {T}}_L(x)}F^1_z\prod _{z\in {\mathbb {T}}_L(y)}F^1_z\right\rangle =\left\langle F^2_{\vartheta x}F^2_{\vartheta y} \prod _{z\in {\mathbb {T}}_L(\vartheta x)}F^1_z\prod _{z\in {\mathbb {T}}_L(\vartheta y)}F^1_z\right\rangle . \end{aligned}$$

(4.6)

An analogous identity holds for $x,y\in Q\cap {\mathbb {T}}_L^-$. Now we use (2.3) with the expansion $(1+x)^(1/2)=1+x/2-x^2/8+O(x^3)$. Note that the $\eta$ terms will cancel by (2.4). Now we compare the $\eta ^2$ terms. We find we have the stated inequality plus an extra term with is zero due to translation invariance and the condition $|Q^+|=|Q^-|$. This completes the proof. $\square$

We take $Q=\{o,z\}$ and $\vartheta$ the reflection in the plane bisecting $\{p\varvec{e}_i,(p+1)\varvec{e}_i\}$ for $p:=\tfrac{1}{2} (z\cdot \varvec{e}_i-1+q\}$, this requires $z\cdot \varvec{e}_i+q\in 2{\mathbb {N}}+1$ and $z\cdot \varvec{e}_i\pm q\in (0,L)$. If we take $q=0$ when $z_i\in 2{\mathbb {N}}+1$ and $q=1$ when $z_i\in 2{\mathbb {N}}\setminus \{0\}$ then Lemma 4.1 gives us (2.6) and (2.7). If we also have reflection positivity for reflections through sites then we can reflect in the plane $R=\{x\in {\mathbb {R}}\,:\, x\cdot \varvec{e}_i=\tfrac{1}{2}(z\cdot \varvec{e}_i+q)\}$, requiring that $z\cdot \varvec{e}_i+q$ is even. If we apply Lemma 4.1 with $q=0$ we find that for $z\cdot \varvec{e}_i\in 2{\mathbb {N}}\setminus \{0\}$ we also have (2.6).

For the monotonicity result (2.8) we take $Q=\{o,z,z_i\varvec{e}_i,z-z_i\varvec{e}_i\}$ with the same reflection as above. We define the function

$$\begin{aligned} G^{\varvec{e}_i}_L(x):=\tfrac{1}{2}\big (G_L(o,x)+G_L(o,(x\cdot \varvec{e}_i)\varvec{e}_i)\big ), \end{aligned}$$

(4.7)

and find, using Lemma 4.1, after rearranging and (2.4) that for $z_i+q$ odd

$$\begin{aligned} G^{\varvec{e}_i}_L(z+q\varvec{e}_i)-G^{\varvec{e}_i}_L(z)\ge G^{\varvec{e}_i}_L(z)+G^{\varvec{e}_i}_L(z-q\varvec{e}_i). \end{aligned}$$

(4.8)

The proof follows the proof of [13, Proposition 4.2]. We can now prove (2.8) by contradiction. Suppose that $y\in {\mathbb {T}}_L$ such that $y\cdot \varvec{e}_i=0$ and odd $n\in (0,L/2)$ satisfy $G^{\varvec{e}_i}_L(y+n\varvec{e}_i)>G^{\varvec{e}_i}_L(y+(n-2)\varvec{e}_i)$. Now by repeatedly using (4.8) with $q=2$ we find

$$\begin{aligned} G^{\varvec{e}_i}_L(y+n\varvec{e}_i)>G^{\varvec{e}_i}_L(y+(n-2)\varvec{e}_i)>G^{\varvec{e}_i}_L(y+(n-4)\varvec{e}_i)>G^{\varvec{e}_i}_L(y+(n-6)\varvec{e}_i)\ldots \end{aligned}$$

(4.9)

Once we have used this inequality n times we find $G^{\varvec{e}_i}_L(y+n\varvec{e}_i)>G^{\varvec{e}_i}_L(y+n\varvec{e}_i-2n\varvec{e}_i)=G^{\varvec{e}_i}_L(y-n\varvec{e}_i)$, but by reflection positivity we must have $G^{\varvec{e}_i}_L(y-n\varvec{e}_i)=G^{\varvec{e}_i}_L(y+n\varvec{e}_i)$. This contradiction completes the proof of (2.8). If, in addition, we have reflection positivity for reflections through sites we can use the reflection in $R=\{x\in {\mathbb {R}}\,:\, x\cdot \varvec{e}_i=\tfrac{1}{2}(z\cdot \varvec{e}_i+q)\}$. We then obtain the inequality (4.8) for $z_i+q$ even. Using this we can obtain a contradiction as before by alternating between the odd and even version of (4.8) with $q=1$ to find that for any $y\in {\mathbb {T}}_L$ such that $y\cdot \varvec{e}_i\pm 1\in (0,L)$

$$\begin{aligned} G^{\varvec{e}_i}_L(y+\varvec{e}_i)-G^{\varvec{e}_i}_L(y)\ge G^{\varvec{e}_i}_L(y)-G^{\varvec{e}_i}_L(y-\varvec{e}_i). \end{aligned}$$

(4.10)

The full monotonicity result then follows similarly to (2.8).

5 Proof of Theorem 2.2

We start with the proof of (i) and we present the proof of (ii) and (iii) afterwards. To begin, fix an arbitrary $\varphi \in (0, C_1)$. We claim that there must exist an $\epsilon > 0$ small enough such that for any $L \in 2 {\mathbb {N}}$ there exists $z_L \in {\mathbb {T}}_L \setminus [0, \epsilon L]^d$ such that $G_L(o,x) \ge \varphi$. The proof of this claim is by contradiction. Suppose that this was not the case, then, under the assumptions of the theorem, we would have that

$$\begin{aligned} \sum _{x \in {\mathbb {T}}_L} G_L(o,x) \le \, \, \varphi \, \, \lceil (\, 1 \, - \, \epsilon \, ) \, L \rceil ^d \, + \, M \lceil \epsilon L \rceil ^d, \end{aligned}$$

which would be in contradiction with (2.9) for small enough $\epsilon$, since we assumed that $\varphi < C_1$. Now define $y_L : = z_L \cdot \varvec{e}_1$ and, if it is odd, we use the first claim in Theorem 2.1 and deduce that, $G_L \big (o, y_L \varvec{e}_1 \big ) \, \, \ge \, \, \varphi ,$ otherwise we use the second claim in Theorem 2.1 and deduce that, $\max \big \{G_L \big (o, (y_L + 1) \varvec{e}_1 \big ), G_L \big (o, (y_L - 1) \varvec{e}_1 \big ) \big \} \, \, \ge \, \, \frac{\varphi }{2}.$ Using the fact that $y_L+ 1 \ge \epsilon L$ and the last claim in Theorem 2.1, we deduce that, for any odd integer in the interval $n \in (o, \epsilon L)$, $G_L \big (o, n \varvec{e}_1 \big ) \ge \frac{\varphi }{2}.$ This concludes the proof of (i). We now proceed with the proof of (ii) and (iii). To begin, for $z\in {\mathbb {T}}_L$ we define

$$\begin{aligned} {\mathbb {Q}}_z:=\{(x_1,\dots ,x_d)\in {\mathbb {Z}}^d\,:\, \forall i\in \{1,\dots ,d\},\, x_i\le |z\cdot \varvec{e}_i| \text { or } x_i>L-|z\cdot \varvec{e}_i]\}. \end{aligned}$$

(5.1)

The proof relies on the following lemmas.

Lemma 5.1

Let $z\in {\mathbb {T}}_L$ and $y\in {\mathbb {Q}}_z$ be such that $z_i$ and $y_i$ are odd for every $i\in \{1,\ldots ,d\}$ then under the same assumptions as Theorem 2.2

$$\begin{aligned} G_L(o,y)\ge 2^dG_L(o,z) -(2^d-1)M. \end{aligned}$$

(5.2)

If, in addition, $\langle \cdot \rangle$ is reflection positive for reflections through vertices then the inequality holds for any $z\in {\mathbb {T}}_L$ and $y\in {\mathbb {Q}}_z$.

Proof

The proof is as in the proof of [13, Proposition 4.7] with minor changes as we only have the monotonicity result (2.8) for odd n. For convenience we assume that $z_i,y_i>0$ for every $i\in \{1,\dots ,d\}$, other cases follow by symmetry. For $i\in \{1,\dots , d\}$ define

$$\begin{aligned} D_i:=(z-y)\cdot \varvec{e}_i, \end{aligned}$$

(5.3)

then $D_i\in 2{\mathbb {N}}$. There is a “path”

$$\begin{aligned} \left( z^1_0,z^1_1,\dots ,z^1_{D_1/2},z^2_0,z^2_1,\dots ,z^2_{D_2/2},\dots ,z^d_0,z^d_1,\dots ,z^d_{D_d/2}\right) , \end{aligned}$$

(5.4)

with the properties that $z^1_0=z$, $z^d_{D_d/2}=y$, and, for every $i\in \{1,\ldots ,d-1\}$, $z^i_{D_i/2}=z^{i+1}_1$. Further, for each $i\in \{1,\ldots ,d\}$ and $j\in [1,D_i/2]$,

$$\begin{aligned} z^i_{j-1}-z^i_j=2\varvec{e}_i. \end{aligned}$$

(5.5)

Now we use both (2.6) and (2.8),

$$\begin{aligned} \begin{aligned} 2G_L(o,z^i_0)&\le G_L(o,z^i_0) +G_L(o,(z^i_0\cdot \varvec{e}_i)\varvec{e}_i)\\&\le G_L(o,z^i_{D_i/2}) + G_L(o,(z^i_{D_i/2}\cdot \varvec{e}_i)\varvec{e}_i), \end{aligned} \end{aligned}$$

(5.6)

and hence using that $G_L(o,x)\le M$ for any $x\in {\mathbb {T}}_L$ we have that

$$\begin{aligned} G_L(o,z^i_{D_i/2}) \ge 2G_L(o,z^i_0)-M. \end{aligned}$$

(5.7)

Iterating this for $i=1,\ldots , d$ gives

$$\begin{aligned} \begin{aligned} G_L(o,y)=G_L(o,z^d_{D_d/2})&\ge 2G_L(o,z^d_0)-M\ge \dots \\&\ge 2^dG_L(o,z)-(2^d-1)M, \end{aligned} \end{aligned}$$

(5.8)

this completes the proof. If $\langle \cdot \rangle$ is also reflection positive for reflections through vertices the proof is exactly as in [13, Proposition 4.7]. We define $D_i$’s and the path $(z_0^1,\dots z^d_{D_d/2}$ as before except that we can take $z^i_{j-1}-z^i_j=\varvec{e}_i$, the rest of the proof then proceeds as before. $\square$

Now, for $r\in {\mathbb {N}}$ let

$$\begin{aligned} {\mathbb {S}}_{r,L}:=\{z\in {\mathbb {T}}_L\, :\, \exists i\in \{1,\ldots ,d\}\text { such that } z\cdot \varvec{e}_i<r\text { or }L-z\cdot \varvec{e}_i\le r\}. \end{aligned}$$

(5.9)

Lemma 5.2

Under the same assumptions as 2.2 there are $x_L\in {\mathbb {T}}_L\setminus {\mathbb {S}}_{\varepsilon L,L}$ and $z_L\in {\mathbb {T}}_L\setminus {\mathbb {S}}_{\varepsilon L,L}$ with $|z_L\cdot \varvec{e}_i|\in 2{\mathbb {N}}+1$ for every $i\in \{1,\ldots ,d\}$ such that

$$\begin{aligned} G_L(o,x_L)&\ge M-(1-2\varepsilon )^{-d}(M-C_1), \end{aligned}$$

(5.10)

$$\begin{aligned} G_L(o,z_L)&\ge M-\big (\tfrac{1}{2}-\varepsilon \big )^{-d}(M-C_1) . \end{aligned}$$

(5.11)

Proof

The proof of (5.10) is exactly as in [13, Lemma 4.9]. The proof of (5.11) is a simple adaptation of [13, Lemma 4.9] and we sketch it here. Now a simple proof by contradiction shows that there must be a $z_L$ as in the statement of the lemma. Indeed, suppose for every $z_L\in {\mathbb {T}}_L$ with $|z_L\cdot \varvec{e}_i|\in [\varepsilon L,L)\cap 2{\mathbb {N}}+1$ for every $i\in \{1,\dots ,d\}$ that $G_L(o,z_L)< M-\big (\tfrac{1}{2}-\varepsilon \big )^{-d}(M-C_1)$. Using this together with the worst-case bound M for every other vertex and the bound $|{\mathbb {T}}_L\setminus {\mathbb {S}}_{r,L}|=(L-2r)^d$ gives a contradiction. $\square$

Statement (i) of Theorem 2.2 follows immediately from (5.10) and Theorem 2.1. For statement (ii) of Theorem 2.2 note that if $z_L$ is as in the statement of Lemma 5.2 then, by Lemma 5.1, for any $y\in {\mathbb {Q}}_{z_L}$ such that $y_i$ is odd for each $i\in \{1,\dots ,d\}$ we have (after rearranging)

$$\begin{aligned} G_L(o,y)\ge 2^dG_L(o,z_L)-(2^d-1)M\ge M-2^d\big (\tfrac{1}{2}-\varepsilon \big )^{-d}(M-C_1). \end{aligned}$$

(5.12)

which is equal to the bound in the Theorem. Finally for statement (iii) of Theorem 2.2 we note that by Lemmas 5.1 and 5.2 for any $y\in {\mathbb {Q}}_{x_L}$ we have (after rearranging)

$$\begin{aligned} G_L(o,y)\ge 2^dG_L(o,x_L)-(2^d-1)M\ge M-2^d(1-2\varepsilon )^{-d}(M-C_1). \end{aligned}$$

(5.13)