Isothermic constrained Willmore tori in 3-space

Abstract

We show that the homogeneous and the 2-lobe Delaunay tori in the 3-sphere provide the only isothermic constrained Willmore tori in 3-space with Willmore energy below $8\pi$. In particular, every constrained Willmore torus with Willmore energy below $8\pi$ and non-rectangular conformal class is non-degenerated.

1 Introduction

The Willmore functional of an immersions $f:M\rightarrow S^3$ from a oriented surface M into the 3-sphere is given by

$$\begin{aligned} {\mathcal {W}}(f)=\int _M (H^2+1) {\text {d}}A \end{aligned}$$

where H is the mean curvature and dA is the induced area form of f. Geometrically speaking, $\mathcal{W}$ measures the roundness of a surface, physically the degree of bending, and in biology, $\mathcal{W}$ appears as a special instance of the Helfrich energy for cell membranes. The Willmore functional is invariant under Möbius transformations (conformal transformations of the 3-sphere with its standard conformal structure). Critical points of the Willmore functional are Willmore surfaces. Examples are given by minimal surfaces in the Riemannian subgeometries of constant curvature of the conformal 3-sphere.

If M is equipped with a Riemann surface structure, it is natural to consider only conformal immersions $f:M\rightarrow S^3$, i.e. the complex structure is given by rotating tangent vectors by $\frac{\pi }{2}$ in the 3-space. Critical points of the Willmore functional restricted to a given conformal class are called constrained Willmore surfaces. The conformal constraint augments the Euler–Lagrange equation by a holomorphic quadratic differential $\omega \in H^0(K^2_M)$ paired with the trace-free second fundamental form $\mathring{A}$ of the immersion

$$\begin{aligned} \triangle H+ 2H(H^2+1-K)=\,<\omega ,{\mathring{A}}>, \end{aligned}$$

see [7, 27]. The first examples of these constrained Willmore tori are given by those of constant mean curvature (CMC) in a 3-dimensional space form.

It is well known (and obvious by the holomorphicity of the Hopf differential) that CMC (constant mean curvature) surfaces admit conformal curvature line parametrizations away from their umbilical points. Surfaces with this property are called isothermic. Isothermic surfaces play an important role in conformal surface geometry, see [10, 11], since the notion is independent of the specific metric in the conformal class of the ambient manifold. For a compact surface M, there is a natural map from the space of immersions into the 3-space to the Teichmüller space

$$\begin{aligned} \pi :f\in Imm(M,S^3)\mapsto [f^*g_{round}]\in Teich(M), \end{aligned}$$

where $g_{round}$ is the round metric on $S^3,$ and [.] denotes the conformal class in the Teichmüller space. The map $\pi$ is a submersion except at isothermic immersions, see [7]. Hence, the Lagrange multiplier for isothermic constrained Willmore surfaces—the holomorphic quadratic differential—is no longer uniquely determined by the immersion.

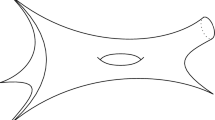
In this paper, we restrict to compact Riemann surfaces of genus 1. We classify isothermic constrained Willmore tori with Willmore energy below $8\pi .$ Our main theorem is the following one (see also Fig. 1).

Theorem 1

Isothermic constrained Willmore tori in the conformal 3-sphere with Willmore energy below $8 \pi$ are CMC surfaces in the round 3-sphere.

Fig. 1

The vertical stalk represents the family of homogenous tori, starting with the Clifford torus at the bottom. Along this stalk are bifurcation points at which the embedded Delaunay tori appear along the horizontal lines. The rectangles indicate the conformal types. Images by Nicholas Schmitt

1.1 Strategy of proof

Richter [26] shows that isothermic constrained Willmore tori in the conformal 3-sphere are locally of constant mean curvature in a 3-dimensional space form. The solution of the Lawson and Pinkall-Sterling conjectures by Brendle [8] and Andrews-Li [2] further gives that embedded CMC tori in the 3-sphere are rotationally symmetric and thus consist only of the families of k-lobed Delaunay tori [19]. Moreover, the Willmore energy along every embedded family is monotonically increasing in the conformal class b. Thus, since for $k\ge 3$ the k-lobes bifurcates from the homogenous tori with Willmore energy above $8\pi$, the 2-lobed family is the CMC-family with minimal Willmore energy in their respective conformal classes. The aim is to exclude the existence of constrained Willmore surfaces of constant mean curvature in ${\mathbb {R}}^3$ or hyperbolic 3-space $\mathcal H^3$ that can be compactified to a torus in $S^3$ with Willmore energy below $8 \pi .$ By Li and Yau [21] these surfaces must be embedded.

The Alexandrov maximum principle [1] shows that there are no closed CMC tori with Willmore energy below $8\pi$ in ${\mathbb { R}}^3$ or $\mathcal H^3$. The only non-closed CMC surfaces in ${\mathbb {R}}^3$ that can be compactified to conformal embeddings in $S^3$ are minimal surfaces with planar ends ($H\ne 0$ is excluded by local analysis [20]), which have quantized energy $4 \pi k,$ with $k\ge 2$ being the number of ends. Thus, those surfaces have Willmore energy $\ge 8\pi$. Similar arguments work for constant mean curvature surfaces in $\mathcal H^3$ with mean curvature $H = 1$ giving quantized Willmore energy $\mathcal W=4 \pi k,$ where $k\in {\mathbb {N}}$ denotes the number of ends see [6] and one-punctured CMC 1 torus in $\mathcal H^3$ does not exist by [23].

To prove Theorem 1, it is thus sufficient to show that isothermic constrained Willmore tori in $S^3$, whose intersection with $\mathcal H^3\subset S^3$ is of constant mean curvature, cannot have Willmore energy below $8 \pi$. Those surfaces intersect the infinity boundary of $\mathcal H^3\subset S^3$—a round 2-sphere—with an angle $\alpha$ satisfying ${\mathbb {C}}os(\alpha ) = H.$ In particular, the constant mean curvature must satisfy $|H| <1$ or the surface is entirely contained in $\mathcal H^3,$ and therefore cannot be embedded by maximum principle. It hence remains to show that CMC surfaces in $\mathcal H^3$ with mean curvature $|H| <1$ and Willmore energy below $8 \pi$ cannot be embedded, see Theorem 3.

We will call isothermic constrained Willmore tori into $S^3$ which are CMC in $\mathcal H^3$ with $|H| <1$ on the intersection with the two hyperbolic balls Babich–Bobenko tori in the following. The first examples have been constructed by Babich and Bobenko [3] in the case of $H=0$. The main idea of the proof is now to use the quaternionic Plücker estimate [13], which links lower bounds of the Willmore energy to the dimension of holomorphic sections of a certain quaternionic holomorphic vector bundle. This dimension is then related to the (necessarily odd) genus g of the spectral curve for Babich–Bobenko tori.

The paper is organized as follows: In Sect. 2, we study the spectral curve of Babich–Bobenko tori in detail. In Sect. 3, we use the special structure of the spectral curve to apply the Plücker estimate which yields a proof of Theorem 3.

2 The constrained Willmore spectral curves of Babich–Bobenko tori

We consider two different approaches to the spectral curve theory of Babich–Bobenko tori. The aim of this section is to show that these two approaches towards the spectral curve are in fact equivalent. The lightcone model one is used to show that the spectral curve of a Babich–Bobenko torus—the Riemann surface parametrizing the eigenlines of $d^\uplambda _q$—is hyper-elliptic, while the Plücker estimate uses the multiplier spectral curve, which by [4] corresponds to the spectral curve of $\nabla ^\mu$ from the quaternionic approach. Subtleties arise from the non-uniqueness of the Lagrange multipliers.

2.1 Quaternionic geometry

The spectral curve theory for conformal immersions f from a 2-torus $T^2$ into the conformal 4-sphere has been developed in [9], where $S^4$ is considered as the quaternionic projective space ${\mathbb {H}} P^1$. To every conformal immersion f, the quaternionic line bundle

$$\begin{aligned} L= f^* \mathcal T \subset T^2 \times {\mathbb {H}}^2 \end{aligned}$$

given by the pull-back of the tautological bundle $\mathcal T$ of ${\mathbb {H}} P^1$ is associated. Another quaternionic line bundle associated to f is V/L,  where $V= T^2 \times {\mathbb {H}}^2.$ On V/L there exists a natural quaternionic holomorphic structure D (see [4, 9] for a detailed definition and discussion) by demanding the projections of the constant sections (0, 1) and (1, 0) of V to be holomorphic. The immersion f is then recovered (up to conformal transformations) by

$$\begin{aligned}{}[0,1] = - [1,0] f. \end{aligned}$$

The (multiplier) spectral curve $\Sigma$ of a conformally immersed torus f is the normalization of the Riemann surface parametrizing all holomorphic sections of V/L with (complex) monodromy, i.e. every point of the spectral curve corresponds to a holomorphic section with monodromy [5]. Therefore, we can define maps from $\Sigma$ to ${\mathbb {C}}$—so-called monodromy maps $\nu _i$—by assigning to every point in $\Sigma$ the monodromy of the underlying holomorphic section along generators $\gamma _i$ of the fundamental group $\pi _1(T^2)$.

Bohle [4] gives an alternative approach to the spectral curve for constrained Willmore tori. For constrained Willmore surfaces $f:M\longrightarrow S^3\subset S^4$, Bohle defined the following ${\mathbb {C}}_*$-family of flat SL$(4,{\mathbb {C}})$-connections

$$\begin{aligned} \nabla ^\mu =d+(\mu -1)A_{\mathbb {C}}irc^{1,0}+(\mu ^{-1}-1)A_{\mathbb {C}}irc^{0,1}. \end{aligned}$$

(1)

Here, d is the trivial connection on the trivial ${\mathbb {H}}^2$-bundle considered as a ${\mathbb {C}}^4$-bundle,

$$\begin{aligned} A_{\mathbb {C}}irc=A+*\eta \end{aligned}$$

where A is the Hopf field of the conformal immersion and q is the Lagrange multiplier of the constrained Willmore Euler–Lagrange equation (which is not unique for isothermic surfaces). He showed that the flatness of an associated ${\mathbb {C}}^*$-family $\nabla ^\mu$ of ${\mathrm {SL}}(4, {\mathbb {C}})$-connections defined on the trivial bundle V, considered as a ${\mathbb {C}}^4$-bundle, is equivalent to f being constrained Willmore. The (holonomy) spectral curve is then given by the Riemann surface parametrizing the eigenlines of the holonomy of $\nabla ^\mu .$ Bohle [4] showed that the (holonomy) spectral curve is always of finite genus and that both approaches to the spectral curve coincide. To be more precise, Bohle showed that $\nabla ^\mu$-parallel sections with monodromy are the unique prolongations of the holomorphic sections with monodromy of the quaternionic holomorphic line bundle (V/L, D) to V. The genus g of the associated spectral curve is called the spectral genus of the immersion f.

Remark 1

In the case of f mapping into the 3-sphere $S^3\subset S^4$, the spectral curve $\Sigma$ admits an additional involution $\sigma$, see [16, Lemma 1]. Another involution $\rho$ on $\sigma$ arises from the quaternionic construction, i.e. by an appropriate multiplication by j. If the quotient $\Sigma /\sigma$ is biholomorphic to ${\mathbb {C}} P^1$, there are two cases to distinguish depending on whether the real involution $\rho {\mathbb {C}}irc \sigma$ has fix points or not. In the first case the surface is of constant mean curvature in ${\mathbb {R}}^3,$ $S^3$ or $\mathcal H^3$ (with mean curvature $|H|>1$). If $\rho {\mathbb {C}}irc \sigma$ has no fixed points, then the corresponding immersion is of Babich–Bobenko type. We want to show the converse, i.e. that $\Sigma /\sigma {\mathbb {C}}ong {\mathbb {C}} P^1$ for Babich–Bobenko tori.

2.2 The light cone model

CMC surfaces in 3-dimensional space forms can also be described by associated families of flat ${\mathrm {SL}}(2,{\mathbb {C}})$-connections $\nabla ^\uplambda ,$ $\uplambda \in {\mathbb {C}}_*$, on a rank 2 bundle $\tilde{V} \rightarrow M$ [3, 18]. In the case of tori, these families of flat connections can be described by (algebraic–geometric) spectral data consisting of a (compact) hyper-elliptic curve $\tilde{\Sigma }$ (the spectral curve), two meromorphic differentials and a holomorphic line bundle. In the case of Babich–Bobenko tori [3] $\tilde{\Sigma }$ is the spectral curve of a finite gap solution of the Cosh–Gordon equation and admits a real involution covering $\uplambda \mapsto -{\bar{\uplambda }}^{-1}$. Therefore, ${\tilde{\Sigma }}$ hyper-elliptic and of odd genus. In this alternate approach the light cone model as developed in [10, 11] is used. Its relation to quaternionic holomorphic geometry can be found in [12, $\S$5], details of the computations is also included in the thesis of Quintino [24] and in [25]. We only recall the main constructions here. The Plücker estimate cannot be applied to this approach directly, since $\tilde{\nabla }^\uplambda$ have singularities on M, corresponding to the intersection of the surface with the infinity boundary of $\mathcal H^3,$ see [17].

As in [12] we start with ${\mathbb {C}}^4$ equipped with a quaternionic structure, i.e. a complex anti-linear map

$$\begin{aligned} j:{\mathbb {C}}^4\rightarrow {\mathbb {C}}^4 \end{aligned}$$

with $j^2=-1$ and identify ${\mathbb {C}}^4 {\mathbb {C}}ong {\mathbb {H}}^2.$ Moreover, we choose a determinant $\det \in \varLambda ^4({\mathbb {C}}^4)^*$ with

$$\begin{aligned} j^*\det =\overline{\det } \end{aligned}$$

and

$$\begin{aligned} \det (e_1,e_2,je_1,je_2)=1 \end{aligned}$$

for $\{e_1, e_2, e_3:= j e_1, e_4 := j e_2\}$ being the standard basis of ${\mathbb {C}}^4.$ The quaternionic structure induces a real structure on $\varLambda ^2{\mathbb {C}}^4$ (also denoted by j by abuse of notation) via

$$\begin{aligned} v\wedge w\mapsto j v\wedge jw, \end{aligned}$$

and the determinant induces an inner product $\langle .,.\rangle$ on $\varLambda ^2{\mathbb {C}}^4$ by

$$\begin{aligned} \langle \alpha ,\beta \rangle =\det (\alpha \wedge \beta ). \end{aligned}$$

The 6-dimensional real subspace V is spanned by

$$\begin{aligned} v_1= & {} e_1\wedge e_3,\\ v_2= & {} e_2\wedge e_4,\\ v_3= & {} e_1\wedge e_2+e_3\wedge e_4,\\ v_4= & {} ie_1\wedge e_2-ie_3\wedge e_4,\\ v_5= & {} e_1\wedge e_4+e_2\wedge e_3,\\ v_6= & {} ie_1\wedge e_4-ie_2\wedge e_3. \end{aligned}$$

Restricted to V the inner product $\langle .,.\rangle$ is of signature (5, 1).

For a general $(n+2)$-dimensional real vector space V with inner product of signature $(n+1,1)$, the n-sphere can be naturally identified with projectivation ${\mathbb {P}}{\mathcal {L}}$ of the light cone

$$\begin{aligned} \mathcal L=\{ v\in V\mid \langle v,v\rangle =0\}. \end{aligned}$$

Moreover, ${\mathbb {P}} {\mathcal {L}}$ is equipped with a natural conformal structure: For a lift l of $\pi :\mathcal L\rightarrow {\mathbb {P}}{\mathcal {L}}$ the Riemannian metric $g_l$ is defined as

$$\begin{aligned} g_l(X,Y):=\langle dl(X),dl(Y)\rangle . \end{aligned}$$

(2)

The space of orientation preserving conformal transformations—the Möbius group—can be identified with

$$\begin{aligned} {\mathrm {SO}}(n+1,1)^+:=\{g\in {\mathrm {SO}}(n+1,1)\mid \langle g(v),v\rangle<0 \; {\mathrm {if}}\; \langle v,v\rangle <0\}. \end{aligned}$$

For V being the real subspace of $\varLambda ^2{\mathbb {C}}^4$, a real nonzero lightlike vector of V is given by a complex 2-plane in ${\mathbb {C}}^4$ (nullity) invariant under j (reality), i.e. it gives rise to a quaternionic line in $({\mathbb {C}}^4,j).$ This identifies the 4-sphere with the quaternionic projective line ${\mathbb {H}} P^1$, and relates the quaternionic holomorphic geometry to the lightcone model, see [12, $\S$4].

Constant curvature subgeometries of the Möbius geometry $({\mathbb {P}}{\mathcal {L}}, {\mathrm {SO}}(5,1)^+)$ are specified by a choice $v_\infty \in V\setminus \{0\}.$ Such a choice provides a natural lift l of ${\mathbb {P}} {\mathcal {L}}$ onto the subset

$$\begin{aligned} S_\infty :=\{[x]\in {\mathbb {P}}{\mathcal {L}}\mid \langle x, v_\infty \rangle =-1\}, \end{aligned}$$

(3)

and the induced Riemannian metric $g_l$ defined in (2) is of constant sectional curvature $-\langle v_\infty ,v_\infty \rangle .$ The corresponding group of orientation preserving isometries of the subgeometry is then given by

$$\begin{aligned} {\mathrm {SO}}(5,1)^+_\infty =\{g\in {\mathrm {SO}}(5,1)^+\mid g(v_\infty )=v_\infty \}, \end{aligned}$$

and is isomorphic to ${\mathrm {SO}}(5)$ if $\langle v_\infty ,v_\infty \rangle <0$ and isomorphic to ${\mathrm {SO}}(4,1)$ if $\langle v_\infty ,v_\infty \rangle >0.$

To define the associated family of connections, we need the mean curvature sphere congruence S for the immersion $f: M \rightarrow S^4$. This is a map S from M into the space of oriented 2-spheres in $S^4,$ such that at every $p \in M$ the corresponding 2-sphere S(p), touches the immersion at f(p) and has the same oriented tangent plane, and the same mean curvature. An oriented 2-sphere $S\subset {\mathbb {P}}{\mathcal {L}}$ is determined by an oriented (real) 4-dimensional vector space $V_S\subset V$ of signature (3, 1) via $S= {\mathbb {P}} V_S\cap {\mathbb {P}}{\mathcal {L}}.$ This space is uniquely determined by its orthogonal complement, $V_N:=V_S^\perp ,$ which is a oriented real 2-plane with positive definite inner product, and therefore admits a unique compatible complex structure

$$\begin{aligned} J_N:V_N\rightarrow V_N,\quad J_N^2=-id. \end{aligned}$$

A conformal immersion $f:M\rightarrow {\mathbb {P}}{\mathcal {L}}$ is naturally equipped with the real rank 4 subbundle

$$\begin{aligned} V_S\longrightarrow M \end{aligned}$$

of the trivial rank 6 bundle V, with complexification locally given by

$$\begin{aligned} V_S \otimes {\mathbb {C}} = {\mathrm {span}}\{\hat{f},\hat{f}_z,\hat{f}_{\bar{z}}, \hat{f}_{z,\bar{z}}\} \end{aligned}$$

for some local lift $\hat{f}:U\subset M\rightarrow \mathcal L$ (and where $f_z=\frac{\partial f}{\partial z}$, etc.), see [10,11,12]. The bundle $V_S$ has induced signature (3, 1) and a natural orientation. Therefore, $V_S$ gives rise to a sphere congruence, i.e. to a smooth map into the space of oriented 2-spheres in $S^4.$ It can be computed (see [10, 11]) that the sphere congruence $V_S$ is the mean curvature sphere congruence, i.e. $(V_S)_p$ is the unique oriented 2-sphere in $S^4$ which touches (with orientation) the surface at f(p) to second order. Analogous to the classical case of surface geometry in Euclidean 3-space ${\mathbb {R}}^3$, we consider the induced splitting of the trivial connection d with respect to

$$\begin{aligned} V=V_S\oplus V_N, \end{aligned}$$

where $V_N :=V_S^\perp$ given by

$$\begin{aligned} d={\mathcal {D}}+{\mathcal {N}} \end{aligned}$$

into diagonal part ${\mathcal {D}}$ and off-diagonal part ${\mathcal {N}}.$ While ${\mathcal {D}}$ is a connection, ${\mathcal {N}}$ is tensorial.

Another related vector bundle Z is the bundle of skew-symmetric maps of $(V,\langle .,.\rangle )$ which map ${\mathbb {R}}\hat{f}$ to ${\mathrm {span}}\{\hat{f},\hat{f}_z,\hat{f}_{\bar{z}}\}$ and vice versa vanishing on other components.

With these notations, we list a few further important properties of the mean curvature sphere congruence:

• (see [10]) f is isothermic if and only if there exists $\eta \in \varOmega ^1(M,Z)$ with

  $$\begin{aligned} d\eta =d^{{\mathcal {D}}}\eta +[{\mathcal {N}}\wedge \eta ]=0; \end{aligned}$$

• (see [11]) the Willmore energy of f is given by

  $$\begin{aligned} \mathcal W(f)=-\frac{1}{4}\int _M tr( *{\mathcal {N}}\wedge \mathcal N) \end{aligned}$$

  where $*dz=idz, *d\bar{z}=-id\bar{z};$

• (see [7, 10, 11]) a surface is Willmore if and only if

  $$\begin{aligned} d^{{\mathcal {D}}}*{\mathcal {N}}=0, \end{aligned}$$

  and constrained Willmore if and only if there exists a $q\in \varOmega ^1(M, Z)$ satisfying $d^{{\mathcal {D}}}q=0$ and

  $$\begin{aligned} d^{{\mathcal {D}}}*{\mathcal {N}}=2[q\wedge *{\mathcal {N}}]; \end{aligned}$$

  q is called the Lagrange multiplier of f;

• (see [10] or [12, $\S$3.3]) a surface f has parallel mean curvature vector H in the constant sectional curvature subgeometry $S_\infty$ of ${\mathbb {P}}{\mathcal {L}}$ defined by $v_\infty$ in (3) if and only if

  $$\begin{aligned} {\mathcal {D}} v_\infty ^\perp =0, \end{aligned}$$

  where $v_\infty ^\perp$ is the projection to $V_N=V_S^\perp ;$ in particular, f is minimal in $S_\infty$ if and only if $v_\infty ^\perp =0;$

• a surface with parallel mean curvature vector H in $S_\infty$ is constrained Willmore with Lagrange multiplier q which is determined by

  $$\begin{aligned} q^{1,0}v_\infty ^\perp :=-{\mathcal {N}}^{1,0} (v_\infty ^\perp )^+, \end{aligned}$$

  where $v_\infty ^\perp =(v_\infty ^\perp )^++(v_\infty ^\perp )^-$ is with respect to the decomposition of the normal bundle $V_N\otimes {\mathbb {C}}=V_N^+\oplus V_N^-,$ see [24, $\S$7.2.2].

In particular, the Lagrange multiplier q of a constrained Willmore surface f is unique if and only if f is non-isothermic, as for two Lagrange multipliers $q_1,q_2$ the 1-form

$$\begin{aligned} \eta =*q_1-*q_2\in \varOmega ^1(M,Z) \end{aligned}$$

solves $d\eta =0.$

The following theorem reduces the constrained Willmore property of a given immersion f to the flatness of an associated family of flat connections in the language of the light cone model.

Proposition 1

[10, 11] The surface $f:M\rightarrow {\mathbb {P}}{\mathcal {L}}$ is constrained Willmore with Lagrange multiplier $q\in \varOmega ^1(M, Z)$ if and only if

$$\begin{aligned} d^\uplambda _q:={\mathcal {D}}+\uplambda ^{-1}\mathcal N^{(1,0)}+\uplambda {\mathcal {N}}^{(0,1)}+(\uplambda ^{-2}-1) q^{(1,0)}+(\uplambda ^2-1) q^{(0,1)} \end{aligned}$$

is flat for all $\uplambda \in {\mathbb {C}}^*,$ where (1, 0) and (0, 1) are the complex linear and complex anti-linear parts of a 1-form.

2.3 Compatibility of the quaternionic and the lightcone theory

The two approaches, the quaternionic and the lightcone one, towards the associated family of flat connections are in fact equivalent, as both associated families are gauge equivalent, when choosing suitable parameters. In order to provide a link between these families, we need to relate the two different ways to obtain the mean curvature sphere congruence S.

Oriented 2-spheres in quaternionic geometry are given by complex structures $\tilde{S}$ of $V= M \times \mathbb H^2$. To be more precise, a 2-sphere is a map

$$\begin{aligned} \tilde{S} \in {\mathrm {SL}}(4, {\mathbb {C}}) \quad {\mathrm {satisfying}} \quad \tilde{S}^2=-id. \end{aligned}$$

On the other hand, an oriented 2-sphere $S\subset {\mathbb {P}}{\mathcal {L}}$ is determined by an oriented 4-dimensional vector space $V_S\subset V$ of signature (3, 1) via $S ={\mathbb {P}} V_S\cap {\mathbb {P}}{\mathcal {L}}.$ Moreover, $V_N:=V_S^\perp$ is a oriented real 2-plane with positive definite inner product, and therefore admits a compatible complex structure

$$\begin{aligned} J_N:V_N\rightarrow V_N,\quad J_N^2=-id. \end{aligned}$$

We therefore obtain a decomposition

$$\begin{aligned} \varLambda ^2 {\mathbb {C}} ^4 = V\otimes {\mathbb {C}}=V_S\otimes \mathbb C\oplus V_N^+\oplus V_N^- \end{aligned}$$

such that

$$\begin{aligned} V_N^\pm =\{v\in V_N\otimes {\mathbb {C}}\mid J_N v=\pm i v\} \end{aligned}$$

are complex null lines that are complex conjugated to each other, i.e.

$$\begin{aligned} jV_N^\pm =V_N^\mp . \end{aligned}$$

In particular, $V_N^\pm$ gives rise to complex planes $W^\pm$ in ${\mathbb {C}}^4$ satisfying

$$\begin{aligned} {\mathbb {C}}^4=W^+\oplus W^-. \end{aligned}$$

Hence, there exists a unique $\tilde{S}\in {\mathrm {SL}}(4,{\mathbb {C}})$ with

$$\begin{aligned} \tilde{S}^2=-id,\quad \tilde{S}_{\mid W^\pm }= \pm i\;\;{\mathrm {and}}\;\;\tilde{S}j=j\tilde{S}, \end{aligned}$$

(4)

which is a 2-sphere in $\mathbb H P^1$ in the quaternionic sense.

Conversely, every quaternionic 2-sphere $\tilde{S}$ determines its $\pm i$ eigenspaces $W_{\tilde{S}}^\pm$ which are interchanged via j. They define complex null-lines $V^\pm _N$ satisfying $jV^\pm _N=V^\mp _N,$ and therefore define a real oriented 2-plane of signature (2, 0). Its orthogonal complement in V is a real oriented vector space $V_S$ of signature (3, 1), hence a 2-sphere in ${\mathbb {P}}{\mathcal {L}}.$

In the quaternionic description of $f :M \rightarrow S^4 \subset \mathbb H P^1$, we consider the quaternionic line bundle $L = f^*\mathcal T,$ the pull-back of the tautological bundle $\mathcal T$ of $\mathbb H P^1$, which can be viewed as a M-family of j-invariant complex 2-planes in ${\mathbb {C}}^4$ determined by $f:M\rightarrow {\mathbb {P}}{\mathcal {L}}.$ Its mean curvature sphere congruence

$$\begin{aligned} \tilde{S}_f:M\rightarrow \{\tilde{S}\in {\mathrm {SL}}(4,{\mathbb {C}})\mid \tilde{S}\; {\mathrm {satisfies}} \;(4)\} \end{aligned}$$

is determined by the above identifications. We consider the bundle decomposition

$$\begin{aligned} {\mathbb {C}}^4=W^+\oplus W^- \end{aligned}$$

into the $\pm i$-eigenbundles of $\tilde{S}_f$, and the decomposition of the trivial connection d as

$$\begin{aligned} d={\mathcal {D}}_{\tilde{S}}+{\mathcal {N}}_{\tilde{S}} \end{aligned}$$

into ${\tilde{S}}_f$ commuting and anti-commuting parts, i.e. ${\mathcal {D}}_{\tilde{S}}{\tilde{S}}_f=0$ and ${\mathcal {N}}_{\tilde{S}}{\tilde{S}}_f=-{\tilde{S}}_f{\mathcal {N}}_{\tilde{S}}.$ Again $\mathcal D_{\tilde{S}}$ is a connection and ${\mathcal {N}}_{\tilde{S}}$ is tensorial. Moreover, ${\mathcal {D}}_{\tilde{S}}$ induces ${\mathcal {D}}$ on $\varLambda ^2{\mathbb {C}}^4$, and ${\mathcal {N}}_{\tilde{S}}$ acts as ${\mathcal {N}}\in \varOmega ^1(M, \mathfrak {so}(\varLambda ^2\mathbb C^4,\det ))$. Note that reality of ${\mathcal {N}}_{\tilde{S}}$ is equivalent to anti-commutation with $S_f$, For details, see [12, $\S$ 4.5]. The Lagrange multiplier $q\in \varOmega ^1(M,Z)$ is then given by $\eta \in \varOmega ^1(M,\mathfrak {sl}(4,{\mathbb {C}}))$ satisfying

$$\begin{aligned} {\mathrm {image}}(\eta )\subset L\subset {\mathrm {ker}}( \eta ) \quad d^{{\mathcal {D}}_{\tilde{S}}}\eta =0 \end{aligned}$$

and the Euler–Lagrange equation of a CW surface with Lagrange multiplier $\eta$ is

$$\begin{aligned} d^{{\mathcal {D}}_{\tilde{S}}}*{\mathcal {N}}_{\tilde{S}}=2[\eta \wedge *{\mathcal {N}}_{\tilde{S}}]. \end{aligned}$$

Consequently, a surface is constrained Willmore in the 4-sphere if and only if the connections

$$\begin{aligned} d^\uplambda _{\eta ,{\tilde{S}}}:={\mathcal {D}}_{\tilde{S}}+\uplambda ^{-1}{\mathcal {N}}_{\tilde{S}}^{1,0}+\uplambda {\mathcal {N}}_{\tilde{S}}^{0,1}+(\uplambda ^{-2}-1) \eta ^{1,0}+(\uplambda ^2-1) \eta ^{0,1} \end{aligned}$$

(5)

are flat for all $\uplambda \in {\mathbb {C}}^*.$ Moreover, the induced family of flat connections on $\varLambda ^2{\mathbb {C}}^4$ satisfies

$$\begin{aligned} \varLambda ^2 d^\uplambda _{\eta ,{\tilde{S}}}=d^\uplambda _q \end{aligned}$$

(6)

for $\eta$ corresponding to q under the above identifications.

The following Proposition is proven in [24, $\S$ 9], and is used below to determine the structure of the spectral curves of the Babich–Bobenko tori:

Proposition 2

The family of ${\mathrm {SL}}(4,{\mathbb {C}})$-connections $\nabla ^\mu$ as in (1) is gauge equivalent to $d^\uplambda _{\eta ,{\tilde{S}}}$ for $\mu =\uplambda ^2.$

2.4 The structure of the spectral curve of a Babich–Bobenko torus

The aim of this section is to show the holonomy spectral curve of a Babich–Bobenko torus defined by the rank 4 family $\nabla ^\mu$ has the same properties as the Cosh–Gordon spectral curve by taking the Lagrange multiplier $\eta$ corresponding to $q_\infty$ as defined in [24, page 130]. Note that we consider the immersions maps into $S^3 \subset S^4 {\mathbb {C}}ong \mathbb H P^1$ (to make the relation to quaternionic holomorphic surface geometry transparent). We first study the structure of the spectral curve for the case of $H=0$, which is equivalent to the vanishing of the Lagrange multiplier $\eta \mathop {\widehat{=}} q=0$. The case $0<|H|<1$ is morally the same, though the details are slightly different, see Sect. 2.5. The application of the Plücker estimate in Sect. 3 works totally analogous in both cases.

Proposition 3

For a Babich–Bobenko torus $f:M\longrightarrow S^3$ with $H=0$, the associated constrained Willmore family of flat connections $\nabla ^\mu$ is gauge equivalent to a $\mathbb C_*$-family of flat ${\mathrm {SL}}(4,{\mathbb {C}})$-connections ${\tilde{\nabla }}^{\uplambda }$ of the form

$$\begin{aligned} {\tilde{\nabla }}^{\uplambda }=d+ \begin{pmatrix}\omega (\uplambda ) &{} 0 \\ 0&{}\overline{\omega ({\bar{\uplambda }}^{-1})} \end{pmatrix} \end{aligned}$$

with $\mu =\uplambda ^2$ through a $\uplambda$-dependent family of complex gauge transformations, where

$$\begin{aligned} \omega (\uplambda )=\uplambda ^{-1}\omega _{-1}+\omega _0+\uplambda \omega _1\in \varOmega ^1(M,\mathfrak {sl}(2,\mathbb C)) \end{aligned}$$

(7)

with $*\omega _{\pm 1}=\pm i\omega _{\pm 1}.$

Moreover,

$$\begin{aligned} d+\omega (-\uplambda ) \quad {\text {and}} \quad d+\overline{\omega ({\bar{\uplambda }}^{-1})} \end{aligned}$$

are gauge equivalent for all $\uplambda \in {\mathbb {C}}^*$, and the monodromies of $d+\omega (-\uplambda )$ along non-trivial elements of the first fundamental group have neither unimodular nor real eigenvalues for generic $\uplambda \in S^1.$

Proof

Let $f:M\rightarrow S^3\subset {\mathbb {P}}{\mathcal {L}}$ be a Babich–Bobenko torus with mean curvature $H = 0.$ Then, the family of connections

$$\begin{aligned} {\tilde{\nabla }}^\uplambda =d^\uplambda _{0,S} \end{aligned}$$

as defined in (5) with Lagrange multiplier $\eta =0$ is flat for all $\uplambda \in {\mathbb {C}}_*.$

Because the Babich–Bobenko surface is minimal in the intersection with the hyperbolic space $S_\infty$, the parallel vector $v_\infty$ is space-like and is contained in the mean curvature sphere bundle V for all $p\in M.$ In particular, we have $\mathcal N(v_{\infty })=0$. Hence, by Proposition 1 and (6) together with $q=0$ $v_\infty$ is parallel with respect to $\varLambda ^2 {\tilde{\nabla }}^\uplambda$ for all $\uplambda \in {\mathbb {C}}^*$. Recall that the 3-sphere $S^3\subset S^4$ is determined by a space-like vector v via

$$\begin{aligned} S^3=\{[x]\in {\mathbb {P}}{\mathcal {L}}\mid \langle x,v\rangle =0\}. \end{aligned}$$

Thus, v is contained in $V_N$ for all $p\in M$ and hence v is also parallel with respect to $\varLambda ^2 {\tilde{\nabla }}^\uplambda$ for all $\uplambda \in {\mathbb {C}}^*$. Note also that v and $v_\infty$ are perpendicular. There exists a conformal transformation of $S^4$ given by a real element of ${\mathrm {SO}}(\varLambda ^2{\mathbb {C}}^4,\det )$ which transforms the (real and space-like) 2-vectors v and $v_\infty$ (which are perpendicular to each other as they define perpendicular 3-spheres in the 4-sphere) as follows.

$$\begin{aligned} v \mapsto \tilde{v}:=e_1\wedge e_2+e_3\wedge e_4, \quad v_\infty \mapsto \tilde{v}_\infty :=ie_1\wedge e_2-ie_3\wedge e_4. \end{aligned}$$

Hence, we can assume without loss of generality that $v=\tilde{v}$ and $v_\infty =\tilde{v}_\infty$ are parallel for all $\uplambda \in {\mathbb {C}}^*.$ For a connection $d+A$ with $A\in \varOmega ^1(M,\mathfrak {sl}(4,{\mathbb {C}}))$, the 2-vectors $v,w\in \varGamma (M,\varLambda ^2{\mathbb {C}}^4)$ are parallel if and only if it $e_1\wedge e_2$ and $e_3\wedge e_4$ are parallel. This is equivalent to A being of the form

$$\begin{aligned} A=\begin{pmatrix}A_1&{}0\\ 0&{}A_2\end{pmatrix} \end{aligned}$$

for $A_1,A_2\in \varOmega ^1(M,\mathfrak {sl}(2,{\mathbb {C}}))$ as can be seen as follows: for $A=(a_{i,j})$ we get

$$\begin{aligned} A (e_1\wedge e_2)= (A e_1)\wedge e_2+e_1\wedge (A e_2)=(a_{3,1} e_3+a_{4,1} e_4)\wedge e_2+e_1\wedge (a_{3,2} e_3+a_{4,2} e_4) \end{aligned}$$

which vanishes if and only if

$$\begin{aligned} a_{3,1}=a_{3,2}=a_{4,1}=a_{4,2}=0, \end{aligned}$$

and similarly for $A( e_3\wedge e_4).$ Moreover, if A commutes with j or equivalently $\varLambda ^2(d+A)$ is real, then $A_2=\overline{A_1}:$ in fact,

$$\begin{aligned} j (d+A)(e_1)=jA_1(e_1)=j(a_{1,1} e_1+a_{2,1} e_2)=\overline{a_{1,1} }j e_1+\overline{a_{2,1}} j e_2=\overline{a_{1,1}} e_3+\overline{a_{2,1}} e_4 \end{aligned}$$

and

$$\begin{aligned} (d+A)(je_1)= a_{3,3}e_3+a_{4,3}e_3, \end{aligned}$$

and similarly for $e_2.$

Hence, with $q\widehat{=}\eta =0$ we see that ${\tilde{\nabla }}^\uplambda$ has the form

$$\begin{aligned} {\tilde{\nabla }}^\uplambda =d+\begin{pmatrix}\omega (\uplambda )&{}0\\ 0&{}\overline{\omega ({\bar{\uplambda }}^{-1})}\end{pmatrix}, \end{aligned}$$

where $\omega (\uplambda )$ is as stated in (7). By [24, Lemma 9.14] and [4, Equation (2.11)], ${\tilde{\nabla }}^\uplambda$ is gauge equivalent to $\nabla ^\mu$ as defined in (1) (with $\mu =\uplambda ^2$).

If the monodromies of $d+\omega (-\uplambda )$ along non-trivial elements $\gamma _i$ of $\pi _1(M)$ would have either unimodular or real eigenvalues for generic $\uplambda \in S^1$, then [4, Proposition 3.2] shows that the eigenvalues of $\nabla ^\mu$ must be all equal to 1 for all $\mu \in {\mathbb {C}}_*$ and therefore this case can be excluded by [4, Theorem 5.1].

It remains to prove that $d+\omega (-\uplambda )$ and $d+\overline{\omega ({\bar{\uplambda }}^{-1})}$ are gauge equivalent for all $\uplambda \in {\mathbb {C}}^*.$ We make use of the fact that ${\tilde{\nabla }}^\uplambda$ and ${\tilde{\nabla }}^{-\uplambda }$ are gauge equivalent (as both are gauge equivalent to $\nabla ^{\mu = \uplambda ^2}$), and want to determine the gauge as explicit as possible. Consider first the case that at some point $p\in M$

$$\begin{aligned} w=(e_1\wedge e_3-e_2\wedge e_4) \end{aligned}$$

is (twice) the oriented normal of f at p. Then, $S^+_p$ is the 2-plane determined by

$$\begin{aligned} w+ i {\tilde{v_\infty }}=(e_1-e_4)\wedge (e_3-e_2) \end{aligned}$$

and $S^-_p$ is the 2-plane determined by

$$\begin{aligned} w-i {\tilde{v_\infty }}=(e_1+e_4)\wedge (e_2+e_3), \end{aligned}$$

i.e.

$$\begin{aligned} S^+_p={\text {span}}(e_1-e_4,e_3-e_2) \end{aligned}$$

and

$$\begin{aligned} S^-_p={\text {span}}(e_1+e_4,e_2+e_3). \end{aligned}$$

By [12, $\S 3.2$ ] or [24, Lemma 9.14],

$$\begin{aligned} {\tilde{\nabla }}^{-\uplambda }={\tilde{\nabla }}^{\uplambda }.H, \end{aligned}$$

where $H:{\mathbb {C}}^4\rightarrow {\mathbb {C}}^4$ is determined by

$$\begin{aligned} H(s_\pm )=\pm i s_\pm \quad {\text {for}} \quad s_\pm \in S^\pm . \end{aligned}$$

Using the standard basis of ${\mathbb {C}}^4,$ $H_p$ is given by

$$\begin{aligned} H_p=\begin{pmatrix} 0&{}0&{}0&{}-i\\ 0&{}0&{}-i&{}0\\ 0&{}-i&{}0&{}0\\ -i&{}0&{}0&{}0 \end{pmatrix}. \end{aligned}$$

Now, let (twice) the normal of f at the point $q\in M$ be arbitrary, i.e. $N_q$ is in the real part of $\varLambda ^2{\mathbb {C}}^4$ perpendicular to $\tilde{v}$ and $\tilde{v}_\infty$ and of length 2. There is a conformal transformation $\varPsi _q$ of $S^4$ which fixes the 3-sphere and the sphere at infinity, and maps $N_p$ to w. It must be (considered as a ${\mathrm {SL}}(4,{\mathbb {C}})$-matrix commuting with j) of the form

$$\begin{aligned} \varPsi _q=\begin{pmatrix} P_q &{}0\\ 0&{} {\bar{P}}_{q}\end{pmatrix} \end{aligned}$$

where $P_q$ is a 2 by 2 matrix of unimodular determinant. Denote

$$\begin{aligned} K=\begin{pmatrix} 0&-i\i&0\end{pmatrix}. \end{aligned}$$

Then,

$$\begin{aligned} H_q=\begin{pmatrix}P^{-1}_q&{}0\\ 0&{}\bar{P}^{-1}_q\end{pmatrix} \begin{pmatrix} 0 &{}K\\ K&{} 0\end{pmatrix}\begin{pmatrix} P_q &{}0\\ 0&{} \bar{P}_q\end{pmatrix}= \begin{pmatrix} 0 &{}P^{-1}_qK\bar{P}_q\\ \bar{P}^{-1}_qKP_q&{} 0\end{pmatrix}. \end{aligned}$$

Because the space of ${\mathrm {SL}}(4,{\mathbb {C}})$ matrices commuting with j and fixing

$$\begin{aligned} {\tilde{v}},{\tilde{v_\infty }} \quad {\text {and}} \quad {e_1{\wedge }} {e_3-e_2{\wedge }e_4} \end{aligned}$$

is given by

$$\begin{aligned} \begin{pmatrix}{\alpha {a}}&{}{\alpha {b}}&{}0&{}0\\ {\alpha {\bar{b}}}&{}{\alpha {\bar{a}}}&{}0&{}0\\ 0&{}0&{}{\alpha ^{-1}} {\bar{a}}&{}{\alpha ^{-1}} {\bar{b}}\\ 0&{}0&{}{\alpha ^{-1}} b&{}\alpha ^{-1} a\end{pmatrix}, \end{aligned}$$

where where $a,b\in {\mathbb {C}}$, $\alpha \in S^1$ with

$$\begin{aligned} a{\bar{a-b}}{\bar{b}}=1, \end{aligned}$$

$P_q$ is unique up to

$$\begin{aligned} P_q\longmapsto \alpha \begin{pmatrix}a&{}b\\ {\bar{b}}&{}{\bar{a}}\end{pmatrix}. \end{aligned}$$

Note that

$$\begin{aligned} {\bar{\alpha }}^{-1} \begin{pmatrix} {\bar{a}}&{}-{\bar{b}}\\ -b&{}a \end{pmatrix} {K{\alpha }} \begin{pmatrix} a&{}b\\ {\bar{b}}&{}{\bar{a}} \end{pmatrix} ={\alpha ^{2K.}} \end{aligned}$$

As P can be locally chosen to be smooth on M we find a well-defined global gauge transformation

$$\begin{aligned} g:M\rightarrow {\mathrm {GL}}(2,{\mathbb {C}}) \end{aligned}$$

with unimodular determinant which is locally given by

$$\begin{aligned} g_q={\bar{P}}^{-1}_qKP_q \end{aligned}$$

and satisfies

$$\begin{aligned} (d+\omega (\uplambda )).g=d+\overline{\omega ({\bar{\uplambda }}^{-1})}. \end{aligned}$$

Moreover, due to the quadratic factor $\alpha ^2,$ one can deduce that g can actually be chosen to be ${\mathrm {SL}}(2,{\mathbb {C}})$-valued. $\square$

As an immediate corollary, the spectral curve $\Sigma$ has the same properties as a Cosh–Gordon spectral curve.

Corollary 1

The spectral curve $\Sigma$ of a Babich–Bobenko torus (with $H=0$) considered as a Willmore torus, i.e. as the Riemann surface parametrizing the eigenlines of $\nabla ^\mu ,$ is given by a double covering of $\uplambda : \Sigma \longrightarrow {\mathbb {C}} P^1$ with $\uplambda ^2 =\mu$ satisfying:

• $\uplambda$ is branched over $\uplambda = 0$ and $\uplambda = \infty$

• there exist two holomorphic functions—the monodromy maps—

  $$\begin{aligned} \nu _1,\nu _2:\Sigma \setminus \{0,\infty \}\longrightarrow \mathbb C^* \end{aligned}$$

  such that the hyper-elliptic involution $\sigma$ satisfies

  $$\begin{aligned} \sigma ^*\nu _i=\frac{1}{\nu _i},\quad {\text {for}}\,\,i = 1,2 \end{aligned}$$

• $\Sigma$ has an anti-holomorphic involution $\rho$ covering $\uplambda \mapsto -{\bar{\uplambda }}^{-1}$ with

  $$\begin{aligned} \rho ^*\nu _i=\bar{\nu }_i, \quad {\text {for}}\,\,i = 1,2 \end{aligned}$$

• $\mu : \Sigma \longrightarrow {\mathbb {C}} P^1$ is a fourfold covering, i.e. for generic $\mu \in {\mathbb {C}}_*$ the connection $\nabla ^\mu$ has 4 distinct eigenvalues along the generators $\gamma _k$ $k=1,2$ of $\pi _1(T^2)$ given by the four elements of the set

  $$\begin{aligned} \{\nu _k(\xi ) \mid \quad \xi \in \Sigma : \mu =(\uplambda (\xi ))^2\}. \end{aligned}$$

Proof

By the previous proposition, the spectral curve $\Sigma$ is given by the holonomy spectral curve of the family of flat connections $\hat{\nabla }^\uplambda = d+\omega (\uplambda ).$ Since $\hat{\nabla }^\uplambda$ is SL$(2, {\mathbb {C}}),$ the hyper-elliptic involution $\sigma$ maps an eigenvalue of the monodromy to its inverse. The other involution $\rho$ is induced by the quaternionic multiplication j, which covers $\uplambda \mapsto -{\bar{\uplambda }}^{-1}$ and (complex) conjugates the eigenvalues of the monodromy. Moreover, the parameter covering $\mu = \uplambda ^2$ is unbranched over $\mathbb C^*$. Thus, the quotient $\Sigma /\sigma$ is biholomorphic to ${\mathbb{C}} P^1.$ $\square$

2.5 Non-minimal Babich–Bobenko tori

We show a modified version of Corollary 1 for Babich–Bobenko surfaces

$$\begin{aligned} f : M \longrightarrow S^3 \end{aligned}$$

with mean curvature $H \ne 0$ (and $|H| <1$) in the hyperbolic space $\mathcal H^3 \subset S^3$. Again we use the notations as introduced in Sect. 2.3 (or [24] for more details) and consider the ${\mathbb {C}}^*$-associated family of flat connections

$$\begin{aligned} d^{\uplambda }_{\eta ,S} \end{aligned}$$

on the trivial ${\mathbb {C}}^4$-bundle for the Lagrange multiplier $\eta$ given by

$$\begin{aligned} \eta =H\eta _\infty , \end{aligned}$$

where $\eta _\infty$ is defined in [24, Theorem 8.16]. For further references, see [11, 12, 25]. The connections $d^{\uplambda }_{\eta ,S}$ induce the family of flat connections

$$\begin{aligned} d^\uplambda _{\eta }={\mathcal {D}}+\uplambda ^{-1}{\mathcal {N}}^{(1,0)}+\uplambda \mathcal N^{(0,1)}+(\uplambda ^{-2}-1)\eta ^{(1,0)}+(\uplambda ^{2}-1)\eta ^{(0,1)}, \end{aligned}$$

on the $\varLambda ^2{\mathbb {C}}^4$ with Lagrange multiplier $\eta$. By [24, Lemma 9.14] and [4, Equation (2.11)] the connections $d^{\uplambda }_{\eta ,S}$ and the constrained Willmore associated family of flat connections $\nabla ^\mu$ defined in (1) are gauge equivalent for $\mu =\uplambda ^2$.

The surface f is an isothermic constrained Willmore torus by assumption and admits a conserved quantity [24, Proposition 8.20]. Since we are considering surfaces in $S^3\subset S^4$, there is for every $\uplambda \in {\mathbb {C}}^*$ a complex 2-dimensional subspace of $\varLambda ^2{\mathbb {C}}^4$ on which $d^\uplambda _{\eta }$ acts trivially, see (6). Applying a suitable $SL(4,\mathbb C)$-transformation (depending on $\uplambda$ and $p\in M$), we can assume without loss of generality that the invariant subspace is spanned by

$$\begin{aligned} v= e_1\wedge e_2,\ e_3\wedge e_4. \end{aligned}$$

A short computation as in Sect. 2.4 shows that $d^{\uplambda }_{\eta ,S}$ is of the form

$$\begin{aligned} d+\begin{pmatrix} A(\uplambda ) &{}0\\ 0&{} B(\uplambda )\end{pmatrix} \end{aligned}$$

(8)

for $A(\uplambda ),B(\uplambda )\in \varOmega ^1(M,\mathfrak {sl}(2,\mathbb C))$ (with respect to the chosen $\uplambda$-dependent frame). Recall that the reality condition implies that $d^\uplambda _{\eta }$ reduces to a ${\mathrm {SO}}(3,1)$-connection for every $\uplambda \in S^1$. This implies

$$\begin{aligned} \bar{A}(\uplambda )=B(\uplambda ) \quad {\text {for}}\,\, \uplambda \in S^1. \end{aligned}$$

Remark 2

For CMC surfaces in $S^3$, the connection $d^\uplambda _{\eta }$ reduces to a ${\mathrm {SO}}(4)$-connection with reality condition $-\bar{A}^T=A$ and $-\bar{B}^T=B.$

Proposition 4

The spectral curve of a Babich–Bobenko torus $f: T^2 \longrightarrow S^3$ (corresponding to the Lagrange multiplier $\eta$ defined in [24, Theorem 8.16]) is a hyper-elliptic surface

$$\begin{aligned} \uplambda :\Sigma \longrightarrow {\mathbb {C}}P^1 \end{aligned}$$

with an anti-holomorphic involution $\rho$ covering $\uplambda \mapsto -{\bar{\uplambda }}^{-1}.$ Moreover, $\Sigma$ is endowed with two meromorphic differentials $\theta _1,\theta _2$ of the second kind satisfying

$$\begin{aligned} \sigma ^*\theta _k=-\theta _k,\;\;\rho ^*\theta _k=\bar{\theta }_k, \end{aligned}$$

where $\sigma$ is the hyper-elliptic involution and two holomorphic functions $\nu _1,\nu _2:\Sigma \setminus \uplambda ^{-1}\{0,\infty \}$ with $d\log \nu _k=\theta _k$.

The functions $\nu _i$ parametrizes the eigenvalues of $\nabla ^\mu$ along the generator $\gamma _k,$ of the first fundamental group of $T^2.$ The (generically) four eigenvalues of $\nabla ^\mu$ are given by

$$\begin{aligned} \{\nu _k(\xi ) \mid k= 1,2 \quad {\text {and}} \quad \xi \in \Sigma : \mu =(\uplambda (\xi ))^2\}. \end{aligned}$$

Proof

Let $\tilde{\Sigma }$ be the constrained Willmore spectral curve given as the parametrization of the (generically 4 distinct) eigenvalues of $\nabla ^\mu .$ Since $\nabla ^\mu$ is gauge equivalent to (8), it is the direct sum of two flat SL$(2, \mathbb C)$-connections

$$\begin{aligned} d + A(\uplambda ) \quad {\text {and}}\,\, d + B(\uplambda ) \end{aligned}$$

for $\uplambda ^2=\mu .$ Let h be an eigenvalue of the monodromy of $\nabla ^\mu$. We assume without loss of generality that it is an eigenvalue of $d+A(\uplambda )$. Since $d+A(\uplambda )$ is a SL$(2,{\mathbb {C}})$-connection, $h^{-1}$ is also an eigenvalue of $d+A(\uplambda ).$ Thus we can define an involution

$$\begin{aligned} \sigma : \Sigma \longrightarrow \Sigma , \quad h \longmapsto h^{-1} \end{aligned}$$

(note that $\sigma$ holomorphically extends to $\mu =0,\infty$ and therefore is well defined on $\Sigma$). Since the decomposition into blocks is valid for all $\mu \in {\mathbb {C}}^*$, the quotient $\Sigma /\sigma$ is ${\mathbb {C}}P^1.$ The remaining properties can be easily proved using [4, Proposition 3.1] together with the reality condition $\bar{A}=B.$ $\square$

Remark 3

Note that for $H\ne 0$, the connections $d^{\uplambda }_{\eta ,S}$ and the connections given by (8) are gauge equivalent by a $\uplambda$-dependent gauge transformation. Thus, the map $\uplambda :\Sigma \longrightarrow \Sigma /\sigma$ is not necessarily branched over 0 and $\infty$ as in the $H=0$ case.

3 Plücker estimates

We show that all isothermic constrained Willmore tori of Babich–Bobenko type have Willmore energy above $8\pi .$ The following Plücker estimate is relating the dimension of the holomorphic sections of V/L (without monodromy) to the Willmore energy of the corresponding immersion.

Theorem 2

[13, Theorem 4.12] Let $f:T^2 \longrightarrow S^3$ be a conformal immersion and (V/L, D) be the quaternionic holomorphic line bundle associated to it. Let $k \in {\mathbb {N}}$ be the dimension of $H^0(T^2,V/L)$ (with trivial monodromy). Then, a lower bound for the Willmore energy of f is given by

$$\begin{aligned} W(f) \ge {\left\{ \begin{array}{ll} \pi k^2 &{} k \; even \\ \pi (k^2 - 1) &{} k \; odd .\end{array}\right. } \end{aligned}$$

Remark 4

For every immersion into $S^3$, the sections [1, 0] and [0, 1] are holomorphic sections without monodromy. Thus, $H^0(V/L)$ is at least 2-dimensional. The most relevant cases in the following are: if there exists a third quaternionic linearly independent holomorphic section, then the Willmore energy of f is at least $8 \pi$, if there exists a fourth quaternionic linearly independent holomorphic section, the lower bound is $16\pi .$

Remark 5

We have shown in Sects. 2.4 and 2.5 that the associated family of flat connections $\nabla ^\mu$ of a Babich–Bobenko torus has four distinct eigenvalues for generic $\mu \in {\mathbb {C}}_*$. Thus, by Bohle [4] $\hat{L}=$Ker$A_{\mathbb {C}}irc$ is a non-constant quaternionic line subbundle of V.

Lemma 1

Let $f: T^2 \longrightarrow S^3$ be a Babich–Bobenko torus with Willmore energy below $8\pi .$ Then every branch point of the spectral curve $\uplambda :\Sigma \longrightarrow \Sigma /\sigma {\mathbb {C}}ong{\mathbb {C}} P^1$ except those over $\uplambda =0$ and $\uplambda =\infty$ corresponds to a non-constant holomorphic section of V/L with $\mathbb Z_2$-monodromy.

Proof

The spectral curve $\Sigma$ is the surface parametrizing the eigenlines of $\nabla ^\mu$—the constrained Willmore associated family of flat connections. It admits two involutions: $\sigma$ and $\rho .$ While the involution $\rho$ corresponds to the quaternionic multiplication by j and is fixpoint free, the involution $\sigma$ maps a holomorphic section $\psi$ with monodromy h to a holomorphic section with monodromy $h^{-1}$. Therefore, the branch points of $\Sigma$ correspond to those $\nabla ^\mu$-parallel sections $\psi$ of V with $\mathbb Z_2$-monodromy, i.e. prolongations of holomorphic sections of V/L with $\mathbb Z_2$-monodromy. It is thus crucial to show that these $\psi$ are non-constant sections of V, which clearly holds whenever the monodromy of the section $\psi$ is non-trivial. Thus, we restrict to the case where $\psi$ has trivial monodromy.

Let $\uplambda _0$ be a branch point of $\Sigma$ and $\psi _0$ be the $\nabla ^{\mu _0}$-parallel section of V without monodromy associated to $\uplambda _0$ where $\mu _0=\uplambda _0^2$. If $\mu _0 \ne 1$ then $\psi$ must be non-constant, since $\psi$ being constant would imply that $\tilde{\psi }\in \varGamma ($Ker${A_\mathbb Circ})$ and then $\hat{L}=$Ker$A_{\mathbb {C}}irc$ would be constant in contradiction to [4, Theorem 5.3].

It remains to show that also for the case $\mu _0=\uplambda _0^2=1$ there exists a non-constant section $\tilde{\psi }$, given by a prolongation of a holomorphic section of V/L,  with trivial monodromy. Let $\nabla ^\mu$ be the CW associated family, and $\mu _0=1$ be a branch point of the spectral curve $\Sigma$. Because of the $\rho$-symmetry (interchanging the two points over $\mu _0=1$) $\Sigma$ is not totally branched at $\mu _0$, i.e. we can use a local coordinate $\xi$ on $\Sigma$ with $\xi ^2=\mu -1.$ Assume that the Willmore energy is below $8\pi .$ By [5, Theorem 4.3 (iii)], there is a smooth family of $\nabla ^{\mu (\xi )}$-parallel sections $\psi ^\xi$ parametrized on an open subset of $\Sigma$ around $\xi =0$ depending smoothly on $\xi$, i.e. we have

$$\begin{aligned} \nabla ^{\mu (\xi )}\psi ^\xi =0. \end{aligned}$$

Differentiating this equation with respect to $\xi$ (denoted by $()^{\prime }$) at $\xi =0$ (and therefore $\mu =1$) gives

$$\begin{aligned} 0=(\nabla ^{\mu (x)})^{\prime }\psi +d \psi ^{\prime }=\left( \frac{d \mu (\xi )}{d\xi }_{\mid \xi =0} A_{\mathbb {C}}irc^{1,0}+\frac{d \mu ^{-1}(\xi )}{d\xi }_{\mid \xi =0} A_\mathbb Circ^{0,1}\right) \psi +d\psi ^{\prime }=d\psi ^{\prime }, \end{aligned}$$

where $\psi =\psi ^{\xi =0}$ is constant in $z \in T^2$(as $\nabla ^{\mu =1}=d$). Differentiating once more and evaluating at $\xi =0$ thus gives

$$\begin{aligned} 0=(\nabla ^{\mu (x)})^{\prime \prime }\psi +2(\nabla ^{\mu (x)})^{\prime }\psi ^{\prime }+d \psi ^{\prime \prime }=(-2A_{\mathbb {C}}irc^{1,0}+2A_{\mathbb {C}}irc^{0,1})\psi +d \psi ^{\prime \prime }. \end{aligned}$$

Since $(-2A_{\mathbb {C}}irc^{1,0}+2A_{\mathbb {C}}irc^{0,1})\psi$ is contained in $L = f^* \mathcal T =$ Im $(A_{\mathbb {C}}irc)$, $d\psi ^{\prime \prime }$ is contained in L as well showing that $\psi ^{\prime \prime }$ is the prolongation of a (locally) holomorphic section of V/L. Since the monodromy takes the value 1 with at least second order (because the monodromy is trivial at the branch point $\mu = 1$), $\psi ^{\prime \prime }$ has also trivial monodromy. If $\psi ^{\prime \prime }$ would be constant then

$$\begin{aligned} 0=(-2A_{\mathbb {C}}irc^{1,0}+2A_{\mathbb {C}}irc^{0,1})\psi , \end{aligned}$$

which yields that Ker$A_{\mathbb {C}}irc$ is constant giving a contradiction. $\square$

Lemma 2

Two holomorphic sections of V/L with non-trivial $\mathbb Z_2$-monodromy corresponding to different branch points of $\uplambda :\Sigma \rightarrow \Sigma /\sigma ={\mathbb {C}}P^1$ not lying over 0 or $\infty$, which are not interchanged by the involution $\rho ,$ are quaternionic linear independent.

Proof

Let $\tilde{\psi }_1$ and $\tilde{\psi }_2$ be two holomorphic sections of V/L with $\mathbb Z_2$-monodromy. If these sections have different $\mathbb Z_2$-monodromies, then they are clearly quaternionic linear independent. Thus, let the $\psi _i$ have the same non-trivial $\mathbb Z_2$-monodromy in the following.

Due to [4, Section 2.5] and the fact that their monodromy is non-trivial on $T^2$, it is enough to prove that their prolongations $\psi _1$ and $\psi _2$, which are parallel sections with respect to $\nabla ^{\mu _1}$ and $\nabla ^{\mu _2}$ (corresponding to the branch points $\uplambda _1$ and $\uplambda _2$ of $\Sigma \longrightarrow \Sigma /\sigma$), are linear independent. If $\mu _1=\mu _2$, it follows from Proposition 3 that $\psi _1$ and $\psi _2$ are (quaternionic) linear independent since $\xi _1\ne \xi _2$ and $\xi _1\ne \rho (\xi _2).$

If $\mu _1\ne \mu _2$, we obtain that $\tilde{\psi }_1$ and $\tilde{\psi }_2$ are complex linear independent. Assume that they are not independent as quaternionic sections, then we would have w.l.o.g.

$$\begin{aligned} \tilde{\psi }_1=a\tilde{\psi }_2+b\tilde{\psi }_2 j \end{aligned}$$

for some $a,b \in {\mathbb {C}}.$ Moreover, from

$$\begin{aligned} \nabla ^{\mu _1}\tilde{\psi }_1=0; \quad \nabla ^{\mu _2}\tilde{\psi }_2=0\quad \nabla ^{{\bar{\mu }}_{2}^{-1}}\tilde{\psi }_2 j=0 \end{aligned}$$

we obtain

$$\begin{aligned} \begin{aligned} 0&= (\mu _1^{-1}-\mu _2^{-1}) A_{\mathbb {C}}irc^{1,0} a\tilde{\psi }_2\\&\quad +(\mu _1^{-1}-\bar{\mu }_2) A_{\mathbb {C}}irc^{1,0} a\tilde{\psi }_2j\\&\quad +(\mu _1-\mu _2) A_{\mathbb {C}}irc^{0,1} a\tilde{\psi }_2\\&\quad +(\mu _1-\bar{\mu }_2^{-1}) A_{\mathbb {C}}irc^{1,0} a\tilde{\psi }_2j.\\ \end{aligned} \end{aligned}$$

(9)

By type decomposition (see [13, Section 2.1]), we obtain $A_{\mathbb {C}}irc\psi _2=0$. Since $\psi _2$ is $\nabla ^{\mu _2}$-parallel this implies $\psi _2$ being constant, which is a contradiction by [4, Theorem 5.3] $\square$

Lemma 3

Let $f:T^2\longrightarrow S^3$ be a constrained Willmore torus of Babich–Bobenko type with spectral genus $g \ge 3$. Then, either one of the branch points of the spectral curve over the unit disc $D \subset {\mathbb {C}}$ corresponds to the trivial monodromy or at least two of the branch points of the spectral curve on the punctured unit disc $D_*$ correspond to the same (non-trivial) $\mathbb Z_2$-monodromy.

Proof

For $g >3$, we have at least 5 branch points over the punctured unit disc

$$\begin{aligned} D:=\{\uplambda \in {\mathbb {C}}\mid 0<|\uplambda |\le 1\}. \end{aligned}$$

The claim follows from the fact that there exist only 3 different non-trivial spin structures of the torus.

It remains to show the lemma in the case of $g=3$, where we have 4 branch points over the unit disc (that are not interchanged by $\rho$). Assume that none of the 4 branch points on the unit disc corresponds to the trivial spin structure and moreover, for $\mu \ne 0$ the other 3 branch points correspond to different spin structures. Then, the spin structure at $\mu = 0$ must coincide with the one at $P_k$ for a $k \in \{1, 2, 3\}$, since there exist only 3 different non-trivial spin structures of a torus. Without loss of generality we can assume $k=1$. We want to show that the spin structures corresponding to $P_2$ and $P_3$ must then coincide.

In this case, the closed non-trivial curve, the green curve in Fig. 2, through the branch points $P_2$ and $P_3$ denoted by $\gamma _{23}$, is homologous to the difference of the closed (red) curve $\gamma _S$ through the Sym-points $S_1$ and $S_2$ and the closed (blue) curve $\gamma _{01}$ connecting 0 and $P_1$. Let $\theta _i = d\log \nu _i$ ($i=1,2$) be the logarithmic differentials of the monodromy maps $\nu _i$ and consider integrals of $\theta _i$ along these curves. Using the hyper-elliptic symmetry, we want to show that

$$\begin{aligned} 2 \int _{P_2}^{P_3} \theta _i = \int _{\gamma _{23}} \theta _i \in 4 \pi i \mathbb Z. \end{aligned}$$

Since 0 and $P_1$ correspond to the same spin structure by assumption, we first show that

$$\begin{aligned} \int _{\gamma _{01}} \theta _k \in 4 \pi i \mathbb Z \end{aligned}$$

for $k=1,2$. As $\theta _k$ has trivial residue, we can interpret the above integral as the integral of $\theta _k$ along any curve homotopic to $\gamma _{01}$ which does not pass through $0\in \Sigma$.

In order to analyse the integral, we apply a renormalization: For $k=1,2$, there exists a closed 1-form $\eta _k$ on $\Sigma \setminus \{0\}$ with support in a small neighbourhood of 0 which satisfies $\sigma ^*\eta _k=-\eta _k$ and such that

$$\begin{aligned} \theta _k+\eta _k \end{aligned}$$

extends smoothly through 0,  compare with the limiting analysis of [18, Proposition 3.10]. Note that $\int _{\gamma _{01}}\eta _k=0$. Using an analogous computation as in [18, Proposition 3.10] again, we can associate to $0\in \Sigma$ renormalized eigenvalues $\tilde{\nu }_1$ and $\tilde{\nu }_2$ which take values in $\{\pm 1\}$ and encode the spin structure of the surface. The sign is encoded in the parity of the constant part of the expansion in [18, Proposition 3.10]. Then, we obtain

$$\begin{aligned} \int _{\gamma _{01}} \theta _k=\int _{\gamma _{01}} \theta _k+\eta _k=2\int _{\gamma _{01}^+} \theta _k+\eta _k\in 4\pi i\mathbb Z, \end{aligned}$$

where $\gamma _{01}^+$ is given by a part of $\gamma _{01}$ which goes from 0 to $P_1$, and the last equality follows from the fact that the values $\nu _k(0)$ and $\nu _k(P_1)$ coincide as 0 and $P_1$ correspond to the same spin structure.

Thus it remains to prove that the integral of $\theta _i$ along the red curve $\gamma _S$ satisfies

$$\begin{aligned} \int _{\gamma _{S}} \theta _k \in 4\pi i\mathbb Z. \end{aligned}$$

This follows from the $\rho$-symmetry of the spectral data: the integral of $\theta _k$ along the red curve $\gamma _S$ is twice the integral along the curve $\tilde{\gamma }$ which is defined to be the part of $\gamma _S$ from the point $S_1$ lying over the Sym point $\mu _1$ to the point $S_2$ lying over $-\bar{\mu }_1^{-1}$, i.e.

$$\begin{aligned} \int _{\gamma _S}\theta _k=\int _{\tilde{\gamma }}\theta _k+\int _{\sigma \mathbb Circ\rho (\tilde{\gamma })}\theta _k=\int _{\tilde{\gamma }}\theta _k-\int _{\tilde{\gamma }}\overline{\theta _k}=2\int _{\tilde{\gamma }}\theta _k, \end{aligned}$$

where the last equality uses the fact that the integral takes imaginary values. The well-definedness of f then gives $\int _{\tilde{\gamma }}\theta _k\in 2\pi i\mathbb Z$ proving the claim. $\square$

Theorem 3

The Willmore energy of a constrained Willmore torus $f: T^2 \longrightarrow S^3$ of Babich–Bobenko type is at least $8\pi .$

Fig. 2

A spectral curve of genus 3, with branch points and certain cycles

Proof

Since the spectral curve $\Sigma$ admits an involution $\rho$ covering $\uplambda \mapsto -{\bar{\uplambda }}^{-1}$, it must be of odd genus g, or $\uplambda$ is unbranched. For $g\in \{0,1\}$ the surface f is equivariant, see [15]. For $g=0$ the surface must be homogenous. This case cannot appear, since it would be a surface entirely contained in hyperbolic 3-space. For $g=1$, the surface is rotational symmetric and obtained by rotating a closed wavelike elastic curve in the hyperbolic plane $\mathcal H^2$ around the infinity boundary of $\mathcal H^2.$ The only periodic solution in this class is the family of elastic figure-8 curves in $\mathcal H^2$. These surfaces are non-embedded, see for example [14] or [28], and therefore they have Willmore energy above $8\pi$ by [21].

Let $g \ge 3$. By Lemma 1, we can associate to every branch point of $\Sigma$ a holomorphic section $\psi$ with $\mathbb Z_2$-monodromy of V/L. There exist exactly 4 possible $\mathbb Z_2$-monodromies for $\psi$ arising from the 4 different spin structures of $T^2$. To be more concrete, the two monodromy maps $\nu _i$ of $\psi$ satisfies:

$$\begin{aligned} (\nu _1(\psi ),\nu _2(\psi ))\in \{(1,1),(1,-1),(-1,1),(-1,-1)\}. \end{aligned}$$

Every $\psi$ with $\pm 1$ monodromy gives rise to a proper holomorphic section of V/L considered as a bundle over a suitable double cover $\tilde{T}^2$ of $T^2.$ Thus the theorem follows from the previous Lemma by applying the Plücker estimate (Theorem 2). If the trivial monodromy arises over $\uplambda =0$, the immersion f has trivial spin structure and by [22] the surface cannot be embedded and hence its Willmore energy is at least $8\pi$. $\square$