Isogeometric analysis of bending, vibration, and buckling behaviors of multilayered microplates based on the non-classical refined shear deformation theory

Abstract

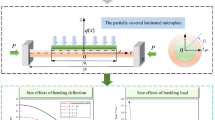
This paper presents a non-classical refined shear deformation theory model in conjunction with the isogeometric analysis for the static bending, free vibration, and buckling behaviors of multilayered microplates. The modified couple stress theory is used to account for the small-scale effect. Taking a five-layer (Al, P3HT: PCBM, PEDOT: PSS, ITO, and Glass) organic solar cell as an example, it is found that the small-scale effects lead to a decrease in deflection, but an increase in the natural frequency and buckling load. With consideration of the size effect (l/h = 1), the stresses are almost 5 times as much as that without the size effect (l/h = 0). This is why the size effect should be taken into account. Besides, the maximum tensile stress occurs in the ITO layer, which is the dangerous layer. In addition, the normalized deflections increase with increasing aspect ratio, but the normalized natural frequencies and normalized buckling loads decrease with increasing aspect ratio.

Appendices

Appendix A: a brief on NURBS basis functions

For the sake of completeness, the NURBS basis function is introduced in this section. More details can be found in Refs. [37, 46]. A knot vector, ${\varvec{k}}\left( \xi \right)$, is a set of non-decreasing numbers between zero and one, ${\varvec{k}}\left( \xi \right) = \left\{ {\xi_{1} = 0, \ldots ,\xi_{i} , \ldots ,\xi_{n + p + 1} = 1} \right\}^{{\text{T}}}$ with i representing the knot index, $\xi_{i}$ is the ith knot, n is the number of basis functions, and p the order of the polynomial [34]. By using the given knot vector ${\varvec{k}}\left( \xi \right)$, the ith B-spline basis function of degree p, termed as $N_{i,p} \left( \xi \right)$, is defined recursively as follows:

$$N_{i,0} (\xi ) = \left\{ {\begin{array}{*{20}l} 1 \hfill &\quad {{\text{if}}\;\xi_{i} \le \xi < \xi_{i + 1} } \hfill \\ 0 \hfill &\quad {{\text{otherwise}}} \hfill \\ \end{array} } \right.\;{\text{for}}\;p = 0\, ,$$

(A1)

and

$$N_{i,p} (\xi ) = \frac{{\xi - \xi_{i} }}{{\xi_{i + p} - \xi_{i} }}N_{i,p - 1} (\xi ) + \frac{{\xi_{i + p + 1} - \xi }}{{\xi_{i + p + 1} - \xi_{i + 1} }}N_{i + 1,p - 1} (\xi )\;\;{\text{for}}\;\;p \ge 1\, .$$

(A2)

For two-dimensional (2D) problems, the NURBS basis functions can be constructed by taking the tensor product of two 1D B-spline basis functions [37]:

$$R_{i,j}^{p,q} (\xi ,\eta ) = \frac{{N_{i,p} (\xi )N_{j,q} (\eta )w_{i,j} }}{{\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{m} {N_{i,p} (\xi )N_{j,q} (\eta )w_{i,j} } } }}\, ,$$

(A3)

where w_i,j is the weight in 2D; $N_{i,p} (\xi )$ and $N_{j,q} (\eta )$, respectively, are the B-spline basis functions of order p in the ξ direction and order q in the η direction; $N_{j,q} (\eta )$ follows the recursive formula shown in Eq. (13) with knot vector ${\varvec{k}}\left( \eta \right)$. The definition of ${\varvec{k}}\left( \eta \right)$ is the same as that of ${\varvec{k}}\left( \xi \right)$.

In addition, the C²-continuity is required in this paper. The second-order derivatives of the NURBS basis function can be described as [51]

$$\frac{{\partial R_{i,j}^{2p,q} \left( {\xi ,\eta } \right)}}{{\partial \xi^{2} }} = w_{i,j} \frac{{\frac{{\partial^{2} N_{i,p} \left( \xi \right)}}{{\partial \xi^{2} }}N_{j,q} \left( \eta \right)W\left( {\xi ,\eta } \right) - \frac{{\partial W\left( {\xi ,\eta } \right)}}{\partial \xi }N_{i,p} \left( \xi \right)N_{j,q} \left( \eta \right)}}{{\left( {W\left( {\xi ,\eta } \right)} \right)^{2} }} - w_{i,j} \frac{{2\left( {\frac{{\partial N_{i,p} \left( \xi \right)}}{\partial \xi }\frac{{\partial W\left( {\xi ,\eta } \right)}}{\partial \xi }N_{j,q} \left( \eta \right)W\left( {\xi ,\eta } \right) - \left( {\frac{{\partial W\left( {\xi ,\eta } \right)}}{\partial \xi }} \right)^{2} N_{i,p} \left( \xi \right)N_{j,q} \left( \eta \right)} \right)}}{{\left( {W\left( {\xi ,\eta } \right)} \right)^{3} }}\, ,$$

(A4)

$$\frac{{\partial R_{i,j}^{2p,q} \left( {\xi ,\eta } \right)}}{{\partial \eta^{2} }} = w_{i,j} \frac{{\frac{{\partial^{2} N_{j,q} \left( \eta \right)}}{{\partial \eta^{2} }}N_{i,p} \left( \xi \right)W\left( {\xi ,\eta } \right) - \frac{{\partial W\left( {\xi ,\eta } \right)}}{\partial \eta }N_{i,p} \left( \xi \right)N_{j,q} \left( \eta \right)}}{{\left( {W\left( {\xi ,\eta } \right)} \right)^{2} }} - w_{i,j} \frac{{2\left( {\frac{{\partial N_{j,q} \left( \eta \right)}}{\partial \eta }\frac{{\partial W\left( {\xi ,\eta } \right)}}{\partial \eta }N_{i,p} \left( \xi \right)W\left( {\xi ,\eta } \right) - \left( {\frac{{\partial W\left( {\xi ,\eta } \right)}}{\partial \eta }} \right)^{2} N_{i,p} \left( \xi \right)N_{j,q} \left( \eta \right)} \right)}}{{\left( {W\left( {\xi ,\eta } \right)} \right)^{3} }}\, ,$$

(A5)

$$\frac{{\partial R_{i,j}^{2p,q} \left( {\xi ,\eta } \right)}}{\partial \xi \partial \eta } = w_{i,j} \frac{{\frac{{\partial N_{i,p} \left( \xi \right)}}{\partial \xi }\frac{{\partial N_{j,q} \left( \eta \right)}}{\partial \eta }W\left( {\xi ,\eta } \right) + \frac{{\partial N_{i,p} \left( \xi \right)}}{\partial \xi }\frac{{\partial W\left( {\xi ,\eta } \right)}}{\partial \eta }N_{j,q} \left( \eta \right)}}{{\left( {W\left( {\xi ,\eta } \right)} \right)^{2} }} - w_{i,j} \frac{{\frac{{\partial^{2} W\left( {\xi ,\eta } \right)}}{\partial \xi \partial \eta }N_{i,p} \left( \xi \right)N_{j,q} \left( \eta \right) + \frac{{\partial W\left( {\xi ,\eta } \right)}}{\partial \xi }\frac{{\partial N_{j,q} \left( \eta \right)}}{\partial \eta }N_{i,p} \left( \xi \right)}}{{\left( {W\left( {\xi ,\eta } \right)} \right)^{2} }} - w_{i,j} \frac{{2\left( {\frac{{\partial N_{i,p} \left( \xi \right)}}{\partial \xi }\frac{{\partial W\left( {\xi ,\eta } \right)}}{\partial \eta }N_{j,q} \left( \eta \right)W\left( {\xi ,\eta } \right) - \frac{{\partial W\left( {\xi ,\eta } \right)}}{\partial \xi }\frac{{\partial W\left( {\xi ,\eta } \right)}}{\partial \eta }N_{i,p} \left( \xi \right)N_{j,q} \left( \eta \right)} \right)}}{{\left( {W\left( {\xi ,\eta } \right)} \right)^{3} }}\, ,$$

(A6)

with

$$\frac{{\partial^{2} W\left( {\xi ,\eta } \right)}}{{\partial \xi^{2} }} = \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\frac{{\partial^{2} N_{i,p} (\xi )}}{{\partial \xi^{2} }}N_{j,q} (\eta )w_{i,j} } }\, ,$$

(A7)

$$\frac{{\partial^{2} W\left( {\xi ,\eta } \right)}}{{\partial \eta^{2} }} = \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\frac{{\partial^{2} N_{j,q} (\eta )}}{{\partial \eta^{2} }}N_{i,p} (\xi )w_{i,j} } }\, ,$$

(A8)

$$\frac{{\partial^{2} W\left( {\xi ,\eta } \right)}}{\partial \xi \partial \eta } = \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\frac{{\partial N_{i,p} (\xi )}}{\partial \xi }\frac{{\partial N_{j,q} (\eta )}}{\partial \eta }w_{i,j} } }\, .$$

(A9)

Appendix B: discrete equations for bending, free vibration, and buckling

The displacements in the middle plane are approximated as

$${\mathbf{u}}^{m} = \sum\limits_{I = 1}^{NP} {R_{I} {\mathbf{u}}_{I} }$$

(B1)

with

$${\mathbf{u}}_{I} = \left[ {\begin{array}{*{20}c} {u_{I} } &\quad {v_{I} } &\quad {w_{bI} } &\quad {w_{sI} } \\ \end{array} } \right]^{T}\, ,$$

(B2)

where NP = (p+1)(q+1) is the number of control points per physical element, R_I and u_I denote the shape function and the unknown displacement vector at the control point I.

Substituting Eq. (15a) into both Eqs. (7) and (9), one can obtain

$${{\varvec{\upvarepsilon}}}_{0} = \sum\limits_{I = 1}^{{{\text{NP}}}} {{\mathbf{B}}_{I}^{0} } {\mathbf{u}}_{I} ,\;{{\varvec{\upvarepsilon}}}_{1} = \sum\limits_{I = 1}^{{{\text{NP}}}} {{\mathbf{B}}_{I}^{1} } {\mathbf{u}}_{I} ,\;{{\varvec{\upvarepsilon}}}_{2} = \sum\limits_{I = 1}^{{{\text{NP}}}} {{\mathbf{B}}_{I}^{2} } {\mathbf{u}}_{I} ,\;{{\varvec{\upvarepsilon}}}_{3} = \sum\limits_{I = 1}^{{{\text{NP}}}} {{\mathbf{B}}_{I}^{3} } {\mathbf{u}}_{I}\, ,$$

(B3)

$${{\varvec{\upchi}}}_{0} = \sum\limits_{I = 1}^{{{\text{NP}}}} {{\mathbf{B}}_{I}^{4} } {\mathbf{u}}_{I} ,\;{{\varvec{\upchi}}}_{1} = \sum\limits_{I = 1}^{{{\text{NP}}}} {{\mathbf{B}}_{I}^{5} } {\mathbf{u}}_{I} ,\;{{\varvec{\upchi}}}_{2} = \sum\limits_{I = 1}^{{{\text{NP}}}} {{\mathbf{B}}_{I}^{6} } {\mathbf{u}}_{I} ,\;{{\varvec{\upchi}}}_{3} = \sum\limits_{I = 1}^{{{\text{NP}}}} {{\mathbf{B}}_{I}^{7} } {\mathbf{u}}_{I}\, ,$$

(B4)

$${\mathbf{B}}_{I}^{0} = \left[ {\begin{array}{*{20}c} {R_{I,x} } & 0 & 0 & 0 \\ 0 & {R_{I,y} } & 0 & 0 \\ {R_{I,y} } & {R_{I,x} } & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right],\;{\mathbf{B}}_{I}^{1} = \left[ {\begin{array}{*{20}c} 0 & 0 & { - R_{I,xx} } & 0 \\ 0 & 0 & { - R_{I,yy} } & 0 \\ 0 & 0 & { - 2R_{I,xy} } & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]\, ,$$

(B5)

$${\mathbf{B}}_{I}^{2} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & { - R_{I,xx} } \\ 0 & 0 & 0 & { - R_{I,yy} } \\ 0 & 0 & 0 & { - 2R_{I,xy} } \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right],\;{\mathbf{B}}_{I}^{3} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {R_{I,x} } \\ 0 & 0 & 0 & {R_{I,y} } \\ \end{array} } \right]\, ,$$

(B6)

$${\mathbf{B}}_{I}^{4} = \left[ {\begin{array}{*{20}c} 0 & 0 & {R_{I,xy} } & 0 \\ 0 & 0 & { - R_{I,xy} } & 0 \\ 0 & 0 & {0.5\left( {R_{I,yy} - R_{I,xx} } \right)} & 0 \\ \end{array} } \right],\;{\mathbf{B}}_{I}^{5} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {R_{I,xy} } \\ 0 & 0 & 0 & { - R_{I,xy} } \\ 0 & 0 & 0 & {0.5\left( {R_{I,yy} - R_{I,xx} } \right)} \\ \end{array} } \right]\, ,$$

(B7)

$${\mathbf{B}}_{I}^{6} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {R_{I,y} } \\ 0 & 0 & 0 & { - R_{I,x} } \\ \end{array} } \right],\;{\mathbf{B}}_{I}^{7} = \left[ {\begin{array}{*{20}c} { - R_{I,xy} } & {R_{I,xx} } & 0 & 0 \\ { - R_{I,yy} } & {R_{I,xy} } & 0 & 0 \\ \end{array} } \right]\, .$$

(B8)

The strain energy of the OSC microplate is

$$\delta U = \int_{\Omega } {\left( {{{\varvec{\upsigma}}}^{{\text{T}}} \delta {{\varvec{\upvarepsilon}}} + {\mathbf{m}}^{{\text{T}}} \delta {{\varvec{\upchi}}}} \right){\text{d}}\Omega }\, .$$

(B9)

The virtual work done by external forces is

$$\delta W = - \int_{\Omega } {\left[ {q_{z} \delta \left( {w_{b} + w_{s} } \right) + N_{ij}^{0} \left( {w_{{b,x_{i} }} + w_{{s,x_{i} }} } \right)\left( {\delta w_{{b,x_{j} }} + \delta w_{{s,x_{j} }} } \right)} \right]{\text{d}}\Omega } \;\;\;\left( {i,j = 1,2} \right)\, ,$$

(B10)

where $N_{ij}^{0}$ and q_s are in-plane critical buckling load and applied transverse loading, x₁ and x₂ represent x and y, respectively.

The variation of the kinetic energy of the mass system is written as

$$\delta K = \int_{\Omega } {\left( {\delta u^{{\text{T}}} \overline{m}\ddot{u}} \right)d\Omega }\, .$$

(B11)

According to Hamilton’s principle, we have

$$0 = \int_{0}^{t} {\left( {\delta U + \delta W - \delta K} \right)} {\text{d}}t\, .$$

(B12)

Substituting Eqs. (B3)–(B11) into Eq. (B12), and applying the weak formulation [52], then we can obtain the weak form for static deformation, free vibration, and buckling.