1 Introduction

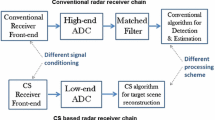
Modern radar is being developed with increasingly wide bandwidth and high resolution [1]. These systems generate large amounts of data, require more storage space, and necessitate a higher level of data processing [2]. According to the classic Nyquist sampling theorem, if undistorted reconstruction is performed on the signal, the sampling frequency of the system must be at least twice the highest frequency of the sampled signal; this is a challenge for real-time signal processing [3]. The proposed theory of compressed sensing (CS) [4, 5] addresses the traditional Nyquist problems [6]. This theory has been widely used in the field of radar signal processing

The radar target signal is sparse. According to the CS theory, when the signal is sparse or compressible, solving an optimization problem can accurately or approximately reconstruct the original signal from low-dimensional observation data [10]. Current signal reconstruction methods include the greedy algorithm [11, 12], orthogonal matching pursuit [13, 14], basis pursuit [4, 15], and other methods [16-18]. However, the process of signal reconstruction is difficult and involves complex iterative algorithms that increase the amount of data. Therefore, a new signal processing method based on compressive detection (CD) has attracted increasing attention [19,20,21,22,23,24].

Radar experiences interference from clutter in the process of detecting a target. A constant false alarm rate (CFAR) detector adaptively changes the detection threshold as the reference cell changes to achieve CFAR detection of targets [25]. Extensive radar target detection results have been achieved with CFAR [26,27,28]. In radar target recognition, sparse representation research focuses on extracting accurate target feature information from the received echo data [29]. Combining CS with traditional CFAR detection has been a research trend for target detection [30, 31]. In [30] and [31], the compressed signal is reconstructed first, and cell average CFAR (CA-CFAR) detection is then performed. However, the reconstruction of the signal requires a high signal-to-noise ratio (SNR). For the signal detection, it is necessary to determine only whether the target exists; it is not necessary to perform the detection after the signal is reconstructed [22, 32,33,34,35]. In [22, 32, 34], compressive detection algorithms based on traditional matched filter methods were proposed. For unknown parameter signal detection, providing all the signal information before detection is inefficient. Additionally, the compression matched filter is greatly affected by the SNR. An algorithm for detecting signals in the sub-space with a low SNR was proposed in [33]. The author determined the subspace with a smaller dimension according to the known sparse characteristics of signals, and then designed and determined the measurement matrix to complete the detection of signals according to the properties of the subspace matrix. However, the algorithm fails to detect unknown sparse signals. In [35], Bayesian CS is studied in detail for signal detection, which needs the prior probability information of the sparse signal. However, when the background distribution characteristics of clutter are relatively complicated, it is difficult to detect the target in the clutter background [28]. Therefore, based on the combination of CD and CFAR detection, in this paper, a support vector data description (SVDD) is used to further classify the signal, which can further reduce the amount of data and improve the detection accuracy [36].

In this paper, the signal is not reconstructed after compression and detection, and the sparseness of the target in the distance cell in the radar echo signal is used to design a deterministic measurement matrix. Then, CFAR detection is directly performed to complete the first-order classification of the signal. This method has better detection performance than the compressive matched filter (CMF) algorithm in [32]. Compared with the traditional matched filtering (MF) algorithm, the data storage space is reduced under the premise of ensuring the detection probability. To address the problem of false alarms after first-order CFAR processing, the SVDD one-class classifier is used to train and classify the characteristic signal to achieve target detection through extraction of the feature difference between the target and the false alarm signal in the power spectrum.

2 System model descriptions

2.1 CD model

From the theory of CS [4, 5], a discrete signal x of length \( \mathtt{L} \) can be represented by a linear combination of a set of bases \( \Psi \in \left[{\psi}_1,{\psi}_2,\cdots, {\psi}_{\mathtt{N}}\right] \)

$$ \mathtt{x}=\sum \limits_{i=1}^{\boldsymbol{N}}{\uptheta}_i{\uppsi}_i=\Psi \theta $$
(1)

in which θ ∈ RN × 1 is the sparse vector, θi = 〈x, ψi〉, \( x\in {R}^{\mathtt{L}\times 1} \) is the signal to be detected, and \( {\Psi}^{\mathtt{L}\times \mathtt{N}} \) is the sparse basis or sparse dictionary. If θ has only \( \mathtt{K}\left(\mathtt{K}=\mathtt{N}\right) \) nonzero elements, then θ is termed the \( \mathtt{K} \)-sparse representation of the signal x. \( \mathtt{K} \) is the sparsity of the signal.

When the signal x can be sparsely represented [22], the problem of CD can be expressed by the following mathematical model of hypothesis testing

$$ \left\{\begin{array}{l}{\mathtt{H}}_0:y=\Phi {s}_n\\ {}{\mathtt{H}}_1:y=\Phi \left(x+{s}_n\right)\end{array}\right. $$
(2)

in which \( \Phi \in {R}^{\mathtt{M}\times \mathtt{N}}\left(\mathtt{M}=\mathtt{N}\right) \) is the measurement matrix and sn is the Gaussian white noise. The hypothesis \( {\mathtt{H}}_0 \) is that the signal does not exist, and the hypothesis \( {\mathtt{H}}_1 \) is that the signal exists. Using Eq. (1), Eq. (2) can be rewritten as

$$ \left\{\begin{array}{l}{\mathtt{H}}_0:y=\Phi {s}_n\\ {}{\mathtt{H}}_1:y=\Phi \left(\Psi \theta +{s}_n\right)\end{array}\right. $$
(3)

2.2 Sparse representation model for radar signals

Assuming that the radar target contains a number \( \mathtt{K} \) of strong scattering centers located at different distance cells, the model of the pulse signal emitted sT(t) ∈ RL × 1 by the radar is

$$ {\boldsymbol{s}}_T(t)= rect\left(t/{T}_P\right)\exp \left(j2\pi {f}_0t+ j\pi {K}_r{t}^2\right) $$
(4)

The complex base-band echo signal received by the radar system xR(τ, t) can be described as

$$ {\displaystyle \begin{array}{c}{x}_{\mathtt{R}}\left(\tau, \mathtt{t}\right)=\sum \limits_{\mathtt{k}=1}^{\mathtt{K}}{\sigma}_{\mathtt{k}}\exp \left[-\mathtt{j}4\pi {\mathtt{f}}_0{\mathtt{r}}_{\mathtt{k}}\left(\tau \right)/\mathtt{c}\right]\\ {}\cdot \mathtt{rect}\left[\left(\mathtt{t}-2{\mathtt{r}}_{\mathtt{k}}\left(\tau \right)/\mathtt{c}\right)/{\mathtt{T}}_{\mathtt{P}}\right]\\ {}\cdot \exp \left\{\mathtt{j}\pi {\mathtt{K}}_{\mathtt{r}}{\left[\mathtt{t}-2{\mathtt{r}}_{\mathtt{k}}\left(\tau \right)/\mathtt{c}\right]}^2\right\}\\ {}+{\boldsymbol{s}}_{\mathtt{c}}\left(\mathtt{t}\right)+{\boldsymbol{s}}_{\mathtt{n}}\left(\mathtt{t}\right)\end{array}} $$
(5)

in which σk is the backscattering coefficient of the scattering point k; TP is the time width of the pulse signal; f0 is the center frequency of the signal; rk(τ) is the distance between the scattering point k and the radar platform at the moment of pulse emission; c is the speed of light; Kr is the frequency modulation coefficient; sc(t) is the clutter, which generally follows the Weibull distribution; and sn(t) is the Gaussian white noise [37].

With s0(t) = [rect(t/TP)/(TP|Kr|)] ⋅ exp(jπKrt2) substituted into Eq. (5), the following is obtained

$$ {\displaystyle \begin{array}{c}{\boldsymbol{x}}_R\left(\tau, t\right)=\sum \limits_{k=1}^K\left\{{\alpha}_k\left(\tau \right){\boldsymbol{s}}_0\left[t-2{r}_k\left(\tau \right)/c\right]\right\}\\ {}+{\boldsymbol{s}}_c(t)+{\boldsymbol{s}}_n(t)\\ {}={\boldsymbol{s}}_r(t)+{\boldsymbol{s}}_c(t)+{\boldsymbol{s}}_n(t)\end{array}} $$
(6)

in which \( {\alpha}_k\left(\tau \right)={T}_P\left|{K}_r\right|{\sigma}_{\mathtt{k}}\exp \left[-\mathtt{j}4\pi {\mathtt{f}}_0{\mathtt{r}}_{\mathtt{k}}\left(\tau \right)/\mathtt{c}\right] \).

For the entire radar scene, the position occupied by the target is very small and is sparse for the total scanning area. The distance resolution of the radar in the observation interval [r1, r2] is denoted Δr, and thus, the target scattering center in the distance cell can be represented by a one-dimensional vector θ

$$ {\theta}^{\mathrm{T}}=\left[{\mathtt{\theta}}_1,{\mathtt{\theta}}_2,\cdots, {\mathtt{\theta}}_{\mathtt{l}},\cdots, {\mathtt{\theta}}_{\mathtt{L}-1},{\mathtt{\theta}}_{\mathtt{L}}\right] $$
(7)

in which θl = σl exp[−j4πf0rl(τ)/c], σl is the backscattering coefficient of the scattering center of distance cell rl, rl = r1 + lΔr, l ∈ [1 : L], and L = 1 + (r2 − r1)/Δr. When there is no target in a certain distance cell k, θk = 0. Through the delay of s0(t), the sparse dictionary basis Ψ ∈ RL × N of the radar signal is constructed:

$$ {\displaystyle \begin{array}{c}{\psi}_i=\left[{s}_0\left({t}_i-2\frac{r_1}{c}\right)\right.{s}_0\left({t}_i-2\frac{r_1+\varDelta r}{c}\right)\\ {}\cdots {s}_0\left({t}_i-2\frac{r_1+ l\varDelta r}{c}\right)\\ {}\ {\left.\cdots {s}_0\left({t}_i-2\frac{r_2-\varDelta r}{c}\right){s}_0\left({t}_i-2\frac{r_2}{c}\right)\right]}^H\\ {}={\left[s\left({t}_i-{\uptau}_1\right)s\left({t}_i-{\uptau}_2\right)\cdots s\left({t}_i-{\uptau}_L\right)\right]}^H\end{array}} $$
(8)

Ψ = [ψ1, ψ2, ⋯, ψN], in which i = 1, 2, ⋯, N, and τi is the time delay corresponding to each distance cell. Given that the clutter and noise are not considered, according to Eqs. (1) and (8), the target scattering center can be sparsely expressed as

$$ {\theta}_r={\Psi}^{\mathrm{H}}{\boldsymbol{s}}_r(t) $$
(9)

2.3 Measurement matrix model

According to the theory of CS, with the complex base-band echo signal sr(t) and through the design of the measurement matrix, the signal after CD can be directly detected. Let the measurement matrix be

$$ \Phi ={\Phi}_1{\Psi}^{\mathrm{H}} $$
(10)

in which Φ1 ∈ RM × N, N/M = l, and l is an integer. Then, Φ1 is defined as

$$ {\displaystyle \begin{array}{c}{\Phi}_1=\left[\begin{array}{cccc}1& & & \\ {}& 1& & \\ {}& & \ddots & \\ {}& & & 1\end{array}\cdots \begin{array}{cccc}1& & & \\ {}& 1& & \\ {}& & \ddots & \\ {}& & & 1\end{array}\right]\\ {}=\left[\mathrm{eye}\left(M,M\right)\kern0.5em \cdots \kern0.5em \mathrm{eye}\left(M,M\right)\right]\end{array}} $$
(11)

According to Eq. (3), the following is obtained

$$ \left\{\begin{array}{l}{H}_0:\boldsymbol{y}={\Phi}_1{\Psi}^{\mathrm{H}}\left({\boldsymbol{s}}_c+{\boldsymbol{s}}_n\right)\\ {}{H}_1:\boldsymbol{y}={\Phi}_1{\Psi}^{\mathrm{H}}\left(\boldsymbol{x}+{\boldsymbol{s}}_c+{\boldsymbol{s}}_n\right)\end{array}\right. $$
(12)

Substituting Eq. (11) into Eq. (12), the signal expression of hypothesis H1 is obtained:

$$ {\displaystyle \begin{array}{c}\boldsymbol{y}={\Phi}_1{\Psi}^{\mathtt{H}}\left(\boldsymbol{x}+{\boldsymbol{s}}_c+{\boldsymbol{s}}_n\right)\\ {}={\Phi}_1\left({\theta}_r+\boldsymbol{D}\right)\\ {}=\left[\mathtt{eye}\left(M,M\right)\kern0.5em \cdots \kern0.5em \mathtt{eye}\left(M,M\right)\right]\\ {}\cdot \left\{\left[\begin{array}{c}0\\ {}\vdots \\ {}{\upsigma}_1^2\\ {}\vdots \\ {}0\\ {}{\upsigma}_L^2\\ {}\vdots \\ {}0\end{array}\right]+\left[\begin{array}{c}\boldsymbol{D}(1)\\ {}\boldsymbol{D}(2)\\ {}\\ {}\vdots \\ {}\\ {}\boldsymbol{D}\left(N-1\right)\\ {}\boldsymbol{D}(N)\end{array}\right]\right\}\end{array}} $$
(13)

Therefore, D = ΨH(sc + sn). Since the radar target signal x is sparse, Eq. (13) shows that \( {\sigma}_1^2,\cdots, {\sigma}_L^2 \) are L targets’ projections on the dictionary basis. When the i-th line (1 ≤ i ≤ L) element 1 of Φ1 is multiplied by \( {\sigma}_i^2 \) and D, the results are all 0 except D multiplied by the i-th element 1 of Φ1. Good noise reduction performance is thus achieved. The noise reduction performance increases with increasing M. Through the CD of the echo signal, the sampling rate is reduced. Additionally, a storage space savings of 1/l is achieved, and the direct detection of the compressed signal is realized without reconstruction.

2.4 SVDD model

Currently, the classifier is divided into a one-class classifier and a multiclass classifier according to the number of categories of training samples [38]. The multiclass classifiers are used mainly for classification problems where the training samples are sufficient and the data of different categories are relatively balanced. Different types of training samples are needed to construct the classification function, and the sample classification is achieved by determining the optimization points between different categories. A one-class classifier is mainly used in scenarios where multiple types of training samples cannot be obtained or are too expensive to obtain. This classifier needs a training sample from only one target category. The training sample of this category is used to construct a closed cover. The unknown test sample is determined as a target or non-target. An SVDD is often used in the field of abnormal data detection and is a very typical classifier. In the training phase, training samples from only one type of target are needed to obtain the optimal classification surface [36]. Assuming that the radius of the hypersphere found in the high-dimensional feature space is Rϕ and that the sphere center vector of the hypersphere is aϕ , the expression for any point on the hypersphere ϕ(xi) is \( {\left\Vert \phi \left({x}_i\right)-{a}_{\phi}\right\Vert}^2={R}_{\phi}^2 \). Therefore, the solution process for the optimal classification surface of the SVDD can be expressed as

$$ \left\{\begin{array}{l}\min\;{\mathtt{R}}_{\phi}^2+\mathtt{C}\sum \limits_{\mathtt{i}=1}^l{\xi}_i\\ {}s.t.{\left\Vert \phi \left({x}_i\right)-{a}_{\phi}\right\Vert}^2\le {\mathtt{R}}_{\phi}^2+{\xi}_i,{\xi}_i\ge 0,i=1,2,\cdots, l\end{array}\right. $$
(14)

in which l is the number of sample points, C is the penalty coefficient, and ξi is the Lagrange multiplier corresponding to the i-th sample. With the Lagrange multiplier method, we can obtain the dual optimization problem

$$ \left\{\begin{array}{l}\max \sum \limits_{i=1}^l{\beta}_i\mathtt{K}\left({\mathtt{x}}_i,{\mathtt{x}}_j\right)\hbox{-} \sum \limits_{i=1}^l\sum \limits_{j=1}^l{\beta}_i{\beta}_j\mathtt{K}\left({\mathtt{x}}_{\mathtt{i}},{\mathtt{x}}_{\mathtt{j}}\right)\\ {}s.t.\sum \limits_{i=1}^l{\beta}_i=1,{\beta}_i\in \left[0,C\right],i=1,2,\cdots, l\end{array}\right. $$
(15)

in which the kernel function K(xi, xj) = ϕT(xi)ϕ(xi) and βi is the Lagrange multiplier. In the process of solving the dual optimization problem, the expression of the sphere center vector of the hypersphere is obtained:

$$ {a}_{\phi }=\sum \limits_{i=1}^l{\beta}_i\phi \left({x}_i\right) $$
(16)

With the Lagrange multiplier and any support vector on the hypersphere ϕ(x), the radius of the hypersphere can be obtained:

$$ {\displaystyle \begin{array}{c}{R}_{\phi }=K\left(x,x\right)-2\sum \limits_{i=1}^l{\beta}_iK\left({x}_i,x\right)\\ {}+\sum \limits_{i=1}^l\sum \limits_{j=1}^l{\beta}_i{\beta}_jK\left({x}_i,{x}_j\right)\end{array}} $$
(17)

Any sample point x becomes ϕ(x) after being mapped to the high-dimensional feature space, and the decision-making method is

$$ {f}_{\phi }(x)={\left\Vert \phi (x)-{a}_{\phi}\right\Vert}^2-{R}_{\phi}^2 $$
(18)

When fϕ(x) ≤ 0, x is the target sample. Otherwise, x is an abnormal sample.

3 Two-stage classification algorithm

3.1 Algorithm flow

The traditional CFAR detectors mainly include CA-CFAR, ordered statistic CFAR (OS-CFAR), etc. [39] CA-CFAR, which is the most widely used CFAR detection algorithm, detects whether or not the signal exists by comparing the arithmetic mean values of the measured cell and several adjacent reference cells. OS-CFAR sorts the data in the reference cell, then selects the value of the k-th element as an estimate of cell’s the clutter level and multiplies this value by a scale factor T as the detection threshold to detect whether or not the signal exists. In addition, we still need to establish how to set the detection threshold, which references [25, 39] show how to do. In the CA-CFAR detector, the estimate of the background clutter power level is the sum of 2n reference cells.

$$ Z=\sum \limits_{i=1}^{2n}{\boldsymbol{y}}_i $$
(19)

The CFAR condition can be obtained by multiplying the scale factor T by the estimated background level. The detection probability of the CA-CFAR detector is

$$ {P}_d={\left(1+\frac{T}{1+S}\right)}^{-2n} $$
(20)

Here, T is a scale factor, and S is the average SNR. In the OS-CFAR detector, the 2n reference cell signals are sorted by amplitude (y1 ≤ y2 ≤ ⋯ ≤ yk ≤ ⋯ ≤ y2n); the k-th value is taken as the background noise estimate:

$$ Z={\boldsymbol{y}}_k $$
(21)

The detection probability of OS-CFAR can be expressed as

$$ {P}_d=\prod \limits_{i=0}^{k-1}\frac{2n-i}{2n-i+T/\left(1+S\right)} $$
(22)

The CFAR models used in this algorithm are CA-CFAR and OS-CFAR, and the classifier is the SVDD one-class classifier. Figure 1 shows the detection scheme of the two-stage classification algorithm. The overall algorithm is divided into two stages.

Fig. 1
figure 1

Detection scheme of the two-stage classification algorithm

Full size image

The first stage of classification:

  • Step 1: Design the sparse dictionary basis according to the complex base-band echo signal, and then design the measurement matrix Φ = Φ1ΨH with Eq. (10);

  • Step 2: Compress and detect the echo signal by the measurement matrix of Eq. (10) to obtain Eq. (12) y;

  • Step 3: Send the CD signal y to the CFAR detector, and perform CA-CFAR or OS-CFAR processing on the 2n data except for the measured cell to obtain the result Z. If the signal is greater than the threshold (Y > TZ), the state is H1, namely, the target exists; otherwise, the state is H0, and the target does not exist.

The second stage of classification (divided into training section and test section):

  • Step 4: Take the non-target signal (H0) in the first stage as the training data, extract the power spectrum feature of each group of training samples to form a feature vector, and form the feature vector matrix using the feature vectors of all training samples. Then, train the SVDD classifier;

  • Step 5: Use the target or false alarm echo data (H1) in the first stage as the test data, then extract the power spectrum feature for each set of test samples, send the feature vector to the trained SVDD classifier, and complete the target detection.

Through the two-stage classification algorithm for radar targets, after the radar echo signal is compressed and detected in the first stage after the CFAR processing, the signal is divided into background clutter and target signals (including false alarm signals). In the second stage, the power spectrum feature is used to perform SVDD classification and to achieve classification of the target signals and false alarm signals.

3.2 Power spectrum feature extraction

For radar echo signals, the power spectrum of the signal can be obtained by using the fast Fourier transform. In the SVDD classifier, the power spectrum of the radar echo signal is extracted as a feature vector for target algorithm classification. Since the power spectrum is high-dimensional data, extensive calculations will be needed if the power spectrum is directly used as a feature vector. Therefore, in this paper, dimensionality reduction is performed on the power spectrum feature vector, and the two-dimensional features are extracted; that is, the second-order central moment of the power spectrum and the power spectrum entropy are used to describe the dispersion characteristics of the power spectrum, which is used as a feature vector. Let the radar echo signal be x = [x1, x2, ⋯, xK]. Then, the frequency spectrum is F = FFT(x) = [F1, F2, ⋯, FK]T, and the power spectrum is p = |F|2 = [p1, p2, ⋯, pK]T, where K is the dimension of the signal.

Feature 1: The second-order central moment of the power spectrum is

$$ {\mathrm{S}}_1=\sum \limits_{k=1}^K{\left(k-\tilde{k}\right)}^2{b}_k $$
(23)

in which \( {b}_k={p}_k/{\sum}_{k=1}^K{x}_k \) and \( \tilde{k}={\sum}_{k=1}^Kk\times {b}_k \). In the random process, the second-order central moment describes the distribution of the power spectrum energy distribution relative to its geometric centroid. If the second-order central moment is smaller, the energy distribution is more scattered relative to the centroid.

Feature 2: The power spectrum entropy is

$$ {\mathrm{S}}_2=-\sum \limits_{k=1}^K{b}_k\lg \left({b}_k\right) $$
(24)

The power spectrum entropy is used to describe the energy distribution characteristics of the power spectrum. The more concentrated the power spectrum energy distribution is, the lower the entropy.

4 Experiment results and discussion

4.1 First-order target classification experiment

In this section, simulation experiments are conducted on two kinds of radar echo in 15 km scenarios (a single-target radar echo scenario and a multi-target radar echo scenario) and compared with the performance of the traditional MF and CMF [32] detection algorithms to evaluate the detection performance of the proposed algorithm. In all the simulations, the radar echo signal is

$$ {\boldsymbol{s}}_r(t)=\sum \limits_{i=1}^m\exp \left( j\pi {\mathtt{K}}_r{\left(t-{\tau}_i\right)}^2\right)+{\boldsymbol{s}}_c(t)+{\boldsymbol{s}}_n(t) $$
(25)

in which m is the number of targets, τi is the time delay of the i-th target, sc(t) is the Weibull background clutter, and sn(t) is the Gaussian white noise.

In Experiment 1, the minimum detection distance of the radar was Rmin = 5000 m, the maximum detection distance was Rmax = 15000 m, the pulse width was B = 30 MHz, the frequency modulation slope was Kr = B/T = 3 × 1012 Hz/s, the sampling frequency was fs = 150 MHz, and a single target location was set at R = 9000 m. In Experiment 2, four target positions were set at R = [6000 6500 7000 8000] m, and the sparse dictionary base Ψ is designed based on Eq. (8). Fig. 2 is the detection effect of the algorithm on the direct CD of CFAR for a single-target radar echo signal. Fig. 3 represents the detection effect of the algorithm on the direct CD of CFAR for multi-target radar echo signals. Fig. 4 compares the performances of the algorithm in this paper, the traditional MF detection algorithm, and the CMF algorithm [32]. Fig. 5 compares the detection performances of the three detection algorithms in CA-CFAR and OS-CFAR. The variation curve of the detection probability with the SNR ratio and different compressive ratios over 1,000 Monte Carlo experiments is depicted in Fig. 6.

Fig. 2
figure 2

Comparison between single target radar echo signal CD and CFAR detection threshold

Full size image
Fig. 3
figure 3

Comparison between multi-target radar echo signal CD and CFAR detection threshold

Full size image
Fig. 4
figure 4

Comparison of the detection performance of the three detection algorithms

Full size image
Fig. 5
figure 5

Comparison of the detection performance of the three detection algorithms in CA-CFAR and OS-CFAR

Full size image
Fig. 6
figure 6

CFAR detection probability under different compressive ratios

Full size image

Figure 2 compares the CD signal and the CFAR detection threshold for SNR =  − 10 dB, a signal-to-clutter ratio SCR =  − 10 dB, M/N = 0.5. For a low SNR, the direct compression and detection of the signal can still clearly determine the target position without reconstruction of the signal.

Figure 3 compares the multi-target CD signal and the CFAR detection threshold for SNR =  − 10 dB, SCR =  − 10 dB, and M/N = 0.5. With four targets, in the case of a low SNR and a low SCR, the first-order classification of the target can be completed through CFAR detection.

Figure 4 compares the detection performances of the algorithm in this paper, the traditional MF algorithm and the CMF algorithm. Under the same compressive ratio, the detection performance of the algorithm in this paper is significantly better than that of the CMF algorithm (Fig. 4). When SNR =  − 15 dB, the detection probability of the algorithm in this paper reaches 96%; this detection performance is close to that of the traditional MF algorithm, while its data storage requirement is reduced by half.

Figure 5 illustrates a comparison of the detection performance of the three detection algorithms in CA-CFAR and OS-CFAR, where SCR =  − 10 dB, M/N = 0.5, and the false alarm probability Pf = 10−3. With the same false alarm probability, the detection performance of CA-CFAR and OS-CFAR is similar. Additionally, the algorithm in this paper reduces the data calculations to half of those of the traditional MF algorithm.

Figure 6 gives the detection probabilities for different compressive ratios with the SNR when SCR =  − 10 dB and the false alarm probability Pf = 10−3. Under the same SNR, the detection probability of the signal increases as the compressive ratio increases. When the SNR =  − 12 dB and M/N = 0.25, the target detection probability reaches 95%.

4.2 Two-stage target classification experiment

Since radar targets are usually non-cooperative, there are usually no target training samples or false alarm signals available in advance, and only targets such as background clutter are used as training samples. Therefore, the SVDD one-class classifier is selected to classify the targets. In this section, the first-stage target after CD of CFAR is further classified by the SVDD one-class classifier to differentiate targets and false alarm signals. For the second-stage classification experiment, the signal is set as x = [x1, x2, ⋯, xK], the signal dimension K = 200, and the power spectrum features of the signal are extracted. Figures 7(a) and 7(b) show the average power spectra (APS) of the background clutter, false alarm signals, and target signals in the first-stage target classification experiment.

Fig. 7
figure 7

APS of the background clutter, the false alarm signal, and the target signal. a Power spectrum of single target scene. b Power spectrum of multi-target scene

Full size image

The target signal exhibits obvious feature differences from the background clutter and false alarm signal in the power spectrum domain (Fig. 7). The overall distribution trends of the power spectra of the three signals show that the shape of the power spectrum curve of the target signal changes relatively smoothly. However, the power spectrum curves of the false alarm signal and the background clutter change more quickly, and their distribution characteristics are very similar and consistent, which is obviously different from that of the target signal. The power spectrum of the target signals in Fig. 7 is more even than its centroid distribution, and the second-order central moment of its power spectrum is larger than the second-order central moments of the false alarm signals and background clutter. From an energy perspective, the power spectrum energy distribution of the target signals is more even and its entropy is greater than those of the false alarm signals and background clutter.

For a given training set that contains n target samples, X = {x1, x2, ⋯, xn}, the goal of SVDD is to find a hypersphere with the smallest volume in a high-dimensional space so that all target samples or as many as possible are enclosed in the hypersphere instead of the scenario where the target sample is as small as possible or none of the target samples are in the hypersphere. In this experiment, according to the SVDD model, the Gaussian kernel function is selected. After the feature vector of the background clutter is selected as the training data, the SVDD one-class classifier is trained to obtain the optimal classification surface. Figures 8(a) and 8(b) show the results of using the SVDD optimal classification to classify the test sample during the test phase. In addition to the background clutter in the training sample, false alarm signals are present in the test sample that are determined to be background clutter inside the classification surface. The test samples outside the classification surface are determined to be the target signals.

Fig. 8
figure 8

Two-dimensional feature classification results for the power spectrum. a Single target scene features. b Multi-target scene features

Full size image

The SVDD experiment results show that the target signals are all outside the optimal classification surface and that the classification results are correct (Fig. 8). All of the false alarm signals are included inside the optimal classification surface and are determined to be background clutter. In single-target and multi-target scenarios, the proposed algorithm can effectively reduce the number of false alarms and increase the probability of signal detection. In the radar target detection process, false alarms usually increase the detection workload, but a missed alarm can cause a serious accident. The algorithm in this paper has good adaptability to such situations. The amount of data storage is reduced, and the number of false alarms can be effectively lowered.

5 Conclusions

In this paper, the CD CFAR is used and combined with an SVDD classifier to form a two-stage classification algorithm for radar target detection. In the distance domain, through the design of the measurement matrix, the radar echo signal is directly compressed and detected without reconstruction of the signal, and the first-stage classification of the radar echo signal is then completed through the CFAR detection structure. To separate false alarm signals and target signals after the first stage of classification, the SVDD is introduced as the second stage of classification. Features of the signal power spectrum are extracted after compression and detection of CFAR, and the SVDD one-class classifier is used in the feature domain. The background clutter is used as training data to complete the classification of false alarm signals and target signals. The analysis of the experimental results shows that the algorithm in this paper can still detect the target position under the conditions of a low SNR and a low SCR. Additionally, under the premise of ensuring a high detection probability, the necessary data storage space is reduced. The detection performance is improved, the number of false alarms is effectively lowered, and good adaptability is maintained.