Abstract
The TLS 1.3 0-RTT mode enables a client reconnecting to a server to send encrypted application-layer data in “0-RTT” (“zero round-trip time”), without the need for a prior interactive handshake. This fundamentally requires the server to reconstruct the previous session’s encryption secrets upon receipt of the client’s first message. The standard techniques to achieve this are session caches or, alternatively, session tickets. The former provides forward security and resistance against replay attacks, but requires a large amount of server-side storage. The latter requires negligible storage, but provides no forward security and is known to be vulnerable to replay attacks. In this paper, we first formally define session resumption protocols as an abstract perspective on mechanisms like session caches and session tickets. We give a new generic construction that provably provides forward security and replay resilience, based on puncturable pseudorandom functions (PPRFs). We show that our construction can immediately be used in TLS 1.3 0-RTT and deployed unilaterally by servers, without requiring any changes to clients or the protocol. To this end, we present a generic composition of our new construction with TLS 1.3 and prove its security. This yields the first construction that achieves forward security for all messages, including the 0-RTT data. We then describe two new constructions of PPRFs, which are particularly suitable for use for forward-secure and replay-resilient session resumption in TLS 1.3. The first construction is based on the strong RSA assumption. Compared to standard session caches, for “128-bit security” it reduces the required server storage by a factor of almost 20, when instantiated in a way such that key derivation and puncturing together are cheaper on average than one full exponentiation in an RSA group. Hence, a 1 GB session cache can be replaced with only about 51 MBs of storage, which significantly reduces the amount of secure memory required. For larger security parameters or in exchange for more expensive computations, even larger storage reductions are achieved. The second construction combines a standard binary tree PPRF with a new “domain extension” technique. For a reasonable choice of parameters, this reduces the required storage by a factor of up to 5 compared to a standard session cache. It employs only symmetric cryptography, is suitable for high-traffic scenarios, and can serve thousands of tickets per second.
Similar content being viewed by others
1 Introduction
0-RTT Protocols A major innovation of TLS 1.3 [51] is its 0-RTT (zero round-trip time) mode, which enables the resumption of sessions with minimal latency and without the need for an interactive handshake. A 0-RTT protocol allows the establishment of a secure connection in “one-shot”, that is, with a single message sent from a client to a server, such that cryptographically protected payload data can be sent immediately (“in 0-RTT”) along with the key establishment message, without the need for a latency-incurring prior handshake protocol. This significant speedup of connection establishment yields a smoother Web browsing experience and, more generally, better performance for applications with low-latency requirements. This is particularly noticeable in networks with relatively high latency, such as mobile networks.
The huge practical demand for 0-RTT is exemplified by the fact that many large Internet companies have developed and experimented with such protocols in the recent past, for example Google’s QUIC [16] and Facebook’s Zero [35] protocols. The content distribution provider Cloudflare has deployed the 0-RTT mode of TLS 1.3 as early as March 2017 at large scale, long before the finalization of the standard [57]. Google and Facebook declared that the cryptography in QUIC and Zero will soon be replaced by TLS 1.3 0-RTT [5, 35].
The TLS 1.3 0-RTT Handshake A full TLS 1.3 handshake (not 0-RTT) is always used in the very first connection between a client and a server. If the server supports 0-RTT, then both the client and server can derive a resumption secret from their shared key and session parameters. The client will simply store this secret. Naturally, the server then needs to retrieve the resumption secret during a subsequent handshake. There are two standard approaches for this, session caches and session tickets, which have different advantages and drawbacks. During the first handshake, the server sends to the client either a lookup key pointing to an entry in the session cache of the server, or a session ticket—depending on the configuration of the server. These approaches essentially work as follows:
- Session caches::
-
The server stores all resumption secrets of recent sessions in a local database and issues each client a unique lookup key. When a client reconnects, it includes that lookup key in its 0-RTT messages, enabling the server to retrieve and use the matching resumption secret.
- Session tickets::
-
The server uses a long-term symmetric encryption key, called the session ticket encryption key (STEK). Instead of storing the resumption secret in a local database, the server encrypts it with the STEK to create a session ticket. The session ticket is stored by the client. When a client reconnects, it includes that session ticket in its 0-RTT messages, which enables the server to decrypt it and recover the resumption secret. Note that the same STEK is used for many sessions and clients.
On a subsequent 0-RTT handshake, the client will include in its first message either the lookup key or the encrypted session ticket, in addition to a Diffie–Hellman key exchange message. The client can also send, in the same message, encrypted application-layer data, termed 0-RTT data. This data will be encrypted with a key derived from the resumption secret and a public client random value, without any input from the server.
In its reply, the server will typically include a Diffie–Hellman key exchange message, and further messages (in either direction) will be encrypted with a key derived also from the DH secret, not only the resumption secret. Hence, the only data protected by the resumption secret alone is the 0-RTT data. We note that the use of DH is not mandatory, and it is possible to rely only on the resumption secret for the security of the entire session; we expect most traffic will use DH as described above.
We stress that the use of session caches or session tickets is opaque to clients. That is, in either case the server sends a NewSessionTicket message containing an opaque sequence of bytes, which may be either a lookup key for the session cache, or an encrypted session ticket, without specifying which is the case. This property ensures that our proposed techniques are compatible with the final TLS 1.3 standard [51] and can be implemented on the server-side without requiring modifications to the protocol or to clients.
Confusingly, the message containing this opaque sequence of bytes is always termed a “NewSessionTicket message”, for both session caches and encrypted self-contained session tickets. To our knowledge there is no standard nomenclature, in [51] or elsewhere, for these two different approaches when used in TLS 1.3; see e.g. [51, §8.1]. TLS 1.2 referred to “Session ID Resumption" and “Session Ticket Resumption", but these terms are not used in TLS 1.3.
Forward Security and Replay Resilience of 0-RTT Protocols Forward security essentially means that the protocol provides security of sessions, even if an attacker is able to corrupt one party after the session has terminated (e.g., by breaking into a Web server and learning the long-term secret key). Resilience to replay attacks is a fundamental, classical design goal of cryptographic protocols, which prevents an attacker from replaying the same payload data to a server repeatedly.
Both forward security and replay resilience are standard design goals of modern security protocols. However, achieving these properties is well-known to be difficult for 0-RTT protocols. This is because classical (“non-0-RTT”) protocols include fresh input from the server (e.g., a Diffie–Hellman message) generated using ephemeral randomness, which provides a leverage to achieve forward security. However, there is no such interactivity in 0-RTT protocols. Furthermore, an attacker is able to replay the 0-RTT key establishment message along with the 0-RTT payload data over and over again to a server, which is not detectable without additional server-side countermeasures.
For a more general treatment of the notion of “forward security” and “forward secrecy” in non-interactive contexts (such as 0-RTT protocols or instant messaging), we refer to a work by Boyd and Gellert [13].
Forward Security and Replay Resilience of TLS 1.3 0-RTT With session caches the server stores a “unique” resumption secret in a local database for each client. In most cases, it is able to delete the resumption secret immediately after retrieving it. This provides forward security, as an attacker obtaining the server state cannot decrypt past sessions. It also provides resilience against replay attacks, as the server is not able to decrypt replayed messages.
If session tickets are used, then an attacker that obtains access to the server can learn the STEK, and thus decrypt all tickets encrypted with this key to learn the resumption keys. Hence, servers using session tickets do not provide forward security. They are also generally vulnerable to replay attacks, as explained below. Since an attacker learning the STEK has catastrophic implications for security, large server operators usually rotate the STEK. Such deployments typically generate a new STEK roughly once per hour, and limit the STEK lifetime to roughly a day [46]. An attacker that learns one STEK can therefore decrypt approximately one hour’s worth of traffic. However, most current TLS implementations do not provide out-of-the-box support for STEK rotation, and this (welcome) defensive measure is usually limited to large operators who can afford to modify TLS implementations [43, 46]. Long-lived STEKs are unfortunately prevalent, and even among high-profile websites, some reuse the same STEK for many weeks, or even for many months [56].
STEK-based deployments are also generally vulnerable to replay attacks. When using resumption, the client must include in its first message the ticket’s age, i.e. the time elapsed between receiving the ticket from the server in a previous session. The server expects this time interval to be precise up to a small window of error allowing for propagation delay, typically on the order of 10 seconds. An attacker can perform replay attacks within this time window (unless there is additional server-side logging of tickets that have already been used, which is rare).
To summarize, session caches are generally forward-secure and replay-resistant, while session tickets are not. Naïvely, it would therefore appear that session caches are the superior solution. However, session caches require the server to store the session state for each (recent) connection. This is often infeasible, in particular for high-traffic server operators. Such server operators often reluctantly use session tickets, knowingly forgoing forward secrecy. Additionally, even if forward security is not prioritized by a particular server operator and thus session tickets are used, the prevention of replay attacks may still require additional storage at the server, since the only way to prevent replay attacks in this case is to log used tickets.
In this context it is sometimes claimed that so-called idempotent requests, that is, requests that have the same effect on the server state whether they are served once or several times, are safe to use with TLS 1.3 0-RTT. However, it is well-known [48] and also discussed in the TLS 1.3 specification [51] that even replays of idempotent requests may give rise to attacks that, e.g., reveal the target URL of HTTP requests. See Appendix A for an example.
All of these issues are well-known to apply to TLS 1.3 0-RTT and have raised significant concerns about its secure deployability in practice [48]. Eric Rescorla, the main author of the TLS 1.3 RFC draft, acknowledges that this poses a “difficult application integration issue” [50]. However, due to the huge practical demand, 0-RTT is also considered “too big a win not to do” [50]. At EUROCRYPT 2017 [33] and 2018 [19, 20], the first 0-RTT protocols that simultaneously achieve forward security and replay resilience were proposed, but these require relatively heavy cryptographic machinery, such as hierarchical or broadcast identity-based encryption, and thus are not yet suitable for large-scale deployment in TLS 1.3.
Our Contributions We give the first formal definition for secure 0-RTT session resumption protocols, as an abstraction of the constructions currently used in practice in TLS 1.3. We propose new techniques to achieve forward security and replay resilience that are ready-to-use with TLS 1.3 as it is standardized, without any changes to the protocol. Our proposal is based on session tickets, and thus requires minimal storage at the server side, but we extend this approach with efficient puncturable pseudorandom functions (PPRFs) that enable us to achieve forward security and replay resilience for session tickets. We provide new constructions of PPRFs with short keys and formal security proofs based on standard hardness assumptions. We propose two variants:
-
1.
The first variant is based on the strong RSA assumption. It reduces the server storage by a factor of at least 11 compared to a session cache, increases ticket size by a negligible length, and requires the server to perform two exponentiations (one per issuance and one per resumption).
-
2.
The second variant reduces server storage by a factor of up to 5 compared to a session cache, while using tickets that are roughly 400 bytes longer than standard tickets. It extends a standard GGM-style [30] binary tree-based PPRF, as described in [12, 14, 38], with a new domain extension idea. It employs only symmetric cryptography, is suitable for very-high-traffic scenarios, and can serve thousands of tickets per second, at the cost of hundreds of megabytes in server storage.
Our Approach At the base of our approach is the concept of puncturing a pseudorandom function (PRF) to obtain a puncturable symmetric-key encryption scheme. Puncturable PRFs are a special case of constrained PRFs [12, 14, 38], which make it possible to derive constrained keys that allow computation of PRF output only for certain inputs.
In our approach, a server initially maintains a STEK k that allows decryption of any session ticket; when receiving ticket t, the server uses k to decrypt t in order to recover the resumption secret. Using the puncturing feature of the PPRF, it then derives from k a new key, \(k'\), that can decrypt any ticket except for t. The server then discards k and stores only \(k'\). It repeats this process for every ticket received. This yields forward secrecy and replay-resistance: an attacker that compromises the server learns a key that is not capable of decrypting past tickets. Similarly, an attacker cannot successfully replay a message, since the server is only able to decrypt each ticket once.
The naïve way to employ this approach in TLS 1.3 0-RTT would be to use public-key puncturable encryption, as in [19, 20, 33]. However, this approach results in impractically long puncturing times or very long secret keys. Moreover, the most practical constructions require relatively expensive pairing-based cryptography by both the client and the server, thereby obviating the efficiency benefit of TLS 1.3 0-RTT. To be precise, since the puncturing times are in the order of hundreds of milliseconds, they introduce additional latency that is larger/comparable to the additional RTT they save. Rather than using public-key puncturable encryption, we observe that in TLS 1.3 0-RTT, the server itself generates the tickets it would later need to decrypt. It therefore suffices to use symmetric cryptography, and to maintain a key that allows decryption of only a limited set of ciphertexts, generated by the server itself. To achieve this, we use PPRFs to derive keys for standard TLS 1.3 tickets. Concretely, we describe two new PPRF constructions that are particularly suitable for our application:
-
The first builds a new PPRF from the Strong RSA Assumption. The PPRF has a polynomially-bounded input size, but this is sufficient for our application (and probably for certain other PPRF applications as well). Its main distinguishing feature is that its secret key size is independent of the number of puncturings. It consists of an RSA modulus N, a number \(g \in {\mathbb {Z}} _N\), and a bitfield, indicating positions where the PPRF was punctured. Due to the short secret key, our construction may find other applications in applied and theoretical cryptography. Since our primary objective is to provide an as-efficient-as-possible solution for practical protocols such as TLS 1.3 0-RTT, we describe a construction with security proof in the random oracle model [7]. It seems likely that our construction can be lifted to the standard model in a straightforward way, via standard techniques like hardcore predicates [8, 10, 31], but this would yield less efficient constructions and is therefore outside the scope of this paper.
-
The second construction is based on a standard tree-based PPRF [12, 14, 38], instantiated with a cryptographic hash function, such as SHA-3.
The size of punctured keys depends linearly on the depth of the tree, which in turn depends on the size of the domain of the PPRF. We describe a new domain extension technique that reduces the size of punctured keys by trading secret key size for ticket size, while preserving the puncturing functionality. Domain extension makes it possible to use a PPRF with a smaller domain (and thus smaller punctured keys). To save a factor of up to n in server-side storage, the ticket size rises roughly as \((n-1)!\). Thus, this is only useful for small values of n, but choosing e.g. \(n=5\) can yield significant savings with a modest increase in ticket size on the wire. Concretely, for \(n=5\) and “128-bit security”, ticket size is increased by 384 bytes. As discussed in Sect. 7.1, experiments done by Google estimate that this will impose only a small impact on latency [44].
Integration in TLS 1.3 We show how to generically integrate any 0-RTT session resumption protocol in the TLS 1.3 resumption handshake. In particular, we can show that the security of the 0-RTT session resumption protocol allows achieving forward secrecy for all messages (including the 0-RTT data) of the resumption handshake without modifications to any client implementations. This yields the first variant of the TLS 1.3 resumption handshake with full forward secrecy, whereas current implementations are unable to provide this for the client’s first flight of messages.
We note that our protocol is incompatible with ticket re-use. That is, a client reusing tickets may undesirably fail to resume its session, which is unavoidable if the server wants to provide forward secrecy for 0-RTT data. As forward secrecy of 0-RTT data is desirable, we hope that client implementations will not reuse tickets when sending 0-RTT data, minimizing failed session resumption attempts. We note that the TLS 1.3 standard explicitly discourages, but does not outright forbid, ticket reuse by clients [51, §C.4].
The security of the new TLS 1.3 resumption handshake variant is proven in the multi-stage key exchange model by Fischlin and Günther [27, 28]. Their model was used in several proofs of key exchange protocols with similar levels of complexity, such as Google’s QUIC protocol [27], and several drafts and handshake modes of the TLS 1.3 protocol [23, 24, 28]. We adopt and extend the proof of the TLS 1.3 draft-14 resumption handshake in [28]. Namely, we model the TLS 1.3 resumption handshake in its finalized version, which follows a different key derivation schedule as considered in previous works, and generically integrate a 0-RTT session resumption protocol to immediately achieve forward secrecy.
Large-Scale Server Clusters and Load Balancing Large TLS server deployments typically consist of many servers that share the same public key. This complicates any logic that relies on the server storing some state, since these servers will typically not share a globally-consistent state. Such discussion is beyond the scope of this paper, and we will assume a single server with consistent storage throughout. When many servers share a session cache, the cache is likely to be distributed, and any logic relying on an atomic retrieve-and-delete operation becomes more complex. Therefore, distributed session caches are not necessarily replay-resistant nor forward-secure, as this requires synchronous deletion of resumption secrets at all servers, and thus synchronized state. When using session tickets, the same holds for mechanisms that store used tickets, which are likely to be distributed as well. See [51, §2.3, §8, §E.5], [48, 49] for more in-depth discussion. However, in large-scale settings it is highly desirable to minimize the amount of memory that must be consistently synchronized across different servers. Our techniques are therefore useful to that end as well.
Further Applications to Devices with Restricted Resources Our techniques may also be useful for devices with very restricted resources, such as battery-powered IoT devices with a wireless network connection. For such devices, it is usually extremely expensive to send data, because each transmitted bit costs energy, which limits the battery lifetime and thus the range of possible applications. In order to maximize the battery lifetime, it is useful to avoid expensive interactive handshakes and use a 0-RTT protocol whenever data is sent to such devices. Note that here the main gain from using 0-RTT is not minimal latency, but rather that no key exchange messages must be sent by the receiver. Ideally, transmitted data should be forward-secure, but such devices have low storage capacity and we cannot use large amounts of storage to achieve forward security.
For such devices, it is reasonable to relax the requirement for very efficient computation, since adding unnecessary transmissions to even a fraction of connections is likely more costly than using moderately more expensive computations. By instantiating our session resumption protocol in a way that puncturing is more expensive (say, five full RSA exponentiations, which may still be reasonable for most IoT devices), we achieve reductions in storage by factors close to 100. Thus, our techniques make it possible to use forward-secure 0-RTT protocols even on such devices. Instead of requiring, say, 1 GB of memory for a session cache, we need only about 10 MBs of memory.
Related Work Puncturable encryption [32] was used to construct forward-secure instant messaging [32] and 0-RTT protocols [19, 20, 33, 45], for instance. Green and Miers [32] first proposed puncturable encryption as a practical building block for the case of asynchronous messaging. They used pairing-based puncturable encryption, and as a result observed impractically long processing times for their construction. Günther et al. [33] proposed using puncturable encryption for 0-RTT protocols, again proposing concrete constructions based on pairings that are also impractical for high-traffic scenarios. Derler et al. [19, 20] proposed trading off space in exchange for processing time, with the use of their proposed Bloom filter encryption. Their construction essentially precomputes many already-punctured keys, and these keys are used only once, so puncturing becomes simply key deletion. Bloom Filter Encryption may be considered practical for low-traffic scenarios, but supporting a large number of puncturings per key requires precomputation and storage of keys on the order of many gigabytes. A proof-of-concept 0-RTT key exchange based on Bloom filter encryption was implemented and analyzed by Dallmeier et al. [18]. However, their approach is incompatible with the standardized TLS protocol, which only allows a 0-RTT mode for session resumption.
Over the past years there have been several papers formally analyzing the security of TLS 1.2 [9, 36, 42] and TLS 1.3 [21,22,23, 28]. Particularly noteworthy are the analyses of the 0-RTT mode of TLS 1.3 [28] and QUIC [27] by Fischlin and Günther, who analyze both protocols in a multi-stage key exchange model [27]. Lychev et al. [47] further formally analyzed QUIC in a security model that additionally captures the secure composition of authenticated encryption and key exchange. A security definition and construction for QUIC-like 0-RTT protocols were given in [34]. However, all these publications do not consider forward secrecy for the very first message in their security models. Hence, we believe that our techniques may also influence the design of protocols providing a 0-RTT key exchange, such as TLS 1.3 and QUIC, in order to achieve forward secrecy for all messages.
Differences to the Eurocrypt 2019 Version This work is the full version of a paper, which appeared in Advances in Cryptology—Eurocrypt 2019—38th Annual International Conference on the Theory and Applications of Cryptographic Techniques [1]. The full version discusses how our construction and its benefits can be composed with the TLS 1.3 protocol, without modifying client side implementations or the TLS 1.3 standard. In Sect. 4 we provide the composed protocol and prove its security in the multi-stage key exchange model by Fischlin and Günther [27, 28]. In contrast to previous security proofs of TLS 1.3 resumption handshake drafts [23, 24, 28], we incorporate the finalized key derivation schedule of TLS 1.3, and are able to achieve forward secrecy for all messages by utilizing the techniques described in this work. This contribution resolves an open problem stated in a previous version of this work.
Outline The rest of this paper is organized as follows. In Sect. 2 we provide formal definitions for secure 0-RTT Session Resumption Protocols. In Sect. 3 we describe a generic construction, based on abstract PPRFs, and formally prove forward security and replay resilience. In Sect. 4 we show how our generic construction can be composed with TLS 1.3 and prove the composition’s security. Section 5 describes the Strong-RSA-based PPRF and an analysis of the efficiency when used in the protocol construction in Sect. 3. Section 6 describes the tree-based PPRF and a novel “domain extension” technique for standard binary tree PPRFs, along with an efficiency analysis.
Notation We denote the security parameter as \(\lambda \). For any \(n \in {\mathbb {N}} \) let \(1^n\) be the unary representation of n and let \([n] = \{1, \ldots , n\}\) be the set of numbers between 1 and n. Moreover, |x| denotes the length of a bitstring x, while \(|{\mathcal {S}}|\) denotes the size of a set \({\mathcal {S}}\). We write  to indicate that we choose element x uniformly at random from set \({\mathcal {S}}\). For a probabilistic polynomial-time algorithm \({\mathcal {A}}\) we define
to indicate that we choose element x uniformly at random from set \({\mathcal {S}}\). For a probabilistic polynomial-time algorithm \({\mathcal {A}}\) we define  as the execution of \({\mathcal {A}}\) (with fresh random coins) on input \(a_1, \ldots , a_n\) and assigning the output to y.
as the execution of \({\mathcal {A}}\) (with fresh random coins) on input \(a_1, \ldots , a_n\) and assigning the output to y.
2 0-RTT Session Resumption Protocols and Their Security
In this section we provide formal definitions for secure 0-RTT session resumption protocols. These definitions capture both our new techniques and the existing solutions already standardized in TLS 1.3. We later show that the techniques used to formally analyze and verify TLS 1.3 0-RTT [17, 24, 28] can be extended to use our abstraction of a session resumption protocol within TLS 1.3. This leads us to believe that our definitions capture a reasonable abstraction of the cryptographic core of the TLS 1.3 0-RTT mode (and likely also of similar protocols that may be devised in the future).
For simplicity, in the following we will refer to pre-shared values as session keys, as they are either previously established session keys, or a resumption secret derived from a session key, as e.g. in TLS 1.3. The details of how to establish a shared secret and potentially derive a session key from it are left to the individual protocol and are outside the scope of our abstraction. Session keys are elements of a keyspace \({\mathcal {S}}\).
Definition 1
A 0-RTT session resumption protocol consists of three probabilistic polynomial-time algorithms \(\mathsf {Resumption} = (\mathsf {Setup}, \mathsf {TicketGen}, \mathsf {ServerRes})\) with the following properties.
-
\(\mathsf {Setup} (1^\lambda )\) takes as input the security parameter \(\lambda \) and outputs the server’s long-term key k.
-
\(\mathsf {TicketGen} (k, s)\) takes as input a long-term key k and a session key s, and outputs a ticket t and a potentially modified long-term key \(k'\).
-
\(\mathsf {ServerRes} (k, t)\) takes as input the server’s long-term key k and the ticket t, and outputs a session key s and a potentially modified key \(k'\), or a tuple \((\bot , k)\) where \(\bot \) is a failure symbol.
Using a Session Resumption Protocol A 0-RTT session resumption scheme is used by a set of clients C and a set of servers S. If a client and a server share a session key s, the session resumption is executed as follows (cf. Fig. 1).
-
1.
The server uses its long-term key k and the session key s to generate a ticket t by running
 . The ticket is sent to the client. Additionally, the server replaces its long-term key k by \(k'\) and deletes the session key s and ticket t, i.e. it is not required to keep any session state.
. The ticket is sent to the client. Additionally, the server replaces its long-term key k by \(k'\) and deletes the session key s and ticket t, i.e. it is not required to keep any session state. -
2.
For session resumption at a later point in time, the client sends the ticket t to the server.
-
3.
Upon receiving the ticket t, the server runs \((s, k') := \mathsf {ServerRes} (k, t)\) to retrieve the session key s. Additionally, k is deleted and replaced by the updated key \(k'\).
Execution of a generic 0-RTT session resumption protocol based on session tickets with early data m, where client and server initially are in possession of a shared secret s. The procedures \(\mathsf {Enc}\) and \(\mathsf {Dec}\) are symmetric encryption and decryption procedures respectively. Note that procedures \(\mathsf {TicketGen}\) and \(\mathsf {ServerRes}\) both potentially modify the server’s key k
Compatibility with TLS 1.3 As explained in Sect. 1, using either session tickets or session caches in TLS 1.3 is transparent to clients, i.e. clients are generally unaware of which is used. In either case, the client stores a sequence of bytes which is opaque from the client’s point of view. Since all algorithms of a session resumption protocol are executed on the server, while a client just has to store the ticket t (encoded as a sequence of bytes), this generic approach of TLS 1.3 is immediately compatible with our notion of session resumption protocols. Thus, a session resumption protocol can be used immediately in TLS 1.3, without requiring changes to clients or to the protocol. Furthermore, session tickets and session caches are specific examples of such protocols.
2.1 Security in the Single-Server Setting
We define the security of a 0-RTT session resumption protocol \(\mathsf {Resumption}\) by a security game \({\mathsf {G}}_{{\mathcal {A}}, \mathsf {Resumption}}^{\mathsf {0\text {-}RTT\text {-}SR}}(\lambda )\) between a challenger \({\mathcal {C}}\) and an adversary \({\mathcal {A}}\). For simplicity, we will start with a single-server setting and argue below that security in the single-server setting implies security in a multi-server setting. Let \(\mu \) be the number of sessions.
-
1.
\({\mathcal {C}}\) runs
 , samples a random bit
, samples a random bit  and generates session keys
and generates session keys  for all sessions \(i \in [\mu ]\). Furthermore, it generates tickets \(t_i\) and updates key k by running
for all sessions \(i \in [\mu ]\). Furthermore, it generates tickets \(t_i\) and updates key k by running 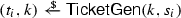 for all sessions \(i \in [\mu ]\). The sequence of tickets \((t_i)_{i \in [\mu ]}\) is sent to \({\mathcal {A}}\).
for all sessions \(i \in [\mu ]\). The sequence of tickets \((t_i)_{i \in [\mu ]}\) is sent to \({\mathcal {A}}\). -
2.
The adversary gets access to oracles it may query.
-
(a)
\({{\mathcal {O}}_\mathsf {Dec}} (t)\) takes as input a ticket t. It computes \(({s}, k') := \mathsf {ServerRes} (k, t)\) and outputs \(\bot \) if \(\mathsf {ServerRes}\) failed. Otherwise, it returns the session key \({s}\) and replaces \(k := k'\). Note that ticket t can either be a ticket of the initial sequence of tickets \((t_i)_{i \in [\mu ]}\) or an arbitrary ticket chosen by the adversary.
-
(b)
\({{\mathcal {O}}_\mathsf {Test}} (t)\) takes as input a ticket t. It computes \(({s}, k') := \mathsf {ServerRes} (k, t)\) and outputs \(\bot \) if the output of \(\mathsf {ServerRes}\) was \((\bot , k)\). Otherwise, it updates \(k := k'\). If \(b=1\), then it returns the session key \({s}\). Otherwise, a random
 is returned. Note that ticket t can either be a ticket of the initial sequence of tickets \((t_i)_{i \in [\mu ]}\) or an arbitrary ticket chosen by the adversary.
is returned. Note that ticket t can either be a ticket of the initial sequence of tickets \((t_i)_{i \in [\mu ]}\) or an arbitrary ticket chosen by the adversary.The adversary is allowed to query \({{\mathcal {O}}_\mathsf {Test}}\) only once.
-
(c)
\({{\mathcal {O}}_\mathsf {Corr}} \) returns the current long-term key k of the server. The adversary must not query \({{\mathcal {O}}_\mathsf {Test}}\) after \({{\mathcal {O}}_\mathsf {Corr}}\), as this would lead to a trivial attack.
-
(a)
-
3.
Eventually, adversary \({\mathcal {A}}\) outputs a guess \(b^*\). Challenger \({\mathcal {C}}\) outputs 1 if \(b = b^*\) and 0 otherwise.
Note that this security model reflects both forward secrecy and replay protection. Forward secrecy is ensured, as an adversary may corrupt the challenger after issuing the \({{\mathcal {O}}_\mathsf {Test}}\)-query. If the protocol did not ensure forward secrecy, an attacker could corrupt its long-term key and trivially decrypt the challenge ticket. Replay protection is ensured, as an adversary is allowed to issue \({{\mathcal {O}}_\mathsf {Dec}} (t_i)\) after already testing \({{\mathcal {O}}_\mathsf {Test}} (t_i)\) and vice versa (as both queries invoke the \(\mathsf {ServerRes}\) algorithm). If the protocol did not ensure replay protection, an attacker could use the decryption oracle to distinguish a real or random session key of the \({{\mathcal {O}}_\mathsf {Test}}\)-query.
Definition 2
We define the advantage of an adversary \({\mathcal {A}}\) in the above security game \({\mathsf {G}}_{{\mathcal {A}}, \mathsf {Resumption}}^{\mathsf {0\text {-}RTT\text {-}SR}}(\lambda )\) as
We say a 0-RTT session resumption protocol is secure in a single-server environment if the advantage \(\mathsf {Adv}_{{\mathcal {A}}, \mathsf {Resumption}}^{\mathsf {0\text {-}RTT\text {-}SR}}(\lambda )\) is a negligible function in \(\lambda \) for all probabilistic polynomial-time adversaries \({\mathcal {A}}\).
2.2 Security in the Multi-server Setting
A 0-RTT session resumption protocol that is secure in our model, only guarantees security in a single-server setting. However, session resumption protocols are meant to be executed in a multi-server environment. In this section, we provide the respective security model and a proof that single-server security implies multi-server security with a standard polynomial loss in the number of servers, provided each server has a different long-term key.
We define the security of a 0-RTT session resumption protocol \(\mathsf {Resumption}\) with multiple servers in the following security game between a challenger \({\mathcal {C}}\) and an adversary \({\mathcal {A}}\). Let \(\mu \) be the number of sessions and d be the number of servers.
-
1.
To simulate the server, \({\mathcal {C}}\) runs
 for \(j \in [d]\), samples a random bit
for \(j \in [d]\), samples a random bit  and generates session keys
and generates session keys  for all \((i,j) \in [\mu ] \times [d]\). Furthermore it generates tickets
for all \((i,j) \in [\mu ] \times [d]\). Furthermore it generates tickets  for all \((i,j) \in [\mu ] \times [d]\). The sequence of tickets \((t_{i,j})_{(i,j) \in [\mu ] \times [d]}\) is sent to \({\mathcal {A}}\).
for all \((i,j) \in [\mu ] \times [d]\). The sequence of tickets \((t_{i,j})_{(i,j) \in [\mu ] \times [d]}\) is sent to \({\mathcal {A}}\). -
2.
The adversary gets access to oracles it may query.
-
(a)
\({{\mathcal {O}}_\mathsf {Dec}} (t, j)\) takes as input a ticket t and an identifier j. It computes \(({s}, k_j') := \mathsf {ServerRes} (k_j, t)\) and outputs \(\bot \) if \(\mathsf {ServerRes}\) failed. Otherwise, it returns the session key \({s}\) and replaces \(k_j := k_j'\). Note that ticket t can either be a ticket of the initial sequence of tickets \((t_i)_{i \in [\mu ]}\) or an arbitrary ticket chosen by the adversary.
-
(b)
\({{\mathcal {O}}_\mathsf {Test}} (t, j)\) takes as input a ticket t and a server identifier j. It computes \({s} := \mathsf {ServerRes} (k_j, t)\) and outputs \(\bot \) if the output of \(\mathsf {ServerRes}\) was \((\bot , k_j)\). Otherwise it replaces \(k_j := k_j'\) and returns either the session key \({s}\) if \(b = 1\) or a random
 if \(b = 0\). Note that ticket t can either be a ticket of the initial sequence of tickets \((t_i)_{i \in [\mu ]}\) or an arbitrary ticket chosen by the adversary.
if \(b = 0\). Note that ticket t can either be a ticket of the initial sequence of tickets \((t_i)_{i \in [\mu ]}\) or an arbitrary ticket chosen by the adversary.The adversary is only allowed to query \({{\mathcal {O}}_\mathsf {Test}}\) once and only for tickets t which have not been queried using \({{\mathcal {O}}_\mathsf {Dec}} (t)\) before.
-
(c)
\({{\mathcal {O}}_\mathsf {Corr}} (j)\) takes as input a server identity \(j \in [d]\). It returns the server’s long-term key \(k_j\). The adversary is not allowed to query \({{\mathcal {O}}_\mathsf {Test}} (t, j)\) after \({{\mathcal {O}}_\mathsf {Corr}} (j)\), as this would lead to trivial attacks.
-
(a)
-
3.
Eventually, \({\mathcal {A}}\) outputs a guess \(b^*\). Challenger \({\mathcal {C}}\) outputs 1 if \(b = b^*\) and 0 otherwise.
Definition 3
We define the advantage of an adversary \({\mathcal {A}}\) in the above security game \({\mathsf {G}}_{{\mathcal {A}}, \mathsf {Resumption}}^{\mathsf {M0\text {-}RTT\text {-}SR}}(\lambda )\) as
We say a 0-RTT session resumption protocol is secure in a multi-server environment if the advantage \(\mathsf {Adv}_{{\mathcal {A}}, \mathsf {Resumption}}^{\mathsf {M0\text {-}RTT\text {-}SR}}(\lambda )\) is a negligible function in \(\lambda \) for all probabilistic polynomial-time adversaries \({\mathcal {A}}\).
Theorem 1
From each probabilistic polynomial-time adversary \({\mathcal {A}}\) against the security of a 0-RTT session resumption protocol \(\mathsf {Resumption}\) in a multi-server environment with advantage \(\mathsf {Adv}_{{\mathcal {A}}, \mathsf {Resumption}}^{\mathsf {M0\text {-}RTT\text {-}SR}}(\lambda )\), we can construct an adversary \({\mathcal {B}}\) against the security of \(\mathsf {Resumption}\) in the single-server environment with advantage \(\mathsf {Adv}_{{\mathcal {A}}, \mathsf {Resumption}}^{\mathsf {0\text {-}RTT\text {-}SR}}(\lambda )\), such that
Proof
Let \({\mathcal {A}}\) be an adversary against the \(\mathsf {M0\text {-}RTT\text {-}SR}\) security of \(\mathsf {Resumption}\). We will use this adversary to construct an adversary \({\mathcal {B}}\) against the \(\mathsf {0\text {-}RTT\text {-}SR}\) security of \(\mathsf {Resumption}\). The \(\mathsf {0\text {-}RTT\text {-}SR}\) challenger \({\mathcal {C}}\) starts its security game by sending a tuple of tickets \((t_i)_{i \in [\mu ]}\).
In order to initialize \({\mathcal {A}}\) we need to prepare a tuple of tickets \((t_{i,j})_{(i,j) \in [\mu ] \times [d]}\). We generate \(\mu \cdot (d - 1)\) tickets by ourselves and use tickets \((t_i)_{i \in [\mu ]}\) the \(\mathsf {0\text {-}RTT\text {-}SR}\) challenger sent us for the leftover \(\mu \) tickets. At first we guess an index  and hope that \({\mathcal {A}}\) queries \({{\mathcal {O}}_\mathsf {Test}} (t_{i,\nu }, \nu )\) for some \(i \in [\mu ]\). Let \(\delta = [d] \setminus \{\nu \}.\) We generate \(\mu \cdot |\delta |\) tickets honestly by running
and hope that \({\mathcal {A}}\) queries \({{\mathcal {O}}_\mathsf {Test}} (t_{i,\nu }, \nu )\) for some \(i \in [\mu ]\). Let \(\delta = [d] \setminus \{\nu \}.\) We generate \(\mu \cdot |\delta |\) tickets honestly by running  for \(j \in \delta \), generating
for \(j \in \delta \), generating  and invoking
and invoking  for all \((i,j) \in [\mu ] \times \delta \). We embed our challenge as \(t_{i,\nu } = t_i\) for \(i \in [\mu ]\). We send \((t_{i,j})_{(i,j) \in [\mu ] \times [d]}\) to \({\mathcal {A}}\).
for all \((i,j) \in [\mu ] \times \delta \). We embed our challenge as \(t_{i,\nu } = t_i\) for \(i \in [\mu ]\). We send \((t_{i,j})_{(i,j) \in [\mu ] \times [d]}\) to \({\mathcal {A}}\).
We need to distinguish two possible cases. We can simulate all queries \({\mathcal {A}}\) can ask for server identities \(j \in \delta \) by ourselves, as we know all secret values for those servers. In the case of \(j = \nu \) we forward all queries to the challenger \({\mathcal {C}}\) and send the answers back to \({\mathcal {A}}\).
If \({\mathcal {A}}\) queries \({{\mathcal {O}}_\mathsf {Test}} (t_{i,j}, j)\) we behave in the following way. If \(j = \nu \) we continue the security game and forward the final bit output of \({\mathcal {A}}\) as our solution of the challenge to \({\mathcal {C}}\). If \(j \ne \nu \) we abort the security game and output a random bit to \({\mathcal {C}}\).
In the case of \(j = \nu \) we win the security game with the advantage \(\mathsf {Adv}_{{\mathcal {A}}, \mathsf {Resumption}}^{\mathsf {0\text {-}RTT\text {-}SR}}(\lambda )\). This happens with a probability of 1/d as  is drawn at random. If \(j \ne \nu \), we have no advantage compared to guessing. In conclusion, we have
is drawn at random. If \(j \ne \nu \), we have no advantage compared to guessing. In conclusion, we have

\(\square \)
On Theoretically-Sound Instantiation Tight security in a multi-server setting is a major issue for classical AKE-like protocols. First tightly-secure protocols were described by Bader et al. [2], and by Gjøsteen–Jager [29]). Similar to classical AKE protocols, our extension to the multi-server setting is non-tight as we have a security loss in the number of protocol participants (which is the “standard security loss” for many AKE-like protocols). So, if parameters are chosen in a theoretically-sound way (which is currently rather uncommon in practice, but would be a desirable goal in our opinion), then this factor needs to be compensated with larger parameters.
3 Constructing Secure Session Resumption Protocols
In this section we will show how session resumption protocols providing full forward security and replay resilience can be constructed. We will start with a generic construction, based on authenticated encryption with associated data and any puncturable pseudorandom function that is invariant to puncturing. Later we describe new constructions of PPRFs, which are particularly suitable for use in session resumption protocols.
3.1 Building Blocks
We briefly recall the basic definition of puncturable pseudorandom functions and authenticated encryption with associated data.
Puncturable PRFs A puncturable pseudorandom function is a special case of a pseudorandom function (PRF), where it is possible to compute punctured keys which do not allow evaluation on inputs that have been punctured. We recall the definition of puncturable pseudorandom functions and its security from [54].
Definition 4
A puncturable pseudorandom function (PPRF) with keyspace \({\mathcal {K}}\), domain \({\mathcal {X}}\) and range \({\mathcal {Y}}\) consists of three probabilistic polynomial-time algorithms \(\mathsf {PPRF} = (\mathsf {Setup}, \mathsf {Eval}, \mathsf {Punct})\), which are described as follows.
-
\(\mathsf {Setup} (1^\lambda )\): This algorithm takes as input the security parameter \(\lambda \) and outputs an evaluation key \(k \in {\mathcal {K}}\).
-
\(\mathsf {Eval} (k, x)\): This algorithm takes as input a key \(k \in {\mathcal {K}}\) and a value \(x \in {\mathcal {X}}\), and outputs a value \(y \in {\mathcal {Y}}\), or a failure symbol \(\bot \).
-
\(\mathsf {Punct} (k, x)\): This algorithm takes as input a key \(k \in {\mathcal {K}}\) and a value \(x \in {\mathcal {X}}\), and returns a punctured key \(k' \in {\mathcal {K}}\).
Definition 5
A PPRF is correct if for every subset \(\{x_1, \ldots , x_n\} = {\mathcal {S}} \subseteq {\mathcal {X}}\) and all \(x \in {\mathcal {X}} \setminus {\mathcal {S}}\), we have that

A new property of PPRFs that we will need is that puncturing be “commutative”, i.e. the order of puncturing operations does not affect the resulting secret key. That is, for any \(x_0, x_1 \in {\mathcal {X}}, x_0 \ne x_1\), if we first puncture on input \(x_0\) and then on \(x_1\), the resulting key is identical to the key obtained from first puncturing on \(x_1\) and then on \(x_0\). This implies that puncturing by any set of inputs always gives the same result, regardless of the order of puncturing. Formally:
Definition 6
A PPRF is invariant to puncturing if for all keys \(k \in {\mathcal {K}}\) and all elements \(x_0, x_1 \in {\mathcal {X}}, x_0 \ne x_1\) it holds that
We define two notions of PPRF security. The first notion represents the typical pseudorandomness security experiment with adaptive evaluation queries by an adversary. The second notion is a weaker, non-adaptive security experiment. We show that it suffices to prove security in the non-adaptive experiment if the PPRF is invariant to puncturing and has a polynomial-size domain.
Definition 7
We define the advantage of an adversary \({\mathcal {A}}\) in the \(\mathsf {rand}\) (resp. \(\mathsf {na\text {-}rand}\)) security experiment \({\mathsf {G}}_{{\mathcal {A}}, \mathsf {PPRF}}^{\mathsf {rand}}(\lambda )\) (resp. \({\mathsf {G}}_{{\mathcal {A}}, \mathsf {PPRF}}^{\mathsf {na\text {-}rand}}(\lambda )\)) defined in Fig. 2 as
We say a puncturable pseudorandom function \(\mathsf {PPRF}\) is \(\mathsf {rand}\) -secure (resp. \(\mathsf {na\text {-}rand}\) -secure), if the advantage \(\mathsf {Adv}_{{\mathcal {A}}, \mathsf {PPRF}}^{\mathsf {rand}}(\lambda )\) (resp. \(\mathsf {Adv}_{{\mathcal {A}}, \mathsf {PPRF}}^{\mathsf {na\text {-}rand}}(\lambda )\)) is a negligible function in \(\lambda \) for all probabilistic polynomial-time adversaries \({\mathcal {A}}\).
It is relatively easy to prove that \(\mathsf {na\text {-}rand}\)-security and \(\mathsf {rand}\)-security are equivalent, up to a linear security loss in the size of the domain of the PPRF if the PPRF is invariant to puncturing. In particular, if the PPRF has a polynomially-bounded domain size, then both are polynomially equivalent.
Theorem 2
Let \(\mathsf {PPRF}\) be a \(\mathsf {na\text {-}rand}\)-secure PPRF with domain \({\mathcal {X}}\). If \(\mathsf {PPRF}\) is invariant to puncturing, then it is also \(\mathsf {rand}\)-secure with advantage
Proof
The proof is based on a straightforward reduction. We give a sketch. Let \({\mathcal {A}}\) be an adversary against the \(\mathsf {rand}\) security of \(\mathsf {PPRF}\). We guess \({\mathcal {A}}\) ’s challenge value in advance by sampling  uniformly at random. We initialize the \(\mathsf {na\text {-}rand}\) challenger by sending it \(\nu \). In return we receive a challenge y (either computed via \(\mathsf {Eval}\) or random) and a punctured key k that cannot be evaluated on input \(\nu \).
uniformly at random. We initialize the \(\mathsf {na\text {-}rand}\) challenger by sending it \(\nu \). In return we receive a challenge y (either computed via \(\mathsf {Eval}\) or random) and a punctured key k that cannot be evaluated on input \(\nu \).
The punctured key k allows us to correctly answer all of \({\mathcal {A}}\) ’s \({{\mathcal {O}}_\mathsf {Eval}}\) queries, except for \(\nu \). When the adversary outputs its challenge \(x^*\) we will abort if \(x^* \ne \nu \). Otherwise, we forward y and a punctured key \(k'\) that has been punctured on all values of the \({{\mathcal {O}}_\mathsf {Eval}}\) queries. Note that the key has a correct distribution, as we require that the PPRF is invariant to puncturing.
Eventually, \({\mathcal {A}}\) outputs a bit \(b^*\) which we forward to the \(\mathsf {na\text {-}rand}\) challenger.
The simulation is perfect unless we abort it, which happens with polynomially-bounded probability \(1/|{\mathcal {X}}|\), due to the fact that \(|{\mathcal {X}}|\) is polynomially bounded. \(\square \)
Authenticated Encryption with Associated Data We will furthermore need authenticated encryption with associated data (AEAD) [52], along with the standard notions of confidentiality and integrity.
Definition 8
An authenticated encryption scheme with associated data is a tuple \(\mathsf {AEAD} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Dec})\) of three probabilistic polynomial-time algorithms:
-
\(\mathsf {KGen} (1^\lambda )\) takes as input a security parameter \(\lambda \) and outputs a secret key k.
-
\(\mathsf {Enc} (k, m, ad )\) takes as input a key k, a message m, associated data \( ad \) and outputs a ciphertext c.
-
\(\mathsf {Dec} (k, c, ad )\) takes as input a key k, a ciphertext c, associated data \( ad \) and outputs a message m or a failure symbol \(\bot \).
An AEAD scheme is called correct if for any key  , any message \(m \in \{0,1\} ^*\), any associated data \( ad \in \{0,1\} ^*\) it holds that \(\mathsf {Dec} (k, \mathsf {Enc} (k, m, ad ), ad ) = m\).
, any message \(m \in \{0,1\} ^*\), any associated data \( ad \in \{0,1\} ^*\) it holds that \(\mathsf {Dec} (k, \mathsf {Enc} (k, m, ad ), ad ) = m\).
Definition 9
We define the advantage of an adversary \({\mathcal {A}}\) in the \(\mathsf {IND\text {-}CPA}\) experiment \({\mathsf {G}}_{{\mathcal {A}}, \mathsf {AEAD}}^\mathsf {IND\text {-}CPA} (\lambda )\) defined in Fig. 3 as
We say an AEAD scheme \(\mathsf {AEAD}\) is indistinguishable under chosen-plaintext attacks (\(\mathsf {IND\text {-}CPA}\) -secure), if the advantage \(\mathsf {Adv}_{{\mathcal {A}}, \mathsf {AEAD}}^\mathsf {IND\text {-}CPA} (\lambda )\) is a negligible function in \(\lambda \) for all probabilistic polynomial-time adversaries \({\mathcal {A}}\).
Definition 10
We define the advantage of an adversary \({\mathcal {A}}\) in the \(\mathsf {INT\text {-}CTXT}\) experiment \({\mathsf {G}}_{{\mathcal {A}}, \mathsf {AEAD}}^\mathsf {INT\text {-}CTXT} (\lambda )\) defined in Fig. 3 as
We say an AEAD scheme \(\mathsf {AEAD}\) provides integrity of ciphertexts (\(\mathsf {INT\text {-}CTXT}\) -secure), if the advantage \(\mathsf {Adv}_{{\mathcal {A}}, \mathsf {AEAD}}^\mathsf {INT\text {-}CTXT} (\lambda )\) is a negligible function in \(\lambda \) for all probabilistic polynomial-time adversaries \({\mathcal {A}}\).
The \(\mathsf {IND\text {-}CPA}\) and \(\mathsf {INT\text {-}CTXT}\) security experiment for AEAD [52]
3.2 Generic Construction
Now we are ready to describe our generic construction of a 0-RTT session resumption protocol, based on a PPRF and an AEAD scheme, and to prove its security.
Construction 1
Let \(\mathsf {AEAD} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Dec})\) be an authenticated encryption scheme with associated data and let \(\mathsf {PPRF} = (\mathsf {Setup}, \mathsf {Eval}, \mathsf {Punct})\) be a PPRF with range \({\mathcal {Y}}\). Then we can construct a 0-RTT session resumption protocol \(\mathsf {Resumption} = (\mathsf {Setup},\mathsf {TicketGen}, \mathsf {ServerRes})\) in the following way.
-
\(\mathsf {Setup} (1^\lambda )\) runs \(k_\mathsf {PPRF} = \mathsf {PPRF}.\mathsf {Setup} (1^\lambda )\), and outputs \(k := (k_\mathsf {PPRF}, 0)\), where “0” is a counter initialized to zero.
-
\(\mathsf {TicketGen} (k, s)\) takes a key \(k = (k_\mathsf {PPRF}, n)\). It computes \(\kappa = \mathsf {PPRF}.\mathsf {Eval} (k_\mathsf {PPRF}, n)\). Then it encrypts the ticket as
 . Finally, it defines \(t = (t', n)\) and \(k := (k_\mathsf {PPRF}, n+1)\), and outputs (t, k).
. Finally, it defines \(t = (t', n)\) and \(k := (k_\mathsf {PPRF}, n+1)\), and outputs (t, k). -
\(\mathsf {ServerRes} (k, t)\) takes \(k = (k_\mathsf {PPRF}, n)\) and \(t = (t', n')\). It computes a key \(\kappa := \mathsf {PPRF}.\mathsf {Eval} (k_\mathsf {PPRF}, n')\). If \(\kappa = \bot \), then it returns \((\bot , k)\). Otherwise it computes a session key \(s := \mathsf {AEAD}.\mathsf {Dec} (\kappa , t', n')\). If \(s = \bot \), it returns \((\bot , k)\). Else it punctures \(k_\mathsf {PPRF}:= \mathsf {PPRF}.\mathsf {Punct} (k_\mathsf {PPRF}, n')\), and returns \((s, (k_\mathsf {PPRF}, n))\).
Note that the associated data n is sent in plaintext when the client resumes the session, posing a potential privacy leak: Assume an attacker that observes all communication to and from the server. When the attacker observes a client resuming using a ticket with associated data n, the attacker learns that it is the same client that first connected when the server issued the n-th ticket. Newly-generated tickets are first sent encrypted from the server to the client, but it is feasible for the attacker to identify sessions where the server issued tickets by performing traffic analysis (and then identifying the n-th such session). In essence, using the above construction as-is, sessions are linkable.
This can be circumvented by additionally encrypting n under a dedicated symmetric key. Compromise of this key would only allow an attacker to link sessions by the same returning client, not to decrypt past traffic, therefore this symmetric key needs not be punctured to achieve forward security.
We remark that the natural solution would be to encrypt n using public-key puncturable encryption, but this would be costly, and obviate most of the efficiency benefits described in this work. We are unfortunately unaware of a good solution that achieves session unlinkability in the event of server compromise. We further note that TLS 1.3 0-RTT includes a mechanism named “obfuscated ticket age” that solves a similar session linkability concern; that mechanism as well is not applicable here.
Theorem 3
If \(\mathsf {PPRF} \) is invariant to puncturing, then from each probabilistic polynomial-time adversary \({\mathcal {A}}\) against the security of \(\mathsf {Resumption}\) in a single-server environment with advantage \(\mathsf {Adv} _{{\mathcal {A}}, \mathsf {Resumption}}^{\mathsf {0\text {-}RTT\text {-}SR}}(\lambda )\), we can construct five adversaries \({\mathcal {B}} _{\mathsf {PPRF} 1}\), \({\mathcal {B}} _{\mathsf {PPRF} 2}\), \({\mathcal {B}} _{\mathsf {AEAD} 1}\), \({\mathcal {B}} _{\mathsf {AEAD} 2}\), and \({\mathcal {B}} _{\mathsf {AEAD} 3}\) such that
where \(q_\mathsf {Dec} \) is the number of decryption queries and \(\mu \) is the number of sessions.
Proof
We will conduct this proof in a sequence of games between a challenger \({\mathcal {C}}\) and an adversary \({\mathcal {A}}\). We start with an adversary playing the \(\mathsf {0\text {-}RTT\text {-}SR}\) security game. Over a sequence of hybrid arguments, we will stepwise transform the security game to a game where the \({{\mathcal {O}}_\mathsf {Test}}\)-query is independent of the challenge bit b. The claim then follows from bounding the probability of distinguishing any two consecutive games. By \(\mathsf {Adv} _i\) we denote \({\mathcal {A}}\) ’s advantage in the i-th game.
Game 0
We define Game 0 to be the original \(\mathsf {0\text {-}RTT\text {-}SR}\) security game. By definition we have
Game 1
In this game, we want to bound the probability that an adversary is able to forge a new ticket with \(n > \mu \). Formally, this game is identical to Game 0, but we change how \({{\mathcal {O}}_\mathsf {Dec}}\) and \({{\mathcal {O}}_\mathsf {Test}}\) queries are answered. That is, whenever the adversary queries \({{\mathcal {O}}_\mathsf {Dec}}\) or \({{\mathcal {O}}_\mathsf {Test}}\) for a ticket \(t = (t', n)\) with \(n > \mu \), we always reply with \(\bot \). This change is only detectable by the adversary if it forges a ticket t such that \({{\mathcal {O}}_\mathsf {Dec}} (t) \ne \bot \) or \({{\mathcal {O}}_\mathsf {Test}} (t) \ne \bot \). Let X be the event that the adversary produces such a forgery \(t = (t', n)\) with \(n > \mu \). Hence, we have
We bound the probability of X occurring by using the following lemma:
Lemma 1
Let \(q_\mathsf {Dec} \) be the number of decryption queries by the adversary. Then we have
Proof
Intuitively, in order to make even X happen, the adversary would have to break \(\mathsf {INT\text {-}CTXT}\) security. But the reduction to show this is not completely straightforward, since we have to use both the security of the PPRF and the \(\mathsf {INT\text {-}CTXT}\) security to show this. This is done by the short “branch sequence of games” considered in this lemma.
For the sake of clarity, we emphasize that the lemma only claims a bound on the probability that the event X occurs. Therefore, we bound only the probability of this event, and not the probability that an adversary wins. That is, as soon as the event X has happened, the adversary does not require a consistent simulation anymore, as the occurrence of X cannot be reverted.
We prove the lemma by following a sequence of games. By \(\Pr [X_i]\) we denote probability of X occurring in the i-th game. We define Game 0.0 to be Game 0 of the main proof. By definition we have
Game 0.1 This game is identical to Game 0.0 but we guess which \({{\mathcal {O}}_\mathsf {Dec}}\) or \({{\mathcal {O}}_\mathsf {Test}}\) query the adversary uses for its first forgery \(t = (t', n)\) with \(n > \mu \) such that \({{\mathcal {O}}_\mathsf {Dec}} (t) \ne \bot \) or \({{\mathcal {O}}_\mathsf {Test}} (t) \ne \bot \). Formally, let  where \(q_\mathsf {Dec} \) is the number of \({{\mathcal {O}}_\mathsf {Dec}}\) queries made by the adversary. Since the choice of j is oblivious to the adversary, we can bound the probability of guessing correctly by \(1/(q_\mathsf {Dec} + 1)\). Let \(X_{\text {0.1}}\) be the event that \(X_0\) occurs and j was guessed correctly. We can then bound
where \(q_\mathsf {Dec} \) is the number of \({{\mathcal {O}}_\mathsf {Dec}}\) queries made by the adversary. Since the choice of j is oblivious to the adversary, we can bound the probability of guessing correctly by \(1/(q_\mathsf {Dec} + 1)\). Let \(X_{\text {0.1}}\) be the event that \(X_0\) occurs and j was guessed correctly. We can then bound
and subsequently assume that j was guessed correctly.
Game 0.2 The difference between Games 0.1 and 0.2 is whether we use the “real” or a “random” PPRF key in the j-th query. If this changes the probability of event \(X_{0.1}\) significantly, then we can construct a successful PPRF distinguisher \({\mathcal {B}} _{\mathsf {PPRF} 1}\).
Formally, this game is identical to Game 0.1 but we change how the j-th query in the sequence of \({{\mathcal {O}}_\mathsf {Dec}}\) and \({{\mathcal {O}}_\mathsf {Test}}\) queries is computed. Let  be a value chosen by the experiment. Normally, the j-th query would need to compute \(\mathsf {PPRF}.\mathsf {Eval} (k, n^*)\) for some ticket \(t^* = (t', n^*)\). However, we will now replace the result this computation with the independent and precomputed value \(\rho \).
be a value chosen by the experiment. Normally, the j-th query would need to compute \(\mathsf {PPRF}.\mathsf {Eval} (k, n^*)\) for some ticket \(t^* = (t', n^*)\). However, we will now replace the result this computation with the independent and precomputed value \(\rho \).
Everything else works exactly as before. We will show that any adversary that is able to distinguish Game 0.1 from Game 0.2, can be used to construct an adversary against the security of the underlying PPRF. Concretely, we have
Construction of \({\mathcal {B}} _{\mathsf {PPRF} 1}\) \({\mathcal {B}} _{\mathsf {PPRF} 1}\) simulates Game 0.1 for \({\mathcal {A}}\) by utilizing the PPRF challenger. That is, the initial sequence of tickets is computed via the \(\mathsf {Eval}\) query of the PPRF challenger. Likewise, we can answer all \({{\mathcal {O}}_\mathsf {Dec}}\) and \({{\mathcal {O}}_\mathsf {Test}}\) queries up until the \(j-1\)-th query with aid of the \(\mathsf {Eval}\) oracle. However, for every query to \({{\mathcal {O}}_\mathsf {Dec}}\) or \({{\mathcal {O}}_\mathsf {Test}}\) with \(t = (t', n)\) with \(n > \mu \), we always return \(\bot \). Note that the change in Game 0.1 ensures that this is a valid behavior as the correct guess of j ensures that all previous calls to \({{\mathcal {O}}_\mathsf {Dec}}\) or \({{\mathcal {O}}_\mathsf {Test}}\) with \(t = (t', n)\) and \(n > \mu \) are \(\bot \) by definition.
As soon as the adversary uses its j-th \({{\mathcal {O}}_\mathsf {Dec}}\) or \({{\mathcal {O}}_\mathsf {Test}}\) query with \(t = (t', n^*)\) and \(n^* > \mu \), we relay \(n^*\) as challenge to the PPRF challenger. Note that we have never used \(n^* > \mu \) as input to the \(\mathsf {Eval}\) oracle, making \(n^*\) an admissible challenge. The challenger responds with a punctured key \(k' := \mathsf {PPRF}.\mathsf {Punct} (k, n^*)\) and a value \(\gamma \), where either  or \(\gamma := \mathsf {PPRF}.\mathsf {Eval} (k, n^*)\).
or \(\gamma := \mathsf {PPRF}.\mathsf {Eval} (k, n^*)\).
We use \(\gamma \) to check whether the ticket \(t'\) is a valid AEAD ciphertext. That is, if \(\mathsf {AEAD}.\mathsf {Dec} (\gamma , t', n^*) \ne \bot \), the adversary forges for a real key and invokes event \(X_{\text {0.1}}\). In this case, we return 1 to the challenger. If, on the other hand, \(\mathsf {AEAD}.\mathsf {Dec} (\gamma , t', n^*) = \bot \), the adversary forges for a random key and invokes event \(X_{\text {0.2}}\). In this case, we return 0 to the challenger. This implies that any adversary that can distinguish Game 0.1 from Game 0.2, can be transformed into a successful adversary \({\mathcal {B}} _{\mathsf {PPRF} 1}\) breaking the security of the PPRF.
Bounding \(\Pr [X_\text {0.2}]\) We conclude the proof of the lemma by showing that any adversary invoking event \(X_{0.2}\) in Game 0.2 breaks the \(\mathsf {INT\text {-}CTXT}\) security of \(\mathsf {AEAD}\). To this end, consider the following adversary \({\mathcal {B}} _{\mathsf {AEAD} 1}\).
Construction of \({\mathcal {B}} _{\mathsf {AEAD} 1}\) \({\mathcal {B}} _{\mathsf {AEAD} 1}\) proceeds exactly like the challenger in Game 0.2 but we use the AEAD challenger as the encryption/decryption procedure with respect to the ticket associated to the j-th query. As soon as the adversary issues the j-th \({{\mathcal {O}}_\mathsf {Dec}}\) or \({{\mathcal {O}}_\mathsf {Test}}\) query for some ticket t, \({\mathcal {B}} _{\mathsf {AEAD} 1}\) outputs t to its AEAD challenger. Note that t is the first valid forgery with \(n > \mu \) by \({\mathcal {A}}\) due to our changes in Game 0.1 and note that t is encrypted under a uniformly random key \(\rho \) (which is perfectly hidden from the adversary) due to our changes in Game 0.2. Hence the AEAD challenger accepts t as a valid forgery, and we have
Summing up all probabilities proves the lemma. \(\square \)
Continuing with our proof, we now have that
Now, after proving the above lemma, we return to our original sequence of games. Using Lemma 1, we can now assume that the adversary never forges a ticket \(t = (t', n)\) with \(n > \mu \) such that \({{\mathcal {O}}_\mathsf {Dec}} (t) \ne \bot \) or \({{\mathcal {O}}_\mathsf {Test}} (t) \ne \bot \).
Game 2
This game is identical to Game 1, except for the following changes. At the beginning of the experiment the challenger picks an index  . It aborts the security experiment and outputs a random bit
. It aborts the security experiment and outputs a random bit  , if the adversary queries \({{\mathcal {O}}_\mathsf {Test}} (t)\) with \(t = (t', i)\) such that \(i \ne \nu \). Since the choice of
, if the adversary queries \({{\mathcal {O}}_\mathsf {Test}} (t)\) with \(t = (t', i)\) such that \(i \ne \nu \). Since the choice of  is oblivious to \({\mathcal {A}}\) until an abort occurs, we have
is oblivious to \({\mathcal {A}}\) until an abort occurs, we have
Game 3
This game is identical to Game 2, except that at the beginning of the game we compute \(\kappa _\nu = \mathsf {PPRF}.\mathsf {Eval} (k,\nu )\) and then \(k := \mathsf {PPRF}.\mathsf {Punct} (k,\nu )\). Furthermore, we replace algorithm \(\mathsf {PPRF}.\mathsf {Eval} \) with the following algorithm \(F_{3}\):
Everything else works exactly as before. Note that we have simply implemented algorithm \(\mathsf {PPRF}.\mathsf {Eval} \) in a slightly different way. Since \(\mathsf {PPRF} \) is invariant to puncturing, the fact that \(\kappa _\nu \) was computed early, immediately followed by \(k := \mathsf {PPRF}.\mathsf {Punct} (k,\nu )\), is invisible to \({\mathcal {A}} \). Hence, Game 3 is perfectly indistinguishable from Game 2, and we have
Game 4
This game is identical to Game 3, except that the challenger now additionally picks a random key  from the range of the PPRF. Furthermore, we replace algorithm \(F_{4}\) with the following algorithm \(F_{4}\):
from the range of the PPRF. Furthermore, we replace algorithm \(F_{4}\) with the following algorithm \(F_{4}\):
Everything else works exactly as before. We will now show that any adversary that is able to distinguish Game 3 from Game 4 can be used to construct an adversary \({\mathcal {B}} _{\mathsf {PPRF} 2}\) against the \(\mathsf {na\text {-}rand}\)-security of the PPRF. Concretely, we have
Construction of \({\mathcal {B}} _{\mathsf {PPRF} 2}\) \({\mathcal {B}} _{\mathsf {PPRF} 2}\) initially picks  and outputs \(\nu \) to its PPRF-challenger, which will respond with a punctured key \(k := \mathsf {PPRF}.\mathsf {Punct} (k,\nu )\) and a value \(\gamma \), where either \(\gamma = \mathsf {PPRF}.\mathsf {Eval} (k, \nu )\) or
and outputs \(\nu \) to its PPRF-challenger, which will respond with a punctured key \(k := \mathsf {PPRF}.\mathsf {Punct} (k,\nu )\) and a value \(\gamma \), where either \(\gamma = \mathsf {PPRF}.\mathsf {Eval} (k, \nu )\) or  . Now \({\mathcal {B}} _{\mathsf {PPRF} 2}\) simulates Game 4, except that it uses the following function F in place of \(F_{4}\).
. Now \({\mathcal {B}} _{\mathsf {PPRF} 2}\) simulates Game 4, except that it uses the following function F in place of \(F_{4}\).
Eventually, \({\mathcal {A}} \) will output a guess \(b^*\). \({\mathcal {B}} _{\mathsf {PPRF} 2}\) forwards this bit to the PPRF-challenger. Note that if \(\gamma = \mathsf {Eval} (k, \nu )\), then function F is identical to \(F_{3}\), while if \(\gamma = \rho \) then it is identical to \(F_{4}\). This proves the claim.
Game 5
This game is identical to Game 4, except that we raise an event \(\mathsf {abort_{\mathsf {AEAD} 2}}\), abort the game, and output a random bit  , if the adversary \({\mathcal {A}}\) ever queries \({{\mathcal {O}}_\mathsf {Test}} (t)\) for a ticket \(t = (t', \nu ) \ne t_\nu \) (i.e., t differs from the \(\nu \)-th ticket in the first position), but \(\mathsf {AEAD}.\mathsf {Dec} (\rho , t', \nu ) \ne \bot \), where \(\rho = F_{4}(k, \nu )\). We have
, if the adversary \({\mathcal {A}}\) ever queries \({{\mathcal {O}}_\mathsf {Test}} (t)\) for a ticket \(t = (t', \nu ) \ne t_\nu \) (i.e., t differs from the \(\nu \)-th ticket in the first position), but \(\mathsf {AEAD}.\mathsf {Dec} (\rho , t', \nu ) \ne \bot \), where \(\rho = F_{4}(k, \nu )\). We have
and we claim that we can construct an adversary \({\mathcal {B}} _{\mathsf {AEAD} 2}\) on the \(\mathsf {INT\text {-}CTXT}\)-security of the AEAD with advantage at least \(\Pr [\mathsf {abort_{\mathsf {AEAD} 2}}]\).
Construction of \({\mathcal {B}} _{\mathsf {AEAD} 2}\) \({\mathcal {B}} _{\mathsf {AEAD} 2}\) proceeds exactly like the challenger in Game 5, except that it uses its challenger from the AEAD security experiment to create ticket \(t_\nu \). To this end, it outputs the tuple \((s_\nu , \nu )\) for some  to the AEAD challenger. The AEAD challenger responds with \(t_\nu ' := \mathsf {AEAD}.\mathsf {Enc} (\rho , s_\nu , \nu )\), computed with an independent AEAD key \(\rho \). Finally, \({\mathcal {B}} _{\mathsf {AEAD} 2}\) defines the ticket as \(t_\nu = (t_\nu ', \nu )\). Apart from this, \({\mathcal {B}} _{\mathsf {AEAD} 2}\) proceeds exactly like the challenger in Game 5.
to the AEAD challenger. The AEAD challenger responds with \(t_\nu ' := \mathsf {AEAD}.\mathsf {Enc} (\rho , s_\nu , \nu )\), computed with an independent AEAD key \(\rho \). Finally, \({\mathcal {B}} _{\mathsf {AEAD} 2}\) defines the ticket as \(t_\nu = (t_\nu ', \nu )\). Apart from this, \({\mathcal {B}} _{\mathsf {AEAD} 2}\) proceeds exactly like the challenger in Game 5.
Whenever the adversary \({\mathcal {A}}\) makes a query \({{\mathcal {O}}_\mathsf {Test}} (t)\) with a ticket \(t = (t', i)\) with \(i \ne \nu \), then we abort, due to the changes introduced in Game 2. If it queries \({{\mathcal {O}}_\mathsf {Test}} (t)\) with \(t = (t', \nu )\) such that \(t \ne t_\nu \), then \({\mathcal {B}} _{\mathsf {AEAD} 1}\) responds with \(\bot \) and outputs the tuple \((t', \nu )\) to its AEAD challenger. With probability \(\Pr [\mathsf {abort_{\mathsf {AEAD} 2}}]\) this ticket is valid, which yields
Game 6
This game is identical to Game 5, except that when the adversary queries \({{\mathcal {O}}_\mathsf {Test}} (t_\nu )\), then we will always answer with a random value, independent of the bit b. More precisely, recall that we abort if the adversary queries \({{\mathcal {O}}_\mathsf {Test}} (t)\), \(t = (t', \nu )\) such that \(t \ne t_\nu \), due to the changes introduced in Game 5. If the adversary queries \({{\mathcal {O}}_\mathsf {Test}} (t_\nu )\), then the challenger in Game 5 uses the bit  sampled at the beginning of the experiment as follows. If \(b=1\), then it returns the session key \(s_\nu \). Otherwise, a random
sampled at the beginning of the experiment as follows. If \(b=1\), then it returns the session key \(s_\nu \). Otherwise, a random  is returned.
is returned.
In Game 6, the challenger samples another random value  at the beginning of the game. When the adversary queries \({{\mathcal {O}}_\mathsf {Test}} (t_\nu )\), then if \(b=1\) the challenger returns \(s_\nu '\). Otherwise, it returns a random
at the beginning of the game. When the adversary queries \({{\mathcal {O}}_\mathsf {Test}} (t_\nu )\), then if \(b=1\) the challenger returns \(s_\nu '\). Otherwise, it returns a random  . Note that in either case the response of the \({{\mathcal {O}}_\mathsf {Test}} (t_\nu )\)-query is a random value, independent of b. Therefore, the view of \({\mathcal {A}}\) in Game 6 is independent of b. Obviously, we have
. Note that in either case the response of the \({{\mathcal {O}}_\mathsf {Test}} (t_\nu )\)-query is a random value, independent of b. Therefore, the view of \({\mathcal {A}}\) in Game 6 is independent of b. Obviously, we have
We will now show that any adversary who is able to distinguish Game 5 from Game 6 can be used to construct an adversary \({\mathcal {B}} _{\mathsf {AEAD} 3}\) against the \(\mathsf {IND\text {-}CPA}\)-security of \(\mathsf {AEAD} \).
Construction of \({\mathcal {B}} _{\mathsf {AEAD} 3}\) Recall that the key used to generate ticket \(t_\nu \) is \(\rho = F_{4}(k,\nu )\). By definition of \(F_{4}\), \(\rho \) is an independent random string chosen at the beginning of the security experiment. This enables a straightforward reduction to the \(\mathsf {IND\text {-}CPA}\)-security of the AEAD.
\({\mathcal {B}} _{\mathsf {AEAD} 3}\) proceeds exactly like the challenger in Game 6, except for the way the ticket \(t_\nu \) is created. \({\mathcal {B}} _{\mathsf {AEAD} 3}\) computes \(\rho _\nu = F_{4}(k,\nu )\). Then it outputs \((s_\nu , s_\nu ', \nu )\) to its challenger, which returns
where \(\rho \) is distributed identically to \(\rho _\nu \) and \(b'\) is the hidden bit used by the challenger of the AEAD. Apart from this, \({\mathcal {B}} _{\mathsf {AEAD} 3}\) proceeds exactly like the challenger in Game 6. Eventually, \({\mathcal {A}} \) will output a guess \(b^*\). \({\mathcal {B}} _{\mathsf {AEAD} 3}\) forwards this bit to its challenger.
Note that if \(b'=0\), then the view of \({\mathcal {A}}\) is perfectly indistinguishable from Game 5, while if \(b'=1\) then it is identical to Game 6. Thus, we have
By summing up probabilities from Game 0 to Game 6, we obtain
\(\square \)
4 Composition with the TLS 1.3 Resumption Handshake
In this section we show how to compose a 0-RTT session resumption protocol with the TLS 1.3 resumption handshake, also called pre-shared key (PSK) mode. We start with a brief section on building blocks used in TLS. Next we recap the multi-stage key exchange model, and finally we describe our protocol composition and prove its security.
4.1 Building Blocks and Security Assumptions
Before we can describe our construction, we need to introduce a few more primitives and their respective security notions. The first two notions cover collision resistant hash functions and pseudorandom functions.
Unkeyed hash functions \(H : \{0,1\} ^* \rightarrow \{0,1\} ^\lambda \), as deployed in practice, always imply the existence of collisions, as the range of H is smaller than the domain. Instead of assuming that no efficient adversary is able to find collisions, we follow the approach by Rogaway [53] and assume that it is hard to efficiently construct an adversary that can efficiently find collisions.
Definition 11
A hash function \(H : \{0,1\} ^* \rightarrow \{0,1\} ^\lambda \) that maps arbitrary finite-length bit strings to strings of fixed length \(\lambda \) is called collision resistant if we cannot efficiently construct an efficient adversary \({\mathcal {A}}\) whose advantage

is non-negligible.
Definition 12
Let \(\mathsf {PRF}: \{0,1\} ^* \times \{0,1\} ^{i(\lambda )} \rightarrow \{0,1\} ^{o(\lambda )}\) be an efficient keyed function with input length \(i(\lambda )\) and output length \(o(\lambda )\). We call f pseudorandom if for all probabilistic polynomial-time adversaries \({\mathcal {A}}\) the advantage

is negligible in \(\lambda \), where  and f is randomly chosen from the set of all functions mapping \(\{0,1\} ^{i(\lambda )} \rightarrow \{0,1\} ^{o(\lambda )}\).
and f is randomly chosen from the set of all functions mapping \(\{0,1\} ^{i(\lambda )} \rightarrow \{0,1\} ^{o(\lambda )}\).
TLS 1.3 additionally relies on the hash-based key derivation function (HKDF) [40, 41] which utilizes the HMAC construction [6, 39] as a core building block. The HKDF follows the extract-then-expand paradigm, that is, it employs special functions to extract and expand keys. The extract function \(\mathsf {Ext} ( salt , src )\) takes a (potentially fixed) salt \( salt \) and a source key material \( src \) as input and computes a pseudorandom key as output. The expand function \(\mathsf {Exp} ( key , ctxt )\) takes a pseudorandom key \( key \) and a context \( ctxt \) as input and computes a new pseudorandom key. Formally, the expand function also takes an additional length parameter, determining the length of the computed key, as input. We omit this parameter for simplicity and assume that the length is equal to the security parameter \(\lambda \) unless stated otherwise.
For our security proof in Sect. 4.3, we rely on the assumption that both functions \(\mathsf {Ext}\) and \(\mathsf {Exp}\) are pseudorandom functions [41]. Additionally, we rely on the \(\mathsf {HMAC} (0,\$)\text {-}\$\) assumption introduced in [28]. This assumption states that \(\mathsf {HMAC} (0, x)\) is computationally indistinguishable from  if
if  and was used to prove the security of draft-14 of TLS 1.3 in [28].
and was used to prove the security of draft-14 of TLS 1.3 in [28].
Definition 13
Let \(\mathsf {HMAC}\) be the function defined in [6]. We say the \(\mathsf {HMAC} (0,\$)\text {-}\$\) assumption holds for \(\mathsf {HMAC}\) if for all probabilistic polynomial-time adversaries \({\mathcal {A}}\) the advantage

is negligible in \(\lambda \).
4.2 Multi-stage Key Exchange
The TLS 1.3 protocol establishes multiple keys during execution. Some of these keys are used to encrypt parts of the communication during protocol execution, while others are used for external (application layer) purposes only. To formally analyze such a multi-key protocol, we use an extension [28] of the multi-stage key exchange model introduced by Fischlin and Günther [27], which has been used to prove security of various drafts of the TLS 1.3 protocol. Their model allows dividing the key exchange protocols into so-called stages, where each stage yields a key that supports a certain level of security. Since we only consider session resumption protocols in this work, we will only briefly describe the relevant parts of the model. See [28] for a more comprehensive description of the model.
Changes to the Model The model is taken verbatim from [28], except for the following minor changes.
-
We removed all model features that are unnecessary for proving TLS 1.3 in its pre-shared key mode, composed with our generic 0-RTT session resumption protocol. Namely, we removed key dependent aspects (TLS 1.3 supports key independence), authentication levels other than mutual authentication (our protocol provides mutual authentication), and replayable stages (our protocol is non-replayable across all stages).
-
We modified the corruption query. Instead of revealing the pre-shared keys of a server, we equip each server with a long-term key k which is used to issue and open tickets. Corruption of a server will leak the current state of the server’s secret key k. Due to the nature of our 0-RTT session resumption protocol introduced earlier, the server’s secret key will change with each protocol execution.
Protocol-Specific and Session-Specific Properties The multi-stage key exchange model separates protocol-specific and session-specific properties. Protocol-specific properties capture, for example, the number of stages and whether established keys are used externally only, while session-specific properties capture, for example, the state of a running session. We begin by listing the protocol-specific properties which are represented by a vector \(({\mathsf {M}}, \mathsf {USE})\) holding the following information:
-
\({\mathsf {M}} \in {\mathbb {N}} \): The number of stages, that is, the number of keys derived.
-
\(\mathsf {USE} = \{\mathsf {internal}, \mathsf {external} \}^{\mathsf {M}} \): The set of key usage indicators for each stage, indicating how a stage-i key is used. We call a key internal if it used within (and possibly outside of) the key exchange protocol, and external if it is only used outside of the key exchange protocol.
We denote the set of users by \({\mathcal {U}} \), where each user is associated with a unique identity \(U \in {\mathcal {U}} \). Sessions are identified by a unique label \(\mathsf {label} \in {\mathcal {U}} \times {\mathcal {U}} \times {\mathbb {N}} \), where \(\mathsf {label} = (U, V, d)\) denotes the d-th local session of user (and owner of the session) U with the intended communication partner V.
Each session is associated with a key index d for the pre-shared secret \(\mathsf {pss}\) and its unique identifier \(\mathsf {psid}\). The challenger maintains vectors \(\mathsf {pss} _{U,V}\) and \(\mathsf {psid} _{U,V}\) of created pre-shared secrets, where the d-th entry is the d-th pre-shared secret (resp. d-th identifier) shared between users U and V. We write \(\mathsf {pss} _{U,V,d}\) (resp. \(\mathsf {psid} _{U,V,d}\)) as shorthand for the d-th entry of \(\mathsf {pss} _{U,V}\) (resp. \(\mathsf {psid} _{U,V}\)).
A session is represented by a tuple \(\sigma \) and comprises of the following information:
-
\(\mathsf {label} \in {\mathcal {U}} \times {\mathcal {U}} \times {\mathbb {N}} \): The unique session label.
-
\(\mathsf {id} \in {\mathcal {U}} \): The identity of the session owner.
-
\(\mathsf {pid} \in {\mathcal {U}} \): The identity of the intended communication partner.
-
\(\mathsf {role} \in \{\mathsf {initiator}, \mathsf {responder} \}\): The role of the session owner.
-
\(\mathsf {execstate} \in \{\mathsf {RUNNING} \cup \mathsf {ACCEPTED} \cup \mathsf {REJECTED} \}\): The state of execution where
$$\begin{aligned} \mathsf {RUNNING}&= \{\mathsf {running} _i \mid i \in {\mathbb {N}} \cup \{0\}\},\\ \mathsf {ACCEPTED}&= \{\mathsf {accepted} _i \mid i \in {\mathbb {N}} \}, \text { and}\\ \mathsf {REJECTED}&= \{\mathsf {rejected} _i \mid i \in {\mathbb {N}} \}. \end{aligned}$$The state is set to \(\mathsf {accepted} _i\) if the session accepts the i-th key. It is set to \(\mathsf {running} _i\) if the session proceeds with the protocol after accepting the i-th key. It is set to \(\mathsf {rejected} _i\) if the session rejects the i-th key (we assume that a session does not continue in this case). The default value is \(\mathsf {running} _0\).
-
\(\mathsf {stage} \in [{\mathsf {M}} ]\): The session’s current stage, where the value \(\mathsf {stage}\) is incremented to i after the state \(\mathsf {execstate}\) accepts or rejects the i-th key. The default value is \(\mathsf {stage} = 0\).
-
\(\mathsf {sid} \in (\{0,1\} ^* \cup \{\bot \})^{\mathsf {M}} \): \(\mathsf {sid} _i\) is the session identifier in stage i. It is set once after the i-th key has been accepted. The default value is \(\mathsf {sid} = (\bot , \ldots , \bot )\).
-
\(\mathsf {cid} \in (\{0,1\} ^* \cup \{\bot \})^{\mathsf {M}} \): \(\mathsf {cid} _i\) is the contributive identifier in stage i. It may be set multiple times until the i-th key has been accepted. The default value is \(\mathsf {cid} = (\bot , \ldots , \bot )\).
-
\(\mathsf {key} \in (\{0,1\} ^* \cup \{\bot \})^{\mathsf {M}} \): \(\mathsf {key} _i\) is the established session key in stage i. It set once after the i-th key has been accepted. The default value is \(\mathsf {key} = (\bot , \ldots , \bot )\).
-
\(\mathsf {keystate} \in \{\mathsf {fresh}, \mathsf {revealed} \}^{\mathsf {M}} \): \(\mathsf {keystate} _i\) is the state of the key in stage i. The state \(\mathsf {fresh}\) indicates that the key is fresh and the state \(\mathsf {revealed}\) indicates that the key has been revealed to the adversary. The default value is \(\mathsf {keystate} = (\mathsf {fresh}, \ldots , \mathsf {fresh})\).
-
\(\mathsf {tested} \in \{\mathsf {true}, \mathsf {false} \}^{\mathsf {M}} \): \(\mathsf {tested} _i\) is a boolean value indicating whether the session key of stage i has been tested. The default value is \(\mathsf {tested} = (\mathsf {false}, \ldots , \mathsf {false})\).
-
\(d \in {\mathbb {N}} \): The index of the pre-shared secret used in a protocol execution.
-
\(\mathsf {pss} \in \{0,1\} ^* \cup \{\bot \}\): The pre-shared secret to be used in the session.
-
\(\mathsf {psid} \in \{0,1\} ^* \cup \{\bot \}\): The identifier of the pre-shared secret to be used in the session.
Each session is stored and maintained in a session list \(\mathsf {SList} \). If an incomplete session tuple \(\sigma \) is added to the session list \(\mathsf {SList}\), we set all empty values to their defined default values. For a more convenient notation, we write \(\mathsf {label}.\mathsf {sid} \) to denote the entry \(\mathsf {sid}\) in the tuple \(\sigma \) with the unique label \(\mathsf {label}\) in \(\mathsf {SList}\).
Following Günther et al. [28], we define two distinct sessions \(\mathsf {label}, \mathsf {label} '\) to be partnered if the session’s session identifiers are equal (i.e., \(\mathsf {label}.\mathsf {sid} = \mathsf {label} '.\mathsf {sid} ' \ne \bot \)). Additionally, we require for correctness that two sessions are partnered if the sessions have a non-tampered joint execution and both parties have reached an acceptance state. This means that a protocol is correct if, in the absence of an adversary, any two sessions executing the protocol are partnered upon acceptance.
Adversary Model We consider a probabilistic polynomial-time adversary \({\mathcal {A}}\) that controls the communication between all parties, and is capable of intercepting, injecting, and dropping messages. We capture adversarial behavior where the adversary trivially loses via a flag \(\mathsf {lost}\) initialized to \(\mathsf {lost}:= \mathsf {false} \). The adversary has access to the following queries:
-
\(\mathsf {NewSecret} (U, V, d, \mathsf {psid})\): This query generates a new pre-shared secret \(\mathsf {pss}\) with identifier \(\mathsf {psid}\). The secret \(\mathsf {pss}\) is the d-th secret shared between users U and V. If \(\mathsf {psid}\) is a used identifier for an already registered secret or if the d-th secret between U and V has already been set, return \(\bot \). Otherwise, sample the secret \(\mathsf {pss}\) uniformly at random from the pre-shared secret space and store \(\mathsf {pss}\) in \(\mathsf {pss} _{U, V}\) and \(\mathsf {pss} _{V, U}\) (as well as \(\mathsf {psid}\) in \(\mathsf {psid} _{U, V}\) and \(\mathsf {psid} _{V, U}\)) as the d-th entry.
-
\(\mathsf {NewSession} (U, V, \mathsf {role}, d)\): Creates a new session with a unique new label \(\mathsf {label}\) for session owner identity \(\mathsf {id} = U\) with role \(\mathsf {role}\), having \(\mathsf {pid} = V\) as intended partner. The value d indicates the key index of the pre-shared secret \(\mathsf {pss}\) between U and V.
If the d-th pre-shared secret \(\mathsf {pss} = \mathsf {pss} _{U, V, d}\) does not exist, return \(\bot \). Otherwise, set \(\mathsf {label}.\mathsf {pss}:= \mathsf {pss} \) and \(\mathsf {label}.\mathsf {psid}:= \mathsf {psid} _{U, V, d}\). Add \(\sigma = (\mathsf {label}, U, V, \mathsf {role}, d,\mathsf {pss}, \mathsf {psid})\) to \(\mathsf {SList}\) and return \(\mathsf {label}\).
-
\(\mathsf {Send} (\mathsf {label}, m)\): Sends a message m to the session with label \(\mathsf {label}\). If there is no tuple \(\sigma \) with label \(\mathsf {label}\) in \(\mathsf {SList}\), return \(\bot \). Otherwise run the protocol as the session owner of \(\mathsf {label}\) when receiving message m and return the output and the updated state of execution \(\mathsf {label}.\mathsf {execstate} \). If \(\mathsf {label}.\mathsf {role} = \mathsf {initiator} \) and \(m = \mathsf {init} \), the protocol is initiated without any input message.
If the state of execution changes to an accepted state for stage i, the protocol execution is suspended and \(\mathsf {accepted} _i\) is send to the adversary. The adversary can later resume execution by issuing a \(\mathsf {Send} (\mathsf {label}, \mathsf {continue})\) query, receiving the next protocol message and the next state of execution.
If the state of execution changes to \(\mathsf {accepted} _i\) for some \(i \in [{\mathsf {M}} ]\) and there is a partnered session \(\mathsf {label} ' \ne \mathsf {label} \) in \(\mathsf {SList}\) with \(\mathsf {label} '.\mathsf {keystate} _i = \mathsf {revealed} \), then \(\mathsf {label}.\mathsf {keystate} _i\) is set to \(\mathsf {revealed}\) as well.
If the state of execution changes to \(\mathsf {accepted} _i\) for some \(i \in [{\mathsf {M}} ]\) and there is a partnered session \(\mathsf {label} ' \ne \mathsf {label} \) in \(\mathsf {SList}\) with \(\mathsf {label} '.\mathsf {tested} _i = \mathsf {true} \), then set \(\mathsf {label}.\mathsf {tested} _i := \mathsf {true} \) and also set set \(\mathsf {label}.\mathsf {key} _i := \mathsf {label}.\mathsf {key} _i\) if \(\mathsf {USE} _i = \mathsf {internal} \). If the state of execution changes to \(\mathsf {accepted} _i\) for some \(i \in [{\mathsf {M}} ]\) and the intended partner \(\mathsf {pid} \) is corrupted, then set \(\mathsf {label}.\mathsf {keystate} _i := \mathsf {revealed} \).
-
\(\mathsf {Reveal} (\mathsf {label}, i)\): Reveals the i-th key of session \(\mathsf {label}\). If there is no session with label \(\mathsf {label}\) in \(\mathsf {SList}\) or if \(\mathsf {label}.\mathsf {stage} < i\) (i.e., the session key has not yet been established), then return \(\bot \). Otherwise, set \(\mathsf {label}.\mathsf {keystate} _i := \mathsf {revealed} \) and if there exists a partnered session \(\mathsf {label} '\) in \(\mathsf {SList}\) with \(\mathsf {label}.\mathsf {stage} \ge i\), then additionally set \(\mathsf {label}.\mathsf {keystate} _i := \mathsf {revealed} \). Finally, send the session key \(\mathsf {label}.\mathsf {key} _i\) to the adversary.
-
\(\mathsf {Corrupt} (U)\): This query provides the adversary with the long-term secret k of participant \(U \in {\mathcal {U}}\). For stage-j forward secrecy we additionally set \(\mathsf {keystate} _i\) to \(\mathsf {revealed}\) if \(i < j\) (i.e., revelation of non-forward-secret keys) or if \(i > \mathsf {stage} \) (i.e., revelation of future keys).
-
\(\mathsf {Test} (\mathsf {label}, i)\): Tests the i-th key in the session \(\mathsf {label}\). If there is no session with the label \(\mathsf {label}\) in \(\mathsf {SList}\) or \(\mathsf {label}.\mathsf {tested} _i = \mathsf {true} \), return \(\bot \). If \(\mathsf {label}.\mathsf {execstate} \ne \mathsf {accepted} _i\) or if there is a partnered session \(\mathsf {label} '\) in \(\mathsf {SList}\) with \(\mathsf {label}.\mathsf {execstate} \ne \mathsf {accepted} _i\), set \(\mathsf {lost}:= \mathsf {true} \) (i.e., only allow testing if the key has not been used yet). Otherwise, set \(\mathsf {label}.\mathsf {tested} _i := \mathsf {true} \).
The \(\mathsf {Test}\) oracle maintains a global bit
 . If \(b_\mathsf {test} = 0\), sample a random session key
. If \(b_\mathsf {test} = 0\), sample a random session key  . Else set \(K := \mathsf {label}.\mathsf {key} _i\) to the real session key.
. Else set \(K := \mathsf {label}.\mathsf {key} _i\) to the real session key.If \(\mathsf {USE} _i = \mathsf {internal} \), set \(\mathsf {label}.\mathsf {key} _i := K\) (i.e., we replace the internally used session key with the random and independent test key K). Additionally, if a partnered session \(\mathsf {label} '\) exists, we set \(\mathsf {label} '.\mathsf {tested}:= \mathsf {true} \) if the i-th key was accepted. Furthermore, we also set \(\mathsf {label} '.\mathsf {key} _i := \mathsf {label}.\mathsf {key} _i\) if \(\mathsf {USE} _i = \mathsf {internal} \).
Finally, return K.
Match Security The notion of \(\mathsf {Match}\) security ensures that session identifiers properly identify partnered sessions in the following sense:
-
1.
Sessions with the same session identifier for some stage hold the same key at that stage.
-
2.
Sessions with the same session identifier for some stage share the same contributive identifier at that stage.
-
3.
Sessions are partnered with the intended participant, and share the same key index.
-
4.
Session identifiers do not match across different stages.
-
5.
At most two sessions have the same session identifier at any stage.
Formally, we define the \(\mathsf {Match}\) security game \(\mathsf G^\mathsf {Match} _{{\mathcal {A}}, \mathsf {KE}}(\lambda )\) as follows:
Definition 14
Let \(\mathsf {KE}\) be a multi-stage key exchange protocol with properties \(({\mathsf {M}},\mathsf {USE})\) and \({\mathcal {A}}\) a probabilistic polynomial-time adversary interacting with \(\mathsf {KE}\) in the following game \({\mathsf {G}}^\mathsf {Match} _{{\mathcal {A}}, \mathsf {KE}}(\lambda )\):
-
1.
The challenger generates a long-term k key for each participant \(U \in {\mathcal {U}}\).
-
2.
The adversary gets access to the queries \(\mathsf {NewSecret}, \mathsf {NewSession}, \mathsf {Send}, \mathsf {Reveal},\mathsf {Corrupt}, \mathsf {Test} \).
-
3.
Eventually, \({\mathcal {A}}\) stops with no output.
We say that \({\mathcal {A}}\) wins the game, denoted by \(\mathsf G^\mathsf {Match} _{{\mathcal {A}}, \mathsf {KE}}(\lambda ) = 1\), if at least one of the following events occurs:
-
1.
Different session keys in some stage of partnered sessions. More formally, if there exist two distinct labels \(\mathsf {label}, \mathsf {label} '\) such that \(\mathsf {label} = \mathsf {label} ' \ne \bot \) for some stage \(i \in [{\mathsf {M}} ]\) and \(\mathsf {label}.\mathsf {execstate} \ne \mathsf {rejected} _i\) and \(\mathsf {label} '.\mathsf {execstate} \ne \mathsf {rejected} _i\), but \(\mathsf {label}.\mathsf {key} _i \ne \mathsf {label} '.\mathsf {key} _i\).
-
2.
Different or unset contributive identifiers in some stage of partnered sessions. More formally, if there exist two distinct labels \(\mathsf {label}, \mathsf {label} '\) such that \(\mathsf {label} = \mathsf {label} ' \ne \bot \) for some stage \(i \in [{\mathsf {M}} ]\), but \(\mathsf {label}.\mathsf {cid} _i \ne \mathsf {label} '.\mathsf {cid} _i\) or \(\mathsf {label}.\mathsf {cid} _i = \mathsf {label} '.\mathsf {cid} _i = \bot \).
-
3.
Different stages share the same session identifier. More formally, if there exist two (not necessarily distinct) labels \(\mathsf {label}, \mathsf {label} '\) such that \(\mathsf {label}.\mathsf {sid} _i = \mathsf {label} '.\mathsf {sid} _j \ne \bot \) for some stages \(i, j \in [{\mathsf {M}} ]\) with \(i \ne j\).
-
4.
More than two sessions share the same session identifier in any stage. More formally, if there exist three distinct labels \(\mathsf {label}, \mathsf {label} ', \mathsf {label} ''\) such that \(\mathsf {label}.\mathsf {sid} _i = \mathsf {label} '.\mathsf {sid} _i = \mathsf {label} ''.\mathsf {sid} _i\) for some stage \(i \in [{\mathsf {M}} ]\).
We say \(\mathsf {KE}\) is \(\mathsf {Match}\)-secure if for all probabilistic polynomial-time adversaries \({\mathcal {A}}\) the advantage
is negligible in \(\lambda \).
Multi-stage Security The notion of \(\mathsf {MultiStage}\) security ensures that, for each stage, keys are indistinguishable from randomly sampled keys in the multi-stage setting.
Definition 15
Let \(\mathsf {KE}\) be a multi-stage key exchange protocol with key distribution \({\mathcal {D}}\) and properties \(({\mathsf {M}}, \mathsf {USE})\) and \({\mathcal {A}}\) a probabilistic polynomial-time adversary interacting with \(\mathsf {KE}\) in the following game \({\mathsf {G}}^{\mathsf {MultiStage}, {\mathcal {D}}}_{{\mathcal {A}}, \mathsf {KE}}(\lambda )\):
-
1.
The challenger generates a long-term key k for each participant \(U \in {\mathcal {U}}\). Additionally, the challenger samples a random test bit
 and sets \(\mathsf {lost}:= \mathsf {false} \).
and sets \(\mathsf {lost}:= \mathsf {false} \). -
2.
The adversary gets access to the queries \(\mathsf {NewSecret}, \mathsf {NewSession}, \mathsf {Send}, \mathsf {Reveal},\mathsf {Corrupt}, \mathsf {Test} \). Note that such queries may set the flag \(\mathsf {lost}\) to \(\mathsf {true}\).
-
3.
Eventually, \({\mathcal {A}}\) stops and outputs a guess b.
-
4.
The challenger \({\mathcal {C}}\) sets the flag \(\mathsf {lost}:= \mathsf {true} \) if there exist two (not necessarily distinct) session labels \(\mathsf {label}, \mathsf {label} '\) and some stage \(i \in [{\mathsf {M}} ]\) such that \(\mathsf {label}.\mathsf {sid} _i = \mathsf {label} '.\mathsf {sid} _i\) and \(\mathsf {label}.\mathsf {keystate} _i = \mathsf {revealed} \) and \(\mathsf {label} '.\mathsf {tested} _i = \mathsf {true} \) (i.e., if the adversary has tested and revealed the key of some stage in a single session or in two partnered sessions).
We say that \({\mathcal {A}}\) wins the game, denoted by \(\mathsf G^{\mathsf {MultiStage}, {\mathcal {D}}}_{{\mathcal {A}}, \mathsf {KE}}(\lambda ) = 1\), if \(b = b_\mathsf {test} \) and \(\mathsf {lost} = \mathsf {false} \). We say \(\mathsf {KE}\) is \(\mathsf {MultiStage}\)-secure, providing stage-j forward-secrecy, with key usage \(\mathsf {USE}\) if \(\mathsf {KE}\) is \(\mathsf {Match}\)-secure and for all probabilistic polynomial-time adversaries \({\mathcal {A}}\) the advantage
is negligible in \(\lambda \).
4.3 Composition and Security
In this section we show how to generically compose a 0-RTT session resumption protocol with the TLS 1.3 resumption handshake and prove the composition’s security in the multi-stage key exchange model, achieving a stage-1-forward-secret resumption handshake. In contrast, without such a session resumption protocol it is only possible to show that the TLS 1.3 resumption handshake only achieves stage-3 forward-secrecy via an additional execution of a Diffie–Hellman key exchange [28].
Integrating a 0-RTT Session Resumption Protocol into TLS 1.3 As explained in the Introduction, the TLS 1.3 standard allows the server to unilaterally choose a mechanism for issuing tickets and serving resumption handshakes. The only interoperability requirement is correctness, i.e. when resuming a session, the server should correctly compute the relevant resumption secret and use it as prescribed by the key schedule. The client is generally not aware of the resumption mechanism in use by the server; the client merely receives an opaque ticket, and sends it to the server when resuming.
In our construction, tickets are computed using a 0-RTT session resumption protocol. Let \(\mathsf {Resumption} = (\mathsf {Setup}, \mathsf {TicketGen}, \mathsf {ServerRes})\) be a 0-RTT session resumption protocol. The server uses  to compute its long-term key k for ticket encryption. Tickets are computed as \(\mathsf {ticket} = \mathsf {TicketGen} (k, \mathsf {RMS} || {\mathsf {N}} _{T})\) and can be opened using the \(\mathsf {ServerRes}\) algorithm.
to compute its long-term key k for ticket encryption. Tickets are computed as \(\mathsf {ticket} = \mathsf {TicketGen} (k, \mathsf {RMS} || {\mathsf {N}} _{T})\) and can be opened using the \(\mathsf {ServerRes}\) algorithm.
Note that by computing \((\mathsf {RMS} {||} {\mathsf {N}} _{T}, k') := \mathsf {ServerRes} (k, \mathsf {ticket})\) a modified secret key of the server \(k'\) is produced. Replacing \(k := k'\) guarantees forward secrecy if \(\mathsf {Resumption}\) is a \(\mathsf {0\text {-}RTT\text {-}SR}\)-secure protocol. That is, forward secrecy is invoked immediately after the ticket has been processed on the server side. Should k leak at a later point in time, the resumption master secret \(\mathsf {RMS}\) (and all keys derived from it) will not be compromised.
On Sending Multiple PSKs TLS 1.3 allows the client to send multiple pre-shared key identifiers in its first message if no 0-RTT data is sent. If, however, 0-RTT data is sent, the standard explicitly states that the handshake will be aborted unless the server picks the first pre-shared key identifier from the client’s list [51, §4.2.10, §4.2.11]. This restriction exists to ensure that the early data only has to be encrypted under one pre-shared key chosen by the client. In this work we only allow the client to send one pre-shared key identifier, as we are specifically interested in the 0-RTT mode. Should a client choose not to send 0-RTT data, then previous analyses of the TLS 1.3 handshake protocol apply [28]. Hence, our change leads to a cleaner protocol and is purely cosmetic.
Protocol Description In the following, we describe our modified version of the TLS 1.3 resumption handshake. We assume that client and server have performed a prior full handshake, allowing them to agree on a pre-shared secret. The pre-shared secret is denoted as resumption master secret \(\mathsf {RMS}\). The client stores \(\mathsf {RMS}\) (and an associated nonce \({\mathsf {N}} _T\)) alongside a server-issued ticket \(\mathsf {ticket}\). The ticket \(\mathsf {ticket}\) was computed by the server using its secret key k and holds \(\mathsf {RMS}\) and \({\mathsf {N}} _T\) as contents.
We provide an illustration of the protocol in Fig. 4. For readability, the figure slightly deviates from the message format in the TLS 1.3 specification. In the figure we separated the binder value \(\mathsf {Fin} _0\) and the \(\mathsf {ticket}\) message from the \(\mathsf {ClientHello}\) message, while in the standard both are included in the \(\mathsf {ClientHello}\) message. Outside of the figure, we consider \(\mathsf {Fin} _0\) and \(\mathsf {ticket}\) as a part of the \(\mathsf {ClientHello}\).
The following messages are exchanged during protocol execution:
- \(\mathsf {ClientHello}\)::
-
The \(\mathsf {ClientHello}\) message is the first message sent by the client. It contains the protocol version, a random nonce \({\mathsf {N}} _C\) chosen by the client, a list of supported cryptographic primitives and extensions, and a pre-shared key identifier. Additionally, it contains \(\mathsf {ticket}\) which is an encryption of the resumption master secret \(\mathsf {RMS}\) and the ticket nonce \({\mathsf {N}} _T\).
- \(\mathsf {Fin} _0\)::
-
The binder value \(\mathsf {Fin} _0\) comprises of an HMAC over a (partial) \(\mathsf {ClientHello}\) message to ensure integrity.
- \(\mathsf {ServerHello}\)::
-
The \(\mathsf {ServerHello}\) message contains a server nonce \({\mathsf {N}} _S\), a selected protocol version, extensions, and supported cryptographic primitives.
- \(\mathsf {Fin} _S\)::
-
The \(\mathsf {Fin} _S\) message comprises of an HMAC over the protocol transcript up to this point and is encrypted under the server handshake traffic key.
- \(\mathsf {Fin} _C\)::
-
The \(\mathsf {Fin} _C\) message comprises of an HMAC over the protocol transcript up to the \(\mathsf {Fin} _S\) message and is encrypted under the client handshake traffic key.
More information on the computation of the hashed finished messages is given in Appendix B.
The \(\mathsf {TLS13wRES}\) protocol executed between a client and a server. The client possesses a pre-shared secret \(\mathsf {RMS}\) and a ticket \(\mathsf {ticket}\) (encrypted under the server’s secret key k) issued by the server. All values \(\ell _i\) are publicly known labels and all hash values \(H_i\) are computable from the communication’s transcript. We provide a technical overview of label values and hash values in Appendix B
Security Analysis Preliminaries In the following, we will analyze the security of our modified TLS 1.3 protocol in the multi-stage key exchange model in its pre-shared secret mode. That is, we will show that our protocol satisfies both \(\mathsf {Match}\) and \(\mathsf {MultiStage}\) security. We start by discussing some preliminaries for both proofs. The vector of protocol-specific properties \(({\mathsf {M}}, \mathsf {USE})\) looks as follows:
-
\({\mathsf {M}} = 5\): The number of stages is equal to five (cf. Fig. 4), deriving traffic keys \(\mathsf {tk} _\mathsf {ets} \), \((\mathsf {tk} _\mathsf {chts}, \mathsf {tk} _\mathsf {shts})\), \((\mathsf {tk} _\mathsf {cats}, \mathsf {tk} _\mathsf {sats})\), the exporter master secret \(\mathsf {EMS}\), and the resumption master secret \(\mathsf {RMS}\).
-
\(\mathsf {USE} = (\mathsf {external}, \mathsf {internal}, {\mathsf {internal}}, \mathsf {external}, \mathsf {external})\): The handshake traffic keys \((\mathsf {tk} _\mathsf {chts}, \mathsf {tk} _\mathsf {shts})\) are used to protect internal protocol messages, while all other keys are only used outside of the protocol.
We define session matching with the following session identifiers (implicitly) consisting of all messages sent in each stage:
Note that neither “ems,” nor “rms” contributes to the established key and they are instead included to ensure distinct session identifiers across stages. We set the contributive identifier of Stage 2 to \(\mathsf {cid} _2 = (\mathsf {ClientHello})\) after the client has sent (resp. after the server has received) the \(\mathsf {ClientHello}\) message and set, on sending (resp. receiving) the \(\mathsf {ServerHello}\) message the contributive identifier to \(\mathsf {cid} _2 = \mathsf {sid} _2\). The other contributive identifiers are set to \(\mathsf {cid} _i = \mathsf {sid} _i\) (for stages \(i \in \{1,3,4,5\}\)) after the respective stage’s session identifier was set.
\(\mathsf {Match}\) Security We start by proving \(\mathsf {Match}\) security of our construction. Our proof follows the proof by Fischlin and Günther [28, Theorem 5.1] as the constructions are very similar.
Theorem 4
The protocol \(\mathsf {TLS13wRES}\) is \(\mathsf {Match}\)-secure with the above properties \(({\mathsf {M}}, \mathsf {USE})\). For any probabilistic polynomial-time adversary we have
where \(n_s\) is the maximum number of sessions.
Proof
In order to prove the \(\mathsf {Match}\) security of \(\mathsf {TLS13wRES}\) we need to show that the five properties of \(\mathsf {Match}\) security hold for \(\mathsf {TLS13wRES}\).
-
1.
Sessions with the same session identifier for some stage hold the same key at that stage. This property holds, as all session identifiers contain the \(\mathsf {ClientHello}\) message which fixes the ticket and thus the resumption master secret \(\mathsf {RMS}\). The \(\mathsf {RMS}\) in turn determines all following keys, guaranteeing that sessions with the same identifier hold the same key at each stage.
-
2.
Sessions with the same session identifier for some stage share the same contributive identifier at that stage. This property holds trivially for Stage 1 as \(\mathsf {sid} _1 = \mathsf {cid} _1\). For all other stages \(i \in \{2,3,4,5\}\), the contributive identifier is set to its final value \(\mathsf {cid} _i := \mathsf {sid} _2\) as soon as the sender and receiver set the session identifier.
-
3.
Sessions are partnered with the intended participant, and share the same key index. This property holds as honest senders only use a legitimate ticket \(\mathsf {ticket}\) (included in the \(\mathsf {ClientHello}\) message), which ensures that both parties agree on the same partner and key index.
-
4.
Session identifiers do not match across different stages. This property holds trivially, as \(\mathsf {sid} _1, \mathsf {sid} _2, \mathsf {sid} _3\) include distinct non-optional messages and \(\mathsf {sid} _4, \mathsf {sid} _5\) include separating identifier strings.
-
5.
At most two sessions have the same session identifier at any stage. Note that each session identifier includes the \(\mathsf {ClientHello}\) message and hence the client nonce \({\mathsf {N}} _C\) of bit length \(\lambda \). The first session identifier is only set after the sever has processed the \(\mathsf {ClientHello}\) (and thus the ticket \(\mathsf {ticket}\)), implying that the server’s secret key has been replaced before accepting the Stage 1 session key. Hence, replaying the \(\mathsf {ClientHello}\) message to the server cannot lead to an accepting stage in a different session, but will incur protocol abortion. A collision can hence only occur if a third party picks the same random nonce \({\mathsf {N}} _C\). We can upper-bound the collision probability by \(n_s \cdot 2^{-\lambda }\), where \(n_s\) is the maximum number of sessions.
\(\square \)
\(\mathsf {MultiStage}\) Security We proceed with proving \(\mathsf {MultiStage}\) security of our construction. Our proof follows the proof of TLS 1.3 draft-14 by Fischlin and Günther [28, Theorem 5.2] as the constructions are very similar, but is different in two main aspects.
-
1.
The proof by Fischlin and Günther only considers TLS 1.3 resumption handshake in draft-14. We adopted and extended their proof to the finalized TLS 1.3 key schedule.
-
2.
The resumption master secret is derived from a 0-RTT session resumption protocol \(\mathsf {Resumption}\), requiring an additional reduction to the security of \(\mathsf {Resumption}\). This way we can achieve forward secrecy for all messages in the very first stage of the resumption handshake, by only modifying the key management on the server side and without any changes to clients or the standardized TLS 1.3 protocol flow.
Theorem 5
The protocol \(\mathsf {TLS13wRES}\) is \(\mathsf {MultiStage}\)-secure in a key-independent and stage-1-forward-secret manner with the above properties \(({\mathsf {M}}, \mathsf {USE})\) and key distribution \({\mathcal {D}}\) if \(\mathsf {Resumption}\) is invariant to puncturing. That is, for any probabilistic polynomial-time adversary \({\mathcal {A}}\) against the \(\mathsf {MultiStage}\) security, we can construct adversaries \({\mathcal {B}} _1, \ldots , {\mathcal {B}} _{15}\) such that
where \(n_s\) is the maximum number of sessions.
Proof
We will conduct this proof in a sequence of games between a challenger \({\mathcal {C}}\) and an adversary \({\mathcal {A}}\). We start with an adversary playing the \(\mathsf {MultiStage}\) security game. Over a sequence of hybrid arguments, we will stepwise transform the security game to a game where the \(\mathsf {Test}\)-query is independent of the challenge bit \(b_\mathsf {test} \). The claim then follows from bounding the probability of distinguishing any two consecutive games. By \(\mathsf {Adv} _i\) we denote \({\mathcal {A}}\) ’s advantage in the i-th game.
Game 0
We define Game 0 to be the original \(\mathsf {MultiStage}\) security game. By definition we have
Game 1
This game is identical to Game 0, except that we restrict the adversary to a single \(\mathsf {Test}\) query. We can apply the hybrid argument by Dowling et al. [23, Appendix A] which reduces the adversary’s advantage in a five stage protocol by a factor of at most \(5n_s\), where \(n_s\) is the number of sessions. The hybrid argument essentially consists of \(5n_s\) hybrids (\(n_s\) possible \(\mathsf {Test}\) queries in each of the five stages) where the first \(j \in [5n_s]\) tested keys are replaced with random keys. This allows implicitly guessing the session to be tested by the adversary. This argument also implicitly guesses which session \(\mathsf {label}\) (which can be either a client or a server session) will be tested by the adversary, allowing us to identify it in advance. In conclusion, we now have
Game 2
This game is identical to Game 1, except that we abort if during protocol execution the same hash value is computed for two distinct inputs. Should this happen, we can construct an adversary \({\mathcal {B}} _1\) that breaks the collision resistance of the hash function H by outputting the two distinct input values to the challenger of the collision resistance game. We can thus bound the probability of aborting as
Game 3
This game is identical to Game 2, except that we now guess the index of the pre-shared secret used within the tested session amongst the maximum number of pre-shared secrets. If the tested session uses a different pre-shared secret, we abort the game. As the guess is oblivious to the adversary until an abort occurs, we have
where \(n_p\) is the maximum number of pre-shared secrets. Note that a correct guess allows us to identify the pre-shared secret \(\mathsf {pss} _{U,V,d}\) in the tested session and hence the intended partner of the tested session. Without loss of generality let us assume that U is the client session and V is the server session.
Game 4
In this game, we modify the output of the \(\mathsf {ServerRes}\) function. To be precise, we proceed as in Game 3, but replace the output of \(\mathsf {ServerRes}\) for both the owner of the tested session and its intended partner with a random value \({\overline{\mathsf {RMS}}} || \overline{{\mathsf {N}} _T}\). We will now show that any adversary that is able to distinguish Game 3 from Game 4 can be used to construct an adversary against the \(\mathsf {0\text {-}RTT\text {-}SR}\) security of \(\mathsf {Resumption}\). Concretely, we have
Construction of \({\mathcal {B}} _2\) against \(\mathsf {Resumption}\) The adversary behaves like the challenger in Game 3, except for all interactions involving the server V associated to the tested session, which we simulate as follows. At first, the adversary initializes the \(\mathsf {0\text {-}RTT\text {-}SR}\) challenger and receives a sequence of tickets \(t_1, \ldots , t_\mu \). It tests the first ticket by invoking \({{\mathcal {O}}_\mathsf {Test}} (t_1) \rightarrow \gamma \in \{s_1, r_1\}\) and immediately corrupts the challenger to receive the challenger’s secret key k. Note that this secret key k has been modified by the challenger and thus cannot be used to open ticket \(t_1\).
As we are now in possession of the secret key k, we are able to simulate all sessions but the one using ticket \(t_1\). We utilize ticket \(t_1\) as the ticket sent within the \(\mathsf {ClientHello}\) message of the tested session between client U to server V. Note that we can perfectly simulate all queries of \({\mathcal {A}}\), since it is not allowed to query \(\mathsf {Reveal}\) for the tested session or its partner. Likewise, it can query \(\mathsf {Corrupt}\) only after the keys have been accepted by U and V, implying replacement of the server’s secret key k. If the adversary issues a corrupt query on the tested server, we are able to puncture the server’s secret key in accordance with all queries issued in other sessions of the server. The invariance to puncturing of \(\mathsf {Resumption}\) guarantees us, that this (possibly wrong order of) key replacements cannot be efficiently detected by the adversary.
Eventually, the adversary will output a guess \(b'\) which we forward to the challenger. If the challenger bit \(b = 0\), we perfectly simulate Game 3 (i.e., \(s_1\) is the actual expected output) and if \(b = 1\), we perfectly simulate Game 4 (i.e., \(r_1\) is a uniformly random output). This proves the claim.
Note that the security of \(\mathsf {Resumption}\) ensures that the adversary cannot learn the value \(\mathsf {RMS}\) for the tested session or its partner, even when corrupting immediately after the \(\mathsf {ClientHello}\) message and the ticket have been processed. This ensures the achievement of forward secrecy in Stage 1.
The next sequence of games aims to replace all traffic keys with random values. That is, we will step by step replace the outputs of the functions \(\mathsf {Ext}\) and \(\mathsf {Exp}\) with random values.
Game 5
This game is identical to Game 4, other than replacing \(\mathsf {Exp} ({\overline{\mathsf {RMS}}}, \cdot )\) with a lazily-sampled random function, such that the pre-shared key \(\mathsf {PSK}\) is replaced by a random value \({\overline{\mathsf {PSK}}}\) in the tested session. Any adversary that is able to distinguish this replacement can be used to construct an adversary that breaks the pseudorandomness of the HKDF. We have
Construction of \({\mathcal {B}} _3\) against \(\mathsf {Exp}\) The adversary \({\mathcal {B}} _3\) behaves exactly like in Game 4, but evaluates \(\mathsf {Exp} ({\overline{\mathsf {RMS}}}, \cdot )\) via the PRF evaluation oracle provided by the PRF challenger. Since the adversary \({\mathcal {A}}\) is not able to learn the real resumption master secret \(\mathsf {RMS}\) by corrupting the tested session (cf. Game 4), it is only known to be a uniformly random value. Hence, \({\mathcal {B}} _3\) perfectly simulates Game 4 if the PRF oracle computes \(\mathsf {Exp}\) and perfectly simulates Game 5 if the PRF oracle is a random function, which proves the claim.
Game 6
This game is identical to Game 5, other than replacing \(\mathsf {Ext} (0, {\overline{\mathsf {PSK}}})\) with a random value \({\overline{\mathsf {ES}}}\) in the tested and partnered session. Recall that \(\mathsf {Ext} (x,y) = \mathsf {HMAC} (x,y)\). Any adversary that is able to distinguish this replacement can be used to break the \(\mathsf {HMAC} (0,\$)\text {-}\$\) assumption of \(\mathsf {Ext}\).
Construction of \({\mathcal {B}} _4\) against \(\mathsf {Ext}\) The \(\mathsf {HMAC}\) assumption states that no probabilistic polynomial-time adversary is able to distinguish \(\mathsf {HMAC} (0, x)\) from  , for uniformly chosen inputs
, for uniformly chosen inputs  . \({\mathcal {B}} _4\) behaves exactly like the challenger in Game 5, but uses the value \(\mathsf {Ext} (0, {\overline{\mathsf {PSK}}})\) as challenge. If \(\mathsf {Ext} (0, {\overline{\mathsf {PSK}}}) = \mathsf {HMAC} (0, x)\) for \(x \in \{0,1\} ^\lambda \) it perfectly simulates Game 5 and if \(\mathsf {Ext} (0, {\overline{\mathsf {PSK}}}) = y\) for \(y \in \{0,1\} ^\lambda \), it perfectly simulates Game 6. In conclusion, we have
. \({\mathcal {B}} _4\) behaves exactly like the challenger in Game 5, but uses the value \(\mathsf {Ext} (0, {\overline{\mathsf {PSK}}})\) as challenge. If \(\mathsf {Ext} (0, {\overline{\mathsf {PSK}}}) = \mathsf {HMAC} (0, x)\) for \(x \in \{0,1\} ^\lambda \) it perfectly simulates Game 5 and if \(\mathsf {Ext} (0, {\overline{\mathsf {PSK}}}) = y\) for \(y \in \{0,1\} ^\lambda \), it perfectly simulates Game 6. In conclusion, we have
Game 7
This game is identical to Game 6, except that we replace all evaluations \(\mathsf {Exp} ({\overline{\mathsf {ES}}}, \cdot )\) by a lazily-sampled random function. In particular, this yields a random early traffic secret \({\overline{\mathsf {ets}}}\), a random binder key \({\overline{\mathsf {bk}}}\), and a random expanded early secret \({\overline{\mathsf {dES}}}\).
Note that the hash value for deriving the early traffic secret is dependent on the session identifier. The changes introduced in Game 2 guarantee that the hash value does not collide across non-partnered users. Furthermore, all three values for the second input of the \(\mathsf {Exp}\) function are distinct labels, ensuring distinct outputs.
Any adversary that is able to recognize this change can be used to construct an adversary against the pseudorandomness of the HKDF in the same fashion as done in Game 5, leading to a bound
Game 8
This game is identical to Game 7, other than replacing \(\mathsf {Exp} ({\overline{\mathsf {ets}}}, \cdot )\) with a lazily-sampled random function, yielding a random value \(\overline{\mathsf {tk} _\mathsf {ets}}\) for the early traffic key in the tested and partnered session. Following the same arguments as in Game 5, we can bound
Game 9
This game is identical to Game 8, other than replacing \(\mathsf {Exp} ({\overline{\mathsf {bk}}}, \cdot )\) with a lazily-sampled random function, yielding a random value \(\overline{\mathsf {fk} _0}\) for the early finished key in the tested and partnered session. Following the same arguments as in Game 5, we can bound
Game 10
This game is identical to Game 9, other than replacing \(\mathsf {Ext} ({\overline{\mathsf {ES}}}, 0)\) with a lazily-sampled random function, yielding a random \({\overline{\mathsf {HS}}}\) in the tested and partnered session. Following the same arguments as in Game 5, we can bound
Game 11
This game is identical to Game 10, except that we replace all evaluations \(\mathsf {Exp} ({\overline{\mathsf {HS}}}, \cdot )\) by a lazily-sampled random function. In particular, this yields a random client handshake traffic secret \({\overline{\mathsf {chts}}}\) (resp. server handshake traffic secret \({\overline{\mathsf {shts}}}\)), and a random expanded handshake secret \({\overline{\mathsf {dHS}}}\).
Note that the hash value for deriving the handshake traffic secrets is dependent on the session identifier. The changes introduced in Game 2 guarantee that the hash value does not collide across non-partnered users. Furthermore, all three values for the second input of the \(\mathsf {Exp}\) function are distinct labels, ensuring distinct outputs.
Following the same arguments as in Game 5, we can bound
Game 12
This game is identical to Game 11, other than replacing \(\mathsf {Exp} ({\overline{\mathsf {chts}}}, \cdot )\) with a lazily-sampled random function, yielding a random client handshake traffic key \(\overline{\mathsf {tk} _\mathsf {chts}}\) and a random client finished key \(\overline{\mathsf {fk} _C}\) in the tested and partnered session. Following the same arguments as in Game 5, we can bound
Game 13
This game is identical to Game 12, other than replacing \(\mathsf {Exp} ({\overline{\mathsf {shts}}}, \cdot )\) with a lazily-sampled random function, yielding a random server handshake traffic key \(\overline{\mathsf {tk} _\mathsf {shts}}\) and a random server finished key \(\overline{\mathsf {fk} _S}\) in the tested and partnered session. Following the same arguments as in Game 5, we can bound
Game 14
This game is identical to Game 13, other than replacing \(\mathsf {Ext} ({\overline{\mathsf {MS}}}, 0)\) with a lazily-sampled random function, yielding a random \({\overline{\mathsf {MS}}}\) in the tested and partnered session. Following the same arguments as in Game 5, we can bound
Game 15
This game is identical to Game 14, except that we replace all evaluations \(\mathsf {Exp} ({\overline{\mathsf {MS}}}, \cdot )\) by a lazily-sampled random function. In particular, this yields a random client application traffic secret \({\overline{\mathsf {cats}}}\) (resp. server application traffic secret \({\overline{\mathsf {sats}}}\)), a random exporter master secret \({\overline{\mathsf {EMS}}}\), and a random new resumption master secret \(\overline{\mathsf {RMS} '}\).
Note that the hash value for deriving the application traffic secrets is dependent on the session identifier. The changes introduced in Game 2 guarantee that the hash value does not collide across non-partnered users. Furthermore, all four values for the second input of the \(\mathsf {Exp}\) function are distinct labels, ensuring distinct outputs.
Following the same arguments as in Game 5, we can bound
Game 16
This game is identical to Game 15, other than replacing \(\mathsf {Exp} ({\overline{\mathsf {cats}}}, \cdot )\) with a lazily-sampled random function, yielding a random client application traffic key \(\overline{\mathsf {tk} _\mathsf {cats}}\) in the tested and partnered session. Following the same arguments as in Game 5, we can bound
Game 17
This game is identical to Game 16, other than replacing \(\mathsf {Exp} ({\overline{\mathsf {sats}}}, \cdot )\) with a lazily-sampled random function, yielding a random server application traffic key \(\overline{\mathsf {tk} _\mathsf {sats}}\) in the tested and partnered session. Following the same arguments as in Game 5, we can bound
In Game 17, all keys \(\overline{\mathsf {tk} _\mathsf {ets}}\), \(\overline{\mathsf {tk} _\mathsf {chts}}\), \(\overline{\mathsf {tk} _\mathsf {shts}}\), \(\overline{\mathsf {tk} _\mathsf {cats}}\), \(\overline{\mathsf {tk} _\mathsf {sats}}\), \({\overline{\mathsf {EMS}}}\), and \(\overline{\mathsf {RMS} '}\) derived in the tested session are chosen uniformly at random. Observe that (contrary to standard TLS session resumption) the security of the \(\mathsf {Resumption}\) protocol ensures that replaying the \(\mathsf {ClientHello}\) message to multiple server sessions does not cause multiple sessions to be partnered to the original client session. We hence achieve replay protection across all stages of the protocol. All sessions that are not partnered with the tested session derive different traffic keys as explained in Games 7, 11, and 15. Therefore, the view of \({\mathcal {A}}\) in Game 17 is independent of \(b_\mathsf {test} \). Obviously, we have
By summing up probabilities from Game 0 to Game 17, we conclude the proof. \(\square \)
Remark on the Optional Diffie–Hellman Key Exchange TLS 1.3 allows including an optional Diffie–Hellman Key Exchange (DHKE) in its resumption handshake. This additional key exchange has an important function in the TLS 1.3 Resumption Handshake. Namely, including the Diffie–Hellman key into the derivation of the handshake key, will achieve stage-3-forward-secrecy as shown by [28, Theorem 5.4]. We deliberately excluded this optional key exchange from our analysis, as the multi-stage key exchange model does not capture any property of the DHKE beyond the forward secrecy aspect, which we already obtain through other means. Hence, including the DHKE as computational step does not offer any security benefits (within this model). We stress that the optional DHKE can be added to the resumption handshake (as done in TLS 1.3) if wanted, without any loss of security.
5 A PPRF with Short Secret Keys from Strong RSA
In order to instantiate our generic construction of forward-secure and replay-resilient session resumption protocol with minimal storage requirements, which is the main objective of this paper, it remains to construct suitable PPRFs with minimal storage requirements and good computational efficiency. Note that a computationally expensive PPRF may void all efficiency gains obtained from the 0-RTT protocol.
In this section we describe a PPRF based on the Strong RSA (sRSA) assumption with secret keys that only consist of three elements, even after an arbitrary number of puncturings. More precisely, a secret key consists of an RSA modulus N, an element \(g \in {\mathbb {Z}} _N\) and a bitfield r, indicating positions where the PPRF was punctured. The secret key size is linear in the size of the PPRF’s domain, since the bitfield needs to be of the same size as the domain (which is determined at initialization, and does not change over time). Hence, the PPRF’s secret key size is independent of the number of puncturings. Moreover, for any reasonable choice of parameters, the bitfield is only several hundred bits long, yielding a short key in practice. Servers can use many instances in parallel with the instances sharing a single modulus, so it is only necessary to generate (and store) the modulus once, at initialization.
Since our primary objective is to provide an efficient practical solution for protocols such as TLS 1.3 0-RTT, the PPRF construction described below is analyzed in the random oracle model [7]. However, we note that we use the random oracle only to turn a “search problem” (sRSA) into a “decisional problem” (as required for a pseudorandom function). Therefore, we believe that our construction can be lifted to the standard-model via standard techniques, such as hardcore predicates [8, 10, 31]. All of these approaches would yield less efficient constructions, and therefore are outside the scope of our work. Alternatively, one could formulate an appropriate “hashed sRSA” assumption, which would essentially boil down to assuming that our scheme is secure. Therefore, we consider a random oracle analysis based on the standard sRSA problem as the cleanest and most insightful approach to describe our ideas.
Idea Behind the Construction The construction is inspired by the RSA accumulator of Camenisch and Lysyanskaya [15]. The main idea is the following. Given a modulus \(N = pq\), a value \(g \in {\mathbb {Z}} _N\), and a prime number P, it is easy to compute \(g \mapsto g^P \mod N\), but hard to compute \(g^P \mapsto g \mod N\) without knowing the factorization of N.
In the following let \(p_i\) be the i-th odd prime. That is, we have \((p_1, p_2, p_3, p_4, \ldots ) = (3, 5, 7, 11, \ldots )\). Let n be the size of the domain of the PPRF. Our PPRF on input \(\ell \) produces an output of the form \(H(g^{p_1 \cdot \ldots \cdot p_n /p_\ell })\), where H is a hash function that will be modeled as a random oracle in the security proof. Note that g is raised to a sequence of prime numbers except for the \(\ell \)-th prime number. As long as we have access to g, this is easy to compute. However, if we only have access to \(g^{p_\ell }\) instead of g, we are unable to compute the PPRF output without knowledge of the factorization of N. This implies that by raising the generator to certain powers, we prevent the computation of specific outputs. We will use this property to puncture values of the PPRF’s domain.
5.1 Formal Description of the Construction
Definition 16
Let p, q be two random safe primes of bitlength \(\lambda /2\) and let \(N = pq\). Let  . We define the advantage of algorithm \({\mathcal {B}}\) against the Strong RSA Assumption [3] as
. We define the advantage of algorithm \({\mathcal {B}}\) against the Strong RSA Assumption [3] as
The following lemma, which is due to Shamir [55], is useful for the security proof of our construction.
Lemma 2
There exists an efficient algorithm that, on input \({Y, Z} \in {\mathbb {Z}} _N\) and integers \(e, f \in {\mathbb {Z}} \) such that \(\gcd (e, f) = 1\) and \(Z^e \equiv Y^f \mod N\), computes \(X \in {\mathbb {Z}} _N\) satisfying \(X^e = Y \bmod N\).
Construction 2
Let \(H : {\mathbb {Z}} _N \rightarrow \{0,1\} ^\lambda \) be a hash function and let \(p_i\) be the i-th odd prime number. Then we construct a PPRF \(\mathsf {PPRF} = (\mathsf {Setup}, \mathsf {Eval}, \mathsf {Punct})\) with polynomial-size \({\mathcal {X}} = [n]\) in the following way.
-
\(\mathsf {Setup} (1^\lambda )\) computes an RSA modulus \(N = pq\), where p, q are safe primes. Next, it samples a value
 and defines \(r := 0^n\) and \(k = (N, g, r)\). The primes p, q are discarded. Output is k.
and defines \(r := 0^n\) and \(k = (N, g, r)\). The primes p, q are discarded. Output is k. -
\(\mathsf {Eval} (k, x)\) parses \(k = (N, g, (r_1, \ldots , r_n))\). If \(r_x = 1\), then it outputs \(\bot \). Otherwise it computes and returns
$$\begin{aligned} y := H\left( g^{P_x} \bmod N\right) . \end{aligned}$$where \(p_i\) is the i-th odd prime and
$$\begin{aligned} P_x := \prod _{i \in [n], i \ne x, r_i \ne 1} p_i \end{aligned}$$is the product of the first n odd primes, except for \(p_x\) and previously “punctured primes” (indicated by \(r_i \ne 1\)).
-
\(\mathsf {Punct} (k, x)\) parses \(k = (N, g, (r_1, \ldots , r_n))\). If \(r_x = 1\), then it returns k. If \(r_x = 0\), it computes \(g' := g^{p_x}\) and \(r' = (r_1, \ldots , r_{x-1},1,r_{x+1},\ldots , r_n)\) and returns \(k' = (N, g', r')\).
It is straightforward to verify the correctness of Construction 2 and that it is invariant to puncturing in the sense of Definition 6.
5.2 Security Analysis
In the following we will prove that Construction 2 is pseudorandom at punctured points, if H is modeled as a random oracle [7] and the Strong RSA assumption holds.
Theorem 6
Let \(\mathsf {PPRF} = (\mathsf {Setup}, \mathsf {Eval}, \mathsf {Punct})\) be as above with polynomial-size input space \({\mathcal {X}} = [n]\). From each probabilistic polynomial-time adversary \({\mathcal {A}}\) with advantage \(\mathsf {Adv}_{{\mathcal {A}}, \mathsf {PPRF}}^{\mathsf {na\text {-}rand}}(\lambda )\) against the \(\mathsf {na\text {-}rand}\)-security (cf. Definition 7) we can construct an efficient adversary \({\mathcal {B}}\) with advantage \(\mathsf {Adv}_{{\mathcal {B}}}^\mathsf {sRSA} (\lambda )\) against the Strong RSA problem, such that
Proof
\({\mathcal {B}}\) receives as input a Strong RSA challenge (N, y). It starts \({\mathcal {A}}\), which outputs a set \({{\mathcal {X}}}' = \{x_1, \ldots , x_\ell \} \subseteq [n]\) of values. \({\mathcal {B}}\) responds as follows to \({\mathcal {A}}\). We write \(P_j := \prod _{i \in [n], i \ne j} p_i\) for the product of the first n odd primes except for \(p_j\), and
to be the product of the first n odd primes, except for those contained in \({{\mathcal {X}}}'\).
\({\mathcal {B}}\) defines \(r = (r_1, \ldots , r_n)\) as
for \(i \in [n]\), and then sets \(k := (N, y, r)\).
Let \(P^* := \prod _{i \in {{\mathcal {X}}}'} p_i\) be the product of the first n odd primes contained in \({{\mathcal {X}}}'\). To show that this is a properly distributed punctured key, we have to show that there exists \(g \in {\mathbb {Z}} _N\) such that \({g^{P^*}} = y \bmod N\), and that y is distributed as if g was uniform over \({\mathbb {Z}} _N\). To this end, note that \(N=pq\) is a product of two safe primes \(p = 2p'+1\) and \(q = 2q'+1\) with \(p',q'\) prime. Furthermore, we have \(p',q' \gg p_n\), because \(p_n\) is the n-th odd prime for polynomially-bounded n, which implies \(\gcd (\varphi (N),{g^{P^*}}) = 1\), where \(\varphi \) is Euler’s Phi-function. Hence, the map \(y \mapsto y^{1/{g^{P^*}}}\) is a permutation over \({\mathbb {Z}} _N\), and therefore there exists an element \(g \in {\mathbb {Z}} _N\) such that
Since y is uniformly random, g is uniformly distributed, too. Hence, \(k := (N, y, r)\) is a properly distributed punctured key.
\({\mathcal {B}}\) picks \(\ell \) random strings  and outputs \((k, (h_1, \ldots , h_\ell ))\) to \({\mathcal {A}}\). \({\mathcal {A}}\) now has to distinguish whether
and outputs \((k, (h_1, \ldots , h_\ell ))\) to \({\mathcal {A}}\). \({\mathcal {A}}\) now has to distinguish whether
for all \(x_i \in {{\mathcal {X}}}'\), or whether the \(h_i\) are uniformly random. Since H is a random oracle, this is perfectly indistinguishable for \({\mathcal {A}}\), unless at some point it queries the random oracle on input \(a \in {\mathbb {Z}} _N\) such that there exists \(i \in {[\ell ]}\) with \(a = g^{P_{x_i}} \bmod N\). Since \({\mathcal {A}}\) has advantage \(\mathsf {Adv}_{{\mathcal {A}}, \mathsf {PPRF}}^{\mathsf {na\text {-}rand}}(\lambda )\), this must happen with probability at least \(\mathsf {Adv}_{{\mathcal {A}}, \mathsf {PPRF}}^{\mathsf {na\text {-}rand}}(\lambda )\) at some point throughout the security experiment.
Whenever \({\mathcal {A}}\) outputs a value \(a \in {\mathbb {Z}} _N\) in order to query for H(a), \({\mathcal {B}}\) checks whether
holds for any \(i \in \ell \). Since \({\mathcal {B}}\) does not know g explicitly, it cannot check this directly. However, it can equivalently check whether
holds for any \(i \in [\ell ]\). If (1) indeed holds for some \(i \in [\ell ]\), then \({\mathcal {B}}\) applies Lemma 2 to solve the Strong RSA instance. Concretely, since \(\gcd (p_{x_i}, P') = 1\), it can run the algorithm on input
The algorithm returns X such that \(X^e = Y \bmod N\). Thus, \((X,e) = (X,p_{x_i})\) is a valid solution to the Strong RSA instance (N, y). Note that if \({\mathcal {A}}\) is efficient, then so is \({\mathcal {B}}\), and that the reduction is tight. \(\square \)
5.3 Efficiency Analysis
Note that a server is able to create multiple instances of our construction to serve more tickets than one instance is able to. Using multiple instances allows using smaller exponents, but in return, the storage cost grows linearly in the number of instances.
Serving a ticket requires two exponentiations, one for computing the key and one for puncturing. Computing the key requires raising the state g to the power of \(\prod _{p \in S} p\) for some subset of primes S. Puncturing requires exponentiating by a single prime. Therefore, all exponentiations feature exponents smaller than \(\prod _{i = 1}^n p_i\). We start by comparing to 2048-bit RSA, which according to the NIST key size recommendations [4] corresponds to “112-bit security”, before comparing to larger RSA key sizes.
Worst-Case Analysis We compare to standard exponentiation in the group, i.e. raising to the power of \(d \in {\mathbb {N}} \), where \(\log d \approx 2048\). For puncturing to be comparable in the worst-case, we require \(\log \left( \prod _{i = 1}^n p_i \right) \le 2048\). Choosing \(p_i\) to be the i-th odd prime yields \(n \le 232\). An economic server may store only one 2048-bit group element for the current state, and a bitfield indicating which of the 232 primes have been punctured, requiring 2280 bits in total. This allows serving 232 tickets, resulting in a storage cost of 1.22 bytes per ticket. Alternatively, a standard session cache would require \(112 \cdot 232 = 25984\) bits to serve those 232 tickets, assuming symmetric keys of 112 bits. Therefore, our construction decreases storage size compared to a Session Cache by a factor of \(25984 / 2280 = 11.4\).
Averaged Analysis Note that in the above worst-case analysis we consider an upper bound on the exponentiation cost. That is, we guarantee that a puncturing and key derivation operation is never more expensive than a full exponentiation. Indeed, the first key computation raises to the power of \(p_1 \cdot \ldots \cdot p_n /p_\ell \), i.e. to the product of \(n-1\) primes. However, subsequent key calculations raise to smaller powers, i.e. to the product of \(n-2\) primes, then \(n-3\), and so on. Therefore, serving tickets arriving later is much cheaper than serving the first. In particular in settings where a server uses many PPRF instances in parallel, in order to deal with potentially thousands of simultaneously issued tickets, an alternative and more reasonable efficiency analysis considers the average cost of serving a ticket to be comparable to exponentiation in the group. In the worst-case, primes are punctured in order, so \(p_n\) is included in the exponent in all key derivations, \(p_{n-1}\) in all derivations except the last, etc. Each prime is also used once for puncturing. Requiring \(\sum _{i=1} ^n i \cdot \log (p_i) \le n \cdot 2048\) yields a maximum \(n = 387\), and a savings factor of \(112 \cdot 387 / (2048 + 387) = 17.8\). The required storage is therefore 0.79 bytes per ticket.
Considering Other Security Parameters and Efficiency Requirements Generalizing the above calculations, Table 1 gives concrete parameters for various security levels, following the NIST recommendations for key sizes [4]. Larger key sizes result in larger reductions in storage, especially when requiring average cost similar to exponentiation in the RSA group. We also show the improvement factor in storage when relaxing the above heuristic choice that serving a ticket must not cost more than one full RSA-exponentiation, by considering the case where serving a ticket is cheaper on average than 5 group exponentiations. This demonstrates that the proposed PPRF can yield very significant storage savings in general cryptographic settings, while keeping computation costs on the same order of magnitude as common public key operations. In the context of TLS, however, we expect most server operators would prefer parameters that keep processing time comparable to a single exponentiation. We emphasize that the improvement factor in storage is determined at initialization time, and is deterministic rather than probabilistic. The largest prime used in exponentiations determines how many tickets are served using a single group element. The worst-case and average-case refer to the processing time, not to the savings in storage.
Additional Storage for the Primes The server will also need to store the first n primes, but this requires negligible additional storage. Storing the primes requires on the order of magnitude of ten kilobytes, where we expect typical caches to use many megabytes. For the minimal storage requirement, we consider 2048-bit RSA while requiring that the worst case puncturing time is cheaper than group exponentiation. In this case \(n = 232\) and \(p_n = 1471\), therefore all primes fit in 32-bit integers. Storing all the primes would require at most \(4 \cdot 232 = 928\) bytes.
The largest value of n for the parameter choices presented in this work is \(n = 9704\), for the “average cheaper than 5 exponentiations” case with 15360-bit RSA. \(p_{9704} = 101341\). The required additional storage is therefore \(4 \cdot 9704 =\) 38,816 bytes. To reiterate, we expect typical caches to use many megabytes.
Concrete Benchmarks We now give concrete performance estimates for this construction, using OpenSSL [58]. OpenSSL is a well-known production-grade library that implements the TLS and SSL protocols, as well as low-level cryptographic primitives. For each key size, we measure the computation time of exponentiating by all primes \(\prod _{i=1}^n p_i\), by calling the OpenSSL “BigNum” exponentiating function. This is analogous to the computation required to serve the first ticket and then puncture the key: Serving requires exponentiating to the power of all primes except one, \(p_i\), and puncturing requires exponentiating to the power of \(p_i\). This is the worst-case, since serving later tickets is cheaper.
We measure the performance of this calculation for two of the above cases, which determine the value of n: (1) Worst-case is cheaper than exponentiation, and (2) The average case is cheaper than exponentiation. We note the latter case is slightly unintuitive: we measure the worst-case performance, under the requirement that the average case is comparable to one exponentiation in the group.
Table 2 gives our results. We observe that performance is comparable to, but slower than, RSA decryption. In typical cases, it requires only a few additional milliseconds compared to RSA decryption. We argue the additional latency and computation requirement are small enough to allow the construction to be deployed as-is, in current large scale TLS deployments. It is unsurprising that RSA decryption is faster than our construction, since OpenSSL performs RSA decryption using the Chinese Remainder Theorem.
6 Tree-Based PPRFs
This section will consider a different approach to instantiating Construction 1 based on PPRFs using trees. At first we will recap the idea behind tree-based PPRFs and explain how we utilize tree-based PPRFs as an instantiation of our session resumption protocol and highlight implications. Finally, we will describe our new “domain extension” technique for PPRFs and analyze its efficiency.
6.1 Tree-Based PPRFs
We will briefly recap the main idea behind tree-based PPRFs. It is well known that the GGM tree-based construction of pseudorandom functions (PRFs) from one-way functions [30] can be modified to construct a puncturable PRF, as noted in [12, 14, 38]. It works as follows.
Let \(G : \{0,1\} ^\lambda \rightarrow \{0,1\} ^{2\lambda }\) be a pseudorandom generator (PRG) and let \(G_0(k)\), \(G_1(k)\) be the first and second half of string G(k), where k is a random seed. The GGM construction defines a binary tree on the PRF’s domain, where each leaf represents an evaluation of the PRF. We label each edge with 0 if it connects to a left child, and 1 if it connects to a right child. We label each node with the binary string determined by the path from the root to the node. The PRF value of \(x = x_1 \ldots x_n \in \{0,1\} ^n\) is \((G_{x_n} \circ \ldots \circ G_{x_1})(k) \in \{0,1\} ^\lambda \), i.e. we compose G according to the path from root to leaf x.
We briefly describe how this construction can be transformed into a PPRF. In order to puncture the PPRF at input \(x = x_1 \ldots x_n\) we compute a tuple of n intermediate node evaluations for prefixes \(\overline{x_1}, x_1\overline{x_2}, \ldots , x_1x_2\ldots \overline{x_n}\) and discard the initial seed k. The intermediate evaluations enable us to still compute evaluations on all inputs but x. Successive puncturing is possible if we apply the above computations to an intermediate evaluation. Note that we have to compute at most \(n \cdot m\) intermediate values if we puncture at random, where m is the number of puncturing operations performed.
The PPRF is secure if an adversary is not able to distinguish between a punctured point and a truly random value, even when given the values of all computed “neighbor nodes”. This holds as long as the underlying PRG is indistinguishable from random [12, 14, 38]. Furthermore, note that the PPRF is also invariant to puncturing as puncturing always deletes all nodes from a leaf up to the root without leaving any trace which leaf is “responsible” for the deletion. Hence, if an adversary is given a punctured key, it cannot deduce in which order it has been punctured.
6.2 Combining Tree-Based PPRFs with Tickets
In our session resumption scenario the tree-based PPRF will act as a puncturable STEK. That is, evaluating the PPRF returns a ticket encryption key. Upon resumption with a ticket we will retrieve the ticket encryption key from the PPRF by evaluating it and puncture the PPRF at that very value to ensure the ticket encryption key cannot be computed twice. Note that each ticket encryption key essentially corresponds to a leaf of the tree. Thus we will subsequently use the terms leaf and ticket (encryption key) interchangeably depending on the context.
For simplicity, we consider tickets which consist of a ticket number i and a ticket lifetime t. Following Construction 1 we will issue the tickets one after another while incrementing the ticket number for each. Note that the ticket number i corresponds to the i-th leftmost leaf of the tree. The ticket lifetime t determines how long an issued ticket is valid for resumption. That is, if \(t' > t\) time has passed, the server will reject the ticket.
We assume that the rate at which tickets are issued is roughly the same as the rate tickets are used for session resumption. This holds as for each session resumption we will issue a new ticket to again resume the session at a later point in time. Similarly, we argue that tickets are roughly used in the same order for resumption as we issued them. Again, if we consider multiple users, repeatedly requesting tickets and resuming sessions, we are able to average the time a user takes until a session is resumed (Cloudflare have suggested that these assumptions seem reasonable; unfortunately, they cannot provide data on returning clients’ behavior yet). This yields an implicit window of tickets in usage. The window is bounded left by the ticket lifetime and bounded right by the last ticket the server issued. Within the lifetime of the tree-based PPRF this implicit window will shift from left to right over the tree’s leaves. It immediately follows that tickets are also roughly used in that order.
6.3 Efficiency Analysis of the Tree-Based PPRF
We will now discuss how the performance of tree-based PPRFs depends on the ticket lifetime. We consider a scenario where the ticket lifetime t equals the number of leaves \(\ell \). It is also possible to consider a scenario where the ticket lifetime is smaller than the number of leaves. If both number of leaves \(\ell \) and ticket lifetime t are powers of 2, we can divide the leaves in \(\ell /t\) windows, which span a subtree each. The subtrees are all linked with the “upper part” of the tree. A different approach would be to instantiate a new tree when a tree runs out of tickets. We stress that this does not affect our analysis. As soon as one subtree runs out of tickets, the next subtree is used. If the rate at which we issue tickets stays the same, we are able to delete parts of the former tree when issuing tickets of the next one. Hence, for analysis, it is sufficient to consider a single tree.
If we were to puncture leaves strictly from left to right, we would need to store at most \(\log (\ell )\) leaves (one leaf per layer). Note that if we puncture leaves at random, we would need to store at most \(p \cdot \log (\ell )\) nodes, where p is the number of punctures performed. We can also bound the number of nodes we need to store by \(p \cdot \log (\ell ) \le \ell /2\). This is due to the tree being binary. Essentially each node (except for the lowest layer) represents at least two leaves. To be more precise, in a tree with L layers, storing a node on layer i allows evaluating its \(2^{L - i}\) children. Thus it is preferable to store those nodes instead of storing leaves in order to save memory. In the worst-case only every second leaf is punctured. This results in precomputation of all other leaves without being able to save memory by only storing an intermediary node. Note that this would actually resemble a session cache, where all issued tickets are stored. However, note that a session cache needs to store each ticket when it has been issued, whereas our construction only needs to increase its storage if a ticket is used for resumption. Thus, our tree-based construction performs (memory-wise) at least as well as a session cache. In practice, where user behavior is much more random, our approach is always better than session caches.
The tree-based PPRF performs more computations compared to a session cache. When issuing tickets we need to compute all nodes from the closest computed node to a leaf. For puncturing we need to compute the same, plus computation of some additional sibling nodes. However, when instantiating the construction with a cryptographic hash function, such as SHA-3, evaluation and puncturing of the PPRF consists only of several hash function evaluations. This makes our construction especially suitable for high-traffic scenarios.
Table 3 gives worst-case secret key sizes based on the above analysis. However, we expect the secret key size to be much smaller in practice. Unfortunately, we are not able to estimate the average key size as this would depend on the exact distribution of returning clients’ arrival times.
7 Generic Domain Extension for PPRFs
Most forward-secure and replay-resilient 0-RTT schemes come with large secret keys (possibly several hundred megabytes) when instantiated in a real-world environment [19, 20, 33]. This is especially problematic if the secret key needs to be synchronized across multiple server instances. Therefore, it is often desirable to minimize the secret key size.
In this section we will describe a generic domain extension. In the context of our work, the domain extension reduces the size of punctured keys by trading secret key size for ticket size, while preserving the puncturing functionality.
Idea Behind the Construction Our session resumption protocol uses the output of the PPRF as a ticket encryption key. Normally, a PPRF only allows one output per input as it is designed to be a function. Our protocol, however, does not rely on this property. Instead of only using one ticket encryption key we could generate multiple ticket encryption keys. Ticket issuing would work as follows. First, we generate an intermediary symmetric key to encrypt the resumption secret. The intermediary symmetric key is then encrypted under each of the ticket encryption keys. The ticket will consist of one encryption of the resumption secret and several (redundant) encryptions of the intermediary symmetric key. We note that typically a ticket contains not only the resumption secret but also the chosen cipher suite and other additional session parameters, and is thus larger than just the resumption secret. It is therefore desirable to encrypt this data only once, while encrypting the shorter intermediary symmetric key multiple times. This makes the ticket as short as possible.
As long as the PPRF is able to recompute at least one of those ticket encryption keys, the server will still be able to resume the session. This allows us to construct a wrapper around the PPRF that extends the PPRF’s domain by relaxing the requirement that every input has only a single output.
Before formally describing our construction, we will provide an example to illustrate the idea. Let \({\mathcal {X}}\) be the PPRF’s domain. We will extend the domain to \({\mathcal {X}} \times [n]\) with a domain extension factor of n. That is, we will allow \((x, i), i \in [n]\) for any \(x \in {\mathcal {X}}\) as input. Let \(G : \{0,1\} ^\lambda \rightarrow \{0,1\} ^{n\lambda }\) be a pseudorandom generator and let \(G_j(x)\) be the j-th bitstring of size \(\lambda \) of G on input x. We define the evaluation of (x, i) as all possible compositions of \(G_j\) which end with \(G_i\). That is, for any input (x, i) there will be \((n-1)!\) different outputs, as there are \((n-1)!\) ways to compose \(G_j\) with \(j \ne i\). The possible compositions of PRGs can be illustrated as a tree as shown in Fig. 5.
Possible composition of PRGs for \(n = 3\) illustrated as a tree. Each path from parent to child illustrates an evaluation of the PRG shown next to the path. Upon puncturing (x, 3), the value \(y_3\) is computed and stored and y is discarded. Thus, only the white nodes are computable, whereas the gray nodes cannot be computed without inverting \(G_3\)
After puncturing the PPRF’s key for a value (x, i), it must not be possible to evaluate the value anymore. This requires a mechanism to ensure that composing the PRGs which end with \(G_i\) is no longer possible. We achieve this by forcing an evaluation of \(y_i := G_i(y)\), where y is the evaluation of the underlying PPRF on input x. In order to render recomputation of y impossible, we additionally need to puncture the PPRF’s key on value x and delete the computed y. Formally, the construction is defined as follows.
Construction 3
Let \(G : \{0,1\} ^\lambda \rightarrow \{0,1\} ^{n\lambda }\) be a PRG and let \(G_i(k)\) be the i-th bitstring of size \(\lambda \) of G. Let \(\mathsf {PPRF} '= (\mathsf {Setup} ', \mathsf {Eval} ', \mathsf {Punct} ')\) be a PPRF with domain \({\mathcal {X}}\). We construct a domain extended PPRF \(\mathsf {DE} = (\mathsf {Setup}, \mathsf {Eval}, \mathsf {Punct})\) with domain \({\mathcal {X}} \times [n]\) for \(n \in {\mathbb {N}} \) as follows.
-
\(\mathsf {Setup} (1^\lambda )\) computes \(k_\mathsf {PPRF}:= \mathsf {Setup} '(1^\lambda )\). Next, it defines an empty list \({\mathcal {L}} = \emptyset \). Output is \(k = (k_\mathsf {PPRF},{\mathcal {L}})\)
-
\(\mathsf {Eval} (k, x)\) parses \(x = (x_\mathsf {PPRF}, x_\mathsf {ext}) \in {\mathcal {X}} \times [n]\) and \(k = (k_\mathsf {PPRF}, {\mathcal {L}})\). It computes \(y := \mathsf {Eval} {'}(k_\mathsf {PPRF}, x_\mathsf {PPRF})\). If \(y = \bot \), it checks whether there exists a value \(x_\mathsf {PPRF} \) with
$$\begin{aligned} (x_\mathsf {PPRF}, y', (r_1, \ldots , r_n)) \in {\mathcal {L}}. \end{aligned}$$If it exists, assign \(y := y'\). Otherwise it outputs \(\bot \).
Furthermore, it defines a set \({\mathcal {R}} = \{i \in [n]~|~r_i = 1\}\). If \(r_i\) are undefined, set \({\mathcal {R}}\) is empty. Next, it computes
$$\begin{aligned} {\mathcal {Y}} = \{(G_{i_{n - |{\mathcal {R}}| - 1}} \circ \ldots \circ G_{i_1})(y)\}, \end{aligned}$$where \((i_1, \ldots , i_{n - |{\mathcal {R}}| - 1})\) are all \((n - |{\mathcal {R}}| - 1)!\) possible permutations of elements in \([n] \setminus ({\mathcal {R}} \cup \{x_\mathsf {ext}\})\). Output is \(\mathcal Y\).
-
\(\mathsf {Punct} (k, x)\) parses \(k = (k_\mathsf {PPRF}, {\mathcal {L}})\) and \(x = (x_\mathsf {PPRF}, x_\mathsf {ext}) \in {\mathcal {X}} \times [n]\). It computes \(y := \mathsf {Eval} (k_\mathsf {PPRF}, x_\mathsf {PPRF})\). If \(y \ne \bot \), it appends \({\mathcal {L}} := {\mathcal {L}} \cup \{x_\mathsf {PPRF}, y, (r_1, \ldots , r_n)\}\), where \(r_i = 0\), but \(r_{x_\mathsf {ext}} = 1\). Additionally, it punctures \(k_\mathsf {PPRF} ' := \mathsf {Punct} '(k_\mathsf {PPRF}, x_\mathsf {PPRF})\). If \(y = \bot \) and no value \(x_\mathsf {ext}\) with \((x_\mathsf {ext}, y',r) \in {\mathcal {L}}\) exists, it outputs k.
Otherwise it retrieves \(\ell = (x_{\mathsf {PPRF}}, y', (r_1, \ldots , r_n)) \in {\mathcal {L}}\). If \(r_i = 1\) for all \(i \in [n] \setminus \{x_{\mathsf {PPRF}}\}\), remove \(\ell \) from \({\mathcal {L}}\). Else it sets
$$\begin{aligned} {y'' = G_{x_\mathsf {ext}}(y') \text { and } r_i' := {\left\{ \begin{array}{ll} 1, \text { if } i = x_\mathsf {ext}\\ r_i, \text { else,} \end{array}\right. }} \end{aligned}$$and updates \(\ell \in {\mathcal {L}}\) by computing \({\mathcal {L}} := ({\mathcal {L}} \setminus \{\ell \}) \cup \{{ (x_{\mathsf {PPRF}}, y'', (r_1', \ldots , r_n')}\}\). Output is \(k = (k_\mathsf {PPRF} ', \mathcal L)\).
7.1 Efficiency Analysis of the Generic Domain Extension
Increased Ticket Size Note that a ticket is longer than a standard ticket by \((n-1)!\) encrypted blocks. Assuming 128-bit AES, and choosing \(n = 5\), this translates to \(4! \cdot 16 = 384\) additional bytes. This is likely to be insignificant on the modern Internet. For example, Google has pushed for increasing the maximum initial flight from 4 TCP packets to 10 [25], as most server responses span several packets already (a typical full packet is about 1500 bytes). A basic experiment performed by Google and Cloudflare in 2018 measured a similar scenario: It added 400 bytes for both the client’s and server’s first flights [44]. They observed relatively small additional latencies: 2–4 milliseconds in the median, and less than 20 milliseconds for the 95th percentile. However, choosing \(n = 6\) or larger is likely to be not cost-effective. This would translate to \(5! \cdot 16 = 1920\) additional bytes, larger than a standard TCP packet.
Storage Requirements Comparing the storage requirements of the tree-based construction to standard session caches depends on the specific distribution of returning clients. In the best case, tickets arrive in large contiguous blocks. In this case, a tree-based construction uses negligible storage (logarithmic in the number of tickets), making the savings factor in storage huge. However, this is unrealistic in practice. In the worst-case, tickets arrive in blocks of \(n-1\) tickets of the form \((x_\mathsf {PPRF}, i)\) for \(i \in [n-1]\), adversarially rendering the domain extension technique useless as each subtree is reduced to a single node. As before, this is unrealistic in practice.
We have therefore resorted to simulations in order to assess the improvement in storage requirements. Our simulation constructs two trees: a standard binary tree with \(\ell \) layers, and a domain-extended tree with \(n = 4\). For the domain-extended tree, the first \(\ell - 2\) layers are constructed as a standard binary tree, and the last \(\log (4) = 2\) layers are represented by the domain extension.
We simulated the storage requirements for trees of 10,000 tickets. We note that results for trees of 10,000 tickets should closely follow results for larger tree sizes. Trees are quickly split into smaller sub-trees when puncturing, regardless of the initial tree size. In the first puncturing operation we delete the root and (implicitly) store smaller sub-trees with at most half the nodes in each, and so forth. We focused on the relationship between ticket puncturing rate and savings in storage. The ticket puncturing rate denotes the percentage of tickets that are punctured, out of the 10,000 outstanding tickets. This can also be thought of as the percentage of returning clients. After fixing the puncturing rate to r, we simulate the arrival of \(r\%\) of clients according to two distributions: Gaussian and uniform. With the uniform distribution, the next ticket to be punctured is sampled uniformly out of the outstanding tickets. With the Gaussian distribution, the next ticket to be punctured is sampled using a discrete Gaussian distribution with mean \(\mu = 5000\) and standard deviation \(\sigma \) (for varying values of \(\sigma \)). We then simulate the state of both trees after puncturing the sampled ticket. We repeatedly sample tickets and puncture them, until we reach the desired puncturing rate. We then report the ratio between the storage for the standard binary tree and the storage for the domain-extended tree, in their final states.
Intuitively, the Gaussian distribution aims to simulate the assumption where tickets arrive in some periodic manner. For example, assume the tickets most likely to arrive are the tickets issued roughly one hour ago. Then the distribution of arriving tickets will exhibit a noticeable mode (“peak”), where tickets close to the mode are much more likely to arrive than tickets far from it. The Gaussian distribution is a natural fit for this description. On the other hand, the uniform distribution makes no assumptions on which ticket is likely to arrive next. In personal communication, Cloudflare have advised us that it is reasonable to assume tickets are redeemed roughly in order of issuance (they do not have readily-available data on returning clients’ behavior). This motivated our use of Gaussian distributions. We hope to see additional research in this area. In particular, it would be helpful if large server operators could release anonymized datasets that allow simulating the behavior of returning clients in practice.
Using our domain extension technique with \(n=4\) results in a typical factor of 1.4 (or more) reduction in storage compared to a tree-based PPRF. Figure 6 plots the results when using the uniform distribution and a Gaussian distribution with \(\sigma = 2000\). We encountered similar results when using other values for \(\sigma \). We estimate ticket redeeming rates in large-scale deployments are roughly 50%. We therefore focus on cases where the puncturing rate is at least 40% and at most 60%. We note that in the worst-case, the domain extension performs as well as the binary tree.
Average storage improvement factor of the domain-extended binary tree (with \(n = 4\)) compared to a standard binary tree, depending on the ticket puncturing rate. All simulations used trees of 10,000 tickets. The dashed blue line (resp. continuous red line) shows the storage improvement when modeling client’s arrivals with a uniform distribution (resp. discrete Gaussian distribution with mean \(\mu = 5000\) and standard deviation \(\sigma = 2000\))
8 Comparison of Solutions and Conclusion
Comparison of Solutions To summarize this work, Table 4 compares our two constructions with the standard solutions of session tickets and session caches. Note that we decided to exclude implementation-specific costs (such as database access) from our “dominant cost” column and only focus on cryptographically expensive factors.
Conclusion In most facets, TLS 1.3 offers significant improvements in security compared to earlier TLS versions. However, when 0-RTT mode is used, it surprisingly weakens standard security guarantees, namely forward security and replay resilience. This was noted as the protocol was standardized, but the latency reduction from 0-RTT was considered “too big a win not to do” [50].
This paper presented formal definitions for secure 0-RTT session resumption protocols, and two new constructions that allow achieving the aforementioned security guarantees at a practical cost. We expect continued research in the coming years in this area, of achieving secure 0-RTT traffic as cheaply as possible. Currently, many large server operators serve 0-RTT traffic using STEK-encrypted session tickets. As more Internet traffic becomes 0-RTT traffic, this solution rolls back the security guarantees offered to everyday secure sessions.
The Eurocrypt 2019 version of this paper does not show if TLS 1.3 can be securely composed with the presented 0-RTT session resumption protocol. In this work we resolved this open problem and showed that any secure 0-RTT session resumption protocol can be generically composed with the TLS 1.3 resumption handshake. In particular, this yields the first variant of the TLS 1.3 resumption handshake that achieves forward secrecy for all messages (including the 0-RTT data) without modifying client implementations of TLS 1.3.
References
N. Aviram, K. Gellert, T. Jager, Session resumption protocols and efficient forward security for tls 1.3 0-rtt. In: Ishai, Y., Rijmen, V. (eds.) Advances in Cryptology – EUROCRYPT 2019. pp. 117–150. Springer International Publishing, Cham 2019
C. Bader, D. Hofheinz, T. Jager, E. Kiltz, Y. Li, Tightly-secure authenticated key exchange. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 629–658. Springer, Heidelberg, Germany, Warsaw, Poland (Mar 23–25, 2015)
N. Bari, B. Pfitzmann, Collision-free accumulators and fail-stop signature schemes without trees. In: Fumy, W. (ed.) EUROCRYPT’97. LNCS, vol. 1233, pp. 480–494. Springer, Heidelberg, Germany, Konstanz, Germany (May 11–15, 1997)
E. Barker, Recommendation for key management part 1: General (revision 4). NIST special publication 2016
M. Behr, I. Swett, Introducing QUIC support for HTTPS load balancing 2018, https://cloudplatform.googleblog.com/2018/06/Introducing-QUIC-support-for-HTTPS-load-balancing.html
M. Bellare, R. Canetti, H. Krawczyk, Keying hash functions for message authentication. In: Koblitz, N. (ed.) CRYPTO’96. LNCS, vol. 1109, pp. 1–15. Springer, Heidelberg, Germany, Santa Barbara, CA, USA (Aug 18–22, 1996)
M. Bellare, P. Rogaway, Random oracles are practical: A paradigm for designing efficient protocols. In: Ashby, V. (ed.) ACM CCS 93. pp. 62–73. ACM Press, Fairfax, Virginia, USA (Nov 3–5, 1993)
M. Bellare, I. Stepanovs, S. Tessaro, Poly-many hardcore bits for any one-way function and a framework for differing-inputs obfuscation. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 102–121. Springer, Heidelberg, Germany, Kaoshiung, Taiwan, R.O.C. (Dec 7–11, 2014)
K. Bhargavan, C. Fournet, M. Kohlweiss, A. Pironti, P.Y. Strub, Zanella Béguelin, S.: Proving the TLS handshake secure (as it is). In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 235–255. Springer, Heidelberg, Germany, Santa Barbara, CA, USA (Aug 17–21, 2014)
L. Blum, M. Blum, M. Shub, A simple unpredictable pseudo-random number generator. SIAM J. Comput. 15(2), 364–383 (1986), https://doi.org/10.1137/0215025
H. Böck, Fuzz-compare the OpenSSL function \(\text{BN}\_\text{ mod }\_\text{ exp }()\) and the libgcrypt function \(\text{ gcry }\_\text{ mpi }\_\text{ powm }()\), https://github.com/hannob/bignum-fuzz/blob/master/openssl-vs-gcrypt-modexp.c
D. Boneh, B. Waters, Constrained pseudorandom functions and their applications. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part II. LNCS, vol. 8270, pp. 280–300. Springer, Heidelberg, Germany, Bengalore, India (Dec 1–5, 2013)
C. Boyd, K. Gellert, A Modern View on Forward Security. The Computer Journal (08 2020), https://doi.org/10.1093/comjnl/bxaa104
E. Boyle, S. Goldwasser, I. Ivan, Functional signatures and pseudorandom functions. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 501–519. Springer, Heidelberg, Germany, Buenos Aires, Argentina (Mar 26–28, 2014)
J. Camenisch, A. Lysyanskaya, Dynamic accumulators and application to efficient revocation of anonymous credentials. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 61–76. Springer, Heidelberg, Germany, Santa Barbara, CA, USA (Aug 18–22, 2002)
W.T. Chang, A. Langley, QUIC crypto 2014, https://docs.google.com/document/d/1g5nIXAIkN_Y-7XJW5K45IblHd_L2f5LTaDUDwvZ5L6g
C. Cremers, M. Horvat, S. Scott, T. van der Merwe, Automated analysis and verification of TLS 1.3: 0-RTT, resumption and delayed authentication. In: 2016 IEEE Symposium on Security and Privacy. pp. 470–485. IEEE Computer Society Press, San Jose, CA, USA (May 22–26, 2016)
F. Dallmeier, J.P. Drees, K. Gellert, T. Handirk, T. Jager, J. Klauke, S. Nachtigall, T. Renzelmann, R. Wolf, Forward-secure 0-rtt goes live: Implementation and performance analysis in quic. In: S. Krenn, H. Shulman, S. Vaudenay, (eds.) Cryptology and Network Security. pp. 211–231. Springer International Publishing, Cham 2020
D. Derler, K. Gellert, T. Jager, D. Slamanig, C. Striecks, Bloom filter encryption and applications to efficient forward-secret 0-RTT key exchange. Cryptology ePrint Archive, Report 2018/199 2018, https://eprint.iacr.org/2018/199
D. Derler, T. Jager, D. Slamanig, C. Striecks, Bloom filter encryption and applications to efficient forward-secret 0-RTT key exchange. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part III. LNCS, vol. 10822, pp. 425–455. Springer, Heidelberg, Germany, Tel Aviv, Israel (Apr 29 – May 3, 2018)
D. Diemert, T. Jager: On the tight security of tls 1.3: Theoretically-sound cryptographic parameters for real-world deployments. Cryptology ePrint Archive, Report 2020/726 2020, https://eprint.iacr.org/2020/726
B. Dowling, M. Fischlin, F. Günther, D. Stebila, A cryptographic analysis of the tls 1.3 handshake protocol. Cryptology ePrint Archive, Report 2020/1044 2020, https://eprint.iacr.org/2020/1044
B. Dowling, M. Fischlin, F. Günther, D. Stebila, A cryptographic analysis of the TLS 1.3 handshake protocol candidates. In: Ray, I., Li, N., Kruegel:, C. (eds.) ACM CCS 15. pp. 1197–1210. ACM Press, Denver, CO, USA (Oct 12–16, 2015)
B. Dowling, M. Fischlin, F. Günther, D. Stebila, A cryptographic analysis of the TLS 1.3 draft-10 full and pre-shared key handshake protocol. Cryptology ePrint Archive, Report 2016/081 2016, http://eprint.iacr.org/2016/081
N. Dukkipati, T. Refice, Y. Cheng, J. Chu, T. Herbert, A. Agarwal, A. Jain, N. Sutin, An argument for increasing TCP’s initial congestion window. Computer Communication Review 40(3), 26–33 2010
T. Duong, T. Valverde, Q. Nguyen, Bad life advice - Replay attacks against HTTPS 2015, https://blog.valverde.me/2015/12/07/bad-life-advice/
M. Fischlin, F. Günther, Multi-stage key exchange and the case of Google’s QUIC protocol. In: Ahn, G.J., Yung, M., Li, N. (eds.) ACM CCS 14. pp. 1193–1204. ACM Press, Scottsdale, AZ, USA (Nov 3–7, 2014)
M. Fischlin, F. Günther, Replay attacks on zero round-trip time: The case of the TLS 1.3 handshake candidates. In: 2017 IEEE European Symposium on Security and Privacy, EuroS&P 2017, Paris, France, April 26-28, 2017. pp. 60–75. IEEE 2017, https://doi.org/10.1109/EuroSP.2017.18
K. Gjøsteen, T. Jager, Practical and tightly-secure digital signatures and authenticated key exchange. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part II. LNCS, vol. 10992, pp. 95–125. Springer, Heidelberg, Germany, Santa Barbara, CA, USA (Aug 19–23, 2018)
O. Goldreich, S. Goldwasser, S. Micali, How to construct random functions. J. ACM 33(4), 792–807 (Aug 1986), https://doi.org/10.1145/6490.6503
O. Goldreich, L.A. Levin, A hard-core predicate for all one-way functions. In: 21st ACM STOC. pp. 25–32. ACM Press, Seattle, WA, USA (May 15–17, 1989)
M.D. Green, I. Miers, Forward secure asynchronous messaging from puncturable encryption. In: 2015 IEEE Symposium on Security and Privacy. pp. 305–320. IEEE Computer Society Press, San Jose, CA, USA (May 17–21, 2015)
F. Günther, B. Hale, T. Jager, S. Lauer, 0-RTT key exchange with full forward secrecy. In: Coron, J., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part III. LNCS, vol. 10212, pp. 519–548. Springer, Heidelberg, Germany, Paris, France (Apr 30 – May 4, 2017)
B. Hale, T. Jager, S. Lauer, J. Schwenk, Simple security definitions for and constructions of 0-RTT key exchange. In: Gollmann, D., Miyaji, A., Kikuchi, H. (eds.) ACNS 17. LNCS, vol. 10355, pp. 20–38. Springer, Heidelberg, Germany, Kanazawa, Japan (Jul 10–12, 2017)
S. Iyengar, K. Nekritz, Building zero protocol for fast, secure mobile connections 2017, https://code.fb.com/android/building-zero-protocol-for-fast-secure-mobile-connections/
T. Jager, F. Kohlar, S. Schäge, J. Schwenk, On the security of TLS-DHE in the standard model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 273–293. Springer, Heidelberg, Germany, Santa Barbara, CA, USA (Aug 19–23, 2012)
H. Kario, Add 3072, 7680 and 15360 bit RSA tests to openssl speed, https://groups.google.com/forum/#!topic/mailing.openssl.dev/bv8t7QcXrqg
A. Kiayias, S. Papadopoulos, N. Triandopoulos, T. Zacharias, Delegatable pseudorandom functions and applications. In: Sadeghi, A.R., Gligor, V.D., Yung, M. (eds.) ACM CCS 13. pp. 669–684. ACM Press, Berlin, Germany (Nov 4–8, 2013)
H. Krawczyk, M. Bellare, R. Canetti, Hmac: Keyed-hashing for message authentication (February 1997), http://tools.ietf.org/rfc/rfc2104.txt, rFC2104
H. Krawczyk, P. Eronen, Hmac-based extract-and-expand key derivation function (hkdf) (May 2010), http://tools.ietf.org/rfc/rfc5869.txt, rFC5869
H. Krawczyk, Cryptographic extraction and key derivation: The HKDF scheme. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 631–648. Springer, Heidelberg, Germany, Santa Barbara, CA, USA (Aug 15–19, 2010)
H. Krawczyk, K.G. Paterson, H. Wee, On the security of the TLS protocol: A systematic analysis. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 429–448. Springer, Heidelberg, Germany, Santa Barbara, CA, USA (Aug 18–22, 2013)
A. Langley, How to botch TLS forward secrecy 2013, https://www.imperialviolet.org/2013/06/27/botchingpfs.html
A. Langley, Post-quantum confidentiality for TLS 2018, https://www.imperialviolet.org/2018/04/11/pqconftls.html
S. Lauer, K. Gellert, R. Merget, T. Handirk, J. Schwenk, T0rtt: Non-interactive immediate forward-secret single-pass circuit construction. Proceedings on Privacy Enhancing Technologies 2020(2), 336 – 357 (01 Apr 2020), https://content.sciendo.com/view/journals/popets/2020/2/article-p336.xml
Z. Lin, TLS Session Resumption: Full-speed and Secure (2015), https://blog.cloudflare.com/tls-session-resumption-full-speed-and-secure/
R. Lychev, S. Jero, A. Boldyreva, C. Nita-Rotaru, How secure and quick is QUIC? Provable security and performance analyses. In: 2015 IEEE Symposium on Security and Privacy. pp. 214–231. IEEE Computer Society Press, San Jose, CA, USA (May 17–21, 2015)
C. MacCarthaigh, Security Review of TLS 1.3 0-RTT. https://github.com/tlswg/tls13-spec/issues/1001, accessed: 2018-07-29
E. Rescorla, TLS 0-RTT and Anti-Replay 2015, https://www.ietf.org/mail-archive/web/tls/current/msg15594.html
E. Rescorla, TLS 1.3 2015, http://web.stanford.edu/class/ee380/Abstracts/151118-slides.pdf
E. Rescorla, The Transport Layer Security (TLS) Protocol Version 1.3. RFC 8446 2018, https://rfc-editor.org/rfc/rfc8446.txt
P. Rogaway, Authenticated-encryption with associated-data. In: Atluri, V. (ed.) ACM CCS 02. pp. 98–107. ACM Press, Washington D.C., USA (Nov 18–22, 2002)
P. Rogaway, Formalizing human ignorance. In: P.Q. Nguyen, (ed.) Progress in Cryptology - VIETCRYPT 2006. pp. 211–228. Springer Berlin Heidelberg, Berlin, Heidelberg 2006
A. Sahai, B. Waters, How to use indistinguishability obfuscation: deniable encryption, and more. In: Shmoys, D.B. (ed.) 46th ACM STOC. pp. 475–484. ACM Press, New York, NY, USA (May 31 – Jun 3, 2014)
A. Shamir, On the generation of cryptographically strong pseudorandom sequences. ACM Trans. Comput. Syst. 1(1), 38–44 (Feb 1983), http://doi.acm.org/10.1145/357353.357357
D. Springall, Z. Durumeric, J.A. Halderman, Measuring the security harm of TLS crypto shortcuts. In: Proceedings of the 2016 Internet Measurement Conference. pp. 33–47. ACM 2016
N. Sullivan, Introducing Zero Round Trip Time Resumption 2017, https://blog.cloudflare.com/introducing-0-rtt/
The OpenSSL Project: OpenSSL: The open source toolkit for SSL/TLS, www.openssl.org
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Colin Boyd.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supported by the German Research Foundation (DFG), project JA 2445/2-1, the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme, grant agreement 802823, scholarships from The Israeli Ministry of Science and Technology, The Check Point Institute for Information Security, and The Yitzhak and Chaya Weinstein Research Institute for Signal Processing. We thank Colin Boyd, Sven Hebrok, Nick Sullivan, and all anonymous reviewers for their valuable comments. We also thank Felix Günther and Matilda Backendal for spotting an issue in the proof of Theorem 3 and for suggesting a fix.
Appendices
A Accepting Replay Attacks and Idempotent Requests
When using session tickets, one option is to simply allow replay attacks, in cases where the server can be certain they do not harm security. This was proposed primarily in the case of HTTPS, where TLS encapsulates HTTP requests. Theoretically, HTTP GET requests only retrieve an HTTP resource located on the server, without changing server state. The argument then goes that an attacker replaying an HTTP GET request can only cause a resource to be retrieved several times instead of one, and this is harmless [51, §E.5]. It then follows that it is “safe” to allow replayable HTTP GET requests, and disallow other request types, such as HTTP POST, to be sent such that they can be replayed. This logic can be generalized to allow replay of any idempotent [51] request: a request that has the same effect on the server state whether it is served once or several times.
Furthermore, an attacker is able to cause most modern web browsers to replay any request, idempotent or not [26]. Therefore, the naïve conclusion is that investing resources defending against replay attacks, either in the standard or in deployment practices, is futile.
Colm MacCárthaigh [48] describes several convincing counterarguments against this reasoning. As a simple example, consider the following attack. An HTTP server provides two different medical documents, say DiseaseA.pdf and DiseaseB.pdf. A user downloads one of these documents with TLS 1.3 0-RTT, and doesn’t want the attacker to learn which one. An attacker records the encrypted HTTP GET requests, and wants to learn which file was downloaded.
At some later point in time, document DiseaseA.pdf is deleted from the server (or moved to a different URL, which is equivalent for this attack). The attacker then replays the encrypted HTTP GET request. If the user has downloaded DiseaseA.pdf, then an encrypted HTTP 404 error will be returned, resulting in a relatively “short” response. If the user downloaded DiseaseB.pdf, the server responds with an encrypted pdf document, which is typically much longer.
B Detailed Description of Protocol Values
In this section we provide additional technical details of our modified protocol, introduced in Sect. 4. The details include a table of labels and their values (cf. Table 5) and a short description of how the transcript hashes are computed.
Computation of Transcript Hashes TLS 1.3 includes hash values in the derivation of traffic secrets and the computation of finished messages. In most cases the hashes are computed over the concatenation of all previously-sent and -received messages. The only exception is the computation of the binder value \(\mathsf {Fin} _0\), which only includes a partial transcript of the client’s first flight of messages, ignoring the “binder value” (which is technically part of the client’s first messages) [51, §4.2.11.2]. All other hash values are computed as described in [51, §4.4.1].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aviram, N., Gellert, K. & Jager, T. Session Resumption Protocols and Efficient Forward Security for TLS 1.3 0-RTT. J Cryptol 34, 20 (2021). https://doi.org/10.1007/s00145-021-09385-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00145-021-09385-0





 . The ticket is sent to the client. Additionally, the server replaces its long-term key k by
. The ticket is sent to the client. Additionally, the server replaces its long-term key k by 
 , samples a random bit
, samples a random bit  and generates session keys
and generates session keys  for all sessions
for all sessions 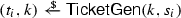 for all sessions
for all sessions  is returned. Note that ticket t can either be a ticket of the initial sequence of tickets
is returned. Note that ticket t can either be a ticket of the initial sequence of tickets  for
for  and generates session keys
and generates session keys  for all
for all  for all
for all  if
if 

 . Finally, it defines
. Finally, it defines  . If
. If  . Else set
. Else set  and sets
and sets 
 and defines
and defines 
