On three-dimensional dynamics of fibre-reinforced functionally graded plates when fibres resist bending

Abstract

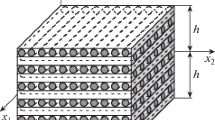
This communication aims to initiate an investigation towards understanding the influence that fibre bending stiffness has on the three-dimensional dynamic behaviour of fibrous composites with embedded functionally graded stiff fibres. In this context, it (i) formulates the general dynamical problem of a rectangular plate with embedded a single family of straight fibres that possess bending resistance and are distributed in a controlled, functionally graded manner through the plate thickness, and (ii) for simple support boundary conditions, it solves the free relevant vibration problem. The problem formulation is based on principles of polar linear elasticity and leads to a high-order set of Navier-type partial differential equations with variable coefficients. For simply supported edge boundaries, solution of these equations is achieved with the use of a computationally efficient semi-analytical (so-called fictitious layer) mathematical method. Two types of possible inhomogeneous distributions of straight fibres are considered for computational and numerical result presentation purposes. These are both regarded as possible, realistic types of inhomogeneous redistributions of stiff fibres that in previous studies have been assumed homogeneously distributed throughout the plate body. The presented numerical results examine to a considerable extent the manner that either of the employed types of inhomogeneous fibre redistribution, in conjunction with the fibre ability to resist bending, affects the dynamic behaviour of the fibrous composite plate of interest.

Appendices

Appendix A: Entries of the matrices G, T and $\varvec{\varGamma }$

The entries of matrix G appearing in (21) are as follows:

$$\begin{aligned} d_{1}= & {} -h^{2}\left( M^{2}+N^{2}\left( \frac{C_{55}}{C_{11}} \right) \right) , \nonumber \\ d_{2}= & {} \frac{C_{55}}{C_{11,}}, \nonumber \\ d_{3}= & {} \frac{{-h}^{2}MN\left( C_{13}+C_{55} \right) }{C_{11}}, \nonumber \\ d_{4}= & {} \frac{hM\left( C_{13}+C_{55} \right) }{C_{11}}, \nonumber \\ d_{5}= & {} \frac{{-h}^{2}\left( {M^{2}C}_{13}+C_{55} \right) }{C_{11}}, \nonumber \\ d_{6}= & {} \frac{C_{44}}{C_{11}}, \nonumber \\ d_{7}= & {} \frac{\left( Nh \right) \left( C_{23}+C_{44} \right) }{C_{11}}, \nonumber \\ d_{8}= & {} \frac{{-h}^{2}\left( C_{55}M^{2}+C_{44}N^{2} \right) }{C_{11}} \nonumber \\ d_{9}= & {} \frac{C_{33}}{C_{11}}, \nonumber \\ d_{10}= & {} -\frac{1}{2}hM^{3}NlL_{1}\left( \frac{C_{11}^{f}V^{f}}{C_{11}} \right) , \nonumber \\ d_{11}= & {} -\frac{1}{2}hM^{3}lL_{1}\left( \frac{C_{11}^{f}V^{f}}{C_{11}} \right) , \nonumber \\ d_{12}= & {} -\frac{1}{2}hM^{4}lL_{1}\left( \frac{C_{11}^{f}V^{f}}{C_{11}} \right) , \nonumber \\ d_{13}= & {} -\frac{1}{2}hM^{3}lL_{1}\left( \frac{C_{11}^{f}V_{,z}^{f}}{C_{11}} \right) , \nonumber \\ d_{21}= & {} \frac{C_{55,z}}{C_{11}}, \nonumber \\ d_{22}= & {} \frac{C_{44,z}}{C_{11}}, \nonumber \\ d_{23}= & {} \frac{C_{13,z}h^{2}M}{C_{11}}, \nonumber \\ d_{24}= & {} \frac{C_{33,z}}{C_{11}}, \nonumber \\ d_{25}= & {} \frac{C_{23,z}h^{2}N}{C_{11}}, \nonumber \\ d_{26}= & {} \frac{C_{55,z}h^{2}M}{C_{11}} ,\nonumber \\ d_{27}= & {} \frac{C_{44,z}h^{2}N}{C_{11}}, \end{aligned}$$

(A.1)

where

$$\begin{aligned} M=\frac{m\pi }{L_{1}} N=\frac{n\pi }{L_{2}}. \end{aligned}$$

(A.2)

The elements of the matrix T appearing in (23) are as follows:

$$\begin{aligned} T_{11}= & {} {-d}_{21} / d_{2}, \quad T_{12}=-{(d}_{1}+\omega ^{2}h^{2}\rho /C_{11})/d_{2}, \quad T_{14}=-{(d}_{3}+d_{10})/d_{2}, \quad T_{15}=-{(d}_{4}+d_{11})/d_{2}, \nonumber \\ T_{16}= & {} -{(d}_{26}+d_{31})/d_{2}, \quad T_{21}=T_{44}=T_{66}=1, \nonumber \\ T_{32}= & {} \frac{{-d}_{3}}{d_{6}}, \quad T_{33}=\frac{{-d}_{22}}{d_{6}}, \quad T_{34}=-{(d}_{5}-d_{12}+\omega ^{2}h^{2}\rho /C_{11})/d_{6}, \quad T_{35}=\frac{{-d}_{7}}{d_{6}}, ~T_{36}=\frac{{-d}_{27}}{d_{6}}, \nonumber \\ T_{51}= & {} \frac{d_{4}}{d_{9}}, \quad T_{52}=\frac{d_{23}}{d_{9}}, \quad T_{53}=\frac{d_{7}}{d_{9}}, \quad T_{54}=\frac{d_{25}}{d_{9}}, ~T_{55}=\frac{{-d}_{24}}{d_{9}}, \nonumber \\ T_{56}= & {} -{(d}_{8}-d_{12}+\omega ^{2}h^{2}\rho /C_{11})/d_{9}. \end{aligned}$$

(A.3)

Finally, the entries of matrix $\varvec{\varGamma }$ appearing in (32) are as follows:

$$\begin{aligned} \mathrm {\Gamma }_{1i}= & {} {\alpha _{1}S}_{1i}+\alpha _{N_{L}2}S_{6i}, \nonumber \\ \mathrm {\Gamma }_{21}= & {} \alpha _{1}, \mathrm {\Gamma }_{22}=\mathrm {\Gamma }_{23}{=\mathrm {\Gamma }}_{24}=\mathrm {\Gamma }_{25}=0, \mathrm {\Gamma }_{26}=\alpha _{6}, \nonumber \\ \mathrm {\Gamma }_{3i}= & {} S_{3i}+\alpha _{3}S_{6i}, \nonumber \\ \mathrm {\Gamma }_{43}= & {} 1,\mathrm {\Gamma }_{46}=\alpha _{3}, \mathrm {\Gamma }_{41}=\mathrm {\Gamma }_{42}=\mathrm {\Gamma }_{44}{=\mathrm {\Gamma }}_{45}=0, \nonumber \\ \mathrm {\Gamma }_{52}= & {} \alpha _{4}, \mathrm {\Gamma }_{54}=\alpha _{5}, \mathrm {\Gamma }_{55}=6, \quad \mathrm {\Gamma }_{51}=\mathrm {\Gamma }_{53}=\mathrm {\Gamma }_{56}=0, \nonumber \\ \mathrm {\Gamma }_{6i}= & {} \alpha _{N_{L}4}S_{2i}+\alpha _{N_{L}5}S_{4i} \quad i=1, 2,\ldots , 6. \end{aligned}$$

(A.4)

where

$$\begin{aligned} \alpha _{1}= & {} \frac{C_{55}^{\left( 1 \right) }}{h}\quad , \quad \alpha _{N1}=\frac{C_{55}^{\left( N_{L} \right) }}{h}, \nonumber \\ \alpha _{2}= & {} MC_{55}^{\left( 1 \right) }-d^{\left( 1 \right) }M^{3}\quad , \quad \alpha _{N2}=MC_{55}^{\left( 1 \right) }-d^{\left( 1 \right) }M^{3}\quad , \nonumber \\ \alpha _{3}= & {} N, \quad \alpha _{4}=-C_{13}^{\left( 1 \right) }M, \quad \alpha _{5}=-C_{23}^{\left( 1 \right) }N, \quad \alpha _{6}=C_{33}^{\left( 1 \right) }h, \nonumber \\ \alpha _{N4}= & {} -C_{13}^{\left( N_{L} \right) }M, \quad \alpha _{N5}=-C_{23}^{\left( N_{L} \right) }N, \quad \alpha _{N6}=\frac{C_{33}^{\left( N_{L} \right) }}{h}. \end{aligned}$$

(A.5)

Appendix B: On the in-plane distortional modes (0, 1) and (1, 0)

In dealing with the in-plane distortional mode (m, $n) = (0, 1)$, the displacement field (19) yields

$$\begin{aligned} U=hf\left( z \right) \sin \left( \frac{\pi y}{L_{2}} \right) \mathrm{sin}\,\omega ~t \quad V=W=0, \end{aligned}$$

(B.1)

and this enables the equations of motion (12) or, equivalently (14) to reduce to the single equation

$$\begin{aligned} C_{55}\frac{\mathrm{d}^{2}f\left( z \right) }{\mathrm{d}z^{2}}+C_{55,z}\frac{\mathrm{d}f\left( z \right) }{\mathrm{d}z}-\left[ {{C}_{55}\left( \frac{\pi }{L_{2}} \right) }^{2}-\rho \omega ^{2}\right] f\left( z \right) =0. \end{aligned}$$

(B.2)

Due to the plate inhomogeneity, (B.2) is generally a second-order ordinary differential equation with variable coefficients that can be solved either with standard power-series methods or with the fictitious layer method employed in this communication.

However, in the case of a homogeneous plate, where $C_{55}$ is constant, (B.2) simplifies further and becomes

$$\begin{aligned} C_{55}\frac{\mathrm{d}^{2}f\left( z \right) }{\mathrm{d}z^{2}}-\left[ {C_{55}\left( \frac{\pi }{L_{2}} \right) }^{2}-\rho \omega ^{2}\right] f\left( z \right) =0. \end{aligned}$$

(B.2)

The lowest frequency associated with this mode is thus seen associated with the linear mode shape

$$\begin{aligned} f\left( z \right) =Az, \end{aligned}$$

(B.3)

where A is a constant. This solution of (B.2) returns the natural frequency

$$\begin{aligned} \omega =\left( \frac{\pi }{L_{2}} \right) \sqrt{\frac{C_{55}}{\rho } ,} \end{aligned}$$

(B.4)

which, by virtue of (43), obtains the non-dimensional form

$$\begin{aligned} \varOmega _{01}=\pi \left( \frac{h}{L_{2}} \right) . \end{aligned}$$

(B.5)

The fact that all $\varOmega _{01}$-values illustrated in Tables 1, 2, 3, 4, and 5 for homogeneous plates ($\varepsilon = 0$) can alternatively be obtained with direct use of (B.5) verifies the efficiency and correctness of the employed computational code. The latter was naturally used for the evaluation of the remaining of the $\varOmega _{01}$-values shown in Tables 1, 2, 3, 4, and 5 for $\varepsilon \ne 0$. These values clearly demonstrate a small influence that the assumed, top-stiff plate inhomogeneity exerts on the values (B.5) of their homogeneous plate counterparts. Nevertheless, Table 6 reveals that the $\varOmega _{01}$-values are influenced more severely from the enhanced inhomogeneity encountered in a through-thickness symmetric fibre redistribution.

Similar observations apply with regard to the in-plane distortional mode (m, $n) = (1, 0)$, for which the displacement field (19) yields

$$\begin{aligned} V=hr\left( z \right) \sin \left( \frac{\pi y}{L_{1}} \right) \mathrm{sin}\,\omega t, \quad U=W=0. \end{aligned}$$

(B.6)

This enables the equations of motion to reduce to the single equation

$$\begin{aligned} C_{44}\frac{d^{2}r\left( z \right) }{dz^{2}}+C_{44,z}\frac{dr\left( z \right) }{dz}-\left[ {{C}_{55}\left( \frac{\pi }{L_{1}} \right) }^{2}+\frac{1}{2}lL_{1}{C_{11}^{f}V}^{f}\left( \frac{\pi }{L_{1}} \right) ^{4}-\rho \omega ^{2}\right] r\left( z \right) =0, \end{aligned}$$

(B.7)

which, due to the plate inhomogeneity, is generally again a second-order ordinary differential equation with variable coefficients. It should be noted though that, unlike (B.2), (B.7) is now influenced by resistance that the fibres may exhibit if/when subjected to in-plane bending.

However, in the case of a homogeneous plate, where $C_{44}$ is constant, (B.7) simplifies further and becomes

$$\begin{aligned} C_{44}\frac{d^{2}r\left( z \right) }{dz^{2}}-\left[ {{C}_{55}\left( \frac{\pi }{L_{1}} \right) }^{2}+\frac{1}{2}lL_{1}{C_{11}^{f}V}^{f}\left( \frac{\pi }{L_{1}} \right) ^{4}-\rho \omega ^{2}\right] r\left( z \right) =0. \end{aligned}$$

(B.8)

The lowest frequency associated with this mode is again associated with the linear mode shape

$$\begin{aligned} g\left( z \right) =Bz, \end{aligned}$$

(B.9)

where B is a constant. This solution of (B.8) returns the natural frequency

$$\begin{aligned} \omega =\left( \frac{\pi }{L_{1}} \right) \sqrt{\frac{C_{55}}{\rho }\left[ 1+\frac{1}{2}lL_{1}{\frac{C_{11}^{f}}{C_{55}}V}^{f}\left( \frac{\pi }{L_{1}} \right) ^{2} \right] } , \end{aligned}$$

(B.10)

and, by virtue of (43), obtains the non-dimensional form

$$\begin{aligned} \varOmega _{10}=\pi \left( \frac{h}{{L_{1}}} \right) \quad \sqrt{ \left[ 1+\frac{1}{2}lL_{1}{\frac{{C_{11}}^{f}}{C_{55}}V}^{f} \left( \frac{\pi }{L_{1}}\right) ^{2} \right] .} \end{aligned}$$

(B.11)