Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-26T06:59:16.532Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE 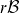$r\mathcal{B}$ELL FAMILY OF DISTRIBUTIONS WITH ACTUARIAL APPLICATIONS

Published online by Cambridge University Press:  18 May 2021

Deepesh Bhati  and
Enrique Calderín-Ojeda Open the ORCID record for Enrique Calderín-Ojeda [Opens in a new window]
Deepesh Bhati
Affiliation:
Department of Statistics Central University of RajasthanKishangarh, India E-Mail: deepesh.bhati@curaj.ac.in
Enrique Calderín-Ojeda*
Affiliation:
Centre for Actuarial Studies Department of Economics The University of Melbourne, Australia E-Mail: enrique.calderin@unimelb.edu.au
*
E-Mail: enrique.calderin@unimelb.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, a new three-parameter discrete family of distributions, the 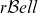$r{\mathcal B}ell$ family, is introduced. The family is based on series expansion of the r-Bell polynomials. The proposed model generalises the classical Poisson and the recently proposed Bell and Bell–Touchard distributions. It exhibits interesting stochastic properties. Its probabilities can be computed by a recursive formula that allows us to calculate the probability function of the amount of aggregate claims in the collective risk model in terms of an integral equation. Univariate and bivariate regression models are presented. The former regression model is used to explain the number of out-of-use claims in an automobile insurance portfolio, by showing a good out-of-sample performance. The latter is used to describe the number of out-of-use and parking claims jointly. This family provides an alternative to other traditionally used distributions to describe count data such as the negative binomial and Poisson-inverse Gaussian models.

Keywords

Automobile insurancebivariate regressionmultiple Poisson processout-of-sampler-Bell Polynomials60E0562E1562H12
Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 52 , Issue 1 , January 2022 , pp. 185 - 210
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The International Actuarial Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bell, E. T. (1934a). Exponential polynomials. Annals of Mathematical, 35(2), 258–277.CrossRefGoogle Scholar
Bell, E. T. (1934b). Exponential numbers. The American Mathematical Monthly, 41(7), 411–419.CrossRefGoogle Scholar
Bender, E. A., and Canfield, E. R. (1996). Log-concavity and related properties of the cycle index polynomials. Journal of Combinatorial Theory, Series A, 74(1), 57–70.CrossRefGoogle Scholar
BolancÉ, C. and Vernic, R. (2019). Multivariate count data generalized linear models: Three approaches based on the Sarmanov distribution. Insurance: Mathematics and Economics, 85(2019), 89–103.Google Scholar
Broder, A.Z. (1984). The r-Stirling numbers, Discrete Mathematics, 49, 241–259.CrossRefGoogle Scholar
Boucher, J.P., Denuit, M. and GuillÉn, M. (2008). Models of insurance claim counts with time dependence based on generalization of Poisson and negative binomial distributions. Variance, 2(1):135–162.Google Scholar
CalderÍn-Ojeda, E., GÓmez-DÉniz, E. and Barranco-Chamorro, I. (2019). Modelling zero-inflated count data with a special case of the generalised poisson distribution. Astin Bulletin, 49(3):689–707.CrossRefGoogle Scholar
Castellares, F., Ferrari, S. L., and Lemonte, A. J. (2018). On the Bell distribution and its associated regression model for count data. Applied Mathematical Modelling, 56, 172–185.CrossRefGoogle Scholar
Castellares, F., Lemonte, A. J., and Moreno-Arenas, G. (2019). On the two-parameter Bell-Touchard discrete distribution. Communications in Statistics-Theory and Methods, 1–19.Google Scholar
Denuit, M., and Lamber, P. (2005). Constraints on concordance measures in bivariate discrete data. Journal of Multivariate Analysis, 93(1), 40–57.CrossRefGoogle Scholar
Famoye, F. (2010). On the bivariate negative binomial regression model. Journal of Applied Statistics, 37(6), 969–981.CrossRefGoogle Scholar
JÁnossy, L., RÉnyi, A. and AczÉl, J. (1950). On composed Poisson distributions, I, Acta Mathematica Academiae Scientiarum Hungaricae, 1(2-4):209–224.CrossRefGoogle Scholar
Johnson, N.L, Kemp, A.W and Kotz, S. (2005). Univariate discrete distributions, Third Edition. Wiley Series in Probability and Statistics. Hoboken, NJ.Google Scholar
Kamp, U. (1998). On a class of premium principles including the Esscher principle. Scandinavian Actuarial Journal, 1, 75–80.CrossRefGoogle Scholar
Kemp, C.D. (1967). On a contagious distribution suggested for accident data, Biometrics, 23(2):241–255.CrossRefGoogle ScholarPubMed
Keilson, J., and Gerber, H.(1971). Some result for discrete unimodality. Journal of American Statistical Association, 66 (334), 386–389.CrossRefGoogle Scholar
Panjer, Klugman, S.A. and Willmot, G.E. (2008). Loss Models: From Data to Decisions, 3rd ed., Wiley, New York, 2008.Google Scholar
Lee, S.C.K (2021). Addressing imbalanced insurance data through zero-inflated Poisson regression with boosting. Astin Bulletin 51(1): 27–55.CrossRefGoogle Scholar
Li, C.S., Lu, J.C., Park, J., Kiim, K., Brinkley, P., and Peterson, J. (1999). Multivariate zero-inflated Poisson models and their applications. Technometrics, 41(1):29–38.CrossRefGoogle Scholar
Liu, F., and Pitt, D. (2017) Application of bivariate negative binomial regression model in analysing insurance count data, Annals of Actuarial Science, 11(2), 390–411.CrossRefGoogle Scholar
Touchard, J. (1933). PropriÉtÉs arihtmÉtiques de certains nombres rÉcurrents. Annales de la SociÉtÉ Scientifique de Bruxelles, 53, 21–31.Google Scholar
MezÖ, I. (2011). The r-Bell Numbers, Journal of Integer Sequences, 14(1), 1–14.Google Scholar
Papageorgiou, H. and Piperigou, V.E. (1997). On bivariate ‘Short’ and related distributions, In: Advances in the Theory and Practice of Statistics-A Volume in Honor of Samuel Kotz (N.L. Johnson, and N. Balakrishnan, Eds.), 397–413, New York: John Wiley & SonsGoogle Scholar
Puig, P. and Valero, J. (2006). Count Data Distributions: Some Characterizations with applications. Journal of the American Statistical Association, 101 (473), 332–340.CrossRefGoogle Scholar
Rolski, T., Schmidli, H., Schmidth, V., Teugels, J. (1999). Stochastic Process for Insurance and Finance. John Wiley and Sons, New York.CrossRefGoogle Scholar
Vuong, Q. (1989). Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica, 57, 2, 307–333.CrossRefGoogle Scholar
Yan, H. R., Zhang, Q. L., and Xu, A. M. (2019). Some Inequalities for Generalized Bell-Touchard Polynomial. Journal of Mathematical Inequalities, 13(3), 645–653.CrossRefGoogle Scholar
Supplementary material: File

Bhati and Calderín-Ojeda supplementary material

Bhati and Calderín-Ojeda supplementary material

Download Bhati and Calderín-Ojeda supplementary material(File)
File 558.8 KB