Abstract
A new analytical model (R-toroid), representing a 3D generalization of the precessing Gaussian ring, is constructed for the study of secular perturbations in celestial mechanics. Our approach is based on triple averaging of the motion of a material point and is reduced to a chain of transformations: 1D Gaussian ring–2D R-ring–3D R-toroid. The figure, structure and gravitational potential of the R-toroid are studied. We obtained the expression for the mutual energy of the R-toroid and the outer Gaussian ring to study the motion of bodies in the gravitational field of the model in two forms (in the integral and in the form of a power-law series). Two equation systems of the secular evolution of osculating orbits (Gaussian rings), in the gravitational field of an R-toroid and in the field of a central precessing star, are derived using the mutual energy. The periods of nodal TΩ and apsidal Tω orbital precession were obtained. Examples of three hot Jupiters with a known period of nodal precession are considered. For the exoplanet Kepler-413b, the R-toroid describes the evolution of any orbit with a ≥ 5.48 AU, and for the exoplanet PTFO 8-8695b, the critical value of the semi-major axis turned out to be only amin ≈ 0.2 AU. The frequency profile of the precession of the test orbit in the field of the star and planet PTFO 8-8695b has been calculated. The minimum value of the period of nodal precession was TΩ ≈ (26.1 ± 3.0) × 103 years.










Similar content being viewed by others
REFERENCES
B. P. Kondratyev, Theory of Potential: New Methods and Problems with Solutions (Mir, Moscow, 2007).
B. P. Kondratyev, Solar Syst. Res. 46, 352 (2012).
V. A. Antonov, I. I. Nikiforov, and K. V. Kholshevnikov, Elements of the Theory of Gravitational Potential and Some Cases of its Explicit Expression (SPbGU, St. Petersburg, 2008) [in Russian].
M. A. Vashkovyak and S. N. Vashkovyak, Solar Syst. Res. 46, 69 (2012).
J. R. Touma, S. Tremaine, and M. V. Kazandjian, Mon. Not. R. Astron. Soc. 394, 1085 (2009).
B. P. Kondratyev and V. S. Kornoukhov, Astron. Rep. 64, 434 (2020).
B. P. Kondratyev, N. G. Trubitsyna, and E. Sh. Mukhametshina, ASP Conf. Ser. 316, 326 (2004).
B. P. Kondratyev, Mon. Not. R. Astron. Soc. 442, 1755 (2014).
B. P. Kondratyev and V. S. Kornoukhov, Astron. Rep. 64, 870 (2020).
Y. Judkovsky, A. Ofir, and O. Aharonson, Astron. J. 160, 195 (2020).
C. D. Murray and S. F. Dermott, Solar System Dynamics (Cambridge Univ. Press, Cambridge, UK, 2000).
J. L. Simon, P. Bretagnon, J. Chapront, M. Chapront-Touze, G. Francou, and J. Laskar, Astron. Astrophys. 282, 663 (1994).
K. Batygin and M. E. Brown, Astron. J. 151, 22 (2016).
K. Batygin, F. C. Adams, M. E. Brown, and J. C. Becker, Phys. Rep. 805, 1 (2019).
JPL Small-Body Database.
R. A. Wittenmyer, M. Endl, W. D. Cochran, and H. F. Levison, Astron. J. 134, 1276 (2007).
V. B. Kostov, P. R. McCullough, J. A. Carter, M. Deleuil, et al., Astrophys. J. 784, 14 (2014).
M. C. Johnson, W. D. Cochran, A. Collier Cameron, and D. M. Bayliss, Astrophys. J. Lett. 810, 23 (2015).
St. Raetz, T. O. B. Schmidt, S. Czesla, T. Klocová, et al., Mon. Not. R. Astron. Soc. 460, 2834 (2016).
J. W. Barnes, J. C. van Eyken, B. K. Jackson, D. R. Ciardi, and J. J. J. W. Fortney, Astrophys. J. 774, 53 (2013).
ACKNOWLEDGMENTS
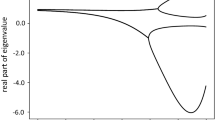
The authors are grateful to the Interdisciplinary Scientific and Educational School of Moscow State University “Fundamental and Applied Space Research,” as well as I.A. Strakhov for his help with Figure 5.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated by E. Seifina
APPENDIX
APPENDIX
EXPANSION OF THE EXTERNAL POTENTIAL OF AN R-TOROID IN A SERIES
To derive formula (24), it is advisable to introduce the function
which we expand in a series in the variables x and u. As a result, we get the series
which can be rewritten, taking into account the form of the function (A1), in the form
where \(\bar {F}(R,z,a,g) = F(R,z,x = 0,a,g).\) After substituting the series (A3) in (22), considering (A1) and rearranging the places of summation and integration, the double integral is divided into the sum of the products of two single integrals
From here, introducing coefficients (25), as a result, we obtain formula (24).
Rights and permissions
About this article
Cite this article
Kondratyev, B.P., Kornoukhov, V.S. R-Toroid as a Three-Dimensional Generalization of a Gaussian Ring and Its Application in Astronomy. Astron. Rep. 65, 412–426 (2021). https://doi.org/10.1134/S1063772921050048
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1063772921050048