Abstract
We provide a school choice model where the student priority orders for schools are allowed not to be total. We introduce a class of algorithms, each of which derives a student optimal stable matching once we have an initial stable matching, when the priorities are represented by partial orders. Since a method to derive a stable matching exists when the priorities are partial orders, we can use it to derive a student optimal stable matching. Moreover, we show that any student optimal stable matchings that Pareto dominate the starting stable one are obtained via an algorithm within this class. For the problem of improving efficiency by allowing some priorities to be violated, the algorithms can also be applied, with a weaker assumption on the violations than in the previous study. Finally, we suggest some specific rules of priorities that can be introduced by weakening the requirement of total ordering.
Similar content being viewed by others
Notes
They show that their algorithm is a polynomial-time one.
Note that this definition is equivalent to the standard definition in terms of a reflexive relation. That is, for any weak order B, there exists a reflexive, weakly connected and transitive \(B'\) that satisfies xBy if and only if \(xB'y\) and
 . Moreover, for any reflexive, weakly connected and transitive \(B'\), there exists a weak order B that satisfies this relationship. (Note that being “complete” is equivalent to satisfying both reflexivity and weak connectedness.) In particular, for the former, construct \(B'\) as \(xB'y\) if and only if
. Moreover, for any reflexive, weakly connected and transitive \(B'\), there exists a weak order B that satisfies this relationship. (Note that being “complete” is equivalent to satisfying both reflexivity and weak connectedness.) In particular, for the former, construct \(B'\) as \(xB'y\) if and only if 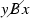 . (For the latter, simply construct B in the above standard manner.)
. (For the latter, simply construct B in the above standard manner.)While the definitions of the orders basically also follow those of Fishburn (1970, Ch.2), our definitions and terminology are different from the Fishburn’s ones in the following points. First, Fishburn (1970, Definition 2.2) calls a binary relation as a strict partial order if it is irreflexive and transitive. Since irreflexivity and transitivity imply asymmetry, our definition is equivalent to his, although we omit “strict”. Second, Fishburn (1970, Definition 2.1) calls a binary relation as a weak order if it is asymmetric and negative transitive. Then, it is also transitive and irreflexive, and hence is also equivalent to ours, because asymmetry implies irreflexivity, and asymmetry and negative transitivity implies transitivity. Third, Fishburn (1970, Definition 2.1) calls a weakly connected weak order a strict order, but we call it a total order.
See Footnote 2.
Since the objective here is only to find a stable matching, the school proposing one is also an alternative, and may be a better choice in the sense of expanding the set of available student optimal stable matchings. For given \(\left( P,\succ \right) \in {\mathcal {P}}^{n}\times \Pi ^{m}\), let \( {\hat{\succ }}\in {\mathcal {T}}^{m}\) be an extension of \(\succ \). As is well known, a resulting matching of the school proposing DA algorithm \(\mu \) and that of the SPDA algorithm \(\mu ^{\prime }\) may differ, and then \(\mu \) is Pareto dominated by \(\mu ^{\prime }\). Thus, there may exist a student optimal matching (with respect to \(\succ \)) that Pareto dominates \(\mu \) but does not \(\mu ^{\prime }\). To be clearer, let M and \(M^{\prime }\) be the set of all matchings that Pareto dominates \(\mu \) and \(\mu ^{\prime }\), respectively. Then, \(M^{\prime }\subseteq M\) must be satisfied. Since we introduce the class of algorithms that can derive all stable matchings that Pareto dominates the starting stable matching, thus, for the case of \( M^{\prime }\subsetneq M\), we can expand the set of available student optimal stable matchings by adopting \(\mu \) as the initial matching of the algorithms.
Note that in Erdil and Ergin (2008), the counterparts of \(X_{i}\left( \mu \right) \) and \(Y_{i}\left( \mu \right) \) are denoted as \(D_{\mu \left( i\right) }\) and \(B_{\mu \left( i\right) }\), respectively.
For the importance of the computational efficiency, see, for example, Korte and Vygen (2000, Ch.1).
In the case of \(\succ \in {\mathcal {T}}^{m}\), since \(i^{\prime }\succ _{\mu \left( i\right) }j\) is equivalent to \(j\nsucc _{\mu \left( i\right) }i^{\prime }\), the algorithm of Dur et al. (2019) works even if \(\left( \succ ,C\right) \) does not satisfy Assumption 1 but satisfies Assumption 2.
The essence of the problem here is: with \(\succ _{s}\in \Pi \), both i \(\nsucc _{s}\) j and j \(\nsucc _{s}\) i are possible. Therefore, even when i’s assignment to s does not violate the priority of j for s, one cannot include i in \(X_{\mu ^{-1}\left( s\right) }^{\prime }(\mu )\). This issue is resolved with \(\succ _{s_{1}}\in {\mathcal {T}}\). Indeed, when \(\succ \in {\mathcal {T}}^{m}\), the algorithm of Dur et al. (2019) works even when \(\left( \succ ,C\right) \) does not satisfy Assumption 1 but satisfies Assumption 2. For instance, in Example 1, the algorithm of Dur et al. (2019) obtains \(\mu ^{\prime }\).
The interesting connection between Examples 1 and 2 is: the binary relation we construct \(\succ _{s_{1}}^{C}\) for both problems is identical. This suggests a way forward for recovering the algorithm of Dur et al. (2019): beginning with a problem in \(\succ _{s}\in \Pi \setminus {\mathcal {T}}\), one can “transform” the problem into another problem with \(\succ _{s}\in {\mathcal {T}}\) such that \(\succ _{s}^{C}\) remains the same. One can then execute Dur et al. (2019)’s algorithm. We discuss this possibility in Sect. 6.
For example, in Boston city, students who lived within 1 mile from elementary school, within 1.5 miles from middle school, and within 2 miles from high school were considered to be in the school’s walk zone (Abdulkadiroğlu et al. 2006). However, as is mentioned by Dur et al. (2013), the walk zone priority has recently been eliminated in Boston.
In the nursery school assignment of several wards in Tokyo, the priority for a school in the ward of a resident child is higher than that of a child living in another ward if the other circumstances of the two children are the same. See, for example, the rules of Bunkyo ward: https://www.city.bunkyo.lg.jp/var/rev0/0182/2053/pamphlet31.pdf.
We heavily owe the discussion here, including the alternative random algorithm as it is, to an associate editor.
We show this fact to introduce a modification of Example 2. Everything is as in Example 2, with the exception of \((\succ _{s_{1}},C (s_{1}))\). Let \(\succ _{s_{1}}\) be such that \(i_{1}\succ _{s_{1}}i\) for all \(i=\) \(i_{2},i_{3},i_{4}\) and \(i_{2}\succ _{s_{1}}i_{3}\). There are only two stable matchings \(\mu \) and \(\mu ^{\prime }\) in Example 2 for \(\left( P,\succ \right) \) and one of them is chosen as the SPDA outcome depending on the total orders extending \(\succ _{s_{1}}\). If fact, if the total order \({\hat{\succ }}_{s_{1}}\) is such that \(i_{1}{\hat{\succ }}_{s_{1}}i_{4} {\hat{\succ }}_{s_{1}}i_{2}{\hat{\succ }}_{{s_{1}}}i_{3}\), then \(\mu ^{\prime }\) is the SPDA outcome. On the other hand, if \({\hat{\succ }}_{s_{1}}\) is such that \(i_{1}{\hat{\succ }}_{s_{1}}i_{2}{\hat{\succ }}_{{s_{1}}}i_{3}{\hat{\succ }}_{{ s_{1}}}i_{4}\), then the SPDA outcome is \(\mu \), which is Pareto dominated by \(\mu ^{\prime }\). Therefore, if we randomly choose an extension of \(\succ _{s_{1}}\), the SPDA outcome is \(\mu \) with a positive probability. On the other hand, our algorithm obtains \(\mu ^{\prime }\) regardless to the starting matching. Therefore, the outcome of the random method is (stochastically) dominated by that of any of our algorithms.
Note that, strictly speaking, this example is beyond the scope of the discussion of this section thus far [where in terms of Sect. 4, Assumption 1 can be satisfied as in Dur et al. (2019)], but is in the scope of those introduced later.
See, for example, the assignment systems in China (Chen and Kesten 2019), Taiwan (Dur et al. 2018) and Turkey (Balinski and Sönmez 1999). The systems of public high schools in many prefectures in Japan are similar. See a description of the system of the Kanagawa prefecture: http://www.pref.kanagawa.jp/docs/dc4/nyusen/nyusen/r2/nyusenseidogaiyou.html.
For example, in the Kanagawa prefecture in Japan, the examination includes a mathematics test, a national language test, an English test, a social science test and a natural science test. Schools may use different combinations and weights of tests to decide their students priority order. In several regions such as China, Taiwan and Turkey, schools also may use different combinations and weights.
It may be more allowable if i is one of students whose welfares are to be improved. For this point, see Kesten (2010).
For example, the magnitude relationship in the total score may be just caused by the difference between the difficulty of the two exams, and some standardization before the summation may easily change the total score relationship. In fact, the average and variance of the scores of A are higher than those of B.
The discussion here may also be extended to public housing course allocation. We thank an anonymous referee suggesting us these examples including the school choice extension here.
In the example of Dur et al. (2019), for some s, \(\succ _{s}^{C}\) is not transitive but acyclic; that is, for any s and any \(\left\{ j_{1},j_{2},\ldots ,j_{g}\right\} \subseteq I\), \(j_{1}\succ _{s}^{C}j_{2},\) \( j_{2}\) \(\succ _{s}^{C}j_{3},\ldots ,\) and \(j_{g-1}\) \(\succ _{s}^{C}j_{g}\) imply \(j_{g}\nsucc _{s}^{C}j_{1}\). The acyclicity is weaker than the transitivity. See, for example, Sen (1970, Ch 1*) on this property. Replacing the transitivity with the acyclicity makes the algorithm fail to work.
On the other hand, Lemma 2 also implies that each algorithm does not decrease the number of matches, hence finding a largest student optimal matching is reduced to finding one of the largest stable matchings (or a total order priority profile \({\hat{\succ }}\) satisfying (1) for all s that yields such a matching).
References
Abdulkadiroğlu A, Sönmez T (2003) School choice: a mechanism design approach. Am Econ Rev 93:729–747
Abdulkadiroğlu A, Pathak PA, Roth AE, Sönmez T (2006) Changing the Boston Public School Mechanism: strategy-proofness as equal access. NBER Working paper, 11965
Abdulkadiroğlu A, Pathak PA, Roth AE (2009) Strategy-proofness versus efficiency in matching with indifferences: redesigning the NYC high school match. Am Econ Rev 99:1954–1978
Alva S, Manjunath V (2019) Strategy-proof Pareto-improvement. J Econ Theory 181:121–142
Balinski M, Sönmez T (1999) A tale of two mechanisms: student placement. J Econ Theory 84(1):73–94
Chen Y, Kesten O (2019) Chinese college admissions and school choice reforms: an experimental study. Games Econ Behav 115:83–100
Cho WJ, Doğan B (2017) Stability and the immediate acceptance rule when school priorities are weak. Int J Game Theory 46:991–1014
Dur U, Kominers SD, Pathak PA, Sönmez T (2013) The demise of walk zones in Boston: priorities vs. precedence in school choice. NBER Working paper, w18981
Dur U, Pathak PA, Song F, Sönmez T (2018) Deduction dilemmas: the Taiwan assignment mechanism. NBER Working paper, w25024
Dur U, Gitmez A, Yılmaz Ö (2019) School choice under partial fairness. Theor Econ 14(4):1309–1346
Ehlers L, Erdil A (2010) Efficient assignment respecting priorities. J Econo Therory 145(3):1269–1282
Erdil A, Ergin H (2008) What’s the matter with tie-breaking? Improving efficiency in school choice. Am Econ Rev 98(3):669–689
Erdil A, Kumano T (2019) Efficiency and stability under substitutable priorities with ties. J Econ Theory 184:104950
Fishburn PC (1970) Utility theory for decision making. Wiley, New York
Gale D, Shapley LS (1962) College admissions and the stability of marriage. Am Math Mon 69(1):9–15
Han X (2018) Stable and efficient resource allocation under weak priorities. Games Econ Behav 107:1–20
Kahn AB (1962) Topological sorting of large networks. Commun ACM 5(11):558–562
Kamada Y, Kojima F (2020) Fair matching under constraints: theory and applications. Rev Econ Stud (forthcoming)
Kesten O (2010) School choice with consent. Q J Econ 125:1297–1348
Kitahara M, Okumura Y (2019) On the number of employed in the matching model. J Math Econ 83:63–69
Korte B, Vygen J (2000) Combinatorial optimization: theory and algorithms. Springer, Berlin
Kumano T (2017) Nash implementation of constrained efficient stable matchings under weak priorities. Games Econ Behav 104:230–240
Okumura Y (2019) School choice with general constraints: a market design approach for the nursery school waiting list problem in Japan. Jpn Econ Rev 70(4):497–516
Roth AE (1982) The economics of matching: stability and incentives. Math Oper Res 7:617–628
Roth AE (2008) Deferred acceptance algorithms: history, theory, practice, and open questions. Int J Game Theory 36:537–569
Sen AK (1970) Collective choice and social welfare. Holden-Day, San Francisco
Szpilrajn E (1930) Sur l’extension de l’ordre partiel. Fundamenta Mathematicae 16:386–389
Tang Q, Yu J (2014) A new perspective on Kesten’s school choice with consent idea. J Econ Theory 154:543–561
Troyan P, Delacrétaz D, Kloosterman A (2020) Essentially stable matchings. Games Econ Behav 120:370–390
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Previous versions of this work were presented at the 9th MAEDA in Kwansei Gakuin University, the Kansai Game Theory Workshop in Yokohama National University and the Microeconomics Workshop in Keio University. We would like to express our gratitude to participants for their helpful comments. We also are grateful to three anonymous referees and an associate editor for many valuable comments and suggestions. This work was supported by JSPS KAKENHI Grant Number JP20K01675, JP19K01542, JP18K01513 and JP16K03612.
Rights and permissions
About this article
Cite this article
Kitahara, M., Okumura, Y. Improving efficiency in school choice under partial priorities. Int J Game Theory 50, 971–987 (2021). https://doi.org/10.1007/s00182-021-00777-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-021-00777-x


 . Moreover, for any reflexive, weakly connected and transitive
. Moreover, for any reflexive, weakly connected and transitive 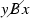 . (For the latter, simply construct B in the above standard manner.)
. (For the latter, simply construct B in the above standard manner.)