A delay model for persistent viral infections in replicating cells

Abstract

Persistently infecting viruses remain within infected cells for a prolonged period of time without killing the cells and can reproduce via budding virus particles or passing on to daughter cells after division. The ability for populations of infected cells to be long-lived and replicate viral progeny through cell division may be critical for virus survival in examples such as HIV latent reservoirs, tumor oncolytic virotherapy, and non-virulent phages in microbial hosts. We consider a model for persistent viral infection within a replicating cell population with time delay in the eclipse stage prior to infected cell replicative form. We obtain reproduction numbers that provide criteria for the existence and stability of the equilibria of the system and provide bifurcation diagrams illustrating transcritical (backward and forward), saddle-node, and Hopf bifurcations, and provide evidence of homoclinic bifurcations and a Bogdanov–Takens bifurcation. We investigate the possibility of long term survival of the infection (represented by chronically infected cells and free virus) in the cell population by using the mathematical concept of robust uniform persistence. Using numerical continuation software with parameter values estimated from phage-microbe systems, we obtain two parameter bifurcation diagrams that divide parameter space into regions with different dynamical outcomes. We thus investigate how varying different parameters, including how the time spent in the eclipse phase, can influence whether or not the virus survives.

Proofs

1.1 Proof of Theorem 1

Proof

To study the behavior of the solutions near an equilibrium, we first linearize the model (1) about the equilibrium $(S^*, \ E^*,\ C^*,\ P^*)$ by taking $S(t)= S^* + x(t), E(t)= E^*+ y(t), C(t)= C^* + z(t)$, and $V(t)= V^* + v(t).$ We look for eigenvalues of the linear operator - that is we look for solutions of the form $x(t)= {\overline{x}}e^{\lambda t}, y(t)= {\overline{y}}e^{\lambda t}, z(t)= {\overline{z}}e^{\lambda t}$, and $v(t)={\overline{v}}e^{\lambda t}$, where $\lambda \in {\mathbb {C}}$ and ${\overline{x}},\ {\overline{y}}, \ {\overline{z}}, \ {\overline{v}}$ are arbitrary non-zero constants, but the eigenvalue $\lambda$ is common. This process results in the following system (the bars have been omitted):

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda x&{}=-r S^*\dfrac{n}{K} +r x\left( 1-\dfrac{N^*}{K}\right) -\phi S^*v-\phi xV^*-dx \\ \lambda y &{}=\phi S^*v+\phi xV^*-\hat{d} y-\phi e^{-\hat{d}\tau }S^*v e^{-\lambda \tau }-\phi e^{-\hat{d}\tau }xe^{-\lambda \tau }V^*, \\ \lambda z&{}=-r_0 C^*\dfrac{n}{K} +r_0 z\left( 1-\dfrac{N^*}{K}\right) -{\tilde{d}}z+\phi e^{-\hat{d}\tau }S^*ve^{-\lambda \tau }+\phi e^{-\hat{d}\tau }x e^{-\lambda \tau }V^*, \\ \lambda v&{}=\alpha z-\phi S^*v-\phi xV^*-\mu v, \end{array}\right. } \end{aligned}$$

(15)

where $N^*=S^*+E^*+C^*$ and $n=x+y+z$.

At the equilibrium, ${\mathcal {E}}_0=(S_0,0,0,0)$, system (15) simplifies to:

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda x&{}=-r S_0\dfrac{n}{K} +r x\left( 1-\dfrac{S_0}{K}\right) -\phi S_0 v-dx \\ \lambda y &{}=\phi S_0 v-\hat{d} y-\phi e^{-\hat{d}\tau }S_0ve^{-\lambda \tau }, \\ \lambda z&{}=r_0 z\left( 1-\dfrac{S_0}{K}\right) -{\tilde{d}}z+\phi e^{-\hat{d}\tau }S_0 ve^{-\lambda \tau }, \\ \lambda v&{}=\alpha z-\phi S_0 v-\mu v. \end{array}\right. } \end{aligned}$$

(16)

We obtain the following characteristic equation:

$$\begin{aligned} 1=\dfrac{ r_0}{({\tilde{d}}+\lambda )}\left( 1-\dfrac{S_0}{K}\right) +\dfrac{\phi S_0 e^{-(\hat{d}+\lambda )\tau } }{\lambda +\phi S_0+\mu }\dfrac{\alpha }{(\tilde{d}+\lambda )}. \end{aligned}$$

(17)

Let

$$\begin{aligned} G (\lambda ) = \dfrac{ r_0}{({\tilde{d}}+\lambda )}\left( 1-\dfrac{S_0}{K}\right) +\dfrac{\phi S_0 e^{-(\hat{d}+\lambda )\tau } }{\lambda +\phi S_0+\mu }\dfrac{\alpha }{({{\tilde{d}}}+\lambda )}. \end{aligned}$$

First, we show that if ${\mathcal {R}}_0>1$, then (17) has a positive real solution, and hence ${\mathcal {E}}_0$ is unstable. Since $S_0<K$, it follows that $G(\lambda )$ is a decreasing function of $\lambda \in {\mathbb {R}}$. Note also that $\lim _{t \rightarrow \infty } G(\lambda )=0.$ Therefore, if $G(0)>1$, there exists $\lambda ^*>0$ such that $G(\lambda ^*)=1$. Since $G(0)=\mathcal R(0)>1$, it follows that (17) has a positive solution, and hence ${\mathcal {E}}_0$ is unstable.

Next, assume that ${\mathcal {R}}_0<1$. Since, $S_0<K$, we have $0<G(0)=\mathcal R_0<1$. By continuity, there exists $0<\sigma <\min \{{\tilde{d}},\hat{d},\mu \}$, such that $|G(-\sigma )|<1$. If $\lambda =a+i b$ and $a\ge -\sigma$, then since ${\tilde{d}}-\sigma >0$ and $\mu -\sigma >0$,

$$\begin{aligned} |G(\lambda )|\le & {} \left| \frac{1}{{\tilde{d}}+ a + i b}\right| \left[ \left| r_0\left( 1-\frac{S_0}{K}\right) \right| +\left| \alpha \frac{\phi S_0 e^{-(\hat{d} +a +i b)\tau } }{\phi S_0+(\mu +a+ib)} \right| \right] \\\le & {} \left| \frac{1}{{\tilde{d}}+a + i b)}\right| \left( r_0\left( 1-\frac{S_0}{K}\right) +\alpha \frac{\left| \phi S_0 e^{-(\hat{d} +a +i b)\tau }\right| }{\left| \phi S_0+(\mu +a+ib)\right| } \right) \\\le & {} \left| \frac{1}{{\tilde{d}}-\sigma )}\right| \left( r_0\left( 1-\frac{S_0}{K}\right) +\alpha \frac{\left| \phi S_0 e^{-(\hat{d} +a )\tau }\right| }{\left| \phi S_0+(\mu +a+i b)\right| } \right) \\\le & {} \left| \frac{1}{{\tilde{d}}-\sigma )}\right| \left( r_0\left( 1-\frac{S_0}{K}\right) +\alpha \frac{\phi S_0 e^{-(\hat{d} +a )\tau } }{\phi S_0+(\mu +a)} \right) \\\le & {} \left| \frac{1}{{\tilde{d}}-\sigma )}\right| \left( r_0\left( 1-\frac{S_0}{K}\right) +\alpha \frac{\phi S_0 e^{-(\hat{d}-\sigma )\tau } }{\phi S_0+(\mu -\sigma )} \right) \\= & {} |G(-\sigma )| <1. \end{aligned}$$

Hence one can conclude that $\sup \{ Re\lambda : G(\lambda )=1\} <-\sigma$. The conclusion follows from Theorem 4.8 in Smith (Smith 2011). $\square$

1.2 Proof of Theorem 2

Proof

We consider the local stability of ${\mathcal {E}}_c.$ Evaluated at this equilibrium, (15) becomes,

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda x&{}=r x(1-\dfrac{C_0}{K})-\phi xV_c-dx, \\ \lambda y &{}=\phi xV_c-\hat{d} y-\phi e^{-\hat{d}\tau }xe^{-\lambda \tau }V_c, \\ \lambda z&{}=-r_0 C_0\dfrac{n}{K} +r_0 z(1-\dfrac{C_0}{K})-{\tilde{d}}z+\phi e^{-\hat{d}\tau }xe^{-\lambda \tau }V_c, \\ \lambda v&{}=\alpha z-\phi xV_c-\mu v. \end{array}\right. } \end{aligned}$$

(18)

Since $V_c=\dfrac{\alpha }{\mu }C_0$, the characteristic equation is given by

$$\begin{aligned} \left[ -\mu -\lambda \right] \left[ -\hat{d}-\lambda \right] \left[ r_0\left( 1-\frac{C_0}{K}\right) -{\tilde{d}}\right] \left[ r\left( 1-\frac{C_0}{K}\right) -\phi \dfrac{\alpha }{\mu }C_0-d-\lambda \right] =0, \end{aligned}$$

a polynomial of degree 4 with roots:

$$\begin{aligned} \lambda _1=-\mu , \quad \lambda _2=-\hat{d}, \quad \lambda _3=-r_0+{\tilde{d}}, \quad \lambda _4= r \left( 1-\dfrac{C_0}{K}\right) -\phi \dfrac{\alpha }{\mu }C_0-d \end{aligned}$$

$\lambda _1$ and $\lambda _2$ are always negative. $\lambda _3$ is negative provided $C_0>0$, i.e., when ${\mathcal {E}}_c$ is biologically relevant.

$$\begin{aligned} \lambda _4= & {} C_0 \left[ r \left( \dfrac{1}{C_0}-\dfrac{1}{K}\right) -\phi \dfrac{\alpha }{\mu }-\dfrac{d}{C_0} \right] =C_0\left[ \frac{r-d}{C_0}-\frac{r}{K}-\frac{K\phi \alpha }{r\mu } \right] \\= & {} \frac{rC_0}{K}\left[ \frac{S_0}{C_0}-\frac{K\phi \alpha }{r \mu }-1 \right] =\frac{rC_0}{K}\left[ {\mathcal {R}}^{C_0}_S-1\right] . \end{aligned}$$

Therefore, when ${\mathcal {E}}_c$ is biologically meaningful, it is locally asymptotically stable if ${\mathcal {R}}^{C_0}_S<1$ and unstable if ${\mathcal {R}}^{C_0}_S>1$. $\square$

1.3 Proof of Proposition 1.

Proof

Let

$$\begin{aligned} \mathcal E^\dagger _i=(S^\dagger _i,E^\dagger _i,C^\dagger _i,V^\dagger _i): \mathcal E^\dagger _i \in {\mathbb {R}}^4_{>0}, \, i=1,2 \end{aligned}$$

denote the interior equilibria of system (1), provided they exist. Then, if we define

$$\begin{aligned} N^\dagger _i=S^\dagger _i+E^\dagger _i+C^\dagger _i, \end{aligned}$$

(19)

equating the right-hand sides of (1) equal to zero to obtain expressions for the components of the equilibria, it follows that

$$\begin{aligned} N^\dagger _i=S_0-\dfrac{K}{r} \phi V^\dagger _i, \ V^\dagger _i=\dfrac{\alpha C^\dagger _i}{\phi S^\dagger _i+\mu },\ E^\dagger _i=\dfrac{\phi S^\dagger _i}{\phi S^\dagger _i+\mu } \dfrac{\alpha C^\dagger _i}{\hat{d}}[1-e^{-\hat{d}\tau }] . \end{aligned}$$

(20)

and

$$\begin{aligned} 0=\dfrac{r_0 C_0}{K} C^\dagger _i(1-\dfrac{N^\dagger _i}{C_0}) +\phi e^{-\hat{d} \tau }S^\dagger _i V^\dagger _i. \end{aligned}$$

(21)

Substituting both equations for $N^\dagger _i$ and $V^\dagger _i$ in (20) into equation (21), we obtain (7), i.e.,

$$\begin{aligned} C^\dagger _i=S^\dagger _i(B-\dfrac{r e^{-\hat{d}\tau }}{r_0})+\dfrac{\mu }{\phi } B, \quad \text{ where } \quad B=\dfrac{r}{K\alpha }[S_0-C_0]. \end{aligned}$$

(22)

In addition, substituting the expression for $E^\dagger _i$ in (20) and the expression for $C^\dagger _i$ in (7) into (19),

we obtain,

$$\begin{aligned} N^\dagger _i=S^\dagger _i+\left[ S^\dagger _i(B-\dfrac{r e^{-\hat{d}\tau }}{r_0})+\dfrac{\mu }{\phi } B\right] \left[ 1+ \dfrac{\phi S^\dagger _i}{\phi S^\dagger _i+\mu } \dfrac{\alpha }{{\hat{d}}}[1-e^{-\hat{d}\tau }] \right] . \end{aligned}$$

(23)

Then, by substituting the expression for $V^\dagger _i$ in (20) into (21), we obtain

$$\begin{aligned} N^\dagger _i=\dfrac{\alpha \phi S^\dagger _i e^{-\hat{d}\tau } K }{(\phi S^\dagger _i+\mu )r_0}+C_0. \end{aligned}$$

(24)

By equating (23) and (24), we obtain

$$\begin{aligned} S^\dagger _i+\left[ S^\dagger _i(B-\dfrac{r e^{-\hat{d}\tau }}{r_0})+\dfrac{\mu }{\phi } B\right] \left[ 1+ \dfrac{\phi S^\dagger _i}{\phi S^\dagger _i+\mu } \dfrac{\alpha }{{\hat{d}}}[1-e^{-\hat{d}\tau }] \right] =\dfrac{\alpha \phi S^\dagger _i e^{-\hat{d}\tau } K }{(\phi S^\dagger _i+\mu )r_0}+C_0.\nonumber \\ \end{aligned}$$

(25)

Rearranging equation (25), we obtain $h(S^\dagger )_i=g(S^\dagger _i),$ where

$$\begin{aligned} h(S^\dagger _i)&=S^\dagger _i[\phi S^\dagger _i+\mu ]+\left[ S^\dagger _i(B-\dfrac{r e^{-\hat{d}\tau }}{r_0})+\dfrac{\mu }{\phi } B\right] \nonumber \\&\quad \left[ (\phi S^\dagger _i+\mu )+ \phi S^\dagger _i\dfrac{\alpha }{{\hat{d}}}[1-e^{-\hat{d}\tau }] \right] , \quad \text{ and }\nonumber \\ g(S^\dagger _i)&= \dfrac{\alpha \phi S^\dagger _i e^{-\hat{d}\tau } K }{r_0}+C_0(\phi S^\dagger _i+\mu ). \end{aligned}$$

(26)

Note that $g(S^\dagger _i)$ is a linear increasing function and $h(S^\dagger _i)$ is a quadratic polynomial. Therefore, these two curves can have at most two intersection points, and hence there are at most two possible candidates for $S^\dagger _i$ and only real, positive roots are candidates for the component of an interior equilibrium.

First rearranging equation (26), and then simplifying the expressions of coefficients (verified also by the symbolic package Maple [32]), we obtain the quadratic polynomial (5), with coefficients defined in (6). Using (20), to find the corresponding $E^\dagger _i$ and $V^\dagger _i$, it follows that ${\mathcal {E}}^\dagger _i$ is an interior equilibrium of system (1) whenever $S^\dagger _i>0$ and the corresponding expression given in (7) for $C^\dagger _i>0.$ Hence, there can be at most two interior equilibria.

Alternatively, we can find the quadratic equation (9) for the $C^\dagger _i$ component of ${\mathcal {E}}^\dagger _i$ by first rearranging (7) to find the expression for $S^\dagger _i$ as a function of $C^\dagger _i$ and substituting this expression into (26). Then by simplifying the coefficients by multiplying the equation (verified also by Maple [32]) by $\phi \alpha r_0^2\left( B-\frac{r e^{-\hat{d}\tau }}{r_0}\right) ^2$ and rearranging them, we obtain the expressions for the coefficients in (10). $\square$

1.4 Proof of Theorem 3

Proof

To determine whether there is a forward or a backward bifurcation when $r_0=r_0^c$, we find the sign of the derivative of the component $C^\dagger$ of ${\mathcal {E}}^\dagger$ with respect to $r_0$ at $r_0=r_0^c$, the transcritical bifurcation involving ${\mathcal {E}}_0$ and ${\mathcal {E}}^\dagger$, where these two equilibria cross and exchange stability, i.e., where ${\mathcal {E}}^\dagger ={\mathcal {E}}_0$, and so $C^\dagger =0$.

By Lemma 1, we know that $B-\frac{re^{-\hat{d} \tau }}{r_0}\ne 0$ near $r_0=r_0^c.$ Therefore by Proposition 1, the C component of $\mathcal E^\dagger$, must satisfy $P(C^\dagger )=0$ near $r_0^c,$ where P(C) is defined in (9) with coefficients defined in (10).

First by the Implicit Function Theorem, we will guarantee that whenever $a_1(r_0^c)\ne 0,$ there exists an open interval set ${\mathcal {U}}$ of ${\mathbb {R}},$ containing $r_0^c,$ such that there exists a unique continuously differentiable function, $f:{\mathcal {U}} \rightarrow {\mathbb {R}},$ where

$$\begin{aligned} f(r_0^c)=0, \textit{ and } P(r_0, f(r_0)))=0, \ \forall r_0\in {\mathcal {U}}. \end{aligned}$$

Differentiating $P(C)=0$ implicitly with respect to $r_0$ (noting that the coefficients depend on $r_0$), and evaluating at $r_0^c$, where $C^\dagger =0$, we obtain

$$\begin{aligned} \dfrac{dC^\dagger }{dr_0}|_{(r_0=r_0^c,C^\dagger =0)}= \frac{-\frac{\partial a_2}{\partial r_0}(r_0^c)}{a_1(r_0^c)}. \end{aligned}$$

(27)

Therefore if $a_1(r_0^c)\ne 0,$ we can conclude that $C^\dagger (r_0)$, given in (7), is a unique (and continuously differentiable) function of $r_0$ on an open neighborhood of the point $r_0^c.$ Next we will check the sign of the derivative, given in (27), and complete the proof.

Now since,

$$\begin{aligned} \frac{\partial a_2}{\partial r_0}(r_0^c) = -\mu d e^{-\hat{d} \tau }(K{\phi }(r-d)+\mu r)<0, \end{aligned}$$

(28)

the sign of the derivative in (27) is the same as the sign of $a_1(r_0^c)$. Using Maple to evaluate $a_1(r_0^c)$ and defining the positive factor

$$\begin{aligned} \omega (r_0^c)= \frac{\mu \phi \alpha e^{-\hat{d} \tau }}{d \hat{d}(S_0\phi +\mu )^2} \end{aligned}$$

it follows that

$$\begin{aligned} \frac{a_1(r_0^c)}{\omega (r_0^c)}= & {} e^{-\hat{d} \tau }\left( \alpha \hat{d} r^2 \phi ^2 S_0^2 + d \hat{d} \mu ^2 r^2 +r K \mu \phi \left\{ r[ \hat{d}(d+\alpha )+\alpha d ]-d^2(\alpha +\hat{d})\right\} \right) \nonumber \\&- r^2 d \mu \phi \alpha S_0e^{-2\hat{d}\tau } -r^2 \hat{d}{\tilde{d}}(\phi S_0+\mu )^2, \end{aligned}$$

(29)

the expression in (13). Thus, if $a_1(r_0^c)<0$, the transcritical bifurcation at $r_0^c$ is a backward bifurcation and if $a_1(r_0^c)>0$, it is a forward bifurcation. $\square$

1.5 Proof of Theorem 4

Proof

First we show that when $r=r_0^b$, the equilibria ${\mathcal {E}}_c$ and ${\mathcal {E}}^\dagger$ coalesce, i.e., $S^\dagger =0$, $E^\dagger =0$, $C^\dagger =C_0$ and $V^\dagger =V_c$. Recall that $S^\dagger$ satisfies equation (5) with coefficients defined in (6):

$$\begin{aligned} \hat{P}(S^\dagger )=A_0(S^\dagger )^2+A_1S^\dagger + A_2=0. \end{aligned}$$

If $S^\dagger =0$, $\hat{P}(0)=0$ if and only if $A_2=0$. That is precisely when ${\mathcal {R}}_S^{C_0}=1$ or equivalently, when $r_0=r_0^b$. Note that by similar arguments in the Proof of Theorem 3, which is given in (A.4), the Implicit Function Theorem guarantees that the function $S^\dagger (r_0),$ given in (7), is unique (and continuously differentiable) function of $r_0$ on an open neighborhood of the point $r_0^b,$ when $A_1(r_0^b)\ne 0.$ Setting $\hat{P}(S^\dagger )=0$ and differentiating both sides implicitly with respect to $r_0$, noting that $S^\dagger =0$ when $r_0=r_0^b$, it follows that

$$\begin{aligned} \frac{d S^\dagger }{d r_0}(r_0^b,0)= -\frac{\frac{\partial A_2}{\partial r_0}(r_0^b)}{A_1(r_0^b)}= \frac{\mu {\tilde{d}}(K\phi \alpha +\mu r)}{\alpha \phi (r_0^b)^2}\left( \frac{1}{A_1(r^b_0)}\right) , \end{aligned}$$

and hence the sign of this expression depends on the sign of $A_1,$ evaluated at $r_0=r_0^b.$ Using MAPLE to evaluate $A_1(r_0^b)$,

it follows that

$$\begin{aligned} A_1(r_0^b)&=\frac{(-d \hat{d} \mu ^2 r - K \phi \alpha \mu (\hat{d}(d + r) + {\tilde{d}} (r - d)) - (K\phi \alpha )^2 \hat{d})e^{-\hat{d}\tau } - \mu {\tilde{d}}(-\hat{d}\mu r + K \phi ((d - r - \hat{d})\alpha + \hat{d}(d-r )))}{{\tilde{d}} \hat{d}(K\phi \alpha + \mu r)} \end{aligned}$$

(30)

Thus, if $A_1(r_0^b)>0$, the transcritical bifurcation at $r_0^b$ is a backward bifurcation and if $A_1(r_0^b)<0$, it is a forward bifurcation. $\square$

1.6 Proof of Theorem 5

Lemma 2

Consider $B(r_0),$ given in (7), and define $r_0^*=\frac{r {\tilde{d}}}{d}$. Then, $B(r_0^*)=0.$ If $r_0< r_0^*$, then $B(r_0)>0$ and if $r_0>r_0^*$, then $B(r_0)<0$. Furthermore, $\max \{r_0^c,r_0^b\}<r_0^*.$

Proof

Note that $B=\frac{r}{K \alpha }[S_0-C_0]=\frac{r {\tilde{d}}- r_0 d}{\alpha r_0}=\frac{d(r^*-r_0)}{\alpha r_0}$. Therefore, $B(r_0^*)=0.$ In addition,

$B(r_0)>0$ for all $r_0<r_0^*$ and $B(r_0)<0$ for all $r_0>r_0^*$. Also note that $r_0^*-r_0^c= \frac{ r \phi \alpha S_0 e^{-\hat{d}\tau }}{d( \phi S_0 + \mu )} >0$ and $r_0^* -r_0^b=\frac{r \phi \alpha {\tilde{d}}S_0}{d(K \phi \alpha +d \mu )} >0$. Therefore, $r_0^*>\max \{r_0^c,r_0^b\}$. $\square$

Lemma 3

• (a) The function ${\mathcal {R}}_0(r_0)$, defined in (3), is continuous and increasing for $r_0>0$.

  • i) If   $r_0<r_0^c$, then $a_2(r_0)>0$.

  • ii) If   $r_0>r_0^c$, then $a_2(r_0)<0$.

• (b) $r_0^b>{\tilde{d}}$.

• (c) $A_2(r_0)$, defined in (6), has a removeable singularity at $r_0={\tilde{d}}$ and can be redefined by multiplying $C_0$ into the term in square brackets so that it is differentiable and decreasing for all $r_0>0$.

  • i) If $0<r_0<r_0^b$, then $A_2(r_0)>0$.

  • ii) If $r_0>r_0^b$, then $A_2(r_0)<0.$

Proof

(a) :

This follows directly from the definition of ${\mathcal {R}}_0$ in (3), the definition of $r_0^c$ in (11), and the definition of $a_2$ in (10).

(b) :

Note that

$$\begin{aligned} r_0^b-{\tilde{d}}=\frac{{\tilde{d}} \mu r S_0}{K^2 \phi \alpha +d \mu }>0. \end{aligned}$$

(c) :

The function ${\mathcal {R}}_S^{C_0}(r_0)$, defined in (4), has a vertical asymptote at $r_0={\tilde{d}}$.   ${\mathcal {R}}_S^{C_0}(r_0)<0$   if   $r_0<{\tilde{d}}$, Multiplying $C_0$ into the expression in square brackets in (6) and simplifying we obtain,

$$\begin{aligned} A_2(r_0)= \dfrac{\mu ^2 rC_0}{\phi K \alpha }[R^{C_0}_S-1]=\frac{\mu (K \phi \alpha ({\tilde{d}}-r_0)-(r_0 d- r {\tilde{d}}))}{r_0 \phi \alpha }, \end{aligned}$$

(31)

and

$$\begin{aligned} \frac{d A_2(r_0)}{d r_0}=\frac{-{\tilde{d}} \mu (K \phi \alpha +\mu r)}{r_0^2 \phi \alpha }<0. \end{aligned}$$

Substituting $r_0={\tilde{d}}$ into (31), since $r>d$, it follows that $A_2(r_0)|_{r_0={\tilde{d}}}>0$. If $0<r_0<{\tilde{d}}$ then both $C_0(r_0)$ and ${\mathcal {R}}_S^{C_0}(r_0)$ are negative and it follows again that $A_2(r_0)>0$. However, if $r_0>{\tilde{d}}$, then $C_0(r_0)>0$, and the sign of $A_2(r_0)$ depends upon whether or not ${\mathcal {R}}_S^{C_0}(r_0)$ is larger or smaller than 1, and hence whether $r_0>r_0^b$ or $r_0<r_0^b$. Therefore, if $r_0>r_0^b$, then $A_2(r_0)<0$ and if ${\tilde{d}}<r_0<r_0^b$, then $A_2(r_0)>0$.

$\square$

We denote the coefficient of S in (7) by

$$\begin{aligned} B_c(r_0):=B(r_0)-\frac{r e^{-\hat{d}\tau }}{r_0}. \end{aligned}$$

(32)

Lemma 4

If $A_0(r_0)\le 0$, where $A_0(r_0)$ is defined in (6), then $B_c(r_0)<0$.

Proof

$A_0 = \frac{\phi }{\hat{d}}\left( \alpha B_c (1-e^{-\hat{d} \tau }) +\hat{d}(B_c+1) \right) .$ $\square$

Lemma 5

Assume $A({\widehat{r}}_0)=0.$ If either $\alpha \ne {\tilde{d}} e^{\hat{d}\tau }$ or ${\tilde{d}}\ne \frac{d \hat{d} e^{-\hat{d}\tau }}{\hat{d}-d(1-e^{-\hat{d} \tau })}$, then $\frac{ d A_0({\widehat{r}}_0)}{d r_0} \ne 0$. Otherwise, $A(r_0)=0$ (and $a_0(r_0)=0$) for all $r_0\ge 0$.

Proof

If $A_0({\widehat{r}}_0)=0$, then

$$\begin{aligned} r({\tilde{d}}-\alpha e^{-\hat{d}\tau })\left( 1-\dfrac{ \alpha (e^{-\hat{d}\tau } - 1)}{\hat{d}} \right) ={\widehat{r}}_0\left( d(1-\dfrac{ \alpha (e^{-\hat{d}\tau } - 1)}{\hat{d}})- \alpha \right) . \end{aligned}$$

(33)

If the coefficient of ${\widehat{r}}_0$ in (33) equals zero, one of the factors on the left hand side of (33) must equal zero. It cannot be the one in the large brackets, since then coefficient of ${\widehat{r}}_0$ would equal $-\alpha$ with equality if and only if $\alpha =0$, yielding a contradiction. Therefore, the other factor on the left hand side must equal 0, i.e., $\alpha ={\tilde{d}}e^{\hat{d}\tau }.$ Then, substituting this value of $\alpha$ into the coefficient of ${\widehat{r}}_0$ in (33) setting the coefficient equal to zero, it follows that

$$\begin{aligned} {\tilde{d}}= \frac{d \hat{d} e^{-\hat{d}\tau }}{\hat{d}-d(1-e^{-\hat{d} \tau })} \end{aligned}$$

(34)

Therefore, as long as $\alpha \ne {\tilde{d}} e^{\hat{d}\tau }$ or condition (34) does not hold, then the coefficient of ${\widehat{r}}_0$ in (33) is nonzero and so $\frac{d A_0(r_0)}{d r_0}|_{r_0={\widehat{r}}}\ne 0$. Otherwise, $A_0(r_0)=0$ for all $r_0$. $\square$

Definition 1

When

$$\begin{aligned} \alpha = {\tilde{d}} e^{\hat{d}\tau } \quad \text{ and } \quad {\tilde{d}}= \frac{d \hat{d} e^{-\hat{d}\tau }}{\hat{d}-d(1-e^{-\hat{d} \tau })} \end{aligned}$$

(35)

we refer to this as the degenerate case.

Lemma 6

Assume (35) is satisfied. Then, $r_0^c>0$, and

• i) $\hat{d} K \phi -\mu r (1-e^{-\hat{d}\tau }) > 0$,   if and only if   $r_0^c<r_0^b$.

• ii) $\hat{d} K \phi -\mu r (1-e^{-\hat{d}\tau }) = 0$,   if and only if   $r_0^c=r_0^b$.

• iii) $\hat{d} K \phi -\mu r (1-e^{-\hat{d}\tau })< 0$,   if and only if   $r_0^c>r_0^b$.

Proof

We substitute the values for $\alpha$ and ${\tilde{d}}$ given in (35) into the expressions for $r_0^c$ and $r_0^b$ given in (11) and (12), respectively.

$$\begin{aligned} r_0^c= \frac{d \hat{d} \mu r^2 e^{-\hat{d} \tau }}{(\hat{d}-d(1-e^{-\hat{d}\tau }))(\mu r +K \phi (r-d))}>0, \end{aligned}$$

since $r>d$ and ${\tilde{d}}>0$, and so the denominator in the expression for ${\tilde{d}}$ in (35) is therefore positive. Also, by Lemma 3(b), $r_0^b>{\tilde{d}}>0$.

Next we evaluate $r_0^b-r_0^c$ to obtain:

$$\begin{aligned} r_0^b-r_0^c = \left[ \hat{d} K \phi -\mu r (1-e^{-\hat{d}\tau }) \right] \left( \frac{d \hat{d} \, \phi e^{-\hat{d} \tau }S_0}{( \hat{d} K \phi +\mu (\hat{d}- d(1-e^{-\hat{d} \tau }))(\hat{d} - d(1-e^{-\hat{d} \tau }))(\phi S_0 + \mu )} \right) . \end{aligned}$$

(36)

All of the factors in the expression in the large round brackets in (36) are positive, and hence, the sign of (35) is determined by the factor in the square brackets, and the result follows. $\square$

Lemma 7

Assume that (35) holds.

• i) $a_1(r_0)=-d \phi r_0 A_1(r_0)$ for all $r_0$.

• ii) $A_1(r_0),$ $a_1(r_0)$, and $a_2(r_0)$ are all continuous functions of $r_0>0$ and $A_2(r_0)$ has a removeable singularity at $r_0={\tilde{d}}$ and can be defined so that it is continuous for all $r_0>0$.

• iii) $A_1(r_0)$, $A_2(r_0)$, and $a_2(r_0)$ are decreasing functions of $r_0>0$ and $a_1(r_0)$ is increasing for $r_0>0$.

• iv) $A_1(r_0)<0$ if   $r_0^c<r_0<r_0^b$ and $A_1(r_0)>0$ if   $r_0^b<r_0<r_0^c$.

• v) $a_1(r_0)>0$ if   $r_0^c<r_0<r_0^b$ and $a_1(r_0)<0$ if   $r_0^b<r_0<r_0^c$.

• vi) $\hat{P}(S)=A_1(r_0) S + A_2(r_0)=0$ has a unique positive solution if $r_0^c<r_0<r_0^b$ and if $r_0^b<r_0<r_0^c$.

• vii) $P(C)=a_1(r_0) C + a_2(r_0)=0$ has a unique positive solution if $r_0^c<r_0<r_0^b$ and if $r_0^b<r_0<r_0^c$.

• viii) If $r_0\notin (\min \{r_0^c,r_0^b\},\max \{r_0^c,r_0^b\})$, then the solution of at least one of the equations $\hat{P}(S)=A_1(r_0) S + A_2(r_0)=0$ or $P(C)=a_1(r_0) C + a_2(r_0)=0$ is not positive.

Proof

i) :

$$\begin{aligned} \frac{-a_1(r_0)}{d \phi r_0^2}= & {} A_1(r_0) \nonumber \\= & {} \frac{e^{-\hat{d}\tau }[r_0 d(2 d \mu -\hat{d}( K\phi +2 \mu ))+\hat{d}^2\mu r]-r_0[d^2\mu e^{-2\hat{d}\tau }+(\hat{d}-d)(\hat{d} K \phi +\mu (\hat{d}-d)) ] }{r_0 \hat{d}(\hat{d}-d(1-e^{-\hat{d}\tau }))} \end{aligned}$$

(37)

ii) :

Noting that we only consider when ${\tilde{d}}>0$, and in the degenerate case ${\tilde{d}}$ satisfies (35), the factor in the denominator of ${\tilde{d}}$ given in (37) must be positive. It follows that $a_1(r_0)$ and $A_1(r_0)$ are both continuous with respect to $r_0$, for all $r_0>0$. The singularity in $A_2(r_0)$at $r_0={\tilde{d}}$, where both $C_0=0$ and ${\mathcal {R}}_S^{C_0}(r_0)=0$ is removed by multiplying $C_0$ into the term in the square brackets and is continuous with respect to $r_0>0$ and $a_2(r_0)$ is clearly continuous with respect to $r_0$.

iii) :

$$\begin{aligned} \frac{d A_1(r_0)}{ d r_0}= \frac{- r \mu \hat{d} e^{-\hat{d} \tau }}{r_0^2(\hat{d}-d(1-e^{\hat{d} \tau }))}<0. \end{aligned}$$

(38)

Therefore, $A_1(r_0)$ is a decreasing function of $r_0$ and hence by i), $a_1(r_0)$ is an increasing function of $r_0$.

$$\begin{aligned} \frac{d A_2(r_0)}{ d r_0}=\frac{-\mu e^{-\hat{d}\tau }(d\hat{d}K \phi +\mu r(\hat{d}-d(1-e^{\hat{d}\tau } ))}{r_0^2\phi (\hat{d}-d(1-e^{-\hat{d}\tau }))} <0. \end{aligned}$$

(39)

Therefore, $A_2(r_0)$ is a decreasing function of $r_0$.

$$\begin{aligned} \frac{d a_2(r_0)}{d r_0}= -e^{-\hat{d}\tau } \mu d(K \phi (r-d)+\mu r)<0, \end{aligned}$$

and hence $a_2(r_0)$ is decreasing function of $r_0$.

iv) :

$A_1(r_0^c)$ and $A_1(r_0^b)$ have the same sign or are both equal to zero, since

$$\begin{aligned} A_1(r_0^b)= & {} \frac{-d(\hat{d}K\phi -\mu r (1-e^{-\hat{d}\tau }))(\hat{d} K \phi +\mu (\hat{d}-d(1-e^{-\hat{d}\tau })))}{d\hat{d}K \phi + \mu r (\hat{d}-d(1-e^{-\hat{d} \tau }))}, \end{aligned}$$

(40)

$$\begin{aligned} A_1(r_0^c)= & {} \frac{-d(\hat{d} K \phi -\mu r(1-e^{-\hat{d} \tau }))}{r \hat{d}}. \end{aligned}$$

(41)

By Lemma 6, $r_0^c>0$ and so $A_1(r_0)$ is continuous for all $r_0\ge r_0^c.$ By Lemma 6i), if $r_0^c<r_0<r_0^b$, then $A_1(r_0^c)<0$, and by part iii) $A_1(r_0)$ is a decreasing function of $r_0$. Therefore, $A_1(r_0)<0$ for all $r_0\in [r_0^c,r_0^b]$. By Lemma 6iii), if $r_0^b<r_0<r_0^c$, then $A_1(r_0^c)>0$ and by part iii) $A_1(r_0)$ is a decreasing function of $r_0$, and therefore $A_1(r_0)>0$ for all $r_0\in [r_0^b,r_0^c]$.

v) :

By i), $a_1(r_0)$ and $A_1(r_0)$ have opposite signs or are both equal to zero. By iv) $A_1(r_0)<0$ if $r_0^c<r_0^b$. Therefore, $a_1(r_0)>0$ for all $r_0\in (r_0^c,r_0^b)$. Similarly, $a_1(r_0)<0$ for all $r_0^b<r_0<r_0^c$.

vi) :

Since $\hat{P}(S)=0$ is linear, and by iv) and Lemma 3 (c), the coefficients have opposite signs, there is a unique positive solution.

vii) :

Since $P(C)=0$ is linear, and by v) and Lemma 3 (a), the coefficients have opposite signs, there is a unique positive solution.

viii) :

First, consider when $0<r_0<r_0^b<r_0^c$. By Lemma 3 (a)i), $a_2(r_0)>0$ and by (c)i) $A_2(r_0)>0$. Next consider when $0<r_0<r_0^c<r_0^b$. By Lemma 3 (a)ii), $a_2(r_0)<0$ and by (c)ii) $A_2(r_0)<0$. In both cases, $a_2(r_0)$ and $A_2(r_0)$ have the same sign. Howeve, from i), $a_1(r_0)$ and $A_1(r_0)$ have opposite signs or are both equal to zero. Therefore, either $A_1(r_0)$ and $A_2(r_0)$ have the same sign and so the solution of $\hat{P}(S)=0$ is negative, or $a_1(r_0)$ and $a_2(r_0)$ have the same sign and the solution of $P(C)=0$ is negative or $A_1(r_0)=a_1(r_0)=0$ and $\hat{P}(S)=0$ and $P(C)=0$ has no solution. In the case that $r_0>\max \{r_0^c,r_0^b\}$, The result also follows by a similar argument.

$\square$

Proof of Theorem 5

Note that by their definitions in (6) and (10), $A_0(r_0)$ and $a_0(r_0)$ have the same sign or are both equal to zero.

Case (a). Since $r_0\in (r_0^c,r_0^b)$, by Lemma 3(a), $a_2(r_0)<0$ and by (c) $A_2(r_0)>0$.

First assume that $A_0(r_0)>0$ and hence $a_0(r_0)>0$. Since $A_0(r_0)>0$ and $A_2(r_0)>0$, the quadratic equation $\hat{P}(S)=0$, defined in (5), is concave up and has a positive vertical intercept, and therefore either has two real solutions of the same sign or two complex solutions. On the other hand, since $a_2(r_0)<0$, the quadratic equation $P(C)=0$, defined in (9), is concave up and has a negative vertical intercept, and therefore has one negative solution and one positive solution. Therefore there is a most one interior equilibrium. Rearranging (7), we obtain

$$\begin{aligned} S=\frac{C-\frac{\mu }{\phi }B(r_0)}{B(r_0)-\frac{r e^{-{\tilde{d}}\tau }}{r_0}}=\frac{C-\frac{\mu }{\phi }B(r_0)}{B_c(r_0)}, \end{aligned}$$

(42)

where the denominator is negative, since by Lemma 1, ${\bar{r}}_0<r_0^c$. Also, by Lemma 2, $B(r_0)>0$, since $r_0^*>r_0^b$. Substituting the negative solution of $P(C)=0$ into (42) gives a corresponding positive value for S. Therefore, the negative solution of $P(C)=0$ corresponds to a positive solution of $\hat{P}(S)=0$, and since both solutions of $\hat{P}(S)=0$ have the same sign, both solutions of $\hat{P}(S)=0$ must be positive, and so the positive solution of $P(C)=0$ must also give a positive solution of (42). By (8), the corresponding values of $E^\dagger$ and $V^\dagger$ are also positive and hence, there is a unique interior equilibrium if $A_0(r_0)>0$.

Next assume that $A_0(r_0)<0$ and hence $a_0(r_0)<0$. In this case, since $A_2(r_0)>0$, $\hat{P}(S)=0$ has one positive solution and one negative solution and hence there is at most one interior equilibrium. Since $a_2(r_0)<0$, both solutions of $P(C)=0$ have the same sign or are complex. However, using similar reasoning as in the previous case, if both solutions of $P(C)=0$ are negative or complex, substituting them into (42), it would imply that the two corresponding solutions of $\hat{P}(S)=0$ are positive or complex, contradicting the fact that one is positive and one is negative. Hence, when $A_0(r_0)< 0$, both solutions of $P(C)=0$ must be positive, and again there is a unique interior equilibrium.

Finally, assume $A_0({\widehat{r}}_0)=0$ for some ${\widehat{r}}_0\in (r_0^c,r_0^b)$. If the degenerate case (35) holds, then by Lemma 7vi) and vii) both $\hat{P}(S)=0$ and $P(C)=0$ are linear and each equation has a unique positive solution. Hence, there is a unique interior equilibrium. In the non-degenerate case, by Lemma 4, $\frac{d A_0({\widehat{r}}_0)}{d r_0}\ne 0$. Therefore, there exists $\delta >0$ such that $A_0(r_0)\ne 0$ for all $r_0\in ({\widehat{r}}_0-\delta ,{\widehat{r}}_0)\cup ({\widehat{r}}_0, {\widehat{r}}_0+\delta )$. If $(S(r_0),C(r_0))$ denotes the unique positive solution of $\hat{P}(S)=0$ and $P(C)=0$ for $r_0 \in ({\widehat{r}}_0-\delta ,{\widehat{r}}_0)$, then, since this solution is continuous in $r_0$, and since $\lim _{r_0\rightarrow {\widehat{r}}_0}(S(r_0),C(r_0))=(S({\widehat{r}}_0),C({\widehat{r}}_0))$ exists, $(S({\widehat{r}}_0),C({\widehat{r}}_0))$ is also a nonnegative solution of $\hat{P}(S)=0$ and $P(C)=0$. Since both equations are linear now, $(S({\widehat{r}}_0),C({\widehat{r}}_0))$ is the unique solution for $r_0={\widehat{r}}_0$. In fact, both $S({\widehat{r}}_0)$ and $C({\widehat{r}}_0)$ are positive because, otherwise, $S({\widehat{r}}_0)=0$ would imply that ${\widehat{r}}_0=r_0^b$ and $C({\widehat{r}}_0)=0$ woud imply that ${\widehat{r}}_0=r_0^c$, giving a contradiction in both cases. Thus, there is also a unique interior equilibrium when $A_0(r_0)=0$.

Case (b).

Assume that $r_0> \max \{r_0^c,r_0^b\}$. Then, by Lemma 3(a)ii), $a_2(r_0)<0$ and by Lemma 3 (b)ii) $A_2(r_0)<0$. By Lemma 1, ${\bar{r}}_0<r_0^c$ and so $B_c(r_0)<0$, where $B_c$ is the coefficient of S in (7), and is defined in (32).

First assume that $A_0(r_0)>0$ and hence $a_0(r_0)>0$. Since $A_2(r_0)<0$, $\hat{P}(S)=0$ defined in (5) is concave up with vertical intercept negative and so has one positive solution and one negative solution. Similarly, $P(C)=0$ defined in (9), has one positive solution and one negative solution. On $(\max \{r_0^c,r_0^b\},r_0^*)$, by Lemma 2, $B>0$, and since the coefficient of S in (7), $B_c(r_0)<0$, from (7), it follows that the negative solution of $\hat{P}(S)=0$ corresponds to the positive solution of $P(C)=0$, and hence the positive solution of $\hat{P}(S)=0$ must correspond to the negative solution of $P(C)=0$. Thus, there are no interior equilibria in this case. Also, if $r_0\ge r_0^*$, then by Lemma 2, $B\le 0$.

From the rearrangement of (7) given in (42), and noting the denominator is negative, again the negative solution of $P(C)=0$ corresponds to the positive solution of $\hat{P}(S)=0$, and hence there are no interior equilibria in this case.

Next assume that $A_0(r_0)<0$ and hence $a_0(r_0)<0$. Since, $A_2(r_0)<0$, both roots of $\hat{P}(S)=0$ defined in (5) have the same sign or they are both complex. As well, $a_2(r_0)<0$, and so both roots of $\hat{P}(C)=0$, defined in (9), have the same sign or they are both complex. If $r_0\ge r_0^*$, then $B\le 0$ and $B_c(r_0)<0$, and so from (7) the two positive roots of $P(C)=0$ correspond to two negative roots of $\hat{P}(S)=0$, and hence there are no interior equilibria in this case. However, if $r_0\in (\max \{r_0^c,r_0^b\},r_0^*)$, then $B>0$, and although it follows from (42), that the two negative roots of $P(C)=0$ would correspond to the two positive roots of $\hat{P}(S)=0$, we cannot rule out the possibility that the two positive roots of $P(C)=0$ correspond to two positive roots of $\hat{P}(S)=0$, and hence there can be at most two interior equilibria.

Finally, assume that there exists ${\widehat{r}}_0$ such that $A({\widehat{r}}_0)=0$. In the degenerate case, by Lemma 7viii), then the solution of at least one of the equations $\hat{P}(S)=0$ or $P(C)=0$ is not positive and hence there is no interior equilibrium. If the degenerate case (35) is not satisfied, then, $\hat{P}(S)=0$ and $P(C)=0$ are linear, and so there is at most one interior equilbrium. If $r_0\ge r_0^*$, then $B\le 0$ and $B_c(r_0)<0$. Using (7), if the solution of $\hat{P}(S)=0$ is positive, it follows that the corresponding value of C is negative, and hence there are no interior equilibria in this case. However, if there exists ${\widehat{r}}_0\in (\max \{r_0^c,r_0^b\}, r_0^*),$ we have $B(r_0)>0$, so that even though $a_0({\widehat{r}}_0)=0$, and so by Lemma 4, $B_c({\widehat{r}}_0)<0$, we cannot rule out the possibility of a unique interior equilibrium.

Case (c). Assume $r_0\in (r_0^b,r_0^c)$. Therefore, by Lemma 3(a)i), $a_2(r_0)>0$ and by Lemma 3(b) $r_0^b>{\tilde{d}}$ and (c)ii), $A_2(r_0)<0$. Also, by Lemma 1, ${\bar{r}}_0<r_0^c$ and so $B_c(r_0)<0$, where $B_c$ is the coefficient of S in (7), and is defined in (32).

First assume that $A_0(r_0)>0$ and so $a_0(r_0)>0$. By $\hat{P}(S)=0$ is a quadratic equation that is concave up and since $A_2(r_0)<0$, the vertical intercept is negative. Therefore, $\hat{P}(S)=0$ has one positive solution and one negative solution. Hence, there is at most one interior equilibrium. By (7), the corresponding C components are defined and real and by Lemma 2, since $r^*>r_0^c$, $B>0$. Therefore, independent of the sign of the coefficient of S in (7), at least one of the C components is positive. Hence, the roots of $P(C)=0$ defined in (9) must be real, and at least one is positive. Since the coefficient of $P(C)=0$ in (9) are $a_0(r_0)>0$ and $a_2(r_0)>0$, the solutions of $P(C)=0$ must have the same sign, and so they must both be positive. Therefore, the C component defined in (7) corresponding to the positive solution of $\hat{P}(S)=0$, is also positive. By (8), the corresponding values of $E^\dagger$ and $V^\dagger$ are also positive and hence, there is a unique interior equilibrium if $A_0(r_0)>0$.

Next assume that $A_0(r_0)<0$ and hence $a_0(r_0)<0$.

In this case, $P(C)=0$ is concave down and since $a_0(r_0)>0$, the vertical intercept is positive. Hence, there is one positive and one negative solution of $P(C)=0$, and hence, at most one interior equilibrium. As well, $r_0\in (\max \{r_0^b,{\bar{r}}_0\},r_0^c)$, since if $r_0^b<r_0\le {\bar{r}}_0$, then by Lemma 1, $B_c(r_0) \ge 0$, contradicting $A_0(r_0)<0$ and hence $B_c(r_0)<0$ by Lemma 4. When, $A_0(r_0)<0$ and $r_0\in (\max \{r_0^b,{\bar{r}}_0\},r_0^c)$. the denominator in (42) is negative, and by Lemma 2, $B>0$. Therefore, the negative solution, C, of $P(C)=0$ gives a positive value of S in (42). On the other hand, $A_0(r_0)<0$ and $A_2(r_0)<0$ and so both solutions of $\hat{P}(S)=0$ must have the same sign. Therefore, both corresponding values of S are positive, and once again there is a unique interior equilibrium when $A_0(r_0)<0$.

Finally, assume that $A_0({\widehat{r}}_0)=0$ and hence $a_0({\widehat{r}}_0)=0$ for some ${\widehat{r}}_0\in (r_0^b,r_0^c)$. If the degenerate case (35) holds, by Lemma 7vi) and vii), both $\hat{P}(S)=0$ and $P(C)=0$ have a unique positive solution and hence there is a unique interior equilibrium. Next consider the non-degenerate case. By Lemma 5, in the nondegenerate case $\frac{d \,A({\widehat{r}}_0)}{ d \, r_0}\ne 0$, and so the zero of $A_0(r_0)$ at ${\widehat{r}}_0$ is isolated, i.e., ${\widehat{r}}_0$ is the only point in $(r_0^b,r_0^c)$ such that $A_0(r_0)=0$. Note also that, ${\widehat{r}}_0\ne {\bar{r}}_0$, since by Lemma 1, if ${\bar{r}}_0>0$ then ${\tilde{d}}>\alpha e^{\hat{d} \tau }$ and so $a_0({\bar{r}}_0)=\frac{\alpha r\hat{d} \phi ^2({\tilde{d}}-\alpha e^{-\hat{d}\tau })}{d}>0$, contradicting $a_0({\widehat{r}}_0)=0$. By Lemma 4, since $A_0({\widehat{r}}_0)=0$, $B_c(r_0)<0$ and therefore $r_0^c>{\widehat{r}}_0>{\bar{r}}$. Since $A_0({\widehat{r}}_0)=0$, ${\widehat{r}}_0\in (r_0^b,r_0^c)$, and ${\widehat{r}}_0>{\bar{r}}$, there exists $\delta >0$ such that ${\widehat{r}}_0-\delta >{\bar{r}}_0$, $a_0(r_0)\ne 0$ for all $r_0\in ({\widehat{r}}_0-\delta ,{\widehat{r}}_0)\cup ({\widehat{r}}_0,{\widehat{r}}_0+\delta )$, and $B_c(r_0)<0$. If $S(r_0)$ denotes the the unique positive solution of the $\hat{P}(S(r_0))=0$ with corresponding positive solution $C(r_0)$ of $P(C(r_0))=0$ on $({\widehat{r}}_0-\delta ,{\widehat{r}}_0)$, just shown above to exist, then, since this solution is continuous in $r_0$, and since $\lim _{r_0\rightarrow {\widehat{r}}_0}(S(r_0),C(r_0))=(S({\widehat{r}}_0),C({\widehat{r}}_0))$ exists, $(S({\widehat{r}}_0),C({\widehat{r}}_0))$ is also a nonnegative solution of (5) and $P(C({\widehat{r}}_0))=0$. Since both equations $\hat{P}(S)=0$ and $P(C)=0$ are linear, $(S({\widehat{r}}_0),C({\widehat{r}}_0))$ is the unique solution. In fact, both $S({\widehat{r}}_0)$ and $C({\widehat{r}}_0)$ are positive, because otherwise, if $S({\widehat{r}}_0)=0$ ($C({\widehat{r}}_0)=0$), that would mean ${\widehat{r}}_0=r_0^b$ (${\widehat{r}}_0=r_0^c$), contradicting ${\widehat{r}}\in (r_0^b,r_0^c)$. Thus, we also have a unique interior equilibrium when $A_0({\widehat{r}}_0)=0$.

${\mathcal {E}}_c$ exists provided ${\tilde{d}}<r_0$. Since $r_0^b-{\tilde{d}}=\frac{{\tilde{d}} \mu (r-d)}{d(K \phi \alpha d \mu )}>0$, hence ${\tilde{d}}<r_0$ for all $r_0\in [r_0^b,r_0^c]$ and therefore $E_c$ exists for all $r_0\in [r_0^b,r_0^c]$. The local stability of ${\mathcal {E}}_0$ follows from Theorem 1 and of ${\mathcal {E}}_c$ follows from Theorem 2.

Case (d). Assume that $0<r_0<\min \{r_0^c,r_0^b\}$.

Therefore, by Lemma 3 (a)i), $a_2(r_0)>0$ and by Lemma 3 (b) i), $A_2(r_0)>0$.

In case i), since $A_0(r_0)>0$ and hence $a_0(r_0)>0$, therefore, both polynomials $\hat{P}(S)=0$ and $P(C)=0$ either have two positive roots or no positive roots, depending on the sign of $A_1(r_0)$.

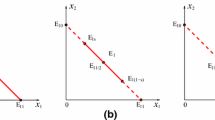
Therefore, there can be 0, 1, or 2 interior equilibria, (one in the case of a double positive root, i.e., at a saddle-node bifurcation). See Fig. 1 b) for an example showing all three possibilities.

In case ii), since $A_0(r_0) \le 0$ and hence $a_0(r_0) \le 0$, both polynomials $\hat{P}(S)=0$ and $P(C)=0$ either have no solution or have one positive solution and one negative solution, and hence there is at most one interior equilibrium. Since we are assuming that $A_0(r_0)\le 0$, by Lemma 4, $B_c<0$ where $B_c$ is defined in (32). Therefore, by Lemma 1, $r_0\in ({\bar{r}}_0,\min \{r_0^c,r_0^b\})$, by Lemma 2, since $\min \{r_0^c,r_0^b\})<r^*$, we have $B>0$. From (42), it follows that the negative root of $P(C)=0$ corresponds to the positive root of $\hat{P}(S)=0$ and from (7) it follows that the negative root of $\hat{P}(S)=0$ corresponds to the postiive root of $P(C)=0$. Hence, there are no interior equilibria in this case.

$\square$

1.7 Proof of Theorem 6

To simplify the notation in system (1), we first use the dimensionless time, ${{\tilde{t}}}=\phi S_0 t,$ and the dimensionless delay, ${\tilde{\tau }}=\phi S_0 \tau ,$ where $S_0=K\left( 1-\dfrac{d}{r}\right)$. Then we rescale the variables of the model (1) by letting $s=\dfrac{S}{S_0}, {{\bar{e}}}=\dfrac{E}{S_0} , c=\dfrac{C}{S_0}, p=\dfrac{V}{S_0}.$ In addition, in dimensionless form, the parameters are as follows: $r_1=\dfrac{r-d}{\phi S_0}, \ r_2=\dfrac{r_0-{\tilde{d}}}{\phi S_0} ,\ b=\dfrac{\alpha }{\phi S_0}, \ d_2=\dfrac{\mu }{\phi S_0}, \ d_1=\dfrac{{\hat{d}}}{\phi S_0}, \ a=\dfrac{S_0}{C_0},$ with $C_0=K\left( 1-\dfrac{{\tilde{d}}}{r_0}\right) .$ For rest of the paper, we will assume that $r>d.$ Also notice that $r_2, a>0,$ whenever $r_0>{\tilde{d}}.$

Now, for notational convenience, we replace ${\tilde{t}}$ and $\tilde{\tau }$ with t and $\tau$, respectively, and obtain the following system:

$$\begin{aligned} \begin{aligned} s'(t)&=r_1s(t)(1-n(t)) -s(t)p(t)\\ {\bar{e}}'(t)&=s(t)p(t)-d_1{\bar{e}}(t)- e^{-d_1 \tau }s(t-\tau )p(t-\tau ) \\ c'(t)&=r_2 c(t)(1-a n(t)) + e^{-d_1 \tau } s(t-\tau ) p(t-\tau )\\ p'(t)&=bc(t)-s(t)p(t)-d_2 p(t),\\ \end{aligned} \end{aligned}$$

(43)

where $n=s+{\bar{e}}+c.$

We can write (43) in the form

$$\begin{aligned} x'(t)=f(x_t), \end{aligned}$$

(44)

where $x=(s,{\bar{e}},c,p)$ and $f\in C_+$ (recall that $C_+:=\{F: [-\tau ,0]\rightarrow {\mathbb {R}}^4_+\mid F \text{ is } \text{ continuous }\}$), where

$$\begin{aligned} f(\phi )= \left( \begin{array}{c} r_1\phi _1(0)[1-(\phi _1(0)+\phi _2(0)+\phi _3(0))]-\phi _1(0)\phi _4(0)\\ \phi _1(0)\phi _4(0)-d_1\phi _2(0)-e^{-d_1\tau }\phi _1(-\tau )\phi _4(-\tau )\\ r_2\phi _3(0)(1-a(\phi _1(0)+\phi _2(0)+\phi _3(0)))+e^{-d_1\tau }\phi _1(-\tau )\phi _4(-\tau )\\ b\phi _3(0)-\phi _1(0)\phi _4(0)-d_2\phi _4(0) \end{array} \right) \end{aligned}$$

(45)

In equation (44), by $x_t(\phi )$ we denote the member of $C_+$ that satisfies $x_t(\phi )(\theta )=x(t+\theta ,\phi )$, where $x(t,\phi )$ is the solution of (43) that satisfies $x(\theta ,\phi )=\phi (\theta )$ for all $\theta \in [-\tau ,0]$. From the theory of delay differential equations (see, e.g., Hale and Lunel 1993) it follows that (43) has a unique solution $x(t,\phi )$ that exists for all $t\ge 0$ and coincides with $\phi$ on the interval $[-\tau ,0]$. It is known that $(t,\phi )\mapsto x_t(\phi )$ is a continuous semiflow.

Let $D=\{\phi \in C_+ \mid \phi _2(0)=0 \Rightarrow \phi _1(0)\phi _4(0)-e^{-d_1\tau }\phi _1(-\tau )\phi _4(-\tau )\ge 0\}$. Then, if $\phi \in D$ such that $\phi _i(0)=0$, we have $f_i (\phi )\ge 0$. Further, from Theorem 2.1 in (Smith 1995), we have that any solution $x(t,\phi )$ of (43) with $\phi \in D$ is nonnegative for all $t\ge 0$. This further implies that D is positively invariant. Thus we consider the set D to be the state space for model (43).

The boundary equilibrium points of (43) are ${\mathcal {E}}_0^0=(0,0,0,0)$, $\tilde{{\mathcal {E}}}_0=(1,0,0,0)$ and $\tilde{{\mathcal {E}}}_c=(0,0,1/a,b/(d_2a))$. Obviously, the stability properties of ${\mathcal {E}}_0^0$, $\tilde{{\mathcal {E}}}_0$ and $\tilde{{\mathcal {E}}}_c$ for system (43) are the same as those of ${\mathcal {E}}_0^0$, ${\mathcal {E}}_0$ and ${\mathcal {E}}_c$ for system (1), respectively.

Abusing notation, we also use $||\cdot ||$ to denote the “sup” norm on a space $\{g:[-\tau ,0]\rightarrow {\mathbb {R}}^k_+ \mid g \text{ is } \text{ continuous }\}$. It will be clear from the context to which norm we will be referring.

Before we give of Theorem 6, we need a few preliminary results. We begin by establishing the existence of a compact attractor of bounded sets. Theorem 5 in Smith and Zhao (2001), which we use for the proof of our theorem, uses a slightly weaker assumption, namely the existence of a compact attractor of points. For mathematical completeness, we provide below the more general result.

Theorem 7

There exists a unique global attractor of bounded sets corresponding to (44).

Proof

First, we show that $x_t(\phi )$ is point dissipative. Recall that $n(t)=s(t)+{\bar{e}}(t)+c(t)$. Then

$$\begin{aligned} n'(t)\le r_1s(t)(1-n(t))+r_2c(t)(1-a n(t)) \end{aligned}$$

(46)

Hence, the set $B_1:=\{x\in {\mathbb {R}}^4_+ \mid x_1+x_2+x_3 \le \max \{1,1/a\}\}$ attracts all solutions of (43), and no solution that enters $B_1$ can escape this set in forward time. Thus, there exists $K>0$ such that, for all large t,

$$\begin{aligned} p'(t) \le K-d_2 p(t) \end{aligned}$$

(47)

From (46) and (47) we obtain that $x(t,\phi )=(s(t),{\bar{e}}(t),c(t),p(t))\in B$ for all large t and all $\phi \in D$, where $B=\{x \in {\mathbb {R}}^4_+ \mid x_1+x_2+x_3 \le 2\max \{1,1/a\},\, x_4\le 2K/d_2\}$. Consequently (recall that $x_t(\phi )(\theta )=x(t+\theta ,\phi )$), $x_t(\phi )\in {\mathcal {B}}:=\{F\in D\mid F(\theta )\in B,\, \forall \, \theta \in [-\tau ,0]\}$ for all large t and all $\phi \in D$.

Next we show that $x_t(\phi )$ is asymptotically smooth. That is, for every positively invariant, bounded, closed set $S \subset D$, every sequence $x_{t_n}(\phi _n)$ with $t_n\rightarrow \infty$, $\phi _n\in S$, has a convergent subsequence. From (45) we see that f maps bounded sets in D to bounded sets in ${\mathbb {R}}^4$. Thus, there exists $k>0$ such that $||f(\phi )||\le k$ for all $\phi \in S$. Further, we have

$$\begin{aligned} ||x_{t_n}(\phi _n)(\tau _2)-x_{t_n}(\phi _n)(\tau _1)||=\left| \left| \int _{t_n+\tau _1}^{t_n+\tau _2} f(x_l)\, dl \right| \right| \le k|\tau _2-\tau _1| \end{aligned}$$

Hence, from the Arzela-Ascoli theorem, the set $\{x_{t_n}(\phi _n)\mid n\ge 0\}$ is precompact and so it has a convergent subsequence.

Finally, we show that (44) is eventually bounded on every bounded set. Thus, let R be a bounded set in D. Let $n_{max}\ge \max \{1,1/a, \sup _{\phi \in R}||\phi _1||+||\phi _2||+||\phi _3||\}$ and $p_{max}\ge \max \{K/d_2, \sup _{\phi \in R} ||\phi _4||\}$. Then, using (46) and (47), we have that the set $R_B:=\{\phi \in D \mid ||\phi _1||+||\phi _2||+||\phi _3||\le n_{max},\, ||\phi _4||\le p_{max}\}$ is bounded, positively invariant and contains R.

Now the conclusion follows from Theorem 2.33 in (Smith and Thieme 2011).

$\square$

Consider the nonautonomous linear systems

$$\begin{aligned} {u^1}'(t)= & {} A_1(x_t(\phi ))u^1(t), \end{aligned}$$

(48)

$$\begin{aligned} {u^2}'(t)= & {} A_2(x_t(\phi ))u^2(t)+B_2(x_t(\phi ))u^2(t-\tau ), \end{aligned}$$

(49)

where

$$\begin{aligned} A_1(x_t(\phi ))= & {} r_1[1-n_t(\phi )(0)]-p_t(\phi )(0), \end{aligned}$$

(50)

$$\begin{aligned} A_2(x_t(\phi ))= & {} \left( \begin{array}{cc} r_2(1-an_t(\phi )(0)) &{} 0\\ b &{} -(d_2 +s_t(\phi )(0)) \end{array} \right) , \end{aligned}$$

(51)

$$\begin{aligned} B_2(x_t(\phi ))= & {} \left( \begin{array}{cc} 0 &{} e^{-d_1\tau }s_t(\phi )(-\tau )\\ 0 &{} 0 \end{array} \right) \end{aligned}$$

(52)

Denote by $L_i(t,\phi )$, $i=1,2$, the solution operators for (48) and (49), respectively. Thus, $L_1(t,\phi ):{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+$, $L_1(t,\phi )\eta =u^1(t,\eta ,\phi )$, and $L_2(t,\phi ): C^2_+\rightarrow C^2_+$, $L_2(t,\phi )\eta =u^2_t(\eta ,\phi )$, where $C^2_+=\{F:[-\tau ,0]\rightarrow {\mathbb {R}}^2_+\mid F \text{ is } \text{ continuous }\}$. Also, $L_i(0,\phi )\eta =\eta$, for all $\phi \in D$, $\eta \in C^i_+$, where, for convenience, we write $C^1_+$ for ${\mathbb {R}}_+$. Then we have that

$$\begin{aligned} L_i(t_2,x_{t_1}(\phi ))L_i(t_1,\phi )\eta =L_i(t_1+t_2,\phi )\eta ,\, \forall \, t_1\ge 0,\, t_1+t_2\ge 0, \, \phi \in D, \, \eta \in C^i_+. \end{aligned}$$

(53)

We define $||L_2(t,\phi )||=\sup \{||L_2(t,\phi )\eta || \mid \eta \in C^2_+,\, ||\eta ||=1\}$. For $\phi \in C_+$ and $\eta > 0$, let

$$\begin{aligned} \lambda _i(\phi ,\eta )=\limsup _{t\rightarrow \infty }\dfrac{1}{t}\ln ||L_i(t,\phi )\eta ||,\, i=1,2. \end{aligned}$$

(54)

The following notation (borrowed from Smith 1995) will prove useful. Thus, for $\eta \in C^2_+$, $\eta \gg 0$ means $\eta _i(\theta )>0,\, \forall \, i=1,2$, $\forall \theta \in [-\tau ,0]$, while $\eta >0$ means $\exists \, \theta \in [-\tau ,0],\, \exists \, i=1,2$ such that $\eta _i(\theta )>0$.

Lemma 8

$\lambda _2(\tilde{{\mathcal {E}}}_0,\eta )=\lambda _2(\tilde{{\mathcal {E}}}_0,\xi )$, for all $\eta ,\xi >0$.

Proof

Equation (49) can be written as

$$\begin{aligned} {u^2}'(t)=Pu^2_t, \end{aligned}$$

(55)

where, for $\eta \in C^2_+$, $P\eta =A_2(x_t(\tilde{{\mathcal {E}}}_0))\eta (0)+B_2(\tilde{{\mathcal {E}}}_0)\eta (-\tau )$.

For every $\eta \in C^2_+$, $\eta _1(0)=0$ implies $P_1(t)\eta =e^{-d_1\tau }\eta _2(-\tau )\ge 0$, while $\eta _2(0)=0$ implies $P_2(t)\eta =b\eta _1(0))\ge 0$. Thus, (49) is cooperative.

For $j=1,2$, let $\hat{e}^j\in C^2_+$ be defined as $\hat{e}^j_k(t)=\delta _{jk}$ (the Kronecker delta), for all $t\in [-\tau ,0]$. Then

$$\begin{aligned} col(P\hat{e}^1,P\hat{e}^2)=\left( \begin{array}{cc} r_2(1-a) &{} e^{-d_1\tau }\\ b &{} -(d_2+1) \end{array} \right) \end{aligned}$$

is an irreducible matrix. Thus, (48) is cooperative and irreducible in $C^2_+\setminus \{0\}$.

Also, we can write $P_j\eta$, $j=1,2$, as

$$\begin{aligned} P_j\eta = a_j\eta _j(0)+\sum _{k=1}^2\int _{-\tau _k}^0 \eta _k(\theta )d_{\theta }\nu _{jk}(t,\theta ), \end{aligned}$$

where $\tau _1=0$, $\tau _2=\tau$, $a_1=r_2(1-a)$, $a_2(t)=-(d_2+1)$, $\nu _{11}=\nu _{22}=0$ (the zero measure), $\nu _{12}(t,\theta )=e^{-d_1\tau }\delta _{-\tau }$, and $\nu _{21}=b\delta _0$, where $\delta _{\theta }$ is the Dirac measure based at $\theta$.

From Lemma 3.2 in Smith (1995) (note that condition (R) on p.86 is satisfied), we obtain that if $u^2(t,\eta )$ is a solution of (49) with $\eta >0$ then $u^2(t,\eta )\gg 0$ for all $t\ge 2\tau$.

Now let $\eta ,\xi \gg 0$. That is, $\eta _i(\theta ),\, \xi _i(\theta )>0$, for all $\theta \in [-\tau ,0]$, $i=1,2$. Then there exist $a,b>0$ such that $a\eta \le \xi \le b\eta$. From (54) and the fact that (49) is cooperative, we obtain $\lambda _2(\phi ,\eta )=\lambda _2(\phi ,\xi )$.

Let $\eta \in C^2_+$, $\eta >0$. Let $\xi =L_2(2\tau ,\phi )\eta$.Then

$$\begin{aligned} \lambda _2(\phi ,\eta )= & {} \displaystyle \limsup _{t\rightarrow \infty }\frac{1}{t}\ln ||L_2(t,\phi )\eta ||\\= & {} \displaystyle \limsup _{t\rightarrow \infty }\frac{1}{t}\ln ||L_2(t-2\tau ,x_{2\tau }(\phi ))L_2(2\tau ,\phi )\eta ||\\= & {} \displaystyle \limsup _{t\rightarrow \infty }\frac{t-2\tau }{t} \cdot \frac{1}{t-2\tau }\ln ||L_2(t-2\tau ,x_{2\tau }(\phi ))\xi ||\\= & {} \displaystyle \limsup _{t\rightarrow \infty }\frac{1}{t}\ln ||L_2(t,x_{2\tau }(\phi ))\xi ||\\= & {} \displaystyle \lambda _2(x_{2\tau }(\phi ),\xi )\\= & {} \displaystyle \lambda _2(x_{2\tau }(\phi ),L_2(2\tau ,\phi )\xi )\\= & {} \displaystyle \limsup _{t\rightarrow \infty }\frac{1}{t}\ln ||L_2(t,x_{2\tau }(\phi ))L_2(2\tau ,\phi )\xi ||\\= & {} \displaystyle \limsup _{t\rightarrow \infty }\frac{1}{t}\ln ||L_2(t+2\tau ,\phi )\xi ||\\= & {} \displaystyle \limsup _{t\rightarrow \infty }\frac{t+2\tau }{t}\frac{1}{t+2\tau }\ln ||L_2(t+2\tau ,\phi )\xi ||\\= & {} \displaystyle \limsup _{t\rightarrow \infty }\frac{1}{t}\ln ||L_2(t,\phi )\xi ||\\= & {} \lambda _2(\phi ,\xi ) \end{aligned}$$

$\square$

Thus, in what follows we will often write, in short, $\lambda (\phi )$ for $\lambda (\phi ,\eta )$.

Lemma 9

There exist $\delta >0$ and a neighborhood V of $\tilde{{\mathcal {E}}}_0$ such that the set

$$\begin{aligned} U_2:=\left\{ \frac{L_2(t+\tau ,\phi ,\gamma )\eta }{||L_2(t,\phi ,\gamma )\eta ||}\, \mid \, t\ge 0,\, \eta \in C^2_+\setminus \{0\},\, ||\gamma -\gamma _0||<\delta ,\, x_T(\phi ,\gamma )\in V, \, \forall \, T\ge 0 \right\} \end{aligned}$$

(56)

is precompact and its closure is contained in $C^2_+\setminus \{0\}$.

Proof

There exists $V'$ a neighborhood of $\tilde{{\mathcal {E}}}_0$ and $\kappa _1>0$ such that $||A_2(\phi )||\le \kappa _1$, $||B_2(\phi )||\le \kappa _1$, for all $\phi \in V'$. First, we show that the following set is precompact

$$\begin{aligned} U_2':=\left\{ \frac{L_2(t+\tau ,\phi ,\gamma )\eta }{||L_2(t,\phi ,\gamma )\eta ||}\, \mid \, t\ge 0,\, \eta \in C^2_+\setminus \{0\},\, x_T(\phi ,\gamma )\in V', \, \forall \, T\ge 0\right\} \end{aligned}$$

(57)

Let $L_2(t+\tau ,\phi ,\gamma )\eta /||L_2(t,\phi ,\gamma )\eta ||\in U_2'$. Then $L_2(t+\tau ,\phi ,\gamma )\eta /||L_2(t,\phi ,\gamma )\eta ||=L_2(\tau ,\psi ,\gamma )\xi$, where $\psi =x_t(\phi ,\gamma )$ and $\xi =L_2(t,\phi ,\gamma )\eta /||L_2(t,\phi ,\gamma )\eta ||$. From (49), we have

$$\begin{aligned} L_2(\tau ,\psi ,\gamma )\xi (\theta )= & {} u_{\tau }^2(\xi ,\psi ,\gamma )(\theta )\nonumber \\= & {} u^2(\tau +\theta ,\xi ,\psi ,\gamma )\nonumber \\= & {} \displaystyle \xi (0)+\int _0^{\tau +\theta } A_2(x_s(\psi ,\gamma ))u^2(s,\xi ,\psi ,\gamma )\, ds\nonumber \\&\displaystyle + \int _0^{\tau +\theta } B_2(x_s(\psi ,\gamma ))u^2(s-\tau ,\xi ,\psi ,\gamma )\, ds\nonumber \\= & {} \displaystyle \xi (0)+\int _{-\theta }^{\tau } A_2(x_{s+\theta }(\psi ,\gamma ))u^2(s+\theta ,\xi ,\psi ,\gamma )\, ds\nonumber \\&\displaystyle + \int _0^{\tau +\theta } B_2(x_s(\psi ,\gamma ))\xi (s-\tau )\, ds\nonumber \\ ||L_2(\tau ,\psi ,\gamma )\xi (\theta )||\le & {} \displaystyle 1+\kappa _1\tau +\kappa _1 \int _{-\theta }^{\tau } ||L_2(s,\psi ,\gamma )\xi (\theta )||\, ds\nonumber \\ ||L_2(\tau ,\psi ,\gamma )\xi (\theta )||\le & {} (1+\kappa _1\tau )e^{\kappa _1\tau }, \end{aligned}$$

(58)

where the last inequality follows from Gronwall’s inequality. Thus, there exists $\kappa _2>0$ such that $||L_2(\tau ,\psi ,\gamma )||\le \kappa _2$, for all $\psi \in V'$, $\gamma \in \varGamma$.

Next we show that $\forall \, \varepsilon>0,\, \exists \, \delta >0$ such that, $\forall \, \theta _1,\theta _2\in [-\tau ,0],\, |\theta _2-\theta _1|<\delta$, $\forall$ $L_2(t+\tau ,\phi ,\gamma )\eta /||L_2(t,\phi ,\gamma )\eta ||\in U_2'$, there holds

$$\begin{aligned} \frac{||L_2(t+\tau ,\phi )\eta (\theta _2)-L_2(t+\tau ,\phi )\eta (\theta _1)||}{||L_2(t,\phi ,\gamma )\eta ||}<\varepsilon \end{aligned}$$

(59)

Again, from (49), we obtain that, for all $t\ge 0$,

$$\begin{aligned} L_2(t+\tau ,\phi ,\gamma )\eta (\theta )= & {} u^2_{t+\tau }(\eta ,\phi ,\gamma )(\theta )\\= & {} u^2(t+\tau +\theta ,\eta ,\phi ,\gamma )\\= & {} \displaystyle \eta (0)+\int _0^{t+\tau +\theta }A_2(x_s(\phi ,\gamma ))u^2(s,\eta ,\phi ,\gamma )\, ds\\&\displaystyle +\int _0^{t+\tau +\theta }B_2(x_s(\phi ,\gamma ))u^2(s-\tau ,\eta ,\phi ,\gamma )\, ds. \end{aligned}$$

Thus, w.l.o.g assuming $\theta _1<\theta _2$, we have

$$\begin{aligned}&||L_2(t+\tau ,\phi ,\gamma )\eta (\theta _2)-L_2(t+\tau ,\phi ,\gamma )\eta (\theta _1)||\\&\quad \le \displaystyle \int _{t+\tau +\theta _1}^{t+\tau +\theta _2}||A_2(x_s(\phi ,\gamma ))|| ||u^2(s,\eta ,\phi ,\gamma )||\, ds\\&\qquad +\displaystyle \int _{t+\tau +\theta _1}^{t+\tau +\theta _2}||B_2(x_s(\phi ,\gamma ))|| ||u^2(s-\tau ,\eta ,\phi ,\gamma )||\, ds\\&\quad \le \displaystyle \kappa _1( \int _{t+\tau +\theta _1}^{t+\tau +\theta _2}||u^2(s,\eta ,\phi ,\gamma )||\, ds\\&\qquad \displaystyle +\int _{t+\tau +\theta _1}^{t+\tau +\theta _2}||u^2(s-\tau ,\eta ,\phi ,\gamma )||\, ds)\\&\quad = \displaystyle \kappa _1\left( \int _{\theta _1}^{\theta _2}||u^2(t+\tau +s,\eta ,\phi ,\gamma )||\, ds\right. \\&\left. \qquad \displaystyle +\int _{\theta _1}^{\theta _2}||u^2(t+s,\eta ,\phi ,\gamma )||\, ds\right) \\&\quad = \displaystyle \kappa _1\left( \int _{\theta _1}^{\theta _2}||u^2_{t+\tau }(\eta ,\phi ,\gamma )(s)||\, ds\right. \\&\left. \qquad \displaystyle +\int _{\theta _1}^{\theta _2}||u^2_{t}(\eta ,\phi ,\gamma )(s)||\, ds\right) \\&\quad \le \displaystyle \kappa _1(\theta _2-\theta _1)(||u^2_{t+\tau }(\eta ,\phi ,\gamma )||+||u^2_{t}(\eta ,\phi ,\gamma )||) \end{aligned}$$

Hence

$$\begin{aligned}&\frac{||L_2(t+\tau ,\phi ,\gamma )\eta (\theta _2)-L_2(t+\tau ,\phi ,\gamma )\eta (\theta _1)||}{||L_2(t,\phi ,\gamma )\eta ||}\nonumber \\&\quad \le \kappa _1(\theta _2-\theta _1) \left( 1+\frac{||u^2_{t+\tau }(\eta ,\phi ,\gamma )||}{||u^2_{t}(\eta ,\phi ,\gamma )||}\right) \end{aligned}$$

(60)

On the other hand, using (53) have that

$$\begin{aligned}&u^2_{t+\tau }(\eta ,\phi ,\gamma )=L_2(\tau ,x_{t}(\phi ,\gamma ),\gamma )L_2(t,\phi ,\gamma )\eta \nonumber \\&\quad =L_2(\tau ,x_{t}(\phi ,\gamma ),\gamma )u^2_{t}(\eta ,\phi ,\gamma ),\, \forall \, t\ge 0, \end{aligned}$$

(61)

from which we obtain

$$\begin{aligned} ||u^2_{t+\tau }(\eta ,\phi ,\gamma )||\le ||L_2(\tau ,x_{t}(\phi ,\gamma ),\gamma )|| ||u^2_{t}(\eta ,\phi ,\gamma )||\le \kappa _2||u^2_{t}(\eta ,\phi ,\gamma )||, \end{aligned}$$

(62)

Then (59) follows from (60) and (62).

Now from (59) and (62) we obtain, applying the Arzela-Ascoli theorem, that $U_2'$ is precompact.

For $\delta >0$ and $V\subset V'$ a neighborhood of $\tilde{{\mathcal {E}}}_0$, $U_2\subset U_2'$, so $U_2$ is also precompact.

Suppose that for every $\delta >0$ and every V a neighborhood of $\tilde{{\mathcal {E}}}_0$, the closure of the corresponding set $U_2$ is not contained in $C^2_+\setminus \{0\}$. Then there exist sequences $(t_n)_n$, $(\phi _n)_n\subset C_+$, $\gamma _n\rightarrow \gamma _0$ and $(\eta _n)_n\subset C^2_+\setminus \{0\}$, $x_{t_n}(\phi _n,\gamma _n)\rightarrow \tilde{{\mathcal {E}}}_0$, such that $L_2(\tau ,x_{t_n}(\phi _n,\gamma _n),\gamma _n)\xi _n\rightarrow 0$, where $\xi _n=L_2(t_n,\phi _n,\gamma _n)\eta _n/||L_2(t_n,\phi _n,\gamma _n)\eta _n||$. For each n let $\theta _n$ be such that $||\xi _n(\theta _n)||=1$. For all large n, the differential equation

$$\begin{aligned} v'(t)=A_2(x_{t+\theta _n+t_n}(\phi _n,\gamma _n))v(t)+B_2(x_{t+\theta _n+t_n}(\phi _n,\gamma _n))v(t-\tau ) \end{aligned}$$

(63)

is satisfied by $L_2(t,x_{t_n}(\phi _n,\gamma _n),\gamma _n)\xi _n(\theta _n)$, for all $t>0$. Consider the ordinary differential equation

$$\begin{aligned} w'(t)=A_2(x_{t+\theta _n+t_n}(\phi _n,\gamma _n))w(t) \end{aligned}$$

(64)

Since matrix $A_2$ is quasipositive and matrix $B_2$ is nonnegative, we have that $L_2(t,x_{t_n}(\phi _n,\gamma _n),\gamma _n)\xi _n(\theta _n)\ge w_n(t)\ge 0$, $\forall \, t\ge 0$, for every solution $w_n(t)$ of (64) with $w_n(0)=\xi _n(\theta _n)$. Hence $w_n(\tau )=w(\tau ,x_{t_n}(\phi _n,\gamma _n),\xi _n(\theta _n))\rightarrow 0$ (where $x_{t_n}(\phi _n,\gamma _n)$ is regarded as a parameter for the solution w). There exists a subsequence $n_k\rightarrow \infty$ such that $\xi _{n_k}(\theta _{n_k})\rightarrow {\bar{\xi }}\in {\mathbb {R}}^2_+$. Then $w(\tau ,\tilde{{\mathcal {E}}}_0,{\bar{\xi }})=0$ and $||{\bar{\xi }}||=1$. By the uniqueness of solutions of (64), ${\bar{\xi }}=0$, which represents a contradiction. This concludes our proof.

$\square$

Lemma 10

The set $\cup _{\phi \in D,\gamma \in \varGamma }\omega _{\gamma }(\phi )$ is precompact.

Proof

Let ${\mathcal {A}}_{\varGamma }= \cup _{\phi \in D,\gamma \in \varGamma }\omega _{\gamma }(\phi )$ and let $\psi \in {\mathcal {A}}_{\varGamma }$. Let $\varepsilon >0$. Then there exists $\gamma \in \varGamma$, ${\bar{\phi }}\in D$ such that $d(\psi ,\omega _{\gamma }({\bar{\phi }}))<\varepsilon$ (where $d(\psi ,\omega _{\gamma }({\bar{\phi }}))$ denotes the distance between $\psi$ and the set $\omega _{\gamma }({\bar{\phi }})$). $\omega _{\gamma }({\bar{\phi }})$ being compact, there exists $\psi _0\in \omega _{\gamma }({\bar{\phi }})$ such that $d(\psi ,\omega _{\gamma }({\bar{\phi }}))=d(\psi ,\psi _0)=||\psi -\psi _0||$. Also, $\omega _{\gamma }({\bar{\phi }})$ being invariant, there exists $\phi _0\in \omega _{\gamma }({\bar{\phi }})$ such that $\psi _0=x_{\tau }(\phi _0,\gamma )$. The system (43) can be written in the form $x'(t)=A(x_t)x(t)+B(x_t)x(t-\tau )$, with

$$\begin{aligned} A(\phi )= & {} \left( \begin{array}{cccc} r_1[1-\sum _{i=1}^3\phi ^i(0)]-\phi ^4(0) &{} 0 &{} 0 &{} 0\\ \phi ^4(0) &{} -d_1 &{} 0 &{} 0\\ 0 &{} 0 &{} r_2[1-a\sum _{i=1}^3\phi ^i(0)] &{} 0\\ 0 &{} 0 &{} b &{} -\phi ^1(0)-d_2 \end{array} \right) \end{aligned}$$

(65)

$$\begin{aligned} B(\phi )= & {} \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -e^{-d_1\tau }\phi ^1(-\tau )\\ 0 &{} 0 &{} 0 &{} e^{-d_1\tau }\phi ^1(-\tau )\\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right) \end{aligned}$$

(66)

Let ${\mathcal {B}}(\gamma )$ be the set ${\mathcal {B}}$, defined in Theorem 7, corresponding to the parameter $\gamma \in \varGamma$. Then, since $\varGamma$ is compact, $\cup _{\gamma \in \varGamma }{\mathcal {B}}(\gamma )$ is bounded. Therefore ${\mathcal {A}}_{\varGamma }$ is bounded (because $\omega _{\gamma }(\phi )\in {\mathcal {B}}(\gamma )$). Now using (65) and (66), we obtain that there exists $\kappa >0$ such that $||\phi ||$, $||A(\phi )||$, $||B(\phi )||$ $\le \kappa$, for all $\phi \in {\mathcal {A}}_{\varGamma }$. Let $\theta _1,\theta _2\in [-\tau ,0]$, $\theta _1\le \theta _2$. We have

$$\begin{aligned} ||\psi (\theta _2)-\psi (\theta _2)||\le & {} ||x(\tau +\theta _2,\phi _0,\gamma )-x(\tau +\theta _1,\phi _0,\gamma )|| +\\&+ ||\psi (\theta _1)-x_{\tau }(\phi _0,\gamma )(\theta _1)||+ ||\psi (\theta _2)-x_{\tau }(\phi _0,\gamma )(\theta _2)||\\\le & {} 2\varepsilon + \int _{\tau +\theta _1}^{\tau +\theta _2} ||A(x_s(\phi ,\gamma ))|| ||x(s,\phi ,\gamma )||\, ds+\\&\int _{\tau +\theta _1}^{\tau +\theta _2} ||B(x_s(\phi ,\gamma ))|| ||x(s-\tau ,\phi ,\gamma )||\, ds\\\le & {} 2\varepsilon + \kappa \left( \int _{\tau +\theta _1}^{\tau +\theta _2} ||x(s,\phi ,\gamma )||\, ds+ \int _{\tau +\theta _1}^{\tau +\theta _2} ||\phi (s)||\, ds\right) \\= & {} 2\varepsilon +\kappa ^2(\theta _2-\theta _1) \end{aligned}$$

Then, from the Arzela-Ascoli theorem, we obtain that $\cup _{\phi \in D,\gamma \in \varGamma }\omega _{\gamma }(\phi )$ is precompact.

$\square$

Proof of Theorem 6

We will work here with the rescaled model (43) and apply Theorem 5 in Smith and Zhao (2001). Using Lemma 10, for each of the cases i)-iv) above we only need to verify the assumptions $\mathbf {(B1)}$ and $\mathbf {(B2)}$ of this theorem.

Let $X_0^1=\{\phi \in D \mid \phi _1(0)=0\}$, $X_0^2=\{\phi \in D \mid \phi _3=\phi _4=0\}$, and $X_0=\{\phi \in D \mid \phi _1(0)=\phi _3(0)=0\}$. Notice that all solutions originating in one of these sets remains in that set for all $t>0$.

(i). It is trivial to verify that all solutions originating in $X_0$ converge to ${\mathcal {E}}_0^0=(0,0,0,0)$. We choose the “generalized distance function” from Theorem 5 in Smith and Zhao (2001) to be ${\tilde{p}}(\phi )=\phi _1(0)+\phi _3(0)$. Next we verify condition (B2) of this theorem for ${\mathcal {E}}_0^0$, arguing by contradiction. Thus, suppose $\forall \, \epsilon>0,\delta _0>0$, $\exists \, {\bar{\gamma }}$, $||{\bar{\gamma }}-\gamma _0||<\delta _0$, and ${\bar{\phi }}\in C_+\setminus X_0$, such that

$$\begin{aligned} d(x_t({\bar{\phi }},{\bar{\gamma }}), {\mathcal {E}}_0^0)\le \epsilon ,\, \forall \, t\ge 0. \end{aligned}$$

(67)

First assume that ${\bar{\phi }}_1(0)>0$. From (43), $s(t)=s(t,{\bar{\phi }})$ satisfies

$$\begin{aligned} s'(t)=s(t)[r_1(1-s(t)-{\bar{e}}(t))-p(t)] \end{aligned}$$

(68)

Hence, using (67) , we see that (for $\epsilon$ small) s would be increasing, thus convergent to a positive value, which would represent a contradiction.

Now assume that ${\bar{\phi }}_1(0)=0$. Then $\phi _1(t)=s(t)=0$ for all $t\ge 0$. Also, $\phi _3(0)>0$, and c(t) satisfies

$$\begin{aligned} c'(t)\ge r_2 c(t)[1-a({\bar{e}}(t)+c(t))],\, \forall \, t\ge 0 \end{aligned}$$

Since ${\bar{e}}(t)\rightarrow 0$ as $t\rightarrow \infty$, and since $c'(t)>0$ if $c(t)<1/(2a)$ for all large t, again we arrive to a contradiction to (67).

Assumption $\mathbf { (B1)}$ is satisfied by Theorem 7 and $\{{\mathcal {E}}_0^0\}$ being the only invariant set in $X_0$ and asymptotically stable (hence isolated and acyclic) in $X_0$. This concludes of this part.

For the remainder of we will assume, without a loss of generality, that the state space is disjoint from a certain neighborhood of ${\mathcal {E}}_0^0$.

(ii). All solutions originating in $X_0^1$ converge to $\tilde{{\mathcal {E}}}_c=(0,0,1/a,b/(d_2a))$. We choose ${\tilde{p}}(\phi )=\phi _1(0)$. Next we verify condition (B2), arguing by contradiction. Thus, suppose $\forall \, \epsilon>0,\delta _0>0$, $\exists \, {\bar{\gamma }}$, $||{\bar{\gamma }}-\gamma _0||<\delta _0$, and ${\bar{\phi }}\in C_+\setminus X_0^1$, such that

$$\begin{aligned} d(x_t({\bar{\phi }},{\bar{\gamma }}), \tilde{{\mathcal {E}}}_c)\le \epsilon ,\, \forall \, t\ge 0. \end{aligned}$$

(69)

We have $\lambda _1(\tilde{{\mathcal {E}}}_c)=r_1(1-1/a)-b/(d_2a)$, which is positive, because ${\mathcal {R}}_S^{C_0}>1$. Then it follows that tere exist $c>1$, $T,\delta >0$, and $V_0$ a bounded neighborhood of $\tilde{{\mathcal {E}}}_c$ such that

$$\begin{aligned} \forall \, \phi \in V_0,\, ||\gamma -\gamma _0||<\delta , L_1(T,\phi ,\gamma )1>c \end{aligned}$$

(70)

Assume that $\delta _0<\delta$ and that $\epsilon$ is so small, so that $x_t({\bar{\phi }},{\bar{\gamma }})\in V_0$, for all $t\ge 0$.

Notice that $L_1(t,\phi ,\gamma )\phi _1(0)=s(t,\phi ,\gamma )$. Applying (70) with $\gamma$ replaced by ${\bar{\gamma }}$, $\phi$ replaced by ${\bar{\phi }}$ and 1 replaced by ${\bar{\phi }}_1(0)/{\bar{\phi }}_1(0)$ we obtain

$$\begin{aligned} s(T,{\bar{\phi }},{\bar{\gamma }})>c {\bar{\phi }}_1(0) \end{aligned}$$

(71)

Next we apply again (70), this time with $\phi$ replaced by $x_{T}({\bar{\phi }},{\bar{\gamma }})$ and $\eta$ replaced by

$L_1(T,{\bar{\phi }},{\bar{\gamma }}){\bar{\phi }}_1(0)/L_1(T,{\bar{\phi }},{\bar{\gamma }}){\bar{\phi }}_1(0)$ and obtain (see (53))

$$\begin{aligned} s(2T,{\bar{\phi }},{\bar{\gamma }})>c^2 {\bar{\phi }}_1(0) \end{aligned}$$

(72)

By continuing this algorithm, we obtain that

$$\begin{aligned} s(nT,{\bar{\phi }},{\bar{\gamma }})>c^n {\bar{\phi }}_1(0),\, \forall \, n\ge 1 \end{aligned}$$

(73)

This contradicts that $x_t({\bar{\phi }},{\bar{\gamma }})\in V_0$, for all $t\ge 0$.

Assumption $\mathbf {(B1)}$ is satisfied by Theorem 7 and $\{\tilde{{\mathcal {E}}_c}\}$ being the only invariant set in $X_0^1$ and asymptotically stable (hence isolated and acyclic) in $X_0^1$. This concludes of this part.

(iii). On the set $X_0^2$ the equilibrium $\tilde{{\mathcal {E}}}_0$ is globally asymptotically stable, and so it is isolated and acyclic.

Next we calculate the Lyapunov exponent corresponding to $\tilde{{\mathcal {E}}}_0$. The characteristic equation associated with the linear, autonomous DDE (49), where $\phi =\tilde{{\mathcal {E}}}_0$, is

$$\begin{aligned} \lambda ^2-[r_2(1-a)-(1+d_2)]\lambda -r_2(1-a)(1+d_2)=be^{-(\lambda +d_1)\tau } \end{aligned}$$

(74)

Further, ${\mathcal {R}}_0>1$ implies that (74) has a positive solution ${\bar{\lambda }}$. A corresponding eigenvector would be $\psi \in C^2$, $\psi (t)=e^{{\bar{\lambda }}t}v$, where $v\in {\mathbb {R}}^2\setminus \{0\}$. Since

$$\begin{aligned} \left( \begin{array}{cc} {\bar{\lambda }}-r_2(1-a) &{} -e^{-({\bar{\lambda }}+d_1)\tau }\\ -b &{} {\bar{\lambda }}+(1+d_2) \end{array} \right) \left( \begin{array}{c} v_1\\ v_2 \end{array} \right) =0, \end{aligned}$$

(75)

we can choose $v\in int({\mathbb {R}}^2_+)$. Hence $\psi \gg 0$. From this it follows that $W^U(0)$, the unstable manifold of 0 for (49), contains points in $C^2_+\setminus \{0\}$. Let $\xi \in (C^2_+\setminus \{0\})\cap W^U(0)$. Then $u(t,\xi )$, the solution of (48) with initial condition $\xi$ does not converge to 0 as $t\rightarrow \infty$.

On the other hand, from Theorem 1.2 in Pituk (2018), $\lambda _2(\tilde{{\mathcal {E}}}_0)=\lambda _2(\tilde{{\mathcal {E}}}_0,\xi )=\lim _{t\rightarrow \infty }(1/t)\ln ||u_t(\xi )||$ is a real root $\mu$ of (74) associated with an eigenvector in $C^2_+$. Hence (75) is satisfied with ${\bar{\lambda }}$ replaced by $\mu$ and with v replaced by some $u\in int({\mathbb {R}}^2_+)$.

Suppose that $\mu <0$. Then, from (75) it follows that $\mu >\max \{-(1+d_2),-r_2(a-1)\}$, which leads to a contradiction to $\mu$ being a real solution to (74), because $be^{-d_1\tau }>r_2(a-1)(1+d_2)$. Hence $\mu >0$.

Next we verify condition (B2) of Theorem 5 in Smith and Zhao (2001) for $\tilde{{\mathcal {E}}}_0$. For convenience, for a $\phi \in C_+$ we denote $(\phi _3,\phi _4)$ by $\phi ^2$. Thus, we show that $\exists \, \epsilon _2,\delta _2>0$, such that

$$\begin{aligned} \limsup _{t\rightarrow \infty } d(x_t(\phi ,\gamma ), \tilde{{\mathcal {E}}}_0)>\epsilon _2,\, \forall \, \phi \in D,\, ||\phi ^2||>0,\, ||\gamma -\gamma _0||<\delta _2 \end{aligned}$$

(76)

We prove this arguing by contradiction. Thus, suppose $\forall \, \epsilon _2,\delta _2>0$, $\exists \, {\bar{\gamma }}$, $||\gamma -\gamma _0||<\delta _2$, and ${\bar{\phi }}\in C_+,\, ||{\bar{\phi }}^2||>0$, such that

$$\begin{aligned} d(x_t({\bar{\phi }},{\bar{\gamma }}),\tilde{{\mathcal {E}}}_0)\le \epsilon _2,\, \forall \, t\ge 0. \end{aligned}$$

(77)

Since $\lambda _2(\tilde{{\mathcal {E}}}_0)>0$, we have $\lambda _2(\tilde{{\mathcal {E}}}_0,\eta )>0$ for all $\eta \in {\bar{U}}_2$ (see Lemma 8). Further, using that $U_2$ (for some $\delta$ and V) is precompact and ${\bar{U}}_2\subset C^2_+\setminus \{0\}$ (Lemma 9), it follows that there exist $c>1$, $T_1,\ldots , T_k,\delta _1\in (0,\delta )$, and $V_2\subset V$ a bounded neighborhood of $\tilde{{\mathcal {E}}}_0$ such that

$$\begin{aligned} \forall \, \phi \in V_2,\, \eta \in U_2,\, ||\gamma -\gamma _0||<\delta _1,\, \exists \, j\in \{1,\ldots ,k\} \text{ such } \text{ that } ||L_2(T_j,\phi ,\gamma )\eta ||>c \end{aligned}$$

(78)

Assume that $\delta _2<\delta _1$ and that $\epsilon _2$ is so small, so that $x_t({\bar{\phi }},{\bar{\gamma }})\in V_2$, for all $t\ge 0$.

Notice that $L_2(t,\phi ,\gamma )\phi ^2=x_t^2(\phi ,\gamma )$. Applying (78) with $\gamma$ replaced by ${\bar{\gamma }}$, $\phi$ replaced by $x_{\tau }({\bar{\phi }},{\bar{\gamma }})$ and $\eta$ replaced by $L_2(\tau ,{\bar{\phi }},{\bar{\gamma }}){\bar{\phi }}^2/||{\bar{\phi }}^2||$ we obtain

$$\begin{aligned} ||x^2_{T_{j_1}+\tau }({\bar{\phi }},{\bar{\gamma }})||>c ||{\bar{\phi }}^2||, \end{aligned}$$

(79)

for some $T_{j_1}\in \{T_1,...,T_k\}$. Next we apply again (78), this time with $\phi$ replaced by $x_{T_{j_1}+2\tau }({\bar{\phi }},{\bar{\gamma }})$ and $\eta$ replaced by $L_2(T_{j_1}+2\tau ,{\bar{\phi }},{\bar{\gamma }}){\bar{\phi }}^2/||L_2(T_{j_1}+\tau ,{\bar{\phi }},{\bar{\gamma }}){\bar{\phi }}^2||$ we obtain

$$\begin{aligned} ||x^2_{T_{j_1}+T_{j_2}+2\tau }({\bar{\phi }},{\bar{\gamma }})||>c^2||{\bar{\phi }}^2||, \end{aligned}$$

(80)

for some $T_{j_2}\in \{T_1,...,T_k\}$. By continuing this algorithm, we obtain that

$$\begin{aligned} ||x^2_{t_n}({\bar{\phi }},{\bar{\gamma }})||>c^n ||{\bar{\phi }}^2||, \end{aligned}$$

(81)

where, for arbitrarily large n, $t_n=\sum _{m=1}^n T_{j_m}+n\tau$, with each $T_{j_m}$ being some member of $\{T_1,\ldots ,T_k\}$. This contradicts that $x_t({\bar{\phi }},{\bar{\gamma }})\in V_2$, for all $t\ge 0$. Hence (76) holds.

Now the conclusion follows from Theorem 5 in Smith and Zhao (2001), applied with the generalized distance function ${\tilde{p}}:C_+\rightarrow {\mathbb {R}}$, ${\tilde{p}}(\phi )=\min _{i=3,4}\min _{\theta \in [-\tau ,0]} \phi _i(\theta )$.

iv). It follows from ii) and iii).

$\square$