Significance of multi-objective optimization in logistics problem for multi-product supply chain network under the intuitionistic fuzzy environment

Abstract

Determining the methods for fulfilling the continuously increasing customer expectations and maintaining competitiveness in the market while limiting controllable expenses is challenging. Our study thus identifies inefficiencies in the supply chain network (SCN). The initial goal is to obtain the best allocation order for products from various sources with different destinations in an optimal manner. This study considers two types of decision-makers (DMs) operating at two separate groups of SCN, that is, a bi-level decision-making process. The first-level DM moves first and determines the amounts of the quantity transported to distributors, and the second-level DM then rationally chooses their amounts. First-level decision-makers (FLDMs) aimed at minimizing the total costs of transportation, while second-level decision-makers (SLDM) attempt to simultaneously minimize the total delivery time of the SCN and balance the allocation order between various sources and destinations. This investigation implements fuzzy goal programming (FGP) to solve the multi-objective of SCN in an intuitionistic fuzzy environment. The FGP concept was used to define the fuzzy goals, build linear and nonlinear membership functions, and achieve the compromise solution. A real-life case study was used to illustrate the proposed work. The obtained result shows the optimal quantities transported from the various sources to the various destinations that could enable managers to detect the optimum quantity of the product when hierarchical decision-making involving two levels. A case study then illustrates the application of the proposed work.

Introduction

Company operations may present a tremendous environmental hazard through carbon emissions, scrapped packaging products, dumped radioactive goods. Due to the diverse and intense global competition, multinational and large companies are progressively researching strategies to develop supply chain practices that increase efficiency and profitability, reduce costs, and preserve long-term sustainability. Manufacturing companies have adopted supply chain (SC) practices to handle consumer desire for environmentally friendly goods and services generated by socially responsible processes apart from environmental policy standards [42, 53]. Such activities allow producers to partner with vendors and consumers to improve environmental sustainability. Enforcement of these practices contributes to better environmental efficiency, as shown by decreases in carbon pollution, effluent and hazardous waste, and harmful material intake. The timeline for becoming environmentally conscious presents a variety of problems worldwide for industrial and service firms. Today's most significant problem is implementing waste management that considers the relationship between toxic waste and environmental conservation. Many studies have recently been conducted that presented the advantages of combining different practices with a conventional supply chain. Several recent researchers have conducted numerous studies on environmental efficiency assessment dependent on SC practices and their long-term effects.

A supply chain network (SCN) consists of several facilities (e.g., manufacturing plants, distribution centers, suppliers) that form a set of operations ranging from raw materials' purchase and conversion of the materials into final products of the final product to the distributors [22]. The SCN forms a chain of the processes involved in transforming raw constituents into finished products readily obtainable by absolute customers. Supply chain management (SCM) is widely spread within multinational companies and becomes an essential part. It includes the acquisition of the whole of SC's management from the procurement of orders to the production and the delivery of products [1]. The SCM composition performs items, the constructed suppliers and distributors, contract, leaders and followers’ relationship, and trading circumstances.

In contrast, dynamic SC is a flexible network that switches between suppliers for each agreement, without fixed trading partners. It operates with set leaders or follower relationships just like SCM. Global supply chain management (GSCM) has been implemented as a series of methods for effectively combining suppliers, distributors, warehouses, and retailers to generate and deliver the right amount of goods to the correct location (place) and at the appropriate time to reduce system-wide costs, thus fulfilling service-level criteria [53]. Companies use GSCM to improve awareness regarding changing market requirements. GSCM involves organizing and overseeing activities involved in the acquisition, sourcing, transformation, and logistics. GSCM also establishes management and relationships with suppliers, intermediates, other service providers, and customers. GSCM is used in SC designed under ambiguities to implement the game-theoretical approach by recognizing the benefit of contractual agreements between several firms [67]. Due to developments in consumer goods' production and volatility, currency risk and exchange shifts have appeared, such as disaster risk. SC needs to be reformed to react flexibly to the various changes and minimize resources subject to some constraints.

In real-life most SC problems involve uncertainties in the parameters. Some researchers used the fuzzy theory/number to present the uncertainties in the formulated model. One of the fuzzy set theory generalizations used to present uncertainty is the intuitionistic fuzzy set (IFS). In situations where the available information is not adequate for defining an impreciseness through a traditional fuzzy set, the IFS can be seen as an appropriate/alternative method for defining the uncertainty. In fuzzy sets, the degree of acceptance is considered only, but IFS is characterized by a membership function and a non-membership function so that the sum of both the values is less than one [5, 6]. Ali et al. [2] formulated SC's inventory problem under an intuitionistic fuzzy environment by considering uncertainty in selling price, purchasing price, holding cost, ordering cost, and demand of items. Niroomand et al. [44] considered a typical SCN design problem consisting of plants, distribution centers, and customers under uncertain environments, and the hybrid approach has been used to convert the trapezoidal IFS into crisp value. Kamal et al. [31] formulated an SCN problem with different kinds of membership functions like linear, exponential, parabolic, hyperbolic, and quadratic membership under uncertainty and presented it with IFS.

This research's stated objective “to determine the optimal order allocation of products from different sources to different destinations in the context of sources, plant, warehouses and distributor” has been carried out. In this study, we have assumed that two types of DM’s operate at two separate groups of SCN. The fuzzy goal programming approach has been used to obtain the formulated problem's compromise solution by attaining each membership goal's highest degree by minimizing their deviational variables. Various scenarios have also been generated for getting the varying allocations with distinct values of degrees of achievement. This research enables the manager to analyze the uncertainty judgment scenarios in SCN when the product's demands and supplies are under vagueness.

Literature review

The multi-objective supply chain network (MOSCN) is a system in which more than two objective functions are optimized simultaneously. Such types of problems are solved by several methods, such as goal programming (GP), fuzzy goal programming (FGP), lexicographic goal programming (LGP), and preemptive goal programming (PGP).

Multi-objective programming in SCN

Various modern frameworks have been introduced for GSCM and service sector preparation, such as Croxton et al. [14], who presented the work related to SCM processes. Srivastava [62] derived a GSCM with several strategies. Fahimnia et al. [17] formulated the decision models for sustainable SCM. Kaur and Awasthi [33] presented the situation of barriers in GSCM, and Gupta et al. [23] considered the vendor selection issue in an SCM. Saberi et al. [56] discussed blockchain technology and its effectiveness in SCM partnership, Gupta et al. [24] developed the SC's transportation and delivery time model. Gupta et al. [25] also formulated a production–distribution model for the SC systems, and Ali et al. [2] considered the inventory management problem of an SC.

Most SC problems involve uncertainties in the parameters. Some researchers used the fuzzy theory/number to solve those problems. Many have uncertain multi-objective optimization problems, and various solution methodologies have been presented on the SCM. To reduce the expenses and time usage in a three-level SC, Chen et al. [13] proposed a “production and distribution planning” model as a mixed-integer nonlinear multi-objective programming problem to derive practical benefit from an SC. Torabi et al. [63] integrated the fuzzy set theory into the hierarchical production planning (HPP) system to resolve complex and infeasibility issues. They subsequently suggested a fuzzy HPP paradigm composed of two stages of decision-making. The first stage involved calculating an overall production strategy by solving a fuzzy framework. At the second stage, another fuzzy framework formulated a disaggregated production plan to determine a quantified production plan at the final stage in an ambiguous environment. A facility-layout decision problem model was suggested by Nobil et al. [45], a discrete binary approach for a nonlinear location-planning facility that considers the orthogonal difference between the various SC stages. Finally, they used a genetic algorithm for this problem. Ghodratnama et al. [19] suggested an order-allocation model for the hub-covering problem based on a fuzzy bi-objective. The model optimized two cases related to time and cost, where the first goal involved travel costs and expense coverage, facilities, setup expenses, and resetting infrastructure cost. The second goal involved reducing the overall delivery period from the source node to the destination node.

Soleimani et al. [61] formulated a fuzzy multi-objective GSCM with a closed-loop, and Gupta et al. [25] addressed a production-planning problem multi-objective modelling approach. Tseng et al. [66] enhanced the GSCM using an interval-valued triangular fuzzy number. Through inter-criteria association approaches in sustainable SC risk assessment, Rostamzadeh et al. [54] used an integrated “technique for the order to prefer similarity to ideal solution”. Tsao et al. [65] developed the SCN model in an unpredictable environment and used multi-objective fuzzy programming, and Uygun and Dede [67] used the embedded multicriteria fuzzy decision-making strategies to improve the GSCM’s success assessment. This model's proposed work found three classes both in the top line and in the descending series. The aims were optimizing SC’s net income, market fulfillment, and client loyalty to obtain appropriate customer prices, delivery canters, and recursive centers.

Cao et al. [10] present some well-known work related to the SCN: modelling for designing a network of reverse logistics was developed by Mutha and Pokharel [43], an optimization model incorporating both environmental and economic performances in the SCN was proposed by Paksoy and Ozceylan [47], and different scenarios for wage contraction models were investigated and documented in Wang et al. [68]. A “closed-loop supply chain (CLSC)” including three stages of manufacturing, distributing, and provision of services has been considered by Rabbani et al. [51], a multiple-objective CLSC model was proposed by Altmann and Bogaschewsky [3], in which the parameter influences were better understood by the decision-maker (DM). Other related works on the SC are documented [16, 18, 30, 39, 46, 48, 49, 52, 57,58,59, 64].

Bi-level programming in SCN

The MOSCN problem has been formulated in terms of a bi-level programming problem (BLPP) in this study, where the first-level decision-maker (FLDM) determines targets or goals and then the maximum entity for each subordinate level in isolation, while the second-level decision-maker (SLDM) considers and changes the FLDM with the analysis of the organization’s overall benefit. This method is then followed until a suitable outcome has been reached. BLPP has a pecking order association between levels, with decentralized planning, wherein the top level is considered the leader, whereas the lower level is regarded as a follower. Many researchers apply this framework to determine the best or most optimal decision regarding the organization's upper and lower pecking order relationship. The best resource distribution is obtained by the collaboration functions of the SC systems. Traditionally, producers are pioneers in the GSM, and the supreme power has recently moved from producer to distributor. This process could maximize production level, inventory, and cost of delivery and improve SC partners' productivity and collaboration. Many studies have analyzed the channel interaction between the producer and distributor from various aspects of management decisions, including advertising, marketing, manufacturing, and inventory control.

The integrated problem of buying, production, and delivery planning in an SC is demanding as businesses push into higher collaboration and competitive situations. Prominent work related to the BLPP in the SCN is discussed in studies by Hajiaghaei-Keshteli and Fathollahi-Fard [27]. They solved the distribution network problem using the two-stage stochastic bi-level decision-making model under efficient heuristics and meta-heuristics approaches. Kolak et al. [34] framed a multi-objective bi-level problem for the traffic network optimization under sustainability. Karimi et al. [32] presented a bi-level multiple-objective optimization method for pricing demand response in real-time retail markets. Amirtaheri et al. [4] used a bi-level programming model (BLPM) for a decentralized manufacturer and distributor of an SC by considering cooperative advertisement. Golpîra et al. [21] presented a robust bi-level optimization model for an SCN. Hsueh [28] accessed BLPP in sustainable SCM for collaboration with corporate social responsibility. Rowshannahad et al. [55] formulated a multi-item commodity problem of SC as a BLPP having multiple by-products that can be remanufactured and reused.

The study is arranged so that the next section discusses BL-MOSCN’s formulation with intuitionistic fuzzy parameters. The following section proposes FGP to solve the problem formulated. In the next section, a demonstration through a case study helps illustrate the effectiveness of the model developed. Finally, in the last section, the conclusions are made.

Problem description

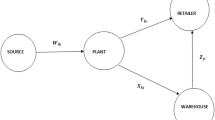
In this study, we have assumed that the two types of DM’s operate at two separate groups of SCN, i.e., at the first level and a second level. The FLDM, who first moves in the decision making or optimization process, determines the amounts of the quantity that are to be transported to distributors, and then the SLDM rationally chooses his amounts to be transported for further shipment. The FLDM objective is to minimize the total transportation costs, and similarly, the SLDM objective is to minimize the total delivery time of the SCN, but at the same point, the appropriate order allocation is balanced between each source, plant, distributor, and warehouse. BLPP has a hierarchical relationship between upper and lower levels. It is developed for decentralized planning for the system in which the upper level is termed as the leader, and the lower level relates to the follower's objective. Many DMs apply it to make the best decision with the upper and lower hierarchical relationship in an organization. The best resource of distribution is obtained by the collaboration functions of the supply chain systems. The proposed work could reduce production, inventory, and distribution costs and increase the efficiency and coordination of supply chain partners. Several articles have been studied before formulating the model of interest so that the channel coordination between manufacturer and retailer from various aspects of business decisions, including pricing, advertising, production, and inventory management, could be more effective and efficient. This research production manager will act as an FLDM, and the logistic manager will act as an SLDM. The considered methodology for the SCN is given below in Fig. 1.

Fig. 1

Supply chain network

Following assumptions have been used to formulate the mathematical model of SCN:

• 1. The plants do not hold an inventory. Demand is considered uncertain. Each plant can handle all forms of packaging.

• 2. No shortage and backlogging are allowed. The buyer pays transportation and other handling costs. The shipping cost of one unit from source to plant, from plant to warehouse, and from the warehouse to distributor may vary from the predetermined shipping cost.

• 3. Shipping time for transporting the units also varies from the predetermined time. The total budget allocated for the logistic may vary from the predetermined value as the shipping cost, and another related cost varies. Retailer demands can be fulfilled by supplying products directly from the distributor (Table 1).

Table 1 Summary of related literature

Mathematical model

The GSCM has become more integral to businesses today and is essential for its success and customer satisfaction. An SCN comprises a broad network for supplying the materials from distinct sources to different plants and various plants to distinct distributors. In contrast, the remainder of the materials has been transported from various plants to distinct warehouses and from different warehouses to distinct distributors depending on market demand. The company acquires raw materials from different vendors and supplies them to various factories and, after processing them into finished products, distributors can make them easily accessible to their customers. A DM usually coordinates networks to incur minimum transportation costs and delivery time. The global manufacturing advancement has made optimization involving multiple suppliers, manufacturers, and distributors (i.e., MOSCN) increasingly precarious. Gupta et al. [24] formulated an SCN as a bi-level programming model wherein the determination of the optimal order allocation of products is the DM’s primary objective, assuming that the products' demands and supply are fuzzy. Charles et al. [12] integrated the various stages of SCN and formulated it as a multi-objective optimization model. To obtain the SCN’s optimal solution, they used three different approaches: a simple additive GP, weighted GP, and PGP. Chalmardi and Camacho-Vallejo [11] developed a BLPP for a sustainable SCN design that considers the government's financial incentives (Fig. 2). The MOSCN problem has formulated using such studies on SCN. The following notations are used in the formulations of the problem:

Fig. 2

Supply chain network with variable

Nomenclature

$D_{k}$ is the yearly demand from kth distributor, $\forall \,\,k = 1,2, \ldots ,K$

$A_{i} -$ is the potential capacity of ith plant, $\forall \,\,i = 1,2,...,I$

$B_{j} -$ is the supply capacity of jth supplier, $\forall \,\,j = 1,2,\ldots,J$

$V_{l} -$ is the potential capacity of lth warehouse, $\forall \,\,l = 1,2,...,L$

$C_{ji} -$ is the unit shipping cost from the jth supply source to the ith plant

$C_{il} -$ is the unit cost of shipment from the ith plant to the lth warehouse

$C_{ik} -$ is the unit cost of shipment from the ith plant to the kth distributor

$C_{lk} -$ is the unit cost of shipment from the lth warehouseto the kth distributor

$T_{il} -$ is the delivery time of the shipping each unit from the plant $i$ to the warehouse $l$

$T_{ik} -$ is the delivery time of the shipping each unit from the plant $i$ to the distributor $k$

$T_{lk} -$ is the delivery time of the shipping each unit from the warehouse $l$ to the distributor $k$

$P_{ji} -$ is the amount of the quantity shipped from the supply source $j$ to the plant $i$

$Q_{il} -$ is the amount of the quantity shipped from the plant $i$ to the warehouse $l$

$R_{ik} -$ is the amount of the quantity shipped from the plant $i$ to the distributor $k$

$S_{lk} -$ is the amount of the quantity shipped from the warehouse $l$ to the distributor $k$

In this study, we assumed that there are two levels of functioning in a SCN with the FLDM and the SLDM; furthermore, the decision variables $P_{ji}$, $Q_{il}$, $R_{ik}$, and $S_{lki}$ have been separated between two DMs. Additionally, the first decision is made by the FLDM and followed by the SLDM, considering the leader’s strategy. In the corresponding SCN, the FLDM controls vector $P_{ji}$, while vectors $Q_{il}$, $R_{ik}$, and $S_{lk}$ are controlled by the SLDM. FLDM’s goal is the minimization of the total transportation cost. Likewise, the SLDM goal effectively minimizes the SCN’s total delivery time as well as maintains equilibrium between the distribution order of every source, distributor, plant, and warehouse. BL-MOSCN can be written as follows:

Transportation costs can be essential in the total logistics expenditure of a company. Transportation relates to moving the item from one place to another as it moves from the start of the SC to the customer's handling. With higher fuel prices, the ratio assigned to transportation may be higher than expected. This cost is passed to the customer, and the price of the products rises. When transportation costs are increasing, even common oversights can lead to unnecessary expenditures that could have been prevented and reduced total profit margins. The total transportation cost of the SCN is minimized as follows:

[1st level]

$$ \mathop {\min \,}\limits_{{P_{ji} }} \,\left( \begin{array}{ll} \,Z_{11} = \sum\limits_{j = 1}^{J} { \, \sum\limits_{i = 1}^{I} {C_{ji} \, P_{ji} + \sum\limits_{i = 1}^{I} { \, \sum\limits_{k = 1}^{K} {C_{ik} {\text{ R}}_{ik} } } } } \hfill \\ \,Z_{12} = \sum\limits_{j = 1}^{J} { \, \sum\limits_{i = 1}^{I} {C_{ji} \, P_{ji} + \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} {C_{il} \, Q_{il} } } } } \hfill \\ \,Z_{13} = \sum\limits_{j = 1}^{J} { \, \sum\limits_{i = 1}^{I} {C_{ji} \, P_{ji} + \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} {C_{il} \, Q_{il} } } } } + \sum\limits_{l = 1}^{L} { \, \sum\limits_{k = 1}^{K} {C_{lk} \, } } S_{lk} \hfill \\ \end{array} \right) $$

(1)

where $Q_{il} ,R_{ik} ,S_{lk}$ solves.

Delivery time in an SCN begins when the customer places an order until it is prepared for delivery. Delivery speed is an increasingly examined aspect of an SCN, especially as consumer demands continually expand. The delivery time of the SCN is minimized and presented as follows:

[2nd Level]

$$ \mathop {\min }\limits_{{Q_{il} ,R_{ik} ,S_{lk} }} \,\,\,\left( \begin{array}{ll} Z_{21} = \sum\limits_{i = 1}^{I} { \, \sum\limits_{k = 1}^{K} {T_{ik} \, R_{ik} } } + \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} {T_{il} \, Q_{il} } } \hfill \\ Z_{22} = \sum\limits_{i = 1}^{I} { \, \sum\limits_{k = 1}^{K} {T_{ik} \, R_{ik} } } + \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} {T_{il} \, Q_{il} } } + \sum\limits_{l = 1}^{L} { \, \sum\limits_{k = 1}^{K} {T_{lk} {\text{ S}}_{lk} } } \hfill \\ \end{array} \right) $$

(2)

There are many considerations for attaining excellent SCN. Coordinating and integrating various activities such as the relationship with suppliers, relationship with customers, value-added process (manufacturing), flexibility, quality, production system, customer satisfaction, and customer service lead to higher competitive advantages.

Subject to the constraint

The total amount of quantity shipped from different suppliers to different plants can be presented as follows:

$$ \sum\limits_{i = 1}^{I} {P_{ji} \le B_{j} } , $$

(3)

The total amount of quantity produced in a different factory cannot exceed their capacity and can be presented as follows:

$$ \sum\limits_{k = 1}^{K} {R_{ik} + \sum\limits_{l = 1}^{L} {Q_{il} \le A_{i} } } , $$

(4)

The total amount of quantity shipped through different warehouses cannot exceed their capacity can be presented as follows:

$$ \sum\limits_{k = 1}^{K} {S_{lk} \, \le \, V_{l} ,} $$

(5)

The total amount of quantity shipped from the various distributors must cover the customer demand and can be presented as follows:

$$ \sum\limits_{l = 1}^{L} {S_{lk} + \sum\limits_{i = 1}^{I} {R_{ik} \ge D_{k} } } , $$

(6)

The total amount of quantity shipped to various warehouses and distributors from different plants cannot be more than the number of raw materials available and is presented as follows:

$$ \sum\limits_{j = 1}^{J} {P_{ji} \ge \sum\limits_{l = 1}^{L} {Q_{il} + \sum\limits_{k = 1}^{K} {R_{ik} } } } , $$

(7)

The total amount of quantity shipped from different warehouses to the various distributors cannot exceed its capacity and is represented as follows:

$$ \sum\limits_{i = 1}^{I} { \, Q_{il} \, \ge \, \sum\limits_{k = 1}^{K} { \, S_{lk} } } , $$

(8)

The nonnegative restriction on the decision variable can be presented as follows:

$$ \left. \begin{aligned} P_{ji} \ge 0,\, \, \,\forall \, j,i \hfill \\ Q_{il} \ge 0,\,\, \, \forall \, i,l \hfill \\ R_{ik} \ge 0,\,\,\,\, \, \forall \, i,k\,\,{\text{ and}} \hfill \\ S_{lk} \ge 0,\,\,\, \, \,\forall \, l,k \hfill \\ \end{aligned} \right\} $$

(8)

Methodology

Uncertainty in SCN relates to the SC decision-making process wherein the DM cannot determine the best decision because of SC accountability. In the model defined above, deterministic values are assumed in the parameters; however, they may approximate values in most practical situations. The DM has no specific knowledge about the unit shipping costs and the distribution time from the various origins to the various destinations throughout the transportation period. The fundamental explanation for the demand volatility is increased expense, most often in surplus inventory, surplus processing capability, or the use of quicker and more costly goods transport. The business typically attempts to produce an SC equilibrium where the cost of stock, transport, and SC capacity is minimized but still meets the customer’s demanded service level. A variety of reasons, including the impact of causative variables, or lumpy demand, make demand challenging to predict. Some of these may be known, but unforeseeable circumstances may also alter the products' demand. Due to the possible scenarios discussed above, we replace deterministic parameters with fuzzy parameters:

Model 1

[1st level]

$$ \mathop {\min \,}\limits_{{P_{ji} }} \,\left( \begin{array}{ll} \,\tilde{Z}_{11} \, = \sum\limits_{j = 1}^{J} { \, \sum\limits_{i = 1}^{I} { \, \tilde{C}_{{_{ji} }}^{I} \, P_{ji} + \, \sum\limits_{i = 1}^{I} { \, \sum\limits_{k = 1}^{K} { \, \tilde{C}_{{_{ik} }}^{I} \, R_{ik} } } } } \hfill \\ \,\tilde{Z}_{12} = \sum\limits_{j = 1}^{J} { \, \sum\limits_{i = 1}^{I} { \, \tilde{C}_{{_{ji} }}^{I} \, P_{ji} + \, \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} { \, \tilde{C}_{{_{il} }}^{I} \, Q_{il} } } } } \hfill \\ \,\tilde{Z}_{13} \, = \, \sum\limits_{j = 1}^{J} { \, \sum\limits_{i = 1}^{I} { \, \tilde{C}_{{_{ji} }}^{I} \, P_{ji} + \, \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} { \, \tilde{C}_{{_{il} }}^{I} \, Q_{il} } } \, } } + \, \sum\limits_{l = 1}^{L} { \, \sum\limits_{k = 1}^{K} { \, \tilde{C}_{{_{lk} }}^{I} } \, } S_{lk} \, \hfill \\ \end{array} \right) $$

where $Q_{il} ,R_{ik} ,S_{lk}$ solves.

[2nd level]

$$ \mathop {\min }\limits_{{Q_{il} ,R_{ik} ,S_{lk} }} \,\,\,\left( \begin{array}{ll} \tilde{Z}_{21} \, = \, \sum\limits_{i = 1}^{I} { \, \sum\limits_{k = 1}^{K} { \, \tilde{T}_{{_{ik} }}^{I} \, R_{ik} } } \, + \, \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} { \, \tilde{T}_{{_{il} }}^{I} \, Q_{il} } } \hfill \\ \tilde{Z}_{22} \, = \, \sum\limits_{i = 1}^{I} { \, \sum\limits_{k = 1}^{K} { \, \tilde{T}_{{_{ik} }}^{I} \, R_{ik} } } + \, \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} { \, \tilde{T}_{{_{il} }}^{I} \, Q_{il} } } \, + \, \sum\limits_{l = 1}^{L} { \, \sum\limits_{k = 1}^{K} { \, \tilde{T}_{{_{lk} }}^{I} \, S_{lk} } \, } \hfill \\ \end{array} \right) $$

Constraints

$$ \begin{aligned} \sum\limits_{i = 1}^{K} { \, P_{ji} \, \le \, \left( {\tilde{B}_{{_{j} }}^{I} } \right) \, } ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall \, j \hfill \\ \sum\limits_{k = 1}^{K} {{\text{ R}}_{ik} \, + \, \sum\limits_{l = 1}^{L} { \, Q_{il} \, \le \, A_{i} \, \,\,\,\,\,\,\,\,\,\forall \, i} } \hfill \\ \sum\limits_{k = 1}^{K} { \, S_{lk} \, \le \, V_{l} \, ,\, \, \,\,\,\,\forall \, l} \hfill \\ \end{aligned} $$

$$ \begin{aligned} \sum\limits_{l = 1}^{L} { \, S_{lk} \, + \, \sum\limits_{i = 1}^{I} { \, R_{ik} \, \ge \, \left( {\tilde{D}_{{_{k} }}^{I} } \right)} } \, , \, \forall \, k \hfill \\ \sum\limits_{j = 1}^{J} { \, P_{ji} \, \ge \, \sum\limits_{l = 1}^{L} { \, Q_{il} \, + \, \sum\limits_{k = 1}^{K} { \, R_{ik} } \, } } , \, \forall \, i \hfill \\ \sum\limits_{i = 1}^{I} { \, Q_{il} \, \ge \, \sum\limits_{k = 1}^{K} { \, S_{lk} { ,}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall \, l} } \hfill \\ \end{aligned} $$

$$ \begin{aligned} P_{ji} \, \ge \, 0 \, ,\,\,\, \, \forall \, j \, , \, i \hfill \\ Q_{il} \, \ge \, 0 \, , \, \,\,\, \, \forall \, i \, , \, l \, \hfill \\ R_{ik} \, \ge \, 0 \, ,\,\,\, \, \,\,\forall \, i \, , \, k \, \hfill \\ S_{lk} \, \ge \, 0 \, ,\,\,\,\, \, \,\forall \, l \, , \, k \hfill \\ \end{aligned} $$

In model (1), it is assumed that parameters such as $\tilde{C}_{{_{ji} }}^{I} ,\tilde{C}_{{_{il} }}^{I} ,\tilde{C}_{{_{ik} }}^{I} ,\,\tilde{C}_{{_{lk} }}^{I} ,$ ${\stackrel{\sim }{T}}_{il}^{I}, {\stackrel{\sim }{T}}_{ik}^{I}, {\stackrel{\sim }{T}}_{lk}^{I}, {\stackrel{\sim }{B}}_{j}^{I}, and\, {\stackrel{\sim }{D}}_{k}^{I}$ are IFN. IFN’s preliminaries related to this study have been adopted from Atanassov [5, 6] and Ali et al. [2]. In Model (1), the following input information, namely, unit shipping cost from the jth supplier to ith plant, production and shipment cost of each unit from the ith plant to the kth distributor, unit production, and shipment cost from the ith plant through lth warehouse, shipment cost of each unit from the lth warehouse to the kth distributor, unit shipment of time for delivery from the ith plant to the kth distributor, unit shipment of time for delivery from the ith plant through the lth warehouse, unit shipment of time for delivery from the lth warehouse through the kth distributor, supply capacity of jth suppliers, and annual demand from kth distributors have been assumed to be IFN. The following definitions are accurate by the assumed fuzzy parameters, which can be presented as follows:

Intuitionistic fuzzy numbers (IFN)

An intuitionistic fuzzy set $\tilde{C}_{{_{ji} }}^{I} = \{ \, < x,\mu_{{\tilde{C}_{{_{ji} }}^{I} }} (x),\gamma_{{\tilde{C}_{{_{ji} }}^{I} }} (x) \, > \,\,:\, \, x \in X\left. {} \right\}$ is known as IFN if and only if these conditions hold:

• I. If $m \, \in \, \Re \,$:$\mu_{{\tilde{C}_{{_{ji} }}^{I} }} ( \, m \, ) \, = \, 1\,$ and $\gamma_{{\tilde{C}_{{_{ji} }}^{I} }} ( \, m \, ) \, = \, 0\,$ exist, where $m$ is the mean value of $\tilde{C}_{{_{ji} }}^{I} .$

• II. If $\mu_{{\tilde{C}_{{_{ji} }}^{I} }} \,$ and $\gamma_{{\tilde{C}_{{_{ji} }}^{I} }}$ are the continuous functions from $\Re$ to the interval $\left[ { \, 0, \, 1 \, } \right]$ and $0 \, \le \mu_{{\tilde{C}_{{_{ji} }}^{I} }} ( \, x \, ) + \gamma_{{\tilde{C}_{{_{ji} }}^{I} }} \,( \, x \, ) \, \le \, 1 \, ,\,\,\forall \, x \, \in \, R, \,$ where

  $$ \mu_{{\tilde{C}_{{_{ji} }}^{I} }} \,( \, x \, ) = \left\{ \begin{array}{ll} g_{1} (x) \, , &\quad \, m - \Delta_{{C_{ji} }} \le x < m \hfill \\ 1, &\quad \, x = \, m \hfill \\ h_{1} \, ( \, x \, ) \, , &\quad m \, < \, x \, \le \, m \, + \, \nabla_{{C_{ji} }} \hfill \\ 0 \, , &\quad {\text{ otherwise}} \hfill \\ \end{array} \right. $$

and

$$ \gamma_{{\tilde{C}_{{_{ji} }}^{I} }} \,( \, x \, ) \, = \, \left\{ \begin{array}{ll} g_{2} \, ( \, x \, ) \, , &\quad m \, - \, \Delta_{{C_{ji} }}^{^{\prime}} \le \, x \, < \, m \, ;\,\,0 \le \, g_{1} \, ( \, x \, ) \, + \, g_{2} \, ( \, x \, ) \, \le \, 1 \hfill \\ 1 \, , &\quad x = \, m \hfill \\ h_{2} ( \, x \, ) \, , &\quad \, m \, < x \le m + \nabla_{{C_{ji} }}^{^{\prime}} ;\,\,0 \, \le \, h_{1} \, ( \, x \, ) \, + \, h_{2} \, ( \, x \, ) \, \le \, 1 \hfill \\ 0 , &\quad {\text{ otherwise}} \hfill \\ \end{array} \right. $$

where m is the mean of IFN $\tilde{C}_{{_{ji} }}^{I}$, $(\Delta_{{C_{ji} }} ,\nabla_{{C_{ji} }} )$ and $(\Delta_{{C_{ji} }}^{^{\prime}} ,\nabla_{{C_{ji} }}^{^{\prime}} )$ are spread over to the left and the right of the linear member function (LMF)$\mu_{{\tilde{C}_{{_{ji} }}^{I} }} (x)\,$ and nonlinear member function (NLMF)$\gamma_{{\tilde{C}_{{_{ji} }}^{I} }} (x)\,,$ respectively. The symbols $g_{1}$ and $h_{1}$ are continuous functions where $g_{1}$ and $h_{1}$ increase and decrease strictly in the interval $[m - \Delta_{{C_{ji} }} \, , \, m)$, $(m \, , \, m + \Delta_{{C_{ji} }} ]$ and $[m - \Delta_{{C_{ji} }}^{^{\prime}} ,m]$ and $[m,m + \Delta_{{C_{ji} }}^{^{\prime}} ]$, respectively. Therefore, the IFN can be defined as $\tilde{C}_{{_{ji} }}^{I} = (m \, ;\, \, \Delta_{{C_{ji} }} ,\nabla_{{C_{ji} }} \, ; \, \Delta_{{C_{ji} }}^{^{\prime}} ,\nabla_{{C_{ji} }}^{^{\prime}} ).$

Triangular IFN

Let $\tilde{C}_{{_{ji} }}^{I} = \{ \, (\phi_{{C_{ji} }} \, , \, m_{{C_{ji} }} \, , \, \phi_{{C_{ji} }} )\, \, ; \, (\theta_{{C_{ji} }} \, , \, m_{{C_{ji} }} \, , \, \vartheta_{{C_{ji} }} ) \, \} ,$ $\forall \, \theta_{{C_{ji} }} \le \, \phi_{{C_{ji} }} \le \, m_{{C_{ji} }} \le \, \varphi_{{C_{ji} }} \le \, \vartheta_{{C_{ji} }}$ is triangular IFN with LMF $\mu_{{\tilde{C}_{{_{ji} }}^{I} }} \,$ and NLMF $\gamma_{{\tilde{C}_{{_{ji} }}^{I} }}$ at $(\alpha ,\beta )$ is given as

$$ \mu_{{\tilde{C}_{{_{ji} }}^{I} }} \,(x) = \left\{ \begin{array}{ll} \frac{{x - \varphi_{{C_{ji} }} }}{{m_{{C_{ji} }} - a_{{C_{ji} }} }}, &\quad \varphi_{{S_{k} }} < x \le m_{{C_{ji} }} \hfill \\ 1, & \quad x = m_{{C_{ji} }} \hfill \\ \frac{{\varphi_{{C_{ji} }} - x}}{{\phi_{{C_{ji} }} - m_{{C_{ji} }} }}, &\quad m_{{C_{ji} }} \le x \le \phi_{{C_{ji} }} \hfill \\ 0, &\quad {\text{otherwise}} \hfill \\ \end{array} \right. $$

(10)

and

$$ \gamma_{{\tilde{C}_{{_{ji} }}^{I} }} \,(x) = \left\{ \begin{array}{ll} \frac{{m_{{C_{ji} }} - x}}{{m_{{C_{ji} }} - \theta_{{C_{ji} }} }}, & \quad \theta_{{C_{ji} }} < x \le m_{{C_{ji} }} \,\, \hfill \\ 1, &\quad x = m_{{C_{ji} }} \hfill \\ \frac{{x - m_{{C_{ji} }} }}{{\vartheta_{{C_{ji} }} - m_{{C_{ji} }} }}, &\quad m_{{C_{ji} }} \le x < \vartheta_{{C_{ji} }} \, \hfill \\ 0, &\quad {\text{otherwise}} \hfill \\ \end{array} \right. $$

(11)

Then, its LMF and NLMF can be expressed as.

$L_{{\mu_{{C_{ji} }} }} ( \, x \, ) = \frac{{x - \phi_{{C_{ji} }} }}{{m_{{C_{ji} }} - \phi_{{C_{ji} }} }}, \, \phi_{{C_{ji} }} \le x \le m_{{C_{ji} }}$ and $R_{{\mu_{{C_{ji} }} }} ( \, x \, ) = \frac{{\phi_{{C_{ji} }} - x}}{{\phi_{{C_{ji} }} - m_{{C_{ji} }} }}, \, m_{{C_{ji} }} \le x \le \phi_{{C_{ji} }}$.

$L_{{\gamma_{{C_{ji} }} }} ( \, x \, ) = \frac{{m_{{C_{ji} }} - x}}{{m_{{C_{ji} }} - \theta_{{C_{ji} }} }}, \, \theta_{{C_{ji} }} \le x \le m_{{C_{ji} }}$ and $R_{{\gamma_{{C_{ji} }} }} ( \, x \, ) = \frac{{x - m_{{C_{ji} }} }}{{\vartheta_{{C_{ji} }} - m_{{C_{ji} }} }}, \, m_{{C_{ji} }} \le x \le \vartheta_{{C_{ji} }}$.

The $L^{ - 1}$ and $R^{ - 1}$ are inverse functions and can be expressed analytically as

$$ L_{{\mu_{{C_{ji} }} }}^{ - 1} ( \, h \, ) = \phi_{{C_{ji} }} + (m_{{C_{ji} }} - \phi_{{C_{ji} }} ) \, h \, , R_{{\mu_{{C_{ji} }} }}^{ - 1} ( \, h \, ) = \phi_{{C_{ji} }} - (\phi_{{C_{ji} }} - m_{{C_{ji} }} ) \, h $$

$$ L_{{\gamma_{{C_{ji} }} }}^{ - 1} ( \, h \, ) = m_{{C_{ji} }} - (m_{{C_{ji} }} - \theta_{{C_{ji} }} ) \, h \, , R_{{\gamma_{{C_{ji} }} }}^{ - 1} ( \, h \, ) = m_{{C_{ji} }} + (\vartheta_{{C_{ji} }} - m_{{C_{ji} }} ) \, h $$

The resultant value of LMF for $\tilde{C}_{{_{ji} }}^{I}$ at $\alpha$ is

$$ \begin{aligned} P_{{\mu_{{C_{ji} }} }} \left( {\tilde{C}_{{_{ji} }}^{I} } \right) &= \frac{{\int\nolimits_{0}^{1} {h\left[ {\alpha \left( {\phi_{{C_{ji} }} + (m_{{C_{ji} }} - \phi_{{C_{ji} }} )h} \right) + (1 - \alpha )\left( {\phi_{{C_{ji} }} - (\phi_{{C_{ji} }} - m_{{C_{ji} }} )h} \right)} \right]dh} }}{{\int\nolimits_{0}^{1} {h\,dh} }} \hfill \\ &= \frac{{\left[ {\frac{{\phi_{{C_{ji} }} \alpha h^{2} }}{2} + \frac{{\alpha (m_{{C_{ji} }} - \phi_{{C_{ji} }} )h^{3} }}{3} + \frac{{(1 - \alpha )\phi_{{C_{ji} }} h^{2} }}{2} - \frac{{(1 - \alpha )(\phi_{{C_{ji} }} - m_{{C_{ji} }} )h^{3} }}{3}} \right]_{0}^{1} }}{{\left[ {\frac{{h^{2} }}{2}} \right]_{0}^{1} }}\hfill \\ &= \frac{{\alpha (\phi_{{C_{ji} }} - \phi_{{C_{ji} }} ) + \phi_{{C_{ji} }} + 2m_{{C_{ji} }} }}{3} \end{aligned} $$

(12)

The resultant value of NLMF for $\tilde{C}_{{_{ji} }}^{I}$ at $\beta$ is:

$$ \begin{aligned} P_{{\gamma_{{C_{ji} }} }} \left( {\tilde{C}_{{_{ji} }}^{I} } \right) &= \frac{{\int\nolimits_{0}^{1} {h\left[ {\beta \left( {m_{{C_{ji} }} - (m_{{C_{ji} }} - \theta_{{C_{ji} }} )h} \right) + (1 - \beta )\left( {m_{{C_{ji} }} + (\vartheta_{{C_{ji} }} - m_{{C_{ji} }} )h} \right)} \right]dh} }}{{\int\nolimits_{0}^{1} {h\,dh} }}\hfill \\ &= \frac{{\left[ {\frac{{\beta m_{{C_{ji} }} h^{2} }}{2} - \frac{{\beta (m_{{C_{ji} }} - \theta_{{C_{ji} }} )h^{3} }}{3} + \frac{{(1 - \beta )m_{{C_{ji} }} h^{2} }}{2} + \frac{{(1 - \beta )(\vartheta_{{C_{ji} }} - m_{{C_{ji} }} )h^{3} }}{3}} \right]_{0}^{1} }}{{\left[ {\frac{{h^{2} }}{2}} \right]_{0}^{1} }} \hfill \\ &= \frac{{2\beta (\theta_{{C_{ji} }} - \vartheta_{{C_{ji} }} ) + m_{{C_{ji} }} + 2\vartheta_{{C_{ji} }} }}{3} \end{aligned} $$

(13)

The magnitude of LMF and NLMF for $\tilde{C}_{{_{ji} }}^{I}$ at $(\alpha ,\beta )$ can be expressed as

$$ P\left( {\tilde{C}_{{_{ji} }}^{I} } \right) = \left[ {\frac{{\alpha (\phi_{{C_{ji} }} - \phi_{{C_{ji} }} ) + \phi_{{C_{ji} }} + 2m_{{C_{ji} }} }}{3},\frac{{2\beta (\theta_{{C_{ji} }} - \vartheta_{{C_{ji} }} ) + m_{{C_{ji} }} + 2\vartheta_{{C_{ji} }} }}{3}} \right] $$

(14)

These assumptions are also valid in the case of intuitionistic fuzzy parameters (IFP), that is, $\tilde{C}_{{_{il} }}^{I} ,$ $\tilde{C}_{{_{ik} }}^{I} ,\, \, \tilde{C}_{{_{lk} }}^{I} ,$ $\tilde{T}_{{_{il} }}^{I} , \, \tilde{T}_{{_{ik} }}^{I} \,, \, \tilde{T}_{{_{lk} }}^{I} , \, \tilde{B}_{{_{j} }}^{I} \,\,{\text{ and }}\,\,\tilde{D}_{{_{k} }}^{I}$ respectively. Using the above procedures for converting triangular IFN for other intuitionistic fuzzy parameters, model (1) is restated as its crisp equivalent considering LMF as follows:

Model (1a)

[1st level]

$$ \mathop {\min \,}\limits_{{P_{ji} }} \,\left( \begin{aligned} \,\left( {\tilde{Z}_{11} } \right)_{\alpha } &= \sum\limits_{j = 1}^{J} {\sum\limits_{i = 1}^{I} {\left( {\frac{{\alpha (\phi_{{C_{ji} }} - \phi_{{C_{ji} }} ) + \phi_{{C_{ji} }} + 2m_{{C_{ji} }} }}{3}} \right) \, P_{ji} + \sum\limits_{i = 1}^{I} {\sum\limits_{k = 1}^{K} {\left( {\frac{{\alpha (\phi_{{C_{ik} }} - \phi_{{C_{ik} }} ) + \phi_{{C_{ik} }} + 2m_{{C_{ik} }} }}{3}} \right) \, R_{ik} } } } } \hfill \\ \,\left( {\tilde{Z}_{12} } \right)_{\alpha } &= \sum\limits_{j = 1}^{J} {\sum\limits_{i = 1}^{I} {\left( {\frac{{\alpha (\phi_{{C_{ji} }} - \phi_{{C_{ji} }} ) + \phi_{{C_{ji} }} + 2m_{{C_{ji} }} }}{3}} \right) \, P_{ji} + \sum\limits_{i = 1}^{I} {\sum\limits_{l = 1}^{L} {\left( {\frac{{\alpha (\phi_{{C_{il} }} - \phi_{{C_{il} }} ) + \phi_{{C_{il} }} + 2m_{{C_{il} }} }}{3}} \right) \, Q_{il} } } } } \hfill \\ \,\left( {\tilde{Z}_{13} } \right)_{\alpha }& = \sum\limits_{j = 1}^{J} {\sum\limits_{i = 1}^{I} {\left( {\frac{{\alpha (\phi_{{C_{ji} }} - \phi_{{C_{ji} }} ) + \phi_{{C_{ji} }} + 2m_{{C_{ji} }} }}{3}} \right) \, P_{ji} + \sum\limits_{i = 1}^{I} {\sum\limits_{l = 1}^{L} {\left( {\frac{{\alpha (\phi_{{C_{il} }} - \phi_{{C_{il} }} ) + \phi_{{C_{il} }} + 2m_{{C_{il} }} }}{3}} \right) \, Q_{il} } } } } \hfill \\ & + \sum\limits_{l = 1}^{L} { \, \sum\limits_{k = 1}^{K} {\left( {\frac{{\alpha (\phi_{{C_{lk} }} - \phi_{{C_{lk} }} ) + \phi_{{C_{lk} }} + 2m_{{C_{lk} }} }}{3}} \right)} } \, S_{lk} \hfill \\ \end{aligned} \right) $$

where $Q_{il} ,R_{ik} ,S_{lk}$ solves.

[2nd level]

$\mathop {\min }\limits_{{X_{kj} ,Y_{ki} ,Z_{ji} }} \,\,\,\left( \begin{aligned} \left( {\tilde{Z}_{21} } \right)_{\alpha } &= \sum\limits_{i = 1}^{I} { \, \sum\limits_{k = 1}^{K} {\left( {\frac{{\alpha (\phi_{{T_{ik} }} - \phi_{{T_{ik} }} ) + \phi_{{T_{ik} }} + 2m_{{T_{ik} }} }}{3}} \right) \, R_{ik} } } + \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} {\left( {\frac{{\alpha (\phi_{{T_{il} }} - \phi_{{T_{il} }} ) + \phi_{{T_{il} }} + 2m_{{T_{il} }} }}{3}} \right) \, Q_{il} } } \hfill \\ \left( {\tilde{Z}_{22} } \right)_{\alpha } &= \sum\limits_{i = 1}^{I} { \, \sum\limits_{k = 1}^{K} {\left( {\frac{{\alpha (\phi_{{T_{ik} }} - \phi_{{T_{ik} }} ) + \phi_{{T_{ik} }} + 2m_{{T_{ik} }} }}{3}} \right) \, R_{ik} } } + \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} {\left( {\frac{{\alpha (\phi_{{T_{il} }} - \phi_{{T_{il} }} ) + \phi_{{T_{il} }} + 2m_{{T_{il} }} }}{3}} \right) \, Q_{il} } } \hfill \\ &\quad + \sum\limits_{l = 1}^{L} { \, \sum\limits_{k = 1}^{K} {\left( {\frac{{\alpha (\phi_{{T_{lk} }} - \phi_{{T_{lk} }} ) + \phi_{{T_{lk} }} + 2m_{{T_{lk} }} }}{3}} \right) \, S_{lk} } } \hfill \\ \end{aligned} \right)$Constraint

$$ \begin{aligned} & \sum\limits_{i = 1}^{I} { \, P_{ji} \le \left( {\frac{{\alpha (\phi_{{B_{j} }} - \phi_{{B_{j} }} ) + \phi_{{B_{j} }} + 2m_{{B_{j} }} }}{3}} \right)} \, , \quad \,\forall \, j \, \hfill \\ & \sum\limits_{k = 1}^{K} { \, R_{ik} + \, \sum\limits_{l = 1}^{L} { \, Q_{il} \, \le \, A_{i} \, , \quad,\,\forall \, i \, } } \hfill \\ & \sum\limits_{k = 1}^{K} { \, S_{lk} \, \le \, V_{l} \, , \quad \,\forall \, l \, } \hfill \\ \end{aligned} $$

$$ \begin{aligned} &\sum\limits_{l = 1}^{L} { \, S_{lk} + \sum\limits_{i = 1}^{I} { \, R_{ik} \, \ge \, \left( {\frac{{\alpha \, (\phi_{{D_{k} }} - \phi_{{D_{k} }} ) \, + \, \phi_{{D_{k} }} \, + \, 2 \, m_{{D_{k} }} }}{3}} \right)} } \, , \, \forall \, k \hfill \\ & \sum\limits_{j = 1}^{J} { \, P_{ji} \, \ge \, \sum\limits_{l = 1}^{L} { \, Q_{il} \, + \, \sum\limits_{k = 1}^{K} { \, R_{ik} } \, } } , \quad \forall \, i \hfill \\ & \sum\limits_{i = 1}^{I} { \, Q_{il} \, \ge \, \sum\limits_{k = 1}^{K} { \, S_{lk} \, , \quad \forall \, l} } \hfill \\ \end{aligned} $$

$\begin{aligned} P_{ji} \, \ge \, 0 \, ,\,\,\, \, \forall \, j, \, i \hfill \\ Q_{il} \, \ge \, 0 \, ,\,\,\, \, \forall \, i, \, l \hfill \\ R_{ik} \, \ge \, 0 \, ,\,\,\,\, \, \,\forall \, i, \, k \hfill \\ S_{lk} \, \ge \, 0 \, ,\,\,\, \, \, \, \,\forall \, l, \, k \hfill \\ \end{aligned}$.

Identically, the crisp equivalent for Model (1) with NLMF can be presented as follows:

Model (1b)

[1st level]

$$ \mathop {\min \,}\limits_{{P_{ji} }} \,\left( \begin{aligned} \,\left( {\tilde{Z}_{11} } \right)_{\beta } &= \sum\limits_{j = 1}^{J} { \, \sum\limits_{i = 1}^{I} {\left( {\frac{{2\beta (\theta_{{C_{ji} }} - \vartheta_{{C_{ji} }} ) + m_{{C_{ji} }} + 2\vartheta_{{C_{ji} }} }}{3}} \right) \, P_{ji} + \sum\limits_{i = 1}^{I} { \, \sum\limits_{k = 1}^{K} {\left( {\frac{{2\beta (\theta_{{C_{ik} }} - \vartheta_{{C_{ik} }} ) + m_{{C_{ik} }} + 2\vartheta_{{C_{ik} }} }}{3}} \right)R_{ik} } } } } \hfill \\ \,\left( {\tilde{Z}_{12} } \right)_{\beta }& = \sum\limits_{j = 1}^{J} { \, \sum\limits_{i = 1}^{I} {\left( {\frac{{2\beta (\theta_{{C_{ji} }} - \vartheta_{{C_{ji} }} ) + m_{{C_{ji} }} + 2\vartheta_{{C_{ji} }} }}{3}} \right) \, P_{ji} + \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} {\left( {\frac{{2\beta (\theta_{{C_{il} }} - \vartheta_{{C_{il} }} ) + m_{{C_{il} }} + 2\vartheta_{{C_{il} }} }}{3}} \right) \, Q_{il} } } } } \hfill \\ \,\left( {\tilde{Z}_{13} } \right)_{\beta } &= \sum\limits_{j = 1}^{J} { \, \sum\limits_{i = 1}^{I} {\left( {\frac{{2\beta (\theta_{{C_{ji} }} - \vartheta_{{C_{ji} }} ) + m_{{C_{ji} }} + 2\vartheta_{{C_{ji} }} }}{3}} \right) \, P_{ji} + \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} {\left( {\frac{{2\beta (\theta_{{C_{il} }} - \vartheta_{{C_{il} }} ) + m_{{C_{il} }} + 2\vartheta_{{C_{il} }} }}{3}} \right) \, Q_{il} } } } } \hfill \\ \&\quad + \sum\limits_{l = 1}^{L} { \, \sum\limits_{k = 1}^{K} {\left( {\frac{{2\beta (\theta_{{C_{lk} }} - \vartheta_{{C_{lk} }} ) + m_{{C_{lk} }} + 2\vartheta_{{C_{lk} }} }}{3}} \right)} } \, S_{lk} \hfill \\ \end{aligned} \right) $$

where $Q_{il} ,R_{ik} ,S_{lk}$ solve.

[2nd level]

$$ \mathop {\min }\limits_{{Q_{il} ,R_{ik} ,S_{lk} }} \,\,\,\left( \begin{aligned} \left( {\tilde{Z}_{21} } \right)_{\beta } &= \sum\limits_{i = 1}^{I} { \, \sum\limits_{k = 1}^{K} {\left( {\frac{{2\beta (\theta_{{T_{ik} }} - \vartheta_{{T_{ik} }} ) + m_{{T_{ik} }} + 2\vartheta_{{T_{ik} }} }}{3}} \right) \, R_{ik} } } + \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} {\left( {\frac{{2\beta (\theta_{{T_{il} }} - \vartheta_{{T_{il} }} ) + m_{{T_{il} }} + 2\vartheta_{{T_{il} }} }}{3}} \right) \, Q_{il} } } \hfill \\ \left( {\tilde{Z}_{22} } \right)_{\beta } &= \sum\limits_{i = 1}^{I} { \, \sum\limits_{k = 1}^{K} {\left( {\frac{{2\beta (\theta_{{T_{ik} }} - \vartheta_{{T_{ik} }} ) + m_{{T_{ik} }} + 2\vartheta_{{T_{ik} }} }}{3}} \right) \, R_{ik} } } + \sum\limits_{i = 1}^{I} { \, \sum\limits_{l = 1}^{L} {\left( {\frac{{2\beta (\theta_{{T_{il} }} - \vartheta_{{T_{il} }} ) + m_{{T_{il} }} + 2\vartheta_{{T_{il} }} }}{3}} \right) \, Q_{il} } } \hfill \\ &\quad + \sum\limits_{l = 1}^{L} { \, \sum\limits_{k = 1}^{K} {\left( {\frac{{2\beta (\theta_{{T_{lk} }} - \vartheta_{{T_{lk} }} ) + m_{{T_{lk} }} + 2\vartheta_{{T_{lk} }} }}{3}} \right) \, S_{lk} } } \hfill \\ \end{aligned} \right) $$

Constraints

$$ \begin{aligned} & \sum\limits_{i = 1}^{I} { \, P_{ji} \, \le \, \left( {\frac{{2 \, \beta \, (\theta_{{B_{j} }} - \vartheta_{{B_{j} }} ) + m_{{B_{j} }} + 2 \, \vartheta_{{B_{j} }} }}{3}} \right)} {,}\,\,\,\,\forall \, j \hfill \\ & \sum\limits_{k = 1}^{K} { \, R_{ik} \, + \, \sum\limits_{l = 1}^{L} { \, Q_{il} \, \le \, A_{i} \, , \quad\forall \, i} } \hfill \\ & \sum\limits_{l = 1}^{L} { \, \sum\limits_{k = 1}^{K} { \, S_{lk} \, \le \, V_{l} \, , \quad,\forall \, l} } \hfill \\ \end{aligned} $$

$$ \begin{aligned} & \sum\limits_{l = 1}^{L} { \, S_{lk} + \sum\limits_{i = 1}^{I} { \, R_{ik} \, \ge \, \left( {\frac{{2 \, \beta \, (\theta_{{T_{k} }} - \vartheta_{{T_{k} }} ) + m_{{T_{k} }} + 2 \, \vartheta_{{T_{k} }} }}{3}} \right)} } \, , \, \forall \, k \hfill \\ & \sum\limits_{j = 1}^{J} { \, P_{ji} \, \ge \, \sum\limits_{l = 1}^{L} { \, Q_{il} + \, \sum\limits_{k = 1}^{K} { \, R_{ik} } } } \, , \quad \forall \, i \hfill \\ & \sum\limits_{i = 1}^{I} { \, Q_{il} \, \ge \, \sum\limits_{k = 1}^{K} { \, S_{lk} \, , \quad \forall \, l} } \hfill \\ \end{aligned} $$

$$ \begin{aligned} P_{ji} \ge \, 0 \, , \, \,\,\,\forall \, j, \, i \hfill \\ Q_{il} \ge \, 0 \, ,\,\, \, \, \, \forall \, i, \, l \hfill \\ R_{ik} \ge \, 0 \, ,\,\,\,\,\, \, \forall \, i, \, k \, \hfill \\ S_{lk} \ge \, 0 \, ,\,\,\,\,\, \, \forall \, l, \, k \hfill \\ \end{aligned} $$

The above-formulated BL-MOSCN model with an intuitionistic fuzzy parameter becomes deterministic at a distinct value of $\alpha \in [0,1]$ and $\beta \in [0,1][0,1]$. After that, the problem was solved using the FGP approach. FGP expands standard goal programming in a decision-making environment to address multi-objective problems with imprecise model parameters. Instead of evaluating the accomplishment of blurred objective values directly, it is already considered in a solution search method to achieve goal membership values of the highest possible degree (unity) by minimizing under deviations. The FGP method's literature lists several contributions [9, 36, 41, 69, 70]. The FGP method is then used to create a practical methodology based on all these studies to solve multi-objective programming problems. Step-by-step procedures are given to solve the formulated BL-MOSCN problem after some manipulations in the FGP method. Following are the steps:

Step 1: First, formulate the BL-MOSCN problem under IFP.

Step 2 Use the classification procedure to transform the IFP of the BL-MOSCN problem to an appropriate deterministic form. Using Eq. (12), formulate the equivalent deterministic form for the BL-MOSCN problem of the model (1) in which IFN has been obtained in LMF form. Similarly, when it is in NLMF form, the consequence of identical deterministic model (1) of BL-MOSCN problem can be obtained from Eq. (13).

Step 3: Step 2 obtains BL-MOSCN’s two equally deterministic models: Models 1a and 1b. Initially, Models 1a and 1b are solved with only one goal function for the different values of $\alpha \in \left[ {0, \, 1} \right]$ and $\beta \in \left[ {0, \, 1} \right]$, respectively, ignoring other goals. Thus, the ideal solutions are obtained, which helps the DM determine the level of aspirations for individual goals; that is, the best ideal solution (individual minimum) $\left( {g_{kl} } \right)_{\alpha }$ and $\left( {g_{kl} } \right)_{\beta }$ for the two-level DMs can be presented as

$$ \left. \begin{aligned} & {\text{Min FLDM }}\,\,\left( {g_{1l} } \right)_{\alpha } = \,\left( { \, \left( { \, \tilde{Z}_{1l} ( \, x \, ) \, } \right)_{\alpha } \, } \right)\,\,, \, & \, l \, = 1, \, 2, \, 3 \hfill \\ &{\text{Min SLDM }}\left( {g_{2l} } \right)_{\alpha } = \left( { \, \left( { \, \tilde{Z}_{2l} ( \, x \, ) \, } \right)_{\alpha } \, } \right) \, ,\,\,\,\, \, l \, = 1,2 \hfill \\ \end{aligned} \right\} $$

(15)

and

$$ \left. \begin{aligned} & {\text{Min FLDM}}\,\,\,\left( {g_{1l} } \right)_{\beta } = \, \, \left( {\left( { \, \tilde{Z}_{1l} \, ( \, x \, ) \, } \right)_{\beta } \, } \right)\,\,, & \, l \, = 1, \, 2, \, 3 \hfill \\ & {\text{Min SLDM }}\left( {g_{2l} } \right)_{\beta } = \left( { \, \left( { \, \tilde{Z}_{2l} \, ( \, x \, ) \, } \right)_{\beta } \, } \right) \, ,\,\,\,\, \, l = 1, \, 2 \hfill \\ \end{aligned} \right\} $$

(16)

Similarly, let the worst individual solution (maximum) for both the FLDM and SLDM be $\left( {u_{kl} } \right)_{\alpha }$ and $\left( {u_{kl} } \right)_{\beta }$, respectively, and determine them as follows:

$$ \left. \begin{aligned} & {\text{Max FLDM }}\,\,\left( {u_{1l} } \right)_{\alpha } = \left( { \, \left( { \, \tilde{Z}_{1l} \, ( \, x \, ) \, } \right)_{\alpha } \, } \right)\,, & \, l = 1, \, 2, \, 3\, \hfill \\ & {\text{Max SLDM}}\,\,\,\left( {u_{2l} } \right)_{\alpha } = \left( { \, \left( { \, \tilde{Z}_{2l} ( \, x \, ) \, } \right)_{\alpha } } \right) \, , & \, l = 1, \, 2 \hfill \\ \end{aligned} \right\} $$

(17)

and

$$ \left. \begin{aligned} & {\text{Max FLDM}}\,\,\,\left( {u_{1l} } \right)_{\beta } = \, \left( { \, \left( { \, \tilde{Z}_{1l} ( \, x \, )} \right)_{\beta } \, } \right)\,, & \, l = 1, \, 2, \, 3\, \hfill \\ & {\text{Max SLDM}}\,\,\,\left( {u_{2l} } \right)_{\beta } = \left( { \, \left( { \, \tilde{Z}_{2l} ( \, x \, ) \, } \right)_{\beta } } \right) \, , & \, l = 1, \, 2 \hfill \\ \end{aligned} \right\} $$

(18)

Let $P_{ji}^{*} ,Q_{il}^{*} ,R_{ik}^{*} ,S_{lk}^{*}$ be the optimal values for both levels of the DM’s objective function, and let $\left( {g_{1l} } \right)_{\alpha } \ge \left( { \, \tilde{Z}_{1l} (x)} \right)_{\alpha } , \, l = \, 1, \, 2, \, 3$ be the aspiration limit for the first-level goal function and $\left( {g_{2l} } \right)_{\alpha } \ge \left( { \, \tilde{Z}_{2l} (x) \, } \right)_{\alpha } \, , \, l = 1, \, 2$ be the second level objective function. If the values of goal functions are higher than $\left( {u_{1l} } \right)_{\alpha }$, then they unacceptable. When $\left( {u_{1l} } \right)_{\alpha }$ is the fuzzy upper limit tolerance goal for the first level goal function, the membership function can be represented as follows:

$$ \mu_{{(\tilde{Z}_{1l} (x))}} = \left\{ \begin{array}{ll} 1, & \quad if\, \, \left( {\tilde{Z}_{1l} ( \, x \, )} \right)_{\alpha } \, \le \,\left( {g_{1l} } \right)_{\alpha } \hfill \\ \frac{{\left( {u_{1l} } \right)_{\alpha } - \left( {\tilde{Z}_{1l} (x)} \right)_{\alpha } }}{{\left( {u_{1l} } \right)_{\alpha } - \left( {g_{1l} } \right)_{\alpha } }}, & \quad if\left( {g_{1l} } \right)_{\alpha } \le \left( {\tilde{Z}_{1l} (x)} \right)_{\alpha } \le \left( {u_{1l} } \right)_{\alpha } \hfill \\ 0, & \quad if\,\left( {\tilde{Z}_{1l} (x)} \right)_{\alpha } \ge \left( {u_{1l} } \right)_{\alpha } \, \hfill \\ \end{array} \right. $$

(19)

For the first level, [$l = 1,2,3$ and $k = 1$] and identically, the membership function for the second level [$l = 1,2$ and $k = 2$] has been constructed as follows (Fig. 3).

Fig. 3

Membership function for minimization type goal function

The final FGP model for the first level is:

$$ {\text{Min}} \sum\limits_{l = 1}^{3} {w_{1l} d_{1l}^{ + } } $$

Subject to the constraints

$$ \frac{{\left( { \, u_{1l} \, } \right)_{\alpha } - \, \left( { \, \tilde{Z}_{1l} (x) \, } \right)_{\alpha } }}{{\left( { \, u_{1l} \, } \right)_{\alpha } \, - \, \left( { \, g_{1l} } \right)_{\alpha } }} + d_{1l}^{ - } - d_{1l}^{ + } = 1 \, ,\,\,\,l = 1, \, 2, \, 3 $$

$$ \,d_{1l}^{ - } , \, d_{1l}^{ + } \, \ge \, 0\,{\text{ with }}\,\,d_{1l}^{ - } \times \, d_{1l}^{ + } = \, 0 \, ,\,\,\,\,j = 1, \, 2, \, 3\, $$

and all sets of constraints of Model 1(a).

Where $d_{1l}^{ - } , \, d_{1l}^{ + } \, \ge \, 0 \, ,\,\,l = 1, \, 2, \, 3$ are used for the deviations resulting from the underachievement and overachievement of the DM's goal and $w_{1l}$ is the weight for each goal function. The following criteria are used for the relative importance of deviations to the target value. That is $w_{1l} = \, \frac{1}{{\left( {u_{1l} } \right)_{\alpha } - \left( {g_{1l} } \right)_{\alpha } }} \, ,\,\,l = \, 1, \, 2, \, 3.$, the FGP has been applied to model (1b) and solved for the different values of $\alpha \in [0,1].$ FLDM’s solution helps set extreme positive and negative tolerance limits for the controllable parameters under the FLDM.

Step 4: Let $t^{L} \,\& \,t^{R}$ be the left and right tolerances and not be undoubtedly identical. The tolerance limit helps allow the SLDM to expand the feasible space to find an ideal solution. The tolerance value can be increased within the feasible space to obtain satisfactory solutions (Fig. 4).

Fig. 4

Membership function for the decision vector

The linear membership function of the decision vector is

$$ \mu (P_{ji} ) = \left\{ \begin{array}{ll} \frac{{P_{ji}^{*} - \, ( \, P_{ji}^{*} \, - \, t^{L} \, )}}{{t^{L} }} \, , & \quad {\text{if }}\,\,P_{ji}^{*} - \, t^{L} \, \le \, x_{i} \, \le \, P_{ji}^{*} \hfill \\ \hfill \\ \frac{{( \, P_{ji}^{*} + \, t^{R} \, ) - \, P_{ji}^{*} }}{{t^{R} }} \, , & \quad {\text{if}}\,\,P_{ji}^{*} \, \le \, x_{i} \, \le \, P_{ji}^{*} \, + \, t^{R} \hfill \\ 0 \, ,& \quad {\text{if otherwise}} \hfill \\ \end{array} \right. $$

(20)

where $P_{ji}^{*}$ is the most favorable solution, which linearly increases in intervals $[\,P_{ji}^{*} - t^{L} ,P_{ji} ]$ and linearly decreases $[x_{i} ,x_{i}^{*} + t^{L} ]$. Thus, the decision vector is defined in the form of membership function as:

$$ \mu (P_{ji} ) + d_{ji}^{ - } - d_{ji}^{ + } = 1 $$

(21)

and, alternatively, equivalently as

$$ \left. \begin{aligned} \frac{{P_{ji}^{*} - (P_{ji}^{*} - t^{L} )}}{{t^{L} }} + d_{ji}^{L - } - d_{ji}^{L + } = 1 \hfill \\ \frac{{(P_{ji}^{*} + t^{R} ) - P_{ji} }}{{t^{R} }} + d_{ji}^{R - } - d_{ji}^{R + } = 1 \hfill \\ \end{aligned} \right\} $$

(22)

where $d_{ji}^{ - } \, = \, ( \, d_{ji}^{L - } , \, d_{ji}^{R - } \, ){ ,}$$d_{ji}^{ + } \, = \, (d_{ji}^{L + } , \, d_{ji}^{R + } ){ ,}$ and $d_{ji}^{L - } , \, d_{ji}^{R - } , \, d_{ji}^{L + } , \, d_{ji}^{R + } \, \ge \, 0$ with the following conditions $d_{ji}^{L - } \, \times \, d_{ji}^{L + } = \, 0$ and $d_{ji}^{R - } \, \times \, d_{ji}^{R + } \, = \, 0$ are deviations in respect of over-and underachievement, respectively, from the dream goals.

Step 5: Finally, by considering the priority function, the model for the FGP of the BL-MOSCN problem can be expressed as follows:

$$ {\text{Min}} \sum\limits_{l = 1}^{3} { \, w_{1l} \, d_{1l}^{ + } } \, + \, \sum\limits_{l = 1}^{2} { \, w_{2l} \, d_{2l}^{ + } } + \sum\limits_{j = 1}^{J} {\sum\limits_{i = 1}^{I} { \, [w_{ji}^{L} \, (d_{ji}^{L - } + \, d_{ji}^{L + } ) \, + \, w_{ji}^{R} \, ( \, d_{ji}^{R - } + \, d_{ji}^{R + } \, ) \, ]} } $$

Subject to the set of constraints

$$ \begin{aligned}& \frac{{ \, \left( {u_{1l} \, } \right)_{\alpha } - \, \left( {\tilde{Z}_{1l} \, ( \, x) \, } \right)_{\alpha } }}{{\left( { \, u_{1l} \, } \right)_{\alpha } - \, \left( { \, g_{1l} \, } \right)_{\alpha } }} + d_{1l}^{ - } - d_{1l}^{ + } = 1 \, ,\,\,\,\, \, \,l = 1, \, 2, \, 3 \hfill \\ &\frac{{ \, \left( {u_{2l} } \right)_{\alpha } - \, \left( { \, \tilde{Z}_{2l} \, ( \, x \, ) \, } \right)_{\alpha } }}{{\left( { \, u_{2l} } \right)_{\alpha } \, - \, \left( { \, g_{1l} \, } \right)_{\alpha } }} \, + \, d_{2l}^{ - } \, - \, d_{2l}^{ + } \, = 1 \, ,\,\,\,\,\,l = \, 1, \, 2 \hfill \\ &\mu \, ( \, P_{ji} \, ) \, + \, d_{ji}^{ - } \, - \, d_{ji}^{ + } \, = \, 1 \, ,\,\,\,\,\,\,\,\, \, i = 1, \, 2, \, \ldots , \, I \,\quad \, \, \,\,j = 1, \, 2, \, \ldots , \, J\,\,\,\, \hfill \\ \end{aligned} $$

$$ \begin{aligned}& d_{1l}^{ - } , \, d_{1l}^{ + } \ge \, 0\,\,{\text{ with }}\,\,d_{1l}^{ - } \times d_{1l}^{ + } = \, 0,\,\,\,\,l = \, 1, \, 2, \, 3 \hfill \\ & d_{2l}^{ - } , \, d_{2l}^{ + } \, \ge \, 0\,\,{\text{ with }}\,\,d_{2l}^{ - } \times d_{2l}^{ + } = \, 0,\,\,\,l = \, 1, \, 2 \hfill \\ & d_{ji}^{L + } ,d_{ji}^{L - } \ge 0\,\,{\text{ with }}\,\,d_{ji}^{L + } \times d_{ji}^{L - } = 0\,\,\, \, \hfill \\ & d_{ji}^{R + } ,d_{ji}^{R - } \ge 0\,\,{\text{ with }}\,\,d_{ji}^{R + } \times d_{ji}^{R - } = 0 \hfill \\ \end{aligned} $$

and set of all constraints of Model 1(b).

Where $w_{1l} , \, w_{2l}$ represent the FLDM and SLDM weights, respectively, and $w_{ji}^{L} , \, w_{ji}^{R}$ are the deviational variable importance weights considering the targeted value measurement, that is,

$\,w_{2l} \, = \, \frac{1}{{ \, \left( {u_{2l} \, } \right)_{\alpha }^{U} - \left( { \, g_{2l} \, } \right)_{\alpha }^{L} }},\,\,l \, = 1, \, 2$ and

$$ w_{i}^{L} \, = \, \frac{1}{{t^{L} }}\,\, \, \& \, \,\,\,w_{i}^{R} = \frac{1}{{t^{R} }} $$

(23)

Similarly, the procedure discussed above for model (1a) has been followed for the model (1b) and solved for the different value of $\beta \in [01].$

Numerical illustration

This section draws an outcome based on available data to illustrate the case study. Five vendors are to supply four manufacturing plants with raw materials. The distribution system comprises six different warehouses that store items. The quantitative information used in the numerical illustrations are not real evidence; according to the developed concept, it is simulated. Tables 2, 3, 4, 5, 6, 7, 8, 9 shows the hypothetical data for illustrating the proposed work.

Table 2 Cost of shipment from the suppliers to the plants (in Rs) with intuitionistic fuzziness

Table 3 Cost of shipment from plants to the distributors (in Rs) with intuitionistic fuzziness

Table 4 Cost of shipment from plants to the warehouse (in Rs) with intuitionistic fuzziness

Table 5 Cost of shipment from warehouses to the distributors (in Rs) with intuitionistic fuzziness

Table 6 Time taken for the shipment of products from plants to distributors (in hours) with intuitionistic fuzziness

Table 7 Time taken for the shipment of product from plants to the warehouses (in hours) with intuitionistic fuzziness

Table 8 Time taken for the shipment of product from warehouse to the distributors (in hours) with intuitionistic fuzziness

Table 9 Right-hand side parameters (‘000)

Table 2 shows the shipping cost from various suppliers (i.e., Supplier A, Supplier B, Supplier C, Supplier D, and Supplier E) to various plants (i.e., Plant G₁, Plant G₂, Plant G₃, and Plant G₄) with intuitionistic fuzzy data.

Table 3 shows the shipping cost from various plants (i.e., Plant G₁, Plant G₂, Plant G₃, and Plant G₄) to various distributors (i.e., Distributor M₁, Distributor M₂, Distributor M₃, Distributor M₄, Distributor M₅, Distributor M₆, Distributor M₆, Distributor M₇, and Distributor M₈) with intuitionistic fuzzy data.

Table 4 presents the shipping cost from various plants (i.e., Plant G₁, Plant G₂, Plant G₃, and Plant G₄) to various warehouses (Warehouse N₁, Warehouse N₁, Warehouse N₂, Warehouse N₃, Warehouse N₄, Warehouse N₅, and Warehouse N₆) with intuitionistic fuzzy data.

Table 5 shows the shipping cost from various warehouses (Warehouse N₁, Warehouse N₁, Warehouse N₂, Warehouse N₃, Warehouse N₄, Warehouse N₅, and Warehouse N₆) to various distributors (i.e., Distributor M₁, Distributor M₂, Distributor M₃, Distributor M₄, Distributor M₅, Distributor M₆, Distributor M₆, Distributor M₇, and Distributor M₈) with intuitionistic fuzzy data.

Table 6 shows the delivery time from various plants (i.e., Plant G₁, Plant G₂, Plant G₃, and Plant G₄) to various distributors (i.e., Distributor M₁, Distributor M₂, Distributor M₃, Distributor M₄, Distributor M₅, Distributor M₆, Distributor M₆, Distributor M₇, and Distributor M₈) with intuitionistic fuzzy data.

Table 7 shows the delivery time from various plants (i.e., Plant G₁, Plant G₂, Plant G₃, and Plant G₄) to various warehouses (Warehouse N₁, Warehouse N₁, Warehouse N₂, Warehouse N₃, Warehouse N₄, Warehouse N₅, and Warehouse N₆) with intuitionistic fuzzy data.

Table 8 shows the delivery time from various warehouses (Warehouse N₁, Warehouse N₁, Warehouse N₂, Warehouse N₃, Warehouse N₄, Warehouse N₅, Warehouse N₆) to various distributors (i.e., Distributor M₁, Distributor M₂, Distributor M₃, Distributor M₄, Distributor M₅, Distributor M₆, Distributor M₆, Distributor M₇, and Distributor M₈) with intuitionistic fuzzy data.

Table 9 shows the intuitionistic demand and supply and the fixed capacities of the plant and warehouses.

The proposed work model is solved using LINGO 16.0 software on an Intel Core i3 (6th Generation) with a 1.7 GHz CPU and 4 GB RAM. Solving a mathematics problem involves many equations, and thus a machine system is better to use. The software we have used for solving the mathematical model is LINGO 16.0. LINGO 16.0 is a powerful and flexible software created by LINDO Systems Inc. “LINGO 16.0 is a comprehensive tool designed to make building and to solve linear, nonlinear (convex and non-convex), quadratic, quadratically constrained, stochastic, multi-choice, integer, and multicriteria optimization models faster, easier and more efficiently”. It includes a wholly optimized program with an efficient optimization model platform for problem-solving, and it allows us to find the solution in a minimum of time. In short, the primary purpose of LINGO consists of allowing the programmer to efficiently implement, correct and evaluate the solution's validity or adequacy, and to quickly change a minor formula and repeat the cycle (if needed). The primary edition of LINGO includes a “graphical user interface”, but under some specific cases like operating under Linux (command line functionality) can be used for finding the problem solution.

By utilizing the above data sets, we have formulated the BL-MOSCN problem with intuitionistic fuzzy parameters. At a different value of $\alpha ,\beta \in [0,1]$, the BL-MOSCN problem changes into its deterministic form. The separate minimum and maximum values of the goal functions at each level have been calculated at distinct values of $\alpha ,\beta \in [0,1].$

Case 1 (Model 1a Solution): Model (1a) was solved by the stepwise algorithm given in Sect. 3. To solve the formulated model SCN, we must first calculate the minimum individual solution for each of the objective functions at a distinct value of $\alpha \in [0,1]$. Since the objective functions are minimized, the best value for all objective functions occurred $\alpha = 0.1$. Therefore, the direct minimum transportation cost incurred from various sources to different distributors through multiple plants is 91,244.44. The direct minimum transportation cost incurred from various sources to different warehouses through multiple plants is 100094.4; the direct minimum transportation cost incurred from various sources to different distributors through multiple plants and warehouses is 110,637.4. Furthermore, the minimum delivery time taken from various multiple sources to different warehouses through multiple plants is 14196.11; and the minimum delivery time taken from various sources to different distributors through multiple plants and warehouses is 26,531.11. The minimum range or limit at the different values of $\alpha \in [0,1]$ for Z₁₁ is (91,244.44, 100,544.4); Z₁₂ is (100,094.4, 109,394.4); Z₁₃ is (110,637.4, 112,187.4); Z₂₁ is (14,196.11, 18,195.56); and Z₂₂ is (26,531.11, 30,925.56).

To solve the formulated model SCN, we must also calculate the maximum individual solution for each objective function at distinct values $\alpha \in [0,1]$. Since the objective functions are changed from minimization type to maximization type, all objective functions' best values occurred $\alpha = 0$. Therefore, the direct maximum transportation cost incurred from various sources to different distributors through multiple plants is 1,186,523. The direct minimum transportation cost incurred from various sources to different warehouses through multiple plants is 1,141,732; the direct minimum transportation cost incurred from various sources to different distributors through multiple plants and warehouses is 1,319,107. Furthermore, the minimum delivery time taken from various sources to different warehouses through multiple plants is 120,438.9, and the minimum delivery time taken from various sources to different distributors through multiple plants and warehouses is 142021.7. The maximum range or limit at the different values of $\alpha \in [0,1]$ for Z₁₁ is (1,143,741, 1,186,523); Z₁₂ is (1,102,081, 1,141,732); Z₁₃ is (1,267,964, 1,319,107); Z₂₁ is (112,344.4, 120,438.9); and Z₂₂ is (131,710.6, 142,021.7). Although the selection of all efficient solutions cannot always be achieved in realistic circumstances, DMs favor a compromise solution for the multi-objective functions. Hence, an acceptable solution needs to be a compromise solution. The final solution for the model (1a) is in Table 10. Since the objective functions are of the minimization type, the most probable value for all the objective functions occurred at $\alpha = 0.5$, while the optimistic solution occurred at $\alpha = 1$, and pessimistic solution at $\alpha = 0.$

Table 10 Compromise optimal values with order quantities

Further, we have discussed the different amounts of quantity transported from various sources to different plants, different plants to different distributors, various sources to a different plant, and different warehouses to the various distributors at different values of $\alpha \in [0,1]$. We have categorized the obtained result into three categories that will provide the DM with more ideas about the uncertain situation.

The most probable result in this uncertain situation occurs at $\alpha = 0.5$, in which the direct minimum transportation cost incurred from various multiple sources to different distributors through multiple plants is 264,350. The direct minimum transportation cost incurred from various sources to different warehouses through multiple plants is 256810, and the direct minimum transportation cost incurred from various sources to different distributors through multiple plants and warehouses is 327,946.7. Furthermore, the minimum delivery time taken from various sources to different warehouses through multiple plants is 25,034, and the minimum delivery time taken from various sources to different distributors through multiple plants and warehouses is 359,49.17. The final quantity of finished goods shipped from various multiple plants to various distributors is 272 units. The quantity to be shipped from various multiple plants to warehouses is 406 units, and the quantity to be shipped from various multiple warehouses to various distributors is 370 units.

The favorable result in this uncertain situation occurs at $\alpha = 1$, for which the direct minimum transportation cost incurred from various multiple sources to different distributors through multiple plants is 247,230. The direct minimum transportation cost incurred from various sources to different warehouses through multiple plants is 246,510, and the direct minimum transportation cost incurred from various sources to different distributors through multiple plants and warehouses is 306351.7. Furthermore, the minimum delivery time taken from various sources to different warehouses through multiple plants is 22,710, and the minimum delivery time incurred from various sources to different distributors through multiple plants and warehouses is 33,918. The final finished goods quantity to be shipped from various multiple plants to various distributors is 246 units. The quantity to be shipped from various multiple plants to various warehouses is 372 units, and the quantity to be shipped from various multiple warehouses to various distributors is 351 units.

The pessimistic result in this uncertain situation occurs at $\alpha = 0$, for which the direct minimum transportation cost incurred from the various multiple sources to different distributors through multiple plants is 252,873.3. The direct minimum transportation cost incurred from various sources to different warehouses through multiple plants is 270,046.7, and the direct minimum transportation cost incurred from various sources to different distributors through multiple plants and warehouses is 361,985. Furthermore, the minimum delivery time taken from various sources to different warehouses through multiple plants is 28,683.33, and the minimum delivery time taken from various sources to different distributors through multiple plants and warehouses is 39,933.33. The final finished goods quantity to be shipped from various multiple plants to various distributors is 515 units. The quantity to be shipped from various multiple plants to various warehouses is 384 units, and the quantity to be shipped from various multiple warehouses to various distributors is 305 units (Fig. 5).

Fig. 5

Distinct values of the objective function

Case 2 (Model 1b Solution): Model (1b) has been solved using stepwise algorithms in Sect. 3. To solve the formulated model SCN, we must first calculate the minimum individual solution for each of the objective functions at the distinct values for $\beta \in [0,1]$. Since the objective functions are minimized, the best value for all the objective functions occurred $\beta = 1.0$. Therefore, the direct minimum transportation cost incurred from various sources to different distributors through multiple plants is 78,321.11. The direct minimum transportation cost incurred from various sources to different warehouses through multiple plants is 86,811.11, and the direct minimum transportation cost incurred from various sources to different distributors through multiple plants and warehouses is 90,637.10. Furthermore, the minimum delivery time taken from various sources to different warehouses through multiple plants is 9055, and the minimum delivery time taken from various sources to different distributors through multiple plants and warehouses is 19,048.89. The minimum range or limit at the different values of $\alpha \in [0,1]$ for Z₁₁ is (78,321.11, 115,161.1); Z₁₂ is (86,811.11, 124,011.1); Z₁₃ is (90,637.10, 134,322.1); Z₂₁ is (9055, 23,353.89); and Z₂₂ is (19,048.89, 36,898.89).

To solve the formulated model SCN, we must also calculate the maximum individual solution for each objective function at distinct values $\beta \in [0,1]$. Since the objective functions are changed from minimization type to maximization type, the best value for all the objective functions occurred at $\beta = 0$. Therefore, the direct maximum transportation cost incurred from various sources to different distributors through multiple plants is 1,239,163. The direct minimum transportation cost incurred from various sources to different warehouses through multiple plants is 1,196,386, and the direct minimum transportation cost incurred from various sources to different distributors through multiple plants and warehouses is 1,393,028. Furthermore, the minimum delivery time taken from various sources to different warehouses through multiple plants is 131,873.3, and the minimum delivery time taken from various sources to different distributors through multiple plants and warehouses is the same 156,731.7. The maximum range or limit at the different values of $\alpha \in [0,1]$ for Z₁₁ is (1,105,630, 1,239,163), Z₁₂ is (1,196,386, 1,066,083), Z₁₃ is (1,219,673, 1,393,028), Z₂₁ is (106,083.3, 131,873.3), and Z₂₂ is (119,960, 156,731.7). Although selecting all efficient solutions cannot always be achieved in realistic circumstances, a compromise solution seems to be a solution favored by the DM for the multi-objective functions. Hence, an acceptable solution needs to be a compromise solution. The final solution for the model (1b) is given in Table 11. Since the objective functions are of minimization type, the most probable value for all the objective functions occurred at $\beta = 0.5$, while the optimistic solution occurred at $\beta = 1$, and pessimistic solution at $\beta = 0.$

Table 11 Compromise optimal objective values

Further, we have discussed the different amounts of quantity transported from various sources to different plants, different plants to different distributors, various sources to different plants, and different warehouses to different distributors at different values $\beta \in [0,1]$. We have categorized the obtained result into three categories that provide the DM with more ideas about the uncertain situation.

The most probable result in this uncertain situation occurs when the direct minimum transportation cost incurred from various sources to different distributors through multiple plants is 275,860. The direct minimum transportation cost incurred from various sources to different warehouses through multiple plants is 262,526.7, and the direct minimum transportation cost incurred from various sources to different distributors through multiple plants and warehouses is 342,715. Furthermore, the minimum delivery time taken from various sources to different warehouses through multiple plants is 25,211.67, and the minimum delivery time taken from various sources to different distributors through multiple plants and warehouses is 37,151.67. The final quantity of finished goods shipped from various multiple plants to various distributors is 272 units. The quantity to be shipped from various multiple plants to various warehouses is 435 units, and the quantity to be shipped from various multiple warehouses to various distributors is 426 units.

The favorable result in this uncertain situation occurs at $\beta = 1$, and the direct minimum transportation cost incurred from various sources to different distributors through multiple plants is 257,280. The direct minimum transportation cost incurred from various sources to different warehouses through multiple plants is 244,506.7, and the direct minimum transportation cost incurred from various sources to different distributors through multiple plants and warehouses is 302,898.3. Furthermore, the minimum delivery time taken from various sources to different warehouses through multiple plants is 21,588.33; and the minimum delivery time taken from various sources to different distributors through multiple plants and warehouses is 30,180. The final finished goods quantity to be shipped from various multiple plants to various distributors is 343 units. The quantity to be shipped from various multiple plants to various warehouses is 298 units, and the quantity to be shipped from various multiple warehouses to various distributors is 292 units.

The pessimistic result in this uncertain situation occurs at $\beta = 0$, for which the direct minimum transportation cost incurred from various multiple sources to different distributors through multiple plants is 322,266.7. The direct minimum transportation cost incurred from various sources to different warehouses through multiple plants is 320,553.3, and the direct minimum transportation cost incurred from various sources to different distributors through multiple plants and warehouses is 412,073.3. Furthermore, the minimum delivery time taken from various sources to different warehouses through multiple plants is 39,956.67, and the minimum delivery time taken from various sources to different distributors through multiple plants and warehouses is 56,176.67. The final finished goods quantity to be shipped from various multiple plants to various distributors is 260 units. The quantity to be shipped from various multiple plants to various warehouses is 460 units, and the quantity to be shipped from various multiple warehouses to various distributors is 452 units (Fig. 6).

Fig. 6

Different values of the objective function

The results show that this approach with efficient solutions gives more compatible results than the existing ones. Consequently, the solutions obtained at distinct $\alpha \,\,{\text{and}}\,\,\beta$ values help the DM select the maximum value that optimizes the problem as per the weight defined. Accurately, $\alpha ,\beta$ = 0 is the most extensive lowest chance, showing that the goal function's value will be in that range. In contrast, the extreme of $\alpha ,\beta$ = 1 provides the most confident goal function value. In the above numerical example, the objective function at both the levels has been fuzzy intuitionistic; therefore, the objective function with the most probable value at a distinct $\alpha$ value is (264,350.0, 256,810.0, 327,946.7, 25,034.00, 35,949.17). While the pessimistic values of the objective function are (252,873.3, 270,046.7, 361,985.0, 28,683.33, 39,933.33) and the optimistic values of the objective function are (247,230.0, 266,510.0, 306,351.7, 24,710.00, 33,918.00); on the other hand, the most probable values of the objective function are at a distinct $\beta$ value of (275,860.0, 262,526.7, 342,715.0, 25,211.67, 37,151.67), while the pessimistic values of the objective function are (322,266.7, 320,553.3, 412,073.3, 39,956.67, 56,176.67). The objective function's optimistic values are (257,280.0, 254,506.7, 302,898.3, 21,588.33, 30,180.00).

Managerial implication

Following are the managerial implication of this study:

• This study's findings allow companies to follow a structured method for the transport and assignment of orders to destinations from multiple sources.

• Manufacturing firms will use the proposed methodology to set up the supply chain for a new product at any location for the first time.

• The uncertainty and its solution methodology can be used for other SCN design problems easily.

• This form of complexity is functional when there is little historical data of the SCN design problem in an organization.

• This analysis allows the manager to assess the best order quantity of items using the optimization process with two stages of hierarchical decision-making.

Conclusions

Most of the prior studies related to the SCN dealt with deterministic circumstances; that is, all the parameters of the problem DM are precisely known. However, some instances show that the model's parameters may be inaccurate and imprecise due to some autonomous factors. This study examined bi-level programming with the intuitionistic fuzzy parameters for modelling an SCN problem under multi-objective and effectively solved it using an FGP approach to reach a satisfying solution for the decision-making environment. In decision-making at the first level, DMs attempt to optimize transportation costs, while DMs at the second level optimize the SCN’s delivery time. The DM's main aim was to present the optimistic and pessimistic view for solving the BL-MOSCN problem, including production, requirements, and distribution planning tasks. The quantities transported from the various sources to the various destinations have been compared independently. This research enables managers to detect the optimum quantity of the product when hierarchical decision-making involving two levels is related to optimization. It also helps managers analyze the results obtained in the SCN under a specific and unspecified circumstance and provides ideas on how to perform in uncertain situations.

To improve the formulated model, certain utility functions affected by SC network functionality—such as store accessibility at the point of demand and proximity level between store and customers—can be specified to examine as needed. Eventually, network configurations are affected by those decisions. This study's limitation is that it does not account for some criteria not included in model formulation, such as the price elasticity of demand and one-day replenishment coverage and their impact on the distribution center. After conducting a more careful analysis of demand elasticity in the market and after knowing the one-day replenishment plan, the research may be continued with actual data gathered from the market. Another limitation of the model established applies to a single period in the study. Hence, the model may be improved by adding more than one of the term details into the study or providing potential hypothetical business company predictions. Potential research involves identifying a more dynamic SC network of more than three echelons and involving recycling centers, aspects of globalization, and other variables that could also improve the model’s importance. The formulated model can also be extended to real-world situations from other intensely dynamic industries such as consumer goods and computer devices to test the concept's value.