Introduction

Since the concept was first described by Malys and Jensen (1990), Héroux and Kouba (1995), and Zumberge et al. (1997), PPP has proven itself as a substantial GNSS positioning method, which is used for various scientific and commercial applications today (Teunissen and Montenbruck 2017). This technique, which uses code and phase observations on multiple frequencies, allows a highly accurate, undifferenced, and absolute positioning for a single receiver. PPP is characterized by the use of precise satellite products and the application of accurate observation models and sophisticated algorithms. In this way, a position accuracy in the decimeter to centimeter level is achieved, and even at the centimeter to millimeter level when the phase ambiguities are fixed to their correct integers (Kouba 2015).

Unlike relative positioning methods, PPP does not require a nearby reference station, network, or, generally, simultaneous observations at reference and rover receivers (Choy et al. 2017). Using globally valid satellite orbits, clocks, and biases, a worldwide homogeneous positioning quality is feasible, which requires data communication only in one direction to the user. Furthermore, in addition to the coordinates, other attractive parameters such as the tropospheric delay and receiver clock error are estimated during a PPP solution. However, PPP requires a long convergence time to reach centimeter coordinate accuracy, which is a major drawback of this technique and limits its application in time-critical applications. The reduction in the convergence time is a major topic in scientific research, and to make PPP more competitive among other high-precision GNSS positioning techniques, researchers have tested different approaches.

First, the inclusion of observations of supplemental GNSS in addition to GPS substantially improves the PPP technique (Tegedor et al. 2014; Pan et al. 2017b). A higher number of observations make the parameter estimation easier and more stable, resulting in a shorter convergence period and higher accuracy (Choy et al. 2017). Second, the uncombined PPP model, which relies directly on the raw GNSS measurements, has become a viable alternative to the conventional PPP model, which uses the ionosphere-free linear combination. This modern approach is auspicious, considering ionospheric constraints and the multitude of frequencies used by today’s GNSS constellations (Li et al. 2015; Aggrey and Bisnath 2019). The uncombined PPP model is based on the idea that although it eliminates the first-order ionospheric delay, the IF LC increases the observation noise, which increases the convergence time (Lou et al. 2016; Boisits et al. 2020). Furthermore, it is much more flexible and suitable for observations on one or any number of frequencies (Ning et al. 2019; An et al. 2020). Finally, PPP with integer ambiguity resolution (PPP-AR) has proven to be an effective method for improving positioning accuracy, especially in the east component, while also reducing or possibly eliminating convergence time (Ge et al. 2008; Teunissen and Montenbruck 2017). Note that instead of PPP-AR also the terms IPPP (integer-PPP) or PPP-RTK are common in the literature.

Since PPP is a zero-difference technique, fixing phase ambiguities to their correct integer number is more complex than in relative positioning methods because it is not possible to build double-differences to eliminate phase biases originating from satellite and receiver hardware. The undifferenced ambiguities absorb these phase biases, and so their integer nature is destroyed (Shi and Gao 2014; Håkansson et al. 2017). Hence, ambiguities are typically estimated as real numbers in PPP, the so-called float solution.

However, researchers have found different ways to fix the undifferenced phase ambiguities to their correct integer value and calculate a fixed PPP solution. Therefore, the PPP user should apply appropriate satellite products provided by the network side consistently. Usually, the ambiguity of the IF LC is decomposed into the ambiguities of the Wide-Lane (WL) and Narrow-Lane (NL) linear combinations, which are fixed consecutively using proper phase biases and algorithms. In principle, two strategies build the basis for all modern satellite products enabling PPP-AR. Their key difference is how the satellite hardware phase biases are separated from the integer ambiguities.

First, Ge et al. (2008) developed a method to determine uncalibrated phase delays (UPDs), which are more likely called fractional phase biases (FCBs) today, for the WL and NL ambiguity by averaging the fractional parts of the float WL and NL estimates in a network solution. The WL and NL FCBs, when forwarded to the user, enable fixing the single-differenced ambiguities between satellites and a fixed PPP solution.

Second, it is possible to estimate “integer” clocks known as the integer recovery clock (IRC) method. Laurichesse et al. (2009) used the same decomposition in WL and NL, but the undifferenced ambiguities are fixed directly to an integer. Unlike Ge et al. (2008), this strategy assimilates the NL FCBs into the clock estimates, thereby introducing phase clocks. Therefore, the NL ambiguities have to be fixed to integers before estimating the satellite clocks in the network solution. The PPP user only has to consider the WL FCB. Similarly, Collins (2010) developed a decoupled clock model where the pseudorange clocks differ from the carrier-phase clocks.

Geng et al. (2010) and Shi and Gao (2014) compared these methods and concluded that they were equivalent for the ambiguity-fixed position. Teunissen and Khodabandeh (2015) looked into more detail, reviewed six strategies enabling PPP-AR and discussed their network and user components. They show how these are connected and provide transformations in between them. Therefore, despite using different strategies in their computation, a combination of PPP-AR satellite products and the production of a combined IGS product is possible and was tested for GPS (Banville et al. 2020).

Recently, PPP-AR performance has improved significantly, and solutions including supplemental GNSS outperform the GPS-only solution in terms of accuracy and, especially, convergence time. Fixing GLONASS ambiguities in PPP is still considered difficult due to the frequency and receiver type-specific interfrequency biases in the GLONASS observations caused by the frequency-division multiple access technique of the GLONASS signals (Reussner and Wanninger 2011) and despite the new approaches by Teunissen and Khodabandeh (2019). For PPP-AR solutions using GPS observation, the convergence time is typically 20–30 min (Ge et al. 2008; Geng et al. 2010; Pan et al. 2017a). For a dual-GNSS PPP-AR with GPS + Galileo or GPS + BeiDou, average times to the first fix and centimeter-level accuracy of about 15 min have been reported (Pan et al. 2017a, b; Li et al. 2018). Including observations from all available GNSS, this can be reduced to about 10 min (Li et al. 2018).

We demonstrate what PPP performance in terms of convergence time and accuracy is feasible for a combined GPS and Galileo PPP-AR solution using modern satellite products and an up-to-date PPP software. Instead of using our own network estimation to enable PPP-AR, existing products from well-established institutions are tested using independent software.

The following section introduces the observation model and PPP-AR algorithm that was used. The third section presents different modern satellite products for PPP-AR and shows how they are integrated into the observation model. Furthermore, we present the selected test case and a detailed look at the PPP results of the various satellite products. The fifth section shows convergence times that are achievable with high-rate observations. Our conclusions are drawn in the final section.

Observation model

The GNSS observation equations in units of meters can be written as (Teunissen and Montenbruck 2017).

$${P}_{i}=\rho +c\left({dt}_{R}-{dt}^{S}\right)+dTrop+{dIon}_{i}+{B}_{R,i} -{B}_{i}^{S}+ \varepsilon $$
(1)
$${L}_{i}=\rho +c\left({dt}_{R}- {dt}^{S}\right)+dTrop-{dIon}_{i}+{\lambda }_{i}\left(N+ {b}_{R,i}- {b}_{i}^{S}\right)+\varepsilon $$
(2)

with the code observable \({P}_{i}\) and the phase observable \({L}_{i}\) on frequency \(i\), the geometric distance between the satellite and receiver \(\rho \), the receiver clock error \({dt}_{R}\) and the satellite clock error \({dt}^{S}\), both multiplied by the speed of light \(c\). \(dTrop\) and \(dIon\) denote the tropospheric and ionospheric delays, respectively. \({B}_{R}\) and \({B}^{S}\) are receiver and satellite code hardware delays converted to the range, and \(\varepsilon \) comprises random and other negligible errors. The ambiguity term of the phase observable, which is multiplied with the wavelength \({\lambda }_{i}\), includes the integer term \(N\) and carrier phase hardware delays from the receiver \({b}_{R}\) and the satellite \({b}^{s}\). To improve the readability, no index for the GNSS is included.

$${P}_{IF}=\frac{{f}_{1}^{2}}{{f}_{1}^{2}-{f}_{2}^{2}}{P}_{1}-\frac{{f}_{2}^{2}}{{f}_{1}^{2}-{f}_{2}^{2}}{P}_{2}$$
(3)
$${L}_{IF}=\frac{{f}_{1}^{2}}{{f}_{1}^{2}-{f}_{2}^{2}}{L}_{1}-\frac{{f}_{2}^{2}}{{f}_{1}^{2}-{f}_{2}^{2}}{L}_{2}.$$
(4)

In PPP, the ionosphere-free linear combination (IF LC) denoted by the subscript \(IF\) is typically used, which is built with the frequencies \({f}_{1}\) and \({f}_{2}\) of the used signals and (3) and (4) for the code and phase measurement. As an alternative to the IF LC, the uncombined model directly relies on raw GNSS measurements. This implicates different handling of the ionospheric delay, which allows including the ionospheric pseudo-observations (Lou et al. 2016; Boisits et al. 2020; An et al. 2020).

$${P}_{IF}=\rho + c\left({dt}_{R}^{gps}+\delta {t}_{R}^{g}\right)+{dTrop}^{wet}+ \varepsilon $$
(5)
$${L}_{IF}=\rho + c\left({dt}_{R}^{gps}+\delta {t}_{R}^{g}\right)+{dTrop}^{wet} +{\lambda }_{IF}({\overline{N} }_{IF}+{b}_{IF,R} -{b}_{IF}^{S}) + \varepsilon $$
(6)

Furthermore, precise satellite orbits, clocks, and biases are applied, and modeled error sources on the measurements are omitted in the mathematical model, such as relativistic effects, phase wind-up, satellite and receiver phase center offset and variations, and deformation of the earth surface. Therefore, the PPP observation equations result in (5) and (6). Because of the use of precise satellite products in PPP, no satellite orbit error is included, and satellite clock error \({dt}^{S}\) and the satellite code biases \({B}_{i}^{S}\) are omitted. Furthermore, compared to the basic GNSS observation equations, the ionospheric delay \(dIon\) is eliminated due to the use of the IF LC as higher order terms of the ionospheric delay are neglected. The tropospheric delay is divided into a hydrostatic part, which is modeled and therefore omitted, and an estimated wet part \(dTro{p}^{wet}\). A receiver clock offset \(\delta {t}_{R}^{g}\) is added to the GPS receiver clock error \(d{t}_{R}^{gps}\) for each processed GNSS other than GPS. The receiver code biases \({\mathrm{B}}_{\mathrm{R},\mathrm{i}}\) are converted into a constant offset that is absorbed by the receiver clock when the IF LC is built.

$${\tilde{N }}_{IF}= {\overline{\mathrm{N}} }_{\mathrm{IF}}+{\mathrm{b}}_{\mathrm{IF},\mathrm{R}} -{\mathrm{b}}_{\mathrm{IF}}^{\mathrm{S}}$$
(7)

For the calculation of the float solution, the receiver \({\mathrm{b}}_{\mathrm{IF},\mathrm{R}}\) and satellite hardware phase delays \({\mathrm{b}}_{\mathrm{IF}}^{\mathrm{S}}\) in (6) are lumped together with the integer term \({\overline{\mathrm{N}} }_{\mathrm{IF}}\) to the float ambiguity \({\tilde{N }}_{IF}\).

Usually, the unknown parameters (coordinates, wet tropospheric delay, float ambiguities, GPS receiver clock error, and a receiver clock offset for each processed GNSS other than GPS) are estimated in the float solution by Kalman Filtering. Based on the float ambiguity estimates, an integer fixing of the ambiguities and a PPP-AR solution is possible. Therefore, for each GNSS, a reference satellite is used to build satellite single differences (SD), and then the SD ambiguities of the Wide-Lane (WL) and Narrow-Lane (NL) are fixed consecutively. Therefore, the receiver phase biases are eliminated, while the satellite phase biases are corrected.

First, to fix the WL, the Hatch–Melbourne–Wübbena (HMW) LC (Hatch 1982) is built for each satellite using (8). This is based on the facts that this LC eliminates all terms except the ambiguity, and its wavelength is that of the WL. To remove the receiver hardware biases \({b}_{WL.R}\) from the HMW LC in (8), the single-differenced HMW LC \({\mathrm{HMW}}_{\mathrm{SD}}\) is calculated using the HMW LC observation of the chosen reference satellite \({\mathrm{HMW}}_{\mathrm{sat}}^{\mathrm{ref}}\). Furthermore, satellite hardware delays \({b}_{WL,\mathrm{SD}}^{s}\) can be corrected with phase biases that correspond to the used satellite orbits and clocks. Then, the SD WL ambiguity is fixed by averaging \({\mathrm{HMW}}_{\mathrm{SD}}\) over the last \(n\) epochs and rounding to the nearest integer value, which is denoted as \({\langle \rangle }_{n}\) in (10).

$$HMW=\frac{{f}_{1}{L}_{1}-{f}_{2}{L}_{2}}{{f}_{1}-{f}_{2}}-\frac{{f}_{1}{P}_{1}+{f}_{2}{P}_{2}}{{f}_{1}+{f}_{2}}= (\overline{WL }+ {b}_{WL.R}-{b}_{WL}^{S}){\lambda }_{WL}$$
(8)
$$HM{W}_{SD}=HM{W}_{sat}^{ref}- HMW$$
(9)
$${\overline{WL} }_{SD}= {\langle HM{W}_{SD}+{b}_{WL,SD}^{s} \rangle }_{n}$$
(10)

In this way, the SD WL ambiguities \({\overline{\mathrm{WL}} }_{\mathrm{SD}}\) can be reliably fixed after a small number of observation epochs (Huber 2015).

Second, the fixing of the NL ambiguity is performed. Therefore, the SD float ambiguities \({\stackrel{\sim }{\mathrm{N}}}_{\mathrm{SD}}\) are calculated using the reference satellite and (11). Afterward, \({\stackrel{\sim }{\mathrm{N}}}_{\mathrm{SD}}\) and \({\overline{\mathrm{WL}} }_{\mathrm{SD}}\) are used to calculate the SD float estimation of the NL ambiguity \({\tilde{NL }}_{SD}\) with (12).

$${\stackrel{\sim }{\mathrm{N}}}_{\mathrm{SD}}= {\stackrel{\sim }{\mathrm{N}}}_{\mathrm{sat}}^{\mathrm{ref}}-\stackrel{\sim }{\mathrm{N}}$$
(11)
$${\tilde{NL }}_{SD}={\tilde{N }}_{SD}\frac{{f}_{1}+{f}_{2}}{{\lambda }_{1}{f}_{1}}- {\overline{WL} }_{SD}\frac{{f}_{2}}{{f}_{1}-{f}_{2}}+ {\mathrm{b}}_{\mathrm{NL},\mathrm{SD}}^{\mathrm{s}}$$
(12)
$${\overline{NL} }_{SD}=LAMBDA({\tilde{NL }}_{SD})$$
(13)
$${\overline{\mathrm{N}} }_{\mathrm{IF},\mathrm{SD}}{\uplambda }_{\mathrm{IF}} = {\uplambda }_{1}\frac{{\mathrm{f}}_{1}{\mathrm{f}}_{2}}{{\mathrm{f}}_{1}^2-{\mathrm{f}}_{2}^2}{\overline{\mathrm{WL}} }_{\mathrm{SD}}+ {\uplambda }_{1}\frac{{\mathrm{f}}_{1}}{{\mathrm{f}}_{1}+{\mathrm{f}}_{2}}\left({\overline{\mathrm{NL}} }_{\mathrm{SD}}-{\mathrm{b}}_{\mathrm{NL},\mathrm{SD}}^{\mathrm{s}}\right)$$
(14)

Using partial ambiguity resolution and the LAMBDA algorithm (Teunissen 1995), the SD NL ambiguities can be fixed for all satellites together by introducing the covariance matrix of \({\tilde{NL }}_{SD}\), which is calculated from the covariance matrix of the float solution using error propagation,

If the SD WL and NL ambiguities are fixed for a specific satellite, the fixed ambiguity \({\overline{N} }_{IF,SD}{\lambda }_{IF}\) of the IF LC is recalculated with (14) using the SD NL FCBs \({b}_{WL,\mathrm{SD}}^{s}\). When three or more ambiguities of the IF LC are fixed in this way, the fixed coordinates are estimated in a separate least squares adjustment. Thus, the fixed ambiguities are introduced as pseudo-observations with extremely high weights in addition to the float solution.

When the fixing procedure is examined, we observed that the WL FCBs are only used to resolve the WL ambiguities. However, the NL FCBs \({b}_{NL,\mathrm{SD}}^{s}\) directly contribute to the ambiguity-fixed PPP solution in (14). Therefore, the accuracy of the NL FCBs has a significant effect on the PPP-AR solution (Pan et al. 2017a). To estimate the float ambiguities reliably and ensure a correct integer fixing, some epochs with a valid float solution are required, which can be seen as the time the solution transitions from a pseudorange-only to a float ambiguity carrier phase solution (Choy et al. 2017). Therefore, to increase the chance for fixing the ambiguities to their correct integer value, the fixing process typically does not start immediately in the first epoch.

Modern satellite products enabling PPP-AR

Nowadays, various analysis centers and institutions compute and provide satellite products, enabling PPP-AR. Therefore, they adopt different strategies and formats to distribute the resulting satellite phase biases. Because of the landscape of modern GNSS signals, PPP-AR satellite products allowing a combined GPS and Galileo solution from the following institutions (Table 1) are investigated: Centre national d’études spatiales (CNES), Center for Orbit Determination in Europe (CODE), School of Geodesy and Geomatics (SGG), and Graz University of Technology (TUG). Real-time correction streams and PPP-AR satellite products solely for GPS (e.g., from Wuhan University (Geng et al. 2019)) are not considered.

Table 1 Overview of the tested PPP-AR satellite products and details of the provided phase biases
Full size table

The satellite orbits and clocks from CNES rely on the IRC approach (Katsigianni et al. 2019; Loyer et al. 2012). Therefore, the user only has to apply the satellite WL FCBs in (8), which are included in the header of the daily clock file, to fix the SD MW LC correctly. Note that not all satellites provided in CNES files have integer fixed clocks every day, as is indicated in the following file: ftp://ftpsedr.cls.fr/pub/igsac/GRG_ELIMSAT_all.dat.

Like CNES, CODE uses the IRC approach (Prange et al. 2020) to provide orbits, clocks, and biases. Unlike CNES, the satellite biases are provided in the new SINEX format 1.00 (Schaer 2016) as observable specific biases (OSBs), and they are applied to the raw observations in (1) and (2) before building any linear combination. Therefore, no biases have to be considered in the fixing process anymore, and from a user's perspective, this is the most convenient representation of biases. CNES and CODE products are available on the IGS FTP servers as part of the IGS MGEX product series.

Unlike other institutions, SGG does not compute satellite orbits and clocks. This institution provides daily WL and quarter-hourly NL FCBs in a modified version of Ge et al. (2008) for the MGEX orbit and clock products of GFZ (GeoForschungsZentrum Potsdam), CNES, and CODE (Li et al. 2016; Hu et al. 2020). They are provided in their own *.fcb format and are publicly available under https://github.com/FCB-SGG/FCB-FILES. In addition to GPS and Galileo, BeiDou and QZSS FCBs are also included in these products. To enable PPP-AR, the FCBs are introduced into (10) and (12) to fix the WL and NL correctly.

Similar to CODE, the products of TUG consist of orbits, clocks, and biases as OSBs. Since these are experimental products, they are not publicly available currently. Unlike all other satellite products relying on the IF LC, TUG products are calculated using a raw observation approach (Strasser et al. 2018). Therefore, this product is suitable for fixing any linear combination, whereas all other products enable PPP-AR only for the IF LC of two specific frequencies. This is quite restrictive given the modern multi-frequency GNSS constellations and makes PPP-AR impossible in PPP models different from the IF LC. Therefore, satellite products based on a raw observation approach (Strasser et al. 2018) or a network approach as presented by Odijk et al. (2016) are critical in a multi-frequency and multi-GNSS landscape.

Test case

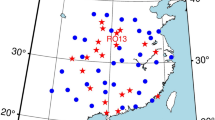
The quality of the different PPP-AR products (Table 1) is evaluated in a combined GPS and Galileo PPP solution using observation data from 45 IGS MGEX stations (Fig. 1) with an interval of 30 s for January 2020. The stations were randomly selected to cover the entire globe. However, only stations with complete data and daily IGS coordinate estimation were considered eligible. Our in-house software raPPPid, the PPP component of the Vienna VLBI and satellite software (VieVS PPP), is used for processing. Principally, it can process up to three frequencies and all four operable GNSS in various PPP models, including the uncombined model with ionospheric constraint (not used here) and the IF LC. Therefore, several different models, input data, and settings can be used. Six PPP-AR solutions were computed using the satellite products from CODE, CNES, SGG, or TUG. GPS observations on L1 and L2 and Galileo observations on E1 and E5a are used to build the IF LC, and ambiguity fixing is performed as described previously. At the start-epoch of the WL fixing, the GPS and Galileo satellite with minimum zenith distance is selected as reference satellite and kept until its elevation angle drops under 20°. In that case, again, the satellite with the currently maximum elevation angle is selected as the new reference satellite. To correct for phase center offsets and variations of the satellites and receivers, the current IGS antenna phase center model igs14.atx is applied, and for missing Galileo corrections, the GPS values are used. Note that the satellite products of CODE are based on the values from Steigenberger et al. (2016) for Galileo observations, while TUG uses the Antex file of the third IGS data reprocessing campaign (repro3). The processing settings are summarized in Table 2. The epoch-wise PPP coordinate estimation is compared with the daily IGS station coordinates to assess the coordinate results in terms of convergence and accuracy. Other metrics for assessing the quality of PPP solutions, such as the estimation of the zenith wet delay or code and phase residuals, are not presented here.

Fig. 1
figure 1

Distribution of the used 45 IGS MGEX stations

Full size image
Table 2 Overview of processing settings
Full size table

The PPP solution is restarted every full hour to study the convergence behavior in detail. This results in 24 so-called convergence periods for a specific day and station and more than 33 000 convergence periods for the whole test case. The convergence time of the coordinates can be described as the time it takes for the position to reach a specific level of accuracy and does not exceed this level later on. In this study, the float solution’s convergence is defined as the point in time when the 2D position difference with respect to the reference coordinates is under the threshold of 10 cm and does not exceed this threshold for the entire remaining convergence period. Note that nowadays, this accuracy level can be reached with Galileo and only broadcast ephemeris after a considerable convergence time (Hadas et al. 2019). For the fixed solution, convergence is defined as the time to first fix (TTFF), which is achieved when the 2D position difference of the fixed solution stays under the threshold of 5 cm until the next reset.

Figure 2 shows a bar plot of the float convergence for the different PPP solutions. The height of a bar corresponds to the percentage of convergence periods that have reached convergence at a specific point in time. There are only small differences between the six PPP solutions. The float convergence of SGGCODE and CODE as well as SGGCNES and CNES are identical because they use the same satellite orbits and clocks, and the use of different phase biases makes no difference in estimating float ambiguities. When the mean convergence times in Table 3 are compared, the PPP solutions using TUG and CODE satellite products converge nearly identical and slightly faster than the solution using GFZ. The float solutions using satellite orbits and clocks from CNES show the worst convergence behavior. Furthermore, there are no significant variations in the accuracy of the various float PPP solutions. Table 3 shows that the median and average 3D position differences differ by only a few millimeters, mirroring the convergence behavior. Generally, the float PPP solution using TUG products performs best, followed by the float solutions using CODE, GFZ, and CNES satellite orbits and clocks.

Fig. 2
figure 2

Bar plot of the convergence of the float solution. The height of a bar indicates the percentage of convergence periods, which have converged for a specific PPP solution at a specific point in time after the last reset

Full size image
Table 3 Convergence time (2D < 10 cm) and accuracy of the float solution using different satellite products
Full size table

Unlike the float solution, the convergence of the fixed solution varies depending on the chosen satellite product. Figure 3 presents the bar plot for the convergence of the fixed solution, and Table 4 lists the corresponding values of the average and median TTFF. The PPP-AR solution using the satellite products from CODE converges the fastest, with an average TTFF of 5.52 min, followed by SGGCODE, SGGGFZ, and TUG, with a similar average TTFF of roughly 6 min. The solutions SGGCNES and CNES show a slightly worse average TTFF of about 6.5 min, originating from the float solution. Considering the observation interval of 30 s, a small number of epochs is sufficient for a correctly fixed position.

Fig. 3
figure 3

Bar plot of the convergence of the fixed solution. The height of a bar indicates the percentage of convergence periods, which have converged for a specific PPP solution at a specific point in time after the last reset

Full size image
Table 4 The average and mean convergence time (2D < 5 cm) and the accuracy of the fixed solution using different satellite products. Furthermore, the percentage of convergence periods, which did not reach convergence within 60 min, is presented
Full size table

By comparing the bar heights of Figs. 2 and 3, it is evident that PPP-AR significantly reduces the coordinate convergence time. Despite using a half-size threshold as convergence criteria, the number of PPP solutions that have reached convergence in Fig. 3 is still significantly higher for the fixed solution than the number of converged periods for the float solution. Figure 4 shows the percent improvement using a linear (top panel) and a logarithmic scale (bottom panel). Regardless of the used satellite product, the number of solutions that have reached convergence increases with PPP-AR by a factor of four to five within the first minutes. Unlike the float solution, the fixed solution remains under the convergence threshold most likely for the remaining convergence period once the position is correctly fixed. Furthermore, the estimation of the float ambiguities converges much faster than the float coordinates, which allows a successful fixing after a short period.

Fig. 4
figure 4

Improvement in the number of converged periods in percentage from the float to the fixed solution for the first 30 min after the last reset, using a linear scale (top) and a logarithmic scale (bottom)

Full size image

Figure 5 shows the 68% and 95% quantile of the 2D and 3D position difference for the fixed solution. The different satellite products converge similarly for the 68% quantile. For the 95% quantile, the differences in convergence get more distinct and confirm the findings from above. The PPP solution using CODE performs best, followed by a similar performance of SGGCODE, SGGGFZ, and TUG, with a small gap to SGGCNES and CNES. Furthermore, Fig. 5 shows that there are no perceptible differences in accuracy between the different PPP solutions after convergence. Also, in Table 4, listing the median and average 3D position difference, the variations are only in the size of one or two millimeters. Therefore, the choice of satellite products makes no difference to accuracy for a correctly fixed position. The 2D position difference is clearly under 5 cm, and the 3D position difference is in the subdecimeter to centimeter level.

Fig. 5
figure 5

68% (left) and 95% (right) quantiles of the 2D position difference (top) and the 3D position difference (bottom) of the fixed PPP solution using different satellite products for the first 15 min after the last reset

Full size image

Figure 6 presents the mean TTFF of all stations for each PPP solution. From left to right, the stations are ordered from small to large TTFF values. As shown in the illustration, the differences between the solutions are similar for all stations and may originate from a differing quality of the phase biases. The performance of a PPP solution using a specific satellite product results from the sum of all stations rather than individual stations. The PPP solution using CODE products performs best for nearly all stations, while SGGCNES and CNES perform notably worse. In between are the solutions using SGGCODE, SGGGFZ, and TUG products.

Fig. 6
figure 6

Mean TTFF for all stations and satellite products. The stations are sorted from a short TTFF (left) to a longer TTFF (right) for the TTFF values of the PPP solution using CODE products

Full size image

Figure 6 shows that regardless of the satellite product used, some stations show a worse convergence behavior than others. There are good and bad stations with a small and large mean TTFF, respectively. Tables 5 and 6 list the ten best and worst stations in terms of mean TTFF, receiver type, and processed observation type. While the ten best stations have a mean TTFF of four minutes or less, the ten worst stations have a mean TTFF ranging from 8 to 12 min. Concerning the receiver type of the ten best and worst stations, it appears that stations with Septentrio receivers tend to deliver better results, while stations with receivers such as Trimble NETR9 or Javad TRE_G3TH Delta perform worse. Furthermore, receivers providing C1X and C5X observations for Galileo perform better than receivers providing C1C and C5Q observations. An explanation could be that the used observation model and fixing process do not fit that well for these receivers. Interestingly, DARW has the second-largest mean, and MAW1 has the sixth-largest mean TTFF, although they are equipped with SEPT POLARX5 receivers. This can be explained with outdated receiver software (5.2.0 versus 5.3.0) in the case of DARW. The phase observations of MAW1 contain many cycle slips in specific time periods, which jeopardizes the overall performance of the fixed solution.

Table 5 Overview of the ten best stations regarding their mean TTFF of all solutions, receiver, and processed code observation. The corresponding processed phase observation is not listed
Full size table
Table 6 Overview of the ten worst stations regarding their mean TTFF of all solutions, receiver, and processed code observation. The corresponding processed phase observation is not listed
Full size table

Another error source deteriorating the fixing process is multipath. Figure 7 shows a skyplot of the color-coded code residuals of the float solution for the station REYK and the entire January. There exist distinctly pronounced areas, denoted by red ellipses, where large code residuals accumulate. If this plot is repeated for a few days only or another PPP solution, the same regions appear. A multipath map can be useful in reducing this effect, but this is a site-specific solution that requires a significant amount of observation data and preparation.

Fig. 7
figure 7

Skyplot of the station REYK for the period of January. The shown float code residuals of the PPP solution using CODE products are color-coded according to their size. Pronounced Multipath regions are emphasized with black ellipses

Full size image

In addition to that, there might be other error sources that deteriorate the fixing process. For example, the IF LC eliminates only the first-order ionospheric delay. There can be residual ionospheric effects for the bad stations near the equator (e.g., PNGM, LMMF).

High-rate observations

Motivated by the small number of epochs, which were necessary to fix the ambiguities with 30-s observation data, the use of high-rate observations is tested. This should reduce the convergence time similar to the float solution (Bahadur and Nohutcu 2020) also for the fixed solution because the float ambiguities are estimated more reliable in a shorter time period. Therefore, observation data with an interval of 1 s from all previously used stations that provide high-rate data is processed for the first five days of January 2020 using raPPPid: AREG, ASCG, BRUX, DJIG, GAMB, KIRU, MAS1, KERG, KOUG, MAYG, NKLG, NNOR, NRC1, YELL, and OWMG. The same processing settings are used again (Table 2), except for the reset of the solution (every 15 min) and the start of the WL and NL fixing (after 15 and 30 s).

The performance of the different PPP solutions among each other is comparable to the previous test case. Figure 8 shows the convergence of the 68% and 95% quantile for the fixed solution, while Table 7 shows the average and median TTFF and its improvement to the use of observations with an interval of 30 s. Again, the PPP solution using CODE products performs best and, interestingly, slightly better than the solution using CNES. This can be explained that nearly all CNES satellite clocks, and significantly more than for the whole of January 2020, are integer-fixed for the first five days of January 2020. These two solutions are followed by the solutions using SGGCODE and SGGGFZ, which converge similarly and slightly better than the PPP solution using SGGCNES and TUG.

Fig. 8
figure 8

The 2D position difference (top) and the 3D position difference (bottom) of the fixed PPP solution using different satellite products and observation data with an interval of 1 s. The left side shows the 68% quantile, and the right side the 95% quantile

Full size image
Table 7 The average and median convergence time (2D < 5 cm) of the fixed solution using observations with an interval of 1 s and different satellite products. The corresponding improvement is calculated to the PPP solution using observations with an interval of 30 s for the same time period and stations. Furthermore, the percentage of periods, which did not reach convergence within 15 min, is presented
Full size table

Figure 9 shows the mean TTFF for all high-rate stations, similar to Fig. 6. Again, individual stations do not influence the overall performance of a PPP solution. Furthermore, using high-rate observations, the assessment of good and bad stations does not change significantly. Compared to the results using 30-s data, the TTFF is reduced for all PPP solutions by 45 to nearly 60 percent, which is a bigger improvement than for the float solution in Bahadur and Nohutcu (2020). With high-rate observations and the best satellite products, the TTFF is reduced to few minutes and, in the best case, to one minute.

Fig. 9
figure 9

Mean TTFF for all high-rate stations and satellite products using observation data with an interval of 1 s. The stations are sorted from a short TTFF (left) to a longer TTFF (right) for the TTFF values of the PPP solution using CODE products

Full size image

Conclusion

We contrasted various modern satellite products that enable PPP-AR in different strategies and presented the correct application of the phase biases. All these products allow PPP-AR for two GPS and Galileo frequencies and the IF LC. However, only TUG enables the inclusion of additional frequencies and application of different PPP models in the fixing process, which is crucial for the developing multi-frequency and multi-GNSS landscape.

The different modern satellite products were tested in a combined GPS and Galileo PPP-AR solution. Unlike the performance of the float solution, the choice of the satellite product has a significant influence on the convergence of the fixed solution. This indicates that the satellite phase biases are of different quality. A 2D position accuracy of few centimeters can be achieved with six minutes using an observation interval of 30 s. Observations with an interval of 1 s reduce the TTFF to a few minutes and, in the best case, to one minute. When the position is fixed correctly, there is no difference in the coordinate accuracy between the different PPP solutions. The following inequality summarizes the performance of the fixed PPP solutions based on the satellite product used:

$$CODE>SG{G}_{CODE},SG{G}_{GFZ} \ge TUG\ge CNES \ge SG{G}_{CNES}$$

The test results have shown that the convergence behavior varies significantly between stations. Besides multipath and other potential error sources, the Galileo observation type and the receiver type influence the convergence performance. Investigations of these effects and an upcoming combined IGS satellite product that enables PPP-AR can reduce the TTFF even more. Future work will concentrate on the uncombined model with ionospheric constraint and the inclusion of additional frequencies and GNSS in the fixing process.