Introduction

Quantum resources promise advances in sensing and metrology1,2,3,4,5,6,7, beyond the fundamental limits of precision set for classical light. They enable overcoming the shot-noise limit (SNL) and achieving the ultimate Heisenberg limit in phase sensing8. Within the quantum states toolbox, most practical are squeezed states. Unlike exotic non-Gaussian states, squeezed states of atoms and light can contain a macroscopic number of particles and survive a reasonable amount of loss while providing reduced uncertainty in a plethora of measurements. As a result, their use noticeably improved the sensitivity of modern gravitational-wave detectors9,10,11,12. There are also numerous proof-of-principle experiments on squeezing-enhanced absorption measurement and spectroscopy13,14,15, imaging and microscopy16,17,18,19, polarimetry20, magnetometry21,22, and other types of sensing23,24.

Although more robust than non-Gaussian states, squeezed states are still very susceptible to loss. Therefore, overcoming the SNL in optical sensing requires extremely efficient detection18,25. The quantum advantage provided by squeezing strongly depends on the detection efficiency η26,27,28, and completely disappears for η < 50%. Similarly, detection noise becomes a problem if the probing state is not very bright. In spectral ranges where detection is inefficient or noise is high, sub-shot-noise optical sensing is impossible.

Here we experimentally demonstrate a solution to this problem, namely strong parametric amplification of the signal before detection. Although proposed long ago29 and already applied to the detection of microwave quantum states30, to the improvement of the homodyne detection bandwidth31, to the tomography of optical non-Gaussian states32, and to atom interferometry33, this method has not been implemented in optical sensing. A similar principle provides loss tolerance of so-called SU(1,1) (nonlinear) interferometers34,35,36, both optical and atomic. But SU(1,1) has certain limitations, among them, a narrow range of phase sensitivity27 and more complexity in realization, at least in the multimode version. For making phase measurement loss- and noise-tolerant, much more practical is to add an amplifier to the output of a linear [SU(2)] interferometer. This is what we do in our experiment; the same method can be applied to sub-shot-noise imaging and absorption measurement.

Results

Phase-space representation

The principle is illustrated in Fig. 1 showing a Mach-Zehnder interferometer as an example. In classical interferometry (a), coherent light is fed into one input port, and direct or homodyne detection is performed in one output port in order to sense a phase difference ϕ between the two arms. The best sensitivity is achieved in the ‘dark fringe’, with no light in the output port. This becomes clear by looking at the Wigner function of the output state. In panel b, it is plotted for ϕ = 0, 0.2 π, . . π for the input coherent state containing 9 photons. Whenever the output states are well separated, the phase sensitivity is high; this happens around ϕ = 0. The phase can be retrieved by measuring the \(\hat{x}\) quadrature (homodyne detection) or the number of photons (direct detection).

Fig. 1: Overcoming detection loss in squeezing-assisted interferometry.
figure 1

Panels a, c, e show the experimental schemes and panels b, d, f, the calculated Wigner functions of the output states for five equidistant phases. a This ideal Mach-Zehnder interferometer fed with a coherent state \(\left|\alpha \right\rangle\) has the best phase sensitivity at ϕ = 0, the detector seeing the `dark fringe', where the output states for different phases are most distinguishable (b). c If, additionally, the second input port is fed with squeezed vacuum (SV) \(\left|\xi \right\rangle\), the neighboring states are squeezed and better distinguishable; however loss or imperfect detection efficiency η makes them overlap (d). e To overcome the loss, a degenerate optical parametric amplifier (DOPA) amplifies the state before detection. f The output states are now anti-squeezed in the quadrature carrying the phase information; the latter is therefore protected against loss. In the calculation, α = 3, η = 0.5, \(\left|\xi \right\rangle\) is 6 dB squeezed, and DOPA provides 9.6 dB quadrature anti-squeezing.

Full size image

To increase the phase sensitivity, a squeezed vacuum state \(\left|\xi \right\rangle\) is injected into the unused input port29,37,38,39 (Fig. 1c). Then, under the ‘dark fringe’ condition ϕ = 0, the detected output port contains the squeezed vacuum (6 dB squeezing is assumed in this example). As the phase changes from ϕ = 0 to ϕ = π, the output state evolves to a coherent state (Fig. 1d). Near the ‘dark fringe’, the states are squeezed in the \(\hat{x}\) quadrature and therefore better distinguishable. However, if the detection is lossy (we assume η = 0.5), the squeezing is degraded, the states overlap, and the advantage of squeezing is fully or partly lost.

As a remedy, the state at the output of the interferometer is amplified by a phase sensitive amplifier (a degenerate optical parametric amplifier, DOPA), see Fig. 1e. The DOPA amplifies the quadrature carrying the phase information, but it also makes this quadrature anti-squeezed. The relative separation of the states at the output (Fig. 1f) remains the same, but the phase information is now in the anti-squeezed quadrature and therefore less susceptible to loss. In the calculation, quadrature anti-squeezing of 9.6 dB completely eliminates the effect of loss; as we will see below, our experiment provides even stronger amplification and a much higher loss can be overcome. If strong enough, amplification also protects the measurement against the detection noise. Importantly, a DOPA does not change the signal-to-noise ratio of the input state and therefore does not add noise.

Experiment

In our experiment, we provide strong phase-sensitive parametric amplification with a nonlinear beta-barium borate (BBO) crystal pumped by picosecond pulses under collinear frequency-degenerate type-I phasematching. The amplification is defined by the squeeze factor \(G\propto {\chi }^{(2)}L\sqrt{P}\), where L is the length of the nonlinear crystal, χ(2) its second-order susceptibility, and P the pump power40. The quadratures after such an amplifier evolve as \({\hat{x}}_{{\rm{out}}}={e}^{G}{\hat{x}}_{{\rm{in}}},\ {\hat{p}}_{{\rm{out}}}={e}^{-G}{\hat{p}}_{{\rm{in}}}\), and the mean photon number of a coherent state, as \({N}_{{\rm{out}}}={N}_{{\rm{in}}}{e}^{2G}+{\sinh }^{2}G\). Generally40, we can achieve up to G ~ 10. The current experiment uses squeeze factors only up to G = 3.6, which still means impressive 1340-fold intensity amplification and 31 dB quadrature variance anti-squeezing.

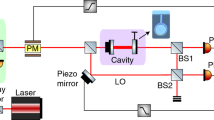
In our proof-of-principle implementation, the interferometer is simulated by a half-wave plate (HWP)39, see Fig. 2a. Instead of two spatial modes, the two arms of the interferometer are the right- and left-circularly polarized modes, and a rotation of the HWP leads to a phase shift between them (see Methods). The inputs and outputs of the interferometer are linear polarization modes. The coherent state is the radiation of a Spectra Physics Spitfire Ace laser with the central wavelength 800 nm, 1.5 ps pulse duration, 5 kHz repetition rate, horizontally polarized (Fig. 2b), attenuated to 1500 photons/pulse. The squeezed vacuum (SV), produced in the first amplifier BBO1 pumped by the second harmonic of the same laser and unseeded, is vertically polarized. The coherent beam, injected through beamsplitter BS2, does not interact with BBO1 because there is no phase matching for its polarization. The output amplifier BBO2 works only for a vertically-polarized input beam; the de-amplification phase is set by properly choosing the distance between the two crystals36, while the amplification phase of the coherent beam is set with a piezoelectric actuator (Supplementary Information Sec. II). The pump is rejected with dichroic mirror DM and the vertical polarization is selected by Glan polarizer GP. To ensure good de-amplification of the SV, we select an angular bandwidth of 130 μrad with 200 μm pinhole P in the focal plane of lens L (f = 1.5 m). The bandpass filter BF has 3 nm spectral bandwidth around the central wavelength 800 nm. Photodetector PD1 registers the number of photons per pulse, with a dark noise of 500 photons.

Fig. 2: Squeezing-assisted interferometer with parametric amplification at the output.
figure 2

a A HWP as a Mach-Zehnder interferometer: left- and right-circularly polarized states play the role of the two arms and linear polarization states, input and output modes. b Vertically polarized squeezed vacuum (SV) is produced in nonlinear crystal BBO1 and the horizontally polarized coherent state is fed through beamsplitter BS2. Vertically polarized output of the interferometer is amplified in the second crystal BBO2, cleaned from the pump by dichroic mirror DM, selected by Glan polarizer GP, and finally detected with photodetector PD1. Lens L and pinhole P provide spatial filtering, while bandpass filter BF, spectral filtering. Beamsplitters BS1, BS2 tap off parts of the pump and coherent beams to monitor intensity fluctuations and lock the phase. c The output intensity of unseeded BBO2 versus the pump power.

Full size image

The loss between BBO1 and BBO2 (internal) amounts to 3% and is impossible to compensate for. The loss after the amplifier (‘detection loss’) is incorporated into the detection efficiency η = 0.50 ± 0.03 (for the detailed description of losses, see Supplementary Information Sec. III). Please note that spatial and spectral filtering, i.e. the pinhole and the bandpass filter, restricts the amount of photons detected but cannot be considered as loss since all the measurements are carried out within the same bandwidths. Meanwhile, the optical transmission of the bandpass filter within the spectral bandwidth is taken into account. The amplification at the interferometer output, if strong enough, can completely overcome the detection inefficiencies. Both the amplification of BBO2 and the squeezing of BBO1 are characterized by measuring the photon numbers at their outputs with a vacuum at the input (see Methods and Fig. 2c). In all measurements, G1 = 1.7 ± 0.3 (measured as described in Methods), from which an initial 15 dB level of squeezing is inferred.

Beamsplitters BS1 and BS2 serve, respectively, for monitoring/stabilizing the pump intensity (Methods) and locking the phase between the coherent and SV beams at the input of the HWP (Supplementary Information Sec. II).

The phase sensitivity is evaluated as

$${{\Delta }}\phi ={{\Delta }}N{\left(\left|\frac{d\langle N\rangle }{d\phi }\right|\right)}^{-1},$$
(1)

where \({{\Delta }}N=\sqrt{\langle {N}^{2}\rangle -{\langle N\rangle }^{2}}\) is the measured uncertainty of the photon number, detector dark noise included, and 〈N〉 is the average number of photons. The slope of the \(\langle N\rangle \left(\phi \right)\) dependence is inferred from the fit.

Figure 3 shows the results of phase sensitivity measurements, with the SNL (measured as described in Methods) marked with a dashed red line. In panel a, the second amplifier has the squeeze factor measured to be G2 = 3.1 ± 0.3 (photon-number amplification 490 times) and the detection efficiency is 50%, 29% and 15%. To vary η, we place a HWP and a GP (not shown in Fig. 2) before lens L. For the highest efficiency (circles), the SNL variance is overcome by 1.8 ± 0.8 dB in the best case, i.e., at ϕ ~ 0. Note that without the output amplifier, the phase sensitivity would not overcome the SNL at all, in particular due to the large detection noise. With the amplifier, the performance just overcomes the SNL for 29% detection efficiency (triangles). Exactly at ϕ = 0, the average number of photons is the lowest and the detector dark noise spoils the sensitivity, hence the peak.

Fig. 3: Phase sensitivity measurements with 15 dB input squeezing and Nα = 1500 photons in the coherent beam.
figure 3

The red dashed line marks the SNL and the solid lines are the theoretical predictions. The error bars represent the standard error of the mean with a sample size of 1000. The insets show the photon number dependence on the phase and the error bars are too small to be seen. a Parametric amplification with G2 = 3.1. Circles, triangles and crosses show measurements with detection efficiency η = 50%, 29% and 15%, respectively. b Parametric amplification with G2 = 3.6. Circles, triangles and crosses are for η = 50%, 16% and 6%, respectively.

Full size image

By increasing the output parametric amplification (the measured squeeze factor G2 = 3.6 ± 0.3), the phase sensitivity is improved (Fig. 3b). The measurements shown with circles, triangles and crosses correspond, respectively, to detection efficiencies η = 50%, 16% and 6%. For the highest value of η, the SNL variance is overcome by 6 ± 1 dB. In addition, with lower detection efficiency we need a stronger amplification for overcoming SNL. Indeed, while it is η = 29% for lower G2 (a), for higher G2 it is only η = 16% (b).

To fit the experimental points, we derive the phase sensitivity for a lossy squeezing-assisted interferometer with an OPA at the output and direct detection27. The model also takes into account the relative excess noise of the coherent beam, i.e. deviation of the normalized second-order correlation function \({g}^{\left(2\right)}\) from unity (see Supplementary Information Secs. IV-V), which we measured to be 0.0020 ± 0.0005. We use two fitting parameters G2 and \({g}^{\left(2\right)}\) for the model (lines), in reasonable agreement with the experiment for G2 = 2.7 and \({g}^{\left(2\right)}=1.003\) (a) and for G2 = 3.2 and \({g}^{\left(2\right)}=1.004\) (b). From now on, we refer to the two different situations in panels (a) and (b) with these fitted squeeze factors.

Ideally, the sub-shot-noise sensitivity phase range should cover half of the 2π period27. In our case, it is at most ~ 0.3 π in panel a and ~ 0.4 π in panel b. The main reason is that our coherent beam is not shot-noise limited. Additionally, the detector dark noise excludes part of this range near ϕ = 0. But even with these imperfections, the sub-shot-noise sensitivity range is broader than the one of the SU(1,1) interferometer36,41.

To demonstrate tolerance to detection inefficiency, Fig. 4a shows the best phase sensitivity \({{\Delta }}{\phi }_{\min }\) versus the detection efficiency η. The photon number for the coherent beam and the input squeezing are kept constant; the common SNL is marked with a red dashed line. We observe that with G2 = 2.7 (green triangles), the system provides sub-shot-noise sensitivity for η > 34%. For G2 = 3.2 (blue circles), the best sensitivity proves more robust and overcomes the SNL for η = 13%.

Fig. 4: Loss tolerance through phase-sensitive amplification.
figure 4

a Best phase sensitivity as a function of detection efficiency η with G2 = 3.2 and G2 = 2.7 amplification (blue circles and green triangles, respectively). The SNL is the red dashed line and the lines show the theoretical model. The error bars in the vertical axis represent the standard error of the mean with a sample size of 1000 and the standard deviation for the horizontal axis. b The quantum advantage Q normalized to the ‘perfect detection' one Q0 = 17 versus the detection efficiency and parametric amplification. Points show the experimental parameters used with standard-deviation error bars.

Full size image

For any detection efficiency, by increasing G2 one can get as close as necessary to perfect-detection performance. Indeed, with an account for amplification, the quantum advantage in phase sensitivity is

$$Q={\left({Q}_{0}^{-1}+\frac{1-\eta }{\eta \mu }{e}^{-2{G}_{2}}\right)}^{-1},$$
(2)

where Q0 is the quantum advantage under perfect detection27 and (1 − μ) the internal loss. Figure 4b shows Q/Q0, where Q0 = 17 is determined by the initial 15 dB squeezing and 3% internal loss, as a function of η and G2. Blue and green points mark the parameters of our experiment. For very low detection efficiency, the required amplification can be unrealistically high, but G = 5, easily achievable in experiment36,40, already enables overcoming 98% loss.

Noteworthy, the detection of pulsed light we perform here has a considerable noise, equivalent to 500 photons per pulse. Yet, although this noise is much stronger than the SV (about 10 photons per pulse) and comparable to the coherent beam (1500 photons per pulse) injected into the interferometer, parametric amplification provides noise robustness and enables sub-shot-noise phase sensitivity. Meanwhile, it is the detection noise that prevents reaching the ‘perfect detection’ quantum advantage (green and blue points in Fig. 4b).

Discussion

We have demonstrated that for a squeezing-assisted interferometer the detrimental effects of detection loss and noise can be eliminated with a phase-sensitive parametric amplifier at the output. In particular, our experiment shows phase sensitivity overcoming the SNL by 6 dB even with 50% detection efficiency and noise comparable to the signal sensing the phase. Increasing the output amplification helps to overcome a higher amount of loss. By amplifying the output photon number about 600 times we overcome the SNL for detection efficiency down to 13%. Even lower detection efficiencies will not be an obstacle for squeezing-assisted measurements if stronger amplification is used; it is realistic to go down to 2% efficiency.

This result is relevant to many schemes where losses in the output optical path, including limited detection efficiency, reduce the advantage brought by squeezing. An example is the gravitational-wave detectors, where, due to the output losses, 7–10 dB of the input squeezing gives only ≈ 3 dB of the sensitivity gain11,12. Compensating for these losses with a continuous-wave scheme similar to ours could revolutionize gravitational-wave detection (note that the 6 dB gain in the phase sensitivity translates to almost an order of magnitude increase of the detection rate). Importantly, the homodyne scheme (used in gravitational-wave detectors) will also benefit from pre-amplification; moreover, unlike direct detection, it is not affected by detector dark noise27.

A similar amplification strategy will be valid for imaging experiments involving multimode radiation, considered theoretically in ref. 28. Indeed, the scheme could be accommodated to support more than a single spatial mode, similarly to ref. 42, and this opens up a considerable amount of experiments on sub-shot-noise imaging. The method will be also applicable to sub-shot-noise measurement of very small loss, where otherwise a very high detection efficiency is required28,43.

Detection efficiency proves to be an especially important constraint for experiments with mid-infrared and terahertz radiation, used for biological and industrial applications. Another case is where the whole angular spectrum of radiation cannot be collected due to small detector sizes. This is an issue in sub-shot-noise microscopy where high resolution compromises the detection efficiency18. In these cases, parametric amplification before detection will be indispensable.

Methods

Polarization Mach-Zehnder interferometer

is implemented using a single HWP (Fig. 2a). The input coherent state \(\left|\alpha \right\rangle\) has horizontal polarization and the SV state \(\left|\xi \right\rangle\), vertical polarization. The 50:50 beam splitters correspond to the transition between linear and circular polarization bases. The HWP with the optic axis at an angle δ introduces a phase shift ϕ = 4δ between the two arms, see Supplementary Information Sec. V. The HWP is a 45-μm-thick dual-wavelength waveplate: a HWP for 800 nm; a full-wave plate for 400 nm.

Parametric amplifiers

BBO1 and BBO2 are 2 mm BBO crystals pumped by the second harmonic of Spectra Physics Spitfire Ace laser (central wavelength 400 nm, horizontal polarization, average power 65 mW, waist intensity FWHM 240 ± 10 μm). Their squeeze factors G1,2 are found by measuring the mean numbers of photons N1,2 per pulse at their outputs in the regime of vacuum amplification (high-gain parametric down-conversion) and fitting with the parameters B1,2 the obtained dependences on the pump power P with the functions \({N}_{1,2}\propto {\sinh }^{2}{G}_{1,2}\), \({G}_{1,2}={B}_{1,2}\sqrt{P}\). By detuning BBO1 from exact phase matching, G1 is reduced compared to G2. The waist of the coherent beam is inside BBO2 and the waist intensity FWHM is chosen close to the one of the first Schmidt mode44, i.e. 80 ± 10 μm. This ensures mode matching for the coherent beam and, as a result, efficient amplification. Meanwhile, the SV is de-amplified efficiently only in the collinear direction due to its divergence, and spatial filtering at the detection stage is necessary for this purpose.

Pump intensity stabilization

We tap off part of the pump beam by BS1 (Fig. 2b), amplify the fluctuations (initially 2% RMS) approximately 7 times using high-gain parametric down-conversion, and post-select measurements for which the pump fluctuations were within 0.3% RMS (see Supplementary Information Sec. I).

The shot-noise limit for the phase sensitivity

is found as

$${{\Delta }}{\phi }_{{\rm{SNL}}}=\frac{1}{\sqrt{{N}_{\alpha }+{N}_{{\rm{SV}}}}},$$
(3)

where Nα and NSV are, respectively, the photon numbers of the coherent and SV beams inside the interferometer, i.e. at the HWP, within the spatial and spectral bandwidths registered at the detector. For the SV beam, we can use the estimate \({N}_{{\rm{SV}}} \sim {\sinh }^{2}{G}_{1}\). For the coherent beam, we measure with the photo-detector at the output of the interferometer an average number of photons per pulse of 720 ± 20, whose uncertainty is reduced by repeated measurements. Dividing this number by the total efficiency 49 ± 3%, we obtain Nα = 1500 ± 100 and, neglecting the small value of NSV, the SNL sensitivity is ΔϕSNL = 26 ± 1 mrad.

We also test the interferometer in the classical regime, by blocking the SV and leaving only the laser beam at the input. In this case, the phase sensitivity is much worse than SNL, due to the detection loss and noise (see Supplementary Information Sec. III). We note that it is this test that identifies the SNL in most of experiments. While it might work for continuous-wave lasers, it leads to the overestimation of the SNL for pulsed light, which usually has stronger intensity fluctuations.