Shannon Entropy Rate of Hidden Markov Processes

Abstract

Hidden Markov chains are widely applied statistical models of stochastic processes, from fundamental physics and chemistry to finance, health, and artificial intelligence. The hidden Markov processes they generate are notoriously complicated, however, even if the chain is finite state: no finite expression for their Shannon entropy rate exists, as the set of their predictive features is generically infinite. As such, to date one cannot make general statements about how random they are nor how structured. Here, we address the first part of this challenge by showing how to efficiently and accurately calculate their entropy rates. We also show how this method gives the minimal set of infinite predictive features. A sequel addresses the challenge’s second part on structure.

1 Introduction

Randomness is as necessary to physics as determinism. Indeed, since Henri Poincaré’s failed attempt to establish the orderliness of planetary motion, it has been understood that both determinism and randomness are essential and unavoidable in the study of physical systems [1,2,3,4]. In the 1960s and 1970s, the rise of dynamical systems theory and the exploration of statistical physics of critical phenomena offered up new perspectives on this duality. The lesson was that intricate structures in a system’s state space amplify uncertainty, guiding it and eventually installing it—paradoxically—in complex spatiotemporal patterns. Accepting this state of affairs prompts basic, but as-yet unanswered questions. How is this emergence monitored? How do we measure a system’s randomness or quantify its patterns and their organization?

The tools needed to address these questions arose over recent decades during the integration of Turing’s computation theory [5,6,7], Shannon’s information theory [8], and Kolmogorov’s dynamical systems theory [9,10,11,12,13]. This established the vital role that information plays in physical theories of complex systems. In particular, the application of hidden Markov chains to model and analyze the randomness and structure of physical systems has seen considerable success, not only in complex systems [14], but also in coding theory [15], stochastic processes [16], stochastic thermodynamics [17], speech recognition [18], computational biology [19, 20], epidemiology [21], and finance [22], to offer a nonexhaustive list of examples.

Shannon showed that given a finite-state predictive hidden Markov chain (HMC), one may directly and accurately calculate the generated process’ irreducible randomness [8]—now called the Shannon entropy rate. Furthermore, for such a process, there is a unique, minimal, and finite set of maximally predictive features, known as the causal states. The features may be used to construct an optimally predictive, finite-state HMC that generates the process [23], known as the $\epsilon -machine$. The $\epsilon -machine$ ’s mathematical description gives a constructive definition of a process’ structural complexity as the amount of memory required to generate the process.

Loosening the predictive constraint to consider a wider class of generated processes, however, leads to major roadblocks. In fact, predicting a process generated by an arbitrary nonpredictive finite-state HMC requires an infinite set of causal states [24]. That is, though “finitely” generated, the process cannot be predicted by any finite HMC. Practically, this precludes determining the process’ entropy rate using Shannon’s result and stymies characterization of its structural complexity. To date, working with infinite causal states required coarse-graining to produce a finite set of suboptimally-predictive features. Fortunately, the tradeoffs between resource constraints and predictive power induced by such coarse graining can be systematically laid out [25,26,27]. Although the problem of HMC entropy rate is well studied [15, 28,29,30,31,32,33], fully quantifying HMC-generated process randomness and structure in general is an open problem.

The following introduces a direct approach to working with this class of processes. First, causal states of an arbitrary nonpredictive HMC are shown to be equivalent (with mild constraints) to the mixed states, a construction formally introduced by Blackwell over a half century ago [29]. Second, the generation of uncountably infinite sets of mixed states is identified as a chaotic dynamical system—specifically, a (place dependent) iterated function system (IFS). This obviates analyzing the process via coarse graining. Rather, the complex dynamics of the chaotic system directly captures the information-theoretic properties of the generated process. Specifically, this allows exactly calculating the entropy rate of the process generated by the original HMC. Additionally, the dynamical systems perspective provides new insight into the causal-state structure and complexity of infinite causal-state processes. This has direct application to the study of randomness and structure in a wide range of physical systems.

In point of fact, the following and its sequel [34] were proceeded by two companions that applied the theoretical results here to two, rather different, physical domains. The first analyzed the origin of randomness and structural complexity engendered by quantum measurement [35]. The second solved a longstanding problem on exactly determining the thermodynamic functioning of Maxwellian demons, aka information engines [36]. That is, the following and its sequel lay out the mathematical and algorithmic tools required to successfully analyze these applied problems. We believe the new approach is destined to find even wider applications.

Section 2 recalls the necessary background in stochastic processes, hidden Markov chains, and information theory. Section 3 reviews the needed results on iterated function systems; while Sect. 4 develops mixed states and their dynamic—the mixed-state presentation. The main result connecting these then follows in Sect. 5, showing that the mixed-state presentation is an IFS and that it produces an ergodic process. Section 6 recalls Blackwell’s theory, updating it for our present purpose of determining the entropy rate of any HMC. The Supplementary Materials provide background on the asymptotic equipartition property and minimality of the mixed states. They also constructively work through the results for several example nonunifilar HMCs. They close with the statistical error analysis underlying entropy-rate estimation.

2 Hidden Markov Processes

A stochastic process $\mathcal {P}$ is a probability measure over a bi-infinite chain $\ldots \, X_{t-2} \, X_{t-1} \, X_{t} \, X_{t+1} \, X_{t+2} \ldots$ of random variables, each denoted by a capital letter. A particular realization $\ldots \, x_{t-2} \, x_{t-1} \, x_{t} \, x_{t+1} \, x_{t+2} \ldots$ is denoted via lowercase letters. We assume values $x_{t}$ belong to a discrete alphabet $\mathcal {A}$. We work with blocks ${X}_{t:t^\prime }$, where the first index is inclusive and the second exclusive: ${X}_{t:t^\prime } = X_{t} \ldots X_{t^\prime -1}$. $\mathcal {P}$’s measure is defined via the collection of distributions over blocks: $\{ \Pr ({X}_{t:t^\prime }): t < t^\prime , t,t^\prime \in \mathbb {Z} \}$.

To simplify the development, we restrict to stationary, ergodic processes: those for which ${\mathrm{Pr}}({X}_{t:t+\ell }) = {\mathrm{Pr}}({X}_{0:\ell })$ for all $t \in \mathbb {Z}$, $\ell \in \mathbb {Z}^+$, and individual infinite realizations capture those statistics. In such cases, we only need to consider a process’s length-$\ell$ word distributions ${\mathrm{Pr}}({X}_{0:\ell })$.

A Markov process is one for which $\Pr (X_t|{X}_{-\infty :t}) = \Pr (X_t|X_{t-1})$. A hidden Markov process is the output of a memoryless channel [37] whose input is a Markov process [16].

2.1 Hidden Markov Chains

Working with processes directly is cumbersome, so we turn to consider finitely-specified mechanistic models that generate them.

Definition 1

A finite-state edge-labeled hidden Markov chain (HMC) consists of:

• 1. a finite set of states ${\varvec{{\mathcal {S}}}}= \{\sigma _1, ... , \sigma _N \}$,

• 2. a finite alphabet $\mathcal {A}$ of k symbols $x \in \mathcal {A}$, and

• 3. a set of N by N symbol-labeled transition matrices $T^{(x)}$, $x \in \mathcal {A}$: $T^{(x)}_{ij} = \Pr (\sigma _j,x|\sigma _i)$. The corresponding overall state-to-state transitions are described by the row-stochastic matrix $T = \sum _{x \in \mathcal {A}} T^{(x)}$.

Fig. 1

A hidden Markov chain (HMC) with two states, $\{\sigma _1, \sigma _2 \}$ and two symbols $\{\square , \triangle \}$. It is unifilar

Any given stochastic process can be generated by any number of HMCs. These are called a process’ presentations.

We now introduce a structural property of HMCs that has important consequences in characterizing process randomness and internal state structure.

Definition 2

A unifilar HMC (uHMC) is an HMC such that for each state $\sigma _i \in {\varvec{{\mathcal {S}}}}$ and each symbol $x \in \mathcal {A}$ there is at most one outgoing edge from state $\sigma _i$ labeled with symbol x.

One consequence is that a uHMC’s states are predictive in the sense that each is a function of the prior emitted sequence—the past ${x}_{-\infty :t} = \ldots x_{t-2} x_{t-1} x_t$. Consider an infinitely-long past that, in the present, has arrived at state $\sigma _t$. For uHMCs, it is not required that this infinitely-long past arrive at a unique state, but it is the case that any state arrived at by this past must have the same past-conditioned distribution of future sequences $\Pr ({X}_{\infty :t} | {x}_{-\infty :t})$. We call this deterministic relationship between the past and the future a prediction.

In comparison, a nonpredictive generative (nonunifilar) HMC may return a set of states with varying conditional future distributions upon seeing this infinite past. All that is required for accurate generation is that, if this were to be repeated many times, averaging over these conditional future distributions returns the the unique conditional future distribution $\Pr ({X}_{\infty :t} | {x}_{-\infty :t})$ given by the predictive uHMC state.

Although there are many generative and predictive presentations for a process $\mathcal {P}$, there is a canonical presentation that is unique: a process’ $\epsilon -machine$.

Definition 3

An $\epsilon -machine$ is a uHMC with probabilistically distinct states: For each pair of distinct states $\sigma _i, \sigma _j \in {\varvec{{\mathcal {S}}}}$ there exists a finite word $w = {x}_{0:\ell -1}$ such that:

$$\begin{aligned} {\mathrm{Pr}}({X}_{0:\ell } = w|{\mathcal {S}}_0 = \sigma _k) \not = {\mathrm{Pr}}({X}_{0:\ell } = w|{\mathcal {S}}_0 = \sigma _j)~. \end{aligned}$$

A process’ $\epsilon -machine$ is its optimal, minimal presentation, in the sense that the set ${\varvec{{\mathcal {S}}}}$ of predictive (or causal) states is minimal compared to all its other unifilar presentations [38].

2.2 Entropy Rate of HMCs

A process’ intrinsic randomness is the information in the present measurement, discounted by having observed the information in an infinitely long history. It is measured by Shannon’s source entropy rate [8].

Definition 4

A process’ entropy rate $h_\mu$ is the asymptotic average entropy per symbol [39]:

$$\begin{aligned} h_\mu = \lim _{\ell \rightarrow \infty } \frac{{\text {H}}[{X}_{0:\ell } ]}{\ell } ~, \end{aligned}$$

(1)

where $H[{X}_{0:\ell } ]$ is the Shannon entropy of block ${X}_{0:\ell }$:

$$\begin{aligned} H[{X}_{0:\ell } ] = - \sum _{{x}_{0:\ell } \in \mathcal {A}^\ell } \Pr ({x}_{0:\ell }) \log _2 \Pr ({x}_{0:\ell }) ~. \end{aligned}$$

(2)

An equivalent, but more rapidly converging version is found using the conditional entropy:

$$\begin{aligned} h_\mu = \lim _{\ell \rightarrow \infty } {\text {H}}[X_0|{X}_{-\ell :0} ] ~. \end{aligned}$$

(3)

Given a finite-state unifilar presentation $M_u$ of a process $\mathcal {P}$, we may directly calculate the entropy rate from the transition matrices of the uHMC [8]:

$$\begin{aligned} h_\mu (\mathcal {P})&= h_\mu (M_u) \nonumber \\&= - \sum _{\sigma \in {\varvec{{\mathcal {S}}}}} \Pr (\sigma ) \sum _{x \in \mathcal {A}} T_{\sigma \sigma ^\prime }^{(x)} \log _2 T_{\sigma \sigma ^\prime }^{(x)} ~. \end{aligned}$$

(4)

Here, $\Pr (\sigma )$ is the internal Markov chain’s stationary state distribution, denoted $\pi$ and determined by T’s left eigenvector normalized in probability: $\pi = \pi T$.

Blackwell showed, though, that in general for processes generated by HMCs there is no closed-form expression for the entropy rate [29]. For a process generated by an nonunifilar HMC M, applying Eq. (4) to M typically overestimates the true entropy rate of the process $h_\mu (\mathcal {P})$:

$$\begin{aligned} h_\mu (M) \ge h_\mu (\mathcal {P}) ~. \end{aligned}$$

Overcoming this limitation is one of our central results. We now embark on introducing the necessary tools for this.

3 Iterated Function Systems

To get there, we must take a short detour to review iterated function systems (IFSs) [40], as they play a critical role in analyzing HMCs. Speaking simply, we show that HMCs are stochastic dynamical systems—namely, IFSs.

Let $(\Delta ^N, d)$ be a compact metric space with $d(\cdot ,\cdot )$ a distance. This notation anticipates our later application, in which $\Delta ^N$ is N-simplex of discrete-event probability distributions (see Sect. 4.1). However, the results here are general.

Let $f^{(x)}: \Delta ^N \rightarrow \Delta ^N$ for $x = 1, \dots , k$ be a set of Lipschitz functions with:

$$\begin{aligned} d\left( f^{(x)} (\eta ), f^{(x)} (\zeta ) \right) \le \tau ^{(x)} d(\eta , \zeta ) ~, \end{aligned}$$

for all $\eta , \zeta \in \Delta ^N$ and where $\tau ^{(x)}$ is a constant. This notation is chosen to draw an explicit parallel to the stochastic processes discussed in Sect. 2 and to avoid confusion with the lowercase Latin characters used for realizations of stochastic processes. In particular, note that the superscript (x) here and elsewhere parallels that of the HMC symbol-labeled transition matrices $T^{(x)}$. The reasons for this will soon become clear.

The Lipschitz constant $\tau ^{(x)}$ is the contractivity of map $f^{(x)}$. Let $p^{(x)} : \Delta ^N \rightarrow [0,1]$ be continuous, with $p^{(x)}(\eta ) \ge 0$ and $\sum _{x=1}^k p^{(x)}(\eta ) = 1$ for all $\eta$ in M. The triplet $\{\Delta ^N,\{p^{(x)}\},\{f^{(x)}\}: x \in \mathcal {A}\}$ defines a place-dependent IFS.

A place-dependent IFS generates a stochastic process over $\eta \in \Delta ^N$ as follows. Given an initial position $\eta _0 \in \Delta ^N$, the probability distribution $\{ p^{(x)}(\eta _0) : x = 1, \dots , k \}$ is sampled. According to the sample x, apply $f^{(x)}$ to map $\eta _0$ to the next position $\eta _1 = f^{(x)}(\eta _0)$. Resample x from the distribution $p^{(x)}(\eta _1)$ and continue, generating $\eta _0, \eta _1, \eta _2, \ldots$.

If each map $f^{(x)}$ is a contraction—i.e., $\tau ^{(x)} < 1$ for all $\eta , \zeta \in \Delta ^N$—it is well known that there exists a unique nonempty compact set $\Lambda \subset \Delta ^N$ that is invariant under the IFS’s action:

$$\begin{aligned} \Lambda = \bigcap _{x=1}^k f^{(x)}(\Lambda ) ~. \end{aligned}$$

$\Lambda$ is the IFS’s attractor.

Consider the operator $V : M(\Delta ^N) \rightarrow M(\Delta ^N)$ on the space of Borel measures on the N-simplex:

$$\begin{aligned} V \mu (B) = \sum ^k_{x =1} \int _{\left( f^{(x)}\right) ^{-1} (B) } p^{(x)}(\eta ) d \mu (\eta ) ~. \end{aligned}$$

(5)

A Borel probability measure $\mu$ is said to be invariant or stationary if $V\mu = \mu$. It is attractive if for any probability measure $\nu$ in $M(\Delta ^N)$:

$$\begin{aligned} \int g d(V^n \nu ) \rightarrow \int g \mu ~, \end{aligned}$$

for all g in the space of bounded continuous functions on $\Delta ^N$.

Let’s recall here a key result concerning the existence of attractive, invariant measures for place-dependent IFSs.

Theorem 1

[41, Thm. 2.1] Suppose there exists $r<1$ and $q>0$ such that:

$$\begin{aligned} \sum _{x\in \mathcal {A}} p^{(x)} (\eta ) d^q \left( f^{(x)} (\eta ), f^{(x)} (\zeta ) \right) \le r^q d^q \left( \eta , \zeta \right) ~, \end{aligned}$$

for all $\eta , \zeta \in \Delta ^N$. Assume that the modulus of uniform continuity of each $p^{(x)}$ satisfies Dini’s condition and that there exists a $\delta > 0$ such that:

$$\begin{aligned} \sum _{x: d(f^{(x)}(\eta ), f^{(x)}(\zeta )) \le r d(\eta , \zeta )} p^{(x)}(\eta ) p^{(x)}(\zeta ) \le \delta ^2 ~, \end{aligned}$$

(6)

for all $\eta , \zeta \in \Delta ^N$. Then there is an attractive, unique, invariant probability measure for the Markov process generated by the place-dependent IFS.

In addition, under these same conditions Ref. [42] established an ergodic theorem for IFS orbits. That is, for any $\eta \in \Delta ^N$ and $g: \Delta ^N \rightarrow \Delta ^N$:

$$\begin{aligned} \frac{1}{n+1} \sum _{k=0}^n g(w_{x_k} \circ \dots \circ w_{x_1} \eta ) \rightarrow \int g d \mu ~. \end{aligned}$$

(7)

4 Mixed-State Presentation

We now return to stochastic processes and their HMC presentations. When calculating entropy rates from various presentations, we noted that nonunifilar HMC presentations led to difficulties: (i) the internal Markov-chain $\{{\varvec{{\mathcal {S}}}}, T\}$ entropy-rate overestimates the process’ entropy rate and (ii) there is no closed-form entropy-rate expression. Furthermore, the states of nonunifilar HMCs are nonpredictive, there is no (known) unique minimal nonunifilar presentation of a given process. This precludes characterizing, in a unique and minimal way, a process’ structural complexity directly from a nonunifilar presentation.

To develop the tools needed to resolve these problems, we introduce HMC mixed states and their dynamic. To motivate our development, consider the problem of observer-process synchronization.

Assume that an observer has knowledge of a finite HMC M generating a process $\mathcal {P}$. The observer cannot directly observe M’s internal states, but wishes to know which internal state M is in at any given time—to synchronize to the machine. Since the observer does have knowledge of M’s transition dynamic, they can improve on their initial guess $\left( \Pr (\sigma _1), \Pr (\sigma _2), \dots , \Pr (\sigma _N) \right)$ by monitoring the output data $x_{0} \, x_{1} \, x_{2} \ldots$ that M generates.

4.1 Mixed States

For a length-$\ell$ word w generated by M let $\eta (w) = {\mathrm{Pr}}({\varvec{{\mathcal {S}}}}|w)$ be the observer’s guess as to the process’ current state after observing w:

$$\begin{aligned} \eta (w)&\equiv {\mathrm{Pr}}({\mathcal {S}}_\ell | {X}_{0:\ell } =w, {\mathcal {S}}_0 \sim \pi ) ~, \end{aligned}$$

(8)

where the initial guess $\Pr ({\mathcal {S}}_0 | \cdot )$ is $\pi$, M’s stationary state distribution. When observing a N-state machine, the vector $\left\langle \eta (w)\right|$ lives in the (N-1)-simplex $\Delta ^{N-1}$, the set such that:

$$\begin{aligned} \{ \eta \in \mathbb {R}^{N} : \langle \eta \left| {\mathbf {1} } \right\rangle = 1, \langle \eta \left| \delta _i\right\rangle \ge 0, i=1, \dots , N \} ~, \end{aligned}$$

where $\left\langle \delta _i\right| = \begin{pmatrix} 0&0&\dots&1&\dots&0 \end{pmatrix}$ and $\left| {\mathbf {1} } \right\rangle = \begin{pmatrix} 1&1&\dots&1 \end{pmatrix}$. We use this notation to indicate components of the belief distribution vector $\eta$ in order to avoid confusion with temporal indexing. When a mixed state appears in probability expressions, the notation refers to the random variable $\eta$, not the row vector $\left| \eta \right\rangle$, and we drop the bra-ket notation. Bra-ket notation is used in vector-matrix expressions.

The 0-simplex $\Delta ^0$ is the single point $\left| \eta \right\rangle = (1)$, the 1-simplex $\Delta ^1$ is the line segment [0, 1] from $\left| \eta \right\rangle = (0,1)$ to $\left| \eta \right\rangle = (1,0)$, and so on.

The set of belief distributions $\eta (w)$ that an HMC can visit defines its set ${\varvec{{\mathcal {R}}}}$ of mixed states:

$$\begin{aligned} {\varvec{{\mathcal {R}}}}= \{ \eta (w): w \in \mathcal {A}^+, \Pr (w) > 0 \} ~. \end{aligned}$$

Generically, the mixed-state set ${\varvec{{\mathcal {R}}}}$ for an N-state HMC is infinite, even for finite N [29].

4.2 Mixed-State Dynamic

The probability of transitioning from $\left\langle \eta (w)\right|$ to $\left\langle \eta (wx)\right|$ on observing symbol x follows from Eq. (8) immediately:

$$\begin{aligned} \Pr (\eta (wx) | \eta (w)) = \Pr (x|{\mathcal {S}}_\ell \sim \eta (w)) ~. \end{aligned}$$

This defines the mixed-state transition dynamic $\mathcal {W}$. Together the mixed states and their dynamic define an HMC that is unifilar by construction. This is a process’ mixed-state presentation (MSP) $\mathcal {U}(\mathcal {P}) = \{{\varvec{{\mathcal {R}}}}, \mathcal {W}\}$.

We defined a process’ $\mathcal {U}$ abstractly. The $\mathcal {U}$ typically has an uncountably infinite set of mixed states, making it challenging to work with in the form laid out in Sect. 4.1. Usefully, however, given any HMC M that generates the process, we can explicitly write down the dynamic $\mathcal {W}$. Assume we have an $N+1$-state HMC presentation M with k symbols $x \in \mathcal {A}$. The initial condition is the invariant probability $\pi$ over the states of M, so that $\left\langle \eta _0\right| = \left\langle \pi \right|$. In the context of the mixed-state dynamic, mixed-state subscripts denote time.

Fig. 2

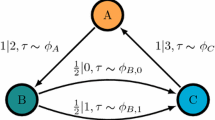
Determining the mixed-state presentation (MSP) of the 2-state unifilar HMC shown in (a): The invariant state distribution $\pi = (2/3, 1/3)$. It becomes the first mixed state $\eta _0$ used in (b) to calculate the next set of mixed states. c The full set of mixed states seen from all allowed words. In this case, we recover the unifilar HMC shown in (a) as the MSP’s recurrent states

The probability of generating symbol x when in mixed state $\eta$ is:

$$\begin{aligned} \Pr (x|\eta ) = \left\langle \eta \right| T^{(x)} \left| {\mathbf {1} } \right\rangle ~, \end{aligned}$$

(9)

where $T^{(x)}$ is M’s symbol-labeled transition matrix associated with the symbol x.

From $\eta _0$, we calculate the probability $\left\langle \eta _{1, x}\right|$ of seeing each $x \in \mathcal {A}$. Upon seeing symbol x, the current mixed state $\left\langle \eta _t\right|$ is updated according to:

$$\begin{aligned} \left\langle \eta _{t+1, x}\right| = \frac{\left\langle \eta _t\right| T^{(x)}}{\left\langle \eta _t\right| T^{(x)} \left| {\mathbf {1} } \right\rangle } ~. \end{aligned}$$

(10)

Fig. 3

Determining the mixed-state presentation of the 2-state nonunifilar HMC shown in (a). The invariant distribution $\pi = (1/2, 1/2)$. It is the first mixed state $\eta _0$ used in (b) to calculate the next set of mixed states. b plots the mixed states along the 1-simplex $\Delta ^1 = [0,1]$. In (c), we translated the points on the simplex to the states of an infinite-state, unifilar HMC

Thus, given an HMC presentation we can restate Eq. (8) as:

$$\begin{aligned} \left\langle \eta (w)\right|&= \frac{\left\langle \eta _0\right| T^{(w)}}{\left\langle \eta _0\right| T^{(w)} \left| {\mathbf {1} } \right\rangle } \\&= \frac{\left\langle \pi \right| T^{(w)}}{\left\langle \pi \right| T^{(w)} \left| {\mathbf {1} } \right\rangle } ~. \end{aligned}$$

Equation (10) tells us that, by construction, the MSP is unifilar, since each possible output symbol uniquely determines the next (mixed) state. Taken together, Eqs. (9) and (10) define the mixed-state transition dynamic $\mathcal {W}$ as:

$$\begin{aligned} \Pr (\eta _{t+1},x|\eta _t)&= \Pr (x|\eta _t) \\&= \left\langle \eta _t\right| T^{(x)} \left| {\mathbf {1} } \right\rangle ~, \end{aligned}$$

for all $\eta \in {\varvec{{\mathcal {R}}}}$, $x \in \mathcal {A}$.

To find the MSP $\mathcal {U}= \{{\varvec{{\mathcal {R}}}}, \mathcal {W}\}$ for a given HMC M we apply mixed-state construction:

• 1. Set $\mathcal {U}= \{ {\varvec{{\mathcal {R}}}}= \emptyset , \mathcal {W}= \emptyset \}$.

• 2. Calculate M’s invariant state distribution: $\pi = \pi T$.

• 3. Take $\eta _0$ to be $\left\langle \delta _\pi \right|$ and add it to ${\varvec{{\mathcal {R}}}}$.

• 4. For each current mixed state $\eta _t \in {\varvec{{\mathcal {R}}}}$, use Eq. (9) to calculate $\Pr (x | \eta _t )$ for each $x \in \mathcal {A}$.

• 5. For $\eta _t \in {\varvec{{\mathcal {R}}}}$, use Eq. (10) to find the updated mixed state $\eta _{t+1, x}$ for each $x \in \mathcal {A}$.

• 6. Add $\eta _{t}$’s transitions to $\mathcal {W}$ and each $\eta _{t+1, x}$ to ${\varvec{{\mathcal {R}}}}$, merging duplicate states.

• 7. For each new $\eta _{t+1}$, repeat steps 4-6 until no new mixed states are produced.

Let us walk through these steps with a simple finite-state example. In Fig. 2a we have a unifilar HMC, which happens to be an $\epsilon -machine$. The invariant state distribution of the machine is $\pi = \left( 2/3, 1/3 \right)$, so in Fig. 2b this becomes our initial mixed state $\eta _0$. Following steps 4 and 5 in the mixed-state construction, we calculate the probabilities of transition for each symbol in the alphabet $\left\{ \triangle , \square \right\}$ and their resultant mixed states $\left\{ \eta _{0, \triangle }, \eta _{0, \square } \right\}$. We then relabel these new mixed states $\left\{ \eta _1, \eta _2\right\}$ and repeat. This process eventually results in Fig. 2c, in which all possible transitions and mixed states have been found.

In Fig. 2c the recurrent states of the MSP, $\left\{ \eta _2,\eta _{3}\right\}$, match exactly with the states of the original machine $\left\{ \sigma _0, \sigma _1 \right\}$. Therefore, the recurrent part of the $\mathcal {U}(M)$ is exactly the $\epsilon -machine$. When starting with the $\epsilon -machine$, trimming the transient states from the $\mathcal {U}(\epsilon -machine)$ in this way always returns the recurrent-state $\epsilon -machine$, as in the above case. In general, if $\mathcal {U}(M)$ is finite, we find the $\epsilon -machine$ by minimizing $\mathcal {U}(M)$ via merging duplicate states: repeat mixed-state construction on $\mathcal {U}(M)$ and trim transient states once more.

Fig. 4

Figures a–c each plot $10^5$ mixed states of the uncountably-infinite state MSP generated by the parametrized 3-state HMC defined in Eq. (S1) at various values of x and $\alpha$. This HMC is capable of generating MSPs with a variety of structures, depending on x and $\alpha$. However, due to rotational symmetry in the symbol-labeled transition matrices, the attractor is always radially symmetric around the simplex center

Is the MSP always the same as the $\epsilon -machine$? When beginning with a finite, unifilar HMC M generating a process $\mathcal {P}$, the MSP $\mathcal {U}(M)$ is a finite, optimally-predictive rival presentation to $\mathcal {P}$’s $\epsilon -machine$. Trimming the transient states will always return the recurrent-state $\epsilon -machine$, as in the above case. The MSPs of unifilar presentations are interesting and contain additional information beyond the unifilar presentations. For example, containing transient causal states, they are employed in calculating many complexity measures that track convergence statistics [43].

However, here we focus on the mixed-state presentations of nonunifilar HMCs, which typically have an infinite mixed-state set ${\varvec{{\mathcal {R}}}}$. Figure 3 illustrates applying mixed-state construction to a finite, nonunifilar HMC. This produces an infinite sequence of states mixed on the 1-simplex, as depicted in Fig. 3b. In this particular example, the MSP is clearly structured and ${\varvec{{\mathcal {R}}}}$ is countably infinite, allowing us to better understand the underlying process $\mathcal {P}$; compared, say, to the 2-state nonunifilar HMC in Fig. 3a. This is, indeed, the $\epsilon -machine$, as is clear from the fact $\eta _n$ are probabilistically distinct and predictive. From the causal states, the process’ structure—a discrete-time renewal process—becomes manifest and the entropy rate may be directly calculated, adapting Eq. (4), as an infinite sum over the states $\eta _n$ as $n \rightarrow \infty$.

That said, MSPs of nonunifilar HMCs typically have an uncountably-infinite mixed-state set ${\varvec{{\mathcal {R}}}}$: Fig. 4 shows three attractors from the same parameterized 3-state HMC (defined in Eq. (S1)) at different points in its parameter space. Our goal then is a set of constructive results for this class of $\mathcal {U}$s: for a given nonunifilar finite-state HMC, determine whether we are guaranteed to have (i) a well-defined, unique, mixed-state set ${\varvec{{\mathcal {R}}}}$, (ii) an invariant measure over $\mu ({\varvec{{\mathcal {R}}}})$, (iii) an ergodic theorem, and (iv) a notion of minimality. With these established, we can use $\mathcal {U}$ as a candidate for a process’ $\epsilon -machine$.

5 MSP as an IFS

With the mixed-state presentation introduced and the goals outlined, our intentions in reviewing iterated function systems (IFSs) become explicit. The MSP exactly defines a place-dependent IFS, where the mapping functions are the set of symbol-labeled mixed-state update functions of Eq. (10) and the set of place-dependent probability functions are given by Eq. (9). We then have a mapping function and associated probability function for each symbol $x \in \mathcal {A}$ that can be derived from the symbol-labeled transition matrix $T^{(x)}$.

If these probability and mapping functions meet the conditions of Theorem 1, we identify the attractor $\Lambda$ as the set of mixed states ${\varvec{{\mathcal {R}}}}$ and the invariant measure $\mu$ as the invariant distribution $\pi$ of the potentially infinite-state $\mathcal {U}$—the original HMC’s Blackwell measure. Since all Lipschitz continuous functions are Dini continuous, the probability functions meet the conditions by inspection.

We now establish that the maps are contractions. For maps defined by nonnegative, aperiodic, and irreducible matrices, we appeal to Birkhoff’s 1957 proof that a positive linear map preserving a convex cone is a contraction under the Hilbert projection metric [44]. This result, which may be extended to any nonnegative $T^{(x)}$ if there is an $N \in \mathbb {N}^+$ such that $\left( T^{(x)} \right) ^N$ is a positive matrix, is summarized in Appendix C.

Although this covers a broad class of nonunifilar HMCs, we are not guaranteed irreducibility and aperiodicity for symbol-labeled transition matrices. Indeed, several of the more interesting examples encountered do not meet this standard. For example, consider the Simple Nonunifilar Source (SNS), depicted in Fig. 3, defined by the symbol-labeled transition matrices:

$$\begin{aligned} T^{(\triangle )} = \begin{pmatrix} 1-p &{} p \\ 0 &{} 1-q \end{pmatrix} ~\text {and}~ T^{(\square )} = \begin{pmatrix} 0 &{} 0 \\ q &{} 0 \end{pmatrix} ~. \end{aligned}$$

(11)

In this case both $T^{(\triangle )}$ and $T^{(\square )}$ are reducible. (A quick check for this property is to examine Fig. 3a and ask if there is a length-n sequence consisting of only a single symbol that reaches every state from every other state.) Nonetheless, the HMC has a countable set of mixed states ${\varvec{{\mathcal {R}}}}$ and an invariant measure $\mu$.

We can show this with the mapping functions:

$$\begin{aligned} f^{(\triangle )}(\eta )&= \left[ \frac{ \langle \eta \left| \delta _1\right\rangle (1-p)}{1 - (1- \langle \eta \left| \delta _1\right\rangle )q} , \frac{\langle \eta \left| \delta _1\right\rangle p + (1-\langle \eta \left| \delta _1\right\rangle )(1-q)}{1 + (1-\langle \eta \left| \delta _1\right\rangle )q} \right] ~\text {and}~ \nonumber \\ f^{(\square )}(\eta )&= \left[ 1, 0 \right] ~. \end{aligned}$$

(12)

Recall here that $\langle \eta \left| \delta _1\right\rangle$ is simply the first component of $\eta$. From any initial state $\eta _0$, other than $\eta _0 = \sigma _0 = \left[ 1,0 \right]$, the probability of seeing a $\square$ is positive. Once a $\square$ is emitted, the mixed state is guaranteed to be $\eta = \sigma _0 = \left[ 1, 0 \right]$. When the mapping function is constant in this way and the contractivity is $-\infty$, we call the symbol a synchronizing symbol. From $\sigma _0$, the set of mixed states is generated by repeated emissions of $\triangle$s, so that ${\varvec{{\mathcal {R}}}}= \left\{ \left( f^{(\triangle ) } \right) ^n (\sigma _0 ) : n = 0, \dots , \infty \right\}$. This is visually depicted in Fig. 3 for the specific case of $p = q = 1/2$. For all p and q, the measure can be determined analytically; see Ref. [45]. This analyticity is due to the HMC’s countable-state structure, a consequence of the synchronizing symbol.

This example, including the uniqueness of the IFS attractor $\Lambda$, helps establish which HMC class generates ergodic processes: those whose total transition matrix $T = \sum _x T^{(x)}$ is nonnegative, irreducible, and aperiodic. Consider an HMC in this class. Define for any word $w = x_1 \ldots x_\ell \in \mathcal {A}^+$ the associated mapping function $T^{(w)} = T^{(x_1)} \circ \cdots \circ T^{(x_\ell )}$. Consider word w in a process’ typical set of realizations (see Appendix A), which approaches measure one as $\vert w \vert \rightarrow \infty$. Due to ergodicity, it must be the case that $f^{(w)}$ is either (i) a constant mapping—and, therefore, infinitely contracting—or (ii) $T^{(w)}$ is irreducible.

As an example of case (i), any composition of the SNS functions Eq. (12) is always a constant function, so long as there is at least one $\square$ in the word, the probability of which approaches one as the word grows in length.

As an example of case (ii), imagine adding to the SNS in Fig. 3a a transition on $\square$ from $\sigma _0$ to $\sigma _1$. For this new machine, both symbol-labeled transition matrices are still reducible, but the composite transition matrices for any word including both symbols will be irreducible. By Birkhoff’s argument, the map associated with that word is contracting. There are only two sequences for which this does not occur: $w = \square ^{N}$ and $w' = \triangle ^{N}$. However, these sequences are measure zero as $N \rightarrow \infty$. Appendix A discusses this argument further.

In short, we extend the result of Theorem 1 to any HMC with nonnegative substochastic transition matrices, as long as $T = \sum _x T^{(x)}$ is nonnegative, irreducible, and aperiodic, regardless of the properties of the individual maps.

Before moving on, let us highlight the implications of this result. For any process $\mathcal {P}$ that may be generated by a finite-state HMC, we now have a guarantee of a unique, attracting set of mixed states ${\varvec{{\mathcal {R}}}}$, with an invariant, attracting measure $\mu ({\varvec{{\mathcal {R}}}})$. Furthermore, we appeal to established IFS results for an ergodic theorem over long words [42]. Then, by introducing a check for minimality (discussed in Appendix B), we identify the MSP $\mathcal {U}(M)$ as the infinite-state $\epsilon -machine$ for the process $\mathcal {P}$ generated by M.

This gives a constructive way to generate the causal states of a broad class of processes and determine their intrinsic randomness and complexity. As Fig. 4 makes clear, $\mathcal {U}$s produce highly structured, fractal-like causal-states sets. The following restricts to these sets to calculate the entropy rate $h_\mu$, but the sequels [34, 46] extend our ability to characterize the structure of these complex systems with tools from dynamical systems, dimension theory, and information theory.

Fig. 5

Entropy rate for 250, 000 parametrized HMCs generated according to the definition in Eq. (S1), over $x \in [0.0,0.5]$ and $\alpha \in [0.0,1.0]$. Examples of the MSPs produced are plotted in Fig. 4. The entropy rate of each, as estimated by Eq. (16), is plotted, showing the gradual change in entropy rate across the parameter space

6 Entropy of General HMCs

Blackwell analyzed the entropy of functions of finite-state Markov chains [29]. With a shift in notation, functions of Markov chains can be identified as general hidden Markov chains. This is to say, both presentation classes generate the same class of stochastic processes. As noted above, the entropy rate problem for finite unifilar hidden Markov chains was solved with Shannon’s entropy rate expression Eq. (4). However, as Blackwell noted, there is no analogous closed-form expression for the entropy rate of a finite nonunifilar HMC.

6.1 Blackwell Entropy Rate

That said, Blackwell gave an expression for the entropy rate of general HMCs, by introducing mixed states over stationary, ergodic, finite-state chains. (Although he does not refer to them as such.) His main result, retaining his original notation, is transcribed here and adapted by us to constructively solve the HMC entropy-rate problem.

Theorem 2

([29, Thm. 1].) Let $\{ x_n, - \infty< n < \infty \}$ be a stationary ergodic Markov process with states $i = 1, \dots , I$ and transition matrix $M = \left\| m(i,j) \right\|$. Let $\Phi$ be a function defined on $1, \dots , I$ with values $a = 1, \dots , A$ and let $y_n = \Phi (x_n)$. The entropy of the $\{y_n\}$ process is given by:

$$\begin{aligned} H = - \int \sum _{a} r_a(w) \log r_a(w) d Q(w) ~, \end{aligned}$$

(13)

where Q is a probability distribution on the Borel sets of the set W of vectors $w = (w_1, \dots , w_I)$ with $w_i \ge 0$, $\sum _i w_i = 1$, and $r_a(w) = \sum _{i=1}^I \sum _{j \ni \Phi (j) = a} w_i m(i,j)$. The distribution Q is concentrated on the sets $W_1, \dots , W_A$, where $W_a$ consists of all $w \in W$ with $w_i = 0$ for $\Phi (i) \ne a$ and satisfies:

$$\begin{aligned} Q(E) = \sum _a \int _{f_a^{-1} E} r_a(w) d Q(w) ~, \end{aligned}$$

(14)

where $f_a$ maps W into $W_a$, with the jth coordinate of $f_a(w)$ given by $\sum _i w_i m(i,j) / r_a(w)$ for $\Phi (j) = a$.

We can identify the w vectors in Theorem 2 as exactly the mixed states of Sect. 4. Furthermore, it is clear by inspection that $r_a(w)$ and $f_a(w)$ are the probability and mapping functions of Eqs. (9) and (10), respectively, with a playing the role of our observed symbol x.

Therefore, Blackwell’s expression Eq. (13) for the HMC entropy rate, in effect, replaces the average over a finite set ${\varvec{{\mathcal {S}}}}$ of unifilar states in Shannon’s entropy rate formula Eq. (4) with (i) the mixed states ${\varvec{{\mathcal {R}}}}$ and (ii) an integral over the Blackwell measure $\mu$. In our notation, we write Blackwell’s entropy formula as:

$$\begin{aligned} h_\mu ^B = - \int _{{\varvec{{\mathcal {R}}}}} d \mu (\eta ) \sum _{x \in \mathcal {A}} p^{(x)}(\eta ) \log _2 p^{(x)}(\eta ) ~. \end{aligned}$$

(15)

Thus, as with Shannon’s original expression, this too uses unifilar states—now, though, states from the mixed-state presentation $\mathcal {U}$. This, in turn, maintains the finite-to-one internal (mixed-) state sequence to observed-sequence mapping. Therefore, one can identify the mixed-state entropy rate itself as the process’ entropy rate.

6.2 Calculating the Blackwell HMC Entropy

Appealing to Ref. [42], we have that contractivity of our substochastic transition matrix mappings guarantees ergodicity over the words generated by the mixed-state presentation. And so, we can replace Eq. (15)’s integral over ${\varvec{{\mathcal {R}}}}$ with a time average over a mixed-state trajectory $\eta _0, \eta _1, \ldots$ determined by a long allowed word, using Eqs. (9) and (10). This gives a new limit expression for the HMC entropy rate:

$$\begin{aligned} \widehat{h_\mu }^B = - \lim _{\ell \rightarrow \infty } \frac{1}{\ell } \sum _{t = 0}^\ell \sum _{x \in \mathcal {A}} \Pr (x |\eta _\ell ) \log _2 \Pr (x |\eta _\ell ) ~, \end{aligned}$$

(16)

where $\eta _\ell = \eta (w_{0:\ell })$ and $w_{0:\ell }$ is the first $\ell$ symbols of an arbitrarily long sequence $w_{0:\infty }$ generated by the process. Note that $w_{0:\ell }$ will be a typical trajectory, if $\ell$ is sufficiently long. To remove convergence-slowing contributions from transient mixed states, one can ignore some number of the initial mixed states. The exact number of transient states that should be ignored is unknown in general and discussed in Appendix E. We can say that it depends on the initial mixed state $\eta _0$, which is generally taken to be $\left\langle \delta _\pi \right|$, and the diameter of the attractor.

Figure 5 plots the entropy rate for 250, 000 HMCs. The HMC definition is given in Eq. (S1) and parametrized by two variables, x and $\alpha$. Three examples of the MSPs from this parameter space displayed in Fig. 4. Despite the visual distinction of the MSPs, the entropy rate smoothly varies across parameters and is often close to $\log _2(3)$. This is partially due to the radial symmetry of the mixed-state attractors. The connection between the MSP structure and information measures will be more fully addressed in the sequel.

6.3 Computational Advantages and Disadvantages

This completes our development of the procedure to determine the HMC entropy rate. We now consider the computational advantages and disadvantages of using the MSP and Eq. (16) to find the entropy rate, in comparison to existing methods, as well as the practical issues of the resources needed for accurate estimation.

One impetus driving our development is a recurring need for an entropy estimation method that is both fast and general—one that applies to extensive surveys of HMCs that may have varying structural elements and transition probabilities. This challenge is broadly encountered. In point of fact, these structural tools and the entropy-rate method introduced here have already been put to practical use in two prior works. One diagnosed the origin of randomness and structural complexity in quantum measurement [35]. The other exactly determined the thermodynamic functioning of Maxwellian information engines [36], when there had been no previous method for this. Both applications relied critically on analyzing parametrized HMCs and required reliable and fast calculation of entropy rates and other information measures across a variety of HMC topologies.

HMC Shannon entropy rate has been studied in terms of upper and lower bounds [37, 47], with exact expressions [8, 48, 49], and as the solution to an integral equation [29]. Naturally, exact expressions are preferable where applicable and needed. Unfortunately, though, they are available only for restricted subsets of HMC topologies, such as unifilar or countable HMCs.

A well-known result is that the upper and lower finite-length conditional entropy estimates [37]:

$$\begin{aligned} H(X_0|X_1,\dots , X_\ell , \sigma _{\ell +1}) \le h_\mu \le H(X_0|X_1, \dots , X_\ell ) \end{aligned}$$

converge exponentially in word length $\ell$ to the entropy rate for path mergeable HMCs, a property that is straightforwardly checked [47]. This being said, while testing for the path mergeability condition is feasible, the algorithm to do so runs in polynomial time in the number of states and symbols, making testing impractical for a large-scale survey of HMCs with many states and/or symbols. Furthermore, while the conditional entropy estimates of $h_\mu$ converge in exponentially in $\ell$, calculating conditional entropies is nontrivial. This is particularly so when the exponential convergence rate $\alpha$ is arbitrarily close to 0. Thus, for accuracy within a desired bound the required $\ell$ may become arbitrarily large. Finally, while $H(X_\ell | X_1, \dots , X_{\ell -1})$ may be calculated exactly for all $\ell$, given knowledge of the HMC, at large $\ell$ this requires calculation of the full distribution over $| \mathcal {A} | ^\ell$ $\ell$-length words. Needless to say, for applications involving many states, large alphabets, and/or many HMCs, bounding the entropy rate in this way becomes computationally impractical.

The new method largely obviates these problems. When mixed-state construction returns a countable-state HMC, we directly apply Shannon’s entropy rate formula Eq. (2) and find the entropy rate exactly. When the MSP is uncountable we apply Eq. (16). It runs in $\mathcal {O}(N)$ where N is the number of mixed states generated, with no direct dependence on number of HMC states or alphabet size. Appendices E and F give a full discussion of the data-length requirements and error of the mixed-state method, respectively.

The net result is that, being cognizant of the data requirements, entropy rate estimation is well behaved, convergent, and accurate. One concludes that the most effective manner of calculating of entropy rate for large-scale surveys will likely employ a combination of our methodology and the other techniques just mentioned, with deployment of exact expressions where possible. Furthermore, we note that the development of the MSP as the $\epsilon -machine$, and the constructive method of producing the causal state set ${\varvec{{\mathcal {R}}}}$, may be of interest beyond computational advantages in characterizing the complexity of the underlying system beyond the entropy rate.

7 Conclusion

We opened considering the role that determinism and randomness play in the behavior of complex physical systems. A central challenge in this has been quantifying randomness, patterns, and structure and doing so in a mathematically-consistent but calculable manner. For well over a half a century Shannon entropy rate has stood as the standard by which to quantify randomness in a time series. Until now, however, calculating it for processes generated by nonunifilar HMCs has been difficult and inaccurate, at best.

We began our analysis of this problem by recalling that, in general, hidden Markov chains that are not unifilar have no closed-form expression for the Shannon entropy rate of the processes they generate. Despite this, these HMCs can be unifilarized by calculating the mixed states. The resulting mixed-state presentations are themselves HMCs that generate the process. However, adopting a unifilar presentation comes at a heavy cost: Generically, they are uncountably-infinite state and so Shannon’s expression cannot be used. Nonetheless, we showed how to work constructively with these mixed-state presentations.

In particular, we showed that they fall into a common class of dynamical system known as place-dependent iterated function systems. Analyzing the IFS dynamics associated with a finite-state nonunfilar HMC allows one to extract useful properties of the original process. For instance, we can easily find the entropy rate of the generated process from long orbits of the IFS. That is, one may select any arbitrary starting point in the mixed-state simplex and calculate the entropy over the IFS’s place-dependent probability distribution. We evolve the mixed state according to the IFS and sequentially sample the entropy of the place-dependent probability distribution at each step. Using an arbitrarily long word and taking the mean of these entropies, the method converges on the process’ entropy rate.

Although the IFS-HMC connection has been considered previously [50, 51], our development complements this by expanding it to address the role of mixed-state presentations in calculating the entropy rate and to connect it to existing approaches to randomness and structure in complex processes. In particular, while our results focused on quantifying and calculating a process’ randomness, we left open questions of pattern and structure. Towards this, we showed how the attractor of the IFS defined by an HMC is, assuming uniqueness of the mixed states as discussed in Appendix B, the set of causal states ${\varvec{{\mathcal {R}}}}$ of the process generated by that HMC. Practically, this gives a method to construct the causal states of a process $\mathcal {P}$, so long as it can be finitely generated. For instance, Fig. 3 demonstrated how the highly structured nature of the Simple Nonunifilar Source is made topologically explicit through calculating its mixed-state presentation—which is also its $\epsilon -machine$.

In point of fact, many information-theoretic properties of the underlying process may be directly extracted from its mixed-state presentation. These sets are often fractal in nature and quite visually striking. See Fig. 4 for several examples. The sequel [34] establishes that the information dimension of the mixed-state attractor is exactly the divergence rate of the statistical complexity—a measure of a process’ structural complexity that tracks memory. Furthermore, the sequel introduces a method to calculate the information dimension of the mixed-state attractor from the mixed-state IFS’s spectrum of the Lyapunov characteristic exponents. In this way, it demonstrates that coarse-graining the simplex—the previous approach to study the structure of infinite-state processes [45]—may be avoided altogether. At this point, however, we must leave to the sequel the full explication of these techniques and further analysis on how mixed states reveal the underlying structure of processes generated by hidden Markov chains.