Introduction of a Scaling Factor for Fracture Toughness Measurement of Rocks Using the Semi-circular Bend Test

Abstract

This article discusses the scale dependence of the mode $\mathrm {I}$ fracture toughness of rocks measured via the semi-circular bend (SCB) test. An extensive set of experiments is conducted to scrutinise the fracture toughness variations with size for three distinct rock types with radii ranging from 25 to 300 mm. The lengths of the fracture process zone (FPZ) for different sample sizes are measured using the digital image correlation (DIC) technique. A theoretical model is also established that relates the value of fracture toughness to the sample size. This theorem is based on the strip-yield model to estimate the length of FPZ, and the energy release rate concept to relate the FPZ length to the fracture toughness. This theoretical model does not rely on any experimental-based curve-fitting parameter, but only on the tensile strength of the rock type as well as the fracture toughness at a specific sample size. The size effects predicted by the theoretical model is in a good agreement with the experimental data on both fracture toughness and the FPZ length. Finally, theoretical correction factors are introduced for various geometrical configurations of the SCB specimen, using which a scale-independent mode $\mathrm {I}$ fracture toughness of the rock material can be estimated from the results of experiments performed on small samples.

1 Introduction

Growing industries and engineering applications including enhanced geothermal systems, CO₂ sequestration projects, waste-water injection procedures, oil and gas shale reservoirs as well as mining excavations all require knowledge on the process of fracture growth in rocks. Being subjected to a combination of mechanical, thermal and hydraulic loads, in addition to embodying inherent fractures of different sizes, rock masses are highly susceptible to fracture initiation and growth. With regard to the quasi-brittle nature of the rock-like materials, their fracturing process is often classified as instantaneous with disastrous consequences such as induced-seismicity, hence requiring precise monitoring.

Mode $\mathrm {I}$ fracture toughness, $K_\mathrm {Ic}$, as an important property of rocks and other quasi-brittle materials, characterises the resistance of the material against crack propagation under static mode $\mathrm {I}$ loading condition. In the context of the linear elastic fracture mechanics (LEFM), the fracture growth commences when the mode $\mathrm {I}$ stress intensity factor (SIF) reaches $K_\mathrm {Ic}$ at a critical load. Among several standardised tests for the measurement of rock fracture toughness, the semi-circular bend (SCB) test has been popular and favourable, thanks to its simple sample preparation and testing procedure as well as the small amount of material required per specimen (Kuruppu et al. 2014). These advantages have attracted a lot of attention to perform SCB tests for rock fracture toughness measurement (Chong et al. 1987; Lim et al. 1994; Dai et al. 2010, 2013; Kuruppu et al. 2014; Kataoka et al. 2015; Chen et al. 2016; Ayatollahi et al. 2016; Wang et al. 2017; Wei et al. 2017b; Bahrami et al. 2020b; Nejati et al. 2020a; Obara et al. 2020).

An important subject when dealing with rock materials is the size effect phenomenon, where tests performed on small-sized rock specimens often yield underestimated values of fracture toughness compared to the scale-independent fracture toughness of the rock mass. Many research studies to date have investigated this size effect behaviour in the mode $\mathrm {I}$ fracture toughness of rock and concrete, using the single edge notch bend (SENB) test (Bažant 1984; Bažant and Pfeiffer 1987; Bažant et al. 1991; Bažant and Kazemi 1991; Karihaloo 1999; Cusatis and Schauffert 2009; Ayatollahi and Akbardoost 2012; Fakhimi and Tarokh 2013; Tarokh et al. 2017; Bhowmik and Ray 2019; Carloni et al. 2019) or the SCB test (Chong et al. 1987; Nath Singh and Sun 1990; Lim et al. 1994; Akbardoost et al. 2014; Wei et al. 2016a, 2017b; Zhang et al. 2019; Nejati et al. 2020b). It is worth noting that this literature consists of experimental, numerical and theoretical approaches, among which the initial studies by Bažant and his co-workers truly stand out and lay the foundation for most of the later research activities in this field. The majority of the experimental size effect studies in the last four decades take account of only one certain type of rock or rock-like material with limited variations in the size of the specimens, and therefore may not evidently generalise their results to other kinds and sizes of rocks. Moreover, in the theoretical studies, the formulations are rather complex and usually depend on inputs from experiments, including curve fittings and empirical determination of size effect parameters. These shortcomings must be addressed thoroughly, which accordingly urges the need for more rigorous studies in this regard.

To bridge the gap, we herein present a combination of the results of an extensive experimental study as well as a novel theoretical model. The former is comprised of mode $\mathrm {I}$ fracture toughness and digital image correlation (DIC) tests on SCB samples made of three different rock types (from sedimentary, metamorphic and igneous categories) with radii ranging from 25 to 300 mm. The latter, i.e. the theoretical model, is based on the strip-yield model and the energy release rate concept which, in hand with a comprehensive numerical analysis, provides an experiment-independent theory which correlates well with experimental findings. A correction (scaling) factor is then introduced for various geometrical conditions in the SCB specimen, based on which one can estimate the true scale-independent mode $\mathrm {I}$ fracture toughness of the rock materials. Furthermore, a method to estimate the length of the fracture process zone (FPZ) without performing experiments such as DIC is described. We point out that the theoretical model proposed in this study does not rely on any experimental-based curve-fitting parameter but only on the tensile strength $\sigma _t$ of the rock type and the fracture toughness $K_{\mathrm {Ic}}$ at a specific sample size.

2 Experimental Study

2.1 Materials

Three distinct rock types are employed for this study, all of which were acquired from different mining sites in Iran. The first type, chosen from sedimentary rocks, is a limestone excavated from Fars province. The second type, from the metamorphic category, is a white marble extracted from West Azerbaijan Province. Finally, the third type is an igneous granitic rock also mined from West Azerbaijan Province. All these rock materials are initially extracted in the form of large blocks at the mines, followed by cutting into slabs with predefined thicknesses in a stone factory. We prepared Brazilian disk and SCB samples from slabs of 2 cm thickness. Only the largest SCBs, i.e. with $R=300$ mm, were extracted from slabs with 3 cm thickness. To reduce the potential influence of the heterogeneity and anisotropy, all the samples from each rock type were prepared from adjacent slabs in a single block and were tested in a predefined direction.

Fig. 1

Measurement of indirect tensile strength using the Brazilian disk tests, with the loading configuration shown in a, and the final failure patterns of b limestone, c marble and d granite

2.2 Brazilian Disk Test

To measure the tensile strength of the rock types, Brazilian disks (BDs) with the radius of $R=50$ mm and the thickness of $t=20$ mm were prepared using the waterjet cutting method. For each rock type, four repetitions were considered, meaning that twelve BD samples were tested overall. Figure 1a pictures a BD specimen of limestone during the test. Circular jaws were used for the exertion of diametrical compressive force, and polymethylmethacrylate (PMMA) cushions with the same curvature to that of jaws were utilised for smoother and better-distributed load transfer to the specimen. In fact, this configuration facilitates a proper execution of the BD test, in which fracturing initiates from a central zone, minimising the potential for failure of disks due to crack initiation near the loading points. Figure 1b–d show sample fractured BD specimens of the three rock materials. As is seen in these photographs, the limestone and granite samples show minimal/no damage at loading points, with minor eccentricity of fracture path observed in the granitic disk. For the marble specimen, however, the surfaces in contact with loading cushions are more pronouncedly damaged as a result of rock fragmentation close to the critical load. This issue was only spotted to exist in the tested marble owing to its crystalline texture, for minimisation of which we employed PMMA flexible jaws. To further diminish undesirable fractures at the loading area, one may use longer flexible jaws with more circumferential coverage, or alternatively, use less stiff wooden jaws.

After conducting the BD test, the peak load $P_c$ corresponding to the fracturing of the disk was recorded by the universal testing machine whereby the indirect tensile strength is calculated from $\sigma _t=0.636 P_c/(2Rt)$ (Bieniawski and Hawkes 1978). The final measurements of the tensile strength are as follows: $5.42 \pm 0.26$ MPa for limestone, $11.41 \pm 0.42$ MPa for marble and $9.50 \pm 0.68$ MPa for granite. Figure 2a visualises typical load-displacement curves obtained for different tested rock materials, emphasising the superiority of marble’s indirect tensile strength. Note that the non-linear behaviour in these curves is mainly attributed to the large non-linear deformation of the PMMA cushions.

Fig. 2

Typical load–displacement curves obtained from a Brazilian disk tests; b three-point bend fracture tests on specimens with ${R=200}$ mm. Tensile strength and fracture toughness superiority of marble is evident

It should be noticed that the BD test is an ISRM-suggested method for the determination of indirect tensile strength. According to ASTM-International (2016), tests other than straight pull are categorised as indirect test methods, which are less difficult and more affordable to be performed compared to direct experiments. Despite the advantages of indirect tensile tests, they are referred to as methods which overestimate the tensile strength of rock materials. As a frequently used specimen in rock mechanics applications, BD has been reported to yield overestimations for tensile strength of about $10\%$ for metamorphic, $20\%$ for igneous and $30\%$ for sedimentary rocks, for practical applications (Perras and Diederichs 2014). However, these empirical figures are not definitive and may vary from one rock material to another, therefore they should be used cautiously.

We also note that the tensile strength used in FPZ characterization models may also in essence differ from the true tensile strength of rock measured via a direct method. This is because the rock material in the process zone is under a biaxial state of stress and not a uniaxial one. In fact, the stress component parallel to the crack, called T-stress, is negative for the SCB specimen configuration used in this study. Hence, the nature of the failures in the SCB and BD are in fact similar in the sense that a compressive stress is applied parallel to the failure plane. In this case, strength obtained from the BD test may be more representative of the failure in the FPZ rather than the true tensile strength obtained from direct tests.

Fig. 3

a Schematic view of the SCB test configuration; b failure of an SCB sample of radius $R=300$ mm in the universal testing machine while the digital image correlation (DIC) set-up is used to capture strain localisation at the notch tip

2.3 Mode I Fracture Toughness Tests

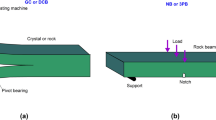
Semi-circular bend test is a standard testing method, suggested by the International Society for Rock Mechanics (ISRM), for the measurement of the mode $\mathrm {I}$ static fracture toughness of rock materials (Kuruppu et al. 2014). This test is conducted under the three-point bend loading configuration, and features the following noticeable virtues: (a) usage of a small amount of core material; (b) requiring relatively simple machining process; and (c) suitability for both isotropic and anisotropic rocks. Hence, the SCB specimen is regarded as a prospective candidate for the measurements of the mode $\mathrm {I}$ fracture toughness. Figure 3a illustrates a 3-D schematic view of the test configuration.

In this research, a total number of 93 SCB specimens were manufactured, with a large range of radii of $R=25$, 50, 75, 100, 150, 200 and 300 mm, and taking account of at least four repetitions per size. The manufacturing process involved water jet cutting to extract semi-circular disks from stone slabs as well as generating notches of length $a/R=0.5$ in the SCB samples. In order to maintain the perpendicularity of the cutting plane with respect to the front (test) plane, and to enhance surface-finishing quality especially at loading and support points, specimen thicknesses were kept at $t=2$ cm for all the specimens with $R=25$ to 200 mm. The only exception was for the largest SCBs of radius $R=300$ mm, which had the thickness $t=3$ cm, to ensure the stability of specimens under three-point bend compression. Note that fracture toughness of rock materials are reported to be independent of the specimen thickness in numerous experimental studies in the literature (Schmidt and Lutz 1979; Laqueche et al. 1986; Kobayashi et al. 1986; Nath Singh and Sun 1990; Haberfield and Johnston 1990; Lim et al. 1994; Khan and Al-Shayea 2000; Chang et al. 2002). Given that our tested rocks have isotropic elasticity response, the roller supports were placed symmetrically to apply pure mode $\mathrm {I}$ loading, with the span length ratio adjusted to $S/R=0.6$ (Bahrami et al. 2019; Sedighi et al. 2020). It is noteworthy that asymmetrical support spans are required to impose mode $\mathrm {I}$ loading for SCB specimens made of anisotropic rocks (Nejati et al. 2019, 2020b).

After the preparation of the test samples, fracture tests were carried out using Santam STM-150 universal testing machine in the displacement-control mode with the crosshead speed of 0.1 mm/min (see Fig. 3b). The fracturing process of the tested rock samples was instantaneous and the load–displacement behaviour was linear up the peak load. Hence, the LEFM theory can be adopted securely to theoretically evaluate the size effects in this study. Figure 4a–c portray samples of fractured specimens for all sizes of the three rock types. As evidenced, the notch had almost always propagated in a self-similar manner as an inherent response of mode $\mathrm {I}$ fracture tests of isotropic materials.

Fig. 4

Samples of fractured specimens in all different sizes: a limestone, b marble, and c granite

In line with the ISRM-suggested method for the SCB test (Kuruppu et al. 2014), once the peak load $P_c$ is measured (from the load-displacement curves for SCB fracture tests as in Fig. 2b), the fracture toughness is calculated from $K_\mathrm {Ic}=K^*_\mathrm {I} P_c \sqrt{\pi a}/(2Rt)$, where R and t represent the radius and thickness of the SCB specimen, and a is the length of the notch. Moreover, the geometry factor $K^*_\mathrm {I}$ is a numerically calculated dimensionless parameter, that depends on the specimen geometry and loading configuration, and is adopted from the results by Nejati et al. (2019, 2020b) for the isotropic case. Figure 5a presents the measured values of $K_\mathrm {Ic}$ against the SCB radius, R. It is observed that, within the entire size range, marble is the strongest material with the largest fracture toughness values, while limestone acquires the least values overall and seems to be rather weaker. Granite, on the other hand, appears to be moderately resistant to fracture growth with $K_\mathrm {Ic}$ values falling in between marble’s and limestone’s. Figure 2b illustrates these trends.

Fig. 5

a Variations of mode $\mathrm {I}$ fracture toughness ($K_\mathrm {Ic}$) against the sample radius, and fitted curves to determine the stabilised value of fracture toughness ($K_\mathrm {Ic}^\infty$); b the variations of the normalised mode $\mathrm {I}$ fracture toughness ($K_\mathrm {Ic}/K_\mathrm {Ic}^\infty$) against the normalised size ($R/(K_\mathrm {Ic}^\infty /\sigma _t)^2$), showing a universal trend in the data

The general trend for all three types of rocks is that the fracture toughness values grow as the specimen radius increases (see Fig. 5a). This phenomenon, referred to as the size effect, occurs due to the formation of a relatively large fracture process zone in front of the crack tip. The FPZ region embodies a zone of highly localised deformation that occurs due to extensive micro-cracking processes. Since $K_\mathrm {Ic}$ is a measure valid only inside the K-dominant zone, the specimen dimensions (and subsequently K-zone) should be enlarged enough so that the FPZ fits inside the K-dominant region (Nejati et al. 2020b). A large FPZ may partially stay out of the K-dominant zone in small samples, whereby inducing size-dependent fracture toughness values (Wei et al. 2016b, 2017a, 2018a, b; Dutler et al. 2018). A clear illustration of this process is given in Nejati et al. (2020b). As our experiments suggest, even by enlarging the specimen radius to $R=200-300$ mm, the fracture toughness values may not still experience a plateau, and a further increase is yet anticipated.

To have experimental reference values for the true scale-independent fracture toughness of the rock materials, $K_\mathrm {Ic}^\infty$, we perform a least squares analysis over the test data utilising an arbitrary exponential model: $K_\mathrm {Ic}=K_\mathrm {Ic}^\infty \left[ {1 - {\lambda _1}\exp \left( { - {\lambda _2}R} \right) } \right]$. Here, $K_\mathrm {Ic}^\infty$, $\lambda _1$ and $\lambda _2$ are unknown parameters that are computed by means of the least squares method with their values given in Fig. 5a. It should be noted that this exponential relation is an arbitrary choice among many possible alternatives which can model a gradually stabilising behaviour, whereby projecting a representative value for the true fracture toughness. We also point out that this estimate for the scale-independent fracture toughness, $K_\mathrm {Ic}^\infty$, will not be used in our theoretical model presented and employed in Sects. 3 and 4. Alternative models also yield relatively similar values to the ones reported for $K_\mathrm {Ic}^\infty$.

A comparison of the results in Fig. 5a reveals that the fracture toughness of the largest specimens of limestone, marble and granite are, respectively, 2.01, 1.41 and 1.49 times greater than the ones of the smallest samples. A comparison between the smallest specimens and $K_\mathrm {Ic}^\infty$ also reveals even greater respective figures of 2.30, 1.45 and 1.58. This significant growth in the fracture toughness values implies a serious effect of size on the fracture toughness that must be taken into account in rock mechanics and engineering applications.

The true (scale-independent) fracture toughness value $K_\mathrm {Ic}^\infty$ for each rock type is then employed to normalise the fracture toughness experimental data, i.e. $K_\mathrm {Ic}/K_\mathrm {Ic}^\infty$, which is plotted versus the normalised disk radius in Fig. 5b. Presenting the data in a normalised manner shows that all the data points irrespective of the rock type follow a universal trend. This behaviour indicates that a proper size effect rule must in fact be material independent. It is noteworthy that if the experimental data are normalised by the fracture toughness of the largest specimen rather than by $K_\mathrm {Ic}^\infty$, again a universal, material-independent pattern similar to that of Fig. 5b will be obtained. Also explicitly shown in Fig. 5b is that $K_\mathrm {Ic}$ values reach a plateau only at larger sizes than $R/(K_\mathrm {Ic}^\infty /\sigma _t)^2 \approx 10$. This finding seriously questions the validity of the minimum size requirement recommended by the ISRM standard, which reads $R \ge (K_\mathrm {Ic}^\infty /\sigma _t)^2$ (Kuruppu et al. 2014). This insufficiency in the minimum size requirement for the SCB specimen has also been pointed out by previous research studies (Nath Singh and Sun 1990; Akbardoost et al. 2014; Wei et al. 2016a, 2017b; Nejati et al. 2020b), all of which urging either the usage of larger specimens or the introduction of correction factors.

2.4 DIC Results on the FPZ Length

We employed the DIC technique to measure the length of FPZ in the tested samples. To prepare the samples for DIC measurements, the surfaces of the samples were painted using a white spray, followed by creating a speckled pattern using a black spray. To prevent the light reflection, matte black and white sprays were employed. The DIC set-up, shown in Fig. 3b, includes a Canon CMOS 600D camera with a mounted macro-lens EF 100 mm f/2.8 to capture images, and two 11-Watt LED lamps to provide an appropriate and stable illumination for the tests. The images corresponding to the undeformed state of the specimens were captured at almost zero load, and images of the deformed samples were taken automatically with intervals of 5 seconds. The deformation states associated with 90% of peak load before fracturing were used to measure the FPZ length.

The Match ID software was used to perform correlation analyses between the reference image (at zero load) and the ones associated to the deformed states at different load levels. The correlation analyses were conducted on a rectangular region of interest in front of the crack tip with the subset size of $55 \times 55$ pixels and the step size of 1 pixel. Also, the normalised sum of squared differences (NSSD) was used as the correlation criterion. More details about the DIC parameters can be found in Bahrami et al. (2020a). Figure 6a, b show samples of displacement and strain fields in front of the crack tip, that represent an area of high displacement gradients and strain concentrations. The formation of a semi-elliptical-shaped FPZ shown in Fig. 6b agrees well with the FPZ shape reported in Dutler et al. (2018); Moazzami et al. (2020); Zhang et al. (2020). It is noteworthy that the strain field is a secondary output of the DIC measurements, that is derived from the gradients of the directly measured displacements by means of numerical smoothing techniques (Pan et al. 2009). We therefore use the displacement field to evaluate the fracture process zone due to its higher accuracy compared to the strain field. Figure 6c demonstrates the variations of the horizontal displacement component u extracted along several parallel horizontal lines in front of the crack tip. As seen, a displacement jump exists along those lines situated adjacent to the crack tip. These jumps indicate highly localised deformation that are indications of the formation of the FPZ in that region. The jump in u decreases and finally vanishes at lines further away from the crack tip. The closest line from the crack tip within which no perceptible displacement jump is observed, indicates the end of FPZ, and the vertical distance between the crack tip and such line is measured as the length of the fracture process zone, i.e. $L_\mathrm {FPZ}$.

Fig. 6

Samples of a displacement and b strain fields obtained from the DIC measurements in front of the crack tip for the granitic rock type. c Schematic view of the method used for measuring the FPZ length based on the gradient of the displacement component u

Figure 7a displays the variations of the FPZ length versus the specimen radius, for all three types of the rock materials. It should be noted that we did not carry out as many DIC tests as the fracture toughness tests, and thus smaller number of experimental data are available in this plot. The scatter of the test data may be attributed to the uncertainty of FPZ length measurement via the DIC technique. Despite fluctuations of $L_\mathrm {FPZ}$ data for limestone that is the weakest rock among the three, the general trend of the data suggests a substantial growth in the FPZ length with specimen size. In the entire size range, granite almost always attains the biggest fracture process zones with values as high as of almost 18 mm for the biggest samples. Similar large fracture process zones in coarse-grained granite  have also been identified by previous experimental studies (Wei et al. 2018c; Dutler et al. 2018). A comparison between the FPZ lengths of the largest and smallest specimens shows ratios of 5.01, 4.15 and 6.27 for limestone, marble and granite, respectively. These figures are indicative of the profound influence of sample size on the development of the FPZ. Small samples significantly constrain the full development of the fracture process zone, consider granite as an example with an average $L_\mathrm {FPZ}=2.8$ mm for the SCB specimen of radius $R=25$ mm. Ayatollahi and Aliha (2008) have confirmed FPZ length of 3.2 mm for specimens with radius $R=37.5$ mm, while Wei et al. (2017b) have obtained $L_\mathrm {FPZ}=2.8~$mm for same-sized granite samples.

Similar to the normalisation procedure taken in Fig. 5b, we also present here the normalised values of the FPZ length $L_\mathrm {FPZ}/a$ against the normalised radius $R/(K_\mathrm {Ic}/\sigma _t)^2$ in Fig. 7b. As seen, the normalisation fades away the highly scattered data especially for limestone, yielding a relatively smooth descending trend of the normalised FPZ length with sample size. The large range chosen for the vertical axis of this figure will be later helpful to demonstrate the curves for theoretical predictions.

Fig. 7

Experimental results of FPZ length ($L_\mathrm {FPZ}$) obtained from the DIC measurements: a the variations of the raw data on the FPZ length $L_\mathrm {FPZ}$ versus the disk radius R; b the variations of the normalised FPZ lengths ($L_\mathrm {FPZ}/a$) versus the normalised size ($R/(K_\mathrm {Ic}/\sigma _t)^2$)

3 Theoretical Study

This section presents a theoretical model that relates the fracture toughness measured at a given size to its scale-independent value. To this end, we first develop a model to estimate the FPZ length at any given size of the SCB sample. This estimate is then used in a second model developed based on the energy release rate to derive a relation that governs the dependency of the fracture toughness on the sample size. In this section, we use the crack tip fields and the associated parameters presented in Appendix A.

3.1 A Model for FPZ Length

Let us consider the FPZ as a cohesive zone ahead of the crack tip as shown in Fig. 8. Employing the superposition principle, one may write the force equilibrium along a segment of the ligament, starting from the crack tip and extending to $m \times (R-a-L_{FPZ})$ along the notch bisector of the SCB specimen (see Fig. 8a):

$$\begin{aligned} \int _0^{m \times (R - a - {L_\mathrm {FPZ}})} {\left( {{\sigma _p}(x) + {\sigma _{cl}}(x)} \right) t \, \text {d}x} = 0 \,, \end{aligned}$$

(1)

where t is the specimen thickness, $\sigma _p$ is the stress induced by the load P when no closure stress exists, i.e. case (b) in Fig. 8, and $\sigma _{cl}$ is the stress induced by the closure stress applied at the FPZ, i.e. case (c) in Fig. 8. We consider the force equilibrium in Eq. (1) being satisfied over half of the ligament, i.e. $m=0.5$, which is a reasonable choice for preserving adequate distance away from the load-point stress concentration area. Inserting the first five terms of the stress expression for $\sigma _y$ from Eq. (16) into Eq. (1) and evaluating at $\theta =0^{\circ }$ yields Eq. (2a), that readily simplifies to Eq. (2b) as

$$\begin{aligned}&\int _0^{m \times (R - a - {L_\mathrm {FPZ}})} \left\{ \frac{{ {\tilde{A}}_1 + {{\tilde{A}}_{1,cl}}}}{{\sqrt{x} }} + 3 \times ( {\tilde{A}}_3 + {{\tilde{A}}_{3,cl}}) \sqrt{x} \right. \nonumber \\&\quad \left. + 5 \times ( {\tilde{A}}_5 + {{\tilde{A}}_{5,cl}}) x\sqrt{x} \right\} \text {d} x = 0 \, , \end{aligned}$$

(2a)

$$\begin{aligned}&({\tilde{A}}_1 + {{\tilde{A}}_{1,cl}}) + ({\tilde{A}}_3 + {{\tilde{A}}_{3,cl}}) \times \Big ( {m \times (R - a - {L_\mathrm {FPZ}})} \Big ) \nonumber \\&\quad + ({\tilde{A}}_5 + {{\tilde{A}}_{5,cl}}) \times {\Big ( {m \times (R - a - {L_\mathrm {FPZ}})} \Big )^2} = 0 \, , \end{aligned}$$

(2b)

Fig. 8

Schematics of a cohesive zone model represented by a closure stress, and the use of the superposition principle to simplify it

Note that the even terms of the stress field ($n=2,4, ...$ in Eq. (16)) vanish along the crack bisector. Eq. (2b) satisfies the force equilibrium along half of the ligament at any load level P. As the load increases, a larger FPZ is developed to satisfy the force equilibrium. This is because the closure stress is limited to the tensile strength of the material, and a compensation for the additional forces applied by P has to be associated with an extension of the FPZ. At the onset of the fracture propagation, the FPZ can no longer extend (no more potential for the energy dissipation within the FPZ), and therefore, the violation of the static equilibrium leads to the fracture growth. It should be noted that the crack length equals $a_\mathrm {eff}=a+L_\mathrm {FPZ}$ in Eq. (2). We refer to the crack parameters as ${\tilde{A}}_n$ in the case associated to Fig 8b and ${\tilde{A}}_{n,cl}$ in the case associated to Fig. 8c. The respective normalised forms are also referred to as ${\tilde{A}}^*_n$ and ${\tilde{A}}^*_{n,cl}$, that are determined numerically as elaborated in Appendix A, and are related to ${\tilde{A}}_n$ and ${\tilde{A}}_{n,cl}$ as

$$\begin{aligned} {\tilde{A}}_n= \,& {} {\tilde{A}}^*_n \, \sigma \, a^{1-\frac{n}{2}}_{\mathrm {eff}} \quad \text {with} \quad {\tilde{A}}^*_n \left( \alpha +\dfrac{L_\mathrm {FPZ}}{R} \right) \nonumber \\= \,& {} {A^*_n} \left( \alpha \right) +\dfrac{\text{d}{{A^*_n}}\left( \alpha \right) }{\text{d} \alpha } \dfrac{L_\mathrm {FPZ}}{R}\nonumber \\=\, & {} {A^*_n}+\alpha {A^*_n}^\prime \dfrac{L_\mathrm {FPZ}}{a} \quad \text {and} \quad \alpha =\,a/R \, , \end{aligned}$$

(3a)

$$\begin{aligned} {\tilde{A}}_{n,cl}= \,& {} -{\tilde{A}}^*_{n,cl} \, \sigma _t \, a \, a_\mathrm {eff} ^{-\frac{n}{2}}, \quad \nonumber \\ {\tilde{A}}^*_{n,cl}=\, & {} \left\{ \begin{array}{l} \left( {\tilde{A}}^*_{n,cl}\right) _{ut} \quad \text {uniform traction model} \\ \left( {\tilde{A}}^*_{n,cl}\right) _{lt} \quad \text {linear traction model} \end{array}\right. \, . \end{aligned}$$

(3b)

Here, $\sigma _t$ is the tensile strength (we assume that stress is limited to $\sigma _t$ in the FPZ) and $\sigma =P/(2Rt)$. We employ two different models to characterise the distribution of cohesive stresses over the fracture process zone: uniform and linear traction models. The former is first introduced by Barenblatt (1959) and Dugdale (1960), and the latter is originally put forward by Labuz et al. (1985), both of which founded upon the singular crack tip stress field. Substituting Eqs. (3a) and (3b) into Eq. (2b), while ignoring the higher order terms of $\sigma _{cl}$, i.e. ${\tilde{A}}_{3,cl}={\tilde{A}}_{5,cl}=0$ (refer to Appendix A.3 for details), delivers the strip-yield model at the incipience of the crack growth

$$\begin{aligned} \begin{aligned}&\left[ {A^*_1 {\sigma _c} \sqrt{{a_\mathrm {eff}}} \left( {1 + \alpha \frac{{A^*_1}^\prime }{{A^*_1}} \frac{{{L_\mathrm {FPZ}}}}{a}} \right) - {{\tilde{A}}^*_{1,cl}} \frac{{{\sigma _t}}}{{\sqrt{{a_\mathrm {eff}}} }} a} \right] \\&\qquad + \left( {A^*_3 + \alpha {A^*_3}^\prime \frac{{{L_\mathrm {FPZ}}}}{a}} \right) \frac{{{\sigma _c}}}{{\sqrt{{a_\mathrm {eff}}} }} \Big ( {m \times \left( {R - a - {L_\mathrm {FPZ}}} \right) } \Big ) \\&\qquad +\left( {{A^*_5} + \alpha {A^*_5}^\prime \frac{{{L_\mathrm {FPZ}}}}{a}} \right) \frac{{{\sigma _c}}}{{{a_\mathrm {eff}} \sqrt{{a_\mathrm {eff}}} }} {\Big ( {m \times \left( {R - a - {L_\mathrm {FPZ}}} \right) } \Big )^2} \\&\quad = 0 \,, \end{aligned} \end{aligned}$$

(4)

where dividing the entire expression into ${A^*_1} {\sigma _c} \sqrt{{a_\mathrm {eff}}}$ and using the effective crack length $a_\mathrm {eff}=a+L_\mathrm {FPZ}$ yields

$$\begin{aligned} \begin{aligned}&\left[ {\left( {1 + \alpha \frac{{{A^*_1}^\prime }}{{A^*_1}}\frac{{{L_\mathrm {FPZ}}}}{a}} \right) - {{\tilde{A}}^*_{1,cl}} \frac{{\sqrt{R\alpha } }}{{\frac{{{A^*_1}{\sigma _c}\sqrt{a} }}{{{\sigma _t}}} }}\frac{a}{{a + {L_\mathrm {FPZ}}}}} \right] \\&\quad + \left( {\frac{{{A^*_3}}}{{{A^*_1}}} + \alpha \frac{{{A^*_3}^\prime }}{{{A^*_1}}}\frac{{{L_\mathrm {FPZ}}}}{a}} \right) \left( {m \times \left( {\frac{1}{\alpha }\frac{a}{{a + {L_\mathrm {FPZ}}}} - 1} \right) } \right) \\&\quad + \left( {\frac{{{A^*_5}}}{{{A^*_1}}} + \alpha \frac{{{A^*_5}^\prime }}{{{A^*_1}}}\frac{{{L_\mathrm {FPZ}}}}{a}} \right) {\left( {m \times \left( {\frac{1}{\alpha }\frac{a}{{a + {L_\mathrm {FPZ}}}} - 1} \right) } \right) ^2} = 0 \,. \end{aligned} \end{aligned}$$

(5)

Recalling that ${A^*_1}{\sigma _c}\sqrt{a}=A_\mathrm {1c}=K_\mathrm {Ic}/\sqrt{2\pi }$ and defining the following coefficients

$$\begin{aligned} {A^*_1}^\prime /{A^*_1}= \,& {} {{\dot{M}}_1}, \quad {A^*_3}/{A^*_1}=\,{M_3},\quad {A^*_3}^\prime /{A^*_1}=\,{{\dot{M}}_3},\quad \nonumber \\ {A^*_5}/{A^*_1}=\, & {} {M_5},\quad {A^*_5}^\prime /{A^*_1}=\,{{\dot{M}}_5} \, , \end{aligned}$$

(6a)

$$\begin{aligned} {\mathcal {R}}^*_\infty= \,& {} R/(K_\mathrm {Ic}^\infty /\sigma _t)^2, \quad \nonumber \\ {\mathcal {K}}^*= \,& {} K_\mathrm {Ic}/K_\mathrm {Ic}^\infty , \quad {\mathcal {L}}^*= L_\mathrm {FPZ}/a \, , \end{aligned}$$

(6b)

Eq. (5) finally reads

$$\begin{aligned} \begin{aligned}&\left[ {\left( {1 + \alpha {{\dot{M}}_1} {\mathcal {L}}^*} \right) - {{\tilde{A}}^*_{1,cl}}\frac{{\sqrt{2\pi \alpha {\mathcal {R}}^*_\infty } }}{{\mathcal {K}}^*}\frac{1}{{1 + {\mathcal {L}}^*}}} \right] \\&\quad + \left( {{M_3} + \alpha {{\dot{M}}_3} {\mathcal {L}}^*} \right) \left( {m \times \left( {\frac{1}{\alpha }\frac{1}{{1 + {\mathcal {L}}^*}} - 1} \right) } \right) \\&\quad + \left( {{M_5} + \alpha {{\dot{M}}_5} {\mathcal {L}}^*} \right) {\left( {m \times \left( {\frac{1}{\alpha }\frac{1}{{1 + {\mathcal {L}}^*}} - 1} \right) } \right) ^2} = 0 \, . \end{aligned} \end{aligned}$$

(7)

Equation (7) depicts the strip-yield model developed for the SCB specimen by considering higher-order parameters of the crack tip stress field, and is in fact an extension of Dugdale’s strip-yield model for plastic zone (Dugdale 1960). By specifying a valid range for the parameter ${\mathcal {R}}^*_\infty$ (as in Fig. 5b), there will remain only two unknowns, namely ${\mathcal {L}}^*$ and ${\mathcal {K}}^*$. In the next section, we develop a second equation based on the energy release rate concept which in hand with Eq. (7) can determine the two unknowns.

3.2 A Model for the Fracture Toughness

Let us consider the energy release rate (ERR) due to crack extension, defined as the amount of potential energy, $\Pi$, released per unit area of crack extension (Anderson 2017):

(8)

Here, A is the crack face area and U is the elastic strain energy. Note that a decrease in the potential energy $\Pi$ is associated to an equivalent increase in the strain energy U in a system that is subjected to a fixed load during crack propagation (Anderson 2017). This increase in the strain energy is due to the additional work put into the system by the fixed load. In the present problem, the incremental crack growth can be considered equivalent to the length of the fracture process zone, i.e. $\Delta a=L_\mathrm {FPZ}$, and $\Delta U$ can be formulated as:

$$\begin{aligned} \Delta U= & {} \int _{r = 0}^{r = {L_\mathrm {FPZ}}} {\text{d} U(r) = } \int _0^{{L_\mathrm {FPZ}}} \frac{1}{2}{P_y}\left( {{v}^ + (r) - {v}^ - (r)} \right) \nonumber \\= & {} \int _0^{{L_\mathrm {FPZ}}} \frac{1}{2} {{{{\sigma _{y}}(r)} \big |}_{\mathop {\theta = 0}\limits _{(r = x)}}}\left( {{{v}(r)} \big |}_{\mathop {\theta = \pi }\limits _{(r = {L_\mathrm {FPZ}} - x)}} \right. \nonumber \\&\left. - {{{v}(r)} \big |}_{\mathop {\theta = - \pi }\limits _{(r = {L_\mathrm {FPZ}} - x)}} \right) \text {d}x \, , \end{aligned}$$

(9)

where the opening displacement v (Fig. 9a) and the normal stress $\sigma _y$ (Fig. 9b) should be acquired through Eqs. (16) and (17). It must be noted that the strain energy U characterised by Eq. (9) is in fact associated to the formation of the FPZ essentially prior to fracture growth, that includes only a portion of fracturing energy dissipation. This is followed by a complete de-cohesioning of the material and the creation of new fracture surfaces that complete the energy dissipation due to fracturing. Therefore, the energy release rate calculated in Eq. (9) may underestimate the actual fracture  energy of the material. It is also noteworthy that the crack length is equal to $a_\mathrm {eff}$ in the analysis of displacements in Fig. 9a, which means that crack parameters must be named as ${\tilde{A}}_n$, with even terms vanishing along the crack flanks. The ERR in pure mode $\mathrm {I}$ can, therefore, be formed as

$$\begin{aligned} {{\mathcal {G}}_\mathrm {I}}= & {} \frac{1}{{{L_\mathrm {FPZ}}}}\int _0^{{L_\mathrm {FPZ}}} \left( {\frac{{{A_1}}}{{\sqrt{x} }} + 3{A_3}\sqrt{x} + 5{A_5}x\sqrt{x} } \right) \nonumber \\&\quad \left( \frac{4}{{{\hat{E}}}}\sqrt{{L_\mathrm {FPZ}} - x} \left( {\tilde{A}}_1 - {\tilde{A}}_3 \left( {{L_\mathrm {FPZ}} - x} \right) \right. \right. \nonumber \\&\left. \left. + {\tilde{A}}_5 {{\left( {{L_\mathrm {FPZ}} - x} \right) }^2} \right) \right) \text {d}x \, , \end{aligned}$$

(10)

where ${\hat{E}}=E$ and ${\hat{E}}=E/(1-\nu ^2)$ are for plane-stress and plane-strain conditions, respectively. Implementing $A_n={A^*_n} \, \sigma \, a^{1-n/2}$ in line with Eqs. (3a) and (6) and collecting ${A^*_1} \,{\sigma }\sqrt{a}=K_\mathrm {I}/\sqrt{2\pi }$ gives the critical ERR as the following analytically integrable expression:

$$\begin{aligned} \begin{aligned} {{\mathcal {G}}_\mathrm {Ic}}&= \frac{2}{\pi }\frac{{{K_{{\mathrm {Ic}}}}^2}}{{{\hat{E}}{\mathcal {L}}^*}}\int _0^{{\mathcal {L}}^*} {\left( {\frac{1}{{\sqrt{\frac{x}{a}} }} + 3{M_3}\sqrt{\frac{x}{a}} + 5{M_5}\frac{x}{a}\sqrt{\frac{x}{a}} } \right) } \\&\quad \times \left( \left( {1 + \alpha {{\dot{M}}_1} {\mathcal {L}}^*} \right) \sqrt{1 + {\mathcal {L}}^*} - \left( {{M_3} + \alpha {{\dot{M}}_3} {\mathcal {L}}^*} \right) \frac{{{\mathcal {L}}^* - \frac{x}{a}}}{{\sqrt{1 + {\mathcal {L}}^*} }} \right. \\&\quad \left. + \left( {{M_5} + \alpha {{\dot{M}}_5} {\mathcal {L}}^*} \right) \frac{{{{\left( {{\mathcal {L}}^* - \frac{x}{a}} \right) }^2}}}{{\left( {1 + {\mathcal {L}}^*} \right) \sqrt{1 + {\mathcal {L}}^*} }} \right) \\&\quad \times \sqrt{{\mathcal {L}}^* - \frac{x}{a}} \ \text {d}\left( {\frac{x}{a}} \right) =\frac{{{K_{\mathrm {Ic}}}}^2}{{{\hat{E}}}} I \left( {\mathcal {L}}^* \right) \, , \end{aligned} \end{aligned}$$

(11)

with I, as a function of ${\mathcal {L}}^*$, representing the integral expression. For a fairly large specimen, i.e. mathematically of infinite size, the critical ERR is obtained by the limit of Eq. (11), as given in Eq. (12a), and the ratio ${{\mathcal {G}}_\mathrm {Ic}}/{\mathcal {G}}_\mathrm {Ic}^\infty$ is thereafter achieved as in Eq. (12b):

$$\begin{aligned}&{\mathcal {G}}_\mathrm {Ic}^\infty = \lim _{\mathop {\scriptstyle R \rightarrow \infty }\limits _{\scriptstyle \left( {a \rightarrow \infty } \right) }} {{\mathcal {G}}_\mathrm {Ic}} = \frac{{K_{\mathrm {Ic}}^\infty }^2}{{{\hat{E}}}} \, , \end{aligned}$$

(12a)

$$\begin{aligned}&\frac{{{{\mathcal {G}}_\mathrm {Ic}}}}{{{\mathcal {G}}_\mathrm {Ic}^\infty }} = I \, { {\frac{{{K_{\mathrm{{Ic}}}}^2}}{{K_{{\mathrm {Ic}}}^\infty }^2}} }=I \, {{\mathcal {K}}^*}^2 \, . \end{aligned}$$

(12b)

Fig. 9

Application of the energy release rate concept: a crack faces opening displacement; b the closure stress applied along the FPZ to hold the crack faces closed

On the other hand, according to Bažant and Kazemi (1991), the brittleness number introduced in Eq. (13a) can be employed to define the ratio ${{\mathcal {G}}_\mathrm {Ic}}/{\mathcal {G}}_\mathrm {Ic}^\infty$ as in Eq. (13b):

$$\begin{aligned} \beta=\, & {} \frac{{\mathcal {G}}^*\left( \alpha + \frac{L_\mathrm {FPZ}}{R} \right) }{\frac{L_\mathrm {FPZ}}{R} {{\mathcal {G}}^*}^\prime \left( \alpha + \frac{L_\mathrm {FPZ}}{R}\right) }-1 \, , \end{aligned}$$

(13a)

$$\begin{aligned} \frac{{{{\mathcal {G}}_\mathrm {Ic}}}}{{{\mathcal {G}}_\mathrm {Ic}^\infty }}= \,& {} \frac{\beta }{1+\beta }=\,1-\alpha {\mathcal {L}}^* \frac{{{\mathcal {G}}^*}^\prime \left( \alpha + \frac{L_\mathrm {FPZ}}{R} \right) }{{\mathcal {G}}^*\left( \alpha + \frac{L_\mathrm {FPZ}}{R}\right) }\nonumber \\=\, & {} 1-\alpha {\mathcal {L}}^* \frac{{{\mathcal {G}}^*}^\prime \left( \alpha \right) +\alpha {{\mathcal {G}}^*}'' \left( \alpha \right) {\mathcal {L}}^*}{{\mathcal {G}}^*\left( \alpha \right) +\alpha {{\mathcal {G}}^*}^\prime \left( \alpha \right) {\mathcal {L}}^*}\nonumber \\=\, & {} 1-\alpha {{\dot{M}}_{\mathcal {G}}} {\mathcal {L}}^* \frac{1+\alpha {{\ddot{M}}_{\mathcal {G}}} {\mathcal {L}}^*}{1+\alpha {{\dot{M}}_{\mathcal {G}}} {\mathcal {L}}^*} \, , \end{aligned}$$

(13b)

where ${{\dot{M}}_{\mathcal {G}}} = {{\mathcal {G}}^*}'/{\mathcal {G}}^*$, ${{\ddot{M}}_{\mathcal {G}}} = {{\mathcal {G}}^*}''/{{\mathcal {G}}^*}'$, and ${\mathcal {G}}^*(\alpha )$ is the normalised form of the energy release rate, i.e. ${\mathcal {G}} ={\mathcal {G}}^*P^2/(4{\hat{E}}Rt^2)$, which is computable via the finite element method (FEM) as explained in Appendix A. Eventually, by equating Eqs. (12b) and (13b), one may obtain the ratio of the measured fracture toughness to the true scale-independent fracture toughness, ${\mathcal {K}}^*$, as a function of the normalised FPZ length ${\mathcal {L}}^*$:

$$\begin{aligned} {\mathcal {K}}^*=\frac{K_\mathrm {Ic}}{K_\mathrm {Ic}^\infty }=\sqrt{\frac{1}{I} \left( 1-\alpha {{\dot{M}}_{\mathcal {G}}} {\mathcal {L}}^* \frac{1+\alpha {{\ddot{M}}_{\mathcal {G}}} {\mathcal {L}}^*}{1+\alpha {{\dot{M}}_{\mathcal {G}}} {\mathcal {L}}^*} \right) } \, . \end{aligned}$$

(14)

Using Eqs. (7) and (14) together, it is now feasible to solve for ${\mathcal {L}}^*$ and ${\mathcal {K}}^*$ simultaneously, over a desired range of ${\mathcal {R}}^*_\infty$. Using Eq. (6b), we also define ${\mathcal {R}}^*={\mathcal {R}}^*_\infty /{{\mathcal {K}}^*}^2=R/(K_\mathrm {Ic}/\sigma _t)^2$ as a dimensionless size measure that is next used to plot figures.

4 Comparison of Theory and Experiment

Figure 10 compares the experimental data on the FPZ length and fracture toughness with the theoretical predictions described in Sect. 3. Figure 10a shows the variations of the normalised FPZ length, ${\mathcal {L}}^*=L_\mathrm {FPZ}/a$, with respect to the normalised size, ${\mathcal {R}}^*=R/(K_\mathrm {Ic}/\sigma _t)^2$. It is seen that the test data are rather enveloped by the theoretical curves obtained from the strip-yield model with two variation types namely uniform and linear traction models. Indeed, the linear traction model (i.e. dashed cyan curve) can be interpreted as somewhat the upper bound of the test data for the normalised FPZ length, while the uniform traction model (i.e. solid pink curve) acts as the lower bound of the experimental data. According to this figure, with the increase in the normalised disk radius ${\mathcal {R}}^*$, the normalised FPZ length ${\mathcal {L}}^*$ decreases dramatically, reaching relatively stabilised values of 0.06 and 0.03 for respectively linear and uniform traction models at ${\mathcal {R}}^*=19$.

Fig. 10

Comparison of the SCB test experimental data with the theoretical predictions ($\alpha =a/R=0.5$, $S/R=0.6$): a the variations of the normalised FPZ length with the normalised SCB size; b the variations of the normalised mode $\mathrm {I}$ fracture toughness with the normalised SCB size

An interesting remark regarding Fig. 10a is that it can be used to estimate the FPZ length in the SCB specimen with $a/R=0.5$ and $S/R=0.6$ without performing any actual DIC measurements. Given that the tensile strength $\sigma _t$ of the rock type is known from the Brazilian disk test, and $K_\mathrm {Ic}$ is also measured at a specific size of the SCB sample, one can simply evaluate the position along the horizontal axis (${\mathcal {R}}^*=R/(K_\mathrm {Ic}/\sigma _t)^2$). Intersecting a vertical line from that particular position with the theoretical curves would then reveal two bounds for the estimates of $L_\mathrm {FPZ}/a$, whereby allowing to have an estimation of the FPZ length using the value of $a/R=0.5$.

To plot the theoretical curves in Fig. 10b, we first employ ${\mathcal {K}}^*$ from Eq. (14) and use it within Eq. (7), allowing the determination of ${\mathcal {L}}^*$ over a given range of ${\mathcal {R}}^*_\infty$. The respective ${\mathcal {L}}^*$ values are then inserted into Eq. (14) to calculate the corresponding ${\mathcal {K}}^*$ values for our employed ${\mathcal {R}}^*_\infty$ range. As illustrated, the results of the two closure stress models are plotted again, based on which, the uniform traction model seems to have a superior correlation with the experimental findings. It is seen that by growing the normalised disk radius ${\mathcal {R}}^*_\infty$, estimations of the normalised fracture toughness ${\mathcal {K}}^*$ ascend remarkably, reaching the values of 0.94 and 0.87 at ${\mathcal {R}}^*_\infty =19$ for uniform and linear traction models, respectively. It is noteworthy that the novel theory we introduced and utilised in this article is thoroughly independent of the experimental results, and its good agreement with the test data indicates the accuracy and efficiency of the theory put forward.

5 Introduction of a Correction Factor

To obtain practical size effect curves to estimate the true scale-independent fracture toughness values, it is required to have the horizontal axis in terms of ${\mathcal {R}}^*=R/(K_\mathrm {Ic}/\sigma _t)^2$ as opposed to ${\mathcal {R}}^*_\infty =R/(K_\mathrm {Ic}^\infty /\sigma _t)^2$ used in Fig. 10b. This is because $K_\mathrm {Ic}^\infty$ is an unknown parameter that is to be determined. To achieve this aim, the theoretical data for ${\mathcal {L}}^*=L_\mathrm {FPZ}/a$ presented in Fig. 10a are to be used in Eq. (14) which outputs ${\mathcal {K}}^*=K_\mathrm {Ic}/K_\mathrm {Ic}^\infty$ over the range ${\mathcal {R}}^*$.

The uniform and linear traction models have unique predictions for the normalised fracture toughness, i.e. ${\mathcal {K}}^*_{ut}$ and ${\mathcal {K}}^*_{lt}$. Let us now introduce a correction factor named $C_k$ as a coefficient to compensate for the underestimation of fracture toughness in small-sized specimens, and define it as the inverse of the average of ${\mathcal {K}}^*_{ut}$ and ${\mathcal {K}}^*_{lt}$:

$$\begin{aligned} C_k=2/({\mathcal {K}}^*_{ut}+{\mathcal {K}}^*_{lt})=K_\mathrm {Ic}^\infty /K_\mathrm {Ic} \, . \end{aligned}$$

(15)

Fig. 11

The variations of the fracture toughness correction factor $C_k=2/({\mathcal {K}}^*_{ut}+{\mathcal {K}}^*_{lt})$ for the semi-circular bend test: a $S/R=0.6$; b $S/R=0.8$

Figure 11 gives the variations of the correction factor $C_k$ with the normalised size for a large range of SCB configurations, i.e. $\alpha =a/R=0.35-0.6$ and $S/R=0.6,0.8$. On the selection of the appropriate correction factor and obtaining the true scale-independent fracture toughness for a particular rock type, the following steps should be taken:

• 1. Measure the tensile strength ($\sigma _t$) from the Brazilian disk test or similar approaches.

• 2. Conduct SCB tests at a specific size (R) and configuration (a/R, S/R) to measure $K_\mathrm {Ic}$ associated to that size.

• 3. Extract the correction factor $C_k$ from Fig. 11 at ${\mathcal {R}}^*=R/(K_\mathrm {Ic}/\sigma _t)^2$ based on the test configuration a/R, S/R.

• 4. Estimate the true scale-independent fracture toughness from $K_\mathrm {Ic}^\infty =C_k \times K_\mathrm {Ic}$.

For a/R and S/R values different from the ones presented in Fig. 11, it is suggested that either interpolation should be performed, or, the correction factor should be found by running a similar analysis to the present work. Moreover, it is advisable to perform toughness experiments on SCB samples with a low a/R ratio. This is in view of the fact that the scale factor $C_k$ experiences higher gradients in small values of ${\mathcal {R}}^*$ as a/R rises. As an instance, by considering a constant normalised radius such as ${\mathcal {R}}^*=7$, it is clearly shown in Fig. 11 that the green curves pertaining to $a/R=0.35$ attain the lowest gradients, thus offering less uncertainty in the procedure of true fracture toughness estimation. In addition, lower ratios of a/R are more preferable since they provide correction factors for wider ranges of $R^*$. This is particularly helpful for small $R^*$ values, where the linear traction model fails to find a solution for ${\mathcal {L}}^*$, and thus the correction factor, $C_k=2/({\mathcal {K}}^*_{ut}+{\mathcal {K}}^*_{lt})$, fails to yield a value. As a remedy, one can establish a scale factor solely based on the uniform traction model, i.e. $C_k=1/{\mathcal {K}}^*_{ut}$, which is responsive even in very low $R^*$ values. However, as shown in Fig. 10b, uniform traction correlates well only with the results of big specimens, yet the small specimens yield results that agree well with the average of the uniform and linear traction models.

To benchmark the applicability and effectiveness of the proposed correction factors, in Table 1 we compare the theoretical estimates for the size-independent fracture toughness (obtained via applying the correction factor) with their experimental counterparts estimated by the least squares method in Fig. 5a. For each rock type, three laboratory-sized SCBs with radii $R=50, 75$ and 100 mm, that are common sizes of cores used for laboratory experiments, are selected, and the dimensionless parameter ${\mathcal {R}}^*$ is calculated accordingly. Since our experiments were performed with $a/R=0.5$ and $S/R=0.6$, the red solid curve from Fig. 11a is to be utilised to calculate the correction factor $C_{k}$ at each particular ${\mathcal {R}}^*$. Next, the theoretical scale-independent fracture toughness $K^\infty _\mathrm {Ic,th}$ is estimated, and finally, the relative error with respect to the experimental estimate of $K^\infty _\mathrm {Ic,ex}$ is given.

As evident in limestone’s and granite’s data, the larger the specimen size, the better the theoretical results match the experimental ones. Due to the high gradients of the correction factor curves in small sizes, any uncertainty or error in the fracture toughness or tensile strength measurement can cause a higher uncertainty and error in the correction factor. Therefore, it is suggested that experiments be conducted on specimens as large as possible to minimise such an error propagation when predicting the true fracture toughness. The relatively high steady errors associated to marble’s data are mainly in view of the fact that these experimental points correlate well with the uniform traction model but not with the linear traction model (refer to Fig. 10b). Since our correction factor is defined as the inverse average of these two models, i.e. $C_k=2/({\mathcal {K}}^*_{ut}+{\mathcal {K}}^*_{lt})$, this unsuitability of the estimations of the linear traction model reflects in the final speculations for $K^\infty _\mathrm {Ic}$. Also noteworthy is that the relatively high errors in Table 1 mostly correspond with small specimens which may also suffer from minor dimensioning errors in specimen manufacturing and test execution. Notwithstanding, even in the worst case, the mentioned errors are yet no more than $27\%$ which are quite comparable with the experimental scatter of this work, especially for small samples. Moreover, the experimental value for size-independent mode $\mathrm {I}$ fracture toughness $K^\infty _\mathrm {Ic,ex}$ is only an estimation. The errors might be decreased when $K^\infty _\mathrm {Ic,ex}$ is actually measured by conducting tests on larger specimens and/or increasing the number of test repetitions.

Table 1 Application of the correction factors given in Fig. 11 to estimate the scale-independent fracture toughness of the tested rocks

6 Conclusions

The main findings of this paper are as follows:

• The results of a total of 93 SCB fracture toughness tests on three different rock materials with sample radii ranging from $R=25$ to 300 mm show a significant dependence of the mode $\mathrm {I}$ fracture toughness on the sample size. The values of both fracture toughness and the FPZ length (measured via DIC technique) grow drastically as the disk radius increases. In the most critical cases, the FPZ length and fracture toughness values associated with the largest and smallest specimens were 6.27 and 2.01 times different, respectively, that indicates a severe size effect behaviour.

• The presented novel theoretical model accurately predicts the size-dependence of the FPZ length and fracture toughness. The proposed theory is totally independent of the rock type, and does not include any experimental curve fittings, thus distinguishing it from the available research work in the literature.

• The ISRM-suggested minimum size requirement for the SCB test does not guarantee a stabilised fracture toughness, and is therefore misleading. Our suggested scale-dependent correction factors are, however, able to accurately adjust the fracture toughness measurements obtained from laboratory-sized SCB specimens in order to provide a scale-independent fracture toughness value. These scale-dependent factors depend on the test configuration of the SCB test, while they are independent of the type of rock material.

Appendix A. Numerical Calculation of Crack Parameters

1.1 A.1. Crack Tip Fields Under Mode I Loading

The series solution of the stress and displacement fields around a crack in an isotropic medium subjected to pure mode $\mathrm {I}$ loading is given by (Williams 1957; Ayatollahi and Nejati 2011)

$$\begin{aligned}&\begin{array}{c} \left\{ {\begin{array}{*{20}{c}} {{\sigma _x}}\\ {{\sigma _y}}\\ {{\tau _{xy}}} \end{array}} \right\} = \sum \limits _{n = 1}^\infty {\frac{n}{2}{A_n}{r^{\left( {\frac{n}{2} - 1} \right) }}} \left\{ {\begin{array}{*{20}{c}} {\left( {2 + \frac{n}{2} + {{\left( { - 1} \right) }^n}} \right) \cos \left( {\frac{n}{2} - 1} \right) \theta - \left( {\frac{n}{2} - 1} \right) \cos \left( {\frac{n}{2} - 3} \right) \theta }\\ {\left( {2 - \frac{n}{2} - {{\left( { - 1} \right) }^n}} \right) \cos \left( {\frac{n}{2} - 1} \right) \theta + \left( {\frac{n}{2} - 1} \right) \cos \left( {\frac{n}{2} - 3} \right) \theta }\\ {\left( {\frac{n}{2} - 1} \right) \sin \left( {\frac{n}{2} - 3} \right) \theta - \left( {\frac{n}{2} + {{\left( { - 1} \right) }^n}} \right) \sin \left( {\frac{n}{2} - 1} \right) \theta } \end{array}} \right\} \end{array} \, , \end{aligned}$$

(16)

$$\begin{aligned}&\begin{array}{c} \left\{ {\begin{array}{*{20}{c}} u\\ v \end{array}} \right\} = \sum \limits _{n = 0}^\infty {\frac{{{A_n}}}{{2\mu }}{r^{\frac{n}{2}}}} \left\{ {\begin{array}{*{20}{c}} {\left( {\kappa + \frac{n}{2} + {{\left( { - 1} \right) }^n}} \right) \cos \frac{n}{2}\theta - \frac{n}{2}\cos \left( {\frac{n}{2} - 2} \right) \theta }\\ {\left( {\kappa - \frac{n}{2} - {{\left( { - 1} \right) }^n}} \right) \sin \frac{n}{2}\theta + \frac{n}{2}\sin \left( {\frac{n}{2} - 2} \right) \theta } \end{array}} \right\} \end{array} \, , \end{aligned}$$

(17)

where $(r,\theta )$ are the polar coordinates with respect to the crack tip (see Fig. 12a), $A_n$ are the mode $\mathrm {I}$ crack coefficients, $\mu =E/(2(1+\nu ))$ is the shear modulus, and the Kolosov constant $\kappa$ is equal to $3-4\nu$ for plane-strain and $(3-\nu )/(1+\nu )$ for plane-stress conditions, respectively.

Fig. 12

a Stresses and strains applied at a material element close to the crack tip; b typical FE mesh used for the numerical modelling of the SCB specimen

1.2 A.2. Crack Parameters in an SCB Sample Subjected to Three-point Bend

To determine crack tip coefficients ($A_n$), we first modelled the SCB specimen in the finite element package Abaqus, where eight-noded plane stress quadratic quadrilateral elements of type CPS8 discretise the solution domain (see Fig. 12b). We then applied the finite element over-deterministic (FEOD) method (Ayatollahi and Nejati 2011; Ayatollahi et al. 2020). This method makes use of the displacements of a large number of finite element nodal points around the crack tip to form an over-determined system of equations, and compute the coefficients of the crack tip fields in a least squares manner. After determining $A_n$ from the FEOD analysis, and the energy release rate ${\mathcal {G}}$ from the FE analysis, Eq. (18, 19) was used to calculate the normalised parameters ${A^*_1}$, ${A^*_3}$, ${A^*_5}$ and ${\mathcal {G}}^*$ that are listed in Table 2 for the two span ratios of $S/R=0.6,0.8$. We note that the terms containing the coefficients $A_2$ and $A_4$ are zero along the notch bisector and therefore are not reported here. Also, note that the parameters $A_n$ and ${\mathcal {G}}$ are dependent only on geometry and loading configuration, and have no dependency on material properties.

$$\begin{aligned}&{A_n}={A^*_n} \dfrac{P}{2Rt} a^{1-\frac{n}{2}} \, , \quad n=1,3,5 \, , \end{aligned}$$

(18)

$$\begin{aligned}&{\mathcal {G}}={\mathcal {G}}^*\dfrac{P^2}{4{\hat{E}}Rt^2} \, . \end{aligned}$$

(19)

Table 2 Normalised crack parameters ${A^*_{n}} \left( \alpha \right)$ and normalised ERR ${\mathcal {G}}^*\left( \alpha \right)$ for different S/R values as sixth order polynomial functions of crack length to disk radius ($\alpha =a/R$)

1.3 A.3. Crack Tip Parameters in a SCB Sample Subjected to a Crack Closure Stress

To determine the crack parameters for the case where closure stress is applied along the FPZ, one should first perform FE analyses for the case schematically shown in Fig. 13a. Therein, a pair of concentrated loads P are applied normal to the crack flanks at a distance x from the crack tip, in an SCB specimen with the crack length a. The exertion of a pair of concentrated forces on the crack flanks invalidates the crack tip series solution in Eq. (16) that is the basis of the FEOD method for determining the crack parameters. Due to the invalidity of the crack tip asymptotic solution in such a case, we may ignore the computation of higher order parameters $A_{3,cl}$ and $A_{5,cl}$, and implement only $A_{1,cl}$ to characterise the effect of the closure stress. We use the directly calculated $K_{\mathrm {I},cl}$ from the domain integral method (that is not disturbed by load application on the crack flanks), and determine $A_{1,cl}=K_{\mathrm {I},cl}/\sqrt{2\pi }$. The normalised form of the first coefficient of the crack tip asymptotic field, $A^*_{1,cl}$, is then calculated from

$$\begin{aligned} {A_{1,cl}}={A^*_{1,cl}} \frac{P}{t\sqrt{a}} \, , \end{aligned}$$

(20)

After performing numerous FE analyses for different values of $\alpha =a/R$, and for each case varying the non-dimensional parameter x/a, we define a two-variable function ${A^*_{1,cl}} \left( x/a,\alpha \right)$ which is represented by a third-order logarithmic expression given in Table 3. Noteworthy is that $A_{1,cl}^\star$ is independent of elastic properties of the material.

Table 3 The curve-fitting parameters for the normalised coefficient ${A^*_{1,cl}} \left( x/a,\alpha \right)$ for the case where concentrated forces are applied at the distance x from the crack tip, on the crack faces of the SCB specimen

Fig. 13

Illustration of how crack tip parameters are obtained for the case where a closure stress is applied on the crack flanks. a A pair of concentrated load applied at a distance x from the crack tip; b uniform traction model; c linear traction model

Having ${A^*_{1,cl}}$ determined for the case of concentrated forces, one can perform integration to obtain solutions for the cases where uniform or linear closure stresses are applied to the crack flanks. For the case of uniform closure stress shown in Fig. 13b (Barenblatt 1959; Dugdale 1960), we consider a crack length of $a_\mathrm {eff}=a+L_\mathrm {FPZ}$, and relate the load P to the closure stress through $P=-\sigma _t t \, \text {d}x$ in Eq. (20), deriving the crack parameter ${\tilde{A}}_{1,cl}$ as

$$\begin{aligned} {{\tilde{A}}_{1,cl}}= & {} - \frac{{{\sigma _t}}}{{\sqrt{{a_\mathrm {eff}}} }}\int _0^{{L_\mathrm {FPZ}}} {{A^*_{1,cl}}\left( {\frac{x}{{a + {L_\mathrm {FPZ}}}},\frac{{a + {L_\mathrm {FPZ}}}}{R}} \right) \text {d}x}\nonumber \\= & {} - \frac{{{\sigma _t}}}{{\sqrt{{a_\mathrm {eff}}} }}\int _0^{{L_\mathrm {FPZ}}} {\left( {{A^*_{1,cl}}\left( {\frac{x}{a},\alpha } \right) + \frac{{\text{d}{A^*_{1,cl}}\left( {\frac{x}{a},\alpha } \right) }}{{\text{d}a}}{L_\mathrm {FPZ}}} \right) \text {d}x} \,. \end{aligned}$$

(21)

By employing the chain rule for derivation, one may expand Eq. (21) as

$$\begin{aligned} {{\tilde{A}}_{1,cl}}= & {} - \frac{{{\sigma _t}}}{{\sqrt{{a_\mathrm {eff}}} }}\int _0^{{L_\mathrm {FPZ}}} \left( {A^*_{1,cl}}\left( {\frac{x}{a},\alpha } \right) \right. \nonumber \\&\left. + \left( {\frac{{\partial {A^*_{1,cl}}\left( {\frac{x}{a},\alpha } \right) }}{{\partial \left( {\frac{x}{a}} \right) }}\frac{{\text{d}\left( {\frac{x}{a}} \right) }}{{\text{d}a}} + \frac{{\partial {A^*_{1,cl}}\left( {\frac{x}{a},\alpha } \right) }}{{\partial \alpha}}\frac{{\text{d} \alpha }}{{\text{d}a}}} \right) {L_\mathrm {FPZ}} \right) \text {d}x \,, \end{aligned}$$

(22)

which with the aid of Table 3 can be transformed into

$$\begin{aligned} {{\tilde{A}}_{1,cl}}&= - \frac{{{\sigma _t}}}{{\sqrt{{a_\mathrm {eff}}} }}a\int _0^{{\mathcal {L}}^*} \left( {A^*_{1,cl}}\left( {\frac{x}{a},\alpha } \right) \right. \\&\quad + \left( - \left( {{d_1} + 2{d_2}\ln \left( {\frac{x}{a}} \right) + 3{d_3}\ln {{\left( {\frac{x}{a}} \right) }^2}} \right) \right. \\&\quad \left. \left. + \alpha \frac{{{A^*_{1,cl}}\left( {\frac{x}{a},\alpha + 0.05} \right) - {A^*_{1,cl}}\left( {\frac{x}{a},\alpha - 0.05} \right) }}{{0.1}} \right) {\mathcal {L}}^* \right) \text {d}\left( {\frac{x}{a}} \right) \\&=- \left( {\tilde{A}}^*_{1,cl}\right) _{ut} \frac{{{\sigma _t}}}{{\sqrt{{a_\mathrm {eff}}} }}a \,. \end{aligned}$$

(23)

while designating the normalised FPZ length as ${\mathcal {L}}^*={{L_\mathrm {FPZ}}}/a$. For the linear traction model illustrated in Fig. 13c (Labuz et al. 1985), we define $P=-\sigma _t \left[ 1-(x/a)/{\mathcal {L}}^*)\right] t \, \text {d}x$ in Eq. (20) and finally reach

$$\begin{aligned} {{\tilde{A}}_{1,cl}}&= - \frac{{{\sigma _t}}}{{\sqrt{{a_\mathrm {eff}}} }}a\int _0^{{\mathcal {L}}^*} \left( 1-\frac{\frac{x}{a}}{{\mathcal {L}}^*}\right) \left( {A^*_{1,cl}}\left( {\frac{x}{a},\alpha } \right) \right. \\&\quad + \left( - \left( {{d_1} + 2{d_2}\ln \left( {\frac{x}{a}} \right) + 3{d_3}\ln {{\left( {\frac{x}{a}} \right) }^2}} \right) \right. \\&\quad \left. \left. + \alpha \frac{{{A^*_{1,cl}}\left( {\frac{x}{a},\alpha + 0.05} \right) - {A^*_{1,cl}}\left( {\frac{x}{a},\alpha - 0.05} \right) }}{{0.1}} \right) {\mathcal {L}}^* \right) \text {d}\left( {\frac{x}{a}} \right) \\&=- \left( {\tilde{A}}^*_{1,cl}\right) _{lt} \frac{{{\sigma _t}}}{{\sqrt{{a_\mathrm {eff}}} }}a \,. \end{aligned}$$

(24)

To summarise our findings here, we may write

$$\begin{aligned} {\tilde{A}}_{1,cl}= \,& {} -{\tilde{A}}^*_{1,cl} \frac{{{\sigma _t}}}{{\sqrt{{a_\mathrm {eff}}} }} a \, , \quad \nonumber \\ {\tilde{A}}^*_{1,cl}= \,& {} \left\{ \begin{array}{l} \left( {\tilde{A}}^*_{1,cl}\right) _{ut} \quad \text {uniform traction model} \\ \left( {\tilde{A}}^*_{1,cl}\right) _{lt} \quad \text {linear traction model} \end{array}\right. \, , \end{aligned}$$

(25)

which has been used in Eq. (3b).