Skip to main content
SpringerLink
Log in

Scattering of cylindrical inclusions in half space with inhomogeneous shear modulus due to SH wave

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

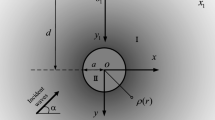
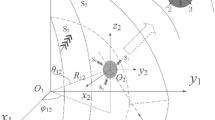
Dynamic responses around cylindrical inclusion in inhomogeneous medium are discussed. A mathematical model of inhomogeneous half space is established. The shear modulus of the medium is assumed to change in two dimensions. Based on complex function theory, the governing equations are derived. Meanwhile, the auxiliary function is introduced. By solving the governing equation, the analytical expressions of the displacement field and stress field formed by Bessel function and Hankel function are obtained. The unknown coefficients can be obtained by boundary conditions. According to numerical examples, the results of this paper are compared with published results to verify the validity of the method. Meanwhile, the effects of inhomogeneous parameters, reference wave number and burial location on the dynamic stress concentration factor (DSCF) around a cylindrical inclusion are discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Pao, Y.H., Mow, C.C.: Diffraction of Elastic Waves and Dynamic Stress Concentrations. New York (1973)s

  2. Achenbach, J.D.: Wave Propagation in Elastic Solids. North-Holland, Amsterdam (1973)

    MATH  Google Scholar 

  3. Liu, D.K., Gai, B.Z., Tao, G.Y.: Applications of the method of complex functions to dynamic stress concentrations. Wave Motion 4, 293–304 (1982)

    Article  MathSciNet  Google Scholar 

  4. Hei, B.P., Yang, Z.L., Wang, Y., Liu, D.K.: Dynamic analysis of elastic waves by an arbitrary cavity in an inhomogeneous medium with density variation. Math. Mech. solids 21(8), 931–940 (2016)

    Article  MathSciNet  Google Scholar 

  5. Yang, Z.L., Zhang, C.Q., Jiang, G.X.X., Yan, P.L., Yang, Y.: A complex function method of SH wave scattering in inhomogeneous medium. Acta Mech. 228(10), 3469–3481 (2017)

    Article  MathSciNet  Google Scholar 

  6. Jiang, G.X.X., Yang, Z.L., Sun, C., Sun, B.T., Yang, Y.: Dynamic response of a circular inclusion embedded in inhomogeneous half-space. Arch. Appl. Mech. 88(10), 1791–1803 (2018)

    Article  Google Scholar 

  7. Zhang, N., Gao, Y.F., Yang, J., Xu, C.J.: An analytical solution to the scattering of cylindrical SH waves by a partially filled semi-circular alluvial valley: near-source site effects. Earthq. Eng. Eng. Vib. 14(2), 189–201 (2015)

    Article  Google Scholar 

  8. Hao, L., Lee, V.W., Liang, J.W.: Anti-plane (SH) waves diffraction by an underground semi-circular cavity: analytical solution. Earthq. Eng. Eng. Vib. 9(3), 385–396 (2010)

    Article  Google Scholar 

  9. Daros, C.H.: Green’s function for SH-waves in inhomogeneous anisotropic elastic solid with power-function velocity variation. Wave Motion 50(2), 101–110 (2013)

    Article  MathSciNet  Google Scholar 

  10. Qi, H., Chen, H.Y., Zhang, X.M., Zhao, Y.B., Xiang, M.: Scattering of SH-wave by an elliptical inclusion with partial debonding curve in half-space. Wave Random Complex Media 29(2), 281–298 (2019)

    Article  MathSciNet  Google Scholar 

  11. Han, X., Liu, G.R.: Effects of SH waves in a functionally graded plate. Mech. Res. Commun. 29(5), 327–338 (2002)

    Article  Google Scholar 

  12. Fang, X.Q., Hu, C., Du, S.Y.: Dynamic Stress of a Circular Cavity Buried in a Semi-Infinite Functionally Graded Material Subjected to Shear Waves. J. Appl. Mech-Trans ASME 74(5), 916–922 (2007)

    Article  Google Scholar 

  13. Martin, P.A.: Scattering by a cavity in an exponentially graded half-space. J. Appl. Mech Trans ASME 76(3), 031009 (2009)

    Article  Google Scholar 

  14. Liu, Q.J., Zhao, M.J., Zhang, C.: Antiplane scattering of SH waves by a circular cavity in an exponentially graded half space. Int. J. Eng. Sci. 78, 61–72 (2014)

    Article  MathSciNet  Google Scholar 

  15. Miiller, R., Dineva, P., Rangelov, T., et al.: Anti-plane dynamic hole–crack interaction in a functionally graded piezoelectric media. Arch. Appl. Mech. 82(1), 97–110 (2012)

    Article  Google Scholar 

  16. Kara, H.F., Aydogdu, M.: Dynamic response of a functionally graded tube embedded in an elastic medium due to SH-Waves. Compos. Struct. 206, 22–32 (2018)

    Article  Google Scholar 

  17. Tsaur, D.H., Chang, K.H., Hsu, M.S.: An analytical approach for the scattering of SH waves by a symmetrical V-shaped canyon: deep case. Geophys. J. Int. 183(3), 1501–1511 (2010)

    Article  Google Scholar 

  18. Tsaur, D.H., Chang, K.H.: An analytical approach for the scattering of SH waves by a symmetrical V-shaped canyon: shallow case. Geophys. J. Int. 174(1), 255–264 (2008)

    Article  Google Scholar 

  19. Zhang, N., Zhang, Y., Gao, Y.F., Pak, R.Y.S., Wu, Y.X., Zhang, F.: An exact solution for SH-wave scattering by a radially multilayered inhomogeneous semicylindrical canyon. Geophys. J. Int. 217(2), 1232–1260 (2019)

    Article  Google Scholar 

  20. Fontara, I., Dineva, P.S., Manolis, G.D., et al.: Seismic wave fields in continuously inhomogeneous media with variable wave velocity profiles. Arch. Appl. Mech. 86(1–2), 65–88 (2015)

    Google Scholar 

  21. Wuttke, F., Fontara, I.K., Dineva, P., Rangelov, T.: SH-wave propagation in a continuously inhomogeneous half-plane with free-surface relief by BIEM. ZAMM-Z Angew Math. Mech. 95(7), 714–729 (2015)

    Article  MathSciNet  Google Scholar 

  22. Chen, J.T., Kao, S.K., Hsu, Y.H., Fan, Y.: Scattering problems of the SH wave by using the null-field boundary integral equation method. J. Earthq. Eng. 22(1), 1–35 (2018)

    Article  Google Scholar 

  23. Chen, T.R., Fehler, M., Fang, X.D., Shang, X.F., Burns, D.: SH wave scattering from 2-D fractures using boundary element method with linear slip boundary condition. Geophys. J. Int. 188(1), 371–180 (2012)

    Article  Google Scholar 

  24. Panji, M., Mojtabazadeh-Hasanlouei, S., Yasemi, F.: A half-plane time-domain BEM for SH-wave scattering by a subsurface inclusion. Comput. Geosci. 134, 104342 (2020)

    Article  Google Scholar 

  25. Weber, W.E., Manolis, G.D.: Dynamic behaviour of rigid inclusions with circumferential damage embedded in an elastic matrix. Arch. Appl. Mech. 87(7), 1–10 (2017)

    Article  Google Scholar 

  26. Emets, V.F., Kunets, Y.I., Matus, V.V.: Scattering of SH waves by an elastic thin-walled rigidly supported inclusion. Arch. Appl. Mech. 73(11), 769–780 (2004)

    Article  Google Scholar 

  27. Shaw, R.P., Manolis, G.D.: A generalized Helmholtz equation fundamental solution using a conformal mapping and dependent variable transformation. Eng. Anal. Bound. Elem. 24(2), 177–188 (1998)

    Article  Google Scholar 

  28. Liu, D.K., Lin, H.: Scattering of SH-waves by a shallow buried cylindrical cavity and the ground motion. Expl. Shock Waves. 23(1), 6–12 (2003). ((in Chinese))

    Google Scholar 

  29. Trifunac, M.D.: Scattering of plane SH-waves by a semi-cylindrical canyon. Earthq. Eng. Struct. Dyn. 1, 267–281 (1973)

    Article  Google Scholar 

Download references

Funding

This work is supported by the National Natural Science Foundation of China (No. 11872156) and the Research Team Project of Heilongjiang Natural Science Foundation (Grant No.TD2020A001) and the Fundamental Research Funds for the Central Universities (Grant No. 3072020CFT0202) and the program for Innovative Research Team in China Earthquake Administration.

Author information

Authors and Affiliations

  1. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin, 150001, China

    Zailin Yang, Jinlai Bian, Yunqiu Song, Yong Yang & Menghan Sun

  2. Key Laboratory of Advanced Material of Ship and Mechanics, Ministry of Industry and Information Technology, Harbin Engineering University, Harbin, China

    Zailin Yang, Yong Yang & Menghan Sun

Authors
  1. Zailin Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jinlai Bian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yunqiu Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Menghan Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Menghan Sun.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

1.1 Expression for stress fields in half space

Incident waves in half-space

$$\begin{aligned} \tau_{rz}^{i} = & \frac{1}{2}\mu_{0} \varphi_{0} \beta \exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta {\text{e}}^{ - i\alpha } + \overline{\zeta }{\text{e}}^{i\alpha } } \right)} \right]\exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right] \\ & \left[ {\left( {\beta \overline{z} + \gamma } \right)\left( {ik_{T} {\text{e}}^{ - i\alpha } - 1} \right){\text{e}}^{i\theta } + \left( {\beta z + \gamma } \right)\left( {ik_{T} {\text{e}}^{i\alpha } - 1} \right){\text{e}}^{ - i\theta } } \right] \\ \end{aligned}$$
(40)
$$\begin{aligned} \tau_{\theta z}^{i} = & \frac{1}{2}i\mu_{0} \varphi_{0} \beta \exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta e^{ - i\alpha } + \overline{\zeta }e^{i\alpha } } \right)} \right]\exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right] \\ & \left[ {\left( {\beta \overline{z} + \gamma } \right)\left( {ik_{T} e^{ - i\alpha } - 1} \right)e^{i\theta } - \left( {\beta z + \gamma } \right)\left( {ik_{T} e^{i\alpha } - 1} \right)e^{ - i\theta } } \right] \\ \end{aligned}$$
(41)

Reflected waves in half-space

$$\begin{aligned} \tau_{rz}^{r} = & \frac{1}{2}\mu_{0} \varphi_{0} \beta \exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta e^{i\alpha } + \overline{\zeta }e^{ - i\alpha } } \right)} \right]\exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right] \\ & \left[ {\left( {\beta \overline{z} + \gamma } \right)\left( {ik_{T} e^{i\alpha } - 1} \right)e^{i\theta } + \left( {\beta z + \gamma } \right)\left( {ik_{T} e^{ - i\alpha } - 1} \right)e^{ - i\theta } } \right] \\ \end{aligned}$$
(42)
$$\begin{aligned} \tau_{\theta z}^{r} = & \frac{1}{2}i\mu_{0} \varphi_{0} \beta \exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta e^{i\alpha } + \overline{\zeta }e^{ - i\alpha } } \right)} \right]\exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right] \\ & \left[ {\left( {\beta \overline{z} + \gamma } \right)\left( {ik_{T} e^{i\alpha } - 1} \right)e^{i\theta } - \left( {\beta z + \gamma } \right)\left( {ik_{T} e^{ - i\alpha } - 1} \right)e^{ - i\theta } } \right] \\ \end{aligned}$$
(43)

Scattering waves generated by inclusion

$$\begin{aligned} \tau_{rz}^{s} = & - \frac{1}{2}\mu_{0} \beta \exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right] \\ & \sum\limits_{n = - \infty }^{\infty } {A_{n} } \left[ {\left( {\left( {\beta \overline{z} + \gamma } \right)\left( {H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{{1}} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n} + H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{{2}} }}{{\left| {\zeta_{{2}} } \right|}}} \right)^{ - n} } \right)} \right.} \right. \\ & + \left. {k_{T} \left( {\beta z + \gamma } \right)\left( {\beta \overline{z} + \gamma } \right)\left( \begin{gathered} \frac{1}{{\beta z_{2} + \gamma }}H_{n + 1}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{{2}} }}{{\left| {\zeta_{{2}} } \right|}}} \right)^{ - n - 1} \hfill \\ - \frac{1}{{\beta z_{1} + \gamma }}H_{n - 1}^{(1)} \left( {k_{T} \left| {\zeta_{{1}} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n - 1} \hfill \\ \end{gathered} \right)} \right){\text{e}}^{i\theta } \\ & + \left( {\left( {\beta z + \gamma } \right)\left[ {H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{{1}} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n} + H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{{2}} }}{{\left| {\zeta_{{2}} } \right|}}} \right)^{ - n} } \right]} \right. \\ & \left. { + \left. {k_{T} \left( {\beta z + \gamma } \right)\left( {\beta \overline{z} + \gamma } \right)\left( \begin{gathered} \frac{1}{{\beta \overline{z}_{1} + \gamma }}H_{n + 1}^{(1)} \left( {k_{T} \left| {\zeta_{{1}} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n + 1} \hfill \\ - \frac{1}{{\beta \overline{z}_{2} + \gamma }}H_{n - 1}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{2} }}{{\left| {\zeta_{2} } \right|}}} \right)^{ - n + 1} \hfill \\ \end{gathered} \right)} \right){\text{e}}^{ - i\theta } } \right] \\ \end{aligned}$$
(44)
$$\begin{aligned} \tau_{\theta z}^{s} = & - \frac{1}{2}i\mu_{0} \beta \exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right] \\ & \sum\limits_{n = - \infty }^{\infty } {A_{n} } \left[ {\left( {\left( {\beta \overline{z} + \gamma } \right)(H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{{1}} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n} + H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{{2}} }}{{\left| {\zeta_{{2}} } \right|}}} \right)^{ - n} } \right.} \right. \\ & + \left. {k_{T} \left( {\beta z + \gamma } \right)\left( {\beta \overline{z} + \gamma } \right)\left( \begin{gathered} \frac{1}{{\beta z_{2} + \gamma }}H_{n + 1}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{{2}} }}{{\left| {\zeta_{{2}} } \right|}}} \right)^{ - n - 1} \hfill \\ - \frac{1}{{\beta z_{1} + \gamma }}H_{n - 1}^{(1)} \left( {k_{T} \left| {\zeta_{{1}} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n - 1} \hfill \\ \end{gathered} \right)} \right){\text{e}}^{i\theta } \\ & - \left( {\left( {\beta z + \gamma } \right)\left[ {H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{{1}} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n} + H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{{2}} }}{{\left| {\zeta_{{2}} } \right|}}} \right)^{ - n} } \right]} \right. \\ & \left. { + \left. {k_{T} \left( {\beta z + \gamma } \right)\left( {\beta \overline{z} + \gamma } \right)\left( \begin{gathered} \frac{1}{{\beta \overline{z}_{1} + \gamma }}H_{n + 1}^{(1)} \left( {k_{T} \left| {\zeta_{{1}} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n + 1} \hfill \\ - \frac{1}{{\beta \overline{z}_{2} + \gamma }}H_{n - 1}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{2} }}{{\left| {\zeta_{2} } \right|}}} \right)^{ - n + 1} \hfill \\ \end{gathered} \right)} \right){\text{e}}^{ - i\theta } } \right] \\ \end{aligned}$$
(45)

Standing waves in inclusion

$$\tau_{rz}^{t} = \frac{1}{2}\mu_{2} k_{2} \sum\limits_{n = - \infty }^{\infty } {B_{n} \left[ {J_{n - 1} \left( {k_{2} \left| {z_{1} } \right|} \right)\left( {\frac{{z_{1} }}{{\left| {z_{1} } \right|}}} \right)^{n - 1} {\text{e}}^{i\theta } - J_{n + 1} \left( {k_{2} \left| {z_{1} } \right|} \right)\left( {\frac{{z_{1} }}{{\left| {z_{1} } \right|}}} \right)^{n + 1} {\text{e}}^{ - i\theta } } \right]}$$
(46)
$$\tau_{\theta z}^{t} = \frac{1}{2}i\mu_{2} k_{2} \sum\limits_{n = - \infty }^{\infty } {B_{n} \left[ {J_{n - 1} \left( {k_{2} \left| {z_{1} } \right|} \right)\left( {\frac{{z_{1} }}{{\left| {z_{1} } \right|}}} \right)^{n - 1} {\text{e}}^{i\theta } + J_{n + 1} \left( {k_{2} \left| {z_{1} } \right|} \right)\left( {\frac{{z_{1} }}{{\left| {z_{1} } \right|}}} \right)^{n + 1} {\text{e}}^{ - i\theta } } \right]}$$
(47)

1.2 Wave fields expression (Sect. 5.1) in boundary conditions

$$\begin{aligned} E^{1} & = \varphi_{0} \exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right]\exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta {\text{e}}^{ - i\alpha } + \overline{\zeta }{\text{e}}^{i\alpha } } \right)} \right] \hfill \\ & + \varphi_{0} \exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right]\exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta {\text{e}}^{i\alpha } + \overline{\zeta }{\text{e}}^{ - i\alpha } } \right)} \right] \hfill \\ \end{aligned}$$
(48)
$$\begin{aligned} E^{2} &= \mu_{0} \varphi_{0} \beta \exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta {\text{e}}^{ - i\alpha } + \overline{\zeta }{\text{e}}^{i\alpha } } \right)} \right]\exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right] \\ & \quad \left[ {\left( {\beta \overline{z} + \gamma } \right)\left( {ik_{T} {\text{e}}^{ - i\alpha } - 1} \right){\text{e}}^{i\theta } + \left( {\beta z + \gamma } \right)\left( {ik_{T} {\text{e}}^{i\alpha } - 1} \right){\text{e}}^{ - i\theta } } \right] \\ & \quad + \mu_{0} \varphi_{0} \beta \exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta {\text{e}}^{i\alpha } + \overline{\zeta }{\text{e}}^{ - i\alpha } } \right)} \right]\exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right] \\ & \quad \left[ {\left( {\beta \overline{z} + \gamma } \right)\left( {ik_{T} {\text{e}}^{i\alpha } - 1} \right){\text{e}}^{i\theta } + \left( {\beta z + \gamma } \right)\left( {ik_{T} {\text{e}}^{ - i\alpha } - 1} \right){\text{e}}^{ - i\theta } } \right] \\ \end{aligned}$$
(49)
$$E_{n}^{11} = - \exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right]\left[ {H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{1} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n} + H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{2} }}{{\left| {\zeta_{2} } \right|}}} \right)^{ - n} } \right]$$
(50)
$$E_{n}^{12} = J_{n} \left( {k_{2} \left| {z_{1} } \right|} \right)\left( {\frac{{z_{1} }}{{\left| {z_{1} } \right|}}} \right)^{n}$$
(51)
$$\begin{aligned} E_{n}^{21} = & \mu_{0} \beta \exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right] \\ & \left[ {\left( {\left( {\beta \overline{z} + \gamma } \right)\left( {H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{1} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n} + H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{2} }}{{\left| {\zeta_{2} } \right|}}} \right)^{ - n} } \right)} \right.} \right. \\ & \left. { + k_{T} \left( {\beta z + \gamma } \right)\left( {\beta \overline{z} + \gamma } \right)\left( \begin{gathered} \frac{1}{{\beta z_{2} + \gamma }}H_{n + 1}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{{2}} }}{{\left| {\zeta_{{2}} } \right|}}} \right)^{ - n - 1} \hfill \\ - \frac{1}{{\beta z_{1} + \gamma }}H_{n - 1}^{(1)} \left( {k_{T} \left| {\zeta_{{1}} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n - 1} \hfill \\ \end{gathered} \right)} \right){\text{e}}^{i\theta } \\ & + \left( {\left( {\beta z + \gamma } \right)\left( {H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{1} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n} + H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{2} }}{{\left| {\zeta_{2} } \right|}}} \right)^{ - n} } \right)} \right. \\ & \left. {\left. { + k_{T} \left( {\beta z + \gamma } \right)\left( {\beta \overline{z} + \gamma } \right)\left( \begin{gathered} \frac{1}{{\beta \overline{z}_{1} + \gamma }}H_{n + 1}^{(1)} \left( {k_{T} \left| {\zeta_{{1}} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n + 1} \hfill \\ - \frac{1}{{\beta \overline{z}_{2} + \gamma }}H_{n - 1}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{2} }}{{\left| {\zeta_{2} } \right|}}} \right)^{ - n + 1} \hfill \\ \end{gathered} \right)} \right){\text{e}}^{ - i\theta } } \right] \\ \end{aligned}$$
(52)
$$E_{n}^{22} = \mu_{2} k_{2} \left[ {J_{n - 1} \left( {k_{2} \left| {z_{1} } \right|} \right)\left( {\frac{{z_{1} }}{{\left| {z_{1} } \right|}}} \right)^{n - 1} {\text{e}}^{i\theta } - J_{n + 1} \left( {k_{2} \left| {z_{1} } \right|} \right)\left( {\frac{{z_{1} }}{{\left| {z_{1} } \right|}}} \right)^{n + 1} {\text{e}}^{ - i\theta } } \right]$$
(53)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, Z., Bian, J., Song, Y. et al. Scattering of cylindrical inclusions in half space with inhomogeneous shear modulus due to SH wave. Arch Appl Mech 91, 3449–3461 (2021). https://doi.org/10.1007/s00419-021-01975-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-021-01975-5

Keywords

Search

Navigation