Large fluctuations in multi-scale modeling for rest hematopoiesis

Abstract

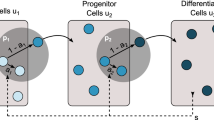
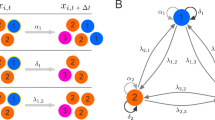
Hematopoiesis is a biological phenomenon (process) of production of mature blood cells by cellular differentiation. It is based on amplification steps due to an interplay between renewal and differentiation in the successive cell types from stem cells to mature blood cells. We will study this mechanism with a stochastic point of view to explain unexpected fluctuations on the mature blood cell number, as surprisingly observed by biologists and medical doctors in a rest hematopoiesis. We consider three cell types: stem cells, progenitors and mature blood cells. Each cell type is characterized by its own dynamics parameters, the division rate and the renewal and differentiation probabilities at each division event. We model the global population dynamics by a three-dimensional stochastic decomposable branching process. We show that the amplification mechanism is given by the inverse of the small difference between the differentiation and renewal probabilities. Introducing a parameter K which scales simultaneously the size of the first component, the differentiation and renewal probabilities and the mature blood cell death rate, we describe the asymptotic behavior of the process for large K. We show that each cell type has its own size and time scales. Focusing on the third component, we prove that the mature blood cell population size, conveniently renormalized (in time and size), is expanded in an unusual way inducing large fluctuations. The proofs are based on a fine study of the different scales involved in the model and on the use of different convergence and average techniques in the proofs.

Appendix

Lemma 3

(Lemma 2.9 of Kang et al. 2014) Let $V^N$ be a sequence of ${\mathbb {R}} _+^{3}$-valued processes. We consider its occupation measure defined for D a Borelian set by

$$\begin{aligned} \varGamma _N(D \times [0,t])= \int _0^t \mathbf{1}_{D}(V^N(s))\, ds. \end{aligned}$$

Let us assume that there exists a function $\psi : {\mathbb {R}} _+^{3} \rightarrow [1,\infty )$ locally bounded such that $\lim _{v \rightarrow +\infty } \psi (v)= +\infty$ and such that for each $t>0$,

$$\begin{aligned} \sup _{N} {\mathbb {E}} \left[ \int _0^t \psi (V^N(s))ds \right] < +\infty . \end{aligned}$$

Then ${\varGamma _N}$ is relatively compact, and if $\varGamma _N$ converges in law to $\varGamma$, then for $f_1,\dots ,f_m \in D_{\psi }$,

$$\begin{aligned}&\left( \int _0^. f_1(V_N(s)) \, ds, \dots , \int _0^. f_m(V^N(s)) \, ds \right) \xrightarrow {\mathscr {L}}\\&\quad \left( \int _{{\mathbb {R}} _+^{3}} f_1(v) \, \varGamma (dv \times [0,.]), \dots , \int _{{\mathbb {R}} _+^{3}} f_m(v) \, \varGamma (dv \times [0,.]) \right) \end{aligned}$$

where $D_{\psi }$ denote the collection of continuous functions f satisfying

$$\begin{aligned} \sup _{v \in {\mathbb {R}} _+^{3}} \frac{\vert f(v) \vert }{\psi (v)}<\infty \quad \text { and } \lim _{k\rightarrow \infty } \sup _{v \in {\mathbb {R}} _+^{3}, \parallel v \parallel >k} \frac{\vert f(v) \vert }{\psi (v)} =0. \end{aligned}$$

(43)