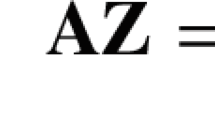Unconstrained representation of orthogonal matrices with application to common principal components

Abstract

Many statistical problems involve the estimation of a $\left( d\times d\right)$ orthogonal matrix $\varvec{Q}$. Such an estimation is often challenging due to the orthonormality constraints on $\varvec{Q}$. To cope with this problem, we use the well-known PLU decomposition, which factorizes any invertible $\left( d\times d\right)$ matrix as the product of a $\left( d\times d\right)$ permutation matrix $\varvec{P}$, a $\left( d\times d\right)$ unit lower triangular matrix $\varvec{L}$, and a $\left( d\times d\right)$ upper triangular matrix $\varvec{U}$. Thanks to the QR decomposition, we find the formulation of $\varvec{U}$ when the PLU decomposition is applied to $\varvec{Q}$. We call the result as PLR decomposition; it produces a one-to-one correspondence between $\varvec{Q}$ and the $d\left( d-1\right) /2$ entries below the diagonal of $\varvec{L}$, which are advantageously unconstrained real values. Thus, once the decomposition is applied, regardless of the objective function under consideration, we can use any classical unconstrained optimization method to find the minimum (or maximum) of the objective function with respect to $\varvec{L}$. For illustrative purposes, we apply the PLR decomposition in common principle components analysis (CPCA) for the maximum likelihood estimation of the common orthogonal matrix when a multivariate leptokurtic-normal distribution is assumed in each group. Compared to the commonly used normal distribution, the leptokurtic-normal has an additional parameter governing the excess kurtosis; this makes the estimation of $\varvec{Q}$ in CPCA more robust against mild outliers. The usefulness of the PLR decomposition in leptokurtic-normal CPCA is illustrated by two biometric data analyses.

1 Introduction

With the term orthogonal matrix we refer to a $\left( d \times d\right)$ matrix $\varvec{Q}$ whose columns are mutually orthogonal unit vectors (i.e., orthonormal vectors). As highlighted by Banerjee and Roy (2014, p. 209), one might, perhaps more properly, call $\varvec{Q}$ an “orthonormal” matrix, but the more conventional name is an “orthogonal” matrix, and we will adopt it hereafter. For further characterizations, properties, and details about orthogonal matrices see, e.g., Lütkepoh (1996, Chapter 9.10), Healy (2000, Chapter 3.5), Schott (2016, Chapter 1.10), and Searle and Khuri (2017, Chapter 5.4). Orthogonal matrices are used extensively in statistics, especially in linear models and multivariate analysis (see, e.g., Graybill 1976 Chapter 11 and James 1954).

The $d^2$ elements of $\varvec{Q}$ are subject to $d\left( d+1\right) /2$ (orthonormality) constraints. It is therefore not surprising that they can be represented by only $d^2-d\left( d+1\right) /2=d\left( d-1\right) /2$ independent parameters. A representation is convenient if $\varvec{Q}$ can be quickly computed from these $d\left( d-1\right) /2$ independent parameters. Such a representation should facilitate the search for an orthogonal matrix that satisfies a certain optimality criterion induced by the chosen estimation method, especially if these independent parameters were real-valued (Khuri 2003). Methods to parameterize an orthogonal matrix are reviewed in Khuri and Good (1989). A similar problem is bumped into when a $\left( d \times d\right)$ positive-definite matrix $\varvec{\Sigma }$, often encountered in statistics in the form of a covariance matrix, needs to be estimated. Luckily, in this case, the Cholesky decomposition allows to map the $d\left( d+1\right) /2$ independent parameters of $\varvec{\Sigma }$ with the $d\left( d+1\right) /2$ real-valued elements of a $\left( d \times d\right)$ lower triangular matrix (Pourahmadi 1999, 2000; Pourahmadi et al. 2007).

Unfortunately, an analogous of the Cholesky decomposition does not exist for $\varvec{Q}$. We fill the gap by using the PLU decomposition, which factorizes any invertible $\left( d\times d\right)$ matrix as the product of a $\left( d\times d\right)$ permutation matrix $\varvec{P}$, a $\left( d\times d\right)$ unit lower triangular matrix $\varvec{L}$, and a $\left( d\times d\right)$ upper triangular matrix $\varvec{U}$. Our merit is the determination of the exact formulation of $\varvec{U}$ when the PLU decomposition is applied to $\varvec{Q}$, and we find that by means of the QR decomposition. We call the result as PLR decomposition; similarly to the Cholesky decomposition, it creates a one-to-one map between $\varvec{Q}$ and $\varvec{L}$, whose $d\left( d-1\right) /2$ entries below the diagonal are advantageously real-valued.

For illustrative purposes, we apply the PLR decomposition in common principal component analysis (CPCA), where the space spanned by the d vectors (principal components) of $\varvec{Q}$ is assumed to be identical across several known groups, whereas the variances associated with the common principal components may vary. When the groups are assumed to be normally distributed, as typically happens, we can use the FG algorithm developed by Flury and Gautschi (1986) for the estimation of $\varvec{Q}$. Although the FG algorithm is distribution-free (Flury 1988, p. 71), under non-normal distributions it may provide an orthogonal matrix which does not maximize the likelihood. Motivated by this consideration, we assume groups having a leptokurtic-normal distribution and use the PLR decomposition to allow $\varvec{Q}$ to be estimated by any standard unconstrained maximization routine. The leptokurtic-normal is an heavy-tailed generalization of the normal distribution that can be preferred, for example, in the presence of mild outliers.

The paper is organized as follow. In Sect. 2 we introduce the PLR decomposition. In Sect. 3 we first define the CPCA based on leptokurtic-normal groups, and then consider the PLR decomposition in the estimation of the common orthogonal matrix. In Sect. 4 we illustrate the leptokurtic-normal CPCA in allometric studies by using two well-known biometric data sets, where the method shows its better performance with respect to the consolidated normal CPCA. Nevertheless, we want to stress that our goal is not to propose a new robust method for estimating the common principal components. Instead, we simply want to illustrate how, regardless of the way the orthogonal matrix enters in the considered model, we can use our PLR decomposition, along with any unconstrained optimization routine, to estimate $\varvec{Q}$, without the need to define ad-hoc estimating algorithms. Finally, we give conclusions and avenues for further research in Sect. 5.

2 PLR decomposition of orthogonal matrices

Before to present the PLR decomposition for orthogonal matrices, Definitions 2.1 and 2.2 recall the well-known QR and PLU decompositions.

Definition 2.1

(QR decomposition) If $\varvec{A}$ is a $\left( d\times d\right)$ invertible matrix, then there is a unique $\left( d\times d\right)$ orthogonal matrix $\varvec{Q}$, and a unique $\left( d\times d\right)$ upper triangular matrix $\varvec{R}$ having a positive diagonal, such that $\varvec{A}= \varvec{Q}\varvec{R}$.

Definition 2.2

(PLU decomposition) If $\varvec{A}$ is a $(d\times d)$ invertible matrix, then there is a $(d\times d)$ permutation matrix $\varvec{P}$, a $\left( d\times d\right)$ unit lower triangular matrix $\varvec{L}$, and a $\left( d\times d\right)$ upper triangular matrix $\varvec{U}$, such that $\varvec{A}= \varvec{P}\varvec{L}\varvec{U}$.

The following theorem presents the PLR decomposition.

Theorem 2.1

(PLR decomposition) If $\varvec{Q}$ is a $\left( d\times d\right)$ orthogonal matrix, then it can be factorized as

$$\begin{aligned} \varvec{Q}= \varvec{P}\varvec{L}\varvec{R}^{-1}, \end{aligned}$$

(1)

where $\varvec{P}$ and $\varvec{L}$ are defined as in Definition 2.2, and $\varvec{R}$ is the upper triangular matrix, having a positive diagonal, coming from the QR decomposition of the matrix $\varvec{P}\varvec{L}$ (see Definition 2.1).

Proof

Because $\varvec{Q}$ is an orthogonal matrix, it is invertible and, according to Definition 2.2, admits the PLU decomposition

$$\begin{aligned} \varvec{Q}= \varvec{P}\varvec{L}\varvec{U}. \end{aligned}$$

(2)

Because any unit lower triangular matrix is invertible, $\varvec{L}$, as well as $\varvec{P}\varvec{L}$, is invertible. Then, according to Definition 2.1, the matrix $\varvec{P}\varvec{L}$ admits the QR decomposition $\varvec{P}\varvec{L}=\varvec{Q}\varvec{R}$, which we recall to be unique. Then, it is easy to verify that $\varvec{U}$ must be equal to $\varvec{R}^{-1}$, and the theorem is proved. $\square$

$\varvec{L}$ is the key matrix of the PLR decomposition in (1); indeed, $\varvec{P}$ can be thought to as a sort of nuisance matrix only affecting the ordering of the columns of $\varvec{Q}$ – and we know that such an ordering is often not of interest – and $\varvec{R}$ is a function of $\varvec{L}$. In particular, $\varvec{R}$ is the (unique) upper triangular matrix, having a positive diagonal, coming from the QR decomposition of $\varvec{P}\varvec{L}$. Note that, the number of free elements in $\varvec{L}$ (which are those below the main diagonal) is $d\left( d-1\right) /2$, as the number of free elements of the orthogonal matrix $\varvec{Q}$. This means that: 1) any orthogonal matrix admits the PLR decomposition in (1), and 2) any pair $\left\{ \varvec{P},\varvec{L}\right\}$ is associated to an orthogonal matrix.

3 Leptokurtic-normal common principal components

The advantages of our PLR decomposition can be appreciated in many statistical fields. Among them there is the common principal component analysis. Below, we give an example by considering groups being distributed according to a multivariate leptokurtic-normal distribution.

3.1 Preliminaries

Let $\left\{ \varvec{x}_{ij};{ i=1,\ldots ,n_j, j=1,\ldots ,k}\right\}$, with $\varvec{x}_{ij}\in \mathbb {R}^d$, be a set of $n=\sum _{j=1}^kn_j$ independent observations from k independent groups (or subpopulations) having mean $\varvec{\mu }_j$ and covariance matrix $\varvec{\Sigma }_j$. If the inferential interest is on $\varvec{\Sigma }_1,\ldots ,\varvec{\Sigma }_k$, then there is the need to estimate $kd\left( d+1\right) /2$ parameters. Such a number may be excessive when k, but especially d, are large, causing problems in the estimation phase. These problems can often be avoided if $\varvec{\Sigma }_1,\ldots ,\varvec{\Sigma }_k$ exhibit some common structures, and several models have been proposed in this direction (see, e.g., Flury 1984, 1986a, 1987; Boik 2002; Greselin et al. 2011). The assessment of a common covariance structure, in addition to allow for parsimony, can provide more information about the group conditional distributions (Greselin et al. 2011; Greselin and Punzo 2013) and it is of intrinsic interest in several fields such as biometry (refer to Sect. 4).

Most of the existing common covariance structures are based on the eigen-decomposition $\varvec{\Sigma }_j=\varvec{Q}_j\varvec{\Lambda }_j\varvec{Q}_j'$, $j=1,\ldots ,k$, where $\varvec{\Lambda }_j=\mathop {\mathrm {diag}}\left( \lambda _{j1},\ldots ,\lambda _{jd}\right)$ and $\varvec{Q}_j$ denote the eigenvalues and eigenvectors matrices, respectively. A famous common structure assumes that the k covariance matrices have possibly different eigenvalues but identical eigenvectors, i.e.,

$$\begin{aligned} \varvec{\Sigma }_j=\varvec{Q}\varvec{\Lambda }_j\varvec{Q}', \quad j=1,\ldots ,k. \end{aligned}$$

(3)

Model (3) was proposed by Flury (1984) and is known as the common principal components (CPC) model. Flury (1984) also derived the maximum likelihood (ML) estimators of $\varvec{Q}$ and $\varvec{\Lambda }_j$, assuming d-variate normality in each group. The asymptotic distribution of these estimators was studied by Flury (1986b). The corresponding log-likelihood function can be written as

$$\begin{aligned} l_{\text {N-CPC}}\left( \varvec{\Psi }\right) = C -\frac{1}{2} \sum _{j=1}^k n_j \left[ \sum _{h=1}^d \ln \lambda _{jh} + \text{ tr }\left( \varvec{Q}\varvec{\Lambda }_j^{-1}\varvec{Q}' \varvec{S}_j\right) \right] , \end{aligned}$$

(4)

where $\varvec{\Psi }=\left\{ \varvec{\mu }_j,\varvec{Q},\varvec{\Lambda }_j;{ j=1,\ldots ,k}\right\}$ is the whole set of parameters of cardinality $m_{\text {N-CPC}}=kd + d\left( d-1\right) /2 + kd$, C is a constant that does not depend on the parameters, and $\varvec{S}_j=n_j^{-1}\sum _{i=1}^{n_j}\varvec{S}_{ij}$, with $\varvec{S}_{ij}= \left( \varvec{x}_{ij}-\varvec{\mu }_j\right) \left( \varvec{x}_{ij}-\varvec{\mu }_j\right) '$. A closed-form solution for the ML estimate of $\varvec{Q}$ does not exist, but the Flury-Gautschi (FG) algorithm of Flury and Gautschi (1986), which is based on pairwise rotations of orthogonal vectors (Flury and Constantine 1985), can be used to obtain such a solution. The more appropriate the CPC model is, the more able the ML-estimated common orthogonal matrix $\varvec{Q}$ is to simultaneously rotate the sample covariance matrices to nearly diagonal form. Flury (1984) also proposed a likelihood-ratio test having the CPC model under the null and the unconstrained model under the alternative. The monograph by Flury (1988) provides a rigorous treatise of the CPC and related models, detailing their properties and offering several examples, with a special focus on biometric data.

3.2 The model

However, as confirmed by the simulations of Hallin et al. (2010), the CPC model discussed above is quite sensitive to the violation of group-specific multivariate normality (see, e.g., Boente and Orellana 2001; Boente et al. 2002, 2006, 2009 for examples of robust CPC approaches). These violations are often due to the presence of mild outliers. Contextualizing in CPCA the definition given by Ritter (2015, p. 4 and pp. 79–80; see also Mazza and Punzo 2020), we can define as mild outlier in group j a point that does not deviate from the reference multivariate normal distribution of that group and is not strongly outlying but, rather, it produces an overall group-specific distribution with heavier tails. Therefore, to reduce the influence of these points, more-flexible elliptically symmetric heavy-tailed distributions can be considered (Ritter 2015, p. 4 and pp. 79). Following this idea, we consider the multivariate leptokurtic-normal distribution (Bagnato et al. 2017) in CPCA. Compared to the normal distribution, the leptokurtic-normal has an additional parameter $\beta$ governing the excess kurtosis and, advantageously with respect to other heavy-tailed elliptical distributions, its parameters correspond to quantities of direct interest (mean, covariance matrix, and excess kurtosis). Such a distribution was successfully applied in the modelling of biometric and financial data (Bagnato et al. 2017; Maruotti et al. 2019).

The probability density function (pdf) of a d-variate leptokurtic-normal (LN) distribution with mean vector $\varvec{\mu }$, covariance matrix $\varvec{\Sigma }$, and excess kurtosis $\beta \in \left[ 0,\beta _{\max }\right]$, where $\beta _{\max }=\min \left[ 4d,4d\left( d+2\right) /5\right]$, is given by

$$\begin{aligned} f_{\text {LN}}\left( \varvec{x};\varvec{\mu },\varvec{\Sigma },\beta \right) = q\left( y;\beta \right) f_{\text {N}}\left( \varvec{x}; \varvec{\mu },\varvec{\Sigma }\right) , \quad \varvec{x}\in \mathbb {R}^d, \end{aligned}$$

(5)

where $y=\left( \varvec{x}-\varvec{\mu }\right) '\varvec{\Sigma }^{-1}\left( \varvec{x}-\varvec{\mu }\right)$, $f_{\text {N}}\left( \cdot ; \varvec{\mu }, \varvec{\Sigma }\right)$ is the pdf of a d-variate normal distribution with mean vector $\varvec{\mu }$ and covariance matrix $\varvec{\Sigma }$, and

$$\begin{aligned} q\left( y;\beta \right) = 1 + \frac{\beta }{8 d\left( d+2\right) }\left[ y^2-2\left( d+2\right) y+d\left( d+2\right) \right] , \quad y\ge 0. \end{aligned}$$

The constraint $\beta \in \left[ 0,\beta _{\max }\right]$ is the intersection of: (i) $\beta \in \left[ 0,4d\right]$, which assures that the pdf is positive elliptical, and (ii) $\beta \in \left[ 0,4d\left( d+2\right) /5\right]$, which guarantees that the pdf is unimodal. As a special case, $f_{\text {LN}}\left( \varvec{x};\varvec{\mu },\varvec{\Sigma },\beta \right)$ coincides with $f_{\text {N}}\left( \varvec{x};\varvec{\mu },\varvec{\Sigma }\right)$ for $\beta =0$.

The log-likelihood function of the CPC model based on leptokurtic-normal groups can be written as

$$\begin{aligned} l_{\text {LN-CPC}}\left( \varvec{\Psi }\right) =&\ C -\frac{1}{2} \sum _{j=1}^k n_j\left[ \sum _{h=1}^d \ln \lambda _{jh} + \text{ tr }\left( \varvec{Q}\varvec{\Lambda }_j^{-1}\varvec{Q}' \varvec{S}_j\right) \right] \nonumber \\&+ \sum _{j=1}^k\sum _{i=1}^{n_j} \ln \left\{ 1 + \frac{\beta _j}{8d(d+2)} \left[ \text{ tr }\left( \varvec{Q}\varvec{\Lambda }_j^{-1}\varvec{Q}' \varvec{S}_{ij}\right) ^2 \right. \right. \nonumber \\&\left. \left. -2(d+2)\text{ tr }\left( \varvec{Q}\varvec{\Lambda }_j^{-1}\varvec{Q}'\varvec{S}_{ij}\right) +d(d+2) \right] \right\} , \end{aligned}$$

(6)

where $\varvec{\Psi }=\left\{ \varvec{\mu }_j,\varvec{Q},\varvec{\Lambda }_j,\beta _j;{ j=1,\ldots ,k}\right\}$ is the whole set of parameters of cardinality $m_{\text {LN-CPC}} = m_{\text {N-CPC}} + k$.

3.3 Computational details

The maximization of $l_{\text {LN-CPC}}\left( \varvec{\Psi }\right)$ with respect to $\varvec{\Psi }$ does not admit a closed-form solution (see Bagnato et al. 2017, for the case $k=1$). Furthermore, the maximization problem is constrained due to $\varvec{Q}$, $\varvec{\Lambda }_j$, and $\beta _j$, $j=1,\ldots ,k$. Finally, even if we were able to split the log-likelihood function as $l_{\text {LN-CPC}}\left( \varvec{\Psi }\right) =l_{\text {LN-CPC}}\left( \varvec{\Psi }_1\right) +l_{\text {LN-CPC}}\left( \varvec{\Psi }_2\right)$, where $\varvec{\Psi }_1=\left\{ \varvec{\mu }_j,\beta _j;{ j=1,\ldots ,k}\right\}$ and $\varvec{\Psi }_2=\left\{ \varvec{Q},\varvec{\Lambda }_j;{ j=1,\ldots ,k}\right\}$, we couldn’t use the FG algorithm to find the ML estimate of $\varvec{\Psi }_2$ because the algorithm is implicitly based on the normality assumption. All these arguments give us the opportunity to appreciate the advantages of the proposed PLR decomposition.

To make the maximization of $l_{\text {LN-CPC}}\left( \varvec{\Psi }\right)$ unconstrained, we follow a transformation/back-transformation approach from the original constrained parameters to unconstrained real values. The constrained orthogonal matrix $\varvec{Q}$ is mapped to a $\left( d\times d\right)$ unit lower triangular matrix $\varvec{L}$, having $d\left( d-1\right) /2$ unconstrained real valued entries, via the PLR decomposition

$$\begin{aligned} \varvec{Q}= \varvec{P}\varvec{L}\varvec{R}^{-1}, \end{aligned}$$

(7)

where we recall that $\varvec{P}$ is a $\left( d\times d\right)$ permutation matrix and $\varvec{R}$ is a $\left( d\times d\right)$ upper triangular matrix depending on $\varvec{L}$ (see Definition 2.1). The back-transformation is

$$\begin{aligned} \varvec{L}= \varvec{P}'\varvec{Q}\varvec{R}, \end{aligned}$$

(8)

which can be easily obtained by starting from the QR decomposition of $\varvec{P}\varvec{L}$. The simple R code (R Core Team 2018) to compute (7) and (8) is given in Appendix A. Concerning diagonal element $\lambda _{jh}$ of $\varvec{\Lambda }_j$, $j=1,\ldots ,k$ and $h=1,\ldots ,d$, the transformation is

$$\begin{aligned} \lambda _{jh}=\exp \left( \widetilde{\lambda }_{jh}\right) , \end{aligned}$$

(9)

with $\widetilde{\lambda }_{jh} \in \mathbb {R}$, while the back-transformation is

$$\begin{aligned} \widetilde{\lambda }_{jh} = \log \left( \lambda _{jh}\right) . \end{aligned}$$

(10)

Finally, regarding $\beta _j$, $j=1,\ldots ,k$, the transformation is

$$\begin{aligned} \beta _j=\beta _{\max }\frac{\exp \left( \widetilde{\beta }_j\right) }{1+\exp \left( \widetilde{\beta }_j\right) }, \end{aligned}$$

(11)

with $\widetilde{\beta }_j \in \mathbb {R}$, while the back-transformation is

$$\begin{aligned} \widetilde{\beta }_j = \log \left( \frac{\beta _j}{\beta _{\max }-\beta _j}\right) . \end{aligned}$$

(12)

Based on (7), (9) and (11), in the transformation step of our procedure we maximize the log-likelihood function $l_{\text {LN-CPC}}$ with respect to $\varvec{\mu }$ (which does not require any transformation), $\widetilde{\lambda }_{jh}$, $\widetilde{\beta }_j$, and to the elements below the diagonal of $\varvec{L}$, $j=1,\ldots ,k$ and $h=1,\ldots ,d$. Operationally, we perform this unconstrained maximization via the general-purpose optimizer optim() for R, included in the stats package. We try two different commonly used algorithms for maximization: Nelder-Mead, which is derivatives-free, and BFGS which uses second-order derivatives. They can be passed to optim() via the argument method. Once the two algorithms are run, we take the best solution in terms of likelihood; see, for instance, Punzo and Bagnato (2020) for a comparison of the two algorithms, in terms of parameter recovery and computational time, for ML estimation. The choice to run both the algorithms is motivated by two facts: 1) sometimes the algorithms do not provide the same solution, and 2) it can happen that an algorithm does not reach convergence. In the back-transformation step of our procedure, the values of $\varvec{L}$, $\widetilde{\lambda }_{jh}$, and $\widetilde{\beta }_j$ maximizing $l_{\text {LN-CPC}}$ can be simply inserted in (7), (9) and (11), respectively, in order to obtain the ML estimates of $\varvec{Q}$, $\lambda _{jh}$, and $\beta _j$, $j=1,\ldots ,k$ and $h=1,\ldots ,d$.

Initial (real) values are required by optim() for maximization. We use the group-specific sample mean vectors for $\varvec{\mu }_1,\ldots ,\varvec{\mu }_k$. For $\varvec{Q}$ and $\varvec{\Lambda }_1,\ldots ,\varvec{\Lambda }_k$ we adopt the the simple intuitive procedure proposed by Krzanowski (1984), which is based on the PCA of the pooled sample covariance matrix and the total sample covariance matrix, followed by comparison of their eigenvectors. Finally, to initialize $\beta _j$, $j=1,\ldots ,k$, we use the empirical excess kurtosis if it falls in $\left[ 0,\beta _{\max }\right]$ (cf. Sect. 3.2); instead, we put $\beta _j=0$, or $\beta _j=\beta _{\max }$, if the empirical excess kurtosis is lower than 0, or greater than $\beta _{\max }$, respectively. By means of (8), (10) and (12), the obtained initial values are transformed so to be passed to optim(). From the transformation (7) related to the initial orthogonal matrix $\varvec{Q}$, we also obtain the permutation matrix $\varvec{P}$ that will be used by optim(). Note that, fixing the permutation matrix to the initial one does not reduce the space of orthogonal matrices considered by optim(), but simply affects the order of the eigenvalues on the diagonal of $\varvec{\Lambda }_j$, $j=1,\ldots ,k$. This means that the ML estimated eigenvalues may not be simultaneously ordered in decreasing order in all groups. However, having eigenvalues in an arbitrary order is not an issue in CPCA (Trendafilov 2010).

4 Application to allometric studies

Allometric studies are a natural area of application of the leptokurtic-normal CPCA proposed in Sect. 3. Allometry can be roughly devised as a tool to study the relation between parts (morphometric variables) in various organisms (Huxley 1993). According to Jolicoeur (1963), allometry can be summarized by the first principal component (PC) of the log-transformed measurements. For the practical and theoretical reasons why it is often useful to transform data to logarithms see, e.g., Pimentel (1979), Reyment (1991), and Bookstein (1997).

When the study involves several groups of specimens, e.g. different sexes or species, the interest is comparing the group-specific allometric patterns. This aim can be handled by comparing the group-specific PCs (see, e.g., Klingenberg 1996). Comparisons of allometry within several groups often show that the PCs differ only minimally. In these cases, it may be feasible to use CPCA, where the groups are assumed to share a common allometric pattern, i.e., that the major axes of their scatters are parallel (Klingenberg et al. 1996). The amount of variation associated with each PC can, instead, vary between groups. However, classical CPCA implies groups having a multivariate normal distribution, and this could be rather restrictive in some cases (cf. Sect. 3.2).

Fig. 1

Scatter plot of the microtus data with variables in logarithmic scale (filled circle denotes microtus subterraneus, while open circle denotes microtus multiplex)

Motivated by the above considerations, and using classical real biometric data, we compare: the CPC model based on normal groups (N-CPC), the CPC model based on leptokurtic-normal groups (LN-CPC), the model with unconstrained covariance matrices and normal groups (N-PC), and the model with unconstrained covariance matrices and leptokurtic-normal groups (LN-PC). The whole analysis is conducted in R. Parameters of the competing models are estimated by the ML approach. For uniformity sake, the PLR decomposition is adopted for both the CPC approaches. For the N-CPC model, the transformation/back-transformation approach based on the PLR decomposition provided the same estimates of $\varvec{Q}$ of the FG-algorithm in all our analyses (also those not reported in this paper). Having the competing models a differing number of parameters, their comparison is accomplished, as usual, via the Akaike information criterion (AIC; Akaike 1974) and the Bayesian information criterion (BIC; Schwarz 1978). Moreover, likelihood-ratio (LR) tests are used to compare nested models, and this gives rise to new testing procedures. Just as an example, the LR test having the N-CPC model under the null and the LN-PC model as alternative represents a more omnibus version of the LR test proposed by Flury (1984) where a more restrictive N-PC model is considered under the alternative. Using Wilks’ theorem, the LR statistic, under the null, is distributed approximately as a $\chi ^2$ with degrees of freedom given by the difference in the number of estimated parameters between the alternative and the null model; this allows us to compute a p value that, in the sequel, will be always compared to the classical 5% significance level.

4.1 Skull dimensions of voles

The first analysis considers the microtus data set accompanying the Flury package (Flury 2012) for R. The data set contains morphological measurements, for eight variables, on the skulls of 288 specimens of voles found at various places in central Europe. For 89 of the skulls, the chromosomes were analyzed to identify their membership to one of $k=2$ species; $n_1 = 43$ specimens were from microtus multiplex, and $n_2 = 46$ from microtus subterraneus. Species was not determined for the remaining 199 specimens. Airoldi et al. (1995) report a discriminant analysis and finite mixture analysis of this data set; see also Flury (2013, Examples 5.4.4 and 9.5.1).

We analyze the sample of $n=89$ labeled skulls – because we need to know the group of membership of the observations for the application of the competing models – and focus the attention on the logarithm of $d=2$ of the available measurements: the length of palatal bone (in mm/1000) and the skull width across rostrum (in mm/100). The scatter plot of the observations, with symbols diversified with respect to the species, is displayed in Fig. 1.

For microtus multiplex voles, the empirical excess kurtosis is 2.341, and the Mardia test of mesokurtosis, as implemented by the mvn() function of the MVN package (Korkmaz et al. 2019), provides a p value of 0.019; this leads to a rejection of the null hypothesis of mesokurtosis. This also implies a rejection of bivariate normality. Instead, for microtus subterraneus voles, the empirical bivariate excess kurtosis is 1.370, corresponding to a p value of 0.170 for the Mardia test. So, the microtus multiplex voles motivate the need of a distribution accounting for heavier than normal tails. Moreover, Fig. 1 seems to suggest that the two scatters for microtus subterraneus and microtus multiplex have approximately the same orientation (i.e., the same principal components).

Table 1 ML estimated parameters of the competing models for the microtus data

To evaluate if a leptokurtic-normal distribution fits the data in each group better, and to assess our conjecture about the similarity between orientations, we proceed with the fitting of the competing models. We could have used the LN distribution only for the microtus multiplex voles, and the fitting procedure outlined in Sect. 3.3 would have been easily adapted to the case. However, this would have gone beyond the scope of this real data application, which is to show the versatility of our PLR decomposition, jointly with any unconstrained optimization routine, in the estimation of an orthogonal matrix, regardless of the model structure. Table 1 reports the ML-estimated parameters. As we can note, the models are very similar in terms of estimated mean vectors. Instead, they differ in terms of estimated eigenvectors and eigenvalues matrices (compare N-CPC with LN-CPC and N-PC with LN-PC). We can realize how constraining the LN model to have $\beta =0$ (yielding the N model) can produce differences in terms of estimated eigenvectors and eigenvalues matrices with respect to the unconstrained case. Moreover, the differences between N-based and LN-based models in terms of eigenvectors and eigenvalues matrices seem to intensify as the estimated $\beta$ departs from zero. Both these facts are evident when comparing the N-PC model with the LN-PC model; here, the estimates of the orthogonal matrices differ mainly in group 1 (microtus multiplex), where a larger empirical/estimated excess kurtosis is present. Finally, as concerns the models based on the leptokurtic-normal distribution, the estimates of the excess kurtoses $\beta _1$ and $\beta _2$ are in line with the empirical excess kurtoses (2.341 and 1.370).

Table 2 presents a model comparison in terms of: number of parameters (m), log-likelihood, AIC, and BIC values (Table 2a) and with respect to the p values from the LR tests (Table 2b). AIC and BIC in Table 2a indicate LN-CPC as the best model. This means that, with respect to a model with unconstrained covariance matrices, a more parsimonious model allowing for common principal components is to be preferred, but without giving up to groups having a heavier-tailed distribution (the leptokurtic-normal in this case). By looking at Table 2b, the null N-CPC model of the LR test by Flury (1984) is not rejected (p value = 0.139). This happens because of the alternative N-PC model used by the test. If we make the test more omnibus by considering the LN-PC model as alternative, then the conclusion changes (p value = 0.020); interestingly, if we change the null hypothesis of this test using a less constrained LN-CPC model, then the conclusion is in favor of the null (p value = 0.459). The null N-CPC model is also rejected, with a greater extent, if we use LN-CPC as alternative (p value = 0.010). Finally, it is also interesting to note that, even if we do not consider a CPC approach, the need for leptokurtic-normal groups arises: the p value of the test of N-PC versus LN-PC is, indeed, 0.022.

Table 2 Model comparison, for the microtus data, in terms of number of parameters (m), log-likelihood, AIC, and BIC (a) and p values from the LR tests (b)

Fig. 2

Matrix of scatter plots of the swiss.soldiers data with variables in logarithmic scale (open circle denotes women and filled circle denotes men)

4.2 Head dimensions of young Swiss soldiers

The second analysis considers the swiss.soldiers data set considered by Flury (1988, Example 2.3). The data were collected by a group of anthropologists on approximately 900 Swiss soldiers, most of them recruits, subdivided in $k=2$ groups according to the gender. All the soldiers were 20 years old at the time of investigation and 25 variables were measured on their heads. The purpose of the study, promoted by the the Swiss government in the mid-1980s, was to provide sufficient data to construct new protection masks for the members of the Swiss army.

We start by the subset of the swiss.soldiers data which can be obtained by merging the swiss.heads (referred to men) and f.swiss.heads (referred to women) data sets included in the Flury package. The merged data contain the values of 6 head measurements for a subsample of $n=259$ soldiers, with $n_1 = 59$ women and $n_2=200$ men. A detailed analysis for the men has been given by Flury (2011, Example 10.2) and Flury (2013, Example 1.2). In particular, we focus on the logarithm of $d=3$ of the available head measurements: the minimal frontal breadth (MFB), the true facial height (TFH), and the length from tragion to gnathion (LTG). All measurements are in millimeters. The matrix of pairwise scatter plots, with symbols diversified with respect to the gender, is displayed in Fig. 2. For women, the empirical excess kurtosis is 1.130, and the Mardia test of mesokurtosis provides a p value of 0.259. As concerns men, the empirical excess kurtosis is 7.621 and the Mardia test of mesokurtosis provides a practically null p value indicating that a leptokurtic distribution should be better than the normal for that group. So, in this example, the group of men justifies the use of the leptokurtic-normal distribution.

Table 3 shows the ML estimated parameters for the competing models. As for the example on the microtus data of Sect. 4.1, the models behave in a similar way in terms of estimated mean vectors, but differ in terms of estimated eigenvectors and eigenvalues matrices if N-CPC is compared with LN-CPC and N-PC with LN-PC. Such a difference is due to the leptokurtic-normal distributional assumption. For the LN-based models, the estimates of the excess kurtoses $\beta _1$ and $\beta _2$ are in line enough with the empirical excess kurtoses (1.130 and 7.621).

Table 3 ML estimated parameters of the competing models for the swiss.soldiers data

Table 4 Model comparison, for the swiss.soldiers data, in terms of number of parameters (m), log-likelihood, AIC, and BIC (a) and p values from the LR tests (b)

Table 4 presents the model comparison. AIC and BIC in Table 4a select LN-CPC as the best model, with a stronger extent with respect to the previous example. Such a greater extent has analogous implications for the p values from the LR tests (see Table 4b). The null N-CPC model is not rejected if N-PC is considered as alternative model (p value = 0.278), but it is strongly rejected (with an approximately null p value) if a LN-based model (LN-CPC or LN-PC) is considered under the alternative. If LN-CPC is considered as the null model, and LN-PC as alternative, then the conclusion is in favor of the null (p value = 0.408). Even if we do not consider a CPC approach, the need for leptokurtic-normal groups is even more evident in this example: the p value of the test of N-PC versus LN-PC is, indeed, practically null.

5 Conclusions

Estimating and modelling a $\left( d \times d\right)$ covariance matrix $\varvec{\Sigma }$ is often difficult because of the constraint that $\varvec{\Sigma }$ must be positive definite. The Cholesky decomposition provides a remedy to this problem by mapping the $d\left( d+1\right) /2$ constrained parameters of $\varvec{\Sigma }$ with the $d\left( d+1\right) /2$ unconstrained real-valued elements of a $\left( d \times d\right)$ lower triangular matrix (Pourahmadi 1999, 2000 and Pourahmadi et al. 2007). Analogously, estimating and modelling a $\left( d \times d\right)$ orthogonal matrix $\varvec{Q}$ is often cumbersome because of its orthonormality constraints. Unfortunately, in this case, an analogous of the Cholesky decomposition does not exist. In this paper we have filled this gap by adapting the well-known PLU decomposition to orthogonal matrices. We have called the result as PLR decomposition; it maps, in a unique way, $\varvec{Q}$ to a $\left( d \times d\right)$ unit lower triangular matrix with $d\left( d-1\right) /2$ unconstrained real entries below the diagonal.

For illustrative purposes, we have applied our PLR decomposition in common principal component analysis (CPCA), based on groups having a heavier-tails leptokurtic-normal distribution, for maximum likelihood estimation of the common orthogonal matrix. We have chosen allometry as a natural area of application of the resulting leptokurtic-normal CPCA and the real data analyses have effectively confirmed its good behavior when compared to the classical normal CPCA.

However, the use of the PLR decomposition of an orthogonal matrix is not limited to CPCA, and other statistical models may benefit from its use. Indeed, the PLR decomposition may be used to simplify the ML estimation of the orthogonal matrix related, only to mention a few, to: CPCA based on further non-normal distributions for the groups, other multiple group models allowing for common covariance structures (Flury 1986a; Greselin and Punzo 2013), parsimonious model-based clustering, classification and discriminant analysis (Banfield and Raftery 1993; Flury et al. 1994; Celeux and Govaert 1995; Fraley and Raftery 2002; Andrews and McNicholas 2012; Bagnato et al. 2014; Lin 2014; Vrbik and McNicholas 2014; Dang et al. 2015; Punzo et al. 2016; Punzo and McNicholas 2016; Punzo et al. 2018; Dotto and Farcomeni 2019), and sophisticated multivariate distributions (Forbes and Wraith 2014; Punzo and Tortora 2019). We pursue to handle these possibilities in future works.

Appendices

Appendix

A PLR decomposition in R