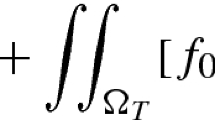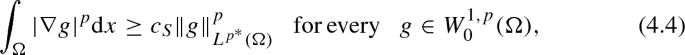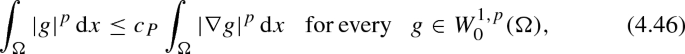Abstract
In this paper, we study the behavior in time of the solutions for a class of parabolic problems including the p-Laplacian equation and the heat equation. Either the case of singular or degenerate equations is considered. The initial datum \(u_0\) is a summable function and a reaction term f is present in the problem. We prove that, despite the lack of regularity of \(u_0\), immediate regularization of the solutions appears for data f sufficiently regular and we derive estimates that for zero data f become the known decay estimates for these kinds of problems. Besides, even if f is not regular, we show that it is possible to describe the behavior in time of a suitable class of solutions. Finally, we establish some uniqueness results for the solutions of these evolution problems.
Similar content being viewed by others
1 Introduction
Let us consider the following nonlinear parabolic problem
where \(\Omega _T = \Omega \times (0,T) \), \(\Omega \) is an open bounded set of \({\mathbb {R}}^N\), \(N > 2\), \(T>0\), \(\alpha _0 \ge 0\) and \(\Gamma = \partial \Omega \times (0,T)\), with \(\partial \Omega \) regular (for example, satisfying the property of positive geometric densityFootnote 1).
Here, the function \(a(x,t,s,\xi ): \Omega \times (0,T) \times {\mathbb {R}}\times {\mathbb {R}}^N \rightarrow {\mathbb {R}}^N\) is a Caratheodory functionFootnote 2 satisfying, for a.e. \((x,t) \in \Omega _{T} \) and for every \(s \in {\mathbb {R}}\), \(\xi \) and \(\eta \in {\mathbb {R}}^N\) the following structure conditions
where
Finally, on the initial datum \(u_0\) we assume
while on f we require
or simply that
Aim of this paper is to study the behavior of the solutions of (1.1).
This evolution problem includes, as particular cases, the heat equation and the p-Laplacian equation, and has been widely studied starting from the sixties by the classical papers of Nash, Moser, Ladyženskaja, Solonnikov, Ural’ceva, J.L. Lions, Aronson, Serrin, Trudinger (see [2, 33, 34, 36, 37, 53] and the references therein) to nowadays and it is really a difficult task to give a complete bibliography on this subject (see for example [1, 3, 4, 6,7,8, 10,11,12, 17, 19,20,26, 29,30,32, 35, 39,40,41, 45, 45, 51, 52, 54, 56, 57] and the references therein).
Nevertheless, we show in this paper some unknown surprising properties of the solutions.
The first issue we want to address stems from the following unexpected and incredible result:
even if the initial datum \(u_0\) is only a summable function, if the reaction term f is the zero function and p is “not too small” (i.e., \(p> \frac{2N}{N+r_0}\)), then there exists a solution u of (1.1) which “immediately” becomes bounded, i.e., such that
Moreover, it is also possible to estimate the \(L^{\infty }\)-norm of u(t) but these estimates differ with p and exhibit a different behavior in the degenerate case from the singular one. In particular, in the degenerate case \(p>2\) the following decay estimate holds true
where C is a constant depending only on \(\alpha \), N, \(|\Omega |\) and p (see [14, 42] and the references therein) and hence is an estimate that doesn’t depend on the initial datum \(u_0\) and for this reason it is also called universal (decay) estimate.
We point out that the universal estimate (1.9) is a peculiarity of the degenerate case (in a bounded domain) and it is no longer true in the singular case \(p < 2\) or for \(p=2\).
If \(p=2\), the same decay of the heat equation appears since the following exponential estimate holds true
where \(\sigma \) is a positive constant depending only on \(\alpha \), N, \(r_0\) and \(\Omega \).
Finally, if \(p > \frac{2N}{N+r_0}\), hence in both the previous cases and in the singular case too with p “not too small,” the following estimate holds true
where C depends only on \(\alpha \), p and N and
(see [28, 42, 54, 55] and the references therein).
The previous estimates, known in the literature as decay or ultracontractive estimates or smoothing effects (see [54]), describe the behavior in time of the solutions and are of interest not only for t large, since they describe in which way u decays to zero letting \(t \rightarrow +\infty \), but also for t near zero, since they describe the “controlled blow-up” of the \(L^\infty \)-norm of u(t) for t that goes to zero.
The first aim of this paper is to understand what happens when the reaction term f is not the zero function. In other words, we want to understand if for suitably regular data f (otherwise the result is false) it is still true that even in the presence of an only summable initial datum \(u_0\) there exists a solution of (1.1) which becomes “instantaneously bounded” and, in case of an affirmative answer, which kind of estimates we can expect.
The author has already studied this problem in the nonsingular case \(p \ge 2\) when the operator a is independent of u (i.e., \(a(x,t,s, \xi )=a(x,t,\xi )\)) and satisfies the following monotony assumption
for a.e. \((x,t) \in \Omega _T\) and for every \(\xi \), \(\eta \in {\mathbb {R}}^N\), where \(\gamma \) is a positive constant (see [46] if \(p =2\) and [47] if \(p>2\)).
Hence, we want to complete here our previous studies considering not only the singular case \(p < 2\), but also the more general case of operators depending also on u and satisfying the weak monotone condition (1.5) instead of the strong monotone condition (1.11), essential in the previous papers for the results obtained there.
We recall that by the classical theory we know that even if we have no information on the initial datum \(u_0\), if f is sufficiently regular (for example, if it is bounded) every solution u belonging to \( L^{\infty }_{loc}((0,T];L^2(\Omega )) \cap L^p_{loc}((0,T];W_0^{1,p}(\Omega ))\) becomes bounded but if \(u_0\) is not regular enough we do not know if we have the starting regularity on u needed to apply these classical results. Moreover, also if we assume more regularity on \(u_0\), like for example that it is in \(L^2(\Omega )\), in order to have the required regularity on u, the \(L^\infty \)-estimates we get by the classical theory are of different types and don’t become the decay estimates presented above when f is the zero function.
Our first result is that even if the initial datum is a summable function, if f is bounded then there exists a solution u of (1.1) that becomes instantaneously bounded (see Sect. 2.1). We prove this regularization phenomenon at first when \(\alpha _0 >0 \) (see Theorem 2.1: the absorption case) and then we show that the immediately boundedness appears also in the absence of the lower-order term \(\alpha _0 u \) (see Theorem 2.2: the case without absorption) or even in the presence of the reaction term \(- \alpha _0 u\) (see Theorem 2.3).
Moreover, we prove \(L^\infty \)-estimates that when f is the zero function become the decay estimates described above.
The second aim of this paper is the study of the behavior in time of solutions that become immediately bounded, even when the initial data are merely summable functions (see Sect. 2.2 for the results).
As a matter of fact, every solution of (1.1) can be extended in a global solution u defined in all \(\Omega \times (0,+\infty )\) (see Definition 2.2 and Theorem 2.4) and we show that if the lower-order term \(\alpha _0 u\) is not identically zero, then all the global solutions of (1.1) that become immediately bounded have the same behavior for t large.
Indeed, we treat not only the case of solutions that become immediately bounded but also solutions that immediately improve their regularity but remain unbounded thus considering a wider class of solutions and of data f.
In all the cases studied here, we prove that if u and v are global solutions that become “immediately suitably regular,” where u solves (1.1) and v satisfies the same problem satisfied by u but with initial datum \(v_0\), i.e.,
then it results
for a suitable \(r \ge 1\). In other words, for t large the “suitably regular” solutions of (1.1) “forget their initial data” and have all the same asymptotic behavior.
The third aim of the paper, is the study of time behavior of the remaining classes of solutions: the ones that do not improve their regularity with time, this can happen when f and \(u_0\) are merely integrable functions, and the ones for which we have no information about their extra regularity.
We point out that in this context the solutions generally are not unique and hence we have the necessity to choose which solution we want to study. We recall that in order to guarantee uniqueness results further requirements on the solutions are needed, like for example to be an entropy solution or a renormalized solution, and also the operator is generally required to be an operator independent of u, i.e., satisfying
for a.e. \((x,t) \in \Omega \times (0,+\infty )\) and for every \(s \in {\mathbb {R}}\) and \(\xi \in {\mathbb {R}}^N\). Hence, we have restricted this study to the case operators satisfying the previous assumption and we have proved that it is possible to distinguish a class of solutions, “the solutions obtained by approximation,” named “sola” (see Definition 2.3), for which we will still be able to describe the behavior in time of the solutions.
As observed in [32], “the definition of these solutions is quite natural” and is motivated by the usual way to find solutions of problems with irregular data by an approximating procedure where the irregular data are replaced by more regular functions.
We prove here that if \(u_0\) and \(v_0\) belong to \(L^1(\Omega )\), then the solutions u and v of, respectively, (1.1) and (1.12), which are obtained by approximation satisfying (1.13).
Moreover, we will also show that the further requirement to be a solution obtained by approximation produces uniqueness despite the fact that the data f and \(u_0\) can be assumed to be only summable functions, thus completing the known uniqueness results on sola that require stronger monotony assumption on the operator than the weak hypothesis (1.5) made here (see Remark 2.9 for further details).
In fact, the assumption (1.14) is also responsible for other interesting phenomena (see Sect. 2.3).
For example, are also unique the solutions that although satisfy only summable initial data then become immediately bounded. Indeed, the uniqueness holds true for a larger class of solutions, eventually unbounded, but which immediately becomes suitably regular (see Theorems 2.13 and 2.14).
We notice that most of the results we prove here remain true replacing the lower-order term \(\alpha _0 u\) in (1.1) with a more general Caratheodory function \(a_0(x,t,u,\nabla u)\) satisfying, for example
but to make clearer the role of the lower-order term in the following results we avoid this full generality.
The plan of the paper is the following: in the next section, we state our results in all the details. In Sect. 3, we give some known and new results we need in the proofs. Finally, Sect. 4 is devoted to the proofs of all the results set out in Sect. 2.
2 Main results
We start showing that in the case of bounded forcing term and integrable initial data there exist solutions that become “instantaneously bounded.” Then, in Sect. 2.2 we will describe the behavior in time of all the solutions that become “instantaneously bounded” and finally in Sect. 2.3 we will discuss the case of operator independent of u.
Before stating our results, we recall that by a solution of (1.1) we mean the following.
Definition 2.1
A measurable function \(u \in L^{\infty }(0,T;L^1(\Omega )) \) is a solution of (1.1) if \(T_k(u) \in L^p(0,T;W_0^{1,p}(\Omega ))\) for every \(k>0\), \(a(x,t,u,\nabla u) \in (L^1(\Omega _T))^N\) and
for every \(\varphi \in W^{1,\infty }(0,T;L^\infty (\Omega ))\cap L^\infty (0,T;W_0^{1,\infty }(\Omega ))\) satisfying \(\varphi (T)=0\), where \(T_k(s)\) is the usual truncated function, i.e.,
and \(\nabla u\) is defined as in [5], i.e., it is equal to \(\nabla T_k(u)\) on the set where \(|u| \le k\).
2.1 The case of bounded forcing term and integrable initial data
Theorem 2.1
(The case with absorption) Let \(f \in L^{\infty }(\Omega _T)\) and \(u_0 \in L^{r_0}(\Omega )\) with \(r_0 \ge 1\). If (1.2)–(1.5) hold true with \(\alpha _0 > 0\) and \(p > \frac{2N}{N+r_0}\), then there exists a solution u of (1.1) such that
Moreover, the following estimate is satisfied (for a.e. \(t \in (0,T)\))
where \(\alpha \) is as in (1.2), \(\sigma = \frac{\alpha c_S c(r_0)}{|\Omega |^{\frac{2}{N}}}\), \(c_S=c_S(N)\) is the Sobolev constant defined in (4.4) and the exponents \(h_0\) and \(h_1\) are defined as follows
Besides, \(\nabla u \) belongs to \( \left[ L^p(\Omega \times (t,T))\right] ^N\) for every \(t \in (0,T)\) and the following estimate holds true
where A(t) is as in (2.4).
Finally, if \(p>2\) also the following estimates hold true
Here and throughout the paper, we adopt the convention that \(\frac{1}{+\infty }=0\) and we denote with c and c(s,v) (respectively) positive constants and functions depending only on the variable in brackets, that can change from one line to the other.
Remark 2.1
We notice that the assumption \(p > \frac{2N}{N+r_0}\) is a necessary condition since it is a sharp condition to have solutions that become immediately bounded when \(f \equiv 0\). Moreover, for zero reaction term f the previous estimates become the sharp estimates of the heat equation if \(p=2\) and those of the p-Laplacian otherwise (see [42, 54] and the references therein). Therefore, for these estimates a sort of continuous dependence on the datum f applies.
Remark 2.2
Notice that by the structure condition (1.3) and the regularity of u proved in the previous theorem it follows that u belongs also to \(C((0,T];L^2(\Omega ))\).
Moreover, by the “immediately boundedness” of u and the classical regularity theory we deduce
(see [22, 33]). In particular, u belongs to \( C((0,T];L^r(\Omega ))\) for every \(r > 1\) arbitrarily fixed and estimate (2.4) holds true for every \(t \in (0,T)\).
Remark 2.3
We point out that when \(p>2\) the \(L^{\infty }\)-estimate (2.7) together with the gradient estimate (2.8) do not depend on the initial datum \(u_0\) and hence are universal estimates.
The following theorem shows that the presence of the lower-order term \(\alpha _0 u\) is not essential in this instantaneous improvement of regularity since the immediately \(L^{\infty }\)-regularization holds true also if \(\alpha _0 = 0\). Moreover, also in this case it is possible to derive \(L^\infty \)-estimates of the solutions depending only on the data.
Theorem 2.2
(The case without absorption) Let \(f \in L^{\infty }(\Omega _T)\) and \(u_0 \in L^{r_0}(\Omega )\) with \(r_0 \ge 1\). If (1.2)–(1.5) hold true with \(p > \frac{2N}{N+r_0}\), then there exists a solution u of (1.1) satisfying (2.9). Moreover, for every \(\rho > 0\) and \(t \in (0,T)\) it results
where
with \(\alpha _p = \alpha e^{- \rho (2-p)_+ T}\) and \(\sigma \) as in estimate (2.4).
Besides, \(\nabla u\) belongs to \(\left[ L^p(\Omega \times (t,T))\right] ^N\) for every \(t \in (0,T)\) and the following estimate holds true
where B(t) is as before.
Finally, if \(p>2\) also the following bounds (independent of \(u_0\)) are satisfied
Remark 2.4
We point out that the estimates in Theorems 2.1 and 2.2 hold true for every solution constructed as limit of sufficiently regular approximating solutions.
Remark 2.5
Notice that if \(f \equiv 0\) and \(p=2\) estimate (2.10) becomes
which implies (due to the arbitrariness of \(\rho \))
Moreover, if otherwise \(p \not = 2\) (\(p > \frac{2N}{N+r_0}\)) and \(f \equiv 0\), by (2.10) and the arbitrariness of \(\rho \) we deduce that
Finally, if \(p>2\) and \(f \equiv 0\) (2.13) becomes
which implies (due again to the arbitrariness of \(\rho \)) the following universal estimate
Thus, all the \(L^{\infty }\)-estimates in Theorem 2.2 for zero data f become the sharp decay estimates (in terms of the power of t and of the dependence on \(\Vert u_0\Vert _{L^{r_0}(\Omega )}\)) known in the literature (see [42, 44, 54, 55] and the references therein).
In conclusion, even if the datum \(u_0\) is not bounded, u becomes bounded also in the presence of a nonzero bounded reaction f and \(L^{\infty }\)-estimates of u hold true depending in a “continuous way on the datum f” (more precisely on the \(L^{\infty }\)-norm of f).
Besides, if \(f \equiv 0\) (2.12) becomes
and hence (using again the arbitrariness of \(\rho \)) we deduce the following estimate of the \(L^p\)-norm of the gradient of the solutions of (1.1) with zero data f
where \( c_1 \equiv \frac{[c(N,\alpha )]^2 |\Omega |}{2 \alpha }\) and if otherwise \(p \not =2\)
where \( c_2 \equiv \frac{[c(N,\alpha ,r_0,p)]^2 |\Omega |}{2 \alpha }\). Moreover, if \(p>2\) and \(f\equiv 0\) estimate (2.14) implies (again by the arbitrariness of \(\rho \))
Notice that estimates (2.17)–(2.19) and (2.12) on \(\nabla u\) seem not available in the literature except in the case \(p \ge 2\) for operators a in (1.1) independent of u (i.e., satisfying \(a(x,t,s,\xi )=a(x,t,\xi )\)) and satisfying stronger monotony assumptions which are essential in the proofs of the results (see [46, 47]).
We conclude this subsection studying the case when in (1.1) the absorption term \(\alpha _0 u\) is replaced by a reaction term \(- \alpha _0u\), i.e.,
The following result shows that what happens is quite similar to the case without absorption. In detail, we have the following result.
Theorem 2.3
(The case with the reaction term \(- \alpha _0 u\)) Let \(f \in L^{\infty }(\Omega _T)\), \(\alpha _0 > 0\) and \(u_0 \in L^{r_0}(\Omega )\) with \(r_0 \ge 1\). If (1.2)–(1.5) hold true with \(p > \frac{2N}{N+r_0}\), then there exists a solution u of (2.20) satisfying (2.9). Moreover, for every \(\rho > \alpha _0\) and \(t \in (0,T)\) it results
where
with \(\alpha _p\) and \(\sigma \) as in estimate (2.4).
Besides, \(\nabla u\) belongs to \(\left[ L^p(\Omega \times (t,T))\right] ^N\) for every \(t \in (0,T)\) and the following estimate holds true
where \(B_{\alpha _0}(t)\) is as before.
Finally, if \(p>2\) also the following bounds (independent of \(u_0\)) are satisfied
2.2 Time behavior of the solutions
In the previous sections, we have considered solutions of our problem (1.1) in \(\Omega _T\). In this subsection, we show that there exist solutions in all the set \(\Omega _{\infty }\) (global solutions) and we study the behavior in time of these global solutions. To this aim, we give the following definition.
Definition 2.2
We say that u is a global solution of (1.1) or, equivalently, that u is a solution of
if u is a solution of (1.1) (according to Definition 2.1) for every arbitrarily fixed \(T>0\).
Moreover, we denote by a “global solution of (1.1) relative to the datum f and to the initial datum \(v_0\)” (\(v_0 \in L^{r_0}(\Omega )\) with \(r_0 \ge 1\)) a global solution v (according to the above definition) of the following problem
We show now that under the structure assumptions (1.2)–(1.5), even if the data f and \(u_0\) are only summable functions, our problem always admits global solutions. Moreover, if f is bounded and p not too small, then there exist also solutions which immediately become bounded. In detail, we have the following result.
Theorem 2.4
Assume that f belongs to \(L^{1}_{loc}([0,+\infty );L^{1}(\Omega ))\) and that (1.2)–(1.6) hold true with \(T=+\infty \). Then, there exists a global solution of (1.1).
Moreover, if \(a(x,t,s,\xi ) \equiv a(x,t,\xi )\) then u belongs to \(C_{loc}([0,+\infty );L^1(\Omega ))\).
Finally, if \(p > \frac{2N}{N+r_0}\) and \(f \in L^{\infty }_{loc}([0,+\infty );L^{\infty }(\Omega ))\), then u belongs to
for every \(r \ge 1\), while if we also assume \(\alpha _0>0\) and \(f \in L^{\infty }(\Omega _{\infty }) \cap L^1(\Omega _{\infty })\) then u belongs also to
for every \(t_0 >0\) and \(r \ge 1\).
We observe that generally these global solutions are not unique (see next section for further details). Anyway, we show now that if the lower-order term \(\alpha _0 u \) is not zero, all the solutions that become “immediately bounded” have the same asymptotic behavior for \(t \rightarrow + \infty \) and this “asymptotic behavior” is the same also for all the global solutions verifying different initial data. In other words, the solutions for large value of t “forget” their initial data.
More in detail, we have the following result.
Theorem 2.5
Let (1.2)–(1.4) hold true with \(T = +\infty \) and \(h \in L^{p'}(\Omega _{\infty })\). Assume \(\alpha _0 > 0\) and that u and v are two global solutions of (1.1) relative to the same datum \(f \in L^{1}_{loc}([0,+\infty );L^{1}(\Omega ))\) and to initial data, respectively, \(u_0\) and \(v_0\), where \(u_0\) and \(v_0\) are functions in \(L^{r_0}(\Omega )\) (\(r_0 \ge 1\)). If there exist \(t_0>0\) and \(r \ge 2\) such that u and v belong to \(L^{\infty }(\Omega \times [t_0,+\infty )) \cap L^p(t_0,+\infty ;W_0^{1,p}(\Omega )) \cap C([t_0,+\infty );L^r(\Omega ))\), then it results
Remark 2.6
It is worth to notice that under the structure assumptions of the previous theorem, if we choose \( p > \frac{2N}{N+r_0}\), \(f \in L^{\infty }(\Omega _{\infty }) \cap L^1(\Omega _{\infty })\) and we assume also the weak monotone condition (1.5), then by Theorem 2.4 for every choice of initial data \(u_0\) and \(v_0\) in \(L^{r_0}(\Omega )\) (\(r_0 \ge 1\)) there exist at least a global solution u of (1.1) and a global solution v of (2.27) belonging to \(L^{\infty }(\Omega \times (t_0,+\infty )) \cap L^p(t_0,+\infty ;W_0^{1,p}(\Omega )) \cap C([t_0,+\infty );L^r(\Omega ))\) for every arbitrarily fixed \(t_0 >0\) and \(r \ge 1\).
Hence, by Theorem 2.5, all these regular global solutions have the same asymptotic behavior (for \(t \rightarrow + \infty \)) free from their initial data and the convergence (2.28) holds true for every \(r \ge 1\).
Indeed, if to the assumptions of Theorem 2.5 we add the boundedness of the reaction term f, we obtain that every solution in \( L^p(t_0,+\infty ;W_0^{1,p}(\Omega )) \cap L^{\infty }(\Omega \times [t_0,+\infty ))\) belongs also to \( C([t_0,+\infty );L^r(\Omega ))\) for every \(r \ge 1\) and satisfies (2.28). In detail, it results.
Corollary 2.1
Let (1.2)–(1.4) hold true with \(T = +\infty \) and \(h \in L^{p'}(\Omega _{\infty })\). Assume \(\alpha _0 > 0\) and that u and v are two global solutions of (1.1) relative to the same datum \(f \in L^{\infty }(\Omega _{\infty })\) and to initial data, respectively, \(u_0\) and \(v_0\), where \(u_0\) and \(v_0\) are functions in \(L^{r_0}(\Omega )\) (\(r_0 \ge 1\)). If there exists \(t_0>0\) such that u and v belong to \( L^p(t_0,+\infty ;W_0^{1,p}(\Omega )) \cap L^{\infty }(\Omega \times [t_0,+\infty ))\) then u and v belong to \( C([t_0,+\infty );L^r(\Omega ))\) for every \(r \ge 1\) and (2.28) holds true (for every \(r \ge 1\)).
We observe that even if the global solutions u and v are not locally bounded (and hence the previous results cannot apply) it is still possible to prove that they exhibit the same asymptotic behavior if they are “sufficiently regular” as the following result shows.
Theorem 2.6
Let (1.2)–(1.4) hold true with \(T = + \infty \) and \(h \in L^{p'}(\Omega _{\infty })\). Assume \(\alpha _0 > 0\) and that u and v are two global solutions of (1.1) relative to the same datum f and to initial data, respectively, \(u_0\) and \(v_0\), where \(u_0\) and \(v_0\) are functions in \(L^{r_0}(\Omega )\) (\(r_0 \ge 1\)). If there exists \(t_0>0\) such that u and v belong to \( L^p(t_0,+\infty ;W_0^{1,p}(\Omega )) \cap L^{\infty }(t_0,+\infty ;L^2(\Omega )) \) and f belongs to \( L^{p'}_{loc}([t_0,+\infty );W^{-1,p'}(\Omega )) \), then u and v belong to \(C_{loc}([t_0,+\infty );L^2(\Omega ))\) and it results
Remark 2.7
We observe that the study of the smoothing effect and time behavior of the solutions to special classes of operators of p-Laplacian type in the absence of reaction terms and in different geometric settings can be found in [13,14,15,16, 19, 28].
We conclude this section studying the particular case of operator a independent of u since in this case many other further interesting properties of the solutions appear.
2.3 The case of operator a independent of u
In this subsection, we prove that under the following condition
many interesting further properties of the solutions of (1.1) appear concerning not only their behavior in time but also their uniqueness properties.
As a first result, we prove that the presence of a bounded reaction term f allows to take \(r = +\infty \) in (2.28). More in detail, we have the following result.
Theorem 2.7
Assume that (1.2)–(1.7) and (2.29) hold true with \(T= + \infty \) and \(\alpha _0 >0\). Let u and v be two global solutions of (1.1) relative to the same datum f and to initial data, respectively, \(u_0\) and \(v_0\), where \(u_0\) and \(v_0\) are functions in \(L^{r_0}(\Omega )\) (\(r_0 \ge 1\)). If these solutions belong to \(L^p_{loc}([t_0,+\infty );W_0^{1,p}(\Omega )) \cap L^{\infty }_{loc}([t_0,+\infty );L^{\infty }(\Omega ))\) (for an arbitrarily fixed \(t_0 >0\)) then u and v belong to \(C(\overline{\Omega }\times [t_0,+\infty ))\) and it results
Moreover, the following estimate holds true
We point out that in the special autonomous case
(for a.e. \(x \in \Omega \) and \(t \ge 0\) and for all \(s \in {\mathbb {R}}\) and \(\xi \in {\mathbb {R}}^N\)) the previous theorem implies that for large value of t the “suitably regular” global solutions behave as the solution \(w \in W_0^{1,p}(\Omega ) \cap L^{\infty }(\Omega ) \) of the associated stationary elliptic problem
Moreover, it is also possible to estimate the difference between these global solutions of (1.1) and the stationary solution w. In detail, we have the following result.
Corollary 2.2
Let (1.2)–(1.7) hold true with \(T= + \infty \) and \(\alpha _0 >0\). If (2.32) is satisfied then every global solution u of (1.1) belonging to \(L^p_{loc}([t_0,+\infty );W_0^{1,p}(\Omega )) \cap L^{\infty }_{loc}([t_0,+\infty );L^{\infty }(\Omega ))\) (where \(t_0 > 0\)) belongs to \(C(\overline{\Omega }\times [t_0,+\infty ))\) and satisfies
where w is the unique solution of (2.33) belonging to \( W_0^{1,p}(\Omega ) \cap L^{\infty }(\Omega ) \).
Moreover, the following estimate holds
Remark 2.8
We recall that analogous results where proved in [46, 47] when \(p \ge 2\) and under stronger monotony assumptions on the operator \(a(x,\xi )\). Hence, the previous result completes the cited ones revealing that the same phenomenon appears in the singular case \(p < 2\) and for a more general class of “weak monotone” parabolic equations.
Until now, we have described the behavior of suitably regular solutions considering different “type of regularity” (for example, immediately boundedness or gradient in \(L^p\)..).
We show now that it is possible to say something also when the solutions generally do not increase their regularity, as for example when f and \(u_0\) are only summable functions, or when we do not have any information on the regularity of the solutions.
As a matter of fact, in all these cases it is possible distinguish a class of solutions, “the solutions obtained by approximation,” for which we will still be able to describe their behavior in time. Moreover, we will also show that the further requirement to be a solution obtained by approximation produces uniqueness despite the fact that the data f and \(u_0\) can be assumed to be only summable functions.
More in detail, let us define what we mean by a “solution constructed by approximation.”
Definition 2.3
A solution u of (1.1) is obtained by approximation (sola) if it is the a.e. limit in \(\Omega _T\) of the solutions \(u_n \in L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega )) \) (denoted “approximating solutions”) of the following (approximating) problems
where \(f_n\) and \(u_{0,n}\) satisfy
Our first result on “sola” is the following.
Theorem 2.8
Let (1.2)–(1.5) and (2.29) hold true. Let \(f \in L^1(\Omega _T)\) and \(u_0 \in L^{r_0}(\Omega )\) with \(r_0 \ge 1\). Then, there exists only one solution u of (1.1) constructed by approximation. Moreover, it results
and the following “estimate of continuous dependence from the data” holds true for every \(t \in (0,T)\)
where v is the (unique) solution constructed by approximation of problem (1.1) which assume initial datum \(v_0 \in L^{1}(\Omega )\) and forcing term \(g \in L^1(\Omega _T)\), i.e., v is the solution constructed by approximation of the following problem
Remark 2.9
We notice explicitly that in Theorem 2.8 we have assumed \(\alpha _0 \ge 0\) and hence the uniqueness of sola holds true also in the absence of the lower-order term \(\alpha _0 u\).
We also point out that the previous uniqueness result completes the result in [20] where when \(p > 2 - \frac{1}{N+1} \) the uniqueness of solutions obtained by approximation is proved assuming the following further structural assumptions
We prove now that if the forcing term f is bounded and p is not too small then the unique solution of (1.1) obtained by approximation is a solution which “immediately becomes bounded.” In detail, we have
Theorem 2.9
Let (1.2)–(1.5) and (2.29) hold true with \(p > \frac{2N}{N+r_0}\). Let \(f \in L^{\infty }(\Omega _T)\) and \(u_0 \in L^{r_0}(\Omega )\) with \(r_0 \ge 1\). Then, there exists only one solution u of (1.1) constructed by approximation belonging to \(L^{\infty }_{loc}((0,T];L^{\infty }(\Omega )) \cap L^{p}_{loc}((0,T];W_0^{1,p}(\Omega )) \cap C([0,T];L^1(\Omega ))\). Moreover, u satisfies the estimates of Theorem 2.1 if \(\alpha _0 >0\) and the estimates of Theorem 2.2 if \(\alpha _0=0\).
Indeed, by the following theorem we can affirm that the solutions obtained by approximations have also a unique extension to a global solution obtained by approximation and all these global solutions exhibit the same behavior for large values of t, independently from the initial data that they assume. We recall that here by a global solution defined by approximation we mean the following
Definition 2.4
A function u is a global solution of (1.1) obtained by approximation (or equivalently is a solution of (2.26) obtained by approximation) if for every arbitrarily fixed \(T>0\), u is a solution of (1.1) obtained by approximation (according to Definition 2.3).
Theorem 2.10
Let (1.2)–(1.5) and (2.29) hold true with \(T = + \infty \). Assume \(u_0 \in L^{r_0}(\Omega )\) with \(r_0 \ge 1\) and \(f \in L^1_{loc}([0,+\infty );L^1(\Omega ))\). Then, there exists a unique global solution u of (1.1) obtained by approximation. Moreover, u belongs to \(C_{loc}([0,+\infty );L^1(\Omega ))\).
Furthermore, if \(v \in C_{loc}([0,+\infty );L^1(\Omega ))\) is the global solution obtained by approximation of (2.40) with \(g \in L^1_{loc}([0,+\infty );L^1(\Omega ))\) and \(v_0 \in L^{r_0}(\Omega )\), then the estimate of continuous dependence from the data (2.39) holds true for every \(t> 0\).
Finally, if \(\alpha _0 >0\) and \(g = f\) (hence now v is the unique global solution obtained by approximation of (2.27)) then the following estimate holds true for a.e. \(t > 0\)
where \(c = |\Omega |^{\frac{1}{r}-\frac{1}{r_0}}\) In particular, it results
Remark 2.10
We point out explicitly that by (2.42) it follows that all these global solutions obtained by approximation have the same asymptotic behavior at infinity even if they satisfy different initial data.
We show now that if p is not too small and in the presence of a more regular datum f the unique global solution of (1.1) obtained by approximation is a solution which “immediately increases its regularity.” In detail, we have
Theorem 2.11
Let (1.2)–(1.5) and (2.29) hold true with \(T = + \infty \), \(p > \frac{2N}{N+r_0}\) and \(f \in L^{\infty }_{loc}([0,+\infty );L^{\infty }(\Omega ))\). Then, there exists a unique global solution u of (1.1) obtained by approximation belonging to
for every \(r \ge 1\).
Moreover, if \(f \in L^{\infty }(\Omega _{\infty }) \cap L^1(\Omega _{\infty })\) and \(\alpha _0 > 0\) then u belongs also to
for every \(t_0 >0\) and \(r \ge 1\).
Indeed, even if a solution is not obtained by approximation, if it is sufficiently regular (belonging to \(L^p_{loc}([0,+\infty );W_0^{1,p}(\Omega ))\)), then it has the same asymptotic behavior for \(t \rightarrow + \infty \) of the solutions constructed by approximation. As a matter of fact, it results.
Theorem 2.12
Let (1.2)–(1.5) and (2.29) hold true with \(T = + \infty \). Assume \(\alpha _0 >0\), \(f \in L^1_{loc}([0,+\infty );L^1(\Omega ))\), \(u_0 \in L^{1}(\Omega )\) and \(v_0 \in L^{1}(\Omega )\). If \(u \in C_{loc}([0,+\infty );L^1(\Omega ))\) is the global solution obtained by approximation of (1.1) and if v is a global solution of (2.27) belonging to \(L^p_{loc}([0,+\infty );W_0^{1,p}(\Omega ))\) then the following estimate holds true
In particular, the limit (2.42) is satisfied.
Indeed, the previous result reveals that if \(\alpha _0 >0\) then all the “sufficiently” regular solutions are unique and coincide with the solutions obtained by approximations. As a matter of fact, an immediate consequence of estimate (2.43) (applied with \(u_0 = v_0\)) is the following result.
Corollary 2.3
Let (1.2)–(1.5) and (2.29) hold true with \(T = + \infty \). Assume \(f \in L^1_{loc}([0,+\infty );L^1(\Omega ))\), \(u_0 \in L^{1}(\Omega )\) and \(\alpha _0 >0\). If u is a global solution of (1.1) belonging to \(L^p_{loc}([0,+\infty );W_0^{1,p}(\Omega ))\) then u is the unique global solution of (1.1) obtained by approximation.
Hence, problem (1.1) can be solved by only one global solution belonging to the space \(L^p_{loc}([0,+\infty );W_0^{1,p}(\Omega ))\).
Moreover, if \(v_0 \in L^1(\Omega )\) and v is the unique global solution of (2.27) in \(L^p_{loc}([0,+\infty );W_0^{1,p}(\Omega ))\) and if u is, as above, the unique global solution of (1.1) belonging to \(L^p_{loc}([0,+\infty );W_0^{1,p}(\Omega ))\) then estimates (2.43) and (2.42) hold true.
We notice that in the previous uniqueness result it was essential the requirement that \(\alpha _0 >0\), otherwise the crucial estimate (2.43) fails. We prove now that the uniqueness of the “sufficiently regular” solutions holds true even if \(\alpha _0 = 0\).
Moreover, we prove that it is sufficient that the solution becomes immediately “sufficiently regular” (i.e., it is not necessary the regularity “up to zero”). In detail, we have the following result.
Theorem 2.13
Let (1.3)–(1.5) and (2.29) hold true. Assume \(f \in L^1(\Omega _T)\) and \(u_0 \in L^{1}(\Omega )\). Then, there is at most one solution of (1.1) belonging to \(L^p_{loc}((0,T];W_0^{1,p}(\Omega )) \cap C([0,T];L^1(\Omega ))\).
Consequently, if (1.3)–(1.5) and (2.29) hold true with \(T \!{=}\! + \infty \) and \(f \in L^1_{loc}([0,+\infty );L^1(\Omega ))\) then there is at most one global solution of (1.1) belonging to \(L^p_{loc}((0,+\infty );W_0^{1,p}(\Omega )) \cap C_{loc}([0,+\infty );L^1(\Omega ))\).
An immediate consequence of Theorems 2.13 and 2.4 is the following result.
Theorem 2.14
Let (1.2)–(1.6) and (2.29) hold true with \(T=+\infty \) and \(p > \frac{2N}{N+r_0}\). Assume \(f \in L^{\infty }_{loc}([0,+\infty );L^{\infty }(\Omega ))\). Then, there exists only one global solution u belonging to
for every \(r \ge 1\).
Moreover, if we also assume \(\alpha _0>0\) and \(f \in L^{\infty }(\Omega _{\infty }) \cap L^1(\Omega _{\infty })\), then u belongs also to
for every \(t_0 >0\) and \(r \ge 1\). Finally, u is also the unique global solution obtained by approximation.
Remark 2.11
We recall, that we have proved above that under the assumptions of the previous theorem there exists a global solution which immediately increases its regularity which is the unique solution obtained by approximation. A priori we do not know if there exist other global solutions which immediately increases their regularity and that are not solutions obtained by approximation. The previous result allows to conclude that there exists one and only one global solution which immediately become regular. Thus, such a unique global solution which becomes immediately regular is also the unique global solution obtained by approximation.
3 Preliminary results
In this section, we give some known and new results which will be essential in the proofs of the results presented here and that can be of interest in themselves.
We start recalling some results about \(L^\infty \)-decay estimates proved in [42] which substantially allow to obtain decays estimates simply by suitable integral estimates (see [48] for a brief description of this method). The proofs of these results make use of a technical Lemma proved in [50] together with a classical Lemma (see Lemma 3.1) often used to prove \(L^{\infty }\)-results. We point out that there are different methods to prove decay estimates. For example, a classical method (completely different from that used here) is the use of suitable Sobolev logarithmic inequalities which reflect the operator involved in the problem (see for example [19, 27, 54] and the references therein).
In detail, let us define
We have the following results.
Theorem 3.1
(Theorem 2.1 in [42]) Assume that
where \(\Omega \) is an open set of \({\mathbb {R}}^N\), (not necessary bounded), \(N \ge 1\), \(0<T\le +\infty \) and
Suppose that u satisfies the following integral estimates for every \(k>0\)
where \(c_1\) and \(c_2\) are positive constants independent of k. Finally, let us define
Then, there exists a positive constant \(C_1\) (see Formula (4.11) in [42]) depending only on N, \(c_1\), \(c_2\), r, \(r_0\), q and b such that
where
Moreover, if \(\Omega \) has finite measure we have an exponential decay if \(b = r\) and universal bounds if \(b > r\). More in detail, we have the following result.
Theorem 3.2
(Theorem 2.2 in [42]) Let the assumptions of Theorem 3.1 hold true.
If \(\Omega \) has finite measure and \(b = r\), the following exponential decay occurs
where \(C_2\) (see Formula (4.17) in [42]) is a positive constant (depending only on N, \(c_1\), \(c_2\), r, \(r_0\) and q), \(u_0\) is as in (3.6), \(h_1\) is as in (3.8), i.e., (recalling that here \(r=b\))
and
where \(|\Omega |\) denotes the measure of \(\Omega \). If otherwise \(\Omega \) has finite measure and \( b > r\), we have the following universal bound
where
and \(C_{\sharp } \) (see Formula (4.19) in [42]) is a constant depending only on r, \(r_0\), q, b, \(c_1\), \(c_2\) and the measure of \(\Omega \).
Remark 3.1
The previous Theorems hold true also if we replace assumption (3.5) with the following weaker assumption
and in this last case all the previous decay estimates hold true with the value \(\Vert u_0 \Vert _{L^{r_0}(\Omega )}\) replaced by \(\frac{c_0}{c_2}\). For details, see Remark 2.4 in [42].
The following three theorems are generalizations of Theorems 3.1 and 3.2 and will be proved at the end of this section.
Theorem 3.3
Let the assumptions of Theorem 3.1 be satisfied with the only change that now inequalities (3.4) and (3.5) are satisfied only for every \(k \ge \sigma _0\), where \(\sigma _0\) is a positive constant. Then, u(t) belongs to \( L^\infty (\Omega )\) for every \(t > 0\) and the following estimate holds true
where \(u_0\) is as in (3.6), the exponents \(h_0 \) and \(h_1\) are as in (3.8) and \(C_0 = \max \{2, C_1\}\) with \(C_1\) as in Theorem 3.1.
Theorem 3.4
Under the assumptions of Theorem 3.3, if \(\Omega \) has finite measure and \(b = r\) then the following estimate occurs
where \(u_0\) is as in (3.6), the exponent \(h_1\) is as in (3.10), \(\sigma \) is as in (3.11) and \(C_3 = \max \{2, C_2\}\) (\(C_2\) as in Theorem 3.2).
Theorem 3.5
Under the assumptions of Theorem 3.3, if \(\Omega \) has finite measure and \(b > r\) then the following estimate occurs
where the exponent \(h_2\) is as in (3.13) and \(C_4 = \max \{2, C_{\sharp }\}\) is a constant independent of \(u_0\) (\(C_{\sharp }\) is as in Theorem 3.2).
In the proofs of Theorems 3.3–3.5 below, we will use the following lemma which, as recalled above, is a very useful tool in proving boundedness results.
Lemma 3.1
(Lemma 5.6, Chapter 2 in [33]) Assume that a sequence \(\{Y_m\}_{m\in {{\mathbb {N}}} \cup \{0\} }\), of nonnegative real numbers satisfies
and
where C and \(\delta \) are positive given constants and \(B\ge 1\). Then, it follows that
To be self-contained, we recall also the following two results, proved, respectively, in [38, 43], which we will use in the proofs of the asymptotic behavior of the solutions.
Theorem 3.6
(Theorem 2.8 of [43]) Let u be in \(C((0,T);L^r(\Omega )) \cap L^{\infty }(0,T;L^{r_0}(\Omega ))\) where \(0< r \le r_0 < + \infty \). Suppose also that \(|\Omega | < +\infty \) if \(r \not = r_0\) (no assumption on \(|\Omega |\) are needed if \(r = r_0\)). If u satisfies
and there exists \(u_0 \in L^{r_0}(\Omega )\) such that
where \(c_i\) (i=1,2) are real positive constants, then the following estimate holds true
where
Theorem 3.7
(Proposition 3.2 of [38]) Assume \(T_0 \in (t_0,+\infty ]\) where \(t_0 \ge 0\) and let \(\Psi (t)\) a continuous and nonnegative function defined on \([t_0,T_0)\) verifying
for every \(t_0< t_1 \le t_2 < T_0\) where M is a positive constant and g is a nonnegative function belonging to \(L^1_{loc}([t_0,T_0))\). Then, it results
We conclude this section by proving Theorems 3.3–3.5.
Proof of Theorem 3.3
Proceeding exactly as in the proof of the Theorem 2.1 in [42] (recalled above as Theorem 3.1), we deduce that the following inequality holds (see (4.7) in [42])
where
Notice that \(\delta \) is a positive constant being, by assumption, \(r>r_0\) and \(b_0< b < q\).
Since (3.24) is obtained applying the integral inequality (3.4) and now such estimate is true only for \( k \ge \sigma _0\), we need to require that \(k_m \ge \sigma _0\) for every \(m \in {{\mathbb {N}}} \cup \{0\}\) and hence, being \(k_0 = \frac{k}{2} = \min \{ k_m \}\), this is true if \( k \ge 2 \sigma _0\). To conclude the proof, we need to show that also the assumption (3.19) of Lemma 3.1 is satisfied, i.e., that it results
Now proceeding exactly as that of Theorem 2.1 in [42] but with the further requirement that k has to be chosen satisfying also the inequality \( k \ge 2 \sigma _0\) we obtain
from which the assertion follows. \(\square \)
Proof of Theorem 3.4
Analogously to the proof of the previous theorem, it is sufficient to proceed exactly as in the proof of Theorem 2.2 (case \(b = r\)) in [42] (recalled above as Theorem 3.2) but with the further requirement that k has to be chosen satisfying also the inequality \( k \ge 2 \sigma _0\). This restriction on k implies that the following estimate holds true (instead of (3.9))
where \(C_2\), \(\sigma \) and \(h_1\) are as in Theorem 3.2. From the last inequality, the assertion follows. \(\square \)
Proof of Theorem 3.5
Analogously to the proof of the previous theorem, it is sufficient to proceed exactly as in the proof of Theorem 2.2 (case \(b > r\)) in [42] but once again with the further requirement that k has to be chosen satisfying also the inequality \( k \ge 2 \sigma _0\). This restriction on k implies that the following estimate holds true (instead of (3.12))
where \(C_{\sharp }\) and \(h_2\) are as in Theorem 3.2. From the last inequality, the assertion follows.
\(\square \)
4 Proofs
Proof of Theorem 2.1
Let u be the solution constructed as the a.e. limit in \(\Omega _T\) of the solutions \(u_n \in L^{\infty }(\Omega _T) \cap L^p(0,T;W_0^{1,p}(\Omega )) \cap C(\overline{\Omega _T})\) to the following approximating problems
where the data \(u_{0,n}(x) \in C^{\infty }_c(\Omega )\) satisfy
The proof proceeds in two steps. Firstly, we prove estimates (2.4) and (2.7) and then we show that also estimates (2.6) and (2.8) hold true.
Step 1. To prove estimate (2.4), it is sufficient to demonstrate that the following inequality holds
where A(t) is as in (2.4). Let \(\varepsilon \) and k be positive constants arbitrarily fixed and take \(\varphi = \{ [\varepsilon + (|u_n|-k)_+]^{r-1} - \varepsilon ^{r-1} \}\mathrm{sign}(u_n)\) as test function in (4.1) where \( r > r_0\) (hence \(r >1\)) is arbitrarily fixed too. Notice that the use of such a test function, together with the following ones, can be made rigorous by means of Steklov averaging process. Using assumption (1.2), we obtain for every \( 0\le t_1 <t_2 \le T\)
where \(G_k\) is the function defined in (3.1) and
Applying SobolevFootnote 3 inequality in the previous estimate, we deduce
where \(c_2=c_1c_S\). Notice that choosing \( k \ge \sigma _0 = \frac{\Vert f\Vert _{L^{\infty }(\Omega _T)}}{\alpha _0} \) the last integral in the previous inequality is nonnegative. Hence, letting \(\varepsilon \rightarrow 0\) we deduce that for every \( 0\le t_1 <t_2 \le T\) and \(k \ge \sigma _0\) the following inequality holds
that is
where we have denoted
We recall that we have chosen \(r > r_0\). Moreover, since it results
the previous inequality is satisfied since we have assumed \(p > \frac{2N}{N +r_0}\). Furthermore, we have
that is, again true by our assumption on p. Thus, the previous choice of b, r and q satisfy (3.3). Observe that if \(r_0 >1\), proceeding as above but with \(r=r_0\) we deduce that (4.5) holds true also with \(r = r_0\), and thus the following estimate follows
and hence (3.5) is satisfied. Otherwise, if \(r_0 = 1\), taking \(\varphi = \left\{ 1- \frac{1}{[1+|G_k(u_n)|]^\delta }\right\} \mathrm{sign}(u_n)\) (\(\delta >1\)) as test function we get
from which choosing again \( k \ge \sigma _0 = \frac{\Vert f\Vert _{L^{\infty }(\Omega _T)}}{\alpha _0} \) and using (1.2) (and that \(\delta >1\)) we obtain for every \(0 \le t_0< t < T\)
from which (letting \(\delta \rightarrow +\infty \)) we deduce for every \(0 \le t_0 \le t <T\) and \(k \ge \sigma _0\)
which is inequality (3.5) with \(r_0 = 1 = c_2\).
Thus, applying Theorem 3.4 if \(p = 2\) and Theorem 3.3 if otherwise \(p \not = 2\) and recalling the construction (4.2), we deduce that estimate (4.3) holds true.
Notice that if \(p >2\) it results \(b>r\). Hence, applying Theorem 3.5 and noticing that \(b-r= p-2\) it follows that
which implies the bound (2.7).
Step 2. As said above, we prove here that also estimates (2.6) and (2.8) hold. To this aim, taking \(u_n\) as test function in the approximating problem (4.1) we obtain for every \(0 < t \le T\)
We estimate now the right-hand side of the previous inequality. By (4.3), it follows
Moreover, we have
Notice that again by (4.3) it results
Hence, by the previous two inequalities we deduce
By (4.10)–(4.12), we conclude that
from which the assertion (2.6) follows.
Finally, if \(p>2\), proceeding exactly as above but using (4.9) instead of (4.3) and hence replacing A(t) with U(t) (see (2.7)) we deduce that also the following estimate holds true
from which (2.8) follows. \(\square \)
Proof of Theorem 2.2
Let \(\rho > 0\) arbitrarily fixed and consider the following nonlinear problem
where we have defined
By the assumptions (1.2)–(1.5), it follows that the operator \(\overline{a}\) satisfies
where h is as in (1.4)
and
Moreover, by assumption (1.7) we deduce that \(\overline{f}\) belongs to \(L^{\infty }(\Omega _T)\). Hence, we can apply Theorem 2.1 with \(\alpha _0 = \rho \) (see also Remark 2.2) and conclude that there exists a solution v of (4.14) belonging to \(C(\overline{\Omega } \times (0,T])\) satisfying (for every \(t \in (0,T)\)) the following estimates
where \(\overline{\alpha }\) is as in (4.19), \(\sigma = \frac{\alpha c_S c(r_0)}{|\Omega |^{\frac{2}{N}}}\) (\(c_S=c_S(N)\) is the Sobolev constant defined in (4.4)) and the exponents \(h_0\) and \(h_1\) are as in (2.5). Moreover, \(\nabla v \in \left[ L^p(\Omega \times (t,T))\right] ^N\) for every \(t \in (0,T)\) and also the following estimate holds true
where \(\overline{A}(t)\) is as in (4.21). Besides, if \(p>2\) also the following estimates are satisfied
Notice that the function \(u = v e^{\rho t}\) is a solution of (1.1). Hence, we can rewrite (4.21)–(4.24) as
Now estimates (2.10) follow by (4.25) while estimate (4.27) implies estimate (2.13). Notice since it results
and
by estimates (4.26) and (4.28) it is possible to derive the following estimates for \(\nabla u\) in \(L^p(\Omega \times (t,T))\)
and if \(p > 2\)
where B(t) and \(B_0\) are as in the statement of the theorem.
Indeed, once we know that estimates (2.10) and (2.13) are satisfied it is possible to derive a slightly better estimate on \(\nabla u\), respect to estimates (2.234.29) and (4.30) obtained above, using directly the equation satisfied by u instead of the estimates of \(\nabla v\). As a matter of fact, it results (recalling the construction of u) for every \(0<t<T\)
which implies
Now, estimate (2.12) is an immediate consequence of estimates (4.32) and (2.10) while (2.14) follows by (4.32) and (2.13) . \(\square \)
Proof of Theorem 2.3
As in the proof of the previous theorem, we consider an auxiliary problem. In detail, let \(\rho > \alpha _0\) and let us consider the following problem
where \(\overline{a}\) and \(\overline{f}\) are as in (4.15). Now it is sufficient to proceed exactly as in the proof of Theorem 2.2 to get the result with the only difference that in applying Theorem 2.1 the absorption term is now \((\rho -\alpha _0)v\) instead \(\rho v\). Notice that this change in the absorption term is the reason of the slow differences in the bounds satisfied by the solution u of (2.20) respect to the bounds satisfied by the solution described in Theorem 2.2 (i.e., the when \(\alpha _0 = 0\)). \(\square \)
Remark 4.1
We notice that the estimates of the previous theorems hold true also replacing assumption (1.4) on h with the weaker hypothesis \(h \in L^{p'}(\Omega _T)\).
Proof of Theorem 2.4
The proof proceeds in two steps. Firstly, we prove the existence of a global solution u when \(f \in L^1_{loc}([0,+\infty );L^1(\Omega ))\) and the regularity \(C_{loc}([0,+\infty );L^1(\Omega ))\) when the operator a is independent of u. Then, in Step 2, we show the further regularity properties of u when \(p > \frac{2N}{N+r_0}\).
Step 1. Let us consider the following approximating problems
where
and \(f_n(x,t) \in L^{\infty }_{loc}([0,+\infty );L^{\infty }(\Omega )) \) satisfy
We recall that for every fixed \(n \in \mathbf{N}\), there exists a unique global solution \(u_n\) of (4.34) in \( L^{\infty }_{loc}([0,+\infty );L^{\infty }(\Omega )) \cap C_{loc}([0,+\infty );L^2(\Omega )) \cap L^p_{loc}([0,+\infty );W_0^{1,p}(\Omega )) \). Moreover, for every arbitrarily fixed \(T>0\), there exists a subsequence of the sequence \(u_n\) converging a.e. in \(\Omega _T\) (indeed a stronger convergence holds) to a solution of our problem (1.1) in \(\Omega _T\) (see for example [6,7,8,9, 44, 52]).
Using the above properties of the sequence \(u_n\) we construct now a global solution u of (1.1). To this aim, let \(T_0\) be a positive constant arbitrarily fixed. As said above, there exists a subsequence \(u^{(1)}_n\) of \(u_n\) satisfying
where \(u_1\) is a solution of (1.1) in \(\Omega _{T_0}\). We know that every term of the sequence \(u^{(1)}_n\) is a global solution, and therefore it is also a solution in \(\Omega _{2T_0}\). Hence, for what recalled above, there exists a subsequence \(u^{(2)}_n\) of \(u^{(1)}_n\) satisfying
where \(u_2\) is a solution of (1.1) in \(\Omega _{2T_0}\).
Iterating this procedure, we can define u (in all the set \(\Omega \times (0,+\infty )\)) in the following way
where \(h \in \mathbf{N}\) is such that \(hT_0 > T\). We point out that u is well defined since (by construction) if \(m \in \mathbf{N}\) is such that \(mT_0 > T\) then it results
We point out that u is a global solution of (1.1) since (by construction) for every arbitrarily fixed \(T >0\) u solves (1.1).
To conclude this step, it remains to show that if \(a(x,t,s,\xi ) \equiv a(x,t,\xi )\) then u belongs to \(C_{loc}([0,+\infty );L^1(\Omega ))\). Notice that it is sufficient to show that for every \(T>0\) arbitrarily fixed the sequence \(u_n\) is a Cauchy sequence in \(C([0,T];L^1(\Omega ))\). The proof of this last fact is similar at all to that in [52] (see also [49]) and hence we omit it.
Step 2. Assume \(p > \frac{2N}{N+r_0}\). We distinguish two cases: the “more regular case” (case 1) with stronger assumptions on f and \(\alpha _0>0\) and the “less regular case” (case 2) with a weaker assumption on f and \(\alpha _0 \ge 0\).
Case 1: Let f be in \( L^{\infty }(\Omega _{\infty }) \cap L^1(\Omega _{\infty })\) and \(\alpha _0 >0\). Let u be the solution constructed in the previous step. Thanks to the further assumptions, we have done here we can choose in the above approximating problems (4.34)
and \(u_{0,n}(x)\) satisfying
Thanks to the above construction of u and recalling the assumption \(\alpha _0 >0\), for every \(T>0\) arbitrarily fixed we can proceed exactly as in the proof of Theorem 2.1 obtaining that u satisfies estimates (2.4) and (2.6) for every \(T>0\) arbitrarily fixed. Consequently, for every \(t_0>0\) it follows
and
where \(\alpha \) is as in (1.2), \(c_S=c_S(N)\) is the Sobolev constant defined in (4.4) and \(\sigma \), \(h_0\) and \(h_1\) are as in (2.4).
Hence, u belongs to \(L^\infty (\Omega \times [t_0,+\infty )) \cap L^p(t_0,+\infty ;W_0^{1,p}(\Omega ))\) for every arbitrarily fixed \(t_0 >0\). To conclude the proof, it remains to show that u belongs also to \(C([t_0,+\infty );L^r(\Omega ))\) for every \(r \ge 1\) arbitrarily chosen. To this aim, we observe that by the structure assumption (1.3), the regularity assumed on f and the above regularity proved on u imply that u belongs also to \(C([t_0,+\infty );L^2(\Omega ))\). Hence, by the classical theory (see [22, 33]) we obtain that u is in \(C(\overline{\Omega } \times [t_0,+\infty ))\). Thus, it follows that u belongs also to \(C([t_0,+\infty );L^r(\Omega ))\) for every \(r \ge 1\).
Case 2: Let f be in \( L^{\infty }_{loc}([0,+\infty );L^{\infty }(\Omega ))\) and \(\alpha _0 \ge 0\). Thanks to the further regularity assumption on f, we have done here we can choose in the approximating problems (4.34) \(f_n\) and \(u_{0,n}(x)\) as in the previous case, i.e., satisfying (4.37) and (4.38). Thanks to the above construction of u and recalling the assumption on p done in this step, for every \(T>0\) arbitrarily fixed we can proceed exactly as in the proof of Theorem 2.2 obtaining that u satisfies estimates (2.10) and (2.12) for every \(T>0\) arbitrarily fixed. Thus, u belongs to \(L^{\infty }_{loc}((0,+\infty );L^{\infty }(\Omega )) \cap L^{p}_{loc}((0,+\infty );W_0^{1,p}(\Omega ))\). Now the remaining regularity \(C_{loc}((0,+\infty );L^r(\Omega ))\) can be proved reasoning as in Case 1 and hence we omit it. \(\square \)
Proof of Theorem 2.5
The assertion follows by the following more general result \(\square \)
Theorem 4.1
Let (1.2)–(1.4) hold true with \(T = + \infty \) and \(\alpha _0 > 0\). Assume that u and v are two global solutions of (1.1) relative to the same datum \(f \in L^{1}_{loc}(0,+\infty ;L^{1}(\Omega ))\) and to initial data, respectively, \(u_0\) and \(v_0\), where \(u_0\) and \(v_0\) are functions in \(L^{r_0}(\Omega )\) (\(r_0 \ge 1\)). If u and v belong to \( L^p_{loc}([t_0,+\infty );W_0^{1,p}(\Omega )) \cap L^{\infty }_{loc}([t_0,+\infty );L^{\infty }(\Omega )) \cap C_{loc}([t_0,+\infty );L^r(\Omega )) \) for an arbitrarily fixed \(t_0 >0\) and \(r \in [2,+\infty )\), then for every \(t_0< t< T_0 < + \infty \) it results
where \(\Lambda _0 = \int _{\Omega }|u-v|^{r}(t_0)\) and \(g(s) \equiv r (r-1)c_1 \int _{\Omega }[ |\nabla u|^p + |\nabla v|^p + |h|^{p'}]\) with \(c_1 = c(\beta ,p,\Omega ,N) [\Vert u-v\Vert _{L^{\infty }(\Omega \times [t_0,T_0))}]^{r-2}\).
Moreover, if in addition we assume that u and v belong to \(L^{\infty }(\Omega \times (t_1, +\infty ))\) for some \(t_1 \ge t_0\), then for every \(t > t_2 \ge t_1\) arbitrarily fixed it results
where \(\Lambda _1 = \Vert u-v\Vert _{L^{\infty }(\Omega \times (t_1, +\infty ))}^r |\Omega |\), \(g_1(s) \equiv r (r-1)C_1 \int _{\Omega }[ |\nabla u|^p + |\nabla v|^p + |h|^{p'}]\) and \(C_1 = c(\beta ,p,\Omega ,N) \Vert u-v\Vert _{L^{\infty }(\Omega \times (t_1, +\infty ))}^{r-2}\).
In particular, if it results
(for example if u and v belong to \( L^p(t_1,+\infty ;W_0^{1,p}(\Omega ))\) and \(h \in L^{p'}(\Omega \times [t_1,+\infty ))\)) then it follows
Remark 4.2
As already noticed in Remark 2.6, under the structure assumptions of Theorem 2.5 if \( p > \frac{2N}{N+r_0}\) and f belongs also to \(L^{\infty }(\Omega \times (0,+\infty ))\) there exists at least a global solution of (1.1) belonging to \(L^{\infty }(\Omega \times (t_0,+\infty )) \cap L^p(t_0,+\infty ;W_0^{1,p}(\Omega )) \cap C([t_0,+\infty );L^2(\Omega ))\) for every arbitrarily fixed \(t_0 >0\). As a matter of fact, thanks to Theorem 2.1 (see also Remark 2.2) it is possible to extend the solution u constructed in Theorem 2.1 in a solution of (2.26) that for sake of simplicity we denote again with u. Again by Theorem 2.1 (and thanks to the assumption that \(f \in L^{\infty }(\Omega \times (0,+\infty )) \cap L^1(\Omega \times (0,+\infty ))\)) it follows that u belongs to \(L^{\infty }(\Omega \times (t_0,+\infty )) \cap L^p(t_0,+\infty ;W_0^{1,p}(\Omega )) \cap C([t_0,+\infty );L^2(\Omega ))\) for every arbitrarily fixed \(t_0 >0\).
Proof of Theorem 4.1
We start proving (4.41). Hence, let \(T_0>0\) be arbitrarily fixed. Choosing \(|u-v|^{r-2}(u-v)\) as a test function in both the equations satisfied by u and v we deduce for every \(t_0 \le t_1 < t_2 \le T_0\)
It results (by (1.3), Young and Poincare inequalityFootnote 4)
where \(c_1 = c(\beta ,p,\Omega ,N) [\Vert u-v\Vert _{L^{\infty }(\Omega \times [t_0,T_0))}]^{r-2}\). By (4.45) and (4.47), it follows that
Notice that g(t) belongs to \(L^1(t_0,T_0)\). Hence, applying Theorem 3.7 with \(\Psi (t) = \int _{\Omega }|u-v|^{r}(t)\) we deduce that the following estimate holds for every \(t_0 \le t < T_0\)
where \(\Lambda _0 = \int _{\Omega }|u-v|^{r}(t_0)\). Moreover, if in addition we assume that u and v belong to \(L^{\infty }(\Omega \times [t_1, +\infty ))\) for some \(t_1 \ge t_0\), then by the previous estimate we deduce that also (4.42) holds true. \(\square \)
We observe that if we do not know if the solutions u and v are locally bounded, it is possible to prove that estimate (4.41) still holds for \(r=2\). In detail, we have the following result.
Theorem 4.2
Let (1.2)–(1.4) hold true with \(T= + \infty \) and \(\alpha _0 > 0\). Assume that u and v are two global solutions of (1.1) relative to the same datum f and to initial data, respectively, \(u_0\) and \(v_0\), where \(u_0\) and \(v_0\) are functions in \(L^{r_0}(\Omega )\) (\(r_0 \ge 1\)). If u and v belong to \( L^p_{loc}([t_0,+\infty );W_0^{1,p}(\Omega )) \cap L^{\infty }_{loc}([t_0,+\infty );L^2(\Omega )) \) (for an arbitrarily fixed \(t_0 >0\)) and if f is in \(L^{p'}_{loc}([t_0,+\infty );W^{-1,p'}(\Omega )) \) then u and v belong to \(C_{loc}([t_0,+\infty );L^2(\Omega ))\) and for every \(t > t_0\) it results
where \(\Lambda _0 = \int _{\Omega }|u-v|^{2}(t_0)\) and \(g(s) \equiv 2 c_1 \int _{\Omega }[ |\nabla u|^p + |\nabla v|^p + |h|^{p'}]\) with \(c_1 = c(\beta ,p,\Omega ,N)\).
Moreover, if in addition we assume that u and v belong to \(L^{\infty }(t_1, +\infty ;L^2(\Omega ))\) for some \(t_1 \ge t_0\), then for every \( t > t_2 \ge t_1\) arbitrarily fixed it results
where
In particular, if it results
it follows
Proof of Theorem 4.2
We observe that by the structure assumption (1.3) and by the regularity assumption done on u, v and f it follows that u and v belong to \(C_{loc}([t_0,+\infty );L^2(\Omega ))\). Now the assertions of the theorem follow choosing \(r=2\) and proceeding exactly as in the proof of Theorem 4.1. \(\square \)
Proof of Corollary 2.1
The proof that both the solutions u and v belong to \(C([t_0,+\infty );L^r(\Omega ))\) for every \(r \ge 1\) is at all similar to that in the proof of Theorem 2.4. In detail, by the structure assumptions and the regularity assumed on u, v and f it follows that the solutions u and v belong to \(C([t_0,+\infty );L^2(\Omega ))\) and hence, by the classical theory (see [22, 33]) they are also in \(C(\overline{\Omega } \times [t_0,+\infty ))\). Thus, the regularity \(C([t_0,+\infty );L^r(\Omega ))\) (for every \(r \ge 1\)) follows and consequently estimate (2.28) holds true by Theorem 2.5 for every \(r \ge 2\) (and hence for every \(r \ge 1\)). \(\square \)
Proof of Theorem 2.6
The assertion follows by Theorem 4.2. \(\square \)
Proof of Theorem 2.7
Reasoning as in the proof of Corollary 2.1, it follows that u and v belong to \(C(\overline{\Omega }\times [t_0,+\infty ))\cap C_{loc}([t_0,+\infty );L^r(\Omega ))\) for every \(r \ge 2\).
Let \(r \in [2,+\infty )\) arbitrarily fixed. Proceeding as in the proof of Theorem 2.5, we deduce that estimate (4.45) holds true for every \(t_0 \le t_1 < t_2 \le T_0\), where \(T_0 > t_0\) is arbitrarily fixed. Since the operator a does not depend on u (i.e., \(a(x,t,s,\xi )=a(x,t,\xi )\)) by the structural assumption (1.5) and by (4.45), we obtain for every \(t_0 \le t_1 < t_2 \le T_0\)
Notice that by the previous estimate it follows that
Now, applying Theorem 3.6 in the set \(\Omega \times (t_0,T_0)\) we deduce the following estimate
Thanks to the arbitrariness of \(T_0\), we can conclude that the previous estimate holds true for every \(t > t_0\) and hence letting \(r \rightarrow +\infty \) we obtain estimate (2.31), i.e.,
Now letting \(t \rightarrow +\infty \), we conclude that also (2.30) holds true. \(\square \)
Remark 4.3
Notice that the previous proofs work replacing the lower-order term \(\alpha _0 u\) with a more general Caratheodory function \(a_0(x,t,u,\nabla u)\) satisfying
and assuming that \(a_0(x,t,u,\nabla u)\) and \(a_0(x,t,v,\nabla v)\) suitable regular \(L^1_{loc}(0,T;L^1(\Omega ))\).
Proof of Corollary 2.2
The assertions follow applying Theorem 2.7 once noticed that the solution w of the stationary problem (2.33) belonging to \( W_0^{1,p}(\Omega ) \cap L^{\infty }(\Omega )\) is also a global solution (in \(L^p([t_0,+\infty );W_0^{1,p}(\Omega ))\cap L^{\infty }([t_0,+\infty );L^{\infty }(\Omega ))\)) of the following evolution problem
\(\square \)
Proof of Theorem 2.8
The existence of a solution constructed by approximation can be find in many papers (depending on the structure assumptions); see for example [6,7,8,9, 44, 52].
We complete the proof by showing the properties of these solutions enunciated in the statement of the theorem.
To this aim, we notice that every approximating sequence \(u_n\) is a Cauchy sequences in \(C([0,T];L^1(\Omega ))\) (see [52] Claim 2 in section 2) and hence every solution u of (1.1) constructed by approximation (and consequently every solution v of (2.40) constructed by approximation) belongs to \(C([0,T];L^1(\Omega ))\) .
Hence, to conclude the proof it is sufficient to show that estimate (2.39) holds true since it implies the uniqueness of the solutions constructed by approximation.
By assumption, u and v are solutions constructed by approximation. Hence, u is the a.e. limit in \(\Omega _T\) of the regular approximating solutions \(u_n \in L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega )) \) of (2.35) and v is the a.e. limit in \(\Omega _T\) of the regular approximating solutions \(v_n \in L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega )) \) of
where \(g_n\) and \(v_{0,n}\) satisfy
Let us choose \(\varphi = \left\{ 1 - \frac{1}{[1+|u_n-v_n|]^{\delta }}\right\} \) sign\((u_n-v_n)\) as test function in (2.35) and in (4.55), where \(\delta > 1\) is arbitrarily fixed. Subtracting the equations obtained in this way, we deduce for every \(t \in (0,T)\)
By (4.58) and assumption (1.5), we deduce
which implies (letting \(\delta \rightarrow + \infty \))
As recalled above, the sequences \(u_n\) and \(v_n\) are Cauchy sequences in \(C([0,T];L^1(\Omega ))\) and hence by (4.59) it follows that
\(\square \)
Proof of Theorem 2.9
The proof is an immediate consequence of Theorem 2.8 once recalled that the solution u considered in Theorem 2.1, if \(\alpha _0 >0\), and in Theorem 2.2, if \(\alpha _0=0\), is a solution obtained by approximation. \(\square \)
Proof of Theorem 2.10
As a first goal, we prove the existence of a global solution obtained by approximation. In detail, we construct our global solution u in the following way: for every \(T > 0\) arbitrarily fixed define u(x, t) in \(\Omega _T\) equal to the unique solution of (1.1) constructed by approximation. We recall that by Theorem 2.8 such a solution exists, is unique and belongs to \(C([0,T];L^1(\Omega ))\). Notice that, again by Theorem 2.8, u is well defined because if v is the solution obtained by approximation of our problem solved in \(\Omega \times (0,T^*)\) with \(T^*\) arbitrarily chosen, then it results \(u = v\) in \(\Omega \times (0,\min \{T,T^*\})\). By construction, u is defined in \(\Omega _{\infty }\), is a solution obtained by approximation of (1.1) for every arbitrarily fixed \(T>0\) and belongs to \(C_{loc}([0,\infty );L^1(\Omega ))\). Hence, u is a global solution of (1.1) obtained by approximation. Since, as recalled above, for every arbitrarily fixed \(T>0\), is unique the solution of (1.1) obtained by approximation, it is also unique the global solution u of (1.1) obtained by approximation. Notice that estimate (2.39) follows by construction thanks again to Theorem 2.8.
Hence, to conclude the proof it remains to show that if \(\alpha _0>0\) then estimate (2.41) holds true.
To this aim, let \(v \in C_{loc}([0,+\infty );L^1(\Omega ))\) be the global solution obtained by approximation of (2.27) and \(0<t<T\) arbitrarily fixed. Thanks to the uniqueness proved above of the global solutions obtained by approximation, we can choose the same approximation \(f_n\) of the datum f in (2.35) and in the approximating solutions \(v_n\) of v, i.e., we can consider \(v_n \in L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega ))\) solutions of
If \(r_0 >1\) let us consider \(1 < r \le r_0\) arbitrarily fixed and choose \(\varphi = \{ [ \varepsilon +|u_n - v_n|]^{r-1}- \varepsilon ^{r-1}\}\) sign\((u_n - v_n)\) as test function in (2.35) and in (4.60) where \(\varepsilon >0\) is arbitrarily fixed. Subtracting the results obtained in this way and thanks to assumptions (1.5) and (2.29), we deduce (letting \(\varepsilon \rightarrow 0\)) for every \(0 \le t_1 < t_2 \le T\)
Notice that by the previous inequality it follows that
Hence, we can apply Theorem 3.6 and conclude that
where \(c_4\) is as in (3.23), that is \(c_4 = |\Omega |^{\frac{1}{r}-\frac{1}{r_0}}\). Now the assertion follows for every \(1 < r \le r_0\) letting \(n \rightarrow +\infty \). Noticing that we are assuming that \(\Omega \) has finite measure, we deduce that the assert follows also in the particular case \(r=1 < r_0\).
If otherwise \(r_0 =1\), we change the test function in \(\varphi = \left\{ 1 - \frac{1}{[1+|u_n-v_n|]^{\delta }}\right\} \) sign\((u_n-v_n)\) where \(\delta > 1\) is arbitrarily fixed. Proceeding as in the proof of estimate (4.59) above, we deduce (being now \(g_n=f_n\))
from which it follows also that
Applying again Theorem 3.6 (with now \(r=r_0 =1\)), we obtain
which implies estimate (2.41) letting \(n \rightarrow +\infty \). \(\square \)
Proof of Theorem 2.11
The result is an immediate consequence of Theorems 2.4 and 2.10 being the solution constructed in Theorem 2.4 a global solution of (2.26) obtained by approximation. \(\square \)
Proof of Theorem 2.12
We start noticing that by the structure bound (1.3) together with the assumption that v is in \(L^p_{loc}([0,+\infty );W_0^{1,p}(\Omega ))\) it follows that v belongs also to \(C_{loc}([0,+\infty );L^1(\Omega ))\). Now let \(T>0\) arbitrarily fixed. Since u is a global solution obtained by approximation it is the a.e. limit in \(\Omega _T\) of the solutions \(u_n \in L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega ))\) of (2.35). Let us choose \(\varphi = \left\{ 1 - \frac{1}{[1+|u_n-v|]^{\delta }}\right\} \) sign\((u_n-v)\) where \(\delta > 1\) is arbitrarily fixed as a test function in (2.35) and in (2.27). Subtracting the results obtained in this way and thanks to assumptions (1.5) and (2.29), we deduce for every \( 0 \le t_1< t_2 < T\) (letting \(\delta \rightarrow + \infty \))
Applying Theorem 3.7, we deduce that for every \(t \in (0,T]\)
from which, recalling that (2.36) holds true, the assert follows letting \(n \rightarrow + \infty \) being \(T>0\) arbitrarily fixed. \(\square \)
Proof of Theorem 2.13
We observe that it is sufficient to prove the uniqueness of the solutions of (1.1) belonging \(L^p_{loc}((0,T];W_0^{1,p}(\Omega )) \cap C([0,T];L^1(\Omega ))\). Now, the proof proceeds by contradiction. Hence, let u and v solutions of (1.1) belonging \(L^p_{loc}((0,T];W_0^{1,p}(\Omega )) \cap C([0,T];L^1(\Omega ))\). Let \(\delta > 1\) be arbitrarily fixed and choose \(\varphi = \left\{ 1 - \frac{1}{[1+|u-v|]^{\delta }}\right\} \) sign\((u-v)\) as a test function in the equations satisfied by u and v. Subtracting the results obtained in this way and thanks to the assumption (2.29), we deduce for every \( 0< t_0 < t \le T\)
Thanks to the assumption (1.5), by the previous inequality (dropping the nonnegative terms) we deduce
and thus, letting \(\delta \rightarrow + \infty \) we conclude that for every \(0< t_0 < t \le T\)
Now, recalling the regularity \(C([0,T];L^1(\Omega ))\) of u and v, the assert follows letting \(t_0 \rightarrow 0^+\). \(\square \)
Notes
We say that \(\Omega \) satisfies the property of positive geometric density if there exists \(\alpha ^* \in (0,1)\) and \(\rho _0 >0\) such that for every \(x_0 \in \partial \Omega \) and for every ball \(B_{\rho }(x_0)\) centered at \(x_0\) and radius \(\rho \le \rho _0\) it results
$$\begin{aligned} | \Omega \cap B_{\rho }(x_0)| \le (1-\alpha ^*) | B_{\rho }(x_0)|. \end{aligned}$$That is, it is continuous with respect to \((s,\xi )\) for almost every \((x,t)\in \Omega _T\), and measurable with respect to (x, t) for every \((s,\xi ) \in {\mathbb {R}}\times {\mathbb {R}}^N\)
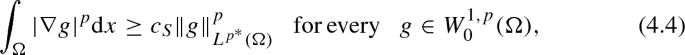
where \(c_S = c_S(p,N)\). Notice that it results \(c_S < \frac{p^*}{p'}=\frac{(N-1)p}{N-p}\) see [18].
Poincare inequality: if \(\Omega \) is an open bounded set it results
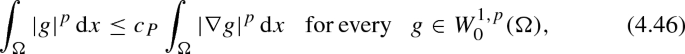
where \(c_P = c_P(p,N,\Omega )\).
References
F. Andreu, J. M. Mazon, S. Segura De Leon, J. Toledo, Existence and uniqueness for a a degenerate parabolic equation with\(L^1(\Omega )\)data, Trans. Am. Math. Soc., 351 (1999), 285–306.
D. G. Aronson, J. Serrin, Local behavior of solutions of quasilinear parabolic equations, Arch. Rational Mech. Anal., 25 (1967), 81–122.
P. Baras, M. Pierre, Problémes paraboliques semilinéaires avec donnés mesures, Appl. Anal., 18 (1984), 11–149.
Ph. Bénilan, M.G. Crandall, Regularizing effects of homogeneous evolution equations, MRC Tech. Rep. n. 2076, Madison, WI (1980).
P. Bénilan, L. Boccardo, T. Gallouët, R. Gariepy, M. Pierre, J.L. Vasquez, An\(L^1\)—theory of existence and uniqueness of solutions of nonlinear elliptic equations, Ann. Scuola Norm. Sup. Pisa Cl. Sci., 22 (1995), 241–273.
D. Blanchard, F. Murat, H. Redwane, Existence and uniqueness of a renormalized solution for a fairly general class of nonlinear parabolic problems, J. Differ. Equ., 177 (2001), 331–374.
L. Boccardo, A. Dall’Aglio, T. Gallouet, L. Orsina, Nonlinear parabolic equations with measure data, J. Funct. Anal., 147 (1997), 237–258.
L. Boccardo, T. Gallouet, Nonlinear elliptic and parabolic equations involving measure data, J. Funct. Anal., 87 (1989), 149–169.
L. Boccardo, L. Orsina, Some borderline cases of nonlinear parabolic equations with irregular data, J. Evol. Equ., 16 (2016), 51–64.
L. Boccardo, M.M. Porzio, A. Primo, Summability and existence results for nonlinear parabolic equations, Nonlinear Anal. TMA, 71 (2009), 978–990.
V. Bögelein, F. Duzaar, J. Kinnunen, C. Scheven, Higher integrability for doubly nonlinear parabolic systems, Journal de Mathématiques Pures et Appliquées. Neuviéme Série, 143 (2020), 31–72.
V. Bögelein, F. Duzaar, P. Marcellini, C. Scheven, Doubly nonlinear equations of porous medium type, Arch. Ration. Mech. Anal., 229 (2018), 503–545.
M. Bonforte, F. Cipriani, G. Grillo, Ultracontractive and convergence to equilibrium for supercritical quasilinear parabolic equations on Riemannian manifold, Adv. Differ. Equ., 7 (2003), 843–872.
M. Bonforte, G. Grillo, Super and ultracontractive bounds for doubly nonlinear evolution equations, Rev. Mat. Iberoamericana, 22 (2006), n. 1, 11–129.
M. Bonforte, G. Grillo, Singular evolution on manifolds, their smoothing properties and Sobolev inequalities, Discrete Cont. Dyn. Syst., (2007), 130–137.
M. Bonforte, G. Grillo, Ultracontractive bounds for nonlinear evolution equations governed by the subcritical p-Laplacian, Progress in Nonlinear Differential Equations and Their Applications, Lecture Notes in Pure and Applied Mathematics. Lecture Notes in Math. vol. 61. 15–26 (Trends in Partial Differential Equations of Mathematical Physics). Birkhäuser Basel (2005).
M. Bonforte, R. G. Iagar, J. L. Vazquez, Local smoothing effects, positivity and Harnack inequalities for the fast p-laplacian equation, Adv. Math., 224 (2010), 2151–2215.
H. Brezis, Analyse fonctionelle, Masson, Paris (1983).
F. Cipriani, G. Grillo, Uniform bounds for solutions to quasilinear parabolic equations, J. Differ. Equ., 177 (2001), 209–234.
A. Dall’Aglio, Approximated solutions of equations with\(L^1\)data. Application to the\(H\)-convergence of quasi-linear parabolic equations, Ann. Mat. Pura Appl., 170 (1996), 207–240.
A. Dall’Aglio, L. Orsina, Existence results for some nonlinear parabolic equations with nonregular data, Differ. Integral Equ., 5 (1992), n. 6, 1335–1354.
E. Di Benedetto, Degenerate parabolic equations, Springer-Verlag, New York (1993).
E. Di Benedetto, M. A. Herrero, On the Cauchy problem and initial traces for a degenerate parabolic equation, Trans. AMS, 314 (1989), 187–224.
E. Di Benedetto, M. A. Herrero, Non negative solutions of the evolution p-Laplacian equation Initial traces and Cauchy problem when\(1<p<2\), Arch. Rational Mech. Anal., 111 (1990), n. 3, 225–290.
C. Ebmeyer, J. M. Urbano, The smoothing property for a class of doubly nonlinear parabolic equations, Trans. Am. Math. Soc., 357 (2005), 3239–3253.
S. Fornaro, M. Sosio, V. Vespri, \(L^r_{loc}\)-\(L^{\infty }_{loc}\)estimates and expansion of positivity for a class of doubly non linear singular parabolic equations, Discrete Contin. Dyn. Syst. Ser. S, 7 (2014), 737–760.
G. Grillo, M. Muratori, M. M. Porzio, Porous media equations with two weights: existence, uniqueness, smoothing and decay properties of energy solutions via Poincaré inequalities, Discrete Contin. Dyn. Syst., 33 (2013), n. 8, 3599–3640.
M. A. Herrero, J. L. Vazquez, Asymptotic behaviour of the solutions of a strongly nonlinear parabolic problem, Ann. Fac. Sci. Toulose Math. (5), 3 (1981), n. 2, 113–127.
K. Ishige, On the existence of solutions of the Cauchy problem for a doubly nonlinear parabolic equation, SIAM J. Math. Anal., 27 (1996), 1235–1260.
A. V. Ivanov, Regularity for doubly nonlinear parabolic equations, Zapiski naucnych seminarov POMI, 209 (1994), 37–59.
P. Juutinen, P. Lindqvist, Pointwise decay for the solutions of degenerate and singular parabolic equations, Adv. Differ. Equ., 14 (2009), 663–684.
T. Kuusi, G. Mingione, Riesz potentials and nonlinear parabolic equations, Arch. Rational Mech. Anal., 212 (2014), 727–780.
O. Ladyženskaja, V. A. Solonnikov, N. N. Ural’ceva, Linear and quasilinear equations of parabolic type, Translations of the American Mathematical Society, American Mathematical Society, Providence (1968).
J. L. Lions, Quelques methodes de resolution des problemes aux limites non lineaires, Dunod et Gauthiers-Villars (1969).
J. J. Manfredi, V. Vespri, Large time behavior of solutions to a class of doubly nonlinear parabolic equations, Electron. J. Differ. Equ. (EJDE), 1994/02 (1994).
J. Moser, A Harnack inequality for parabolic differential equations, Commun. Pure Appl. Math., 17 (1964) 101–134; Correction, ibid., 20 (1967), 231–236.
J. Nash, Continuity of solutions of parabolic and elliptic equations, Am. J. Math., 80 (1958), 931–954.
G. Moscariello, M.M. Porzio, Quantitative asymptotic estimates for evolution problems, Nonlinear Anal. TMA, 154 (2017), 225–240.
A. Porretta, Regularity for entropy solutions of a class of parabolic equations with nonregular initial datum, Dyn. Syst. Appl., 7 (1998), n. 1, 53–71.
M.M. Porzio, Existence of solutions for some noncoercive parabolic equations, Discrete Contin. Dyn. Syst., 5 (1999), n. 3, 553–568.
M.M. Porzio, \(L^\infty _{loc}\)-estimates for degenerate and singular parabolic equations, Nonlinear Anal. Theory Methods Appl., 17 (1991), n. 11, 1093–1107.
M.M. Porzio, On decay estimates, J. Evol. Equ., 9 (2009), n. 3, 561–591.
M.M. Porzio, On uniform and decay estimates for unbounded solutions of partial differential equations, J. Differ. Equ., 259 (2015), 6960–7011.
M.M. Porzio, Existence, uniqueness and behavior of solutions for a class of nonlinear parabolic problems, Nonlinear Anal. TMA, 74 (2011), 5359–5382.
M.M. Porzio, Local regularity results for some parabolic equations, Houston J. Math., 25 (1999), n. 4, 769–792.
M.M. Porzio, Regularity and time behavior of the solutions of linear and quasilinear parabolic equations, Adv. Differ. Equ. 23 (2018), n. 5-6, 329–372.
M.M. Porzio, Asymptotic behavior and regularity properties of strongly nonlinear parabolic equations, Annali di Matematica Pura ed Applicata, 198 (2019), n. 5, 1803–1833.
M.M. Porzio, A new approach to decay estimates. Application to a nonlinear and degenerate parabolic PDE, Rend. lincei Mat. Appl., 29 (2018), 635–659
M.M. Porzio, Uniqueness and estimates for a parabolic equation with\(L^1\)data, to appear on Journal of Convex Analysis. Vol. 28 (2021) n.2.
M.M. Porzio, M.A. Pozio, Parabolic equations with non-linear, degenerate and space-time dependent operators, J. Evol. Equ., 8 (2008), 31–70.
M. M. Porzio, V. Vespri, Hölder estimates for local solutions of some doubly nonlinear degenerate parabolic equations, J. Differ. Equ., 103 (1993), 146–178.
A. Prignet, Existence and uniqueness of entropy solutions of parabolic problems with\(L^1\)data, Nonlinear Anal. TMA, 28 (1997), n. 12, 1943–1954.
N.S. Trudinger, Quasilinear elliptic partial differential equations in n variables, Stanford University, Department of Mathematics (1966).
J. L. Vazquez, Smoothing and decay estimates for nonlinear diffusion equations, Oxford University Press (2006).
L. Veron, Effects regularisants des semi-groupes non linéaires dans des espaces de Banach, Ann. Fac. Sci., Toulose Math. (5), 1 (1979), n. 2, 171–200.
Z. Wu, J. Zhao, J. Yin, H. Li, Nonlinear Diffusion equations, Singapore: World Scientific (2001).
J. Zhao, The Cauchy problem for\(u_t = \text{ div }(|\nabla u|^{p-2} \nabla u)\)when\(\frac{2N}{N+2}<p<2\), Nonlinear Anal. Theory Methods Appl., 24 (1995), 615–630.
Acknowledgements
I would like to thank the anonymous referee for suggesting me to study the case with the reaction term \(- \alpha _0 u\) (see Theorem 2.3), for recommending many references and for all the remarks that have improved the readability and clarity of this paper.
Funding
Open access funding provided by Università degli Studi di Roma La Sapienza within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Porzio, M.M. Regularity and time behavior of the solutions to weak monotone parabolic equations. J. Evol. Equ. 21, 3849–3889 (2021). https://doi.org/10.1007/s00028-021-00709-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00028-021-00709-y