Multiple Retention Mechanisms During Transport in Porous Media

Abstract

Understanding transport and retention mechanisms in porous media is essential in environmental and industrial processes such as subsurface contamination, water filtration and polymer flooding in oil reservoirs. In this article, new averaged equations for colloid transport and retention in porous media are obtained based on the master equation. In addition, new boundary conditions are discussed and an accurate and robust numerical scheme to evaluate the model empirical parameters is proposed. The numerical scheme, which allows incorporating generalized isotherms and retention kinetics, is validated by comparing the obtained solutions with analytical expressions available in the literature. In addition, good agreement between proposed model and the studied experimental data was observed and allowed concluding that the influence of longitudinal hydrodynamic dispersion on retained concentrations can be neglected for large times ($T > 1\ pvi$). Finally, it was shown that transport and retention coefficients (including dispersion coefficient) can be simultaneously obtained by numerically solving the inverse problem for any effluent concentration data, suggesting that tracer injection experiments are not necessary in order to quantify the hydrodynamic dispersion coefficient.

Appendix: Optimization Algorithm for Empirical Coefficients Determination

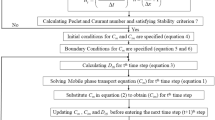
In this section, the optimization algorithm for determining the empirical parameters presented in Sect. 5 is discussed. Firstly, a set of $n \in \mathbb {N}$ measurements represented by $(\mathbf {x}_k,\mathbf {y}_k)$, with $k = \{1,2,\dots ,n\}$ is considered. Then, the model empirical parameter vector $\mathbf {a} := [a_1\ \dots \ a_m]^\top$ is defined and the corresponding model solution (numerical or analytical) is assumed as the objective function $\mathcal {F} = \mathcal {F}(\mathbf {x}_k,\mathbf {a})$. Furthermore, the residual sum of squares (E) is assumed:

$$\begin{aligned} E := \sum \limits _{k=1}^{n} \left( \mathbf {y}_k - \mathcal {F}\left( \mathbf {x}_k,\mathbf {a}\right) \right) ^2. \end{aligned}$$

(48)

The partial derivative of E related to the parameter $a_j$, with $j = {\lbrace }1,\dots ,m{\rbrace }$, is given by:

$$\begin{aligned} \frac{\partial E}{\partial a_j} = 2 \sum \limits _{k}^{n} r_k \frac{\partial r_k}{\partial a_j},\qquad \forall \ j, \end{aligned}$$

(49)

where the residual is defined as $r_k := \mathcal {F}\left( \mathbf {x}_k,\mathbf {a}\right) - \mathbf {y}_k$. In order to minimize the functional (48) and obtain the optimized empirical parameter vector “$\mathbf {a}$,” the following iterative Newton–Raphson algorithm discussed by Bonnans et al. (2006) is applied:

$$\begin{aligned} \mathbf {a}_{p+1} = \mathbf {a}_p - \delta \left[ \mathbf {H}E\left( \mathbf {a}_p\right) \right] ^{-1} \nabla E\left( \mathbf {a}_p\right) , \end{aligned}$$

(50)

where $\delta$ ($0< \delta < 1$) is a step size (Fletcher 2013). Defining the empirical parameter vector increment $\varDelta \mathbf {a}$:

$$\begin{aligned} \mathbf {a}^+ := \mathbf {a} + \varDelta \mathbf {a}\quad \text{ e } \quad \mathbf {a}^- := \mathbf {a} - \varDelta \mathbf {a}, \end{aligned}$$

and considering the finite difference method, the gradient and the Hessian matrix of E ($\nabla E$ and $\mathbf {H}E$, respectively) are given by:

$$\begin{aligned}&\nabla E = \left[ \frac{\mathcal {F}\left( \mathbf {a};a_1^+\right) - \mathcal {F}\left( \mathbf {a}\right) }{\varDelta a_1}\ \dots \ \frac{\mathcal {F}\left( \mathbf {a};a_m^+\right) - \mathcal {F}\left( \mathbf {a}\right) }{\varDelta a_m}\right] ^\top \\&\mathbf {H}E := \left[ \begin{array}{ccc} \displaystyle \frac{\mathcal {F}\left( \mathbf {a};a_1^+\right) - 2\mathcal {F}\left( \mathbf {a}\right) + \mathcal {F}\left( \mathbf {a};a_1^-\right) }{{\varDelta a_1}^2} &{} \cdots &{} \displaystyle \frac{\mathcal {F}\left( \mathbf {a};a_1^+,a_m^+\right) - \mathcal {F}\left( \mathbf {a};a_1^+\right) - \mathcal {F}\left( \mathbf {a};a_m^+\right) + \mathcal {F}\left( \mathbf {a}\right) }{\varDelta a_1 \varDelta a_m}\\ \vdots &{} \ddots &{} \vdots \\ \displaystyle \frac{\mathcal {F}\left( \mathbf {a};a_m^+,a_1^+\right) - \mathcal {F}\left( \mathbf {a};a_m^+\right) - \mathcal {F}\left( \mathbf {a};a_1^+\right) + \mathcal {F}\left( \mathbf {a}\right) }{\varDelta a_m \varDelta a_1} &{} \cdots &{} \displaystyle \frac{\mathcal {F}\left( \mathbf {a};a_m^+\right) - 2\mathcal {F}\left( \mathbf {a}\right) + \mathcal {F}\left( \mathbf {a};a_m^-\right) }{{\varDelta a_m}^2} \end{array} \right] . \end{aligned}$$

For simplicity, the vector $\mathbf {x}_k$ is omitted in the above definitions. Additionally, $\mathcal {F}\left( \mathbf {a};a_j^{\pm }\right)$ represents the objective function $\mathcal {F}$ evaluated in ($\mathbf {x}_k,\mathbf {a}$) with modified parameters $a_j^{\pm }$.

In summary, the optimization algorithm consists of:

Step 1: The model input data and experimental measurements are given. The model input data are space and time discretizations, as well as initial and boundary conditions. Effluent column experimental data (and retention profile, if available) are used for determining the functional defined in Eq. (48).

Step 2: Based on the operating retention mechanisms, the mathematical model is chosen and an initial guess for the corresponding empirical parameter vector $\mathbf {a}_0$ is assumed. Then, the vector of empirical parameters $\mathbf {a}$ is optimized by applying the iterative Eq. (50).

Step 3: Assuming analytical solutions for simplified models as the objective function $\mathcal {F}$ in (48), the empirical parameter vector $\mathbf {a}_1$ is obtained by applying the Step 2. The simplified models should include as much operative retention mechanisms as possible. For this reason, simplified models neglecting hydrodynamic dispersion were also used in this article.

Step 4 Considering $\mathbf {a}_1$ as initial guess, the proposed numerical solution (see Sect. 4) is assumed as the objective function $\mathcal {F}$ in (48) and the empirical parameters are determined by using the iterative Equation (50).

In Steps 3 and 4, Equation (50) is iterated while $|\mathbf {a}_{p+1}-\mathbf {a}_p| \ge \epsilon$ or the maximum number of iterations ($N_\mathrm{{max}}$) is reached. In this article, tolerance ($\epsilon$) and $N_\mathrm{{max}}$ were considered equal to 1E-6 and 1E5, respectively. It is important to mention that, if available, the tracer dispersion coefficient can be assumed as an initial guess in Step 2. However, in all the studied cases, the empirical coefficients converged to the same values when initial guesses for dispersion coefficient varied from 1E-99 to 1E-1 $m^2/s$. It suggests that using the tracer dispersion coefficient as an initial guess is not mandatory. Finally, the optimization can be performed considering the Steps 1, 2 and 4 (with $\mathbf {a}_1 = \mathbf {a}_0$). Although the Step 3 is optional, it allows reducing the computational cost.