A model for the second strain gradient continua reinforced with extensible fibers in plane elastostatics

Abstract

A second strain gradient theory-based continuum model is presented for the mechanics of an elastic solid reinforced with extensible fibers in plane elastostatics. The extension and bending kinematics of fibers are formulated via the second and the third gradient of the continuum deformation. The Euler equations arising in the third gradient of virtual displacement are then formulated by means of iterated integration by parts and variational principles. A rigorous derivation of the associated boundary conditions is also presented from which the expressions of triple forces and stresses are obtained. The obtained triple forces are found to be in conjugation with the Piola-type triple stress and are necessary to determine energy contributions on edges and points of Cauchy cuts. In particular, a complete linear model including admissible boundary conditions is derived within the description of superposed incremental deformations. The obtained analytical solution predicts smooth deformation profiles and, more importantly, assimilate gradual and dilatational shear angle distributions throughout the domain of interest.

Appendix

$\bullet$ Algebraic procedures for $a_{m},b_{m},c_{m}$ and $d_{m}$

$$\begin{aligned} a_{m}= & {} \frac{(T_{2}+T_{1})}{2},b_{m}=\frac{(T_{2}-T_{1})}{2i},c_{m}=\frac{ T_{3}}{i},d_{m}=T_{4}\text {, }m=\frac{n\pi }{2d}(n=1,3,5,etc.), \nonumber \\ T_{1}= & {} \left[ \frac{T_{24}}{4A}-T_{5}-\left\{ -T_{8}(T_{18})^{2}-9T_{8}(T_{10})^{\frac{ 2}{3}}+12T_{17}T_{8}-T_{6}+\frac{12(T_{10})^{\frac{1}{3}}T_{8}T_{18}}{T_{7}} \right\} ^{0.5}\right] ^{0.5}, \nonumber \\ T_{2}= & {} \left[ \frac{T_{24}}{4A}-T_{5}+\left\{ -T_{8}(T_{18})^{2}-9T_{8}(T_{10})^{\frac{ 2}{3}}+12T_{17}T_{8}-T_{6}+\frac{12(T_{10})^{\frac{1}{3}}T_{8}T_{18}}{T_{7}} \right\} ^{0.5}\right] ^{0.5}, \nonumber \\ T_{3}= & {} \left[ \frac{T_{24}}{4A}+T_{5}-\left\{ -T_{8}(T_{18})^{2}-9T_{8}(T_{10})^{\frac{ 2}{3}}+12T_{17}T_{8}+T_{6}+\frac{12(T_{10})^{\frac{1}{3}}T_{8}T_{18}}{T_{7}} \right\} ^{0.5}\right] ^{0.5}, \nonumber \\ T_{4}= & {} \left[ \frac{T_{24}}{4A}+T_{5}+\left\{ -T_{8}(T_{18})^{2}-9T_{8}(T_{10})^{\frac{ 2}{3}}+12T_{17}T_{8}+T_{6}+\frac{12(T_{10})^{\frac{1}{3}}T_{8}T_{18}}{T_{7}} \right\} ^{0.5}\right] ^{0.5}, \nonumber \\ T_{5}= & {} \frac{T8}{6(T_{9})^{\frac{1}{6}}},T_{6}=3\sqrt{6} T_{19}\left[ 27(T_{19})^{2}+3\sqrt{3}T_{15}-72T_{17}T_{18}-2(T_{18})^{3}\right] ^{0.5}, \nonumber \\ T_{7}= & {} 6(T_{9})^{\frac{1}{6}}\left[ 6T_{18}(T_{9})^{\frac{1}{3}}+9(T_{9})^{\frac{ 2}{3}}-T_{12}+\frac{12m^{4}}{A}+(T_{18})^{2}+T_{11}-\frac{3T_{24}T_{16}}{ A^{2}}\right] ^{\frac{1}{4}}, \nonumber \\ T_{8}= & {} \left[ 6T_{18}(T_{10})^{\frac{1}{3}}+9(T_{10})^{\frac{2}{3}}-T_{12}+\frac{ 12m^{4}}{A}+(T_{18})^{2}-\frac{3T_{24}T_{22}}{A^{2}}+T_{11}\right] ^{\frac{1}{2}}, \nonumber \\ T_{9}= & {} \frac{(T_{14})^{2}}{2}-\frac{4T_{18}T_{13}}{3}+\left( \frac{\sqrt{3}}{18} \right) \Big [12(T_{18})^{2}(T_{13})^{2}+27(T_{14})^{4}+16(T_{18})^{4}T_{13}+256(T_{13})^{3} \nonumber \\&-4(T_{18})^{3}(T_{14})^{2}-144T_{18}(T_{14})^{2}T_{13}-\frac{(T_{18})^{3}}{ 27}\Big ]^{0.5}, \nonumber \\ T_{10}= & {} \frac{(T_{19})^{2}}{2}+\frac{\sqrt{3}T_{15}}{18}-\frac{ 4T_{18}T_{17}}{3}-\frac{(T_{18})^{3}}{27},T_{11}=\frac{3(T_{24})^{2}T_{23}}{ 4A^{3}},T_{12}=\frac{9(T_{24})^{4}}{64A^{4}}, \nonumber \\ T_{13}= & {} T_{21}-\frac{m^{4}}{A}-T_{20}+\frac{T_{24}T_{16}}{4A^{2}},T_{14}= \frac{(T_{24})^{3}}{8A^{3}}+\frac{T_{16}}{A}-\frac{T_{24}T_{23}}{2A^{2}}, \nonumber \\ T_{15}= & {} \Big [27(T_{19})^{4}+T_{16}T_{17}(T_{18})^{4}+256(T_{17})^{3}-4(T_{18})^{3}(T_{19})^{2}, \nonumber \\&+128(T_{18})^{2}(T_{17})^{2}-144T_{18}(T_{19})^{2}T_{17}\Big ]^{0.5}, \nonumber \\ T_{16}= & {} (2+E)m^{2},T_{17}=T_{21}-\frac{m^{4}}{A}+\frac{T_{24}T_{22}}{4A^{2} }-T_{20}, \nonumber \\ T_{18}= & {} \frac{3(T_{24})^{2}}{8A^{2}}-\frac{T_{23}}{A},T_{19}=\frac{ (T_{24})^{3}}{8A^{3}}+\frac{T_{22}}{A}+\frac{T_{24}T_{23}}{2A^{2}},T_{20}= \frac{(T_{24})^{2}T_{23}}{16A^{3}},T_{21}=\frac{3(T_{24})^{4}}{256A^{4}}, \nonumber \\ T_{22}= & {} (2+E)m^{2},T_{23}=Cm^{2}+1\text { and }T_{24}=Am^{2}+C. \end{aligned}$$

(A.1)

$\bullet$ Evaluation of the geodesic curvature of the fibers

The geodesic curvature of a parametric curve ($\mathbf {r}(S)$) can be obtained by evaluating the second derivative of $\mathbf {r}(S)$ with respect to the arc length parameter (S);

$$\begin{aligned} \mathbf {g=r}^{\prime \prime }=\frac{d^{2}\mathbf {r(}S\mathbf {)}}{ dS^{2}}. \end{aligned}$$

(A.2)

Using the chain rule (i.e., $\mathrm{{d}}(*)/\mathrm{{d}}S=\frac{\mathrm{{d}}(*)}{\mathrm{{d}}\mathbf {X}}\frac{\mathrm{{d}} \mathbf {X}}{\mathrm{{d}}S}$), we obtain from Eq. (A2) that

$$\begin{aligned} \frac{\mathrm{{d}}^{2}\mathbf {r(}S\mathbf {)}}{\mathrm{{d}}S^{2}}=\frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}\mathbf {r(}S \mathbf {)}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}S}=\frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}\varvec{\chi } (S\mathbf {)}}{\mathrm{{d}}\mathbf {X}} \frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}S}=\left( \frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}\varvec{\chi (}S\mathbf {)}}{\mathrm{{d}} \mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}\mathbf {X}}\right) \frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}. \end{aligned}$$

(A.3)

Since $\mathbf {F}=\mathrm{{d}}\varvec{\chi }/\mathrm{{d}}\mathbf {X}$ and $\mathbf {D}=(\mathrm{{d}}\mathbf {X} (S))/\mathrm{{d}}S$, the above can be rewritten as

$$\begin{aligned} \mathbf {g=r}^{\prime \prime }=\left( \frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}\varvec{\chi (}S \mathbf {)}}{\mathrm{{d}}\mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}\mathbf {X}}\right) \frac{\mathrm{{d}}\mathbf { X}}{\mathrm{{d}}S}=\left( \frac{\mathrm{{d}}(\mathbf {FD})}{\mathrm{{d}}\mathbf {X}}\right) \mathbf {D=}\nabla [\mathbf {FD]D,} \end{aligned}$$

(A.4)

where $\nabla (\mathbf {FD})=\mathrm{{d}}(\mathbf {FD})/\mathrm{{d}}\mathbf {X}$ is the first gradient of “ $\mathbf {FD}$” .

$\bullet$ Evaluation of the rate of changes in curvature of the fibers

The rate of changes in curvature of the fibers can be formulated by taking third derivative of $\mathbf {r}(S)$ with respect to the arc length parameter (S). Hence, from Eq. (A4), we find

$$\begin{aligned} \varvec{\alpha } =\mathbf{r}^{\prime \prime \prime }=\frac{\mathrm{{d}}^{3}\mathbf {r(}S \mathbf {)}}{\mathrm{{d}}S^{3}}=\frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}^{2}\mathbf {r(}S\mathbf {)}}{\mathrm{{d}}S^{2}}\big )}{\mathrm{{d}}S}= \frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}(\mathbf {FD})}{\mathrm{{d}}\mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}S}. \end{aligned}$$

(A.5)

Now applying the chain rule (i.e., $\mathrm{{d}}(*)/\mathrm{{d}}S=\frac{\mathrm{{d}}(*)}{\mathrm{{d}}\mathbf {X}} \frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}$), Eq. (A5) Becomes

$$\begin{aligned} \frac{\mathrm{{d}}^{3}\mathbf {r(}S\mathbf {)}}{\mathrm{{d}}S^{3}}=\frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}(\mathbf {FD})}{\mathrm{{d}} \mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}S}=\frac{\mathrm{{d}}\big (\frac{\mathrm{{d}}(\mathbf {FD})}{\mathrm{{d}} \mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}\big )}{\mathrm{{d}}\mathbf {X}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}=\left[ \frac{\mathrm{{d}}^{2}(\mathbf {FD})}{\mathrm{{d}}\mathbf {X}^{2}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}+\frac{\mathrm{{d}}( \mathbf {FD})}{\mathrm{{d}}\mathbf {X}}\frac{\mathrm{{d}}^{2}\mathbf {X}}{\mathrm{{d}}S^{2}}\right] \frac{\mathrm{{d}}\mathbf {X}}{ \mathrm{{d}}S}. \end{aligned}$$

(A.6)

Since $\mathbf {D}=(\mathrm{{d}}\mathbf {X}(S))/\mathrm{{d}}S$, the above can be rewritten as

$$\begin{aligned} \varvec{\alpha } =\mathbf{r}^{\prime \prime \prime }=\left[ \frac{\mathrm{{d}}^{2}(\mathbf {FD}) }{\mathrm{{d}}\mathbf {X}^{2}}\frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}+\frac{\mathrm{{d}}(\mathbf {FD})}{\mathrm{{d}}\mathbf {X}} \frac{\mathrm{{d}}^{2}\mathbf {X}}{\mathrm{{d}}S^{2}}\right] \frac{\mathrm{{d}}\mathbf {X}}{\mathrm{{d}}S}=[\nabla \{\nabla ( \mathbf {FD})\}{} \mathbf{D}+\nabla (\mathbf {FD})(\nabla \mathbf {(D))}]\mathbf{D,} \end{aligned}$$

(A.7)

where $\nabla (\nabla (\mathbf {FD}))=\mathrm{{d}}^{2}(\mathbf {FD})/\mathrm{{d}}\mathbf {X}^{2}$ is the second gradient of “ $\mathbf {FD}$ ”.

$\bullet$ Implementation of the boundary conditions [Eq. (53)]

The boundary conditions in Eq. (53) can be readily implemented in the desired boundaries via the tangential and normal vectors of the boundary and the director field of the fibers. For example, in the case of aligned fibers in the direction of $\mathbf {X}_{1}$, we find

$$\begin{aligned} \mathbf {D=}D_{1}\mathbf {E}_{1}+D_{2} \mathbf {E}_{2}=D_{1}\mathbf {E}_{1};\text { \ }D_{1}=1\text { and }D_{2}=0. \end{aligned}$$

(A.8)

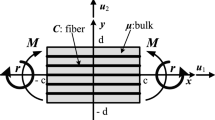
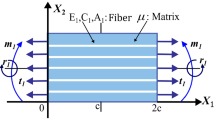
Now on $\Omega _{1}$, the unit normal and tangent to the boundary are defined by (see Fig. 15)

$$\begin{aligned} \mathbf {T}^{1}= & {} T_{1}^{1}\mathbf {E}_{1}+T_{2}^{1}\mathbf {E} _{2}=T_{2}^{1}\mathbf {E}_{2};\text { \ }T_{1}^{1}=0\text { and }T_{2}^{1}=1, \nonumber \\ \mathbf {N}^{1}= & {} N_{1}^{1}\mathbf {E}_{1}+N_{2}^{1}\mathbf {E} _{2}=N_{1}^{1}\mathbf {E}_{1};\text { \ }N_{1}^{1}=1\text { and }N_{2}^{1}=0. \end{aligned}$$

(A.9)

Fig. 15

Schematic demonstration of imposed boundary conditions

Hence, on $\Omega _{1}$, the corresponding boundary conditions can be obtained by

$$\begin{aligned} t_{1}^{1}\mathbf {e}_{1}= & {} \big (P_{11}N_{1}^{1}+P_{12}N_{2}^{1}\big ) \mathbf {e}_{1}=P_{11}\mathbf {e}_{1}, \nonumber \\ t_{2}^{1}\mathbf {e}_{2}= & {} \big (P_{21}N_{1}^{1}+P_{22}N_{2}^{1}\big ) \mathbf {e}_{2}=P_{21}\mathbf {e}_{2}, \nonumber \\ m_{1}^{1}\mathbf {e}_{1}= & {} \big (Cg_{1}-A\alpha _{1,1}D_{1}^{1}-A\alpha _{1,2}D_{2}^{1}\big )\big ( D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}+D_{1}^{1}N_{1}^{1}D_{2}^{1}N_{2}^{1}+D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}+D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}\big ) \mathbf {e}_{1} \nonumber \\= & {} (Cg_{1}-A\alpha _{1,1})\mathbf {e}_{1}, \nonumber \\ m_{2}^{1}\mathbf {e}_{2}= & {} \big (Cg_{2}-A\alpha _{2,1}D_{1}^{1}-A\alpha _{2,2}D_{2}^{1}\big )\big ( D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}+D_{1}^{1}N_{1}^{1}D_{2}^{1}N_{2}^{1}+D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}+D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}\big ) \mathbf {e}_{2} \nonumber \\= & {} (Cg_{2}-A\alpha _{2,1})\mathbf {e}_{2}, \nonumber \\ r_{1}^{1}\mathbf {e}_{1}= & {} A\alpha _{1}\big ( D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}+D_{1}^{1}N_{1}^{1}D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}+D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}+D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}\nonumber \\&+D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}D_{2}^{1}N_{2}^{1}+D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}\big ) \mathbf {e}_{1}=A\alpha _{1}\mathbf {e}_{1},\nonumber \\ r_{2}^{1}\mathbf {e}_{2}= & {} A\alpha _{2}\big ( D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}+D_{1}^{1}N_{1}^{1}D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}+D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}D_{1}^{1}N_{1}^{1}+D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}\nonumber \\&+D_{2}^{1}N_{2}^{1}D_{1}^{1}N_{1}^{1}D_{2}^{1}N_{2}^{1}+D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}D_{2}^{1}N_{2}^{1}\big ) \mathbf {e}_{2}=A\alpha _{2}\mathbf {e}_{2}, \end{aligned}$$

(A.10)

where $\mathbf {t}^{1}=t_{1}^{1}\mathbf {e}_{1}+t_{2}^{1}\mathbf {e}_{2}$, $\mathbf {m}^{1}=m_{1}^{1}\mathbf {e}_{1}+m_{2}^{1}\mathbf {e}_{2}$ and $\mathbf { r}^{1}=r_{1}^{1}\mathbf {e}_{1}+r_{2}^{1}\mathbf {e}_{2}$ are, respectively, the boundary traction, edge moment and the triple force acting on the $\Omega _{1}$ boundary.

For $\Omega _{2}$ boundary, we find (see Fig. 15)

$$\begin{aligned} \mathbf {T}^{2}= & {} T_{1}^{2}\mathbf {E}_{1}+T_{2}^{2}\mathbf {E} _{2}=T_{2}^{2}\mathbf {E}_{2};\text { \ }T_{1}^{2}=0\text { and }T_{2}^{2}=1,\nonumber \\ \mathbf {N}^{2}= & {} N_{1}^{2}\mathbf {E}_{1}+N_{2}^{2}\mathbf {E} _{2}=N_{1}^{2}\mathbf {E}_{1};\text { \ }N_{1}^{2}=1\text { and }N_{2}^{2}=0. \end{aligned}$$

(A.11)

Therefore, repeating the same process as done in the above, it can be shown that

$$\begin{aligned} t_{1}^{2}\mathbf {e}_{1}= & {} \big (P_{11}N_{1}^{2}+P_{12}N_{2}^{2}\big ) \mathbf {e}_{1}=P_{12}\mathbf {e}_{1}, \nonumber \\ t_{1}^{1}\mathbf {e}_{1}= & {} \big (P_{21}N_{1}^{2}+P_{22}N_{2}^{2}\big ) \mathbf {e}_{2}=P_{22}\mathbf {e}_{2}, \nonumber \\ m_{1}^{1}\mathbf {e}_{1}= & {} 0\mathbf {e}_{1} {{, }} m_{2}^{1}\mathbf {e}_{2}=0\mathbf {e}_{2}, \nonumber \\ r_{1}^{1}\mathbf {e}_{1}= & {} 0\mathbf {e}_{1}, r_{2}^{1}\mathbf {e}_{2}=0\mathbf {e}_{2}. \end{aligned}$$

(A.12)

Lastly, Eq. (A12) indicates that the edge moment and triple force cannot be sustained by the $\Omega _{2}$ boundary where no reinforcing fibers are aligned in $\mathbf {e}_{2}$ direction.