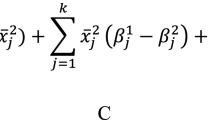Decomposition of the Gini index by income source for aggregated data and its applications

Abstract

The Gini index is well-known for a single measure of inequality. The purpose of this article is to explore a matrix structure of the Gini index in a setting of multiple source income. Using matrices, we analyze the decomposition of the Gini index by income source and derive an explicit formula for the factors in terms of the associated percentile levels based on aggregated data reporting. Each factor is shown to be the sums of the two split off parts of the income within a percentile bracket. Both have unequalizing and equalizing contribution to the total inequality, respectively. We use R code and apply the methodology to several data sets including a sample of European aggregated income reporting in 2014 for illustration. A byproduct from the Gini decomposition provides a matrix approach to the decomposition of the associated Lorenz curve in terms of the density distribution matrix and a Toeplitz matrix.

1 Introduction

There is a long history of the statistical study of income. Consequently, there exists a large body of research articles devoted to the decomposition analysis of inequality trends by income source as well as by population subgroup [see Heshmati (2004), Vernizzi et al. (2010), Mussini (2013), Lerman and Yitzhaki (1985)]. One of the recent papers of Mussini (2013) gives a summary of the historical account (1967–2013) on existing decomposition techniques, including what is known as a matrix approach to income inequality. In general, a measure of income inequality often attracts attention from researchers and policymakers. Much of the attention is focused on the (widening or narrowing) contribution to income inequality from different part of the income composition and different subgroups of the population.

Upon a brief review of various existing decomposition methods for their advantages and disadvantages, a recent existing technique reports a matrix approach to the measure of an inequality by income source and by subgroup. This research work, Mussini (2013), is based on the so-called pairwise difference criterion of the inequality and the use of G-matrix previously appeared in the paper (Silber 1989). Also, some known classical decomposition methods were previously established by computing the covariance between incomes and their ranks. For further details, we refer a reader to the literature by Pyatt (1980). Amongst various limitations in empirical studies, it appears that none of the existing techniques works naturally well or is immediately targeted for aggregated data form, in which economic data are almost always reported. One reason is that the underlying idea of the cited papers strictly relies on the pairwise difference criterion, which is essentially built on the framework of a single income vector. Furthermore, the decomposition methods are mostly developed based on existing techniques which are not directly applicable for aggregated datasets. Often, they are suitable for a single income vector reporting within a typical application setting (Vernizzi et al. 2010; Mussini 2013). Another reason concerns the interpretability, as we notice that the role of G-matrix from the cited papers seems less intuitively descriptive in terms of reducing or increasing the inequality. Therefore, a new method is attempted in order to fulfill an interpretable matrix approach to the Gini index decomposition for a general aggregated dataset.

Working directly with aggregated datasets to achieve the decomposition of inequality is the main motivation for this paper. We do this by developing and implementing a straightforward algorithm, using R package. We further hope the overall contribution of this article may be useful in areas of broad income research as well as in areas of applied and pure mathematics.

In this paper, we begin with any aggregated dataset and present a new approach to the inequality decomposition. We shall only be concerned with the methodology for the decomposition by income source and suggest that it works equally well with that by population subgroup. The result of this article does not rely on any sophisticated statistical calculation such as the aforementioned covariance, nor is it built on any existing decomposition technique. We will utilize elementary matrix algebra to express the decomposition, which is algebraically simple, captures all decomposition components, and facilitates its interpretation.

To keep this article self-contained, we now give a brief review of the Gini index and a Lorenz curve, which originally appeared in Lorenz (1905). The Gini index is a summary statistic of the Lorenz curve and a measure of inequality in a population. A Lorenz curve is essentially the representation of income inequality. It is defined based on the function L(p) that outputs the fraction of the resources owned by the poorest fraction p of the population. For instance, that $L(0.4)=0.1$ means that the poorest 40% of the population owns 10% of the resources. Equivalently, that also means that the top 60% occupy 90% of the resources. Here the reader must be reminded that a general resource shall be concretely interpreted in the context of income for this paper.

The basic theory of characterizing a Lorenz curve demonstrates the two simple facts: (a) L(p) is derivable from a set of economic data distribution, with the extreme cases $L(0)=0$ and $L(1) = 1$; (b) L(p) is nondecreasing and a convex function, whose precise definition may be found in a standard text by Rudin (1987). We will use these facts throughout this paper.

To measure how evenly the income is distributed, the Gini index of a particular Lorenz curve is calculated based on the single quantity that measures how much it is deviated from a perfectly equitable distribution by the Lorenz curve $L(p)=p$, as is shown in Fig. 1a. Using the area enclosed between the two curves to measure such deviation, it is readily seen that the Gini index, G, of a Lorenz curve in question can be defined by the integral

$$\begin{aligned} G=2\int ^1_0 \left( p - L(p)\right) ~ dp, \end{aligned}$$

where the number two is the scaling factor for the range $0 \le G \le 1$. The Gini index can also be used for the measure of health inequality, consumption or some other welfare indicator, etc. For illustrations, we refer the reader to papers by Farris (2010) and Lai et al. (2008).

Fig. 1

a The deviation of L(p) from the perfect equitable distribution. b The income splitting figure for factor $\varPhi _k$ for the income bracket $[p_{j-1},\,p_j]$

The subsequent part of the paper is organized as follows. The main result is encapsulated in (Matrix Representation of Gini Decomposition) Theorem 1 in the following Sect. 2. This section also gives another form of the main result by (Matrix Representation of Factor) Corollary 1 and their with rigorous proofs supported by (Gini Decomposition) Lemma 1.

Various parts of the decomposition formula are interpreted by virtue of Lemma 1 in Sect. 3. Then, we illustrate using R code to perform the decomposition with real data from the US 2007 family and European countries 2014 income households reporting in Sect. 4. Next, by examining various forms of our main result, we derive a matrix representation of a Lorenz curve as well as its decomposition formula in Sect. 5. We finally, in Sect. 6, conclude the paper with some remarks and questions which may be viable for future problems.

2 Decomposition of the Gini index

In order to decompose the Gini index by income source, we assume that there are n observations in the sample and each observation has m components. Let $x_{i k}$ be the kth component of the ith observation in the sample, where $i = 1, 2, \ldots , n,~~ k = 1, \ldots , m$. Since we are mainly concerned with income inequality in this paper, that $x_{i k}$ is tactically referred to the kth component (due to income source k) of the average of all individuals’ income that falls in the associated ith income bracket, and m indicates the total sources of income. The corresponding frequency to each ith income observation is denoted as $h_i$, each of which may be interpreted as the number of individuals (households) that belong to the associated income group. For mathematical convenience, we suppose such aggregated data distribution is reported or formatted as the matrix-like tabulation

$$\begin{aligned} \begin{array}{cccc|c} \hline x_{11} &{}\quad x_{12} &{}\quad \dots &{}\quad x_{1m} &{}\quad h_1 \\ x_{21} &{}\quad x_{22} &{}\quad \dots &{}\quad x_{2m} &{}\quad h_2 \\ \vdots &{}\quad \vdots &{}\quad \cdots &{}\quad \vdots &{}\quad \vdots \\ x_{n1} &{}\quad x_{n2} &{}\quad \dots &{}\quad x_{nm} &{}\quad h_n \\ \end{array} \end{aligned}$$

(1)

Throughout the paper, we make a general assumption for each row-sum

$$\begin{aligned} \displaystyle \sum ^m_{k=1}x_{ik}< \sum ^m_{k=1}x_{jk}\quad \text {whenever}\quad i < j. \end{aligned}$$

(2)

That is, the observations are sorted by the total income of the ith household in ascending order.

To simply state the main result of the paper, we introduce two pieces of notation. First, N denotes the total households and let $p_j$ be the percentile associated with the jth household group given by

$$\begin{aligned} N = \sum ^n_{i=1}h_i,\quad p_j = \frac{1}{N} \sum ^j_{i=1}h_i,\quad 1\le j\le n. \end{aligned}$$

(3)

All values of $p_j$ are in the unit interval [0, 1] right endpoint included, i.e., $p_n=1$. To include the left endpoint, we purposely define $p_0 = 0$. Second, for the total income (all sources combined) earned by the entire households in the population, we denote

$$\begin{aligned} T = \sum ^n_{i=1}\left( \,\sum ^m_{k=1}x_{ik}\right) h_i. \end{aligned}$$

(4)

The purpose of these notations will be simply made clear later in the proof of the main result. Although all notation favors the interpretation of family income, the method and discussion should apply equally well to other situations.

Finally, the main result contained in the following theorem also employs the notation used in the matrix theory by Zhang (1999).

$$\begin{aligned} \text {diag} (\lambda _1,\lambda _2, \ldots , \lambda _n) = \left( \begin{array}{cccc} \lambda _1 &{}\quad &{}\quad &{}\quad 0 \\ &{}\quad \lambda _2 &{}\quad &{}\quad \\ &{}\quad &{}\quad \ddots &{}\quad \\ 0 &{}\quad &{}\quad &{}\quad \lambda _n \\ \end{array} \right) \end{aligned}$$

Similarly, $\text {diag} ({\mathbf {v}})$ generates a diagonal matrix with vector ${\mathbf {v}}$ on the diagonal. Equivalently, if ${\mathbf {v}}$ has m components, then

$$\begin{aligned} \text {diag} ({\mathbf {v}})= \text {diag} \left( ({\mathbf {v}})_1, ({\mathbf {v}})_2, \ldots , ({\mathbf {v}})_m \right) . \end{aligned}$$

2.1 Statements of the main result

Theorem 1

(Matrix Representation of Gini Decomposition) Let

$$\begin{aligned} {\mathbf {X}} = \left( \begin{array}{ccccc} x_{11} &{}\quad x_{12} &{}\quad \ldots &{}\quad x_{1m} \\ x_{21} &{}\quad x_{22} &{}\quad \ldots &{}\quad x_{2m} \\ \vdots &{}\quad \vdots &{}\quad \cdots &{}\quad \vdots \\ x_{n1} &{}\quad x_{n2} &{}\quad \ldots &{}\quad x_{nm} \\ \end{array} \right) ,\quad {\mathbf {h}} = \left( \begin{array}{c} h_1\\ h_2\\ \vdots \\ h_n\\ \end{array} \right) \end{aligned}$$

be the representation for the income-household aggregated data reporting in the form (1) and ranked accordingly as (2), and let $\{p_j\}_{j= 1, 2,\ldots , n}$, and T be defined, in turn, by formula (3) and (4). Then, the Gini index for ${\mathbf {X}}$ associated with ${\mathbf {h}}$ is given by  $G =\varvec{\eta }^\intercal {\varvec{\Theta }}$, where ${\varvec{\eta }}=T^{-1}\mathbf {X}^\mathbf {\intercal } \mathbf {h}$ and

$$\begin{aligned} {\varvec{\Theta }}={\text {diag}}\left( (\mathbf {X}^{\mathbf {\intercal }} \mathbf {h})^{-1}_1, \mathbf {(X}^\mathbf {\intercal } \mathbf {h)}^{-1}_2,\ldots , \mathbf {(X}^\mathbf {\intercal } \mathbf {h)}^{-1}_m \right) \mathbf {X}^\mathbf {\intercal }\,diag \left( \mathbf {T p - 1}_n \right) \, {\mathbf {h}} \end{aligned}$$

respectively, where ${\mathbf {1}}_{n} = (\overbrace{1, 1, \ldots , 1}^{n\text {-tuple}})^\intercal$ is a vector of n entries all one, ${\mathbf {T}}$ is an $n\times n$ Toeplitz matrix given by

$$\begin{aligned} {\mathbf {T}} = \left( \begin{array}{rrrrr} 1 &{}\quad &{}\quad &{}\quad &{}\quad 0\\ 1 &{}\quad 1 &{}\quad &{}\quad &{}\quad \\ &{}\quad \ddots &{}\quad \ddots &{}\quad 1 &{}\quad \\ 0 &{}\quad &{}\quad \ddots &{}\quad 1 &{}\quad 1 \\ \end{array} \right) _{n\times n} \quad \text {and} \quad {\mathbf {p}} = \left( \begin{array}{c} p_1\\ p_2\\ \vdots \\ p_n\\ \end{array} \right) . \end{aligned}$$

Here the matrix transposition $\mathbf {X}^\mathbf {\intercal }$ can be interpreted as the income distribution matrix since its action on the household vector produces a vector of the total income components. We call $\mathbf {\eta }$ and $\varvec{\Theta }$ the income distribution vector and the income centralization index vector, respectively. The interpretations of their components will be given in Sect. 3, which is mainly devoted to a detailed discussion about the principle result that supports the above theorem by the following key lemma.

Lemma 1

(Gini Decomposition) The Gini index for ranked aggregated data (1) is given by $G = \sum ^m_{k=1}\varPhi _k$ and

$$\begin{aligned} \varPhi _k= & {} \frac{1}{T}\sum ^n_{j=1}x_{jk}h_j\left( p_j+p_{j-1} - 1\right) , \end{aligned}$$

(5)

where the percentile level for each associated group $\{p_j\}_{j=0, 1, 2,\ldots , n}$, with $p_0=0$, and the total combined income T, are given by (3) and (4), respectively.

To see other significant and interpretable forms of the Gini decomposition as an immediate consequence from the theorem and lemma above, we additionally introduce the following pieces of notation.

$$\begin{aligned} \mathbf {P_{\!+}} = \text {diag} \left( 0, p_1, \ldots , p_{n-1} \right) \quad \text {and}\quad \mathbf {P_{\!-}}= \text {diag} \left( p_{1}-1, p_{2}-1,\ldots , p_{n}-1\right) \end{aligned}$$

We also need the factor index vector $\varvec{\Phi } = (\varPhi _k)_{k=1,\ldots , m}$. In addition to previously formed definitions, we will use all components of the mean income vector $\mathbf {{\overline{x}}}=({\overline{x}}_k)_{k=1, 2, \ldots , m}$, which is defined by ${\overline{x}}_k = T_k/N$, where

$$\begin{aligned} T_k = \sum ^n_{i=1}x_{ik}h_i \end{aligned}$$

(6)

($T = T_1+T_2+\cdots +T_m$). Lastly, we define the household distribution vector as

$$\begin{aligned} {\mathbf {h}}_N = N^{-1}{\mathbf {h}} . \end{aligned}$$

(7)

These notations shall easily help us simplify and interpret the expression of the Gini decomposition in the following corollary.

Corollary 1

(Matrix Representation of Factors) The matrix form of (5) can be written $\varvec{\Phi }= \varvec{\Phi }^+ + \varvec{\Phi }^-$ where

$$\begin{aligned} \varvec{\Phi }^+= T^{-1}\mathbf {X}^\mathbf {\intercal }\mathbf {P_{\!+}}{\mathbf {h}} \quad \text {and}\quad \varvec{\Phi }^-=T^{-1}\mathbf {X}^\mathbf {\intercal }\mathbf {P_{\!-}}{\mathbf {h}}. \end{aligned}$$

(8)

That is, $\varvec{\Phi } = T^{-1} \mathbf {X}^\mathbf {\intercal }(\mathbf {P_{\!+}} + \mathbf {P_{\!-}}){\mathbf {h}}$. Furthermore, the income distribution vector and the centralization index vector are $\mathbf {\eta } = \left( T_k/T\right) _{k=1, 2,\ldots , m}$ and

$$\begin{aligned} \varvec{\Theta }= diag \left( {\overline{x}}^{-1}_1, {\overline{x}}^{-1}_2, \ldots , {\overline{x}}^{-1}_m \right) \mathbf {X}^\mathbf {\intercal } \mathbf {(P_{\!+} +P_{\!-})\, h}_N, \end{aligned}$$

(9)

respectively for the Gini index $G =\varvec{\eta }^\intercal \varvec{\Theta }$.

We call the matrix sum $\mathbf {P_+ +P_-}$ the percentile income splitting matrix acting on a household vector or a household distribution vector as shown from relation (8) and (9). This results in separating the factor vector $\varvec{\Phi }$ into two parts $\varvec{\Phi }^{\pm }$ for widening and narrowing effect respectively on the measure of the total inequality.

We remark that ${\mathbf {h}}_N$ and $\varvec{\eta }$ are examples of a distribution vector as its components add up to 1 in the theory of applied linear algebra (Bretscher 2013). It is interesting to see how they appear in the decomposition of the Gini index.

2.2 Proof of the main result

As we mentioned earlier, a Lorenz curve is derivable from a set of income data.

The proof of our main result is based on constructing the Lorenz curve L(p). The domain of L is the range of percentile variable p, which can be interpreted as a random variable P equipped with the probability density function $L'(p)$. The probability connection between the Gini index and the expected value ${\overline{P}}$ has been established by Farris (2010), which can be delivered by the following proposition.

Proposition 1

Let G be the Gini index of the Lorenz curve L(p) and let $s(p)=L'(p)$ (almost everywhere) be the probability density function (pdf) for the continuous percentile random variable. Then the expected value of this random variable

$$\begin{aligned} {\overline{P}} = \int ^1_0 p\, s(p)\, dp \end{aligned}$$

is related by

$$\begin{aligned} G=2{\overline{P}} -1. \end{aligned}$$

(10)

It is evident that formula (10) gives another approach to the Gini index once the pdf, s(p), is established. This is what we need for the proof the Gini decomposition Lemma 1 in the sequel. Using this connection, we define the kth income share density function on the interval of ith percentile

$$\begin{aligned} s_{jk}(p)= \frac{x_{jk}}{T/N}~\chi _{(p_{j-1},\,\, p_j]}(p) \end{aligned}$$

(11)

using the percentile variable p and the characteristic function of any subset E of real numbers

$$\begin{aligned} \chi _E(p) = \left\{ \begin{array}{ll} 1 &{}\quad \text {if}~ p\in E\\ 0 &{}\quad \text {if}~p\notin E \\ \end{array} \right. . \end{aligned}$$

This tells us what share of the whole is owned by the portion of the population from the k-source of income that falls in the percentile range $(p_{j-1}, p_j]$.

We now start the proofs of Lemma 1, Theorem 1 and Corollary 1.

Proof

(Gini Decomposition: Lemma 1) By establishing the function correspondence from $\{p_0,~ p_1, \ldots ,~ p_n\}$ to the fraction of the total income earned by each poorest fraction $p_j$, imposing $L(p_0)= 0$, the Lorenz curve at these values can be calculated as follows.

$$\begin{aligned} L(p_j) = \frac{1}{T}\sum ^m_{k=1}\sum ^j_{i=1}x_{ik} h_i, \quad \text {for}\quad j = 1, 2, \ldots , n \end{aligned}$$

(12)

To maintain the convexity of L, the easiest way to extend the correspondence from each interior of percentile range $[p_{j-1}, p_j]$ to a suitable fraction of the total is by linear interpolation, assuming that $L'(p)$ is piecewise constant on each percentile range. (In economic terms, the assumption says that share density, which will be defined and made clear in the sequel, is piecewise fixed in each income bracket).

The convexity of this function can be made clear once the double sum in formula (12) is expressed in terms of p. Noting that the number of households at percentile $p_i$ can be written as

$$\begin{aligned} h_i=(p_i-p_{i-1})N~ \end{aligned}$$

(13)

from relation (3), we now reexpress L function (12) as follows.

$$\begin{aligned} L(p_j)=\sum ^m_{k=1}\sum ^j_{i=1}\frac{x_{ik}}{T/N} ~(p_i - p_{i-1}) \end{aligned}$$

(14)

Quantity T/N is a weighted row-average of $x_{ik}$ in $h_i$ and can be labelled as the average income owned throughout the population. The total density function on (0, 1], using (11), can be defined as

$$\begin{aligned} s(p)= \sum ^m_{k=1} \sum _{i=1}^n s_{ik}(p). \end{aligned}$$

The i-summation can be viewed as the kth component of s(p) with respect to the income source. Thus the inner sum of $L(p_j)$ from (14) is precisely a Riemann sum of this component over $[0,~ p_j]$ and thus, we have

$$\begin{aligned} L(p_j)=\sum ^m_{k=1}\int ^{p_j}_{0} \sum _{i=1}^n s_{ik}(p) ~ dp. \end{aligned}$$

Switching the (easily justified) order of k-summation and integration, we obtain the integral representation of (14).

$$\begin{aligned} L(p_j)=\int ^{p_j}_{0} s(p) ~ dp \end{aligned}$$

(15)

The geometric significance of such representation is that the convexity of function L(p) is immediately established by the standard criteria of midpoint convexity, Rudin (1987), due to the nondecreasing nature of s(p), which is guaranteed by our assumption (2). Another analytic significance of (15) is that $s(p)=L'(p)$ almost everywhere, which we will need in what follows.

We are now in the position to apply Proposition 1, which gives an alternative way of computing the Gini index. Our computation rests on finding ${\overline{P}}$. It follows, by switching the order of summations and integration associated with relation (10), that

$$\begin{aligned} {\overline{P}}= & {} \int ^1_0 p\, \left( \sum ^m_{k=1} \sum _{i=1}^n s_{ik}(p)\right) dp\\= & {} \sum ^m_{k=1} \sum _{i=1}^n \int ^1_0 \frac{x_{ik}}{T/N}\chi _{(p_{i-1},\,\, p_i]}(p)\, p\, dp\\= & {} \sum ^m_{k=1} \sum _{i=1}^n \frac{x_{ik}}{T/N} \int ^{p_{i}}_{p_{i-1}} p\, dp\\= & {} \sum ^m_{k=1} \sum _{i=1}^n \frac{x_{ik}}{T} \frac{p_{i}+p_{i-1}}{2}\,h_i.\\ \end{aligned}$$

The last equality follows from the use of relation (13). Inserting this into (10) and make use of the definition of T, we obtain the following Gini index formula.

$$\begin{aligned} G= & {} \sum ^m_{k=1} \left( \frac{1}{T}\sum _{i=1}^n {x_{ik}} (p_{i}+p_{i-1}) \, h_i \right) - 1\nonumber \\= & {} \sum ^m_{k=1} \left( \frac{1}{T}\sum _{i=1}^n {x_{ik}h_i} (p_{i}+p_{i-1}-1) \, \right) \end{aligned}$$

(16)

The parenthesized expression from the last equality is precisely $\varPhi _k$ for the Gini index decomposition. This completes the proof of Lemma 1. $\square$

To prove Theorem 1, some standard notations about matrices are employed. For a matrix A with entries $a_{ij}$, we write

$$\begin{aligned} {\mathbf {A}} = (a_{ij}) \quad \text {or}\quad ({\mathbf {A}})_{ij} = a_{ij}. \end{aligned}$$

Similarly for a column vector v with entries $v_k$, we write

$$\begin{aligned} {\mathbf {v}} = (v_k) \quad \text {or}\quad ({\mathbf {v}})_k = v_k. \end{aligned}$$

The proof of the various matrix forms of our main result is as follows.

Proof

(Matrix Representation of Gini Decomposition: Theorem 1) First, we notice that for $k=1,\ldots , m$, the k-component of T defined by (6) can be written as

$$\begin{aligned} T_k = \left( \mathbf {X}^\mathbf {\intercal } \mathbf {h}\right) _k \end{aligned}$$

($T = T_1+T_2+\cdots +T_m$). Also, it is straightforwardly verifiable that the corresponding entries of vector $((p_{i}+p_{i-1}-1)h_i)$ and the diagonal matrix $\text {diag} \mathbf {(Tp - 1}_\mathbf {n})\mathbf {h}$ are equal. Simply put.

$$\begin{aligned} (p_{i}+p_{i-1}-1)h_i = \left( \text {diag} (\mathbf {Tp - 1}_\mathbf {n})\mathbf {h} \right) _i \end{aligned}$$

Using these relations, it follows from Lemma 1 that

$$\begin{aligned} G= & {} \sum ^m_{k=1} \frac{T_k}{T}\sum _{i=1}^n \frac{x_{ik}}{T_k}~ (p_{i}+p_{i-1}-1)h_i\\= & {} \sum ^m_{k=1} \frac{T_k}{T}\sum _{i=1}^n \left( \text {diag}( T_1^{-1}, T_2^{-1}, \ldots , T_m^{-1}) \mathbf {X}^\mathbf {\intercal }\right) _{ki} \left( \text {diag} (\mathbf {Tp - 1}_\mathbf {n})\mathbf {h} \right) _i\\= & {} \sum ^m_{k=1} \left( T^{-1}\mathbf {X}^\mathbf {\intercal } \mathbf {h}\right) _k \left( \text {diag}( T_1^{-1}, T_2^{-1}, \ldots , T_m^{-1}) \mathbf {X}^\mathbf {\intercal }(\text {diag} (\mathbf {Tp - 1}_\mathbf {n})\mathbf {h} \right) _k\\= & {} \left( T^{-1}\mathbf {X}^\mathbf {\intercal } \mathbf {h}\right) ^\intercal \text {diag}( T_1^{-1}, T_2^{-1}, \ldots , T_m^{-1})\, \mathbf {X}^\mathbf {\intercal } \text {diag} (\mathbf {Tp - 1}_\mathbf {n})\mathbf {h} \end{aligned}$$

as desired. This completes the proof of Theorem 1. $\square$

We now prove the corollary to conclude this section.

Proof

(Matrix Representation of Factors: Corollary 1) First, we observe the relation.

$$\begin{aligned} \left( p_j+p_{j-1} - 1\right) h_j= & {} p_{j-1}h_j + (p_j - 1)h_j\\= & {} ( \mathbf {P_{\!+}}{\mathbf {h}})_j + (\mathbf {P_{\!-}}{\mathbf {h}})_j \end{aligned}$$

It follow from Lemma 1 that formula (5) can be written as follows.

$$\begin{aligned} \varPhi _k= & {} \frac{1}{T}\sum ^n_{j=1}x_{jk}( \mathbf {P_{\!+}}{\mathbf {h}})_j + x_{jk}(\mathbf {P_{\!-}}{\mathbf {h}})_j\\= & {} (T^{-1}\mathbf {X^\intercal }\mathbf {P_{\!+}}{\mathbf {h}})_k + (T^{-1}\mathbf {X^\intercal }\mathbf {P_{\!-}}{\mathbf {h}})_k\\= & {} (\varvec{\Phi }^+)_k + (\varvec{\Phi }^-)_k \end{aligned}$$

That is required for $\varvec{\Phi }= \varvec{\Phi }^+ + \varvec{\Phi }^-$. Next, the following is easily checked.

$$\begin{aligned} \text {diag} (\mathbf {T p - 1}_n) = \mathbf {P_{\!+}}+ \mathbf {P_{\!-}} \end{aligned}$$

It follows from Theorem 1 and relation (7) that

$$\begin{aligned} \varvec{\Theta }= & {} N~\text {diag}\left( (\mathbf {X}^{\mathbf {\intercal }} \mathbf {h})^{-1}_1, \mathbf {(X}^\mathbf {\intercal } \mathbf {h)}^{-1}_2,\ldots , \mathbf {(X}^\mathbf {\intercal } \mathbf {h)}^{-1}_m \right) \mathbf {X}^\mathbf {\intercal }\,\left( \mathbf {P_{\!+}}+ \mathbf {P_{\!-}} \right) \, {\mathbf {h}}_N\\= & {} \text {diag}\left( (N^{-1}\mathbf {X^\intercal h)}^{-1}_1, (N^{-1}\mathbf {X^\intercal h)}^{-1}_2,\ldots , (N^{-1}\mathbf {X^\intercal h)}^{-1}_m \right) \mathbf {X}^\mathbf {\intercal }\,\left( \mathbf {P_{\!+}}+ \mathbf {P_{\!-}} \right) \, {\mathbf {h}}_N\\= & {} \text {diag}\left( {\overline{x}}^{-1}_1, {\overline{x}}^{-1}_2,\ldots , {\overline{x}}^{-1}_m \right) \mathbf {X}^\mathbf {\intercal }\,\left( \mathbf {P_{\!+}}+ \mathbf {P_{\!-}} \right) \, {\mathbf {h}}_N, \end{aligned}$$

as desired. Finally, it follows from the definition (6) that $T_k=(\mathbf {X}^\mathbf {\intercal } \mathbf {h})_k$. Hence $\eta _k = T_k/T$ by Theorem 1, which is required for the proof of Corollary 1.$\square$

3 Some consequences of the main result

It is worthy noting formula (5) of Lemma 1 as a fundamental result of this paper, for which several interpretations may be made. We shall call $\varPhi _k$ the kth decomposition factor of the Gini index. It involves the quantity $p_j+p_{j-1} - 1$, whose role can be realized as a balancing act between equalizing and unequalizing effect from the jth income bracket towards the total inequality. More precisely, each summand of $\varPhi _k$ indicates the total $x_{jk}h_j$ in jth income bracket from income source k relative to the total income T makes two contributions to the total inequality: one being of positive determined by the fraction from the bottom $p_{j-1}$ income class, and the other being of negative determined by the fraction from the upper $(1-p_j)$ income class. Symbolically, the two parts and the kth factor are denoted as follows and diagramed in Fig. 1b.

$$\begin{aligned} F_{jk}^+= & {} \frac{x_{jk}h_j p_{j-1}}{T}, \quad F_{jk}^- = - \frac{x_{jk}h_j (1-p_{j})}{T}\nonumber \\ \varPhi _k= & {} \sum ^n_{j=1} \left( F_{jk}^+ +F_{jk}^- \right) \end{aligned}$$

(17)

So, formula (17) succinctly indicates that decomposition factor $\varPhi _k$ is the sum of the net contribution from $F_{jk}^+$ and $F_{jk}^-$ over each income bracket from source k in the total income T. It may, therefore, be labelled as the absolute contribution factor from income source k to overall inequality. It provides an unequalizing effect if $\varPhi _k > 0$ and equalizing effect if $\varPhi _k < 0$. A large value of $\varPhi _k$ suggests that it is an important source of the total inequality by the Gini index.

To get a glimpse of various structural perspectives for the total inequality, we now give some consequences of Gini decomposition, noting that relation (5) can be rewritten as

$$\begin{aligned} \varPhi _k = \frac{T_{k}}{T}\sum ^n_{j=1}\frac{x_{jk}h_j}{T_k}~\left( p_j+p_{j-1} - 1\right) . \end{aligned}$$

(18)

Quantity $T_{k}/T$ is the share of the kth income in the total income. The summation part in (18), comparing with a single income case of Lemma 1, may be regarded as a generalized Gini index. In fact, it reduces to the usual (local) Gini index if the k-source income reporting happens to be ordered in accordance with the general assumption (2) for the totals of income brackets. The sign of this summation also indicates a widening or narrowing effect on the total inequality. We call this summation the factor centralization ratio (index) of the kth income component $\varTheta _k$.

In view of formula (18), the upshot is that the Gini index can be termed as a weighted average of factor centralization ratios of all income components, equipped with the weights being the share of all income components in the total income. In symbols, it can be represented below.

$$\begin{aligned} G = \sum ^m_{k=1}\eta _k\varTheta _k \end{aligned}$$

(19)

Interestingly, a slightly different form of (18) may be expressed as

$$\begin{aligned} \varPhi _k = \frac{T_{k}}{T}\sum ^n_{j=1}\frac{x_{jk}h_j}{T_k}\left( 2p_j-\frac{h_j}{N} - 1\right) , \end{aligned}$$

(20)

where the positive contribution of the kth factor to the Gini index is determined by the fraction $(p_{j} - h_{j}/N)$, which gives the deviation of the percentile level from the proportion of the associated household size in the population total. Furthermore, the advantage of such expression of $\varPhi _k$ is that the factor centralization ratio of the kth income component, the summation in (20), can be written as

$$\begin{aligned} \frac{2}{T_k}\left\{ \sum ^n_{j=1}{x_{jk}h_j}p_j-\sum ^n_{j=1}{x_{jk}h_j}~\frac{1}{2}\left( \frac{h_j}{N} + 1\right) \right\} . \end{aligned}$$

The quantity in the braces resembles a covariance between $\{x_{jk}h_j\}$ and $\{p_j\}$ modulo n. When data is disaggregated $N=n, ~~h_j=1$ and $p_j = j/n$, the kth decomposition factor by formula (20) is reduced to the following

$$\begin{aligned} \varPhi _k = \frac{2}{T/n}~ \mathbf{covariance }(\{x_{jk}\},~ \{j/n\}) \end{aligned}$$

since

$$\begin{aligned} \frac{1}{2}\left( \frac{1}{n} + 1\right) = \frac{1}{n}~\sum _{j=1}^n \frac{j}{n}. \end{aligned}$$

When the correlation between income from source k and its income level, $\{j/n\}$, is positive or negative, the kth component of the factor has unequalizing or equalizing influence on the total inequality accordingly. It is also evident that this can be written as

$$\begin{aligned} \varPhi _k = \frac{2}{T}~ \mathbf{covariance }(\{x_{jk}\},~ \mathbf{rank }\{x_{jk}\}) \end{aligned}$$

where $\mathbf{rank }\{x_{jk}\}$ yields the rank for j from 1 to n. Given that rank function is implemented, this may be computationally practical without assumption (2). In particular, $\mathbf{rank }\{x_{jk}\} = \{j\}$ when $\{x_{jk}\}$ is already ordered or with assumption (2). Likewise, the correlation can be termed between $\{x_{jk}\}$ and $\{j\}$ as above for the equalization analysis. One can analyze the scatter diagrams over four quadrants determined by $j=(n+1)/2$ and the kth component of the mean income ${\overline{x}}_k$ section by section (as $k=1, 2, \ldots , m$) for the effect of $\varPhi _k$ on total inequality.

Finally, we mention that $\varPhi _k$ can be termed in terms of income share density function. It follows from formula (11) that

$$\begin{aligned} \varPhi _k = 2~ \mathbf{covariance }(\{s_{jk}\},~ ~ \{j/n\}) \end{aligned}$$

with which we can express the Gini index for disaggregated data in terms of the covariance between the income levels and the local share density functions.

$$\begin{aligned} G = 2~ \mathbf{covariance }\left( \left\{ \sum _{k=1}^m s_{jk}\right\} ,~ ~ \left\{ \frac{j}{n} \right\} \right) \end{aligned}$$

As above, an alternative way of equalization analysis on $\varPhi _k$ can be done section by section using the scatter diagram between $\{s_{jk}\}$ and $\{j/n\}$.

Notably, the parallelism between this formula and the definition of the Gini index by the appearance of the scaling factor 2 appeals to a sense of mathematical elegance.

4 Numerical illustration

As we have deduced all matrix formulas from Gini Decomposition lemma, it is enough to demonstrate the use of formula (5). We point out that the matrix formula either from Theorem 1 or Corollary 1 can be straightforwardly implemented to simply obtain all components of the Gini decomposition when appropriate mathematical software (say Matlab) is available. However, we will give numerical examples for computing and contrasting the factors $\varPhi _k$ using Lemma 1, in which formula (5) can be easily translated into an algorithm and implemented using readily accessible R-package.

Even though a use of Matlab is not presented here for the Gini decomposition and is left for the reader to explore, we actually use Matlab to confirm our results obtained by running the R-code, whose listing is provided as a standalone function in Fig. 5.

To squeeze the most out of the factors, we additionally define and compute the k-source proportion factor by

$$\begin{aligned} \phi _k = \frac{\varPhi _k}{G}, \end{aligned}$$

(21)

which will be a part of the Gini decomposition reporting. In fact, $0 \le \phi _k \le 1$ and that $\phi _k$ closer to 1 (or 0) indicates that the influence of k-source of income on the total inequality is stronger (or weaker).

4.1 Example (single source of income)

Our first example uses the algorithm for the extreme case ($m=1$ and $h_i>1$: an aggregated income reporting from a single source of income). In this case $G=\varPhi _1$ or $\phi _1=1$ and the Gini index is only what we need to compute for the following dataset.

Table 1 U.S. family income from all races in 2017

Table 1 is a partial display of real data from the IRS (2017) government website. Using the R-code (in Fig. 5), we obtain the Gini index $G=0.4425$ for the U.S. family income distribution from all races in 2017.

The point of this illustration is to show how the Gini index can be conveniently obtained when the data is reported aggregately even from a single income source. In this case, the reduced form of formula (5) can also be favorable for entering into spreadsheet with Excel technology, which we purposely use to check the correctness for this essential boundary case of our R-code.

4.2 Example (multiple sources of income)

We now calculate another boundary case ($h_i = 1~ \text {and} ~m > 1$) for disaggregated multiple sources of income reporting, which often appears especially when individuals are reported as countries or states. We download the data from online publication of European income components of households for 36 countries (EUR Data 2014). Table 2 contains a partial listing of the dataset, for which the Gini index is computed to be $G=0.3658$. All factors with relevant components are in turn outputted by the algorithm and recorded in Table 3. In particular, we see the income component pension has the largest inequality (with a generalized Gini index $\varTheta _2=03903$), but the total pension is of only 28.62% in the total income. All income components have widening effect on the total inequality in various magnitudes, since all associated factors are positive.

As we mentioned, the factor centralization ratio $\varTheta _k$ may be regarded as a generalized factor Gini index. It may become the local (factor) Gini index if the factor income happens to be ranked by $x_{ik} \le x_{jk}$ whenever $i < j$ for a particular k (source of income). But this is not guaranteed since the total inequality is based on the total income (and the income brackets, if $h_i > 1$). None appears to be a local Gini index for this dataset, since no income component is ranked in accordance with the gross income.

Table 2 European family income components of households in 2014 (in EUR)

Table 3 Decomposition results: income share $\eta _k$, factor centralization ratio $\varTheta _k$, absolute factor $\varPhi _k$, and proportional factor $\phi _k$ for the dataset Table 2

4.3 Example (aggregated multiple sources of income)

As of this writing, we have not yet found a suitable source of real data reported exactly in the form (1) with $h_i> 1 \text { and } ~ m > 0$. Perhaps it may require a sort of construction to settle the final form for applicability of our algorithm. This is practically not difficult to achieve, when several sources of data reporting become available. For instance, we could reformat the data in Table 2 from our previous example by defining a new set of income brackets so as to run the code to perform Gini decomposition by sources of income.

Table 4 European family income components of households from the five income brackets in 2014 (in EUR)

The Gini index is calculated to be 0.3526 and the factors with associated components are displayed in Table 5. It is evident that the corresponding Gini decomposition data in Table 3 are indeed slightly less than or equal to those in Table 5. This is due to the fact that the associated Lorenz curve is supported by more points from Table 2 than that by those from Table 4. Thus, the resulting Gini index (0.3558) for Table 2 is expected to be slightly larger than that (0.3526) for Table 4. Moreover, the Gini decomposition for the reformatted dataset Table 4 inherits the widening effect of all income components of dataset Table 2. In other words, this scenario does not produce any negative decomposition factor $\varPhi _k$, as expected.

Table 5 Decomposition results: income share $\eta _k$, factor centralization ratio $\varTheta _k$, absolute factor $\varPhi _k$, and proportional factor $\phi _k$ for the dataset Table 4

In general, there is no reason to believe that a factor is always positive because the associated factor centralization ratio $\varTheta _k$ may be negative. As we mentioned that $\varTheta _k$ can be regarded as a generalized local Gini index. It reduces to a local Gini index only if the k source of household incomes are ranked in the same order as household gross income $T_k$.

To make a point for an occurrence of $\varTheta _k < 0$, we use a hypothetical data set Table 6, in which rows are put in a desirable order by form (1). There are, for instance, five income sources: wage income, capital income, transfer income, self-employment income, and special income from the economic data reporting. One way to see such a situation happening is to allow the low-income bracket household to receive a special income through a government program (such as the economic stimulus checks were issued for low income families in the U.S. during the outbreak of COVID-19 lock-down period in 2020), and no such income recipient has family income above a certain upper-income bracket.

Table 6 A hypothetical data for an aggregated family income in thousands from five sources

Table 7 Decomposition results income share $\eta _k$, factor concentration ratio $\varTheta _k$, absolute factor $\varPhi _k$, and proportional factor $\phi _k$ for the dataset Table 6

Running the Gini decomposition R-code in Fig. 5, we obtain the Gini index $G=0.2283$ from the output in Fig. 4. Various preliminary and finer decomposition results of G (factors $\varPhi _k$, proportion factors $\phi _k$, the share of the incomes in the total income $\eta _k$, and the factor centralization ratios $\varTheta _k$) are computed and recorded in Table 7 for further structural analysis of income inequality.

We now conclude with some analysis and interpretation of these results. First, the wage income has the most contribution to unequalizing (widening) effect on the overall income inequality according to the associated factor contribution 0.2149 (being most positive). Only the special income has an equalizing effect due to a negative contribution of the associated factor $-0.0049$. So, a large value of $\varPhi _k$, associated with wage income in this case, suggests that it is an important source of the total inequality. The same can be said for the proportional factor of wage income $\phi _k$. Likewise, one can reach a conclusion for the special income from the equalizing perspective. Finally, the capital income has the largest factor centralization ratio 0.3387, but the smallest income share 0.0085. A reader may wish to draw further analysis as to how the Gini index decomposition sheds light on both the structure and dynamics of income inequality. We believe that these results, computed and plotted in times for multiple years, can be of interest to economists.

4.4 Matrix illustration of Gini decomposition

In this section, we continue to use the hypothetical dataset Table 6 to display the matrix structure for the Gini index decomposition by income source. It is only a numerical illustration of Theorem 1 and Corollary 1 to give an aesthetic beauty of the matrix structure for income inequality. We start with the income matrix and the household vector representations for the dataset Table 6:

$$\begin{aligned} \mathbf{X } =\left( \begin{array}{crccc} 1020.121&{}\quad 8.086&{}\quad 234.848&{}\quad 19.223&{}\quad 65.007\\ 1300.232&{}\quad 9.438&{}\quad 287.614&{}\quad 29.082&{}\quad 58.878\\ 2100.445&{}\quad 14.2&{}\quad 317.534&{}\quad 21.438&{}\quad 50.136\\ 2311.398&{}\quad 16.04&{}\quad 344.556&{}\quad 35.844&{}\quad 63.868\\ 2799.069&{}\quad 38.195&{}\quad 386.723&{}\quad 60.902&{}\quad 0\\ 2964.355&{}\quad 31.242&{}\quad 292.011&{}\quad 36.902&{}\quad 0\\ 5071.598&{}\quad 56.548&{}\quad 533.180&{}\quad 66.385&{}\quad 0\\ \end{array} \right) \quad \text {and}\quad \mathbf{h } =\left( \begin{array}{c} 24410\\ 27492\\ 31633\\ 31952\\ 32291\\ 31664\\ 31519\\ \end{array} \right) . \end{aligned}$$

Using formulas (3) and (4), we get $N=210961$, $T=638852082$, and all values of the percentile. By definition, we obtain the percentile vector and the associated diagonal matrices for Corollary 1 as follows:

$$\begin{aligned} \mathbf{p } =\left( \begin{array}{c} 0.116 \\ 0.246 \\ 0.396 \\ 0.547 \\ 0.700 \\ 0.851 \\ 1.000 \\ \end{array} \right) , \quad \mathbf{P }_{\!+} = \text {diag} \left( \begin{array}{c} 0\\ 0.116 \\ 0.246 \\ 0.396 \\ 0.547 \\ 0.700 \\ 0.851 \\ \end{array} \right) , \quad \mathbf{P }_{\!-} = \text {diag} \left( \begin{array}{c} -0.884 \\ -0.754 \\ -0.604 \\ -0.453 \\ -0.300 \\ -0.149 \\ 0\\ \end{array} \right) . \end{aligned}$$

Using formula (8), we obtain the “canonical” factor decomposition of vector $\varvec{\Phi }$ as follows:

$$\begin{aligned} \varvec{\Phi } = \left( \begin{array}{r} 0.2149\\ 0.0029\\ 0.0128\\ 0.0026\\ -0.0049\\ \end{array} \right) ,\quad \varvec{\Phi }^+ = \left( \begin{array}{c} 0.4710 \\ 0.0051 \\ 0.0553 \\ 0.0069 \\ 0.0022 \\ \end{array} \right) , \quad \varvec{\Phi }^- = \left( \begin{array}{c} -0.2561 \\ -0.0022 \\ -0.0426 \\ -0.0042 \\ -0.0071 \\ \end{array} \right) . \end{aligned}$$

Indeed, the sum of the components of factor $\varvec{\Phi }$ produces the Gini index $G=\sum \varPhi _k = 0.2283$ (also by Lemma 1). Now, for this illustration, we use formula (9) for the factor centralization index vector $\varvec{\Theta } = (\varTheta _k)_{k=1, 2,\ldots , 5}$ from Corollary 1, which has a more simpler as well as interpretable representation:

$$\begin{aligned} \varvec{\Theta }= \text {diag}\left( {\overline{x}}^{-1}_1, {\overline{x}}^{-1}_2, \ldots , {\overline{x}}^{-1}_5 \right) \mathbf {X}^\mathbf {\intercal } \mathbf {(P_{\!\!+} +P_{\!\!-})\, h}_N. \end{aligned}$$

The diagonal matrix can be constructed using formula (6) or $x_k = \mathbf {(X}^\mathbf {\intercal } \mathbf {h)}_k$, where $k=1, 2,\ldots , 5$. We obtain all vectors needed for the Gini decomposition:

$$\begin{aligned} \mathbf {{\overline{x}}} = \left( \begin{array}{r} 2583.6\\ 25.7\\ 347.1\\ 39.4\\ 32.4\\ \end{array} \right) , \quad \mathbf {\eta } = \left( \begin{array}{r} 0.8531\\ 0.0085\\ 0.1146\\ 0.0130\\ 0.0107\\ \end{array} \right) , \quad \mathbf {\Theta } = \left( \begin{array}{r} 0.2519\\ 0.3387\\ 0.1113\\ 0.2017\\ -0.4566\\ \end{array} \right) . \end{aligned}$$

Indeed, we also have that Gini index $G=\varvec{\eta }^\intercal \varvec{\Theta } = 0.2283$, as desired for Corollary 1,

Finally, for a less interpretable but structurally interesting matrix of the Gini decomposition, we have

$$\begin{aligned} {\varvec{\Theta }}=\text {diag}\left( x^{-1}_1, x^{-1}_2,\ldots , x^{-1}_7 \right) \mathbf {X}^\mathbf {\intercal }\, \text {diag}\left( \mathbf {T p - 1}_7 \right) \, {\mathbf {h}} \end{aligned}$$

where ${\mathbf {1}}_{7} = (1, 1, 1, 1, 1, 1, 1)^\intercal$ and ${\mathbf {T}}$ is a Toeplitz matrix

$$\begin{aligned} {\mathbf {T}} = \left( \begin{array}{rrrrrrr} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 1\\ \end{array} \right) \end{aligned}$$

as required for Theorem 1. This operator acting on the percentile variable to extract the percentile range related values for seven income brackets, which in general plays a crucial role for the income decomposition. More exactly, its action in part splits the bracket income total into parts for contributions to equalizing and unequalizing the income inequality.

5 Density matrix and Lorenz curve

In this section, we present two alternative and interpretable matrix forms of factor $\varvec{\Phi }$ appeared in Corollary 1. The purpose is to establish a matrix representation of the associated Lorenz curve. The significance of understanding the structure of Lorenz curve can give insights to improve the Gini index.

5.1 Density matrix for factor

Using the share density functions (11), we define the associated density matrix $\mathbf{S } = (s_{jk})_{j=1, 2, \ldots , n;~k=1,\ldots , m}$. A slightly different form of the matrix equation (9) may be induced by (18), giving another perspective for the structure of income inequality:

$$\begin{aligned} \varvec{\Phi } = \mathbf {S^\intercal }\mathbf {P_{\!+}}{\mathbf {h}}_N + \mathbf {S^\intercal } \mathbf {P_{\!-}} {\mathbf {h}}_N, \end{aligned}$$

(22)

where we notice that the percentile income splitting matrix is acting on the household proportion vector.

Likewise, with an emphasis on a generalized covariance between the share density and income brackets (20), we obtain yet another form:

$$\begin{aligned} \varvec{\Phi } = \mathbf {S^\intercal }({\mathbf {P}}-{\mathbf {H}}_N){\mathbf {h}}_N+\mathbf {S^\intercal P_{\!-}} {\mathbf {h}}_N, \end{aligned}$$

(23)

where the household proportion matrix and the percentile matrix are defined by the diagonal matrices:

$$\begin{aligned} {\mathbf {H}}_N=\text {diag}\left( \frac{h_1}{N}, \frac{h_2}{N},\ldots , \frac{h_n}{N}\right) \quad \text {and}\quad {\mathbf {P}}= \text {diag} \left( p_{1}, p_{2},\ldots , p_{n}\right) . \end{aligned}$$

Fig. 2

A bar graph of $\mathbf{S }$ for seven income brackets

Matrix equations (22) and (23) are displayed purposely to exhibit the two parts of vector $\varvec{\Phi }$, having the widening and narrowing effects on the total income inequality. Each results from the household proportion vector acting on the matrix composition of the transpose of density matrix S with household-percentile deviation matrix ${\mathbf {P}}-{\mathbf {H}}_N$ or an appropriate part of percentile income splitting matrix: $\mathbf {P_{\!+}}+\mathbf {P_{\!-}}$. In view of the integral (15), the appearance of S in these equations leads to investigating a matrix structure for the associated Lorenz curve.

5.2 Matrix representation of Lorenz curve

Now, if we consider a vector given by the values of Lorenz curve for the percentiles and denote $\mathbf {L}({\mathbf {p}})= (L(p_i))_{i=1, 2, \ldots , n}$, then using formula (14), we arrive at the matrix representation for the Lorenz curve

$$\begin{aligned} \mathbf {L}({\mathbf {p}})= & {} \sum ^m_{k=1} \overline{{\mathbf {S}}}_k \mathbf {{\overline{T}} \,p}, \end{aligned}$$

where the matrices in the matrix summation are respectively defined by

$$\begin{aligned} \mathbf {{\overline{S}}}_k = \left( \begin{array}{ccccc} s_{1k} &{}\quad &{}\quad &{}\quad &{}\quad 0 \\ s_{1k} &{}\quad s_{2k} &{}\quad &{}\quad &{}\quad \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad &{}\quad \\ s_{1k}&{}\quad s_{2k} &{}\quad \cdots &{}\quad s_{(n-1) k} &{}\quad \\ s_{1k} &{}\quad s_{2k} &{}\quad \cdots &{}\quad s_{(n-1) k} &{}\quad s_{nk} \\ \end{array} \right) \quad \text {and}\quad \mathbf {{\overline{T}}} = \left( \begin{array}{rrrrr} 1&{}\quad &{}\quad &{}\quad &{}\quad 0\\ -1 &{}\quad 1 &{}\quad &{}\quad &{}\quad \\ &{}\quad -1&{}\quad \ddots &{}\quad &{}\quad \\ &{}\quad &{}\quad \ddots &{}\quad 1 &{}\quad \\ 0 &{}\quad &{}\quad &{}\quad -1 &{}\quad 1 \\ \end{array} \right) _{n\times n}. \end{aligned}$$

Here the triangular matrix $\mathbf {{\overline{S}}}_k$ may be thought of as the kth component of the density distribution matrix, which is defined by

$$\begin{aligned} \mathbf {{\overline{S}}} = \mathbf {{\overline{S}}}_1 + \mathbf {{\overline{S}}}_2 \cdots + \mathbf {{\overline{S}}}_m, \end{aligned}$$

and $\mathbf {{\overline{T}}}$, which may be called the percentile range matrix, is a typical $n\times n$ Toeplitz matrix whose role is to measure the percentile range componentwise for all income brackets. They are all nonsingular and have the explicit inverses, with $\mathbf {{\overline{T}}}^{-1}$ being the lower triangular matrix of having all nonzero entries equal to 1, and

$$\begin{aligned} \mathbf {{\overline{S}}}^{-1} = \left( \! \begin{array}{rrcll} {\overline{s}}_{1}^{\,-1} &{}\quad &{}\quad &{}\quad &{}\quad 0 \\ -{\overline{s}}_{2}^{\,-1} &{}\quad {\overline{s}}_{2}^{\,-1} &{}\quad &{}\quad &{}\quad \\ &{}\quad -{\overline{s}}_{3}^{\,-1} &{}\quad {\overline{s}}_{3}^{\,-1}&{}\quad &{}\quad \\ &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad \\ 0&{}\quad &{}\quad &{}\quad -{\overline{s}}_{n}^{\,-1} &{}\quad {\overline{s}}_{n}^{\,-1} \\ \end{array}\right) \quad \text {where} \quad {\overline{s}}_j (p) = \sum ^{m}_{k=1} s_{jk}(p). \end{aligned}$$

Indeed, quantities $\{{\overline{s}}_1, {\overline{s}}_2, \ldots , {\overline{s}}_n\}$ are the local share density functions on the n percentile intervals respectively. We view these quantities as the components of the total density function with respect to the income bracket, since the total density function s(p) in Sect. 2.2 can be written as

$$\begin{aligned} s(p)=\sum ^n_{j=1} {\overline{s}}_j (p). \end{aligned}$$

It is notable that the inverse of the matrices $\mathbf {{\overline{T}}}$ and $\mathbf {{\overline{S}}}$ can be used for the determination of fractiles $\{p_1, p_2,\ldots , p_n\}$, provided any predetermined fraction of the incomes owned by the poorest fraction of the population. It is also notable that the density distribution matrix $\mathbf {{\overline{S}}}$ becomes $\mathbf {{\overline{T}}}^{-1}$ if it is induced by a uniform share density function. In this case, the resulting Lorenz curve reduces to the curve of perfect equatability $\mathbf {L}({\mathbf {p}})={\mathbf {p}}$.

Finally, using the density distribution and percentile range matrices, we obtain a decomposition of the Lorenz curve by income source

$$\begin{aligned} {\mathbf {L}}({\mathbf {p}}) = \sum ^m_{k=1} \frac{T_k}{T} {\mathbf {L}}_k({\mathbf {p}}) \end{aligned}$$

where ${\mathbf {L}}_k({\mathbf {p}})= (T / T_k) \mathbf {{\overline{S}}}_k \overline{{\mathbf {T}}} {\mathbf {p}}$ can be thought of as a local generalized Lorenz curve (without convexity) for the k-source of income distribution. Evidently, the Lorenz curve is a weighted average of ${\mathbf {L}}_1, {\mathbf {L}}_2,\ldots , {\mathbf {L}}_m$.

5.3 Matrix illustrations of Lorenz curve

We now end Sect. 5 by calculating the density distribution matrix for the Lorenz curve using the dataset Table 6. By the definition of density matrix for the corresponding income matrix X, we compute

$$\begin{aligned} {\mathbf {S}} = \left( \begin{array}{ccccc} 0.3369&{}\quad 0.0027&{}\quad 0.0775&{}\quad 0.0063&{}\quad 0.0215\\ 0.4294&{}\quad 0.0031&{}\quad 0.0950&{}\quad 0.0096&{}\quad 0.0194\\ 0.6936&{}\quad 0.0047&{}\quad 0.1049&{}\quad 0.0071&{}\quad 0.0166\\ 0.7633&{}\quad 0.0053&{}\quad 0.1138&{}\quad 0.0118&{}\quad 0.0211\\ 0.9243&{}\quad 0.0126&{}\quad 0.1277&{}\quad 0.0201&{}\quad 0\\ 0.9789&{}\quad 0.0103&{}\quad 0.0964&{}\quad 0.0122&{}\quad 0\\ 1.6747&{}\quad 0.0187&{}\quad 0.1761&{}\quad 0.0219&{}\quad 0\\ \end{array} \right) . \end{aligned}$$

A plot of this matrix S produces a bar graph in Fig. 2, which can be used to contrast the graph for the share density function s(p) over all sources of income in Fig. 3. The associated density distribution matrix and the corresponding vector for the Lorenz curve are respectively displayed as follows:

$$\begin{aligned}&\mathbf {{\overline{S}}}\! =\! \left( \begin{array}{ccccccc} 0.4449&{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0.4449&{}\quad 0.5565&{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0.4449&{}\quad 0.5565&{}\quad 0.8268&{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0.4449&{}\quad 0.5565&{}\quad 0.8268&{}\quad 0.9153&{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0.4449&{}\quad 0.5565&{}\quad 0.8268&{}\quad 0.9153&{}\quad 1.0847&{}\quad 0 &{}\quad 0\\ 0.4449&{}\quad 0.5565&{}\quad 0.8268&{}\quad 0.9153&{}\quad 1.0847&{}\quad 1.0978&{}\quad 0\\ 0.4449&{}\quad 0.5565&{}\quad 0.8268&{}\quad 0.9153&{}\quad 1.0847&{}\quad 1.0978&{}\quad 1.8914\\ \end{array} \right) ,\quad \\&\mathbf{L } =\left( \begin{array}{c} 0.0515 \\ 0.1240 \\ 0.2480 \\ 0.3866 \\ 0.5526 \\ 0.7174 \\ 1.0000 \\ \end{array} \right) . \end{aligned}$$

A plot of $\mathbf {L}(\mathbf{p })$ together with s(p) in Fig. 3 can be quite useful to envision the linear interpolation for the Lorenz curve one would expect. The visual aspect of s(p), corresponding to all entries at the bottom of matrix $\mathbf {{\overline{S}}}$, can provide geometric intuition for the study of income redistribution over some brackets. Observing striking density changes over some consecutive percentile intervals can be useful for improving the Gini index.

Fig. 3

Total density and a Lorenz curve for seven income brackets

Fig. 4

A verbose output from a sample run of R-code (Fig. 5) for the Gini decomposition of a dataset (Table 6), where all components $\varvec{\Phi }, \varvec{\Phi }^+, \varvec{\Phi }^-$, $\varvec{\Theta }$, ${\varvec{\eta }}$, and $\mathbf {\phi }$ in coding are identified by Fc, Fp, Fm, Theta, Eta, and fc, respectively

Fig. 5

R-code listing for the Gini Decomposition of aggregated data by income source

6 Conclusion and miscellaneous remarks

This paper shows that the Gini index for multiple sources of income can be estimated based on data aggregation. The structure of the overall inequality has been made evident in terms of the Gini index decomposition factors. They can be termed as an algebraic sum of two parts of the associated income over all income brackets in the direction of widening and narrowing the entire inequality respectively. Further variations of the factor have been formulated in terms of the share density function, which offer useful interpretations.

The matrix form of the share density function leads to the finding of a matrix representation of the associated linear interpolated Lorenz curve, which can be useful for further questions about improving the Gini index and modeling the Lorenz curve based on aggregated datasets. This paper also shows that the Lorenz curve can be decomposed by income source and interpreted as a weighted average of local generalized Lorenz curves.

Summing up, this paper has provided a new matrix approach to computing the decomposition factors of Gini index and Lorenz curve under the framework of basic matrix operations. Indeed, such computation schemes are more tractable for algorithmic implementation by R programming as well as easily achievable by matrix software technology such as Matlab. A significant contribution of this paper is to use R code for performing the Gini index decomposition by income source. An extended research, Shao (2020), suggests that this technique works equally well for the Gini decomposition by population subgroup.