Skip to main content
SpringerLink
Log in

An emergent autonomous flow for mean-field spin glasses

  • Published:
Probability Theory and Related Fields Aims and scope Submit manuscript

Abstract

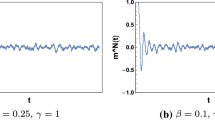
We study the dynamics of symmetric and asymmetric spin-glass models of size N. The analysis is in terms of the double empirical process: this contains both the spins, and the field felt by each spin, at a particular time (without any knowledge of the correlation history). It is demonstrated that in the large N limit, the dynamics of the double empirical process becomes deterministic and autonomous over finite time intervals. This does not contradict the well-known fact that SK spin-glass dynamics is non-Markovian (in the large N limit) because the empirical process has a topology that does not discern correlations in individual spins at different times. In the large N limit, the evolution of the density of the double empirical process approaches a nonlocal autonomous PDE operator \(\Phi _t\). Because the emergent dynamics is autonomous, in future work one will be able to apply PDE techniques to analyze bifurcations in \(\Phi _t\). Preliminary numerical results for the SK Glauber dynamics suggest that the ‘glassy dynamical phase transition’ occurs when a stable fixed point of the flow operator \(\Phi _t\) destabilizes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. One should be able to adapt the methods of this paper to this setting.

  2. See [23, 63] for further discussion of such PDEs.

  3. Private communication.

  4. A quick way to see why this formula holds is to note that the probability of a jump occurring over a small time interval is approximately exponentially distributed, i.e. \({\mathbb {P}}(|\sigma ^{i,j}_{\Delta } - \sigma ^{i,j}_0| > 0 \big ) \simeq c(\sigma ^{i,j}_0, G^{i,j}_0)\exp \big (-\Delta c(\sigma ^{i,j}_0, G^{i,j}_0)\big )\). Taking the ratio of two such densities, multiplying over many time intervals, and then taking \(\Delta \rightarrow 0\), we obtain the formula (124).

  5. This satisfies all of the axioms of a metric, except that \(d_K(\mu ,\nu )=0\) does not necessarily imply that \(\mu =\nu \).

References

  1. Aljadeff, J., Stern, M., Sharpee, T.: Transition to chaos in random networks with cell-type-specific connectivity. Phys. Rev. Lett. 114(8) (2015)

  2. Anderson, D.F., Kurtz, T.G.: Stochastic Analysis of Biochemical Systems. Springer, Berlin (2015)

    Book  MATH  Google Scholar 

  3. Anderson, G.W., Guionnet, A., Zeitouni, O.: An Introduction to Random Matrices. Cambridge University Press, Cambridge (2011)

    MATH  Google Scholar 

  4. Arous, G.B., Dembo, A., Guionnet, A.: Aging of spherical spin glasses. Probab. Theory Relat. Fields 120(1), 1–67 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  5. Arous, G.B.: Aging and spin-glass dynamics. In Proceedings of the International Congress of Mathematicians, volume III, pages 3–14. Higher Ed. Press, (2003)

  6. Arous, G.B., Jagannath, A.: Spectral aap estimates in mean field spin glasses. Commun. Math. Phys. 361, 1–52 (2018)

    Article  MATH  Google Scholar 

  7. Baity-Jesi, M., Sagun, L., Geiger, M., Spigler, S., Arous, G.B., Cammarota, C., LeCun, Y., Wyart, M., Biroli, G.: Comparing Dynamics: Deep Neural Networks versus Glassy Systems. (2018)

  8. Bauerschmidt, R., Bodineau, T.: A very simple proof of the LSI for high temperature spin systems. J. Funct. Anal. 276(8), 2582–2588 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  9. Ben-Arous, G., Guionnet, A.: Large deviations for Langevin spin glass dynamics. Probab. Theory Relat. Fields 102(4), 455–509 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  10. Ben-Arous, G., Dembo, A., Guionnet, A.: Cugliandolo-Kurchan equations for dynamics of spin-glasses. Probab. Theory Relat. Fields 136(4), 619–660 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  11. Arous, G.B., Guionnet, A.: Langevin Dynamics for Sherrington-Kirkpatrick Spin Glasses. In Anton Bovier and P Picco, editors, Mathematical Aspects of Spin Glasses and Neural Networks. Birkhauser, 1 edition, (1998)

  12. Billingsley, P.: Convergence of Probability Measures. Wiley, New York (1999)

    Book  MATH  Google Scholar 

  13. Bolthausen, E., Bovier, A.: Spin Glasses, vol. 2084. Springer (2007)

  14. Brunel, N., Wang, X.-J.: What Determines the Frequency of Fast Network Oscillations With Irregular Neural Discharges? I. Synaptic Dynamics and Excitation-Inhibition Balance. J. Neurophysiol. 90, 415–430 (2003)

    Article  Google Scholar 

  15. Budhiraja, A., Dupuis, P., Fischer, M.: Large deviation properties of weakly interacting processes via weak convergence methods. Annals Probab. 40(1), 74–102 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  16. Cabana, T., Touboul, J.: Large deviations, Dynamics and phase transitions in large stochastic and disordered neural networks. J. Stat. Phys. 153(2), 211–269 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  17. Cessac, B., Doyon, B., Quoy, M., Samuelides, M.: Mean-field equations , bifurcation map and route to chaos in discrete time neural networks. Physica D 74, 24–44 (1994)

  18. Coghi, M., Deuschel, J-D., Friz, P., Maurelli, M.: Pathwise McKean-Vlasov Theory. 1–41, (2018)

  19. Coppini, F., Dietert, H., Giacomin, G.: A law of large numbers and large deviations for interacting diffusions on Erdos-Rényi graphs. Stoch. Dyn. 20(02), 2050010 (2019)

    Article  MATH  Google Scholar 

  20. Crisanti, A., Sompolinsky, H.: Path integral approach to random neural networks. Phys. Rev. E 98(6), 1–20 (2018)

    Article  Google Scholar 

  21. Crisanti, A., Horner, H., Sommers, H.J.: The spherical p-spin interaction spin-glass model. Z. Phys. B: Condens. Matter 92(2), 257–271 (1993)

    Article  Google Scholar 

  22. Cugliandolo, L.F., Kurchan, J.: On the out-of-equilibrium relaxation of the Sherrington-Kirkpatrick model. J. Phys. A: Math. Gen. 27(17), 5749–5772 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  23. Dawson, D., Gartner, J.: Large Deviations, Free Energy Functional and Quasi-Potential for a Mean Field Model of Interacting Diffusions. American Mathematical Society, (1989)

  24. Dembo, A., Lubetzky, E., Zeitouni, O.: Universality for langevin spin glass dynamics. Arxiv Preprint 1, 1–18 (2019)

  25. Dembo, A., Zeitouni, O.: Large Deviations Techniques and Applications, 2nd edn. Springer, Berlin (1998)

    Book  MATH  Google Scholar 

  26. Doiron, B., Litwin-Kumar, A., Rosenbaum, R., Ocker, G., Josic, K.: The mechanics of state dependent neural correlations. Nat. Neurosci. 19(3), 383–393 (2016)

    Article  Google Scholar 

  27. Ethier, S., Kurtz, T.: Markov Processes. Characterization and Convergence. Wiley Series in Probability and Mathematical Statistics, (1986)

  28. Fasoli, D., Faugeras, O., Panzeri, S.: A Formalism for Evaluating Analytically the Cross-Correlation Structure of a Firing-Rate Network Model. J. Math. Neurosc. 5(1), 1–53 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  29. Fasoli, D., Panzeri, S.: Stationary-state statistics of a binary neural network model with quenched disorder. Entropy 21(7), 1–30 (2019)

    Article  MathSciNet  Google Scholar 

  30. Faugeras, O., MacLaurin, J.: Asymptotic description of neural networks with correlated synaptic weights. Entropy 17(7), 4701–4743 (2015)

    Article  Google Scholar 

  31. Faugeras, O., Maclaurin, J., Tanré, E.: A large deviation principle governing the thermodynamic limit of a network of Hopfield neurons with correlated synaptic weights. Archiv Preprint, (2019)

  32. Faugeras, O., Soret, E., Tanré, E.: Asymptotic behaviour of a network of neurons with random linear interactions. Preprint HAL Id : hal-01986927, (2019)

  33. Gheissari, R., Jagannath, A.: On the spectral gap of spherical spin glass dynamics. Annales de l’Institut Henri Poincaré, Probab. et Stat. 5(2), 1–21 (2019)

  34. Gibbs, A.L., Su, F.E.: On choosing and bounding probability metrics. Int. Stat. Rev. 70(3), 419–435 (2002)

    Article  MATH  Google Scholar 

  35. Glauber, R.J.: Time-dependent statistics of the Ising model. J. Math. Phys. 4(2), 294–307 (1963)

    Article  MathSciNet  MATH  Google Scholar 

  36. Green, J.W., Valentine, F.A.: On the Arzela-Ascoli Theorem. Math. Mag. 34(4), 199–202 (1961)

    MathSciNet  MATH  Google Scholar 

  37. Grunwald, M.: Sanov results for Glauber spin-glass dynamics. Probab. Theory Relat. Fields 106, 187–232 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  38. Grunwald, M.: Sherrington-Kirkpatrick Spin-Glass Dynamics. In: Bovier, Anton, Picco, Pierre (eds.) Mathematical Aspects of Spin Glasses. Birkhauser, Basel (1998)

    Google Scholar 

  39. Guerra, F.: Broken replica symmetry bounds in the mean field spin glass model. Commun. Math. Phys. 233(1), 1–12 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  40. Guionnet, A.: Averaged and quenched propagation of chaos for spin glass dynamics. Probab. Theory Relat. Fields 109, 183–215 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  41. Guionnet, A.: Dynamics for Spherical Models of Spin-Glass and Aging. In: Bolthausen, Erwin, Bovier, Anton (eds.) Spin Glasses. Springer, Berlin (2007)

    MATH  Google Scholar 

  42. Houghton, A., Jain, S., Young, A.P.: Role of initial conditions in the mean-field theory of spin-glass dynamics. Phys. Rev. B 28(5), 2630 (1983)

    Article  Google Scholar 

  43. Jacod, J., Shiryaev, A.N.: Limit Theorem for Stochastic Processes, 2nd edn. Springer, New York (2002)

    MATH  Google Scholar 

  44. Jagannath, A.: Dynamics of mean field spin glasses on short and long timescales. Journal of Mathematical Physics 60(8) (2019)

  45. Jourdain, B., Meleard, S.: Propagation of chaos and fluctuations for a moderate model with smooth initial data. Annales De L’I.H.P., Section B, 34(6), (1998)

  46. Jourdain, B., Méléard, S., Woyczynski, W.: Nonlinear SDEs driven by Lévy processes and related PDEs. Alea 4, 1–28 (2007)

    MATH  Google Scholar 

  47. Kadmon, J., Sompolinsky, H.: Transition to chaos in random neuronal networks. Phys. Rev. X 5(4), 1–28 (2015)

    Google Scholar 

  48. Laughton, S.N., Coolen, A.C.C., Sherrington, D.: Order-Parameter Flow in the SK Spin-Glass II : Inclusion of Microscopic Memory Effects. Journal of Physics A: Mathematical and General 29(4), 763 (1996)

    Article  MATH  Google Scholar 

  49. Laughton, S.N., Sherrington, D.: Dynamical Replica Theory for Disordered Spin Systems. Phys. Rev. B 2, 1–7 (1996)

    Google Scholar 

  50. Lindgren, George, Rootzen, Holger, Sandsten, Maria: Stationary Stochastic Processes for Scientists and Engineers. Chapman Hall, London (2013)

    Book  MATH  Google Scholar 

  51. Lucon, E., Stannat, W.: Mean field limit for disordered diffusions with singular interactions 1. Annals Appl. Probab. 24(5), 1946–1993 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  52. Maclaurin, J.: Large Deviations of a Network of Interacting Particles with Sparse Random Connections. arXiv preprintarXiv:1607.05471, (2018)

  53. Mezard, M., Parisi, G., Virasoro, M.A., editors: Spin Glass Theory and Beyond. World Scientific, (1987)

  54. Montanari, A.: Optimization of the Sherrington-Kirkpatrick Hamiltonian. 1–27, (2019)

  55. Panchenko, D.: The Sherrington-Kirkpatrick Model. Springer, Berlin (2013)

    Book  MATH  Google Scholar 

  56. Parisi, G.: Infinite number of order parameters for spin-glasses. Phys. Rev. Lett. 43(23), 1754 (1979)

    Article  Google Scholar 

  57. Poplavskyi, M., Tribe, R., Zaboronski, O.: On the distribution of the largest real eigenvalue for the real ginibre ensemble. Annals Appl. Probab. 27(3), 1395–1413 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  58. Sherrington, D., Kirkpatrick, S.: Solvable model of a spin-glass. Phys. Rev. Lett. 35(26), 1792 (1975)

    Article  Google Scholar 

  59. Sommers, Hans-Jurgen: Path-integral approach to ising spin-glass. Dynamics. 58(12), 1268–1271 (1987)

    Google Scholar 

  60. Sompolinsky, H.: Time-dependent order parameters in spin-glasses. Phys. Rev. Lett. 47(13), 935–938 (1981)

    Article  Google Scholar 

  61. Sompolinsky, H., Zippelius, A.: Dynamic Theory of the Spin-Glass Phase. Phys. Rev. Lett. 47(5), 359–362 (1981)

    Article  Google Scholar 

  62. Stein, D.L., Newman, C.M.: Spin Glasses and Complexity. Princeton University Press, New Jersy (2013)

    Book  MATH  Google Scholar 

  63. Sznitman, A-S.: Topics in Propagation of Chaos. In P.L Henneguin, editor, Lecture Notes in Mathematics. Ecole d’Ete de Probabilites de Saint-Flour XIX - 1989. Springer-Verlag, (1989)

  64. Talagrand, M.: The Parisi formula. Ann. Math. 163(1), 221–263 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  65. Talagrand, M.: Mean Field Models for Spin Glasses: Advanced Replica-Symmetry and Low Temperature. Springer, Berlin (2011)

    Book  MATH  Google Scholar 

  66. Wainrib, G., Touboul, J.: Topological and dynamical complexity of random neural networks. Phys. Rev. Lett. 110(11), 1–4 (2013)

    Article  Google Scholar 

Download references

Acknowledgements

Much thanks to Colin MacLaurin (U. Queensland) for obtaining some preliminary numerical results that were incorporated into the introduction. Much thanks also to Gerard Ben Arous (NYU), David Shirokoff (NJIT), Victor Matveev (NJIT), Bruno Cessac (INRIA) and Etienne Tanre (INRIA) for interesting discussions and very helpful feedback.

Author information

Authors and Affiliations

  1. New Jersey Institute of Technology, Newark, USA

    James MacLaurin

Authors
  1. James MacLaurin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to James MacLaurin.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

MacLaurin, J. An emergent autonomous flow for mean-field spin glasses. Probab. Theory Relat. Fields 180, 365–438 (2021). https://doi.org/10.1007/s00440-021-01040-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00440-021-01040-w

Mathematics Subject Classification

Search

Navigation