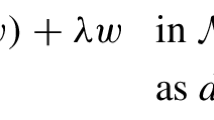Abstract
A new approach in Loewner Theory proposed by Bracci, Contreras, Díaz-Madrigal and Gumenyuk provides a unified treatment of the radial and the chordal versions of the Loewner equations. In this framework, a generalized Loewner chain satisfies the differential equation
where τ: [0, ∞) → \(\overline{\mathbb{D}}\) is measurable and p is called a Herglotz function. In this paper, we will show that if there exists a k ⩽ [0, 1) such that p satisfies
for all z ⩽ \(\mathbb{D}\) and almost all t ⩽ [0, ∞), then, for all t ⩽ [0, ∞), ft has a k-quasiconformal extension to the whole Riemann sphere. The radial case (τ = 0) and the chordal case (τ = 1) have been proven by Becker [J. Reine Angew. Math., vol. 255 (1972), 23–43] and Gumenyuk and the author [Math. Z., vol. 285 (2017), 1063–1089]. In our theorem, no superfluous assumption is imposed on τ ⩽ \(\overline{\mathbb{D}}\). As a key foundation of the proof is an approximation method using a continuous dependence of evolution families and Loewner chains.
Similar content being viewed by others
References
L. V. Ahlfors, Lectures on Quasiconformal Mappings, American Mathematical Society, Providence, RI, 2006.
L. V. Ahlfors and G. Weill, A uniqueness theorem for Beltrami equations, Proc. Amer. Math. Soc. 13 (1962), 975–978.
F. Bracci, M. D. Contreras and S. Díaz-Madrigal, Evolution families and the Loewner equation I. The unit disc, J. Reine Angew. Math. 672 (2012), 1–37.
J. Becker, Löwnersche differentialgleichung und quasikonform fortsetzbare schlichte funktionen, J. Reine Angew. Math. 255 (1972), 23–43.
J. Becker, Conformal mappings with quasiconformal extensions, in Aspects of Contemporary Complex Analysis, Academic Press, London, 1980, pp. 37–77.
L. Bers, Correction to “Spaces of Riemann surfaces as bounded domains”, Bull. Amer. Math. Soc. 67 (1961), 465–466.
Th. Betker, Löwner chains and quasiconformal extensions, Complex Variables Theory Appl. 20 (1992), 107–111.
E. Berkson and H. Porta, Semigroups of analytic functions and composition operators, Michigan Math. J. 25 (1978), 101–115.
M. D. Contreras, S. Díaz-Madrigal and P. Gumenyuk, Loewner chains in the unit disk, Rev. Mat. Iberoamericana 26 (2010), 975–1012.
M. D. Contreras, S. Díaz-Madrigal and P. Gumenyuk, Local duality in Loewner equations, J. Nonlinear Convex Anal. 15 (2014), 269–297.
L. de Branges, A proof of the Bieberbach conjecture, Acta Math. 154 (1985), 137–152.
S. S. Dragomir, Some Gronwall Type Inequalities and Applications, Nova Science Publishers, Hauppauge, NY, 2003.
M. Elin and D. Shoikhet, Linearization Models for Complex Dynamical Systems, Birkhäuser, Basel, 2010.
P. Gumenyuk and I. Hotta, Chordal Loewner chains with quasiconformal extensions, Math. Z. 285 (2017), 1063–1089.
P. Gumenyuk and I. Prause, Quasiconformal extensions, Loewner chains, and the λ-lemma, Anal. Math. Phys. 8 (2018), 621–635.
I. Hotta, Explicit quasiconformal extensions and Löwner chains, Proc. Japan Acad. Ser. A Math. Sci. 85 (2009), 108–111.
I. Hotta, Lowner chains with complex leading coefficient, Monatsh. Math. 163 (2011), 315–325.
J. H. Hubbard, Teichmüller Theory and Applications to Geometry, Topology, and Dynamics. Vol. 1, Matrix Editions, Ithaca, NY, 2006.
Y. Imayoshi and M. Taniguchi, An Introduction to Teichmüller Spaces, Springer, Tokyo, 1992.
F. Johansson Viklund, A. Sola and A. Turner, Scaling limits of anisotropic Hastings-Levitov clusters, Ann. Inst. Henri Poincaré Probab. Stat 48 (2012), 235–257.
P. P. Kufarev, On one-parameter families of analytic functions, Rec. Math. [Mat. Sbornik] N.S. 13(55) (1943), 87–118.
G. F. Lawler, Conformally Invariant Processes in the Plane, American Mathematical Society, Providence, RI, 2005.
O. Lehto, Univalent Functions and Teichmüller Spaces, Springer, New York, 1987.
J. Lind, D. E. Marshall and S. Rohde, Collisions and spirals of Loewner traces, Duke Math. J. 154 (2010), 527–573.
K. Löwner, Untersuchungen über schlichte konforme Abbildungen des Einheitskreises. I, Math. Ann. 89 (1923), 103–121.
O. Lehto and K. I. Virtanen, Quasiconformal Mappings in the Plane, Springer, New York, 1973.
Ch. Pommerenke, Über die Subordination analytischer Funktionen, J. Reine Angew. Math. 218 (1965), 159–173.
Ch. Pommerenke, Univalent Functions, Vandenhoeck & Ruprecht, Göttingen, 1975.
O. Roth, Control Theory in ℋ(\(\mathbb{D}\)), Ph.D. thesis, Universität Würzburg, Würzburg, 1998.
O. Roth and S. Schleißinger, The Schramm-Loewner equation for multiple slits, J. Anal. Math. 131 (2017), 73–99.
O. Schramm, Scaling limits of loop-erased random walks and uniform spanning trees, Israel J. Math. 118 (2000), 221–288.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by JSPS KAKENHI Grant Numbers 17K14205.
Rights and permissions
About this article
Cite this article
Hotta, I. Loewner chains with quasiconformal extensions: an approximation approach. JAMA 143, 123–149 (2021). https://doi.org/10.1007/s11854-021-0149-4
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11854-021-0149-4