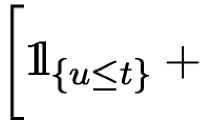New characterizations of multivariate Max-domain of attraction and D-Norms

Abstract

In this paper we derive new results on multivariate extremes and D-norms. In particular we establish new characterizations of the multivariate max-domain of attraction property. The limit distribution of certain multivariate exceedances above high thresholds is derived, and the distribution of that generator of a D-norm on ${\mathbb R}^{d}$, whose components sum up to d, is obtained. Finally we introduce exchangeable D-norms and show that the set of exchangeable D-norms is a simplex.

1 Introduction

Multivariate extreme value theory (MEVT) is the appropriate toolbox for analyzing several extremal events simultaneously. However, MEVT is by no means easy to access; its key results are formulated in a measure theoretic setup in which a common thread is not visible.

Writing the `angular measure’ in MEVT in terms of a random vector, however, provides the missing common thread: Every result in MEVT, every relevant probability distribution, be it a max-stable one or a generalized Pareto distribution, every relevant copula, every tail dependence coefficient etc. can be formulated using a particular kind of norm on multivariate Euclidean space, called a D-norm. Deep results like Takahashi’s characterizations of multivariate max-stable distributions with independent or completely dependent margins (Takahashi 1987; 1988) turn out to be elementary and easily seen properties of D-norms. The letter D means dependence, because a D-norm describes the dependence among the margins of a multivariate max-stable distribution, see Theorem 4.1.

Norms are introduced in each introductory course on mathematics as soon as the multivariate Euclidean space is introduced. The definition of an arbitrary D-norm requires only the additional knowledge of random variables and their expectations. But D-norms do not only constitute the common thread through MEVT; they are of mathematical interest of their own.

D-norms were first mentioned in Falk et al. (2004), equation (4.25), and more elaborated in Falk et al. (2011), Section 4.4. But it was recognized only later that D-norms are actually the skeleton of MEVT and that they simultaneously provide a mathematical topic, which can be studied independently. The monograph Falk (2019) compiles the contemporary knowledge about D-norms and provides an introductory tour through the essentials of MEVT. But D-norms can also be seen from a functional analysis perspective as in Ressel (2013), which is Section 1.11 in Falk (2019), or from a stochastic geometry point of view as in Molchanov (2008), presented in detail in Section 1.12 in Falk (2019).

In this paper we establish new results on MEVT and D-norms. In Section 2 we recall the definition of D-norms and list several basic facts. In Section 3 we specify functions $h:[0,\infty )^{d}\to [0,\infty )$, such that the number E(h(Z)) is generator invariant, i.e., E(h(Z)) depends only on the underlying D-norm generated by Z, but not on the particular generator Z. The dual D-norm function is a prominent example. But this result also entails the definition of the co-extremality coefficient, which is a measure of pairwise tail dependence of a multivariate distribution. The corresponding matrix of co-extremality coefficients turns out to be positive semidefinite.

In Section 4 we link D-norms with MEVT and establish particularly in Theorem 4.4 a new characterization of max-domain of attraction of a random vector ${\boldsymbol {X}}=(X_{1},\dots ,X_{d})$. An immediate consequence, in Corollary 4.6, is for example the fact that the probability of the event ${\sum }_{i=1}^{d} X_{i}>t$ is approximately d/t as t increases, independent of the dependence structure among $X_{1},\dots ,X_{d}$; this was already observed in Barbe et al. (2006).

In Section 5 we derive the limit distribution of certain multivariate exceedances above high thresholds. These results are used in Section 6 to derive among others the distribution of that generator of a D-norm on ${\mathbb R}^{d}$, whose components sum up to d.

It turns out that Mai and Scherer (2020), which is on exchangeable extreme-value copulas, is actually a contribution to the theory of D-norms, as shown in Section 7. To the best of our knowledge, the concept of an exchangeable D-norm is introduced here for the first time, and we prove new results for this subfamily of D-norms.

2 D-Norms

The following result introduces D-norms. For a proof we refer to Lemma 1.1.3 in (Falk 2019).

Lemma 2.1 (D-Norms)

Let $\boldsymbol {Z} = (Z_{1}, \dots , Z_{d})$ be a random vector, whose components satisfy

$$ Z_{i} \geq 0,\quad E(Z_{i}) = 1, \qquad 1 \leq i \leq d. $$

Then

$$ \left\Vert\boldsymbol{x}\right\Vert_{D} := E \left( \underset{1 \leq i \leq d}{\max} (\left\vert x_{i}\right\vert Z_{i}) \right), \qquad \boldsymbol{x} \in \mathbb R^{d}, $$

defines a norm, called a D-norm, and Z is called a generator of this D-norm ${\left \Vert \cdot \right \Vert }_{D}$.

Denote by $\boldsymbol {e}_{j}=(0, \dots , 0,1,0, \dots , 0) \in \mathbb R^{d}$ the j-th unit vector in $\mathbb R^{d}$, 1 ≤ j ≤ d. Each D-norm satisfies

$$ \left\Vert\boldsymbol{e}_{j}\right\Vert_{D}=E \left( \underset{1 \leq i \leq d}{\max} (\delta_{ij}Z_{i}) \right) = E(Z_{j}) = 1, $$

where δ_ij = 1 if i = j and zero elsewhere, i.e., each D-norm is standardized.

Each D-norm is monotone as well, i.e., for 0 ≤x ≤y, where this inequality is taken componentwise, we have

$$ \left\Vert\boldsymbol{x}\right\Vert_{D} = E\left( \underset{1 \leq i \leq d}{\max}(x_{i} Z_{i})\right) \leq E\left( \underset{1 \leq i \leq d}{\max}(y_{i} Z_{i})\right) = \left\Vert\boldsymbol{y}\right\Vert_{D}. $$

Example 2.2

Here is a list of D-norms and their generators, see Section 1.2 in Falk (2019):

• $\displaystyle \left \Vert \boldsymbol {x}\right \Vert _{\infty } = \max \limits _{1\le i\le d}\left \vert x_{i}\right \vert$, generated by $\boldsymbol {Z}=(1,\dots ,1)$.

• $\displaystyle \left \Vert \boldsymbol {x}\right \Vert _{1}=\sum \limits _{i=1}^{d}\left \vert x_{i}\right \vert$, generated by Z = random permutation of $(d,0,\dots ,0)\in \mathbb R^{d}$ with equal probability 1/d.

• $\displaystyle \left \Vert \boldsymbol {x}\right \Vert _{\lambda }=\left (\sum \limits _{i=1}^{d}\left \vert x_{i}\right \vert ^{\lambda }\right )^{1/\lambda }$, $1<\lambda <\infty$. Let $X_{1},\dots ,X_{d}$ be independent and identically Fréchet-distributed random variables, i.e., $P(X_{i}\le x)= \exp (-x^{-\lambda })$, x > 0, λ > 1. Then ${\boldsymbol {Z}}=(Z_{1},\dots ,Z_{d})$ with

  $$ Z_{i}:=\frac{X_{i}}{{{{\varGamma}}}(1-\frac 1\lambda)},\quad i=1,\dots,d, $$

  generates ${\left \Vert \cdot \right \Vert }_{\lambda }$.

• Let the random vector $\boldsymbol {X}=(X_{1},\dots ,X_{d})$ follow a multivariate normal distribution with mean vector zero, i.e., E(X_i) = 0, 1 ≤ i ≤ d, and covariance matrix Σ = (σ_ij)_{1≤i, j≤d} = (E(X_iX_j))_{1≤i, j≤d}. Then $\exp (X_{i})$ follows a log-normal distribution with mean $\exp (\sigma _{ii}/2)$, 1 ≤ i ≤ d, and thus,

  $$ \boldsymbol{Z}=(Z_{1},\dots,Z_{d}):= \left( \exp\left( X_{1}-\frac{\sigma_{11}}2\right),\dots, \exp\left( X_{d}-\frac{\sigma_{dd}}2\right) \right) $$

  is the generator of a D-norm, called a Hüsler-ReissD-norm. This norm depends only on the covariance matrix Σ.

There is a smallest D-norm and a largest one:

$$ \left\Vert\boldsymbol{x}\right\Vert_{\infty}\leq \left\Vert\boldsymbol{x}\right\Vert_{D} \leq \left\Vert\boldsymbol{x}\right\Vert_{1}, \qquad \boldsymbol{x} \in \mathbb R^{d}, $$

see equation (1.4) in Falk (2019).

Note that the univariate distributions of the components $Z_{1},\dots ,Z_{d}$ of Z influence the D-norm, which is generated by Z. Suppose $Z_{1},\dots ,Z_{d}$ are independent and identically distributed (iid) random variables. Then it makes a difference, whether they follow the standard exponential distribution or the uniform distribution on (0,2).

Neither the generator of a D-norm is uniquely determined nor its distribution. Actually, if $\boldsymbol {Z}=(Z_{1},\dots ,Z_{d})$ is the generator of a D-norm, then ${\boldsymbol {Z}}_{X}:=(Z_{1}X,Z_{2}X,\dots ,Z_{d}X)$ generates the same D-norm if X is a random variable with X ≥ 0 and E(X) = 1, which is also independent of Z. But for any D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on ${\mathbb R}^{d}$ and an arbitrary norm ${\left \Vert \cdot \right \Vert }$ on ${\mathbb R}^{d}$ there exists a generator Z of ${\left \Vert \cdot \right \Vert }_{D}$ with the additional property ∥Z∥ = const. The distribution of this generator is uniquely determined. This is the content of the following result, which is Theorem 1.7.1 in Falk (2019).

Theorem 2.3 (Normed Generators)

Let ${\left \Vert \cdot \right \Vert }$ be an arbitrary norm on $\mathbb R^{d}$. For any D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on $\mathbb R^{d}$, there exists a generator Z with the additional property ${\left \Vert {\boldsymbol {Z}}\right \Vert } = \text {const}$. The distribution of this generator is uniquely determined.

The following consequence is Corollary 1.7.2 in Falk (2019).

Corollary 2.4

For any D-norm ${\left \Vert \cdot 1\right \Vert }_{D}$ on $\mathbb R^{d}$, there exist generators Z⁽¹⁾, Z⁽²⁾ with the property ${\left \Vert {\boldsymbol {Z}^{(1)}}\right \Vert }_{1}={\sum }_{i=1}^{d} Z_{i}^{(1)}=d$, and ${\left \Vert {{\boldsymbol {Z}}^{(2)}}\right \Vert }_{\infty }=\max \limits _{1\le i\le d}Z_{i}^{(2)}=\text {const}={\left \Vert {(1,\dots ,1)}\right \Vert }_{D}$.

The following characterization will be used in several proofs in this paper. It goes back to Takahashi (1987) and Takahashi (1988). For a proof see Corollary 1.3.5 in Falk (2019).

Corollary 2.5

Let ${\left \Vert \cdot \right \Vert }_{D}$ be an arbitrary D-norm on $\mathbb R^{d}$. We have the characterizations:

• (i) ${\left \Vert \cdot \right \Vert }_{D} = {\left \Vert \cdot \right \Vert }_{1} \iff \forall 1\leq i<j\leq d \!: {\left \Vert {\boldsymbol {e}_{i}+\boldsymbol {e}_{j}}\right \Vert }_{D}=2=\left \Vert \boldsymbol {e}_{i}+\boldsymbol {e}_{j}\right \Vert _{1},$

• (ii) ${\left \Vert \cdot \right \Vert }_{D} = {\left \Vert \cdot \right \Vert }_{\infty } \iff \exists i \in \{1,\dots ,d\} \forall j \neq i : {\left \Vert {\boldsymbol {e}_{i}+\boldsymbol {e}_{j}}\right \Vert }_{D}=1$.

3 When the number E(h(Z)) is generator invariant

Let Z be the generator of a D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on $\mathbb R^{d}$, and let $h:[0,\infty )^{d}\to [0,\infty )$ be a continuous function that is homogeneous of order one, i.e., h(cy) = ch(y), c ≥ 0, ${\boldsymbol {y}}\in [0,\infty )^{d}$. In Theorem 3.5 we will establish the fact that, with such a function h, the number E(h(Z)) does not depend on the particular generator Z of ${\left \Vert \cdot \right \Vert }_{D}$.

Take, for example, an arbitrary norm ${\left \Vert \cdot \right \Vert }$ on $\mathbb R^{d}$. With $h(\cdot )={\left \Vert \cdot \right \Vert }$ we obtain that the number $E({\left \Vert {\boldsymbol {Z}}\right \Vert })$ does not depend on the particular generator Z of a D-norm ${\left \Vert \cdot \right \Vert }_{D}$. Equally, with $h({\boldsymbol {y}}):=\min \limits _{1\le i\le d}(\left |{x_{i}}\right |y_{i})$, Theorem 3.5 explains, why the function ${\wr \!\!\wr {{\boldsymbol {x}}}\wr \!\!\wr }_{D}=E\left (\min \limits _{1\le i\le d}\left |{x_{i}}\right |Z_{i}\right ) =E(h({\boldsymbol {Z}}))$, known as the dual D-norm function, is generator invariant.

Our proof of Theorem 3.5 uses several auxiliary results, which we establish first. They might be of interest of their own. We will frequently use the equation

$$ E(X)={\int}_{0}^{\infty} P(X>u) du, $$

(3.1)

valid for an arbitrary random variable X ≥ 0; for a proof see, e.g., Lemma 1.2 in Falk (2019). By 1_A(x) we denote the indicator function of a set A, i.e., 1_A(x) = 1 if x ∈ A, and zero elsewhere. All operations on vectors are meant componentwise.

Lemma 3.1

Choose $\boldsymbol {y}\in [0,\infty )^{d}$, $\boldsymbol {y}\not =\boldsymbol {0}\in \mathbb R^{d}$, and z > y. Put $I^{*}:=\{j\in \left \{1,\dots ,d\right \}: y_{j}>0\}$. Then we have for $\boldsymbol {x}\in [0,\infty )^{d}$

$$ 1_{[\boldsymbol{y},\boldsymbol{z})}(\boldsymbol{x}) =\sum\limits_{T\subset I^{*}}(-1)^{\left| T\right|-1}1_{A_{T}}(\boldsymbol{x}), $$

where $\left | T\right |$ denotes the cardinality of the set T, and

$$ A_{T}:=\left\{\boldsymbol{a}\in[0,\infty)^{d}: \max_{j\in T}(a_{j}/y_{j})\ge 1\right\}\cup \left\{\boldsymbol{a}\in[0,\infty)^{d}: \max_{i\in T^{\complement}}(a_{i}/z_{i})\ge 1\right\}, $$

with $T^{\complement }=\left \{1,\dots ,d\right \}\backslash T$.

Proof

Choose $\boldsymbol {x}\in [0,\infty )^{d}$. Suppose first that x_i ≥ z_i for some $i\in \left \{1,\dots ,d\right \}$. Then we have 1_{[y, z)}(x) = 0 and $1_{A_{T}}(\boldsymbol {x})=1$ for each T ⊂ I^∗ and, thus,

$$ \sum\limits_{T\subset I^{*}}(-1)^{\left| T\right|-1}1_{A_{T}}(\boldsymbol{x}) = \sum\limits_{T\subset I^{*}}(-1)^{\left| T\right|-1} = 0 $$

by the fact that

$$ 1= \sum\limits_{\emptyset \neq T \subset \{1, \dots, n\}}(-1)^{\left\vert T\right\vert-1}; $$

(3.2)

for a proof see, e.g., equation (1.10) in Falk (2019).

Suppose next that x_j < y_j for some $j\in \left \{1,\dots ,d\right \}$. This implies j ∈ I^∗; we have $1_{A_{T}}(\boldsymbol {x})=1_{A_{T\cup \left \{j\right \}}}(\boldsymbol {x})$ for each T ⊂ I^∗ and, thus,

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{T\subset I^{*}}(-1)^{\left| T\right|-1}1_{A_{T}}(\boldsymbol{x})\\ &=&\sum\limits_{T\subset I^{*}, j\not\in T}(-1)^{\left| T\right|-1}1_{A_{T}}(\boldsymbol{x}) + \sum\limits_{T\subset I^{*}, j\in T}(-1)^{\left| T\right|-1}1_{A_{T}}(\boldsymbol{x})\\ &=&\sum\limits_{T\subset I^{*}, j\not\in T}(-1)^{\left| T\right|-1}1_{A_{T}}(\boldsymbol{x}) + \sum\limits_{T\subset I^{*}, j\not\in T}(-1)^{\left| T\right|}1_{A_{T\cup\left\{j\right\}}}(\boldsymbol{x})\\ &=&\sum\limits_{T\subset I^{*}, j\not\in T}(-1)^{\left| T\right|-1}1_{A_{T}}(\boldsymbol{x}) - \sum\limits_{T\subset I^{*}, j\not\in T}(-1)^{\left| T\right|-1}1_{A_{T\cup\left\{j\right\}}}(\boldsymbol{x})\\ &=&\sum\limits_{T\subset I^{*}, j\not\in T}(-1)^{\left| T\right|-1} \left( 1_{A_{T}}(\boldsymbol{x})- 1_{A_{T\cup\left\{j\right\}}}(\boldsymbol{x}) \right)\\ &=&0=1_{[\boldsymbol{y},\boldsymbol{z})}(\boldsymbol{x}). \end{array} $$

Suppose finally that y ≤x < z. Then we have x ∈ A_T for each T≠∅, x∉A_∅, and, thus, by Eq. 3.2

$$ \sum\limits_{T\subset I^{*}}(-1)^{\left| T\right|-1}1_{A_{T}}(\boldsymbol{x}) = \sum\limits_{\emptyset\not=T\subset I^{*}}(-1)^{\left| T\right|-1}1_{A_{T}}(\boldsymbol{x}) = 1 = 1_{[\boldsymbol{y},\boldsymbol{z})}(\boldsymbol{x}). $$

□

The measure ν, introduced in the next result, is known as the exponent measure in MEVT; see, for example, Section 4 in Falk (2008). The definition of the exponent measure in equation (1.17) in Falk (2019) is, however, restricted to generators Z that realize in some unit sphere. Different to that, the measure ν in Eq. 3.3 supposes no restriction on Z. This general definition is particulary required for the derivation of Theorem 3.5 below.

Proposition 3.2

Choose a D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on $\mathbb R^{d}$ and an arbitrary generator Z of ${\left \Vert \cdot \right \Vert }_{D}$. Put $\boldsymbol {E}:=[0,\infty )^{d}\backslash \left \{\boldsymbol {0}\right \}$ and define the function $T:(0,\infty )\times {\boldsymbol {E}}\to {\boldsymbol {E}}$ by

$$ T(s,\boldsymbol{z}):=\frac 1s \boldsymbol{z},\qquad s\in(0,\infty), \boldsymbol{z}\in\boldsymbol{E}. $$

Then

$$ \nu(\cdot):=\left( \lambda\times P_{\boldsymbol{Z}}\right)(T^{-1}(\cdot)) $$

(3.3)

defines a measure on the Borel σ-field $\mathbb B_{\boldsymbol {E}}$ of E with

$$ \nu\left( [\boldsymbol{0},\boldsymbol{x}]^{\complement}\right) =\left\Vert\frac{\boldsymbol{1}}{\boldsymbol{x}}\right\Vert_{D},\qquad \boldsymbol{x}>\boldsymbol{0}\in\mathbb R^{d}, $$

(3.4)

where λ denotes the Lebesgue measure on $(0,\infty )$, P_Z(⋅) = P(Z ∈⋅) is the distribution of Z, and “ ⋅×⋅ ” denotes the product measure. The measure ν on E is uniquely determined by Eq. 3.4.

The following consequence of Proposition 3.2 is obvious.

Corollary 3.3

The measure ν, as defined in Eq. 3.3, does not depend on the particular generator Z of ${\left \Vert \cdot \right \Vert }_{D}$.

Proof of Proposition 3.2

First we show that the measure ν satisfies Eq. 3.4. We have for $\boldsymbol {x}=(x_{1},\dots ,x_{d})>\boldsymbol {0}\in \mathbb R^{d}$

$$ \begin{array}{@{}rcl@{}} &&\nu\left( [\boldsymbol{0},\boldsymbol{x}]^{\complement}\right)\\ &=& \left( \lambda\times P_{\boldsymbol{Z}}\right)\left( \left\{(s,\boldsymbol{z}): \frac 1s \boldsymbol{z}\in[\boldsymbol{0},\boldsymbol{x}]^{\complement}\right\}\right)\\ &=& \left( \lambda\times P_{\boldsymbol{Z}}\right)\left( \left\{(s,\boldsymbol{z}): \frac 1s z_{i}>x_{i}\text{ for some }i\in\{1,\dots,d\right\}\right)\\ &=& \left( \lambda\times P_{\boldsymbol{Z}}\right)\left( \left\{(s,\boldsymbol{z}): \max_{1\le i\le d}\frac{z_{i}}{x_{i}}>s\right\}\right)\\ &=&{\int}_{\boldsymbol{E}}{\int}_{0}^{\infty} 1\left( \left\{\max_{1\le i\le d}\frac{z_{i}}{x_{i}}>s\right\}\right) ds P_{\boldsymbol{Z}}(d\boldsymbol{z})\qquad \text{(use Fubini)}\\ &=& {\int}_{\boldsymbol{E}} \max_{1\le i\le d}\frac{z_{i}}{x_{i}} P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& {\int}_{[0,\infty)^{d}} \max_{1\le i\le d}\frac{z_{i}}{x_{i}} P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& E\left( \max_{1\le i\le d}\frac{Z_{i}}{x_{i}}\right) = \left\Vert\frac{\boldsymbol{1}}{\boldsymbol{x}}\right\Vert_{D}. \end{array} $$

Repeating the preceding arguments, one obtains

$$ \nu\left( [\boldsymbol{0},\boldsymbol{x})^{\complement}\right) = \left\Vert\frac{\boldsymbol{1}}{\boldsymbol{x}}\right\Vert_{D},\qquad \boldsymbol{x}>\boldsymbol{0}\in\mathbb R^{d}, $$

(3.5)

as well.

Let μ be another measure on $\mathbb B_{\boldsymbol {E}}$ which satisfies Eq. 3.4. We obtain for $\boldsymbol {y}\in [0,\infty )^{d}$, $\boldsymbol {y}\not =\boldsymbol {0}\in \mathbb R^{d}$, and z > y

$$ \begin{array}{@{}rcl@{}} \nu([\boldsymbol{y},\boldsymbol{z})) &=& {\int}_{\boldsymbol{E}}1_{[\boldsymbol{y},\boldsymbol{z})}(\boldsymbol{x}) \nu(d\boldsymbol{x})\\ &=& {\int}_{\boldsymbol{E}} \sum\limits_{T\subset I^{*}}(-1)^{\left| T\right|-1}1_{A_{T}}(\boldsymbol{x}) \nu(d\boldsymbol{x})\qquad \text{(use Lemma 3.1)}\\ &=& \sum\limits_{T\subset I^{*}}(-1)^{\left| T\right|-1} {\int}_{\boldsymbol{E}} 1_{A_{T}}(\boldsymbol{x}) \nu(d\boldsymbol{x})\\ &=& \sum\limits_{T\subset I^{*}}(-1)^{\left| T\right|-1} \nu\left( A_{T}\right)\\ &=& \sum\limits_{T\subset I^{*}}(-1)^{\left| T\right|-1} \nu\left( \left[\boldsymbol{0},\sum\limits_{j\in T}y_{j}\boldsymbol{e}_{j}+\sum\limits_{i\in T^{\complement}}z_{i}\boldsymbol{e}_{i}\right)^{\complement} \right) \end{array} $$

$$ \begin{array}{@{}rcl@{}} &=& \sum\limits_{T\subset I^{*}}(-1)^{\left| T\right|-1} \left\Vert\frac{\boldsymbol{1}}{{\sum}_{j\in T}y_{j}\boldsymbol{e}_{j}+{\sum}_{i\in T^{\complement}}z_{i}\boldsymbol{e}_{i}}\right\Vert_{D} \qquad\text{(by Eq.~3.5)}\\ &=& \mu([\boldsymbol{y},\boldsymbol{z})) \end{array} $$

(3.6)

by repeating the above arguments. The set of all intervals [y, z), y ≥0, $\boldsymbol {y}\not =\boldsymbol {0}\in \mathbb R^{d}$, and z > y, is intersection stable and generates the Borel σ-field $\mathbb B_{{\boldsymbol {E}}}$ of E. Moreover, the measure ν is σ-finite with

$$ \nu\left( \left[\boldsymbol{0},\left( \frac 1n,\dots,\frac 1n\right)\right)^{\complement}\right) = \left\Vert\frac{\boldsymbol{1}}{\left( \frac 1n,\dots,\frac1n\right)}\right\Vert_{D} = n \left\Vert\boldsymbol{1}\right\Vert_{D} $$

for $n\in \mathbb N$, $\cup _{n\in \mathbb N}\left [\boldsymbol {0},\left (1/n,\dots ,1/n\right )\right )^{\complement } = \boldsymbol {E}$, and, thus, ν = μ on $\mathbb B_{\boldsymbol {E}}$. □

Lemma 3.4

The uniquely determined measure ν in Proposition 3.2 satisfies

$$ \nu(cM)=\frac 1c \nu(M),\qquad c>0, M\in\mathbb B_{\boldsymbol{E}}. $$

Proof

We have, with c > 0 and $M\in \mathbb B_{\boldsymbol {E}}$,

$$ \begin{array}{@{}rcl@{}} \nu(cM)&=& (\lambda\times P_{Z})\left( \left\{(s,\boldsymbol{z}): \frac 1s \boldsymbol{z}\in cM\right\}\right)\\ &=& (\lambda\times P_{Z})\left( \left\{(s,\boldsymbol{z}): \frac 1{sc} \boldsymbol{z}\in M\right\}\right)\\ &=&{\int}_{\boldsymbol{E}}{\int}_{0}^{\infty} 1\left( \frac 1 {sc}\boldsymbol{z}\in M\right) ds P_{\boldsymbol{Z}}(d\boldsymbol{z})\qquad\text{(use Fubini)}\\ &=& \frac 1c {\int}_{\boldsymbol{E}}{\int}_{0}^{\infty} 1\left( \frac 1 s \boldsymbol{z}\in M\right) ds P_{\boldsymbol{Z}}(d\boldsymbol{z})\quad\text{(by substituting $s\mapsto s/c$)}\\ &=&\frac 1c \nu(M)\qquad \text{(use Fubini again)}. \end{array} $$

□

The following theorem is the main result of this section. It shows that a wide class of functions $h:[0,\infty )^{d}\to [0,\infty )$ has the property that the number E(h(Z)) is generator invariant. This result will also be a crucial tool in the proof of Theorem 4.4, which presents a new characterization of max-domain of attraction.

Theorem 3.5

Let Z⁽¹⁾, Z⁽²⁾ be two generators of the D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on $\mathbb R^{d}$. Then we have for each continuous function $h:[0,\infty )^{d}\to [0,\infty )$, which is homogeneous of order one, i.e., h(cx) = ch(x), c ≥ 0, ${\boldsymbol {x}}\in [0,\infty )^{d}$,

$$ E\left( h\left( \boldsymbol{Z}^{(1)}\right)\right) = E\left( h\left( \boldsymbol{Z}^{(2)}\right)\right). $$

Proof

With T and λ as in Proposition 3.2, the measures

$$ \begin{array}{@{}rcl@{}} \nu(M)&:=& \left( \lambda\times P_{\boldsymbol{Z}}^{(1)}\right)\left( T^{-1}(M)\right)\\ \mu(M)&:=& \left( \lambda\times P_{\boldsymbol{Z}}^{(2)} \right)\left( T^{-1}(M)\right) \end{array} $$

coincide on $\mathbb B_{\boldsymbol {E}}$ by Corollary 3.3. As a consequence we obtain

$$ \begin{array}{@{}rcl@{}} &&\nu(\left\{\boldsymbol{x}: h(\boldsymbol{x})\ge 1\right\})\\ &=& \left( \lambda\times P_{\boldsymbol{Z}^{(1)}} \right)\left( \left\{(s,\boldsymbol{z}): h\left( \frac 1s\boldsymbol{z}\right)\ge 1\right\}\right)\\ &=& \left( \lambda\times P_{\boldsymbol{Z}^{(1)}} \right)\left( \left\{(s,\boldsymbol{z}): h(\boldsymbol{z})\ge s\right\}\right)\\ &=&{\int}_{\boldsymbol{E}}{\int}_{0}^{\infty} 1(h(\boldsymbol{z})\ge s) ds P_{\boldsymbol{Z}^{(1)}}(d\boldsymbol{z})\qquad \text{(use Fubini)}\\ &=&{\int}_{\boldsymbol{E}} h(\boldsymbol{z}) P_{\boldsymbol{Z}^{(1)}}(d\boldsymbol{z})\\ &=& {\int}_{[0,\infty)^{d}} h(\boldsymbol{z}) P_{\boldsymbol{Z}^{(1)}}(d\boldsymbol{z})\qquad \text{(because $h(\boldsymbol{0})=0$)}\\ &=& E\left( h\left( \boldsymbol{Z}^{(1)} \right)\right). \end{array} $$

Replacing ν by μ in the preceding list of equations yields the assertion, because ν = μ. □

The preceding result explains, for example, why the dual D-norm function

$$ \wr\!\!\wr\boldsymbol{x}\wr\!\!\wr_{D} := E\left( \min_{1\le i\le d}(\left\vert x_{i}\right\vert Z_{i})\right),\qquad \boldsymbol{x}\in\mathbb R^{d}, $$

does not depend on the particular generator $\boldsymbol {Z}=(Z_{1},\dots ,Z_{d})$ of ${\left \Vert \cdot \right \Vert }_{D}$. Just put, for $\boldsymbol {x}=(x_{1},\dots ,x_{d})\in \mathbb R^{d}$,

$$ h(\boldsymbol{y}):=\min_{1\le i\le d}(\left\vert x_{i}\right\vert y_{i}),\qquad \boldsymbol{y}=(y_{1},\dots,y_{d})\in[0,\infty)^{d}, $$

in Theorem 3.5. For the significance of the dual D-norm function in terms of exceedance probabilities we refer to Falk (2019).

Another promising application of Theorem 3.5 is the co-extremality coefficient.

Definition 3.6

Take an arbitrary D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on $\mathbb R^{d}$ with generator $\boldsymbol {Z}=(Z_{1},\dots ,Z_{d})$. Then

$$ c_{ij}:= E\left( \sqrt{Z_{i}Z_{j}}\right), $$

is the co-extremality coefficient, 1 ≤ i, j ≤ d.

The co-extremality coefficient does not depend on the particular generator $\boldsymbol {Z}=(Z_{1},\dots ,Z_{d})$ of ${\left \Vert \cdot \right \Vert }_{D}$; just put

$$ h(\boldsymbol{y}):=\sqrt{y_{i}y_{j}}. $$

in Theorem 3.5.

The co-extremality coefficient turns out to be a measure of pairwise tail dependence, as revealed by the following result; see also Eq. 4.5. Given a D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on ${\mathbb R}^{d}$, with generator ${\boldsymbol {Z}}=(Z_{1},\dots ,Z_{d})$, we denote by

$$ \left\Vert(x,y)\right\Vert_{D_{ij}}:= \left\Vert x\boldsymbol{e}_{i}+y\boldsymbol{e}_{j}\right\Vert_{D},\qquad x,y\in\mathbb R, $$

the bivariate projection of ${\left \Vert \cdot \right \Vert }_{D}$, which is itself a D-norm, with generator

$$ \boldsymbol{Z}^{(i,j)}:= (Z_{i},Z_{j}),\qquad 1\le i< j\le d. $$

Proposition 3.7

We have c_ij ∈ [0,1], 1 ≤ i, j ≤ d, with c_ii = 1 and, for i≠j,

• (i) $c_{ij}=0\iff \left \Vert \cdot \right \Vert _{D_{ij}}= {\left \Vert \cdot \right \Vert }_{1}$

• (ii) $c_{ij}=1\iff \left \Vert \cdot \right \Vert _{D_{ij}}= {\left \Vert \cdot \right \Vert }_{\infty }$.

Formulated in terms of random variables, the preceding result reads as follows. Suppose the random vector $\boldsymbol {\xi }=(\xi _{1},\dots ,\xi _{d})$ follows a simple max-stable df $G({\boldsymbol {x}})=\exp \left (-{\left \Vert {{\boldsymbol {1}}/{\boldsymbol {x}}}\right \Vert }_{D}\right )$, ${\boldsymbol {x}}>{\boldsymbol {0}}\in {\mathbb R}^{d}$, as in Theorem 4.1 below. Choose 1 ≤ i < j ≤ d. Then ξ_i, ξ_j are independent ⇔ c_ij = 0, and ξ_i = ξ_j a.s. ⇔ c_ij = 1. The co-extremality coefficient is in this sense similar to the extremal dependence measure defined in Larsson and Resnick (2012). Another characterization of the co-extremality coefficient in terms of a random vector X, which is in the domain of attraction of G, is given in Eq. 4.5.

Proof

We first establish part (i). Suppose that $c_{ij}=E\left (\sqrt {Z_{i}Z_{j}}\right )=0$. Then Z_iZ_j = 0 a.s. and, thus, $\min \limits (Z_{i},Z_{j})=0$ a.s. As a consequence,

$$ Z_{i}+Z_{j}=\max(Z_{i},Z_{j})+\min(Z_{i},Z_{j})=\max(Z_{i},Z_{j})\quad\text{a.s.} $$

and thus, taking expectations, we obtain

$$ 2=E(Z_{i}+Z_{j}) = E(\max(Z_{i},Z_{j}))=\left\Vert(1,1)\right\Vert_{D_{ij}}. $$

Corollary 2.5 now implies ${\left \Vert \cdot \right \Vert }_{D_{ij}}={\left \Vert \cdot \right \Vert }_{1}$.

If, on the other hand, ${\left \Vert \cdot \right \Vert }_{D_{ij}}={\left \Vert \cdot \right \Vert }_{1}$, then we can choose by Theorem 3.5 for (Z_i,Z_j) in $c_{ij}=E\left (\sqrt {Z_{i}Z_{j}}\right )$ the random permutation of (2,0) with equal probability 1/2. But then Z_iZ_j = 0 and, thus, c_ij = 0.

Next we establish part (ii). Suppose that ${\left \Vert \cdot \right \Vert }_{D_{ij}}={\left \Vert \cdot \right \Vert }_{\infty }$. Then we can choose by Theorem 3.5 for (Z_i,Z_j) in $c_{ij}=E\left (\sqrt {Z_{i}Z_{j}}\right )$ the constant random vector (1,1) and obtain c_ij = 1.

Now we prove the reverse direction. From Hölder’s inequality we know that

$$ 0\le c_{ij}= E\left( \sqrt{Z_{i}}\sqrt{Z_{j}}\right)\le E(Z_{i})^{1/2} E(Z_{j})^{1/2}=1, $$

with equality c_ij = 1 iff Z_i = Z_j a.s. But (Z_i,Z_j) = (Z_i,Z_i) a.s. generates the bivariate D-norm ${\left \Vert \cdot \right \Vert }_{D_{ij}}={\left \Vert \cdot \right \Vert }_{\infty }$. □

The co-extremality coefficient behaves quite similar to the ordinary coefficient of correlation. But, while the ordinary coefficient of correlation is a measure of overall linear dependence in the data, the co-extremality coefficient addresses the upper tail of a bivariate distribution. Even more, the matrix of pairwise co-extremality coefficients turns out to be positive semidefinite, just like the ordinary correlation matrix. The following result might, therefore, enable the application of standard statistical techniques such as principal component analysis to extremal data. But this is future work. A principal component analysis for the extremal dependence measure defined in Larsson and Resnick (2012) was pursued by Cooley and Thibaud (2019).

Lemma 3.8

The co-extremality matrix

$$ C:=\left( c_{ij}\right)_{1\le i,j\le d} $$

is positive semidefinite.

Proof

We have for $\boldsymbol {y}=(y_{1},\dots ,y_{d})\in \mathbb R^{d}$

$$ \begin{array}{@{}rcl@{}} \boldsymbol{y} C\boldsymbol{y}^{\intercal} &=& \sum\limits_{1\le i,j\le d}y_{i} E\left( \sqrt{Z_{i}Z_{j}}\right)y_{j}\\ &=& E\left( \sum\limits_{1\le i,j\le d}y_{i} \sqrt{Z_{i}}\sqrt{Z_{j}}y_{j}\right)\\ &=&E\left( \left( \sum\limits_{1\le i\le d}y_{i}\sqrt{Z_{i}} \right)^{2} \right)\ge 0. \end{array} $$

□

4 Multivariate Extremes and D-Norms

Next we link D-norms with MEVT. A df G on $\mathbb R^{d}$ is called max-stable, if for every $n\in \mathbb N$ there exists vectors a_n > 0, ${\boldsymbol {b}}_{n}\in {\mathbb R}^{d}$ such that

$$ G^{n}\left( \boldsymbol{a}_{n}\boldsymbol{x}+\boldsymbol{b}_{n}\right)=G(\boldsymbol{x}),\qquad \boldsymbol{x}\in\mathbb R^{d}. $$

(4.1)

Recall that all operations on vectors such as addition, multiplication etc. are always meant componentwise.

A df G on $\mathbb R^{d}$ is a simple max-stable or simple extreme value df iff it is max-stable in the sense of Eq. 4.1, and if it has unit Fréchet margins:

$$ G(x\boldsymbol{e}_{i})=G(0,\dots,0,x,0,\dots,0)=\exp(-1/x),\qquad x > 0, 1\le i\le d. $$

In this case, the norming constants are $\boldsymbol {b}_{n}:=\boldsymbol {0}\in \mathbb R^{d}$ and $\boldsymbol {a}_{n}:=(n,\dots ,n)\in \mathbb R^{d}$. $n\in \mathbb N$.

The theory of D-norms allows a mathematically elegant characterization of an arbitrary simple max-stable df as formulated in the next result; for a proof see Theorem 2.3.3 in Falk (2019). It comes from results found in Balkema and Resnick (1977), de Haan and Resnick (1977), Pickands (1981), and Vatan (1985). By ${\boldsymbol {1}}=(1,\dots ,1)\in {\mathbb R}^{d}$ we denote the vector in ${\mathbb R}^{d}$ with constant entry one.

Theorem 4.1

A df G on $\mathbb R^{d}$ is a simple max-stable df iff there exists a D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on $\mathbb R^{d}$ such that

$$ G(\boldsymbol{x})=\exp\left( -\left\Vert\frac{\boldsymbol{1}}{{\boldsymbol{x}}}\right\Vert_{D}\right),\qquad \boldsymbol{x}>\boldsymbol{0}\in\mathbb R^{d}. $$

A multivariate df F on $\mathbb R^{d}$ is said to be in the max-domain of attraction of a simple EVD G, denoted by $F\in \mathcal D(G)$, if there are vectors a_n > 0, ${\boldsymbol {b}}_{n}\in {\mathbb R}^{d}$, $n\in {\mathbb N}$, such that

$$ F^{n}(\boldsymbol{a}_{n}\boldsymbol{x}+\boldsymbol{b}_{n}){\longrightarrow}_{n\to\infty} G(\boldsymbol{x}),\qquad \boldsymbol{x}\in\mathbb R^{d}. $$

(4.2)

This definition clearly applies to an arbitrary EVD G, but without loss of generality and in view of Theorem 4.1, we restrict our approach in what follows to the case of a simple EVD G.

Put a_t := a_[t], b_t := b_[t], t ≥ 1, where $[t]:=\max \limits \left \{n\in \mathbb N: n\le t\right \}$ is the integer part of t ≥ 1. Then the condition $F\in \mathcal D(G)$ in Eq. 4.2 can be formulated in a continuous way as follows. We have $F\in \mathcal D(G)$ iff there are vectors ${\boldsymbol {a}}_{t}>{\boldsymbol {0}}\in {\mathbb R}^{d}$, ${\boldsymbol {b}}_{t}\in {\mathbb R}^{d}$, t ≥ 1, such that

$$ F^{t}(\boldsymbol{a}_{t}\boldsymbol{x}+\boldsymbol{b}_{t})\to_{t\to\infty} G(\boldsymbol{x}),\qquad \boldsymbol{x}\in\mathbb R^{d}. $$

(4.3)

This equivalent condition will ease later proofs.

Recall that a copula on $\mathbb R^{d}$ is the df of a random vector $\boldsymbol {U}=(U_{1},\dots ,U_{d})$ with the property that each U_i follows the uniform distribution on (0,1). For an exhaustive account on copulas we refer to Nelsen (2006). Sklar’s theorem (Sklar 1959, 1996) plays a major role for the characterization of $F\in \mathcal D(G)$.

Theorem 4.2 (Sklar)

For an arbitrary df F on $\mathbb R^{d}$, with univariate margins $F_{1},\dots ,F_{d}$, there exists a copula C such that

$$ F(\boldsymbol{x}) = C(F_{1}(x_{1}),\dots,F_{d}(x_{d})),\qquad \boldsymbol{x}=(x_{1},\dots,x_{d})\in\mathbb R^{d}. $$

If F is continuous, then C is uniquely determined and given by

$$C(\boldsymbol{u})=F(F_{1}^{-1}(u_{1}),\dots,F_{d}^{-1}(u_{d})), \qquad \boldsymbol{u}=(u_{1},\dots,u_{d})\in(0,1)^{d}, $$

where $F_{i}^{-1}(u)=\inf \{t\in \mathbb R: F_{i}(t)\ge u\}$, u ∈ (0,1), is the generalized inverse of F_i. The copula of a random vector ${\boldsymbol {Y}}=(Y_{1},\dots ,Y_{d})$ is meant to be the copula of its df.

The next result goes back to Deheuvels (1984) and Galambos (1987). It is established in Proposition 3.1.10 in Falk (2019).

Proposition 4.3

A d-variate df F satisfies $F\in \mathcal D(G)$ iff this is true for the univariate margins of F together with the condition that the copula C_F of F satisfies the expansion

$$ C_{F}(\boldsymbol{u})=1-\left\Vert\boldsymbol{1}-\boldsymbol{u}\right\Vert_{D} + o\left( \left\Vert\boldsymbol{1}-\boldsymbol{u}\right\Vert\right) $$

as u →1, uniformly for u ∈ [0,1]^d, where ${\left \Vert \cdot \right \Vert }_{D}$ is the D-norm on $\mathbb R^{d}$ that corresponds to G in the sense of Theorem 4.1.

In the next result we present a new characterization of multivariate max-domain of attraction.

Theorem 4.4

Let $\boldsymbol {X}\ge \boldsymbol {0}\in \mathbb R^{d}$ be a random vector with df F. Then we have

$$ \begin{array}{@{}rcl@{}} & F^{t}(t\boldsymbol{x})\to_{t\to\infty}\exp\left( -\left\Vert\frac{\boldsymbol{1}}{\boldsymbol{x}}\right\Vert_{D}\right),\qquad \boldsymbol{x}>\boldsymbol{0}\in\mathbb R^{d},\\ &\iff tP(h(\boldsymbol{X})>t)\to_{t\to\infty}E(h(\boldsymbol{Z})) \end{array} $$

for each continuous function $h:[0,\infty )^{d}\to [0,\infty )$, which is homogeneous of order one, and Z is an arbitrary generator of the D-norm ${\left \Vert \cdot \right \Vert }_{D}$.

Note that by Theorem 3.5, the number E(h(Z)) does not depend on the particular generator Z of ${\left \Vert \cdot \right \Vert }_{D}$.

Remark 4.5

The conclusion in the preceding result is obvious for X := Z/U, where Z is an arbitrary generator of a D-norm ${\left \Vert \cdot \right \Vert }_{D}$, the random variable U follows the uniform distribution on (0,1), and U and Z are independent. In this case, we obtain for each measurable function $h:[0,\infty )^{d}\to [0,\infty )$ which is homogeneous of order one,

$$ \begin{array}{@{}rcl@{}} tP\left( h\left( \frac 1U \boldsymbol{Z}\right) >t \right) &=&tP(h(\boldsymbol{Z})>tU)\\ &=&t{{\int}_{0}^{1}} P(h(\boldsymbol{Z})>tu) du\qquad \text{(use Fubini)}\\ &=& {{\int}_{0}^{t}} P(h(\boldsymbol{Z})>u) du\\ &\to& {~}_{t\to\infty} {\int}_{0}^{\infty} P(h(\boldsymbol{Z})>u) du = E(h(\boldsymbol{Z})) \end{array} $$

by Eq. 3.1. Note again that by Theorem 3.5, the number E(h(Z)) does not depend on the particular generator Z of ${\left \Vert \cdot \right \Vert }_{D}$.

If the generator Z is in addition bounded, then X = Z/U follows a simple multivariate Generalized Pareto Distribution (GPD). In this case its df is $F_{{\boldsymbol {X}}}({\boldsymbol {x}})=1-{\left \Vert {{\boldsymbol {1}}/{\boldsymbol {x}}}\right \Vert }_{D}$ for large ${\boldsymbol {x}}>{\boldsymbol {0}}\in {\mathbb R}^{d}$. The definition of a multivariate GPD is not unique in the literature. But, if ${\boldsymbol {Y}}=(Y_{1},\dots ,Y_{d})$ is an arbitrary random vector whose copula is excursion stable and each component Y_i follows in its upper tail a standard Pareto distribution, then we call its distribution a simple GPD. The df F_Y(x) of Y coincides for large ${\boldsymbol {x}}>{\boldsymbol {0}}\in {\mathbb R}^{d}$ in this case with that of X = Z/U; see Remark 3.1.3 in Falk (2019).

Proof of Theorem 4.4

The implication “⇐=” is easily seen: Choose $\boldsymbol {x}=(x_{1},\dots , x_{d})>\boldsymbol {0}\in \mathbb R^{d}$ and put $h({\boldsymbol {y}}):=\max \limits _{1\le i\le d}(y_{i}/x_{i})$. Then the assumption implies

$$ tP\left( \max_{1\le i\le d}\frac{X_{i}}{x_{i}}>t\right)\to_{t\to\infty} E\left( \max_{1\le i\le d}\frac{Z_{i}}{x_{i}}\right)= \left\Vert\frac{\boldsymbol{1}}{\boldsymbol{x}}\right\Vert_{D}. $$

But

$$ \begin{array}{@{}rcl@{}} tP\left( \max_{1\le i\le d}\frac{X_{i}}{x_{i}}>t\right)&= t\left( 1- P\left( \max_{1\le i\le d}\frac{X_{i}}{x_{i}}\le t\right)\right)\\ &= t(1-F(t\boldsymbol{x})), \end{array} $$

and thus, we obtain from the fact that $\log (1+\varepsilon )/\varepsilon \to _{\varepsilon \to 0}1$,

$$ \begin{array}{@{}rcl@{}} F^{t}(t\boldsymbol{x})&=& \exp(t\log(F(t\boldsymbol{x})))\\ &=& \exp\big(t\log(1+(F(t\boldsymbol{x})-1))\big)\\ &=& \exp\left( \frac{\log(1+(F(t\boldsymbol{x})-1))}{F(t\boldsymbol{x})-1} t (F(t\boldsymbol{x})-1) \right)\\ &&\to_{t\to\infty}\exp\left( -\left\Vert\frac{\boldsymbol{1}}{\boldsymbol{x}}\right\Vert_{D} \right), \end{array} $$

which is the assertion.

Next we establish the implication “⇒”. Taking the logarithm on both sides of the assumption implies

$$ t\log(F(t\boldsymbol{x}))\to_{t\to\infty}-\left\Vert\frac{\boldsymbol{1}}{\boldsymbol{x}}\right\Vert_{D}, $$

or

$$ t\frac{\log\big(1+(F(t\boldsymbol{x})-1)\big)}{F(t\boldsymbol{x})-1} (1-F(t\boldsymbol{x}))\to_{t\to\infty} \left\Vert\frac{\boldsymbol{1}}{\boldsymbol{x}}\right\Vert_{D}, $$

i.e.,

$$ t(1-F(t\boldsymbol{x}))\to_{t\to\infty} \left\Vert\frac{\boldsymbol{1}}{\boldsymbol{x}}\right\Vert_{D}. $$

In Proposition 3.2 we defined a uniquely determined measure ν on the Borel σ-field $\mathbb B_{\boldsymbol {E}}$ of ${\boldsymbol {E}}=[0,\infty )^{d}\backslash \{{\boldsymbol {0}}\}$, with $\nu \left ([{\boldsymbol {0}},{\boldsymbol {x}}]^{\complement }\right ) = {\left \Vert {{\boldsymbol {1}}/{\boldsymbol {x}}}\right \Vert }_{D}$, ${\boldsymbol {x}}>{\boldsymbol {0}}\in {\mathbb R}^{d}$. Put, for t > 0,

$$ \nu_{t}(M):= t P\left( \frac 1t \boldsymbol{X}\in M\right),\qquad M\in\mathbb B_{\boldsymbol{E}}. $$

Then ν_t, t > 0, defines a sequence of measures on $\mathbb B_{\boldsymbol {E}}$ with

$$ \nu_{t}\left( [\boldsymbol{0},\boldsymbol{x}]^{\complement}\right) \to_{t\to\infty} \left\Vert\frac{\boldsymbol{1}}{\boldsymbol{x}}\right\Vert_{D} = \nu\left( [\boldsymbol{0},\boldsymbol{x}]^{\complement}\right),\qquad \boldsymbol{x}>\boldsymbol{0}\in\mathbb R^{d}. $$

From Eqs. 3.5 and 3.6 we therefore obtain, for $\boldsymbol {y}\ge \boldsymbol {0}\in \mathbb R^{d}$, y≠0, and z > y,

$$ \nu_{t}([\boldsymbol{y},\boldsymbol{z})) \to_{t\to\infty}\nu([\boldsymbol{y},\boldsymbol{z})). $$

But this implies that ν_t converges to ν vaguely as t tends to infinity (Resnick 2008, Proposition 5.17), i.e., $\nu _{t}(M)\to _{t\to \infty }\nu (M)$ for each $M\in \mathbb B_{{\boldsymbol {E}}}$ with ν(∂M) = 0, where $\partial M=\overline {M}\cap \overline {{M^{\complement }}}$ is the topological border of the set M, with $\overline {A}$ denoting the topological closure of a set A ⊂E.

Choose a continuous function $h:[0,\infty )^{d}\to [0,\infty )$, which is homogeneous of order one. Then we have, for t > 0,

$$ tP(h(\boldsymbol{X})>t) = t P\left( h\left( \frac 1t\boldsymbol{X}\right)>1\right) = \nu_{t}(M), $$

with $M:=\left \{\boldsymbol {x}\in \boldsymbol {E}: h(\boldsymbol {x})>1\right \}$. If we can show that ν(∂M) = 0, then we obtain $\nu _{t}(M)\to _{t\to \infty }\nu (M)$, or

$$ tP(h(\boldsymbol{X})>t)\to_{t\to\infty}\nu(M). $$

First we claim that

$$ \nu(M) = E(h(\boldsymbol{Z})). $$

But this can easily be seen as follows:

$$ \begin{array}{@{}rcl@{}} \nu(M)&=&\left( \lambda\times P_{\boldsymbol{Z}}\right)\left( T^{-1}(M)\right)\\ &=&\left( \lambda\times P_{\boldsymbol{Z}}\right)\left( \left\{(s,\boldsymbol{z}): \frac 1s \boldsymbol{z}\in M\right\}\right)\\ &=&\left( \lambda\times P_{\boldsymbol{Z}}\right)\left( \left\{(s,\boldsymbol{z}): h\left( \frac 1s \boldsymbol{z}\right)>1\right\}\right)\\ &=&\left( \lambda\times P_{\boldsymbol{Z}}\right)\left( \left\{(s,\boldsymbol{z}): h(\boldsymbol{z})>s\right\}\right)\\ &=& {\int}_{\boldsymbol{E}}{\int}_{0}^{\infty} 1(h(\boldsymbol{z})>s) ds P_{\boldsymbol{Z}}(d\boldsymbol{z})\qquad \text{(use Fubini)}\\ &=& {\int}_{\boldsymbol{E}}h(\boldsymbol{z}) P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=&{\int}_{[0,\infty)^{d}}h(\boldsymbol{z}) P_{\boldsymbol{Z}}(d\boldsymbol{z})\qquad \text{(as $h(\boldsymbol{0})=0$)}\\ &=& E(h(\boldsymbol{Z})). \end{array} $$

(4.4)

Therefore, all what is left to prove is that ν(∂M) = 0. We have, by the continuity of the function h,

$$ \begin{array}{@{}rcl@{}} \partial M &=&\overline{M}\cap\overline{M}^{\complement}\\ &=&\left\{\boldsymbol{x}\in\boldsymbol{E}: h(\boldsymbol{x})\ge 1\right\}\cap \left\{\boldsymbol{x}\in\boldsymbol{E}: h(\boldsymbol{x})\le 1\right\}\\ &=& \left\{\boldsymbol{x}\in\boldsymbol{E}: h(\boldsymbol{x})=1\right\}. \end{array} $$

Finally, by repeating the arguments in the derivation of Eq. 4.4, we obtain

$$ \nu\left( \left\{\boldsymbol{x}\in\boldsymbol{E}: h(\boldsymbol{x})\ge 1\right\}\right) = \nu\left( \left\{\boldsymbol{x}\in\boldsymbol{E}: h(\boldsymbol{x})> 1\right\}\right) = E(h(\boldsymbol{Z})), $$

and, thus,

$$ \begin{array}{@{}rcl@{}} \nu(\partial M)&=& \nu\left( \left\{\boldsymbol{x}\in\boldsymbol{E}: h(\boldsymbol{x})= 1\right\}\right)\\ &=& \nu\left( \left\{\boldsymbol{x}\in\boldsymbol{E}: h(\boldsymbol{x})\ge 1\right\}\backslash \left\{\boldsymbol{x}\in\boldsymbol{E}: h(\boldsymbol{x})> 1\right\} \right)\\ &=& \nu\left( \left\{\boldsymbol{x}\in\boldsymbol{E}: h(\boldsymbol{x})\ge 1\right\}\right)-\nu\left( \left\{\boldsymbol{x}\in\boldsymbol{E}: h(\boldsymbol{x})> 1\right\} \right) = 0. \end{array} $$

Recall that $E(h(\boldsymbol {Z}))<\infty$, as we can choose, by Theorem 2.3, a generator Z which is bounded. This completes the proof of Theorem 4.4. □

Theorem 4.4 implies, for example, the following characterization of the co-extremality index:

$$ \begin{array}{@{}rcl@{}} c_{ij} &=& E\left( \sqrt{Z_{i}Z_{j}}\right) \\ &=&\lim_{t\to\infty} tP\left( X_{i}X_{j}>t^{2}\right)= \lim_{t\to\infty} \frac{P\left( X_{i}X_{j}>t^{2}\right)}{\sqrt{P(X_{i}>t)P(X_{j}>t)}} \end{array} $$

(4.5)

for 1 ≤ i, j ≤ d, if the random vector $\boldsymbol {X}=(X_{1},\dots ,X_{d})\ge \boldsymbol {0}\in \mathbb R^{d}$ satisfies the first condition in Theorem 4.4.

The fact that tP(X_iX_j > t²) has a limit if t tends to infinity was already observed by (Jessen and Mikosch 2006, Section 4).

Another consequence of Theorem 4.4 is the following result, which was already established in Barbe et al. (2006). It is particularly interesting for risk assessment, as the event ${\sum }_{i=1}^{d} X_{i}>t$ with a large threshold t may describe an unwanted exceedance above a high threshold. By Corollary 4.6, the probability of this event is approximately d/t as t increases, independent of the dependence structure among $X_{1},\dots ,X_{d}$.

Corollary 4.6

Let $\boldsymbol {X}=(X_{1},\dots ,X_{d})\ge \boldsymbol {0}\in \mathbb R^{d}$ be a random vector that satisfies the first condition in Theorem 4.4. For continuous functions $h_{1},\dots ,h_{n}: [0,\infty )^{d}\to [0,\infty )$, $n\in {\mathbb N}$, which are homogeneous of order one, we have

$$ \lim_{t\to\infty} t P\left( \sum\limits_{i=1}^{n} h_{i}(\boldsymbol{X})>t \right) = \sum\limits_{i=1}^{n}\lim_{t\to\infty} tP(h_{i}(\boldsymbol{X})>t)=\sum\limits_{i=1}^{n} E(h_{i}(\boldsymbol{Z})). $$

As a special case we get

$$ \lim_{t\to\infty}t P\left( \sum\limits_{i=1}^{d} X_{i} >t\right) = d, $$

regardless of the tail dependence structure among $X_{1},\dots ,X_{d}$.

Proof

The function $h(\boldsymbol {x}):={\sum }_{i=1}^{n} h_{i}(\boldsymbol {x})$ is continuous, non negative and homogeneous of order one. We can apply Theorem 4.4 and obtain

$$ \begin{array}{@{}rcl@{}} \lim_{t\to\infty}t P\left( \sum\limits_{i=1}^{n} h_{i}(\boldsymbol{X})>t\right)&=& E\left( \sum\limits_{i=1}^{n} h_{i}(\boldsymbol{Z})\right)\\ &=& \sum\limits_{i=1}^{n} E(h_{i}(\boldsymbol{Z}))\\ &=& \sum\limits_{i=1}^{n} \lim_{t\to\infty} tP(h_{i}(\boldsymbol{X})>t). \end{array} $$

By choosing n = d and h_i(x) = x_i, 1 ≤ i ≤ d, $\boldsymbol {x}=(x_{1},\dots ,x_{d})$, we obtain the special case

$$ \lim_{t\to\infty}t P\left( \sum\limits_{i=1}^{d} X_{i}>t \right) = \sum\limits_{i=1}^{d} E(Z_{i}) = d. $$

□

Theorem 4.4 enables the following characterization, when a copula C is in the max-domain of attraction of an EVD G. This time we consider a standard EVD $G({\boldsymbol {x}})=\exp \left (-{\left \Vert {{\boldsymbol {x}}}\right \Vert }_{D}\right )$, ${\boldsymbol {x}}\le {\boldsymbol {0}}\in {\mathbb R}^{d}$, instead of a simple one. This is due to the fact that each univariate margin of C is the uniform distribution on (0,1), with df H(x) = x, x ∈ [0,1]. It satisfies $H\left (1-n^{-1}x\right ) \to _{n\to \infty }\exp (x)$, x ≤ 0, and thus, if $C\in \mathcal D(G)$, then the EVD G has necessarily standard exponential margins. In this case it can be represented as $G({\boldsymbol {x}})=\exp \left (-{\left \Vert {{\boldsymbol {x}}}\right \Vert }_{D}\right )$, ${\boldsymbol {x}}\le {\boldsymbol {0}}\in {\mathbb R}^{d}$, with some D-norm ${\left \Vert \cdot \right \Vert }_{D}$, see Theorem 2.3.3 in Falk (2019).

Corollary 4.7

Suppose the random vector $\boldsymbol {U}=(U_{1},\dots ,U_{d})$ follows a copula C. We have

$$ \begin{array}{@{}rcl@{}} &&C\in\mathcal D(G),\text{ with }G(\boldsymbol{x})=\exp\left( -\left\Vert\boldsymbol{x}\right\Vert_{D}\right),\qquad \boldsymbol{x}\le\boldsymbol{0}\in\mathbb R^{d},\\ &&\iff C^{t}\left( \boldsymbol{1} + \frac 1t \boldsymbol{x}\right)\to_{t\to\infty}\exp\left( -\left\Vert\boldsymbol{x}\right\Vert_{D}\right),\qquad \boldsymbol{x}\le\boldsymbol{0}\in\mathbb R^{d},\\ &&\iff t P\left( h\left( \frac{\boldsymbol{1}}{\boldsymbol{1}-\boldsymbol{U}}\right) >t \right)\to_{t\to\infty} E(h(\boldsymbol{Z})), \end{array} $$

for any continuous function $h:[0,\infty )^{d}\to [0,\infty )$, which is homogeneous of order one, with Z being an arbitrary generator of ${\left \Vert \cdot \right \Vert }_{D}$.

5 Modeling Multivariate Exceedances

The following result can be used for stochastic modeling of multivariate exceedances above high thresholds and the estimation of its probability. By →_D we denote ordinary convergence in distribution of random vectors or, equivalently, ordinary weak convergence of their corresponding distributions. For a thorough presentation of multivariate Peaks-over-Threshold modelling we refer to Rootzén et al. (2018) and the exhaustive literature cited therein.

Theorem 5.1

Let the random vector $\boldsymbol {X}\ge \boldsymbol {0}\in \mathbb R^{d}$ have df F with

$$ F^{t}(t\boldsymbol{x})\to_{t\to\infty}\exp\left( -\left\Vert\frac{\boldsymbol{1}}{\boldsymbol{x}}\right\Vert_{D}\right),\qquad \boldsymbol{x}>\boldsymbol{0}\in\mathbb R^{d}. $$

For an arbitrary norm ${\left \Vert \cdot \right \Vert }$ on $\mathbb R^{d}$, there exists by Theorem 2.3 a generator Z of ${\left \Vert \cdot \right \Vert }_{D}$ with the additional property ${\left \Vert {{\boldsymbol {Z}}}\right \Vert }=\text {const}$. Its distribution P_Z is uniquely determined, and we have

$$ P\left( \text{const}\frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert}\in\cdot \Big| \left\Vert\boldsymbol{X}\right\Vert>t\right) \to_{D} P_{\boldsymbol{Z}}(\cdot) $$

as $t\to \infty$.

The preceding result is in particular applicable with the choice ${\left \Vert \cdot \right \Vert }={\left \Vert \cdot \right \Vert }_{1}$, in which case the typically unknown number $\text {const}={\left \Vert {\boldsymbol {Z}}\right \Vert }_{1}$ equals d, just see the proof of Corollary 2.4.

Corollary 5.2

Under the conditions of Theorem 5.1 we obtain, with ${\left \Vert \cdot \right \Vert }={\left \Vert \cdot \right \Vert }_{1}$,

$$ P\left( d\frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert_{1}}\in\cdot \Big| \left\Vert\boldsymbol{X}\right\Vert_{1}>t\right) \to_{D} P_{\boldsymbol{Z}}(\cdot) $$

as $t\to \infty$, where Z is a generator of ${\left \Vert \cdot \right \Vert }_{D}$ with ${\left \Vert {\boldsymbol {Z}}\right \Vert }_{1}=d$.

If we put in particular X := 1/(1 −U), where U follows a copula $C\in \mathcal D(G)$, $G(\boldsymbol {x})=\exp \left (-\left \Vert \boldsymbol {x}\right \Vert _{D}\right )$, $\boldsymbol {x}\le \boldsymbol {0}\in \mathbb R^{d}$, then we obtain the above conclusion.

If a multivariate exceedance above a high threshold is defined as a realization of the random vector $\boldsymbol {X}=(X_{1},\dots ,X_{d})\ge \boldsymbol {0}\in \mathbb R^{d}$, with ${\left \Vert {{\boldsymbol {X}}}\right \Vert }_{1}=X_{1}+\dots +X_{d}\ge t$ and a large value t , then Corollary 5.2 provides its asymptotic distribution. Having independent copies $\boldsymbol {X}^{(1)},\dots ,\boldsymbol {X}^{(n)}$ of X, the limit distribution P_Z in Corollary 5.2 can be estimated in a straightforward manner by the ordinary empirical measure corresponding to ${\boldsymbol {X}}^{(1)},\dots ,{\boldsymbol {X}}^{(n)}$ as follows. Put, for ${\boldsymbol {x}}\ge {\boldsymbol {0}}\in {\mathbb R}^{d}$ and t > 0,

$$ F_{n,t}(\boldsymbol{x}):= \frac 1{M_{n,t}} \sum\limits_{i=1}^{n} 1\left( d\frac{\boldsymbol{X}^{(i)}}{\left\Vert\boldsymbol{X}^{(i)}\right\Vert_{1}}\le \boldsymbol{x} \right) 1\left( \left\Vert\boldsymbol{X}^{(i)}\right\Vert_{1}>t\right), $$

with

$$ M_{n,t} := \sum\limits_{i=1}^{n} 1\left( \left\Vert\boldsymbol{X}^{(i)}\right\Vert_{1}>t\right). $$

According to Lemma 1.4.1 in Reiss (1993), F_{n, t} is the ordinary empirical df of m independent and identically distributed random vectors $\boldsymbol {Y}^{(1)},\dots ,\boldsymbol {Y}^{(m)}$ with df

$$ P\left( \boldsymbol{Y}^{(i)}\le\boldsymbol{x} \right)= P\left( d\frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert_{1}}\le \boldsymbol{x} \mid \left\Vert\boldsymbol{X}\right\Vert_{1}>t \right),\qquad 1\le i\le m, $$

conditional on M_{n, t} = m, where M_{n, t} is also independent of $\boldsymbol {Y}^{(1)},\dots ,\boldsymbol {Y}^{(m)}$. This representation allows the estimation of the distribution P_Z as n and t both tend to infinity in a straightforward manner. But details are outside the scope of this paper and require future work.

In the proof of Theorem 5.1 we make use of the following auxiliary topological result.

Lemma 5.3

Choose an arbitrary norm ${\left \Vert \cdot \right \Vert }$ on $\mathbb R^{d}$ and let A be a Borel subset of the sphere $S:=\left \{\boldsymbol {x}\in [0,\infty )^{d}: {\left \Vert {\boldsymbol {x}}\right \Vert }=1\right \}$. Put

$$ \begin{array}{@{}rcl@{}} M_{A}&:=& (1,\infty)\cdot A:= \left\{s\boldsymbol{a}: s>1,\boldsymbol{a}\in A\right\}\\ &= &\left\{\boldsymbol{x}\in[0,\infty)^{d}: \frac{\boldsymbol{x}}{\left\Vert\boldsymbol{x}\right\Vert}\in A,\left\Vert\boldsymbol{x}\right\Vert>1\right\}. \end{array} $$

Then, with M_A seen as a subset of $[0,\infty )^{d}$,

$$ \partial M_{A}\subset S\cup (1,\infty)\cdot\left( \overline{A}\cap\overline{S\backslash A} \right). $$

Proof

Let x ∈ ∂M_A. Then $\left \Vert \boldsymbol {x}\right \Vert \ge 1$. If $\left \Vert \boldsymbol {x}\right \Vert =1$, then x ∈ S and we are done. So assume $\left \Vert \boldsymbol {x}\right \Vert >1$. Because x ∈ ∂M_A, there exist sequences x_n ∈ M_A, $n\in {\mathbb N}$, and y_n∉M_A, $n\in {\mathbb N}$, with

$$ \boldsymbol{x}=\lim_{n\in\mathbb N}\boldsymbol{x}_{n}= \lim_{n\in\mathbb N}\boldsymbol{y}_{n}, $$

which implies

$$ \lim_{n\in\mathbb N}\left\Vert\boldsymbol{x}_{n}\right\Vert=\lim_{n\in\mathbb N}\left\Vert\boldsymbol{y}_{n}\right\Vert=\left\Vert\boldsymbol{x}\right\Vert>1. $$

Without loss of generality we can assume $\left \Vert \boldsymbol {x}_{n}\right \Vert >1$, $\left \Vert \boldsymbol {y}_{n}\right \Vert >1$, $n\in \mathbb N$, and, thus, $\boldsymbol {x}_{n}/\left \Vert \boldsymbol {x}_{n}\right \Vert \in A$, $\boldsymbol {y}_{n}/\left \Vert \boldsymbol {y}_{n}\right \Vert \in S\backslash A$, $n\in \mathbb N$. The representation

$$ \frac{\boldsymbol{x}}{\left\Vert\boldsymbol{x}\right\Vert} = \lim_{n\in\mathbb N}\frac{\boldsymbol{x}_{n}}{\left\Vert\boldsymbol{x}_{n}\right\Vert}=\lim_{n\in\mathbb N}\frac{\boldsymbol{y}_{n}}{\left\Vert\boldsymbol{y}_{n}\right\Vert} $$

then implies that $\boldsymbol {x}/\left \Vert \boldsymbol {x}\right \Vert \in \overline {A}\cap \overline {S\backslash A}$ and thus, $\boldsymbol {x}\in (1,\infty )\cdot \left (\overline {A}\cap \overline {S\backslash A}\right )$, because ${\left \Vert {{\boldsymbol {x}}}\right \Vert }>1$. □

Proof of Theorem 5.1

We have to establish the convergence

$$ P\left( \text{const}\frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert}\in M \Big| \left\Vert\boldsymbol{X}\right\Vert>t\right) \to_{t\to\infty} P_{\boldsymbol{Z}}(M) $$

for each Borel subset $M\subset [0,\infty )^{d}$ with P_Z(∂M) = P(Z ∈ ∂M) = 0.

In the proof of Theorem 4.4 we established the convergence $\nu _{t}(M)\to _{t\to \infty }\nu (M)$ for each Borel set $M\in \mathbb B_{\boldsymbol {E}}$, ${\boldsymbol {E}}=[0,\infty )^{d}\backslash \{{\boldsymbol {0}}\}$, with ν(∂M) = 0, where

$$ \nu(\cdot)=\left( \lambda\times P_{\boldsymbol{Z}}\right)\left( T^{-1}(\cdot)\right) $$

as defined in Theorem 3.5, and

$$ \nu_{t}(\cdot) = t P\left( \frac 1t \boldsymbol{X}\in\cdot \right). $$

Put

$$ S_{\text{const}} :=\left\{\boldsymbol{x}\in[0,\infty)^{d}: \left\Vert\boldsymbol{x}\right\Vert=\text{const}\right\}; $$

note that the generator Z realizes in S_const. Let $M\subset [0,\infty )^{d}$ be a Borel subset with P(Z ∈ ∂M) = 0. Put A := M ∩ S_const and

$$ M_{A}:= (1,\infty)\cdot A = \left\{s\boldsymbol{a}: s>1,\boldsymbol{a}\in A\right\}. $$

Check that M_A is a Borel subset of $[0,\infty )^{d}$. Note that 0∉M_A, because 0∉S_const, and hence, $M_{A}\in \mathbb B_{\boldsymbol {E}}$.

From Lemma 5.3, applied to the norm ${\left \Vert \cdot \right \Vert }/\text {const}$, we obtain

$$ \partial M_{A}\subset S_{\text{const}}\cup (1,\infty)\cdot \left( \overline{A}\cap\overline{S_{\text{const}}\backslash A} \right), $$

which implies

$$ \nu(\partial M_{A}) \le \nu\left( S_{\text{const}}\right)+ \nu\left( (1,\infty)\cdot\left( \overline {A}\cap \overline{S_{\text{const}}\backslash A}\right) \right). $$

In what follows we prove that the upper bound in this inequality vanishes.

We have

$$ \nu\left( S_{\text{const}}\right)= \nu\left( \left\{\boldsymbol{x}\ge\boldsymbol{0}: \frac{\boldsymbol{x}}{\text{const}}\ge 1\right\}\right) - \nu\left( \left\{\boldsymbol{x}\ge\boldsymbol{0}: \frac{\boldsymbol{x}}{\text{const}}> 1\right\}\right) = 0 $$

by the arguments in Eq. 4.4, and

$$ \begin{array}{@{}rcl@{}} &&\nu\left( (1,\infty)\cdot\left( \overline A\cap \overline{ S_{\text{const}}\backslash A}\right) \right)\\ &=& \left( \lambda\times P_{\boldsymbol{Z}}\right)\left( \left\{{(s,\boldsymbol{z}): \frac 1s \boldsymbol{z}\in (1,\infty)\cdot\left( \overline A\cap \overline{ S_{\text{const}}\backslash A}\right)}\right\} \right)\\ &= &{\int}_0^{\infty} {\int}_{S_{\text{const}}} 1\left( \boldsymbol{z}\in (s,\infty)\cdot \left( \overline A\cap \overline{ S_{\text{const}}\backslash A} \right) \right) P_{\boldsymbol{Z}}(d\boldsymbol{z}) ds\quad (\text{$\boldsymbol{Z}$ is in $S_{\text{const}}$})\\ &=& {\int}_0^1 {\int}_{\overline A\cap \overline{ S_{\text{const}}\backslash A}} 1 P_{\boldsymbol{Z}}(d\boldsymbol{z}) ds \qquad (\boldsymbol{Z} \text{ is in } S_{\text{const}})\\ &=& P\left( \boldsymbol{Z}\in\left( \overline A\cap \overline{ S_{\text{const}}\backslash A}\right) \right)\\ &\le& P(\boldsymbol{Z}\in\partial M)\qquad (\text{because } \overline A\cap \overline{ S_{\text{const}}\backslash A}\subset \partial M )\\ &=& 0 \end{array} $$

(5.1)

by assumption.

As a consequence of the preceding considerations we have ν(∂M) = 0 and, thus,

$$ \nu_{t}(M)\to_{t\to\infty} \nu(M). $$

From Theorem 4.4 we obtain

$$ \begin{array}{@{}rcl@{}} &&\lim_{t\to\infty}P\left( \text{const} \frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert}\in M \Big| \left\Vert\boldsymbol{X}\right\Vert>t \right)\\ &=& \lim_{t\to\infty}P\left( \text{const} \frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert}\in M \Big| \left\Vert\boldsymbol{X}\right\Vert>\text{const} t \right)\\ &=& \lim_{t\to\infty}P\left( \text{const} \frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert}\in A \Big| \left\Vert\boldsymbol{X}\right\Vert>\text{const} t \right)\quad (\text{recall that } A=M\cap S_{\text{const}})\\ &=& \lim_{t\to\infty}\frac{P\left( \left\Vert\boldsymbol{X}\right\Vert>\text{const} t, \text{const} \frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert}\in A \right)}{P\left( \left\Vert\boldsymbol{X}\right\Vert>\text{const} t\right)}\\ &=& \lim_{t\to\infty} \frac{P\left( \boldsymbol{X}\in t M_{A}\right)}{P\left( \left\Vert\boldsymbol{X}\right\Vert>\text{const} t\right)}\qquad \text{(check equality of the sets)}\\ &=& \frac{\nu\left( M_{A}\right)}{E\left( \left\Vert\boldsymbol{Z}\right\Vert\right)/\text{const}}\\ &=& \nu\left( M_{A}\right)\qquad (\text{recall that } \left\Vert\boldsymbol{Z}\right\Vert=\text{const})\\ &=& P(\boldsymbol{Z}\in A)\qquad \text{(repeat the arguments leading to Eq.~5.1)}. \end{array} $$

This completes the proof of Theorem 5.1. □

Remark 5.4

Theorem 5.1 is implied by Theorem 4.4, but not vice versa. Put X = (X, X) with $P(X>t)=1/\sqrt {t}$, t ≥ 1, and set Z = (1,1), which generates the bivariate D-norm ${\left \Vert \cdot \right \Vert }_{\infty }$.

With an arbitrary norm ${\left \Vert \cdot \right \Vert }$ on $\mathbb R^{2}$ we have ${\left \Vert {\boldsymbol {Z}}\right \Vert }={\left \Vert {(1,1)}\right \Vert }=:\text {const}$, and thus,

$$ \text{const} \frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert} =\text{const} \frac{X(1,1)}{\left\Vert X(1,1)\right\Vert} = (1,1). $$

For all sets $M\in \mathbb B_{\boldsymbol {E}}$, and all t > 0 this implies

$$ \begin{array}{@{}rcl@{}} P\left( \text{const} \frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert}\in M \Big| \left\Vert\boldsymbol{X}\right\Vert>t \right) &= \begin{cases} 1,&\text{if }(1,1)\in M,\\ 0 &\text{elsewhere}, \end{cases}\\ &= P(\boldsymbol{Z}\in M). \end{array} $$

We thus have in particular that the limit result in Theorem 5.1 is valid, but, with h(x₁,x₂) = x₁,

$$ \lim_{t\to\infty}t P(X>t) = \lim_{t\to\infty}\sqrt t\not=E(Z_{1})= 1. $$

6 On Generators Whose Components Sum up to d

In this section we will see that Theorem 5.1 provides a way, how to simulate a generator $\boldsymbol {Z}^{(1)}=\left (Z_{1}^{(1)},\dots ,Z_{d}^{(1)}\right )$ of an arbitrary D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on ${\mathbb R}^{d}$, with the additional property ${\left \Vert {{\boldsymbol {Z}}^{(1)}}\right \Vert }_{1}={\sum }_{i=1}^{d} Z_{i}^{(1)}=d$, and that it delivers the distribution of Z⁽¹⁾, which is unique by Theorem 2.3.

Take a D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on $\mathbb R^{d}$, choose some generator $\boldsymbol {Z}=(Z_{1},\dots ,Z_{d})$ of it, and let U be a random variable, which follows the uniform distribution on (0,1), and which is independent of Z. Put

$$ \boldsymbol{X}:=\frac 1U \boldsymbol{Z}. $$

Then the random vector $\boldsymbol {X}\ge \boldsymbol {0}\in \mathbb R^{d}$ satisfies

$$ P(\boldsymbol{X}\le t\boldsymbol{x})^{t}\to_{t\to\infty}\exp\left( -\left\Vert\frac{\boldsymbol{1}}{\boldsymbol{x}}\right\Vert_{D}\right),\qquad \boldsymbol{x}>\boldsymbol{0}\in\mathbb R^{d}, $$

see Remark 4.5, and thus we obtain from Corollary 5.2

$$ P\left( d \frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert_{1}}\in\cdot \Big| \left\Vert\boldsymbol{X}\right\Vert_{1}>t\right)\to_{D}P\left( \boldsymbol{Z}^{(1)} \in\cdot\right) $$

as $t\to \infty$. But $\boldsymbol {X}/\left \Vert \boldsymbol {X}\right \Vert _{1}=\boldsymbol {Z}/\left \Vert \boldsymbol {Z}\right \Vert _{1}$ and, thus,

$$ P\left( d \frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert_{1}}\in\cdot \Big| \left\Vert\boldsymbol{X}\right\Vert_{1}>t\right) = P\left( d \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert_{1}}\in\cdot \Big| \left\Vert\boldsymbol{Z}\right\Vert_{1}>tU\right). $$

Choosing a large threshold t > 0, this equation enables the simulation of Z⁽¹⁾ in an obvious way. We will see below, in Proposition 6.2, that even the exact distribution of Z⁽¹⁾ can be derived from this equation as well.

Example 6.1

Take, for example, the Dirichlet D-norm ${\left \Vert \cdot \right \Vert }_{D(\alpha )}$, with parameter α > 0. It has the generator

$$ \boldsymbol{Z}=(Z_{1},\dots,Z_{d}) =\frac 1\alpha (V_{1},\dots,V_{d}), $$

where $V_{1},\dots ,V_{d}$ are independent and identically gamma distributed random variables with density $\gamma _{\alpha }(x)= x^{\alpha -1}\exp (-x)/{{{\varGamma }}}(\alpha )$, x > 0. It is well known that the random variables $\left (V_{i}/{\sum }_{j=1}^{d} V_{j}\right )_{i=1}^{d}$ and the sum ${\sum }_{j=1}^{d} V_{j}$ are independent, see, e.g., the proof of Theorem 2.1 in Ng et al. (2011), and thus, by the independence of $(V_{1},\dots ,V_{d})$ and U,

$$ \begin{array}{@{}rcl@{}} &&P\left( d \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert_{1}}\in\cdot \Big| \left\Vert\boldsymbol{Z}\right\Vert_{1}>tU\right)\\ &=& P\left( d\left( \frac{V_{1}}{{\sum}_{j=1}^{d} V_{j}},\dots,\frac{V_{d}}{{\sum}_{j=1}^{d} V_{j}} \right)\in\cdot \Big| \sum\limits_{j=1}^{d} V_{j}>\alpha t U \right)\\ &=& P\left( d\left( \frac{V_{1}}{{\sum}_{j=1}^{d} V_{j}},\dots,\frac{V_{d}}{{\sum}_{j=1}^{d} V_{j}} \right)\in\cdot\right)\\ &=& P\left( \boldsymbol{Z}^{(1)}\in\cdot \right), \end{array} $$

with $\boldsymbol {Z}^{(1)}:= d\left (V_{i}/{\sum }_{j=1}^{d} V_{j}\right )_{i=1}^{d}$.

Suppose, on the other hand, that the generator Z in the definition X = Z/U already satisfies $\left \Vert \boldsymbol {Z}\right \Vert _{1}=d$. Then,

$$ \begin{array}{@{}rcl@{}} P\left( d \frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert_{1}}\in\cdot \Big| \left\Vert\boldsymbol{X}\right\Vert_{1}>t\right) &=& P\left( d \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert_{1}}\in\cdot \Big| \left\Vert\boldsymbol{Z}\right\Vert_{1}>tU\right)\\ &=&P\left( \boldsymbol{Z}\in\cdot \Big| \frac dt >U \right)\\ &=& P(\boldsymbol{Z}\in \cdot),\qquad t>0. \end{array} $$

Theorem 5.1 also provides the distribution of Z⁽¹⁾, given in the following result. This is actually one version of the angular measure, see (Falk 2019, Lemma 1.7.5), and Proposition 6.3 below.

Proposition 6.2

Take an arbitrary D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on $\mathbb R^{d}$ and choose some generator Z of it. Then the distribution of a generator Z⁽¹⁾ of ${\left \Vert \cdot \right \Vert }_{D}$, with ${\left \Vert {{\boldsymbol {Z}}^{(1)}}\right \Vert }_{1}=d$, equals

$$ P\left( \boldsymbol{Z}^{(1)}\in\cdot \right) = \frac 1d E\left( 1\left( d \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert_{1}}\in\cdot\right)\left\Vert\boldsymbol{Z}\right\Vert_{1}\right). $$

Proof

It is easy to see that

$$ Q(\cdot):= \frac 1d E\left( 1\left( d \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert_{1}}\in\cdot\right)\left\Vert\boldsymbol{Z}\right\Vert_{1}\right) $$

defines a probability measure on $[0,\infty )^{d}$ (use the monotone convergence theorem), with $Q\left (\left \{\boldsymbol {x}\ge \boldsymbol {0}\in \mathbb R^{d}: \left \Vert \boldsymbol {x}\right \Vert _{1}=d\right \}\right )=1$. To prove that the distribution of Z⁽¹⁾ equals Q(⋅), we only have to show that their corresponding df coincide on $[0,\infty )^{d}$.

From Theorem 5.1 we know that, with X := Z/U, where U is uniformly on (0,1) distributed and independent of Z,

$$ \begin{array}{@{}rcl@{}} &&P\left( \boldsymbol{Z}^{(1)}\le\boldsymbol{x}\right)\\ &=& \lim_{t\to\infty}P\left( d \frac{\boldsymbol{X}}{\left\Vert\boldsymbol{X}\right\Vert_{1}}\le \boldsymbol{x} \Big| \left\Vert\boldsymbol{X}\right\Vert_{1}>t \right)\\ &=&\lim_{t\to\infty}P\left( d \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert_{1}}\le\boldsymbol{x} \Big| U<\frac {\left\Vert\boldsymbol{Z}\right\Vert_{1}}t\right)\\ &=&\lim_{t\to\infty} \frac{P\left( d \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert_{1}}\le\boldsymbol{x}, U<\frac {\left\Vert\boldsymbol{Z}\right\Vert_{1}}t\right)}{P\left( U<\frac {\left\Vert\boldsymbol{Z}\right\Vert_{1}}t\right)}, \end{array} $$

for each point $\boldsymbol {x}\in [0,\infty )^{d}$, at which the df of Z⁽¹⁾ is continuous.

First we analyze the denominator in the above equation. We have

$$ \begin{array}{@{}rcl@{}} &&P\left( U<\frac {\left\Vert\boldsymbol{Z}\right\Vert_{1}}t\right)\\ &=& {\int}_{\left\{\boldsymbol{z}: \left\Vert\boldsymbol{z}\right\Vert_{1}>t\right\}} P\left( U<\frac {\left\Vert\boldsymbol{z}\right\Vert_{1}}t\right) P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &&{\kern3cm} + {\int}_{\left\{\boldsymbol{z}: \left\Vert\boldsymbol{z}\right\Vert_{1} \le t\right\}} P\left( U<\frac {\left\Vert\boldsymbol{z}\right\Vert_{1}}t\right) P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& {\int}_{\left\{\boldsymbol{z}: \left\Vert\boldsymbol{z}\right\Vert_{1}>t\right\}} 1 P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &&{\kern3cm} + {\int}_{\left\{\boldsymbol{z}: \left\Vert\boldsymbol{z}\right\Vert_{1} \le t\right\}} \frac {\left\Vert\boldsymbol{z}\right\Vert_{1}}t P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& P\left( \left\Vert\boldsymbol{Z}\right\Vert_{1}>t\right) + \frac 1t {\int}_{\left\{\boldsymbol{z}: \left\Vert\boldsymbol{z}\right\Vert_{1} \le t\right\}} \left\Vert\boldsymbol{z}\right\Vert_{1} (_{\boldsymbol{Z}}(d\boldsymbol{z}) \end{array} $$

The fact that $E\left (\left \Vert \boldsymbol {Z}\right \Vert _{1}\right )=d<\infty$ implies

$$ tP\left( \left\Vert\boldsymbol{Z}\right\Vert_{1}>t \right)\to_{t\to\infty}0 $$

(use Lemma 3.1), and

$$ \begin{array}{@{}rcl@{}} &&{\int}_{\left\{\boldsymbol{z}: \left\Vert\boldsymbol{z}\right\Vert_{1} \le t\right\}} \left\Vert\boldsymbol{z}\right\Vert_{1} P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &&\to_{t\to\infty}{\int}_{[0,\infty)^{d}}\left\Vert\boldsymbol{z}\right\Vert_{1} P_{\boldsymbol{Z}}(d\boldsymbol{z}) = E\left( \left\Vert\boldsymbol{Z}\right\Vert_{1}\right)=d. \end{array} $$

As a consequence we obtain

$$ P\left( \left\Vert\boldsymbol{Z}\right\Vert_{1}>t\right) + \frac 1t {\int}_{\left\{\boldsymbol{z}: \left\Vert\boldsymbol{z}\right\Vert_{1} \le t\right\}} \left\Vert\boldsymbol{z}\right\Vert_{1} P_{\boldsymbol{Z}}(d\boldsymbol{z}) = \frac 1t (d+o(1)). $$

Next we investigate the numerator:

$$ \begin{array}{@{}rcl@{}} &&P\left( d \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert_{1}}\le\boldsymbol{x}, U<\frac {\left\Vert\boldsymbol{Z}\right\Vert_{1}}t\right)\\ &=& \int {{\int}_{0}^{1}} 1\left( d \frac{\boldsymbol{z}}{\left\Vert\boldsymbol{z}\right\Vert_{1}}\le\boldsymbol{x}, u<\frac {\left\Vert\boldsymbol{z}\right\Vert_{1}}t\right) du P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& \int {{\int}_{0}^{1}} 1\left( d \frac{\boldsymbol{z}}{\left\Vert\boldsymbol{z}\right\Vert_{1}}\le\boldsymbol{x}\right)\times 1\left( u<\frac {\left\Vert\boldsymbol{z}\right\Vert_{1}}t\right) du P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& \int 1\left( d \frac{\boldsymbol{z}}{\left\Vert\boldsymbol{z}\right\Vert_{1}}\le\boldsymbol{x}\right)\left[{\int}_{0}^{1} 1\left( u<\frac{\left\Vert\boldsymbol{z}\right\Vert_{1}}t\right) du\right] P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& {\int}_{\left\{\boldsymbol{z}: \left\Vert\boldsymbol{z}\right\Vert_{1}\le t\right\}} 1\left( d \frac{\boldsymbol{z}}{\left\Vert\boldsymbol{z}\right\Vert_{1}}\le\boldsymbol{x}\right) \frac{\left\Vert\boldsymbol{z}\right\Vert_{1}}t P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &&+ {\int}_{\left\{\boldsymbol{z}: \left\Vert\boldsymbol{z}\right\Vert_{1}> t\right\}} 1\left( d \frac{\boldsymbol{z}}{\left\Vert\boldsymbol{z}\right\Vert_{1}}\le\boldsymbol{x}\right) P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& \frac 1t \left[E\left( 1\left( d \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert_{1}}\le \boldsymbol{x}\right)\left\Vert\boldsymbol{Z}\right\Vert_{1}\right) + o(1)\right] + o\left( \frac 1t\right)\\ &=& \frac 1t \left[E\left( 1\left( d \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert_{1}}\le \boldsymbol{x}\right)\left\Vert\boldsymbol{Z}\right\Vert_{1}\right) + o(1)\right]. \end{array} $$

As a consequence we obtain

$$ \begin{array}{@{}rcl@{}} F(\boldsymbol{x})&:=& P\left( \boldsymbol{Z}^{(1)}\le\boldsymbol{x}\right)\\ &=&\lim_{t\to\infty}P\left( d \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert_{1}}\le \boldsymbol{x} \Big| U< \frac{\left\Vert\boldsymbol{Z}\right\Vert_{1}}t\right)\\ &=&\frac 1d E\left( 1\left( d \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert_{1}}\le \boldsymbol{x} \right) \left\Vert\boldsymbol{Z}\right\Vert_{1}\right)=:\tilde F(\boldsymbol{x}) \end{array} $$

for each $\boldsymbol {x}\ge \boldsymbol {0}\in \mathbb R^{d}$, at which the df F is continuous. But, being df, the functions F and $\tilde F$ are both upper continuous and, therefore, $F(\boldsymbol {x})=\tilde F({\boldsymbol {x}})$ for each ${\boldsymbol {x}}\in [0,\infty )^{d}$, and thus, Q is the distribution of Z⁽¹⁾. □

The arguments in the proof of Proposition 6.2 can be repeated to establish in general the distribution of a generator ${\tilde {\boldsymbol {Z}}}$ of a D-norm ${\left \Vert \cdot \right \Vert }_{D}$, with the particular property ${\left \Vert {\tilde {\boldsymbol {Z}}}\right \Vert }=\text {const}$, given an arbitrary norm ${\left \Vert \cdot \right \Vert }$ on ${\mathbb R}^{d}$.

Proposition 6.3

Take an arbitrary D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on $\mathbb R^{d}$ and an arbitrary generator Z of ${\left \Vert \cdot \right \Vert }_{D}$. For each norm ${\left \Vert \cdot \right \Vert }$ on $\mathbb R^{d}$ there exists by Theorem 2.3 a generator $\tilde {\boldsymbol {Z}}$ of ${\left \Vert \cdot \right \Vert }_{D}$, with the additional property ${\left \Vert {\tilde {\boldsymbol {Z}}}\right \Vert }=\text {const}$. Its uniquely determined distribution is given by

$$ P\left( {\tilde{\boldsymbol{Z}}}\in\cdot\right) =\frac 1{\text{const}} E\left( 1\left( \text{const} \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert}\in\cdot \right)\left\Vert\boldsymbol{Z}\right\Vert\right). $$

Note that the distribution of ${\tilde {\boldsymbol {Z}}}$ coincides with the angular measure in general, see (Falk 2019, Lemma 1.7.5).

If the arbitrary generator Z in Proposition 6.3 is bounded, then the distribution of ${\tilde {\boldsymbol {Z}}}$ can be specified as follows. Note that the preceding result implies

$$ \text{const} = E\left( \left\Vert\boldsymbol{Z}\right\Vert\right). $$

Proposition 6.4

Suppose in addition to the assumptions in Proposition 6.3 that the arbitrary generator Z of ${\left \Vert \cdot \right \Vert }_{D}$ is bounded, i.e., ${\left \Vert {{\boldsymbol {Z}}}\right \Vert }\le m$ for some number m > 0. Then we have

$$ P\left( {\tilde{\boldsymbol{Z}}}\in\cdot\right) = P\left( \text{const} \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert} \in \cdot \big| \left\Vert\boldsymbol{Z}\right\Vert> U \right), $$

where U is a random variable that is independent of Z and which is uniformly distributed on the interval (0,m).

Proof

According to Proposition 6.3, we have to establish the equation

$$ P\left( \text{const} \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert} \in \cdot \big| \left\Vert\boldsymbol{Z}\right\Vert> U \right) = \frac 1{\text{const}} E\left( 1\left( \text{const} \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert}\in\cdot \right){\left\Vert{{\boldsymbol{Z}}}\right\Vert}\right). $$

First we have, using Fubini’s theorem,

$$ \begin{array}{@{}rcl@{}} P\left( \left\Vert\boldsymbol{Z}\right\Vert>U\right)&=& \int {{\int}_{0}^{m}} 1\left( u<\left\Vert\boldsymbol{z}\right\Vert\right)\frac 1m du P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& \int {\int}_{0}^{\left\Vert\boldsymbol{z}\right\Vert}\frac 1m du P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=&\frac 1m \int\left\Vert\boldsymbol{z}\right\Vert P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& \frac 1m E\left( \left\Vert\boldsymbol{Z}\right\Vert\right) = \frac{\text{const}}m. \end{array} $$

Using very similar arguments we obtain

$$ \begin{array}{@{}rcl@{}} &&P\left( \text{const} \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert} \in \cdot , \left\Vert\boldsymbol{Z}\right\Vert> U \right)\\ &=& \int {{\int}_{0}^{m}} 1\left( \text{const} \frac{\boldsymbol{z}}{\left\Vert\boldsymbol{z}\right\Vert}\in \cdot \right) 1\left( u<\left\Vert\boldsymbol{z}\right\Vert\right) \frac 1m du P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& \int 1\left( \text{const} \frac{\boldsymbol{z}}{\left\Vert\boldsymbol{z}\right\Vert}\in \cdot \right) {\int}_{0}^{\left\Vert\boldsymbol{z}\right\Vert} \frac 1m du P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& \frac 1m \int 1\left( \text{const} \frac{\boldsymbol{z}}{\left\Vert\boldsymbol{z}\right\Vert}\in \cdot \right) \left\Vert\boldsymbol{z}\right\Vert P_{\boldsymbol{Z}}(d\boldsymbol{z})\\ &=& \frac 1m E\left( 1\left( \text{const} \frac{\boldsymbol{Z}}{\left\Vert\boldsymbol{Z}\right\Vert}\in \cdot \right)\left\Vert\boldsymbol{Z}\right\Vert \right). \end{array} $$

The above two equations now imply the assertion. □

The preceding result has the following consequence. If we know a bounded generator Z of a D-norm ${\left \Vert \cdot \right \Vert }_{D}$ and we are able to simulate it, then we can also simulate any normed generator $\tilde {\boldsymbol {Z}}$ of ${\left \Vert \cdot \right \Vert }_{D}$ with the following algorithm; recall that ${\left \Vert {{\boldsymbol {Z}}}\right \Vert }\le m$.

• 1. Sample a realization z of Z.

• 2. Sample a realization u from the uniform distribution on (0,m).

  • (a) If $\left \Vert \boldsymbol {z}\right \Vert \le u$: Go back to step 1.

  • (b) Else: Stop and return ${\tilde {\boldsymbol {z}}}=\text {const}\frac {\boldsymbol {z}}{\left \Vert \boldsymbol {z}\right \Vert }$.

This accept-reject algorithm runs with a random number of steps. As seen in the proof of Proposition 6.4, the probability of stopping is const/m for each iteration, so on average it takes m/const iterations to stop. Note that in the particular case ${\left \Vert \cdot \right \Vert }={\left \Vert \cdot \right \Vert }_{1}$, we have const = d by the fact that E(Z_i) = 1 for each component Z_i of ${\boldsymbol {Z}}=(Z_{1},\dots ,Z_{d})$.

7 On the Structure of Exchangeable D-Norms

In the paper (Mai and Scherer 2020), the authors show that the set of d-variate symmetric stable tail dependence functions, uniquely associated with exchangeable d-dimensional extreme value copulas, is a simplex and they determine its extremal boundary.

It turns out that Mai and Scherer (2020) is actually a contribution to the theory of D-norms, as shown in what follows. To the best of our knowledge, we introduce the concept of an exchangeable D-norm for the first time, and we prove new results for this subfamily of D-norms.

Definition 7.1

A norm ${\left \Vert \cdot \right \Vert }$ on $\mathbb R^{d}$ is called exchangeable, if

$$ \left\Vert(x_{1},\dots,x_{d})\right\Vert = \left\Vert\left( x_{\sigma(1)},\dots,x_{\sigma(d)}\right)\right\Vert,\qquad \boldsymbol{x}=(x_{1},\dots,x_{d})\in\mathbb R^{d}, $$

for each permutation $(\sigma (1),\dots ,\sigma (d))$ of $(1,\dots ,d)$.

Obvious examples are the sup-norm $\left \Vert \boldsymbol {x}\right \Vert _{\infty }=\max \limits _{1\le i\le d}\left \vert x_{i}\right \vert$ and each logistic norm $\left \Vert \boldsymbol {x}\right \Vert _{p}=\left ({\sum }_{i=1}^{d}\left \vert x_{i}\right \vert ^{p}\right )^{1/p}$, p ≥ 1. The norm ${\left \Vert {{\boldsymbol {x}}}\right \Vert }={\sum }_{i=1}^{d} \frac 1i\left |{x_{i}}\right |$ is not exchangeable.

Recall that a random vector $\boldsymbol {X}=(X_{1},\dots ,X_{d})$ is said to have exchangeable components, if

$$ (X_{1},\dots,X_{d}) =_{D} \left( X_{\sigma(1)},\dots,X_{\sigma(d)}\right) $$

for each permutation $(\sigma (1),\dots ,\sigma (d))$ of $(1,\dots ,d)$. By =_D we denote equality in distribution. In this case we say that the random vector X is exchangeable. An obvious example is the case, where the components $X_{1},\dots ,X_{d}$ are iid.

Recall that for each D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on $\mathbb R^{d}$ and each norm ${\left \Vert \cdot \right \Vert }$ on $\mathbb R^{d}$ there exists by Theorem 2.3 a generator Z of ${\left \Vert \cdot \right \Vert }_{D}$, with the additional property ${\left \Vert {{\boldsymbol {Z}}}\right \Vert }=\text {const}$. The distribution of this generator Z is uniquely determined. The name exchangeable D-norm is due to the following characterization.

Theorem 7.1

Let ${\left \Vert \cdot \right \Vert }$ be an arbitrary exchangeable norm on $\mathbb R^{d}$. A D-norm ${\left \Vert \cdot \right \Vert }_{D}$ on $\mathbb R^{d}$ is exchangeable iff the generator Z of ${\left \Vert \cdot \right \Vert }_{D}$ with ${\left \Vert {{\boldsymbol {Z}}}\right \Vert }=\text {const}$ is exchangeable.

The reverse implication can be weakened considerable: If there exists a generator Z of ${\left \Vert \cdot \right \Vert }_{D}$, which is exchangeable, then ${\left \Vert \cdot \right \Vert }_{D}$ is exchangeable.

Proof

The reverse implication is easily seen. Suppose there is a generator $\boldsymbol {Z}=(Z_{1},\dots ,Z_{d})$ of ${\left \Vert \cdot \right \Vert }_{D}$, which is exchangeable. Then we obtain, for ${\boldsymbol {x}}=(x_{1},\dots ,x_{d})\in {\mathbb R}^{d}$,

$$ \begin{array}{@{}rcl@{}} \left\Vert\boldsymbol{x}\right\Vert_{D} &=& E\left( \max_{1\le i\le d}\left( \left\vert x_{i}\right\vert Z_{i}\right)\right) = E\left( \max_{1\le i\le d}\left( \left\vert x_{i}\right\vert Z_{\sigma^{-1}(i)}\right)\right)\\ &= &E\left( \max_{1\le i\le d}\left( \left\vert x_{\sigma(i)}\right\vert Z_{i}\right)\right) = \left\Vert\left( x_{\sigma(1)},\dots,x_{\sigma(d)}\right)\right\Vert_{D}, \end{array} $$

where σ^− 1 is the inverse permutation of σ, i.e., $\sigma \left (\sigma ^{-1}(i)\right )=i$, 1 ≤ i ≤ d.

Next we establish the implication “⇒”. Suppose that ${\left \Vert \cdot \right \Vert }_{D}$ is an exchangeable D-norm on $\mathbb R^{d}$. Choose an arbitrary exchangeable norm ${\left \Vert \cdot \right \Vert }$ on $\mathbb R^{d}$. There exists by Theorem 2.3 a generator ${\tilde {\boldsymbol {Z}}}=(\tilde Z_{1},\dots ,\tilde Z_{d})$ of ${\left \Vert \cdot \right \Vert }_{D}$, with the additional property ${\left \Vert {{\boldsymbol {\tilde Z}}}\right \Vert }=\text {const}$. Its distribution is uniquely determined. The fact that ${\left \Vert \cdot \right \Vert }_{D}$ is exchangeable implies, for ${\boldsymbol {x}}\in {\mathbb R}^{d}$, and an arbitrary permutation $\sigma =(\sigma (1),\dots ,\sigma (d))$ of $(1,\dots ,d)$,

$$ \begin{array}{@{}rcl@{}} \left\Vert\boldsymbol{x}\right\Vert_{D} &=& \left\Vert(x_{1},\dots,x_{d})\right\Vert_{D} = \left\Vert\left( x_{\sigma(1)},\dots,x_{\sigma(d)}\right)\right\Vert_{D}\\ &=& E\left( \max_{1\le i\le d}\left( \left\vert x_{\sigma(i)}\right\vert\tilde Z_{i}\right) \right) = E\left( \max_{1\le i\le d}\left( \left\vert x_{i}\right\vert\tilde Z_{\sigma^{-1}(i)}\right) \right). \end{array} $$

That means that

$$ \boldsymbol{\tilde Z}_{\sigma^{-1}}:= \left( \tilde Z_{\sigma^{-1}(1)},\dots, \tilde Z_{\sigma^{-1}(d)}\right) $$

is a generator of ${\left \Vert \cdot \right \Vert }_{D}$ as well, with the property ${\left \Vert {\boldsymbol {\tilde Z}_{\sigma ^{-1}}}\right \Vert }= {\left \Vert {\boldsymbol {\tilde Z}}\right \Vert }=\text {const}$, due to the exchangeability of ${\left \Vert \cdot \right \Vert }$. But the distribution of this generator ${\boldsymbol {\tilde Z}}$ is uniquely determined, and, thus,

$$ \boldsymbol{\tilde Z}_{\sigma^{-1}}=_{D} \boldsymbol{\tilde Z}. $$

As σ is an arbitrary permutation of $(1,\dots ,d)$, we have established exchangeability of $\boldsymbol {\tilde Z}$. □

Remark 7.2

One might guess that each generator Z of an exchangeable D-norm is exchangeable. But this is not true. Take a random variable U, which follows the uniform distribution on (0,1), and choose arbitrary numbers $a_{0}:=0<a_{1}<\dots <a_{d-1}< a_{d}:=1$. Then ${\boldsymbol {Z}}:= (Z_{1},\dots ,Z_{d})$ with

$$ Z_{i}:= \frac 1{a_{i}-a_{i-1}} 1 (U\in (a_{i-1}, a_{i}]),\qquad 1\le i\le d, $$

is a generator of the D-norm ${\left \Vert \cdot \right \Vert }_{1}$, which is easily seen. But the generator Z is exchangeable only if a_i − a_i− 1 = 1/d, 1 ≤ i ≤ d.

In what follows we will characterize extremal exchangeable D-norms. Let $\sigma ^{*}=\left (\sigma ^{*}(1),\dots ,\sigma ^{*}(d)\right )$ be a random permutation of $(1,\dots ,d)$, with equal probability 1/d! for each possible outcome, and denote by $\mathcal P_{d}$ the set of all permutations of $(1,\dots ,d)$.

Choose $\boldsymbol {t}=(t_{1},\dots ,t_{d})\in S_{d}:= \left \{\boldsymbol {s}\in [0,1]^{d}: \left \Vert \boldsymbol {s}\right \Vert _{1}=d\right \}$ and put, for $\boldsymbol {x}\in \mathbb R^{d}$,

$$ \begin{array}{@{}rcl@{}} \left\Vert\boldsymbol{x}\right\Vert_{D_{\boldsymbol{t}}}&:=& \frac 1{d!} \sum\limits_{\sigma\in\mathcal P_{d}}\max_{1\le i\le d}\left( \left\vert x_{\sigma(i)}\right\vert t_{i} \right) = \frac 1{d!} \sum\limits_{\sigma\in\mathcal P_{d}}\max_{1\le i\le d}\left( \left\vert x_{i}\right\vert t_{\sigma(i)}\right)\\ &=& E\left( \max_{1\le i\le d}\left( \left\vert x_{i}\right\vert t_{\sigma^{*}(i)} \right) \right). \end{array} $$

Then $\left \Vert \cdot \right \Vert _{D_{\boldsymbol {t}}}$ is an exchangeable D-norm on $\mathbb R^{d}$, with generator

$$ \boldsymbol{Z}_{\boldsymbol{t}}:= \left( Z_{\boldsymbol{t},1},\dots,Z_{\boldsymbol{t},d}\right):= \left( t_{\sigma^{*}(1)},\dots,t_{\sigma^{*}(d)}\right). $$

We obviously have $Z_{\boldsymbol {t},i}=t_{\sigma ^{*}(i)}\ge 0$, and

$$ \begin{array}{@{}rcl@{}} E\left( Z_{\boldsymbol{t},i}\right)&=& E\left( t_{\sigma^{*}(i)}\right) = \sum\limits_{j=1}^{d} t_{j} P(\sigma^{*}(i)=j)\\ &=& \sum\limits_{j=1}^{d} t_{j} \frac{\text{number of permutations } \sigma \text{ in } \mathcal P_{d} \text{ with } \sigma(i)=j}{\text{total number of permutations in } \mathcal P_{d}}\\ &=& \sum\limits_{j=1}^{d} t_{j} \frac{(d-1)!}{d!} = \frac 1 d {\sum\limits}_{j=1}^{d} t_{j} = \frac d d = 1. \end{array} $$

The D-norm $\left \Vert \cdot \right \Vert _{D_{\boldsymbol {t}}}$ is obviously exchangeable.

The set of D-norms is convex, see (Falk 2019, Proposition 1.4.1), and, therefore, the set of exchangeable D-norms is convex as well. It turns out that the norms ${\left \Vert {\cdot }\right \Vert }_{D_{{\boldsymbol {t}}}}$, t ∈ S_d, are extremal points of it. This is the content of our next result.

Lemma 7.1

Each D-norm $\left \Vert \cdot \right \Vert _{D_{\boldsymbol {t}}}$, with t ∈ S_d, is an extremal D-norm within the set of exchangeable D-norms on $\mathbb R^{d}$, i.e., if, for some λ ∈ (0,1),

$$ \left\Vert\cdot\right\Vert_{D_{\boldsymbol{t}}} = \lambda \left\Vert\cdot\right\Vert_{D^{(1)}} + (1-\lambda)\left\Vert\cdot\right\Vert_{D^{(2)}}, $$

where $\left \Vert \cdot \right \Vert _{D^{(1)}}$, $\left \Vert \cdot \right \Vert _{D^{(2)}}$ are exchangeable D-norms on $\mathbb R^{d}$, then

$$ \left\Vert\cdot\right\Vert_{D^{(1)}} = \left\Vert\cdot\right\Vert_{D^{(2)}}=\left\Vert\cdot\right\Vert_{D_{\boldsymbol{t}}}. $$

Proof

Let Z⁽ⁱ⁾ be a generator of $\left \Vert \cdot \right \Vert _{D^{(i)}}$, with the additional property $\left \Vert \boldsymbol {Z}^{(i)}\right \Vert _{1}=d$, i = 1,2. Let $\xi \in \left \{1,2\right \}$ be a random variable with P(ξ = 1) = 1 − P(ξ = 2), and which is independent of Z⁽¹⁾ and Z⁽¹⁾. Then the random vector ${\boldsymbol {Z}}^{(\xi )}=\left (Z_{1}^{(\xi )},\dots ,Z_{d}^{(\xi )}\right )$ satisfies, for ${\boldsymbol {x}}=(x_{1},\dots ,x_{d})\in {\mathbb R}^{d}$,

$$ \begin{array}{@{}rcl@{}} E\left( \max_{1\le i\le d}\left( \left\vert x_{i}\right\vert Z_{i}^{(\xi)} \right)\right) = \lambda \left\Vert\boldsymbol{x}\right\Vert_{D^{(1)}} + (1-\lambda) \left\Vert\boldsymbol{x}\right\Vert_{D^{(2)}} = \left\Vert\boldsymbol{x}\right\Vert_{D_{\boldsymbol{t}}}, \end{array} $$

see the proof of Proposition 1.4.1 in Falk (2019). The generator Z^(ξ) realizes in S_d as well, and thus, as the distribution of this generator is by Theorem 2.3 unique, its distribution coincides with that of Z_t. We, consequently, have

$$ P\left( \boldsymbol{Z}^{(\xi)}=\left( t_{\sigma(1)},\dots,t_{\sigma(d)} \right)\right) = P\left( \boldsymbol{Z}_{\boldsymbol{t}}=\left( t_{\sigma(1)},\dots,t_{\sigma(d)} \right)\right) = \frac 1{d!} $$

for each permutation $\sigma =(\sigma (1),\dots ,\sigma (d))\in \mathcal P_{d}$. But this implies, with $\boldsymbol {t}_{\sigma }:=\left (t_{\sigma (1)},\dots ,t_{\sigma (d)} \right )$,

$$ \begin{array}{@{}rcl@{}} &&\lambda \sum\limits_{\sigma\in\mathcal P_{d}} P\left( \boldsymbol{Z}^{(1)}= \boldsymbol{t}_{\sigma}\right) + (1-\lambda) \sum\limits_{\sigma\in\mathcal P_{d}} P\left( \boldsymbol{Z}^{(2)}= \boldsymbol{t}_{\sigma}\right)\\ &=& {\sum\limits}_{\sigma\in\mathcal P_{d}} \left( \lambda P\left( \boldsymbol{Z}^{(1)}= \boldsymbol{t}_{\sigma}\right) + (1-\lambda) P\left( \boldsymbol{Z}^{(2)}= \boldsymbol{t}_{\sigma}\right) \right)\\ &=& \sum\limits_{\sigma\in\mathcal P_{d}} P\left( \boldsymbol{Z}^{(\xi)}=\boldsymbol{t}_{\sigma}\right) = \sum\limits_{\sigma\in\mathcal P_{d}} \frac 1{d!} = 1, \end{array} $$

and, thus,

$$ \sum\limits_{\sigma\in\mathcal P_{d}} P\left( \boldsymbol{Z}^{(1)}=\boldsymbol{t}_{\sigma}\right) = 1 = \sum\limits_{\sigma\in\mathcal P_{d}} P\left( \boldsymbol{Z}^{(2)}=\boldsymbol{t}_{\sigma}\right). $$

Because Z⁽¹⁾ and Z⁽²⁾ are exchangeable by Theorem 7.2, this implies

$$ P\left( \boldsymbol{Z}^{(1)}=\boldsymbol{t}_{\sigma}\right) = \frac 1 {d!} = P\left( \boldsymbol{Z}^{(2)}=\boldsymbol{t}_{\sigma}\right) $$

for each $\sigma \in \mathcal P_{d}$, i.e., $\boldsymbol {Z}^{(1)}=_{D}\boldsymbol {Z}^{(2)} =_{D} \boldsymbol {Z}_{\boldsymbol {t}}$, which is the assertion. □

Our next result shows that the set of exchangeable D-norms on $\mathbb R^{d}$ is a simplex. It parallels Lemma 2.4 in Mai and Scherer (2020).

Lemma 7.2

Let ${\left \Vert \cdot \right \Vert }_{D}$ be an arbitrary exchangeable D-norm on $\mathbb R^{d}$. Then we have, for $\boldsymbol {x}\in \mathbb R^{d}$, the representation

$$ \left\Vert\boldsymbol{x}\right\Vert_{D} = {\int}_{S_{d}}\left\Vert\boldsymbol{x}\right\Vert_{D_{t}} P_{\boldsymbol{\tilde Z}}(d\boldsymbol{t}) = E\left( \left\Vert\boldsymbol{x}\right\Vert_{D_{\boldsymbol{\tilde Z}}}\right), $$

where $\boldsymbol {\tilde Z}$ is a generator of ${\left \Vert \cdot \right \Vert }_{D}$ with ${\left \Vert {\boldsymbol {\tilde Z}}\right \Vert }_{1}=d$, i.e., $\boldsymbol {\tilde Z}$ realizes in S_d. As the distribution of $\boldsymbol {\tilde Z}$ is by Theorem 2.3 uniquely determined, the above representation of ${\left \Vert \cdot \right \Vert }_{D}$ in terms of ${\left \Vert \cdot \right \Vert }_{D_{{\boldsymbol {t}}}}$, t ∈ S_d, and the distribution of ${\boldsymbol {\tilde Z}}$ is uniquely determined as well.

Proof

The assertion is easily seen. Conditioning on $\boldsymbol {\tilde Z}=\boldsymbol {t}$, one obtains from the exchangeability of ${\left \Vert \cdot \right \Vert }_{D}$

$$ \begin{array}{@{}rcl@{}} \left\Vert\boldsymbol{x}\right\Vert_{D}&=& E\left( \max_{1\le i\le d}\left( \left\vert x_{i}\right\vert\tilde Z_{i}\right) \right)\\ &=& \frac 1{d!} \sum\limits_{\sigma\in\mathcal P_{d}} E\left( \max_{1\le i\le d}\left( \left\vert x_{\sigma(i)}\right\vert\tilde Z_{i}\right) \right)\\ &=& \frac 1{d!} \sum\limits_{\sigma\in\mathcal P_{d}} {\int}_{S_{d}} \max_{1\le i\le d} \left( \left\vert x_{\sigma(i)}\right\vert t_{i}\right) P_{\boldsymbol{\tilde Z}}(d\boldsymbol{t})\\ &=& {\int}_{S_{d}} \frac 1{d!} \sum\limits_{\sigma\in\mathcal P_{d}} \max_{1\le i\le d} \left( \left\vert x_{\sigma(i)}\right\vert t_{i}\right) P_{\boldsymbol{\tilde Z}}(d\boldsymbol{t})\\ &=& {\int}_{S_{d}}\left\Vert\boldsymbol{x}\right\Vert_{D_{t}} P_{\boldsymbol{\tilde Z}}(d\boldsymbol{t}) = E\left( \left\Vert\boldsymbol{x}\right\Vert_{D_{\boldsymbol{\tilde Z}}}\right). \end{array} $$

□