Skip to main content
SpringerLink
Log in

Rosette Harmonic Mappings

  • Published:
Complex Analysis and Operator Theory Aims and scope Submit manuscript

Abstract

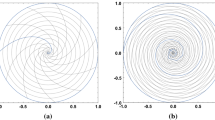
A harmonic mapping is a univalent harmonic function of one complex variable. We define a family of harmonic mappings on the unit disk whose images are rotationally symmetric “rosettes” with n cusps or n nodes, \(n\ge 3\). These mappings are analogous to the n-cusped hypocycloid, but are modified by Gauss hypergeometric factors, both in the analytic and co-analytic parts. Relative rotations by an angle \(\beta \) of the analytic and anti-analytic parts lead to graphs that have cyclic, and in some cases dihedral symmetry of order n. While the graphs for different \(\beta \) can be dissimilar, the cusps are aligned along axes that are independent of \(\beta \). For certain isolated values of \(\beta \), the boundary function is continuous with arcs of constancy, and has nodes of interior angle \(\pi /2-\pi /n\) instead of cusps.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. Subsequent cusp (or node) here indicates the cusp (or node) with the next largest argument.

References

  1. Abdullah, S., McDougall, J.: Rosette minimal surfaces (in preparation) (2021)

  2. Brilleslyper, M.A., Dorff, M.J., McDougall, J.M., Rolf, J.S., Schaubroeck, L.E., Stankewitz, R.L., Stephenson, K.: Explorations in Complex Analysis. Classroom Resource Materials Series. Mathematical Association of America, Washington (2012)

    Book  Google Scholar 

  3. Bshouty, D., Lundberg, E., Weitsman, A.: A solution to Sheil-Small’s harmonic mapping problem for polygons. Proc. Am. Math. Soc. 143(12), 5219–5225 (2015)

    Article  MathSciNet  Google Scholar 

  4. Clunie, J., Sheil-Small, T.: Harmonic univalent functions. Ann. Acad. Sci. Fenn. Ser. A I Math. 9, 3–25 (1984)

    Article  MathSciNet  Google Scholar 

  5. Duren, P., Hengartner, W., Laugesen, R.S.: The argument principle for harmonic functions. Am. Math. Mon. 103(5), 411–415 (1996)

    Article  MathSciNet  Google Scholar 

  6. Duren, P., McDougall, J., Schaubroeck, L.: Harmonic mappings onto stars. J. Math. Anal. Appl. 307(1), 312–320 (2005)

    Article  MathSciNet  Google Scholar 

  7. Duren, P., Thygerson, W.R.: Harmonic mappings related to Scherk’s saddle-tower minimal surfaces. Rocky Mt. J. Math. 30(2), 555–564 (2000)

    Article  MathSciNet  Google Scholar 

  8. Duren, P.: Harmonic Mappings in the Plane, Cambridge Tracts in Mathematics, vol. 156. Cambridge University Press, Cambridge (2004)

    Book  Google Scholar 

  9. Hengartner, W., Schober, G.: On the boundary behavior of orientation-preserving harmonic mappings. Complex Variables Theory Appl. 5(2–4), 197–208 (1986)

    Article  MathSciNet  Google Scholar 

  10. Jenkins, H., Serrin, J.: Variational problems of minimal surface type. II. Boundary value problems for the minimal surface equation. Arch. Ration. Mech. Anal. 21, 321–342 (1966)

    Article  MathSciNet  Google Scholar 

  11. Lewy, H.: On the non-vanishing of the Jacobian in certain one-to-one mappings. Bull. Am. Math. Soc. 42(1), 689–692 (1936)

    Article  MathSciNet  Google Scholar 

  12. McDougall, J.: Harmonic mappings with quadrilateral image, Complex analysis and potential theory. CRM Proc. Lecture Notes, vol. 55, pp. 99–115. American Mathematical Society, Providence, RI (2012)

  13. Merkes, E.P., Scott, W.T.: Starlike hypergeometric functions. Proc. Am. Math. Soc. 12, 885–888 (1961)

    Article  MathSciNet  Google Scholar 

  14. McDougall, J., Schaubroeck, L.: Minimal surfaces over stars. J. Math. Anal. Appl. 340(1), 721–738 (2008)

    Article  MathSciNet  Google Scholar 

  15. Rainville, E.D.: Special Functions, 1st edn. Chelsea Publishing Co., Bronx (1971)

    MATH  Google Scholar 

  16. Schwarz, H.A.: Gesammelte mathematische Abhandlungen. Band I, II, Chelsea Publishing Co., Bronx, N.Y., 1972, Nachdruck in einem Band der Auflage von (1890)

  17. Sheil-Small, T.: On the Fourier series of a step function. Michigan Math. J. 36(3), 459–475 (1989)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Computer Science, Colorado College, Colorado Springs, CO, 80903, USA

    Jane McDougall & Lauren Stierman

Authors
  1. Jane McDougall
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lauren Stierman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jane McDougall.

Additional information

Communicated by Kasso A Okoudjou.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The authors were supported in part by Department of Mathematics and Computer Science summer Grant 2017 and 2019 from Colorado College.

This article is part of the topical collection “Harmonic Analysis and Operator Theory” edited by H. Turgay Kaptanoglu, Aurelian Gheondea and Serap Oztop.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

McDougall, J., Stierman, L. Rosette Harmonic Mappings. Complex Anal. Oper. Theory 15, 67 (2021). https://doi.org/10.1007/s11785-021-01085-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11785-021-01085-8

Keywords

Mathematics Subject Classification

Search

Navigation