Nonlinear hygrothermal effects on the vibrations of a magnetostrictive viscoelastic laminated sandwich plate resting on an elastic medium

Abstract

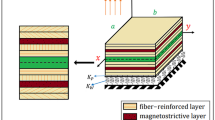
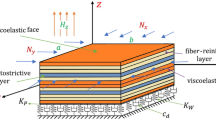
In engineering applications, composite structures supported by elastic foundations are being vastly utilized in various operating environmental conditions. The nonlinear hygrothermal effect on vibration analysis of a magnetostrictive viscoelastic laminated composite sandwich plate rested on two-parameter Pasternak’s foundations is studied in the present article. The material properties of the viscoelastic plate’s layers are considered based on the Kelvin–Voigt model. The governing equation system is derived according to Hamilton’s principle. The analytical solution is obtained to study influences of the hygrothermal change, half wave number, magnitude of the feedback control gain, aspect ratios, thickness ratio, and structural viscoelastic damping coefficients on vibration damping characteristics of the plate including the frequencies, the damping rate, and the deflection. The obtained results indicate that the natural frequency and deflection reduce with increasing the structural viscoelastic damping value. The plate takes a long time for suppressing its vibration due to increasing the hygrothermal factor.

Appendices

Appendix A

The coefficients ${\overline{Q }}_{ij}^{\left(r\right)}$ and ${\overline{q }}_{ij}$ appeared in Eqs. (9) and (10) can be presented as

$$\begin{aligned}{\overline{Q }}_{11}^{\left(r\right)} & ={Q}_{11}^{\left(r\right)}{{\mathrm{cos}}^{4}\theta }^{\left(r\right)}+2\left({Q}_{12}^{\left(r\right)}{+2Q}_{66}^{\left(r\right)}\right){{\mathrm{cos}}^{2}\theta }^{\left(r\right)}{{\mathrm{sin}}^{2}\theta }^{\left(r\right)}+{Q}_{22}^{\left(r\right)}{{\mathrm{sin}}^{4}\theta }^{\left(r\right)},\\ {\overline{Q }}_{23}^{\left(r\right)} & ={Q}_{23}^{\left(r\right)}{{\mathrm{cos}}^{2}\theta }^{\left(r\right)}+{Q}_{13}^{\left(r\right)}{{\mathrm{sin}}^{2}\theta }^{\left(r\right)}, \\ {\overline{Q }}_{12}^{\left(r\right)} & =\left({Q}_{11}^{\left(r\right)}+{Q}_{22}^{\left(r\right)}-{4Q}_{66}^{\left(r\right)}\right){{\mathrm{cos}}^{2}\theta }^{\left(r\right)}{{\mathrm{sin}}^{2}\theta }^{\left(r\right)}+{Q}_{12}^{\left(r\right)}\left({{\mathrm{sin}}^{4}\theta }^{\left(r\right)}+{{\mathrm{cos}}^{4}\theta }^{\left(r\right)}\right), \\ {\overline{Q }}_{22}^{\left(r\right)} & ={Q}_{11}^{\left(r\right)}{{\mathrm{sin}}^{4}\theta }^{\left(r\right)}+2\left({Q}_{12}^{\left(r\right)}{+2Q}_{66}^{\left(r\right)}\right){{\mathrm{cos}}^{2}\theta }^{\left(r\right)}{{\mathrm{sin}}^{2}\theta }^{\left(r\right)}+{Q}_{22}^{\left(r\right)}{{\mathrm{cos}}^{4}\theta }^{\left(r\right)}, \\ {\overline{Q }}_{33}^{\left(r\right)}&={Q}_{33}^{\left(r\right)},\\ {\overline{Q }}_{44}^{\left(r\right)}& ={Q}_{44}^{\left(r\right)}{{\mathrm{cos}}^{2}\theta }^{\left(r\right)}+{Q}_{55}^{\left(r\right)}{{\mathrm{sin}}^{2}\theta }^{\left(r\right)}, \\ {\overline{Q }}_{55}^{\left(r\right)} & ={Q}_{55}^{\left(r\right)}{{\mathrm{cos}}^{2}\theta }^{\left(r\right)}+{Q}_{44}^{\left(r\right)}{{\mathrm{sin}}^{2}\theta }^{\left(r\right)}, \\{\overline{Q }}_{66}^{\left(r\right)} & ={\left({Q}_{11}^{\left(r\right)}+{Q}_{22}^{\left(r\right)}-{2Q}_{12}^{\left(r\right)}-{2Q}_{66}^{\left(r\right)}\right){{\mathrm{sin}}^{2}\theta }^{\left(r\right)}{{\mathrm{cos}}^{2}\theta }^{\left(r\right)}+Q}_{66}^{\left(r\right)}\left({{\mathrm{sin}}^{4}\theta }^{\left(r\right)}+{{\mathrm{cos}}^{4}\theta }^{\left(r\right)}\right),\\ {Q}_{11}^{\left(r\right)} & =\frac{{E}_{1}\left(1-{\upnu }_{23}^{\left(r\right)}{\upnu }_{32}^{\left(r\right)}\right)}{\Delta },\quad{ Q}_{12}^{\left(r\right)}=\frac{{E}_{1}\left({\upnu }_{21}^{\left(r\right)}+{\upnu }_{31}^{\left(r\right)}{\upnu }_{23}^{\left(r\right)}\right)}{\Delta }, \quad{Q}_{13}^{\left(r\right)}=\frac{{E}_{1}\left({\upnu }_{31}^{\left(r\right)}+{\upnu }_{21}^{\left(r\right)}{\upnu }_{32}^{\left(r\right)}\right)}{\Delta },\\ {Q}_{22}^{\left(r\right)} & =\frac{{E}_{2}\left(1-{\upnu }_{13}^{\left(r\right)}{\upnu }_{31}^{\left(r\right)}\right)}{\Delta }, \quad{Q}_{23}^{\left(r\right)}=\frac{{E}_{2}\left({\upnu }_{32}^{\left(r\right)}+{\upnu }_{12}^{\left(r\right)}{\upnu }_{31}^{\left(r\right)}\right)}{\Delta }, \quad{Q}_{33}^{\left(r\right)}=\frac{{E}_{3}\left(1-{\upnu }_{12}^{\left(r\right)}{\upnu }_{21}^{\left(r\right)}\right)}{\Delta } ,\\ {Q}_{44}^{\left(r\right)} & ={G}_{23}^{\left(r\right)}, \quad{Q}_{55}^{\left(r\right)}={G}_{13}^{\left(r\right)},\quad {Q}_{66}^{\left(r\right)}={G}_{12}^{\left(r\right)},\end{aligned}$$

$$\begin{aligned} \Delta &=1- {\upnu }_{21}^{\left(r\right)}{\upnu }_{12}^{\left(r\right)}-{\upnu }_{23}^{\left(r\right)}{\upnu }_{32}^{\left(r\right)}-{\upnu }_{13}^{\left(r\right)}{\upnu }_{31}^{\left(r\right)} -2{\upnu }_{21}^{\left(r\right)}{\upnu }_{13}^{\left(r\right)}{\upnu }_{32}^{\left(r\right)},\\ {\upnu }_{21}^{\left(r\right)} & =\frac{{\upnu }_{12}^{\left(r\right)}{E}_{22}^{\left(r\right)}}{{E}_{1}^{\left(r\right)}},\quad {\upnu }_{31}^{\left(r\right)}={\upnu }_{13}^{\left(r\right)}\frac{{E}_{3}^{\left(r\right)}}{{E}_{1}^{\left(r\right)}},\quad {\upnu }_{32}^{\left(r\right)}={\upnu }_{23}^{\left(r\right)}\frac{{E}_{3}^{\left(r\right)}}{{E}_{2}^{\left(r\right)}},\\ {\stackrel{\sim }{\alpha }}_{xx} & ={\alpha }_{xx}{\mathrm{cos}}^{2}\theta +{\alpha }_{yy}{\mathrm{sin}}^{2}\theta,\quad {\stackrel{\sim }{\alpha }}_{yy}={\alpha }_{yy}{\mathrm{cos}}^{2}\theta +{\alpha }_{xx}{\mathrm{sin}}^{2}\theta ,\\ {\stackrel{\sim }{\alpha }}_{xy}& =\left({\alpha }_{xx}-{\alpha }_{yy}\right)\mathrm{sin}\theta \mathrm{cos}\theta ,\\ {\stackrel{\sim }{\beta }}_{xx} & ={\beta }_{xx}{\mathrm{cos}}^{2}\theta +{\beta }_{yy}{\mathrm{sin}}^{2}\theta,\quad {\stackrel{\sim }{\beta }}_{yy}={\beta }_{yy}{\mathrm{cos}}^{2}\theta +{\beta }_{xx}{\mathrm{sin}}^{2}\theta ,\\ {\stackrel{\sim }{\beta }}_{xy} & =\left({\beta }_{xx}-{\beta }_{yy}\right)\mathrm{sin}\theta \mathrm{cos}\theta ,\\ {\overline{q }}_{31} & ={q}_{31}{\mathrm{cos}}^{2}\theta +{q}_{32}{\mathrm{sin}}^{2}\theta,\quad {\overline{q }}_{32}={q}_{32}{\mathrm{cos}}^{2}\theta +{q}_{31}{\mathrm{sin}}^{2}\theta ,\\ {\overline{q }}_{14} & =\left({q}_{15}-{q}_{24}\right)\mathrm{sin}\theta \mathrm{cos}\theta,\quad {\overline{q }}_{24}={q}_{24}{\mathrm{cos}}^{2}\theta +{q}_{15}{\mathrm{sin}}^{2}\theta ,\\ {\overline{q }}_{15} & ={q}_{15}{\mathrm{cos}}^{2}\theta +{q}_{24}{\mathrm{sin}}^{2}\theta,\quad {\overline{q }}_{25}=\left({q}_{15}-{q}_{24}\right)\mathrm{sin}\theta \mathrm{cos}\theta ,\\ {\overline{q }}_{36} &=\left({q}_{31}-{q}_{32}\right)\mathrm{sin}\theta \mathrm{cos}\theta ,\end{aligned}$$

where ${E}_{i}$, ${v}_{ij}$ and ${G}_{ij}$ are Young’s moduli, Poisson’s ratios, and shear moduli, respectively. Also, the coefficients ${\alpha }_{ij}$ and ${\beta }_{ij}$ are the thermal and hygroscopic expansion coefficients. The coefficients ${q}_{ij}$ indicate the magnetostrictive modules.

Appendix B

The coefficients ${\widehat{S}}_{ij}$, ${\widehat{M}}_{ij}$ and ${\widehat{C}}_{ij}$ ($i=1, 2, 3$) appeared in Eq. (34) are expanded as the following:

$$\begin{aligned} {\widehat{S}}_{11} &=\left(1+{\left.\mathrm{g}\frac{\partial }{\partial t}\right|}_{r=\mathrm{viscoelastic}}\right)\left[{D}_{11}{\left(\frac{n\pi }{a}\right)}^{4}+{D}_{22}{\left(\frac{m\pi }{b}\right)}^{4}+2\left({D}_{12}+2{D}_{66}\right){\left(\frac{n\pi }{a}\right)}^{2}{\left(\frac{m\pi }{b}\right)}^{2}\right] +\left({K}_{P}+{F}_{x}\right){\left(\frac{n\pi }{a}\right)}^{2}+\left({K}_{P}+{F}_{y}\right){\left(\frac{m\pi }{b}\right)}^{2}+{K}_{W}, \\ {\widehat{S}}_{12} & =-\left(1+{\left.\mathrm{g}\frac{\partial }{\partial t}\right|}_{r=\mathrm{viscoelastic}}\right)\left[{E}_{11}^{1}{\left(\frac{n\pi }{a}\right)}^{3}+\left({E}_{21}^{1}+2{E}_{66}^{1}\right)\frac{n\pi }{a}{\left(\frac{m\pi }{b}\right)}^{2}\right],\\ {\widehat{S}}_{13} & =-\left(1+{\left.\mathrm{g}\frac{\partial }{\partial t}\right|}_{r=\mathrm{viscoelastic}}\right)\left[{E}_{22}^{1}{\left(\frac{m\pi }{b}\right)}^{3}+\left({E}_{12}^{1}+2{E}_{66}^{1}\right){\left(\frac{n\pi }{a}\right)}^{2}\frac{m\pi }{b}\right],\\ {\widehat{S}}_{22} & =\left(1+{\left.\mathrm{g}\frac{\partial }{\partial t}\right|}_{r=\mathrm{viscoelastic}}\right)\left[{E}_{11}^{3}{\left(\frac{n\pi }{a}\right)}^{2}+{E}_{66}^{3}{\left(\frac{m\pi }{b}\right)}^{2}+{E}_{55}^{3}\right],\\ {\widehat{S}}_{23} & ={\widehat{S}}_{23}=\left(1+{\left.\mathrm{g}\frac{\partial }{\partial t}\right|}_{r=\mathrm{viscoelastic}}\right)\left({E}_{12}^{3}+{E}_{66}^{3}\right)\frac{n\pi }{a}\frac{m\pi }{b}, \\ {\widehat{S}}_{33} & =\left(1+{\left.\mathrm{g}\frac{\partial }{\partial t}\right|}_{r=\mathrm{viscoelastic}}\right)\left[{E}_{66}^{2}{\left(\frac{n\pi }{a}\right)}^{2}+{E}_{22}^{3}{\left(\frac{m\pi }{b}\right)}^{2}+{E}_{44}^{3}\right],\\ {\widehat{M}}_{11} & =-{\beta }_{31}{\left(\frac{n\pi }{a}\right)}^{2}-{\beta }_{32}{\left(\frac{m\pi }{b}\right)}^{2}, \quad{\widehat{M}}_{21}={\gamma }_{31}\frac{n\pi }{a}, \quad{\widehat{M}}_{31}={\gamma }_{32}\frac{m\pi }{b},\\ {\widehat{M}}_{12} & ={\widehat{M}}_{13}={\widehat{M}}_{22}={\widehat{M}}_{23}={\widehat{M}}_{32}={\widehat{M}}_{33}=0,\\ {\widehat{C}}_{11}& ={I}_{2}\left[{\left(\frac{n\pi }{a}\right)}^{2}+{\left(\frac{m\pi }{b}\right)}^{2}\right]+{I}_{0}, \quad{\widehat{C}}_{12}=-{I}_{e}\frac{n\pi }{a},\quad {\widehat{C}}_{13}=-{I}_{e}\frac{m\pi }{b},\\ {\widehat{C}}_{22} & ={I}_{e}^{2}, \quad{\widehat{C}}_{23}=0, \quad {\widehat{C}}_{33}={I}_{e}^{2}.\end{aligned}$$