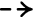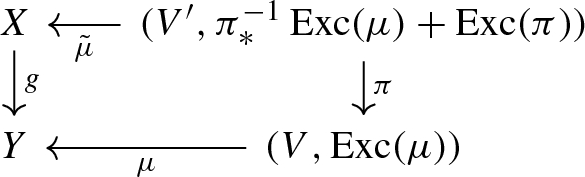On the Kodaira vanishing theorem for log del Pezzo surfaces in positive characteristic

Abstract

We investigate the vanishing of $H^1(X,\mathcal {O}_X(-D))$ for a big and nef $\mathbb {Q}$-Cartier $\mathbb {Z}$-divisor D on a log del Pezzo pair $(X,\Delta )$ over a perfect field of positive characteristic p.

1 Introduction

It has long been known that the (Kodaira and Kawamata–Viehweg) vanishing theorems, so fundamental to birational geometry in characteristic zero, in general fail for surfaces in positive characteristic [20]. Several people have investigated different classes of surfaces over perfect fields of positive characteristic for which the (Kodaira and Kawamata–Viehweg) vanishing theorems may or may not hold. The question is subtle; for example, every smooth rational surface over a perfect field satisfies Kodaira vanishing, however over any algebraically closed field of positive characteristic, there are smooth rational surfaces that violate Kawamata–Viehweg vanishing [4]. On the other hand a smooth surface with ample anti-canonical bundle satisfies Kawamata–Viehweg vanishing theorem over any algebraically closed field [4, Proposition A.1]. This however is no longer true if (klt) singularities are allowed and counterexamples (even to Kodaira vanishing) have been constructed over algebraically closed fields of characteristic 2 [5] and 3 [2].

The situation simplifies in large characteristics. In [6] the authors prove the existence of an integer $p_0$ such that over an algebraically closed field of characteristic $p>p_0$ every log del Pezzo surface satisfies Kawamata–Viehweg vanishing theorem. Finding an effective bound for this $p_0$ is a central open question in positive characteristic birational geometry. For example over an algebraically closed field of characteristic $p>\mathrm {max}\{5, p_0\}$ a three dimensional klt singularity is rational [12, Theorem 1.1], and threefolds satisfy a refined version of the basepoint free theorem [3, Theorem 1.1].

The construction of the integer $p_0$ in [6] is implicit. During the course of the proof of [6, Theorem 1.1] the authors consider log del Pezzo surfaces belonging to a bounded family over ${{\,\mathrm{Spec}\,}}(\mathbb {Z})$. The construction of the integer $p_0$ does in particular depend on this family in an implicit way. It is therefore natural to ask if it is possible to prove vanishing theorems in large explicit characteristics depending on some explicit numerical invariant of a bounded family of log del Pezzo surfaces. In this direction, we show that Kodaira vanishing (for big and nef divisors) holds on a del Pezzo surface of bounded index I in characteristic $p>p_0(I)$ where $p_0(I)$ is an explicit polynomial in the index I. We also determine an explicit bound for $p_0$ (for Kodaira vanishing) in terms of $\epsilon >0$ for an $\epsilon$-klt log del Pezzo surface. Our main results in this direction are the following.

Theorem A

Let X be a projective klt surface over a perfect field k of characteristic $p>0$ with ample anti-canonical divisor $-K_X$ of Cartier index I. Let D be a big and nef $\mathbb {Q}$-Cartier $\mathbb {Z}$-divisor on X.

• (1) If $I=1$, i.e., if $-K_X$ is an ample Cartier divisor then:

  • if $p\ge 9221$, then $H^1(X, \mathcal {O}_X(-D))=0$

  • if $p\ge 5$, then $H^1(X, \mathcal {O}_X(D))=0.$

• (2) If $I\ge 2$ and $p\ge (13-45I)^2(2I^3+4I^2+2I)+1$, then:

  $$H^1(X, \mathcal {O}_X(D))=H^1(X, \mathcal {O}_X(-D))=0.$$

Theorem B

Let $0<\epsilon < 3^{-1/2}$ be a real number. Let $(X,\Delta )$ be a projective $\epsilon$-klt surface with $-(K_X+\Delta )$ ample over a perfect field k of characteristic

$$\begin{aligned} p\ge 2^{\frac{128}{\epsilon ^5}+2}\left( \frac{2}{\epsilon }\right) ^{\frac{(128)^2}{\epsilon ^{25}}} +1. \end{aligned}$$

Then Kodaira vanishing holds on X, i.e., for all ample $\mathbb {Q}$-Cartier $\mathbb {Z}$-divisors D on X we have that $H^i(X,\mathcal {O}_X(D+K_X))=0$, for all $i>0$.

In this note, we use a technique due to Ekedahl [7]. When trying to prove Kodaira vanishing in explicit characteristics using this technique, the difficulties arise from Weil divisors which are far from being Cartier. For example, on a log del Pezzo surface over an algebraically closed field of characteristic $p\ge 4c+1$ we can prove that $H^1(X,\mathcal {O}_X(K_X+A))=0$ for every ample $\mathbb {Q}$-Cartier Weil divisor A of Cartier index $\le c$ (see Remark 3.5). Another strategy is therefore to control the Cartier index of a Weil divisor D in terms of the Cartier index I of $(K_X+\Delta )$. We prove, in this way, that a big and nef $\mathbb {Z}$-divisors D of big volume relative to the index I in characteristic $p\ge 5$ satisfies $H^1(X, \mathcal {O}_X(-D))=0$.

Theorem C

Let $(X, \Delta )$ be a projective klt surface over a perfect field k of characteristic $p\ge 5$ with $-(K_X+\Delta )$ an ample $\mathbb {Q}$-Cartier $\mathbb {Q}$-divisor of Cartier index I. Let D be a big and nef $\mathbb {Q}$-Cartier $\mathbb {Z}$-divisor. Then the following holds true:

• (1) If $I=1$ and $D^2\ge 9$, then $H^1(X, \mathcal {O}_X(-D))=0.$

• (2) If $I\ge 2$ and $D^2\ge {2I^3+4I^2+2I}$, then $H^1(X, \mathcal {O}_X(-D))=0.$

During the preparation of this note we were informed that J. Lacini has classified all log del Pezzo surfaces of Picard rank one over an algebraically closed field of characteristic $p\ge 5$ [17, Theorem 1.1]. From this classification it follows that all log del Pezzo surfaces of Picard rank one over an algebraically closed field of characteristic $p>5$ admit a log resolution that lifts to ${{\,\mathrm{W_2(k)}\,}}$ [17, Theorem 7.2]. It therefore follows from his work that Kodaira vanishing holds for log del Pezzo surfaces of Picard rank one over an algebraically closed field of characteristic $p>5$ (see [6, Lemma 6.1]). Combining his result with the techniques exploited in this paper, one can prove the Kodaira vanishing theorem on a log del Pezzo surface over an algebraically closed field of characteristic $p>5$. At the end of this note we illustrate this argument. Building on the liftability of rank one log del Pezzo surfaces in characteristic $p>5$ by Lacini we can prove the following theorem.

Theorem D

Let $(X,\Delta )$ be a projective log del Pezzo surface over a perfect field of characteristic $p>5$. Then Kodaira vanishing holds on X, i.e., for all ample $\mathbb {Z}$-divisors D on X we have $H^i(X,\mathcal {O}_X(D+K_X))=0$, for all $i>0$.

After this note was made public, the author has, in joint work with Fabio Bernasconi and Justin Lacini, extended the above result. In [1] we show that log del Pezzo surfaces over a perfect field of characteristic $p>5$ satisfy the Kawamata Viehweg vanishing theorem. In [1] we also construct a del Pezzo surface over an algebraically closed field of characteristic $p=5$ on which the Kodaira vanishing theorem fails. This implies that the characteristic $p>5$ in Theorem D is optimal.

2 Preliminaries

By a variety we mean a finite type integral separated scheme over a field. We will work exclusively over a perfect field k.

A $\mathbb {Q}$-divisor D is said to be $\mathbb {Q}$-Cartier if there exists an integer m such that mD is Cartier. A $\mathbb {Q}$-divisor is ample/nef/big if it is $\mathbb {Q}$-Cartier and an integer multiple is ample/nef/big as a line bundle.

If X is a normal variety, then the reflexive sheaves on X are determined (up to isomorphism) by their restriction to a big open subset U (an open subset U of X is big if $\mathrm {codim}_X (X-U)\ge 2$). If $i: U \rightarrow X$ is the inclusion of a big open subset and $\mathcal {M}$ is a reflexive sheaf on U then $i_*\mathcal {M}$ is a reflexive sheaf on X, moreover for any reflexive sheaf $\mathcal {G}$ on X we have an isomorphism $\mathcal {G}\cong i_*\mathcal {G}_{|_U}$ [10, Proposition 1.6]. Let U denote the smooth locus of X. Since X is normal U is big. Therefore, for any Weil divisor D on X the restriction of D to the smooth locus defines a reflexive sheaf $i_*\mathcal {O}_U(U\cap D)$ of rank one on X. Conversely, any reflexive sheaf of rank one $\mathcal {F}$ on X defines a Weil divisor D by setting D to be the closure of a Weil divisor E on U satisfying $\mathcal {F}_{|_U}=\mathcal {O}_U(E)$. This defines a one to one correspondence between the reflexive sheaves of rank one on X up to isomorphism and the set of Weil divisors on X up to rational equivalence [10]. We denote by $\mathcal {O}_X(D)$ the reflexive sheaf corresponding to a divisor D on X. We use the notation $K_X$ for the class corresponding to the closure of a canonical divisor $K_U$ on U in X, hence $\mathcal {O}_X(K_X)\cong i_*\mathcal {O}_U(K_U)$. If X is normal and projective then $\mathcal {O}_X(K_X)$ can be seen to be a dualizing sheaf for X [15, Proposition 5.75]. We use the notation $\omega _X$ for a dualizing sheaf on X.

In general if $D_1$ and $D_2$ are Weil divisors on a normal variety X, then $\mathcal {O}_X(D_1)\otimes \mathcal {O}_X(D_2)$ is not reflexive. However, the dual $\mathcal {M}^\vee$ of a coherent sheaf $\mathcal {M}$ is always reflexive [10, Corollary 1.2] and we may define a product structure on the set of reflexive sheaves by defining $\mathcal {O}_X(D_1)\otimes \mathcal {O}_X(D_2)\mathrel {\mathop :}=(\mathcal {O}_X(D_1)\otimes \mathcal {O}_X(D_2))^{\vee \vee }$. We have the following identities for Weil divisors $D_1, D_2$ and a Cartier divisor C: $\mathcal {O}_X(D_1+D_2)\cong (\mathcal {O}_X(D_1)\otimes \mathcal {O}_X(D_2))^{\vee \vee }$, $\mathcal {O}_X(-D_1)\cong \mathcal {O}_X(D_1)^{\vee }$, $\mathcal {O}_X(D_1+C)\cong \mathcal {O}_X(D_1)\otimes \mathcal {O}_X(C)$ and ${{\,\mathrm{Hom}\,}}_{\mathcal {O}_X}( \mathcal {O}_X(D_1), \mathcal {O}_X(D_2))\cong \mathcal {O}_X(D_2-D_1).$ This product structure makes the set of reflexive sheaves on X (up to isomorphism) into a group such that the correspondence between Weil divisors and reflexive sheaves on X, as described above, becomes an isomorphism of groups.

By a log pair $(X, \Delta )$ we shall mean a normal variety X together with an effective $\mathbb {Q}$-divisor $\Delta$ on X such that $K_X+\Delta$ is $\mathbb {Q}$-Cartier. By a klt (respectively lc) pair we shall mean a log pair with klt (respectively lc) singularities in the sense of [15, Section 2]. By [23, Corollary 4.11] if X is a surface and $(X, \Delta )$ is a klt pair then X is $\mathbb {Q}$-factorial.

A normal surface X is said to be a del Pezzo surface if it has klt singularities and $-K_X$ is $\mathbb {Q}$-Cartier and ample. A log pair (X, B) is said to be a log del Pezzo surface if it has klt singularities and $-(K_X+ B)$ is ample.

2.1 Serre vanishing and Serre duality for $\mathbb {Z}$-divisors

One of the most fundamental vanishing theorems in algebraic geometry is that of Serre. It naturally implies a Weil divisor version.

Theorem 1.1

Let X be a normal projective variety. If D is an ample $\mathbb {Q}$-Cartier $\mathbb {Z}$-divisor and $\mathcal {F}$ is a coherent sheaf on X then

$$H^i(X, \mathcal {F}\otimes \mathcal {O}_X(lD))=0$$

for all l big enough and all $i>0$.

Proof

Let m be an integer such that mD is Cartier. By Serre vanishing there exists, for all $1\le i\le m$, an $n_i$ such that $H^j(X, \mathcal {F}\otimes \mathcal {O}_X(iD)\otimes \mathcal {O}_X(mD)^{\otimes n})=0$, for all $n\ge n_i$ and all $j>0$. Since $\mathcal {O}_X(mD)$ is Cartier $\mathcal {O}_X(iD)\otimes \mathcal {O}_X(mD)^{\otimes n}=\mathcal {O}_X((i+mn)D)$. Set $N=\max _{1\le i \le m} n_i$. For all $l\ge (m+1)N$, we can write $l=i+mk$, for $1\le i\le m-1$, where $k\ge N$. Therefore, we have $H^i(X, \mathcal {F}\otimes \mathcal {O}_X(lD))=H^i(X, \mathcal {F}\otimes \mathcal {O}_X(iD)\otimes \mathcal {O}_X(mD)^{\otimes k})=0$, for all $l\ge (m+1)N$. $\square$

Corollary 1.2

Let D be a big and nef integral divisor on a normal projective surface X, then $H^1(X, \mathcal {O}(-mD))=0$ for all $m>>0$.

Proof

Let r be the Cartier index of D. Let $n>0$ be such that $H^0(X,\mathcal {O}(lD))$ is non zero for all $l\ge n$, this is possible since D is big. By Fujita vanishing [9, Theorem 10] there exists an integer m such that $H^1(X, \mathcal {O}(-(kr+l)D))=0$ for all $l\ge n$ and all $k\ge m$, this proves the Corollary. $\square$

We will repeatedly need to use a form of Serre Duality valid for reflexive sheaves on a normal surface.

Theorem 1.3

(Serre Duality for CM-sheaves) Let X be a projective scheme of pure dimension n over a field k. Let $\mathcal {F}$ be a CM sheaf on X such that ${{\,\mathrm{Supp}\,}}(\mathcal {F})$ is of pure dimension n. Then

$$\begin{aligned} H^i(X,\mathcal {F})\, \hbox {is dual to}\, H^{n-i}(X,{{\,\mathrm{Hom}\,}}_{\mathcal {O}_X}(\mathcal {F},\omega _X)). \end{aligned}$$

Proof

E.g., [15, Theorem 5.71] $\square$

In particular, by [10, Proposition 1.3] for any $\mathbb {Z}$-divisor D on a normal projective surface X the vector space $H^i(X,\mathcal {O}_X(D))$ is dual to $H^{2-i}(X,\mathcal {O}_X(K_X-D))$ for $i=0,1$.

Remark 1.4

If D is a big and nef $\mathbb {Z}$-divisor on a normal projective surface X then $H^0(X, \mathcal {O}_X(-D))=0$ and hence by duality $H^2(X, \mathcal {O}_X(D+K_X))=0$. Therefore, Kodaira vanishing is equivalent to the vanishing of $H^1(X,\mathcal {O}_X(-D))\cong H^{1}(X,\mathcal {O}_X(K_X+D)).$

2.2 Frobenius techniques

Let X be a scheme over a positive characteristic base S, let $F_X$ denote the absolute Frobenius on X. The absolute Frobenius $F_X$ is not a morphism of S-schemes unless $F_S$ on S is the identity. In particular we have the following commuting diagram:

where $F_{X/S}$ denotes the relative Frobenius. When $S=Spec(k)$ for a perfect field k then the absolute Frobenius on S is an isomorphism and

is an isomorphism over S if we consider X as a scheme over S by post-composing the structure morphism to S with $F^{-1}_S$ on S. We often make this identification, under which the relative and the absolute Frobenius coincide, and denote by $F: X\rightarrow X$ the corresponding morphism. Let X be a normal variety over an algebraically closed field of positive characteristic. If D is an integral divisor on X then $(F^*\mathcal {O}_X(D))^{\vee \vee }\cong \mathcal {O}_X(pD)$, since they agree on the regular locus which is a big open subset of X. There is a natural map (unit of adjunction) $\mathcal {O}_X(D)\rightarrow F_*F^*\mathcal {O}_X(D)$. This induces a morphism:

$$\begin{aligned} H^i(X, \mathcal {O}_X(D))\rightarrow H^i(X, F^*\mathcal {O}_X(D)) \rightarrow H^i(X, F^*\mathcal {O}_X(D)^{\vee \vee }). \end{aligned}$$

Therefore, the Frobenius on X induces morphisms for all m:

$$\begin{aligned} H^i(X,\mathcal {O}_X(-p^mD))\rightarrow H^i(X,\mathcal {O}_X(-p^{m+1}D)). \end{aligned}$$

If D is an ample divisor whose associated Weil sheaf is CM, then these groups eventually vanish for $m>>0$ by Theorem 1.3 and Corollary 1.1. Therefore, Kodaira vanishing theorem for such divisors D hold true on X if and only if the morphisms $H^i(X,\mathcal {O}_X(-p^mD))\rightarrow H^i(X,\mathcal {O}_X(-p^{m+1}D))$ are injective for all m and all $i<\mathrm {dim}(X)$.

2.3 Non-vanishing and the associated $\alpha _{\mathcal {O}_{X_0}(D_0)}$-torsor

Let X be a projective normal surface and D be a $\mathbb {Q}$-Cartier $\mathbb {Z}$-divisor on X. Let $X_0\subset X$ denote the smooth locus of X and $D_0\mathrel {\mathop :}=D\cap X_0$ be the restriction of D to the smooth locus. Let $F_0$ denote the Frobenius on $X_0$. We will assume that $H^1(X, \mathcal {O}_X(-D))\ne 0$ and that $H^1(X,\mathcal {O}_X(-pD))=0$. Let $\alpha \in H^1(X, \mathcal {O}_X(-D))$ denote a non-trivial element of the kernel of the map $H^i(X,\mathcal {O}_X(-D))\rightarrow H^i(X,\mathcal {O}_X(-pD))$ described in Sect. 1.2. Since $Z\mathrel {\mathop :}=X-X_0$ is the complement of a big open subset of X and $\mathcal {O}_X(nD)$ is reflexive (and so in particular, $H^0(X,\mathcal {O}_X(nD))\cong H^0(X_0,{\mathcal {O}_X}_0(nD_0))$), we see from the local cohomology long exact sequence that we have an inclusion:

$$H^1(X, \mathcal {O}_X(-nD))\hookrightarrow H^1(X_0, \mathcal {O}_{X_0}(-nD_0))$$

for all n. By our assumptions, $\alpha$ therefore defines a non-trivial element:

$$\alpha _0\in H^1(X_0, \mathcal {O}_{X_0}(-D_0)),$$

which belongs to the kernel of the morphism:

$$\begin{aligned} H^1(X_0, \mathcal {O}_{X_0}(-D_0))\rightarrow H^1(X_0, \mathcal {O}_{X_0}(-pD_0)) \end{aligned}$$

induced by $F_0$. This kernel has a geometric description on $X_0$ which is described in the next section.

2.3.1 $\alpha _{L}$-torsors

An invertible sheaf $\mathcal {L}$ on a scheme X naturally defines a sheaf of groups under addition representable by the affine group scheme $L\mathrel {\mathop :}={{\,\mathrm{Spec}\,}}_X(\bigoplus _i \mathcal {L}^{-i}).$ Let X be defined over a field k of characteristic $p>0.$ Then there exists a homomorphism of sheaves of additive groups $\mathcal {L}\rightarrow \mathcal {L}^p$, defined by raising a local section to its p-power. This is a purely characteristic $p>0$ phenomenon, since for any two local sections s and t of $\mathcal {L}$ we have $(s+t)^p=s^p+t^p$ in characteristic p.

Relative to the Zariski site of X the above morphism of sheaves is not in general a surjection. However, as a morphism of $X_{{{\,\mathrm{fppf}\,}}}$-sheaves it is, i.e., the corresponding morphism of sheaves of groups on the flat site of X is surjective [18, II.2.18]. The kernel of this morphism is a sheaf of groups on $X_{{{\,\mathrm{fppf}\,}}}$ which we denote by $\alpha _{\mathcal {L}}.$ By construction $\alpha _{\mathcal {L}}$ is representable by an affine group scheme over X, denoted $\alpha _L.$ In fact, we have $\alpha _{L}={{\,\mathrm{Spec}\,}}_X( \bigoplus _{i=0}^{p-1} \mathcal {L}^{-i})$.

The short exact sequence of sheaves of groups (relative to the flat- topology on X)

induces a long exact sequence on cohomology [18, 4, Prop 4.5]:

$$\begin{aligned} \dots \rightarrow H^0(X, \mathcal {L}^p)\rightarrow \check{H}^1_{{{\,\mathrm{fppf}\,}}}(X, \alpha _{\mathcal {L}})\rightarrow H^1(X, \mathcal {L})\rightarrow H^1(X, \mathcal {L}^p)\rightarrow \dots \end{aligned}$$

Therefore, a non-trivial element $\alpha$ in the kernel of $H^1(X, \mathcal {L})\rightarrow H^1(X, \mathcal {L}^p)$ defines a non-trivial element $\alpha \in \check{H}^1_{{{\,\mathrm{fppf}\,}}}(X, \alpha _{\mathcal {L}}).$ The group $\check{H}^1_{{{\,\mathrm{fppf}\,}}}(X, \alpha _{\mathcal {L}})$ has a geometric meaning, i.e., a non-trivial element $\alpha \in \check{H}^1_{{{\,\mathrm{fppf}\,}}}(X, \alpha _{\mathcal {L}})$ corresponds to a non-trivial $\alpha _{\mathcal {L}}$-torsors $Y\rightarrow X$, see for example, [18, Proposition 4.6]. The torsor Y corresponding to $\alpha \in \check{H}^1_{{{\,\mathrm{fppf}\,}}}(X, \alpha _{\mathcal {L}})$ constructed as above were studied by Ekedahl.

Proposition 1.5

([7, pp. 106–107], [19, Theorem 2.11]) Let X be a normal variety over an algebraically closed field k of characteristic $p>0$. Let $\mathcal {L}\in Pic(X)$. A non-trivial element of the kernel under the Frobenius action: $H^1(X, \mathcal {L})\rightarrow H^1(X, \mathcal {L}^p),$ gives rise to a non-trivial $\alpha _\mathcal {L}$-torsor $\beta : Y \rightarrow X$. Locally over $U=Spec(A)$, the morphism $\beta ^{-1}U \rightarrow U$ is given by $A\rightarrow A[x]/(x^p-a)$ for some element $a\in A$ which is not a p-power. Therefore, $\beta$ is purely inseparable of degree p. If X is a $G_1$ and $S_2$ variety, then Y is also a $G_1$ and $S_2$ variety which satisfies: $\omega _Y=\beta ^{*}(\omega _X\otimes \mathcal {L}^{p-1})$.

Here $S_2$ denotes Serre’s condition and $G_1$ denotes Gorenstein in codimension one.

Remark 1.6

Y is in general not normal.

2.4 Geometric construction for Weil-divisors

Let X be a projective normal surface over an algebraically closed field of charcteristic $p>0$ and let D a $\mathbb {Q}$-Cartier ample Weil divisor on X such that $H^1(X, \mathcal {O}_X(-D))\ne 0$ and $H^1(X, \mathcal {O}_X(-pD))=0.$ Let $X_0$ denote the smooth locus of X and let $D_0=D\cap X_0$. Let $\alpha _0$ be a non-trivial element of $H^1_{{{\,\mathrm{fppf}\,}}}(X, \alpha _{\mathcal {O}_{X_0}(D_0)})$ coming from a non-trivial element $\alpha \in H^1(X, \mathcal {O}_X(D))$ as described in point Sect. 1.3. Let $\pi _0 :Y_0\rightarrow X_0$ be the corresponding non-trivial $\alpha _{\mathcal {O}_{X_0}(D_0)}$-torsor. Then ${\pi _0}_*\mathcal {O}_{Y_0}$ is a locally free $\mathcal {O}_{X_0}$-algebra. Let $i:X_0\hookrightarrow X$ denote the inclusion of the regular locus. The multiplication on $X_0$ extends (because $i_*{\pi _0}_*\mathcal {O}_{Y_0}$ is reflexive) to make $i_*{\pi _0}_*\mathcal {O}_{Y_0}$ into a sheaf of $\mathcal {O}_X$-algebras. We may therefore define $Y\mathrel {\mathop :}={{\,\mathrm{Spec}\,}}_X(i_*{\pi _0}_*\mathcal {O}_{Y_0})$. Let $\pi : Y\rightarrow X$ denote the natural morphism.

Lemma 1.7

In the situation above $\pi : Y\rightarrow X$ is a finite degree p morphism and Y is a projective $S_2$ and $G_1$ surface that satisfies

$$\begin{aligned} K_Y=\pi ^*(K_X -(p-1)D). \end{aligned}$$

Proof

Since $\pi _*\mathcal {O}_Y=i_*{\pi _0}_*\mathcal {O}_{Y_0}$ is $S_2$ we have by [15, Proposition 5.4] that Y is $S_2.$ Since X and $X_0$ agree in codimension one, Y is $G_1.$ Since everything is $S_2$ and $G_1$ we may replace X with $X_0$ by [11, Theorem 1.12], therefore $\pi ^*(K_X)$ and $\pi ^*(D)$ are well-defined and the formula $K_Y=\pi ^*(K_X -(p-1)D)$ follows from Proposition 1.5. $\square$

Lemma 1.8

With the notation as above, let $\eta :\overline{Y}\rightarrow Y$ be the normalization of Y and let $\overline{\pi }: \overline{Y}\rightarrow X$ denotes the induced morphism. There exists an effective $\mathbb {Z}$-divisor $\Delta \ge 0$ on $\overline{Y}$ such that $K_{\overline{Y}}+\Delta =\overline{\pi }^*(K_X -(p-1)D).$

Proof

Since everything is $S_2$ and $G_1$ we may replace Y with a big open set and assume that Y is Gorenstein and $\overline{Y}$ is regular. Affine locally we may assume that $\omega _Y\cong \mathcal {O}_Y$ and $\omega _{\overline{Y}}\cong \mathcal {O}_{\overline{Y}}$. In this situation [19, Lemma 2.14] proves that the natural map $\omega _{\overline{Y}}\rightarrow \eta ^*\omega _{Y}$ has image equal to the conductor ideal, where $\eta ^*\omega _Y$ is identified with $\mathcal {O}_{\overline{Y}}$. $\square$

2.5 Bend and break

By studying different properties of the variety $\overline{Y}$ appearing in Lemma 1.8 one hopes to arrive at a contradiction to the assumed non-vanishing, $H^1(X, \mathcal {O}_X(-D))\ne 0$. This strategy was successfully employed by Ekedahl [7] and more recently in [19]. The main tool is the use of bend and break, together with the expression for the canonical divisor given by Lemma 1.8. Together, this can be used in order to derive inequalities comparing intersection numbers on X with the characteristic p of the base field. We will repeatedly use the following:

Theorem 1.9

[16, Chapter II, Theorem 5.8] Let X be a projective variety over an algebraically closed field, C a smooth, projective and irreducible curve, $f: C\rightarrow X$ a morphism and M any nef $\mathbb {R}$-divisor. Assume that X is smooth along f(C) and $K_{X} \cdot C>0.$ Then for every $x\in f(C)$ there is a rational curve $\Gamma _x\subset X$ containing x such that

$$\begin{aligned} M\cdot \Gamma _x\le 2\dim (X)\frac{M\cdot C}{-K_X\cdot C}. \end{aligned}$$

3 Kodaira vanishing for divisors of big volume

We will use the following terminology: We will say that a curve C on a surface X is big and basepoint free if the linear system |C| defines a birational morphism. If C is big and basepoint free, then for any finite number of points in X there exists $C'\in |C|$ such that $C'$ avoids all those points.

Lemma 2.1

Let X be a projective normal surface. Suppose that there exists an effective $\mathbb {Q}$-divisor E such that $-(K_X+E)$ is a $\mathbb {Q}$-Cartier ample divisor of Cartier index I. If D is a big $\mathbb {Q}$-Cartier semiample $\mathbb {Z}$-divisor such that $D^2\ge I^2(K_X+E)^2$ then there exists an ample Cartier divisor A and a big basepoint free curve C on X such that $D\cdot C\ge A\cdot C$.

Proof

Suppose, in order to arrive at a contradiction, that for every big basepoint free curve C and every ample Cartier divisor A of X we have $D\cdot C< A\cdot C$. For m divisible enough, $-m(K_X+E)$ is very ample. Therefore, for $A=-I(K_X+E)$ and $C\in |-m(K_X+E)|$ we find $-(K_X+E)\cdot D<I(K_X+E)^2$. Similarly, for n divisible enough, nD is basepoint free and we may consider a curve $C\in |nD|$ to find that $D^2<-I(K_X+E)\cdot D$. Putting this together, we find that $D ^2<I^2(K_X+E)^2$. $\square$

Theorem 2.2

Let X be a projective normal surface over an algebraically closed field k of characteristic $p\ge 5$. Suppose that there exists an effective $\mathbb {Q}$-divisor E such that $-(K_X+E)$ is a $\mathbb {Q}$-Cartier ample divisor of Cartier index I. If D is a $\mathbb {Q}$-Cartier nef and big semiample $\mathbb {Z}$-divisor such that $D^2\ge I^2(K_X+E)^2$ then $H^1(X, \mathcal {O}_X(-D))=0$.

Proof

Suppose that the theorem is not true. Let D be a nef and big semiample $\mathbb {Z}$-divisor on X such $D^2\ge I^2(K_X+E)^2$ and assume that $H^1(X,\mathcal {O}_X(-D))\ne 0$. By Corollary 1.2 there exists some $j\ge 1$ such that $H^1(X,\mathcal {O}_X(-p^jD))= 0$. If we replace D with $p^{j-1}D$ the inequality will be satisfied for $p^{j-1}D$. Suppose we can prove the theorem for $p^{j-1}D$ then $H^1(X,\mathcal {O}_X(-p^{j-1}D))= 0$ and, hence, by descending induction on j, we have proven that $H^1(X,\mathcal {O}_X(-D))= 0$. Therefore, there is no loss of generality to assume that $H^1(X,\mathcal {O}_X(-pD))=0$.

Let $\pi : Y\rightarrow X$ be a degree p-cover corresponding to a non-zero element $y\in H^1(X,\mathcal {O}_X(-D))$ as in Sect. 1.3. By replacing Y with its normalisation, we may assume that Y is normal and that

$$\begin{aligned} K_Y=\pi ^*K_X +(1-p)\pi ^*D -\Delta \end{aligned}$$

(2.1)

where $\Delta$ is effective (Lemma 1.8).

By Lemma 2.1 there exists a big basepoint free curve C on X and an ample Cartier divisor A such that $D\cdot C\ge A\cdot C$. Let $\pi : Y\rightarrow X$ be as above. By replacing C with a large enough multiple we see that there exists a curve $C_Y$ on Y such that:

• $C_Y$ is contained in the smooth locus of Y

• $C_Y$ is not contained in a component of $\Delta$

• $C=\pi _*C_Y$ for some curve C on X not contained in a component of E and such that $D\cdot C\ge A\cdot C.$

By Eq. (2.1) we have $-K_Y\cdot C_Y= -K_X\cdot C + (p-1)D\cdot C +\Delta \cdot C_Y\ge -K_X\cdot C$, where the last inequality comes from the assumption that D is nef and that $C_Y$ is not contained in a component of $\Delta$. By assumption $-(K_X+E)$ is ample, hence $-K_X\cdot C>E\cdot C\ge 0$. Therefore $-K _Y\cdot C_Y>0$. By Theorem 1.9 for $C_Y$ and $\pi ^*A$ on Y, there exists a rational curve $\Gamma _x$ passing through a point $x\in C_Y$ such that:

$$\pi ^*A\cdot \Gamma _x \le 4 \frac{\pi ^*A\cdot C_Y}{-K_Y\cdot C_Y} .$$

By Equation (2.1), we find:

$$\begin{aligned} \left( \pi ^*A\cdot \Gamma _x\right) \left( (-\pi ^*K_X +(p-1)\pi ^*D +\Delta )\cdot C_Y\right) \le 4\pi ^*A\cdot C_Y. \end{aligned}$$

However, since A is an ample Cartier divisor and $\pi$ is finite $\pi ^*A\cdot \Gamma _x\ge 1$. Moreover, $-\pi ^*K_X\cdot C_Y=-K_X\cdot C>0$ and $C_Y\cdot \Delta \ge 0$. By assumption, $\pi ^*A\cdot C_Y\le \pi ^*D\cdot C_Y$, therefore:

$$\begin{aligned} (p-1)\pi ^*A\cdot C_Y < \left( \pi ^*A\cdot \Gamma _x\right) \left( (-\pi ^*K_X +(p-1)\pi ^*D +\Delta )\cdot C_Y \right) . \end{aligned}$$

Putting these inequalities together we find:

$$(p-1)\pi ^*A\cdot C_Y < 4 \pi ^*A\cdot C_Y$$

and, therefore, $p< 5$. $\square$

Theorem 2.2 implies, together with results of [13], our main theorem for divisors of big volume.

Proof of Theorem C

By base change to an algebraic closure of k we can assume that k is algebraically closed. By the Basepoint free theorem [22, Theorem 1.3], D is semiample. Note that a klt surface of index I, necessarily, is $\frac{1}{I}$-klt. By [13, Theorem 1.3], we therefore have that $(K_X+\Delta ) ^2\le \text {max}\{9, 2I +4+\frac{2}{I}\} .$ The result therefore follows from Theorem 2.2. $\square$

Remark 2.3

Recently Kawakami improved both Theorems A and C in the case when $I=1$. In particular, let X be a del Pezzo surface with canonical singularities over an algebraically closed field of positive characteristic p and let D be a big and nef $\mathbb {Q}$-divisor. In [14] it is shown that $H^1(X,\mathcal {O}_X(-D))=0$ if $p\ne 2$ [14, Theorem 1.1] and that $H^1(X,\mathcal {O}_X(D))=0$ in all characteristic [14, Proposition 4.10]. See [14] for the precise statements which are slightly more general.

Corollary 2.4

Let X be a klt del Pezzo surface over an algebraically closed field of characteristic $p\ge 5$, such that $-K_X$ is ample of Cartier index I. Let D be a big and nef $\mathbb {Z}$-divisor of Cartier index c. Then $H^1(X, \mathcal {O}_X(D))=0$ if either of the following holds:

• $K_X^2\ge (c-1)^2D^2$ and D is ample

• $D^2\ge (I-1)^2K_X^2.$

Proof

The assumptions imply that $D-K_X$ is ample and $H^1(X, \mathcal {O}_X(K_X-D))$ is dual to $H^1(X, \mathcal {O}_X(D))$. Assume that the claimed vanishing does not hold. Since the characteristic of the base field is greater than or equal to five, we may argue as in the proof of Proposition 2.2 to assume that for every big basepoint free curve C and every ample Cartier divisor A we have $(D-K_X)\cdot C< A\cdot C.$ The first inequality comes from setting $A=cD$ and $C=-mK_X$ and $C=lD$ respectively, for large and divisible enough l and m. The second inequality comes from setting $A=-IK_X$ and $C=-mK_X$ and $C=lD$ respectively, for large and divisible enough l and m. $\square$

4 Kodaira vanishing in large characteristic

In this section we prove Kodaira vanishing in large characteristic for log del Pezzo surfaces of bounded index. That bounded families of log del Pezzo surfaces over ${{\,\mathrm{Spec}\,}}(\mathbb {Z})$ satisfy Kodaira vanishing in large characteristic (depending only on the family) has been proven by other methods in [6]. In Proposition 3.1 below we show that the existence of a very ample divisor A of bounded volume r on a normal projective surface X over a field of characteristic $p\ge 4r+1$ implies Kodaira Vanishing whenever $-K_X\cdot A>0$. In particular, we do not make any further assumption on the singularities of X.

Proposition 3.1

Let $r>0$ be an integer. Let X be a projective normal surface over an algebraically closed field k of characteristic $p\ge 4r+1$. If there exists a very ample divisor A on X such that $A^2\le r$ and $-K_X\cdot A>0$ then Kodaira vanishing (even for big and nef $\mathbb {Q}$-Cartier $\mathbb {Z}$-divisors) holds on X.

Proof

Suppose that D is a big and nef $\mathbb {Z}$-divisor and suppose that $H^1(X,\mathcal {O}_X(-D))\ne 0$. By replacing D with $p^jD$ for some $j\ge 1$ we may assume that $H^1(X,\mathcal {O}_X(-pD))= 0$ (Corollary 1.2). By Ekedahl’s construction we may assume that there exists a normal variety Y and a purely inseparable degree p morphism $\pi :Y\rightarrow X$ such that

$$\begin{aligned} K_Y=\pi ^*K_X -(p-1)D-E \end{aligned}$$

(3.1)

for $E \ge 0$. Let A be a very ample general curve on X as above. There exists an integer $l>0$ such that $l\pi ^*A$ is very ample on Y. Therefore there exists a curve $A_Y$ on Y such that:

• $A_Y$ is contained in the smooth locus of Y

• $A_Y$ is not contained in a component of E

• $A'=\pi _*A_Y$ for some $A'\in |nA|$ where $n>0$ is an integer.

By Eq. (3.1) we have

$$-K_Y\cdot A_Y= n(-K_X\cdot A + (p-1)D\cdot A) + E\cdot A_Y\ge -nK_X\cdot A.$$

By assumption $-K_X\cdot A> 0$. Therefore $-K _Y\cdot A_Y>0$. By Theorem 1.9 for $A_Y$ and $\pi ^*(A)$ on Y, there exists for every point $x\in A_Y$ a rational curve $\Gamma _x$ passing through x such that

$$\pi ^*(A )\cdot \Gamma _x \le 4 \frac{\pi ^*(A)\cdot A_Y}{-K_Y\cdot A_Y} .$$

However, since A is an ample Cartier divisor and $\pi$ is finite, $\pi ^*A\cdot \Gamma _x\ge 1$. By Eq. (3.1) and the assumption $A^2\le r$, we therefore have:

$$(-\pi ^*K_X +(p-1)\pi ^*D + E)A_Y \le 4rn.$$

Since $-K_X\cdot A>0$ and $E\cdot A_Y\ge 0$, we find that:

$$\begin{aligned} (p-1)\pi ^*D\cdot A_Y < 4rn. \end{aligned}$$

Since $A'\in |nA|$ we have $\pi ^*D\cdot A_Y\ge n$. The result follows. $\square$

Remark 3.2

If $(X, \Delta )$ is a log pair such that $-(K_X+\Delta )$ is ample then $-K_X\cdot A>\Delta \cdot A\ge 0$ for any ample divisor A.

Proof of Theorem A

By base change to an algebraic closure of k we can assume that k is algebraically closed. By [24] the divisor $(13-45I)IK_X$ is very ample. By [13, Theorem 1.3] there is an inequality $K_X ^2\le \text {max}\{9, 2I +4+\frac{2}{I}\} .$ The result therefore follows from Proposition 3.1 and Theorem C. $\square$

For the boundary version of the theorem above we need to use a common bound for the Cartier indices of $K_X$ and $K_X+\Delta$.

Theorem 3.3

Let $(X,\Delta )$ be a log del Pezzo surface over an algebraically closed field k of characteristic $p>0$. Let $m\ge 2$ be such that $m(K_X+\Delta )$ and $mK_X$ are both Cartier. Let D be a big and nef $\mathbb {Z}$-divisor on X. If

$$p\ge 173056m^8-86528m^7 +16200m^5 +32400m^4 +16200m^3+1$$

then $H^1(X, \mathcal {O}_X(-D))=0$.

Proof

Let $H=13mK_X-45m^2(K_X+\Delta )$. According to [24], H is a very ample Cartier divisor. By [24, Lemma 6.2], we have inequalities $(K_X+\Delta )\cdot K_X\ge 0$ and $K_X^2 \le 128m^5(2m-1)$. By [13, Theorem 1.3], we have an inequality $(K_X+\Delta )^2\le 2m +4+\frac{2}{m}$ . Therefore:

$$H^2\le (13)^2128m^7(2m-1)+(45)^2(2m^5 +4m^4+2m^3).$$

We conclude by Proposition 3.1. $\square$

Remark 3.4

A log del Pezzo surface $(X, \Delta )$ where $(K_X+\Delta )$ has Cartier index I is necessarily $\epsilon$-klt for $\epsilon =\frac{1}{I}$. As in the proof below, the Cartier index of $K_X$ can therefore be bounded in terms of the Cartier index of $(K_X+\Delta )$.

Proof of Theorem B

By base change to an algebraic closure of k we can assume that k is algebraically closed. By assumption X is $\epsilon$-klt, therefore the $\mathbb {Q}$-factorial index q at any point $x\in X$ satisfies

$$q\le 2\left( \frac{2}{\epsilon }\right) ^{\frac{128}{\epsilon ^5}}$$

by [24, Prop 6.1]. Moreover, by the same proposition, the Picard rank of a minimal resolution of X is bounded by $\frac{128}{\epsilon ^5}$. Hence, for every $\mathbb {Z}$-divisor D, there exists some $c\le 2^{\frac{128}{\epsilon ^5}}\left( \frac{2}{\epsilon }\right) ^{\frac{(128)^2}{\epsilon ^{25}}},$ depending on D, such that cD is Cartier.

Suppose that $H^1(X,\mathcal {O}_X(-D))\ne 0$. By replacing D with $p^{k-1}D$ for some $k>1$, we may assume that $H^1(X,\mathcal {O}_X(-pD))=0$. We may, therefore, assume that there exists a normal variety Y and a degree p inseparable morphism $Y\rightarrow X$ such that $K_Y= \pi ^*(K_X+(1-p)D)-E$, for some $E \ge 0$. Let $C_Y$ be a general complete intersection curve on Y, not contained in the support of E, such that $\pi _*C_Y=C$ is not contained in the support of $\Delta$. Then $-K_Y\cdot C_Y>0$. By Theorem 1.9 applied to $C_Y$ and

$$\pi ^*(-(K_X+\Delta )+(p-1)D)\equiv -(K_Y+E)-\pi ^*(\Delta ),$$

there exists a rational curve $\Gamma$ through a point on $C_Y$ such that:

$$\begin{aligned} \pi ^*(-(K_X+\Delta )+(p-1)D)\cdot \Gamma \le 4\frac{ (-(K_Y+E)-\pi ^*(\Delta ))\cdot C_Y}{-K_Y\cdot C_Y}. \end{aligned}$$

Since $-\pi ^*(K_X+\Delta )\cdot \Gamma >0$, $E\cdot C_Y\ge 0$ and $\pi ^*(\Delta )\cdot C_Y\ge 0$, we find that

$$\begin{aligned} (p-1)D\cdot \Gamma < 4. \end{aligned}$$

Since cD is Cartier we have an inequality $D\cdot \Gamma \ge \frac{1}{c}.$ Therefore:

$$\begin{aligned} p< 4c+1\le 2^{\frac{128}{\epsilon ^5}+2}\left( \frac{2}{\epsilon }\right) ^{\frac{(128)^2}{\epsilon ^{25}}} +1. \end{aligned}$$

$\square$

Remark 3.5

From the proof of Theorem B we see that on a log del Pezzo surface $(X,\Delta )$ over an algebraically closed field k of characteristic $p \ge 4c+1$ we have $H^1(X,\mathcal {O}_X(-D))=0$, for every ample $\mathbb {Z}$-divisor D of Cartier index $\le c$.

5 Kodaira vanishing in char $p>5$ using the liftability of log del Pezzo surfaces of Picard rank one

In this section we deduce the Kodaira vanishing theorem for log del Pezzo surfaces from the liftability in characteristic $p>5$ of del Pezzo surfaces of Picard rank one, together with the Kodaira vanishing theorem for surfaces Y which admit a Mori fiber space structure $f:Y\rightarrow B$ onto a curve. In fact, for a surface admitting a Mori fiber space structure onto a curve the difficulties arising from non-Cartier divisors in our previous arguments are not present. We learned the main ideas in Proposition 4.1 from Zsolt Patakfalvi.

Proposition 4.1

Let X be a normal projective surface over an algebraically closed field k of characteristic $p>0$ which admits a proper birational morphism $g:X\rightarrow Y$ to a normal projective surface Y admitting a $K_Y$-negative fibration to a curve B. That is, there exists a proper morphism $f:Y\rightarrow B$ such that $f_*\mathcal {O}_Y=\mathcal {O}_B$ and such that the general fiber is isomorphic to $\mathbb {P}^1$. Let D be a $\mathbb {Q}$-Cartier big and nef $\mathbb {Z}$-divisor on X. Then $H^1(X, \mathcal {O}_X(-D))=0$.

Proof

According to Corollary 1.2 by replacing D with $p^mD$, we may assume that $H^1(X, \mathcal {O}_X(-pD))=0.$ Suppose that $H^1(X, \mathcal {O}_X(-D))\ne 0$. We apply Ekedahl’s construction 1.3 to get a degree p finite morphism $\pi : Z\rightarrow X$, where Z is normal, and

$$K_Z+E= \pi ^*K_X+(1-p)\pi ^*D$$

for an effective divisor $E\ge 0.$ We illustrate the situation with a diagram:

Let F be a fiber of f not containing any point which is the image of a curve contracted by g. Then F can be identified with a fiber of $f\circ g:X\rightarrow B$. By abuse of notation we denote a general fiber of $f\circ g$ by F. A general fiber of the composition $f\circ g$ avoids the exceptional locus of g since the curves contracted by g map to a finite number of points on Y. We compute:

$$\begin{aligned} K_Z\cdot \pi ^*F=\pi ^*((K_X-(p-1)D)\cdot F)- E\cdot \pi ^*F. \end{aligned}$$

The morphism $\pi$ is finite of order p, therefore, we have:

$$\begin{aligned} K_Z\cdot \pi ^*F=p((K_X-(p-1)D)\cdot F-E\cdot \pi ^*F. \end{aligned}$$

Since two general fibers F do not intersect we have $F^2=0$ and therefore $K_Y\cdot F=-2$. Since D is big and F is general, we have $D\cdot F> 0$.

Moreover, since E is effective, we see (upon varying F) that the intersection number $E\cdot \pi ^*F\ge 0$. We conclude that:

$$\begin{aligned} \begin{aligned}&K_Z\cdot \pi ^*F\le p(K_X-(p-1)D)\cdot F\\&\quad = p(deg(K_{ F})-(p-1)D\cdot F) \\&\quad =-2p -p(p-1)D\cdot F. \end{aligned} \end{aligned}$$

(4.1)

Denote by $G=\pi ^*F$. We claim that there is an inequality $-2p\le K_Z\cdot G$. Let $F'=G_{red}$ then we have $-2\le K_Z\cdot F'$. It is therefore sufficient to show that if G is non-reduced then it is of multiplicity p, i.e., $G=pF'$. This is clear since $\pi$ is of degree p. This together with the inequality (4.1) implies that

$$\begin{aligned} -2p\le K_Z\cdot G\le -2p -p(p-1)D\cdot F, \end{aligned}$$

but $-p(p-1)D\cdot F<0$ which leads to a contradiction. $\square$

The above proposition treats the case when running a $K_X$-MMP on a log del Pezzo surface X ends with a Mori fiber space $f:Y\rightarrow B$. We will use Lacini’s results on liftability (Theorem 4.3) in the case when Y is a del Pezzo surface of Picard rank one. We first recall the definition of liftability to ${{\,\mathrm{W_2(k)}\,}}$.

Definition 4.2

[8, Definition 8.11] Let k be a perfect field of positive characteristic and let X be a scheme smooth over ${{\,\mathrm{Spec}\,}}(k)$. Let $D=\sum _{i}^nD_i$ be a reduced simple normal crossing divisor on X. A lifting of $D=\sum _{i=1}^nD_i\subset X$ to ${{\,\mathrm{W_2(k)}\,}}$ consists of a scheme $X'$ and subschemes $D'_i$ all defined and flat over ${{\,\mathrm{W_2(k)}\,}}$ such that:

$$\begin{aligned} X=X'\times _{{{\,\mathrm{Spec}\,}}({{\,\mathrm{W_2(k)}\,}})}{{\,\mathrm{Spec}\,}}(k)\, \hbox {and}\,D_i=D_i'\times _{{{\,\mathrm{Spec}\,}}({{\,\mathrm{W_2(k)}\,}})}{{\,\mathrm{Spec}\,}}(k), \end{aligned}$$

for $1\le i\le n$.

For a pair (X, D) consisting of a smooth surface and a reduced simple normal crossing divisor as above, [6] defines the notion of liftability to characteristic zero over a smooth base. We refer the reader to [6, Definition 2.15] for the definition. If the pair (X, D) lifts to characteristic zero over a smooth base then the pair (X, D) lifts to ${{\,\mathrm{W_2(k)}\,}}$ [6, Remark 2.16]. We restate below the liftability theorem for log del Pezzo surfaces of Picard rank one proven by Justin Lacini.

Theorem 4.3

[17, Theorem 7.2] Let S be a log del Pezzo surface of Picard rank one over an algebraically closed field of characteristic $p>5$. Then there exists a log resolution $\mu : V\rightarrow S$ such that $(V,{{\,\mathrm{Exc}\,}}(\mu ))$ lifts to characteristic zero over a smooth base.

We believe the following lemma to be well-known to experts, however since we did not find a reference we include it here. We are indebted to Maciej Zdanowicz for helping us with its proof.

Lemma 4.4

Let X be a smooth surface and $D=\sum _{i=1}^nD_i$ be a reduced simple normal crossing divisor. Suppose that (X, D) lifts to ${{\,\mathrm{W_2(k)}\,}}$. Let $x\in X$ be a closed point. If $\pi : Y \rightarrow X$ is the blow up of X at x then $(Y, Exc(\pi )+\pi _*^{-1}D)$ lifts to ${{\,\mathrm{W_2(k)}\,}}$.

Proof

Let $(X',D')$ be a lift of (X, D) to ${{\,\mathrm{W_2(k)}\,}}$. Let $x\in X$ be a closed point. By formal smoothness there exists a lift $x'\in X'$ of x. We claim the following:

Claim

If $J\subset \{1,2,\ldots , n\}$ is an index set such that $x\in \bigcap _{i\in J}D_i$ but $x\notin D_k$ for $k\notin J$, then, there exists a lift $x'\in X'$, such that $x'\in \bigcap _{i\in J}D'_i$, but $x'\notin D'_k$ for $k\notin J$.

Proof

If $x\in X-{{\,\mathrm{Supp}\,}}(D)$ we can choose a lift $x'\in X'-{{\,\mathrm{Supp}\,}}(D')$ and hence any such lift $x'$ satisfies the claim. Suppose that $x\in {{\,\mathrm{Supp}\,}}(D)$. By [8, Lemma 8.13 d)], we may assume that there is an open subset U containing x and a diagram with all squares being Cartesian:

where $\mathbb {A}^2_k={{\,\mathrm{Spec}\,}}(k[t_1, t_2])$, $\mathbb {A}^2_{{{\,\mathrm{W_2(k)}\,}}}={{\,\mathrm{Spec}\,}}({{\,\mathrm{W_2(k)}\,}}[t_1, t_2])$, U and $U'$ are open subsets of X and $X'$ respectively and the morphisms e and $e'$ are étale. By [8, Lemma 8.14 e)], we may assume that we have chosen local parameters:

$$\begin{aligned} \phi _i=e^*(t_i)\in \mathcal {O}_U\, \hbox {and}\,\phi '={e'}^*(t_i)\in \mathcal {O}_{U'}\,\hbox {for}\,i=1,2, \end{aligned}$$

such that $x={{\,\mathrm{V}\,}}((\phi _1,\phi _2))$ and such that (upon relabeling the components of D) there exists a subset I of $\{ 1, 2\}$, such that $D\cap U={{\,\mathrm{V}\,}}(\prod _{i\in I}\phi _i)$ and $D'\cap U'={{\,\mathrm{V}\,}}(\prod _{i\in I}{\phi '}_i)$. Let $x'={{\,\mathrm{V}\,}}(({\phi '}_1,{\phi '}_2))$, then $x'$ satisfies the claim. $\square$

Let $\pi ': Y'\rightarrow X'$ be the blow up of $x'\in X'$, where $x'$ is chosen as in Claim 4. We want to prove that $(Y', {\pi '}^{-1}_*D'+{{\,\mathrm{Exc}\,}}(\pi '))$ is a lift of $(Y, {{\,\mathrm{Exc}\,}}(\pi )+\pi _*^{-1}D)$ to ${{\,\mathrm{W_2(k)}\,}}$. If $x\notin {{\,\mathrm{Supp}\,}}(D)$, for any choice of $x'\notin {{\,\mathrm{Supp}\,}}(D')$ it is clear that $(Y', {\pi '}^{-1}_*D'+{{\,\mathrm{Exc}\,}}(\pi '))$ is a lift of $(Y, {{\,\mathrm{Exc}\,}}(\pi )+\pi _*^{-1}D)$ to ${{\,\mathrm{W_2(k)}\,}}$. We therefore assume that $x={{\,\mathrm{V}\,}}((\phi _1,\phi _2))$, $x'={{\,\mathrm{V}\,}}((\phi '_1,\phi '_2))$ and that U, $U'$, D and $D'$ are as before. By the commutativity of blowing up with flat base change [21, Lemma 085S] there exists, for any ring S and an étale morphism $T\rightarrow \mathbb {A}^2_S$, a natural Cartesian diagram:

where $\mathbb {A}^2_S={{\,\mathrm{Spec}\,}}(S[t_1, t_2])$. The strict transform of ${{\,\mathrm{V}\,}}(\prod _{i\in I}e^*(t_i))$ is the base change to T of the strict transform of ${{\,\mathrm{V}\,}}(\prod _{i\in I}t_i)$ for any subset $I\subset \{ 1, 2\}$. Using the notation introduced in the beginning or this proof we therefore have:

$$\begin{aligned} {{\,\mathrm{Bl}\,}}_{x'}(U')={{\,\mathrm{Bl}\,}}_{{{\,\mathrm{V}\,}}(t_1,t_2)}(\mathbb {A}^2_{{{\,\mathrm{W_2(k)}\,}}})\times _ {\mathbb {A}^2_{{{\,\mathrm{W_2(k)}\,}}}}U' \end{aligned}$$

and

$$\begin{aligned} {{\,\mathrm{Bl}\,}}_{x}(U)={{\,\mathrm{Bl}\,}}_{{{\,\mathrm{V}\,}}(t_1,t_2)}(\mathbb {A}^2_k)\times _ {\mathbb {A}^2_k}U. \end{aligned}$$

Since the base change of an étale morphism is étale, ${{\,\mathrm{Bl}\,}}_{x'}(U') \rightarrow {{\,\mathrm{Bl}\,}}_{V(t_1, t_2)}\mathbb {A}^2_{{{\,\mathrm{W_2(k)}\,}}}$ is étale. Consequently, we are reduced to the following situation:

The top square, and therefore the whole diagram, is clearly Cartesian. In this situation it is evident that ${{\,\mathrm{Bl}\,}}_{{{\,\mathrm{V}\,}}(t_1, t_2)}\mathbb {A}^2_{{{\,\mathrm{W_2(k)}\,}}}$ is smooth over $W_2(k)$ and that the strict transform of each of the coordinate axes, as well as the exceptional divisor of the blow up, are flat and hence smooth over ${{\,\mathrm{W_2(k)}\,}}$ [8, Lemma 8.13]. Since the base change of an étale morphism is étale this shows that $Y'$ as well as the support of ${\pi '}^{-1}_*D'_i$, for $1\le i \le n$, and ${{\,\mathrm{Exc}\,}}(\pi ')$ are all flat over ${{\,\mathrm{W_2(k)}\,}}$. Consequently $(Y', {\pi '}^{-1}_*D'+{{\,\mathrm{Exc}\,}}(\pi '))$ is a lift of $(Y, {{\,\mathrm{Exc}\,}}(\pi )+\pi _*^{-1}D)$ to ${{\,\mathrm{W_2(k)}\,}}$. $\square$

Theorem 4.5

(Theorem D) Let X be a log terminal projective surface with $K_X$ not pseudo-effective, over a perfect field k of characteristic $p>5$. Then Kodaira vanishing holds on X, i.e., for all ample $\mathbb {Z}$-divisors D on X we have $H^i(X,\mathcal {O}_X(D+K_X))=0$, for all $i>0$.

Proof

By base change to an algebraic closure of k we can assume that k is algebraically closed. Let D be an ample $\mathbb {Q}$-Cartier $\mathbb {Z}$-divisor. It is sufficient to prove that $0=H^1(X,\mathcal {O}_X(-D))=H^1(X,\mathcal {O}_X(K_X+D))$. We run a $K_X$-MMP $g: X\rightarrow Y$, where Y is either a klt del Pezzo surface of Picard rank one or Y admits a Mori fiber space structure $f:Y\rightarrow B$ onto a curve B.

• (1) If $f:Y\rightarrow B$ is a $K_Y$-MFS onto a curve, then the result follows from Proposition 4.1.

• (2) If there exists a birational morphism $X\rightarrow Y$ where Y is a log del Pezzo surface of Picard rank one then by Theorem 4.3 there exists a log resolution $\mu : (V, {{\,\mathrm{Exc}\,}}(\mu ))\rightarrow Y$ such that $(V, {{\,\mathrm{Exc}\,}}(\mu ))$ lifts to characteristic zero over a smooth base where ${{\,\mathrm{Exc}\,}}(\mu )$ denotes the reduced divisor supported at the exceptional locus of $\mu$. There is an induced rational map $\mu ':V$

  

  X. Let $\pi :V'\rightarrow V$ be a resolution of the indeterminacy locus of $\mu '$. The morphism $\pi :V'\rightarrow V$ can be factorised as a composition of blowups at points. By Lemma 4.4, $(V', \pi _*^{-1}{{\,\mathrm{Exc}\,}}(\mu )+ {{\,\mathrm{Exc}\,}}(\pi ))$ lifts to ${{\,\mathrm{W_2(k)}\,}}$. The diagram below illustrates the situation:

  

  The support of ${{\,\mathrm{Exc}\,}}(\tilde{\mu })$ is contained in the support of $\pi _*^{-1}{{\,\mathrm{Exc}\,}}(\mu )+{{\,\mathrm{Exc}\,}}(\pi )$. Therefore $\tilde{\mu }:(V',{{\,\mathrm{Exc}\,}}(\tilde{\mu }))\rightarrow X$ is a log-resolution that lifts to ${{\,\mathrm{W_2(k)}\,}}$. By [6, Lemma 6.1] the result follows.$\square$