Woven electric heaters are already widely used in solving various technical problems: when starting cold mechanical devices; in technological processes related to treatment of plant products, for example, their drying; packing thickened liquid products; melting honey, etc. [1, 2]. Woven electric heaters find application in medicine as well, when solving a wide variety of problems: from trivial ones, such as compensating for heat losses in hypothermic people, to complicated heating complexes providing a multi-level temperature impact (preventing the occurrence of hypothermia, muscle tremors, etc.) on various areas of the body of burn patients. Analysis of the available literature shows that woven electric heaters, due to their elasticity, are mainly used in those very cases when it is necessary to perform one of the most economical forms of heating—contact heating [3–5].

When studying the contact heating mode, one more ability is revealed: not only the ability to generate heat, but also the capability of receiving feedback signals from the person under the influence of this heat. The signals are measured by a thermocouple mounted on the heater surface.

Perspiration is one such response signal in humans [6]. The methods of U. Fere and R. Tarkhanov make it possible to solve some perspiration problems [7]. The Fere method is based on measuring the electrical resistance of the skin surface, whereas the Tarkhanov method focuses on registering changes in the electrical potential. Both methods use the electrolytic properties of sweat and its influence on the electrical changes on the surface of the skin. The difficulty in making an accurate measurement of the amount of sweat excreted is a disadvantage of these methods: when measuring, it is necessary to press the measuring probes to the human body, yet this changes significantly the sweat distribution over the skin surface. Furthermore, in some cases, we might record only the very release of sweat.

Consider the method based on contact body heating in more detail: it allows us not only to fix the perspiration but also to create prerequisites and to get the real perspiration picture in time.

Figure 1 shows this thermal system. It includes a person as an external medium, the gap between the human body and the woven electric heater (hereafter, the gap), the woven electric heater (hereafter, the heater), the heat-insulating layer on the heater surface from the environment side, and the environment.

Fig. 1.
figure 1

Element location in the heating system. X0, surface of the human body; X0–X1, gap (space between the human body and the heater); X1–X2, heater; X2–X3, heat-insulating layer on the woven electric heater surface; X3, environment.

Full size image

We simulate the thermal process taking place in the thermal system: consider how the heat signal occurs in the gap and propagates in time and space, and how it depends on the parameters of the heater, the insulating layer, and the external media constituting this heating system.

First, consider how the variable temperature signal is generated in the gap. Upon the thermal impact (in our case, by means of the heater) on a person, on his/her heat receptors located in the skin, a certain temperature is reached on the skin surface and sweat is released. As a result, thermal parameters such as the heat capacity, density, and thermal conductivity vary in the space between the human body and the heater. Therefore, the temperature varies in the space between the human body and the heater: the temperature decreases. Then, the sweat evaporates. Then, the thermal parameters change again and the temperature increases. When a certain temperature is reached once more, perspiration occurs again, etc. That is, these changes are periodic. The authors of [6] investigated these processes in detail. They note that sweat release occurs from the human skin surface into the gap domain, and then the sweat evaporates. The evaporation has a diffusive nature [8, 9] and proceeds according to the exponential law

$$Q = H({{e}^{{ - gt}}}),$$

where t is the duration of evaporation, Q is the quantity of liquid evaporated per unit area of the interphase surface by the time moment of t, and H and g are constant coefficients.

The parameter variations are related to the processes of replacement of the air medium and displacement by the sweat. Then, a phase transition takes place in the gap medium related to the evaporation of sweat. Here, in these processes, it is impossible to determine the clear boundaries of the phase transition. With account for the fact that the phase transformations take place within a very thin gap, according to [10], they are considered as one-time changes of the thermal parameters throughout the entire gap interval. The authors of [6] performed the mathematical modeling of this process using the analytical method and obtained rather complicated mathematical relations describing those thermal processes. With account for these simulation results, hereafter, we will describe the reaction of the thermal parameters of the gap on the heat signal by a simpler expression

$${{a}_{1}}(t) = k\frac{{{{\lambda }_{1}}}}{{{{\rho }_{1}}{{c}_{1}}}}\cos (gt),$$
(1)

where a1(t) is the gap thermal diffusivity coefficient, ρ1 is the density of the gap medium, c1 is its heat capacity, λ1 is its thermal conductivity, and k and g are constant coefficients.

Now, we answer the main question: how does the reaction on the heat signal propagate along the X-axis within the heating system, under the various thermal parameters of its elements: gap, heater, thermal insulation layer, and environment.

To answer, we conduct mathematical modeling of the thermal processes in the heating system. We formulate the mathematical problem describing the thermal processes occurring in the system (Fig. 1).

We consider the layers constituting the thermal system: the gap medium–the heater–the thermal insulation layer as thin walls: the thickness of each layer is much less than the length and the width of the heater surface impacting the person. Thus, we will consider the heat propagation in this three-layer thin wall as a one-dimensional, nonstationary thermal process and describe it by means of a system of interconnected one-dimensional Fourier equations. Such modeling is also associated with the fact that the layers are so thin that it is almost impossible to perform in situ studies of the thermal processes taking place in them. As the heater size is significantly smaller than the human body, we might assume that the person plays the role of an external medium in relation to this wall. Thus, on one side of the wall, the person is an external medium; and on the other side is the environment. That is, we have the different levels of thermal effects from the “environments.” We assume that the temperatures of these environments do not change in time. At the initial moment, at the point x0 (the surface of a person’s body) we have t = 0, x = x0, and T = Tp, where Tp is the person’s body temperature. For the point x3, we take t = 0, x = x3, and T = Tm, where Tm is the ambient temperature of the medium.

Suppose that, at the point x0, at the boundary between the person’s body and the gap, boundary conditions of the III kind take place:

$$t > 0,\quad x = {{x}_{0}}{\kern 1pt} :\quad - {\kern 1pt} {{\lambda }_{1}}(t)\frac{{\partial \Delta T}}{{\partial x}} = - {{\alpha }_{{\text{p}}}}(\Delta T_{{\text{p}}}^{'} - \Delta T),$$

where λ1 is the gap thermal conductivity coefficient, \(\Delta T = T - {{T}_{{\text{m}}}}\) is the current value of the temperature compared to the ambient medium, αp is the coefficient of the heat transfer to the person’s body, \(\Delta T_{{\text{p}}}^{'} = {{T}_{{\text{p}}}} - {{T}_{{\text{m}}}}\) is the temperature difference at the initial moment, and t = 0 at the point x = x0.

The thermal processes taking place in each thin layer are quite different, and the media of these layers and their physical parameters have significant differences as well. Therefore, we describe each layer by its own expression based on the Fourier equation.

For the first layer, the gap between the person’s body and the heater, the Fourier equation, with account for (1), is

$$t > 0,\quad {{x}_{0}} \leqslant x \leqslant {{x}_{1}}{\kern 1pt} :\quad \frac{{\partial {{\Delta }}T}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {a{\text{(}}t{\text{)}}\frac{{\partial {{\Delta }}T}}{{\partial x}}} \right),\quad {\text{or}}\quad {{{{\rho }}}_{1}}{{c}_{1}}\frac{{\partial {{\Delta }}T}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {{{{{\lambda }}}_{1}}{\text{(}}t{\text{)}}\frac{{\partial {{\Delta }}T}}{{\partial x}}} \right){\text{.}}$$

Then, the gap medium makes contact with the heater; thus, to describe the thermal processes at the boundary of these two media at the point x = x1, we apply boundary conditions of the IV kind

$$t > 0,\quad x = {{x}_{1}}{\kern 1pt} :\quad - {\kern 1pt} {{{{\lambda }}}_{1}}\left. {\frac{{\partial \Delta T}}{{\partial x}}} \right|\frac{{}}{{x = {{x}_{1}}}} = - {{{{\lambda }}}_{2}}\left. {\frac{{\partial \Delta T}}{{\partial x}}} \right|\frac{{}}{{x = {{x}_{1}}}},$$

where λ2 is the thermal conductivity coefficient of the heater material. We consider the whole heater to be a uniform medium.

At the boundary between the first and second media, the following condition is also met:

$$t > 0,\quad x = {{x}_{1}}{\kern 1pt} :\quad \Delta {{T}_{h}}(t,{{x}_{1}}) = \Delta {{T}_{i}}(t,{{x}_{1}}),$$

where \(\Delta {{T}_{h}} = {{T}_{h}} - {{T}_{{\text{m}}}}\), Th is the temperature from the gap side at the point x1; \(\Delta {{T}_{i}} = {{T}_{i}} - {{T}_{{\text{m}}}}\), Ti is the heater temperature at the point x1.

Describe the heater work as \({{q}_{{v}}} = b\frac{P}{S}(1 - {{e}^{{ - j \cdot t}}})\), where \({{q}_{{v}}}\) is the volume density; P is the heater power; S is the heater surface area; and b and j are constant coefficients.

Describe the thermal process along the X axis in the second layer (where the heater is located) by means of the Fourier equation for a nonstationary process with an internal heat source

$$t > 0,\quad {{x}_{1}} \leqslant x \leqslant {{x}_{2}}{\kern 1pt} :\quad {{{{\rho }}}_{2}}{{c}_{2}}\frac{{\partial {{\Delta }}T}}{{\partial t}} = {{{{\lambda }}}_{2}}\frac{{{{\partial }^{2}}{{\Delta }}T}}{{\partial {{x}^{2}}}} + {{q}_{{v}}},$$

where ρ2 is the heater material density and c2 is its heat capacity.

At the boundary of the second (the heater) and the third (the heat-insulating layer on the outer heater surface) layers, conditions of the IV kind will also be met

$$t > 0,\quad x = {{x}_{2}}{\kern 1pt} :\quad - {\kern 1pt} {{{{\lambda }}}_{2}}\left. {\frac{{\partial \Delta T}}{{\partial x}}} \right|\frac{{}}{{x = {{x}_{2}}}} = - {{{{\lambda }}}_{3}}\left. {\frac{{\partial \Delta T}}{{\partial x}}} \right|\frac{{}}{{x = {{x}_{2}}}},$$

where λ3 is the thermal conductivity coefficient of the heat-insulation layer material.

Then, at the second-to-third boundary layer, at the point x2, the following condition is met simultaneously:

$$t > 0,\quad x = {{x}_{2}}{\kern 1pt} :\quad \Delta {{T}_{{h2}}}(t,{{x}_{2}}) = \Delta {{T}_{{i2}}}(t,{{x}_{2}}),$$

where \(\Delta {{T}_{{h2}}} = {{T}_{{h2}}} - {{T}_{{\text{m}}}}\), Th2 is the temperature at the point x2 from the heater side, \(\Delta {{T}_{{i2}}} = {{T}_{{i2}}} - {{T}_{{\text{m}}}}\), and Ti2 is the temperature of the heat-insulation layer at the point x2.

The thermal process in the third layer is described by the expression

$$t > 0,\quad {{x}_{2}} \leqslant x \leqslant {{x}_{3}}{\kern 1pt} :\quad {{{{\rho }}}_{3}}{{c}_{3}}\frac{{\partial {{\Delta }}T}}{{\partial t}} = {{{{\lambda }}}_{3}}\frac{{{{\partial }^{2}}{{\Delta }}T}}{{\partial {{x}^{2}}}},$$

where ρ3 is the heat-insulation material density and c3 is its heat capacity.

Consider that at the external surface of the heat-insulation layer surrounded by the environment, boundary conditions of the III kind take place:

$$t > 0,\quad x = {{x}_{3}}{\kern 1pt} :\quad - {\kern 1pt} {{\lambda }_{3}}\frac{{\partial \Delta T}}{{\partial x}} = - {{\alpha }_{{\text{m}}}}(\Delta T_{{\text{m}}}^{'} - \Delta T),$$

where αm is the heat transfer coefficient to the environment, \(\Delta T_{{\text{m}}}^{'} = {{T}_{{\text{m}}}}_{1} - {{T}_{{\text{m}}}}\), where \(\Delta T_{{\text{m}}}^{'}\) is the temperature difference in the environment, and Tm1 is the surface temperature of the heat-insulation layer at the point x3.

Note that we consider the thermal processes occurring in this three-layer wall not only along the X axis but also in time.

Thus, we assume that the mixed Cauchy problem describing the thermal processes in each layer of the three-layer wall, with the initial and the boundary conditions, both at the edges of the three-layer wall and at the boundaries of the layers, is formulated in the form

$$\left\{ {\begin{array}{*{20}{l}} {T = {{T}_{{\text{p}}}}\quad {\text{for}}\quad t = 0,\quad x = {{x}_{0}},} \\ {T = {{T}_{{\text{m}}}}\quad {\text{for}}\quad t = 0,\quad x = {{x}_{3}},} \\ { - {{\lambda }_{1}}\frac{{\partial \Delta T}}{{\partial x}} = - {{\alpha }_{{\text{p}}}}(\Delta T_{{\text{m}}}^{'} - \Delta T)\quad {\text{for}}\quad t > 0,\quad x = {{x}_{0}},} \\ {{{\rho }_{1}}{{c}_{1}}\frac{{\partial \Delta T}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {{{\lambda }_{1}}(t)\frac{{\partial \Delta T}}{{\partial x}}} \right)\quad {\text{for}}\quad t > 0,\quad {{x}_{0}} < x < {{x}_{1}},} \\ { - {{\lambda }_{1}}\left. {\frac{{\partial \Delta T}}{{\partial x}}} \right|\frac{{}}{{x = {{x}_{1}}}} = - {{\lambda }_{2}}\left. {\frac{{\partial \Delta T}}{{\partial x}}} \right|\frac{{}}{{x = {{x}_{1}}}}\quad {\text{for}}\quad t > 0,\quad x = {{x}_{1}},} \\ {\Delta {{T}_{{h1}}}(t,x) = \Delta {{T}_{{i1}}}(t,x)\quad {\text{for}}\quad t > 0,\quad x = {{x}_{1}},} \\ {{{\rho }_{2}}{{c}_{2}}\frac{{\partial \Delta T}}{{\partial t}} = {{\lambda }_{2}}\frac{{{{\partial }^{2}}\Delta T}}{{\partial {{x}^{2}}}} + {{q}_{{v}}}\quad {\text{for}}\quad t > 0,\quad {{x}_{1}} < x < {{x}_{2}},} \\ { - {{\lambda }_{2}}\left. {\frac{{\partial \Delta T}}{{\partial x}}} \right|\frac{{}}{{x = {{x}_{2}}}} = - {{\lambda }_{3}}\left. {\frac{{\partial \Delta T}}{{\partial x}}} \right|\frac{{}}{{x = {{x}_{2}}}}\quad {\text{for}}\quad t > 0,\quad x = {{x}_{2}},} \\ {\Delta {{T}_{{h2}}}(t,x) = \Delta {{T}_{{i2}}}(t,x)\quad {\text{for}}\quad t > 0,\quad x = {{x}_{2}},} \\ {{{\rho }_{3}}{{c}_{3}}\frac{{\partial \Delta T}}{{\partial t}} = {{\lambda }_{3}}\frac{{{{\partial }^{2}}\Delta T}}{{\partial {{x}^{2}}}}\quad {\text{for}}\quad t > 0,\quad {{x}_{2}} < x < {{x}_{3}},} \\ { - {{\lambda }_{3}}\frac{{\partial \Delta T}}{{\partial x}} = - {{\alpha }_{{\text{m}}}}(\Delta T_{{\text{m}}}^{'} - \Delta T)\quad {\text{for}}\quad t > 0,\quad x = {{x}_{3}}.} \end{array}} \right.$$
(2)

We solved system (2) by means of the numerical difference method: we approximated the equations included in this system. Within this procedure, we applied predominantly the difference approximation method using the well-known and described two-level, four-point patterns of the implicit schemes [10–12].

The thermal processes in the gap medium were an exception. Here, we have the time-varying thermal conductivity coefficient. In this case, to approximate the thermal processes, we engaged the integro-interpolation method [13]. The approximation error for the various heating system elements increased along the X axis linearly in time and quadratically in length. After increasing the approximation level to the second degree, when considering the boundary conditions, the order of the approximation error was about O(τ + h2), where τ is the grid step in time and h is the grid step in space.

By means of the program thus developed, we obtain the possibility to simulate the thermal processes within the heating system with varying parameters of its elements: linear dimensions, time intervals, heater powers, thermal conductivity coefficients, etc.

Application of the implicit scheme made it possible to ensure a high operation stability of the program as a whole while solving the assigned tasks.

Now, by means of the program, we consider the state of the thermal system in the cases when the heaters (the woven type, the water heater, an arbitrary type) operate at the same heating levels.

We begin with modeling the propagation, along the X-axis, of the response arising due to the heat impact on a person by the woven electric heater.

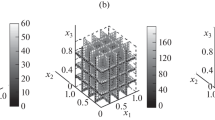
Let the arrangement sequence of the elements of the thermal system considered correspond to Fig. 1. The solution result obtained by means of the program (Fig. 2) shows that this thermal system provides a temperature change not only due to generation of the thermal signal by the heater itself but also receives a time-varying thermal signal-response formed due to a change in the thermal parameters within the gap in time. Moreover, the total variable heat signal-response formed in the gap along the X-axis acts not only within the gap domain but also extends to the heater domain and even to the heat-insulating layer located outside the heater (fluctuations within the range 0 < x < 1). Thus, a heater, such as a woven one, can simultaneously not only serve as a heat source but also receive a response to this heat signal accounting for the perspiration.

Fig. 2.
figure 2

Model of spatio-temporal thermal processes taking place in the heating system using the woven electric heater.

Full size image

Now imagine that the heater is a water heater with the same heat level as the woven electric heater. (We will not separately account for the rubber water heaters as thermal elements because of the significantly lower thermal resistance as compared to the water coolant.) We will assume that this heating system is a two-layer thin wall. In the heating system, we have the same sequence of element arrangement, except for the absent heat-insulating layer. In the first layer in the gap, we have the same thermal parameters as in the first example. In the second layer, certain changes are made: the heater dimensions, the coolant density, the heat capacity, and the thermal conductivity in the heater. The third, heat-insulating, layer is absent. Using a slightly modified program (excluding the cycle associated with the absence of the third, the heat-insulating, layer), we obtain the solution of this problem shown in Fig. 3.

Fig. 3.
figure 3

Model of spatio-temporal thermal processes taking place in the water heater system obtained at the same thermal impact (on a human) level as in the case of the woven electric heater.

Full size image

Note that, in the heating system, the variable thermal signal-response formed due to the thermal impact by the heating pad on a person significantly decreased along the X-axis, within the gap domain (the fluctuations within the range of 0 < x < 0.4), and did not propagate beyond the gap boundaries; within the heating pad area, it is completely absent. Therefore, it is impossible to use a heater with thermal parameters such as a receiver of the reaction to the thermal signal: the water heater, as compared to the woven electric heater, has significantly larger heater dimensions, a higher level of the coolant heat capacity, greater mass, etc. Thus, the water heater is more massive and has a greater thermal inertia.

However, it is not necessary to use only woven electric heaters to obtain the signal-response within the heater domain. By selecting the heater dimensions and properties, in combination with the parameters of the other heating system elements, we might achieve a possibility of the thermal signal-response propagation along the X-axis to the heater domain. Figure 4 shows a variant of the problem solution (obtained by means of the program) under a selection of such parameters of the system element. We fixed the variable signal-response within the range of 0 < x < 0.75.

Fig. 4.
figure 4

Model of spatio-temporal thermal processes in the heating system using an arbitrary heater with the selected thermal parameters of the other heating elements making it possible to receive the human response-signal in the heater domain.

Full size image

CONCLUSIONS

Providing a regime of contact heating of a person, with the simultaneous gap presence, is a necessary, but insufficient condition for formation of a heating system capable of receiving the thermal response signal of perspiration within the heater area. Meeting additional requirements is necessary, that is, a certain combination of the thermal parameters of all elements of the heating system: dimensions, heater powers, thermal conductivity, heat capacity, boundary conditions, etc.

To determine the possibility of using heaters as sensors ensuring stable reception of the signal-response to the thermal impact in the heater area, it is necessary to solve a multicriteria problem of optimizing the parameters of the heating system, including the gap size and the thermal parameters of its medium.

The problem solution within the framework of the model of the thermal system constructed is confirmed: use of electric heaters, such as woven ones having the appropriate dimensions and thermal parameters of their materials, makes it possible stably to receive the thermal signal-response on their own thermal impact, within a wide range of parameters of the system elements. The location of a temperature register on the heater surface provides fixation of the temperature changes in time. The simulation gives an a priori estimate of the thermal signal-response propagation within the framework of the heating system considered.

The method considered, based on the operation of a woven heater within the “person-medium–gap–heater–heat-insulating layer” system considered, makes it possible to study the perspiration processes both in amplitude (by the amount of sweat produced) and in time. Because the heater provides a precise thermal impact, the presence of the gap prevents distortions of the thermal signals in the perspiration studies. This method might be used as a basis for creating a noninvasive method of perspiration study.

The results of this article are of interest to medical professionals as well as to specialists in the development of heating systems, especially those intended for biological objects.