1 Introduction

Precise point positioning (PPP) has been the subject of much research throughout the past years, which has led to many developments. Though the technique is capable of providing highly accurate positions, it still suffers from relatively long initial convergence times (Kouba and Héroux 2001; Bisnath and Gao 2009). Many efforts have been made to reduce PPP initial convergence time; ambiguity resolution (AR) has proved to be a very promising avenue. The ability to remove biases from PPP ambiguities and then fix the ambiguities to their integer values has shown to improve both convergence time and accuracy, especially in a multi-GNSS (Global Navigation Satellite System) context (Collins et al. 2008; Ge et al. 2008; Laurichesse et al. 2009; Teunissen et al. 2010). Three main methods can be utilized to achieve PPP-AR: the fractional cycle bias (FCB) method (Ge et al. 2008; Geng 2010), the decoupled clock model (DCM) (Collins 2008; Collins et al. 2008) and the integer recovery clock (IRC) method (Laurichesse et al. 2009; Laurichesse 2011; Loyer et al. 2012). Geng et al. (2010), Shi and Gao (2014a) and Teunissen and Khodabandeh (2015) have studied the relationship between the models. They have demonstrated equivalence in the ambiguity-fixed user positioning results and that the models are related through transformations. Seepersad and Bisnath (2017) and Banville et al. (2020) have studied the interoperability of AR products from different analysis centres and the latter assessed the capacity to combine different products into a combined product.

For clarity, in this paper, uncombined refers to not using linear combinations of observables, but rather directly using the raw measurements on each frequency, while combined processing refers to forming linear combinations of observables.

This paper focuses on the DCM, which was originally introduced in Collins (2008). The main reasons behind choosing the DCM is that it does not make a-priori assumptions on the receiver biases, which are estimated as clock-like terms instead of being eliminated; as well as its ability to free the ambiguities from biases and to directly estimate them as integers. For instance, Abdelazeem et al. (2016), Zhang et al. (2017, 2019) have studied the temporal variability of the receiver biases and have found that they can vary by several nanoseconds over a few hours. They have found that the variations are due, in part, to the temperature variations of the receiver, its quality and its location. Wang et al. (2020) have analysed the effect of long-term and short-term variations of receiver biases on the stability of the ambiguities and on positioning performance by extracting the receiver biases from the ambiguities and estimating them. Their results have found that doing so leads to more stable ambiguities and therefore faster and more reliable PPP-AR.

It is therefore important to not make assumptions about the receiver biases, which is one of the main principles of the DCM. The model is based on the fact that the pseudorange and carrier-phase measurements are not synchronized to the same level of precision, which means that different clocks need to be used for the pseudorange and carrier-phase measurements. The model is based on the GPS ionosphere-free combination, and therefore to perform AR, it uses the Melbourne-Wübenna (MW) combination. Forming the MW combination allows for the estimation of the widelane (WL) and narrowlane (NL) ambiguities and, consequently, their fixing.

The DCM removes the receiver biases from the ambiguities through implicit differencing by the selection of a reference satellite. Implicit differencing is a consequence of the decoupling of the receiver clocks, and the datum in the phase measurements moves from the receiver clock to the reference satellite’s ambiguities. As a consequence, all estimated ambiguities are relative to the reference satellite’s, and the receiver biases are estimated instead of being eliminated as is the case with explicit differencing. The advantage of the DCM products is that they do not assume any particular behaviour of the biases, which are estimated as white noise.

The DCM was later extended into the Extended DCM in Collins et al. (2012), where the narrowlane pseudorange and widelane carrier-phase measurements were used as two separate measurements instead of forming a single MW measurement. Doing so allows for the estimation of the ionospheric delay, even in combined mode, which offers the possibility of ionospheric constraining.

Shi and Gao (2010) analyzed the integer nature of the ambiguities and the characteristics of the code and phase clocks using the combined DCM. The authors concluded that the DCM is able to recover the integer nature of the ambiguities, and they demonstrated that the receiver phase clock is improved compared to the receiver code clock. They also found that receiver biases can be time-varying and they therefore need to be estimated as white noise.

PPP is typically used by forming ionosphere-free combinations of the raw measurements in order to eliminate the ionosphere from the estimation (e.g., Collins et al. 2010; Katsigianni et al. 2019). However, with multiple frequencies and multiple constellations contemporarily being used, the number of possible combinations increases drastically. Therefore, uncombined processing is becoming much more convenient and practical than forming combinations. Zhang et al. (2011) proposed an uncombined processing concept for PPP-RTK, which was also later used in Zhang et al. (2018). Geng and Bock (2013) analysed the triple-frequency performance on simulated triple-frequency GPS measurements. Since then, GPS, Galileo and BeiDou have started broadcasting three frequencies or more. Xiao et al. (2019) and Geng et al. (2020), among others, proposed multi-frequency AR models, which are based on processing of the raw uncombined measurements on their individual frequencies.

This paper focuses on the Decoupled Clock Model, and extends the original combined DCM to an uncombined, multi-frequency variant at the user-side. The original combined DCM is first introduced. Then, an uncombined dual-frequency variant of the DCM is derived from first principles. The dual-frequency uncombined model is extended to a triple-frequency uncombined model. Finally, the performance of the model is shown through dual- and triple-frequency processing of multiple worldwide datasets using Galileo as the test constellation. The behaviour of some of the model’s parameters are also shown for specific datasets as an example. The paper ends with conclusions and thoughts for future work.

2 Traditional models

In this section, the general PPP equations that define the notation that will be used in this document are introduced. The original combined DCM is then introduced in the same notation to give background understanding of the model.

2.1 PPP observation equations

Considering receiver r and satellite s, the pseudorange and carrier-phase measurements on frequency i, \(i \in \{1,2,3,\ldots ,n\}\), are defined as:

$$\begin{aligned} { \left\{ \begin{array}{ll} P_{r,i}^s &{} = \rho _r^s + c(dt_r - dt^s) + \gamma _i I_1^s + M_r^s.T_r + (b_{r,i} - b^s_i) + \epsilon _{P_i}\\ \Phi _{r,i}^s &{} = \rho _r^s + c(dt_r - dt^s) - \gamma _i I_1^s + M_r^s.T_r + \lambda _i (N_i^s + B_{r,i} - B^s_i)+ \epsilon _{\Phi _i} \end{array} \right. } \end{aligned}$$
(1)

where \(P_{r,i}^s\) and \(\Phi _{r,i}^s\) are, respectively, the pseudorange and carrier-phase measurements, \(\rho _r^s\) is the geometric range between the receiver and the satellite, c is the speed of light in vacuum, \(dt_r\) is the receiver clock error and \(dt^s\) is the satellite clock error. \(\gamma _i = \frac{f_1^2}{f_i^2}\) is the ratio of frequencies that is applied to the first-frequency ionospheric delay \(I_1^s\) to recover the ionospheric delay at frequency i, and \(M_r^s\) is the mapping function that is used to map the zenith troposphere wet delay \(T_r\) to the line-of-sight satellite-station troposphere delay. \(\lambda _i = \frac{c}{f_i}\) is the signal’s wavelength, and \(N_i^s\) is the integer ambiguity on frequency i. \(b_{r,i}\) and \(b^s_i\) are, respectively, the pseudorange receiver and satellite hardware biases and \(B_{r,i}\) and \(B^s_i\) are the receiver and satellite phase biases, respectively. \(\epsilon _{P_i}\) and \(\epsilon _{\Phi _i}\) contain any residual unmodelled errors such as multipath and noise in the pseudorange and carrier-phase measurements, respectively.

All the parameters in Eq. (1) cannot be simultaneously estimated directly due to a rank deficiency of the system. Therefore, it is necessary to re-parameterize the equations by incorporating the receiver and satellites biases into other parameters in order to limit the number of estimated parameters.

2.2 Original combined DCM and EDCM

The original decoupled clock model is based on the ionosphere-free pseudorange and carrier-phase measurements and the Melbourne-Wübenna (MW) widelane observable as introduced in Collins (2008). The MW combination is formed of a narrowlane pseudorange observable and a widelane carrier-phase observable.

In the decoupled clock model, the receiver clocks are decoupled between the pseudorange and carrier-phase measurements. This separation is due to the fact that the pseudorange observables are not synchronized with the carrier-phase observables at the level of precision of the latter, as described in Collins et al. (2012). The equations, from Collins (2008), are summarized as:

$$\begin{aligned} { \left\{ \begin{array}{l} P_{r,3}^s = \rho _r^s + c(dt_{r} - dt^s) + M_r^s.T_r + \epsilon _{P3}\\ \Phi _{r,3}^s = \rho _r^s + c(\delta t_{r} - \delta t^s) + M_r^s.T_r - \lambda _3 (17 N_1^s + 60 N_4^s)+ \epsilon _{\Phi 3}\\ MW_{r,4}^s = b_{r, MW} - b^s_{MW} - \lambda _4 N_4^s + \epsilon _{A4} \end{array} \right. } \nonumber \\ \end{aligned}$$
(2)

where \(P_{r,3}^s\) is the ionosphere-free pseudorange, \(\Phi _{r,3}^s\) is the ionosphere-free carrier-phase and \(MW_{r,4}^s\) is the Melbourne-Wübenna widelane combination. The receiver and satellite clocks are decoupled into pseudorange clocks: \(dt_r\) and \(dt^s\), respectively, and carrier-phase clocks: \(\delta t_r\) and \(\delta t^s\), respectively. The narrowlane \(N_1^s\) and widelane \(N_4^s = N_1^s - N_2^s\) ambiguities are lumped into the ionosphere-free ambiguity with a wavelength \(\lambda _3\). \(\lambda _4=\frac{c}{f_1-f_2}\) is the widelane wavelength, with \(f_1\) and \(f_2\) being the first and second frequencies. In this model, the receiver and satellite biases are moved from the pseudorange and carrier-phase observables to the MW observable. The biases are defined as:

$$\begin{aligned} { \left\{ \begin{array}{ll} b_{r, MW} &{} =\! \frac{c}{f_1-f_2} B_{r,1}\! -\! \frac{c}{f_1-f_2} B_{r,2} - \frac{f_1}{f_1+f_2} b_{r,1} - \frac{f_2}{f_1+f_2} b_{r,2} \\ b^s_{MW} &{} = \frac{c}{f_1-f_2} B_{1}^s - \frac{c}{f_1-f_2} B_{2}^s + \frac{f_1}{f_1+f_2} b_{1}^s + \frac{f_2}{f_1+f_2} b_{2}^s \end{array} \right. } \end{aligned}$$
(3)

The model in Eq. (2) was later expanded to a variant referred to as Extended Decoupled Clock Model (EDCM) in Collins et al. (2012). In this case, the MW observable in Eq. (2) is split into its narrowlane pseudorange and widelane carrier-phase components, and each form a separate observable. This process allows for the estimation and constraining of the ionospheric delays. Therefore, the Extended Decoupled Clock Model relies on the use of four observables: the ionosphere-free code and phase measurements, the narrowlane code measurements and the widelane phase measurements. This model is designed in the dual-frequency case.

3 Uncombined dual-frequency decoupled clock model

In this section, the uncombined dual-frequency DCM is derived from Eq. (1). Seepersad (2019) has derived the uncombined dual-frequency DCM through matrix transformations between combined and uncombined observables. In this paper, the derivation is made from first principles to get the components of each parameter. First, the clocks are decoupled by having a separate parameter for the receiver pseudorange and carrier-phase clocks. For simplicity, in the following derivation, the satellite clocks will be omitted from the equations, as they are corrected by using external products; as well as the tropospheric delay, which is common to all observables. Equation (1) can be simplified to:

$$\begin{aligned} { \left\{ \begin{array}{ll} P_{r,i}^s &{} = \rho _r^s + cdt_r + \gamma _i I_1^s + (b_{r,i} - b^s_i) + \epsilon _{P_i}\\ \Phi _{r,i}^s &{} = \rho _r^s + c\delta t_r - \gamma _i I_1^s + \lambda _i (N_i^s + B_{r,i} - B^s_i) + \epsilon _{\Phi _i}\\ \end{array} \right. } \end{aligned}$$
(4)

where \(dt_r\) is the receiver pseudorange clock and \(\delta t_r\) is the receiver carrier-phase clock. The first step is to focus on the pseudoranges on both frequencies and try to assimilate the receiver pseudorange biases \(b_{r,i}\) into the receiver pseudorange clock \({\overline{dt}}_r\) and ionospheric delays \({\overline{I}}_1^s\) so that the system is as follows:

$$\begin{aligned} \begin{array}{ll} P_{r,i}^s &{} = \rho _r^s + cdt_r + \gamma _i I_1^s + (b_{r,i} - b^s_i) + \epsilon _{P_i}\\ &{}= \rho _r^s + c{\overline{dt}}_r + \gamma _i {\overline{I}}_1^s - b^s_i + \epsilon _{P_i}\\ \end{array} \nonumber \\ \end{aligned}$$
(5)

In order to calculate \(c{\overline{dt}}_r\) and \({\overline{I}}_1^s\), Eq. (5) is written on both frequencies as a system. The terms that are similar on both sides of the equalities are simplified leading to Eq. (6).

$$\begin{aligned} \begin{bmatrix} 1 &{} \quad \gamma _1\\ 1 &{} \quad \gamma _2 \end{bmatrix} \begin{bmatrix} c{\overline{dt}}_r \\ {\overline{I}}_1^s \end{bmatrix} = \begin{bmatrix} 1 &{} \quad \gamma _1 &{} \quad 1 &{} \quad 0\\ 1 &{} \quad \gamma _2 &{} \quad 0 &{} \quad 1 \end{bmatrix} \begin{bmatrix} c dt_r \\ I_1^s \\ b_{r,1} \\ b_{r,2} \end{bmatrix} \end{aligned}$$
(6)

Solving the system in Eq. (6) for the unknowns \({\overline{dt}}_r\) and \(\overline{I_1^s}\) leads to the following expression:

$$\begin{aligned} \left\{ \begin{array}{ll} c {\overline{dt}}_r &{} = c dt_r + \frac{f_1^2}{f_1^2-f_2^2} b_{r,1} - \frac{f_2^2}{f_1^2-f_2^2} b_{r,2}\\ {\overline{I}}_1^s &{} = I_1^s - \frac{f_2^2}{f_1^2-f_2^2} (b_{r,1} - b_{r,2})\\ \end{array} \right. \end{aligned}$$
(7)

By substituting \({\overline{dt}}_r\) and \({\overline{I}}_1^s\) from Eq. (7) into Eq. (4), the code and phase measurements can then be written as:

$$\begin{aligned} { \left\{ \begin{array}{ll} P_{r,1}^s &{}= \rho _r^s + c{\overline{dt}}_r + \gamma _1 {\overline{I}}_1^s - b^s_1 + \epsilon _{P_1}\\ P_{r,2}^s &{}= \rho _r^s + c{\overline{dt}}_r + \gamma _2 {\overline{I}}_1^s - b^s_2 + \epsilon _{P_2}\\ \Phi _{r,1}^s &{} = \rho _r^s + c\delta t_r - \gamma _1 {\overline{I}}_1^s + \lambda _1 (N_1^s + B_{r,1} - B^s_1) - \frac{f_2^2}{f_1^2-f_2^2} (b_{r,1} - b_{r,2}) + \epsilon _{\Phi _1}\\ \Phi _{r,2}^s &{} = \rho _r^s + c\delta t_r - \gamma _2 {\overline{I}}_1^s + \lambda _2 (N_2^s + B_{r,2} - B^s_2) - \frac{f_1^2}{f_1^2-f_2^2} (b_{r,1} - b_{r,2}) + \epsilon _{\Phi _2}\\ \end{array} \right. } \end{aligned}$$
(8)

Proceeding further and being able to eliminate the receiver biases from the carrier-phase observables requires a closer look at the reference satellite’s observables.

3.1 Reference satellite

In order to eliminate the receiver biases, one satellite is chosen as reference and used for between-satellite single-differencing. In the Decoupled Clock Model, the reference satellite’s ambiguities are fixed to arbitrary integer values. These ambiguities are not estimated and they set the datum for the carrier-phase measurements. Indeed, typically in PPP, the carrier-phase measurements’ datum is set by the receiver clock, but because the receiver clocks are decoupled in the DCM, the phase measurements lose the receiver clock datum and therefore require a new datum: the reference satellite’s ambiguities. This situation means that the receiver phase clocks are not absolute but rather relative to the ambiguity datum.

Refer to the reference satellite as ref and set \(N_1^{ref}= N_{01}^{ref} + \delta N_1^{ref}\) and \(N_2^{ref}= N_{02}^{ref} + \delta N_2^{ref}\), where \(N_{0i}^{ref}\) are the arbitrarily set integer ambiguities on frequency i and \(\delta N_i^{ref}\) are the differences between the true integer ambiguities and the arbitrarily set integer ones on frequency i. Re-parametrizing the receiver phase clock so that it absorbs any receiver biases in the L1 observable leads to:

$$\begin{aligned} { \begin{array}{ll} c \overline{\delta t}_r &{} = c \delta t_r + \lambda _1 (\delta N_1^{ref} + B_{r,1}) - \frac{f_2^2}{f_1^2-f_2^2} (b_{r,1} - b_{r,2})\\ \end{array}} \end{aligned}$$
(9)

The phase measurements for the reference satellite can then be expressed as:

$$\begin{aligned} { \left\{ \begin{array}{ll} \Phi _{r,1}^{ref} &{} = \rho _r^s + c\overline{\delta t}_r - \gamma _1 {\overline{I}}_1^{ref} + \lambda _1 (N_{01}^{ref} - B^{ref}_1) + \epsilon _{\Phi _1}\\ \Phi _{r,2}^{ref} &{} = \rho _r^s + c\overline{\delta t}_r - \gamma _2 {\overline{I}}_1^{ref} + \lambda _2 (N_{02}^{ref} - B^{ref}_2) + \delta t_{12} + \epsilon _{\Phi _2}\\ \end{array} \right. } \nonumber \\ \end{aligned}$$
(10)

where \(\delta t_{12} = \lambda _2 (\delta N_2^{ref} + B_{r,2}) - \lambda _1 (\delta N_1^{ref} + B_{r,1}) - (b_{r,1} - b_{r,2})\) will be referred to as the receiver widelane bias to be consistent with the combined model. This term is receiver dependent, as it is only made of receiver biases and the differences between the arbitrarily set integer ambiguities and the unknown integer ones. These differences are constant unless a cycle-slip occurs or a change in the reference satellite happens.

3.2 Non-reference satellites

Based on the definitions of \({\overline{I}}_1\) and \(\overline{\delta t}_r\) in Eqs. (6) and (7), the first frequency’s phase measurement for a given satellite s in Eq. (8) can be rewritten as:

$$\begin{aligned} { \begin{array}{ll} \Phi _{r,1}^s &{}= \rho _r^s + c\overline{\delta t}_r - \gamma _1 {\overline{I}}_1^s + \lambda _1 (N_1^s+B_{r,1}-B_1^s)\\ &{}\quad - \frac{f_2^2}{f_1^2-f_2^2} (b_{r,1} - b_{r,2}) - \lambda _1 (\delta N_1^{ref}+B_{r,1}) + \frac{f_2^2}{f_1^2-f_2^2} (b_{r,1} - b_{r,2})\\ &{}= \rho _r^s + c\overline{\delta t}_r - \gamma _1 {\overline{I}}_1^s + \lambda _1 ({\overline{N}}_1^s - B_1^s) \end{array}} \end{aligned}$$
(11)

where \({\overline{N}}_1^s = N_1^s - \delta N_1^{ref}\). The second frequency’s phase measurement for satellite s can be rewritten from Eq. (8) as:

$$\begin{aligned} { \begin{array}{ll} \Phi _{r,2}^s &{}= \rho _r^s + c\overline{\delta t}_r - \gamma _2 \overline{I_1^s} + \lambda _2 (N_2^s+B_{r,2}-B_2^s) \\ &{}\quad - \frac{f_1^2}{f_1^2-f_2^2} (b_{r,1} - b_{r,2})- \lambda _1 (\delta N_1^{ref}+B_{r,1}) + \frac{f_2^2}{f_1^2-f_2^2} (b_{r,1} - b_{r,2})\\ &{}= \rho _r^s + c\overline{\delta t}_r - \gamma _2 \overline{I_1^s} + \lambda _2 ({\overline{N}}_2^s - B_2^s) + \delta t_{12} \end{array}} \end{aligned}$$
(12)

where \({\overline{N}}_2^s = N_2^s - \delta N_2^{ref}\). Therefore, the carrier-phase measurements on both frequencies for the reference satellite and non-reference satellites have very similar expressions. Note how important it is to set the reference satellite’s ambiguities to integer values, as these arbitrary values (\(N_{01}^{ref}\) and \(N_{02}^{ref}\)) set the datum for the phase measurements and they get lumped into the ambiguities for all the satellites as \(\delta N_1^{ref}\) and \(\delta N_2^{ref}\), which are integers. Having arbitrary float values would mean non-integer \(\delta N_1^{ref}\) and \(\delta N_2^{ref}\), and therefore non-integer \({{\overline{N}}}_1^s\) and \({{\overline{N}}}_2^s\).

3.3 Complete dual-frequency model

Following the phase measurement derivations in Sects. 3.1 and 3.2 and Eq. (8), the complete uncombined dual-frequency model, including the satellite clocks and tropospheric wet delays, can be summarized in Eq. (13).

$$\begin{aligned} { \left\{ \begin{array}{ll} P_1^s &{}= \rho _r^s + c ({\overline{dt}}_r -dt^s) + \gamma _1 {\overline{I}}_1^s + M_r^s.T_r - b^s_1 + \epsilon _{P_1}\\ P_2^s &{}= \rho _r^s + c ({\overline{dt}}_r -dt^s) + \gamma _2 {\overline{I}}_1^s + M_r^s.T_r - b^s_2 + \epsilon _{P_2}\\ \Phi _1^s &{}= \rho _r^s + c (\overline{\delta t}_r -dt^s) - \gamma _1 {\overline{I}}_1^s + M_r^s.T_r + \lambda _1 ({\overline{N}}_1^{s} - B^s_1) + \epsilon _{\Phi _1}\\ \Phi _2^{s} &{}= \rho _r^s + c (\overline{\delta t}_r -dt^s) - \gamma _2 {\overline{I}}_1^s + M_r^s.T_r + \lambda _2 ({\overline{N}}_2^{s} - B^s_2) + \delta t_{12} + \epsilon _{\Phi _2}\\ \end{array} \right. } \end{aligned}$$
(13)

with:

$$\begin{aligned} { \left\{ \begin{array}{ll} c {\overline{dt}}_r &{}= c dt_r + \frac{f_1^2}{f_1^2-f_2^2} b_{r,1} - \frac{f_2^2}{f_1^2-f_2^2} b_{r,2}\\ {\overline{I}}_1^s &{}= I_1^s - \frac{f_2^2}{f_1^2-f_2^2} (b_{r,1} - b_{r,2})\\ \delta t_{12} &{}= \lambda _2 (\delta N_2^{ref} + B_{r,2}) - \lambda _1 (\delta N_1^{ref} + B_{r,1}) - (b_{r,1} - b_{r,2})\\ c \overline{\delta t}_r &{}= c \delta t_r + \lambda _1 (\delta N_1^{ref} + B_{r,1}) - \frac{f_2^2}{f_1^2-f_2^2}(b_{r,1} - b_{r,2})\\ {\overline{N}}_1^{s} &{}= N_1^{s} -\delta N_1^{ref}\\ {\overline{N}}_2^{s} &{}= N_2^{s} -\delta N_2^{ref} \end{array} \right. } \end{aligned}$$
(14)

4 Uncombined triple-frequency decoupled clock model

The triple-frequency model can be extended from the dual-frequency one. The third frequency, \(f_3\), comes with an additional pseudorange and carrier-phase measurement, which have to be arranged from Eq. (1) to an equation similar to (13). Ignoring the satellite clocks and tropospheric zenith wet delay, the third frequency’s measurements’ general expression is:

$$\begin{aligned} { \left\{ \begin{array}{ll} P_{r,3}^s &{} = \rho _r^s + c dt_r + \gamma _3 I_1^s + (b_{r,3} - b^s_3) + \epsilon _{P_3}\\ \Phi _{r,3}^s &{} = \rho _r^s + c dt_r - \gamma _3 I_1^s + \lambda _3 (N_3^s + B_{r,3} - B^s_3)+ \epsilon _{\Phi _3} \end{array} \right. } \end{aligned}$$
(15)

4.1 Third-frequency pseudorange

Replacing the receiver clock and the first frequency’s ionospheric delay’s expressions in the third-frequency pseudorange observable by those in Eq. (7) leads to:

$$\begin{aligned} { \begin{array}{ll} P_{r,3}^s &{} = \rho _r^s + cdt_r + \gamma _3 I_1^s + (b_{r,3} - b^s_3) + \epsilon _{P_3}\\ &{}= \rho _r^s + c{\overline{dt}}_r + \gamma _3 {\overline{I}}_1^s + (b_{r,3} - b^s_3)\\ &{}\quad - \frac{f_1^2}{f_1^2-f_2^2} b_{r,1} + \frac{f_2^2}{f_1^2-f_2^2} b_{r,2} + \frac{f_3^2}{f_1^2-f_2^2} (b_{r,1}-b_{r,2}) + \epsilon _{P_3}\\ &{}= \rho _r^s + c{\overline{dt}}_r + \gamma _3 {\overline{I}}_1^s - b^s_3 + IFB_r + \epsilon _{P_3}\\ \end{array}} \nonumber \\ \end{aligned}$$
(16)

\(IFB_r = \frac{f_3^2 - f_1^2}{f_1^2-f_2^2} b_{r,1} - \frac{f_3^2 - f_2^2}{f_1^2-f_2^2} b_{r,2} + b_{r,3}\) is the Inter-Frequency pseudorange Bias which arises from the fact that \({\overline{dt}}_r\) and \({\overline{I}}_1^s\) cannot absorb all the pseudorange receiver biases on the three frequency. This term only contains receiver biases and it is therefore not satellite dependent. This term varies slowly throughout the day and can be estimated as constant (Xiang et al. 2020). However, because the DCM does not make any assumptions regarding the behaviour of biases, the \(IFB_r\) is estimated as white noise, similarly to the receiver clocks.

4.2 Third-frequency carrier-phase

Replacing the phase receiver clock and first frequency’s ionospheric delay’s expressions by those in Eq. (7) leads to:

$$\begin{aligned} { \begin{array}{ll} \Phi _{r,3}^s &{} = \rho _r^s + c \delta t_r - \gamma _3 I_1^s + \lambda _3 (N_3^s + B_{r,3} - B^s_3) + \epsilon _{\Phi _3}\\ &{}= \rho _r^s + c \overline{\delta t}_r - \gamma _3 {\overline{I}}_1^s + \lambda _3 (N_3^s + B_{r,3} - B^s_3) + \frac{f_2^2}{f_1^2-f_2^2} (b_{r,1}-b_{r,2})\\ &{}\quad - \lambda _1 (\delta N_1^{ref} + B_{r,1}) - \frac{f_3^2}{f_1^2-f_2^2} (b_{r,1}-b_{r,2})+ \epsilon _{\Phi _3} \end{array}} \end{aligned}$$
(17)

Similarly to the dual-frequency derivation, the reference satellite’s phase measurements are looked into first.

4.2.1 Reference satellite

Set \(N_3^{ref} = N_{03}^{ref} + \delta N_3^{ref}\) where \(N_{03}^{ref}\) is the arbitrarily set integer ambiguity at frequency \(f_3\) and \(\delta N_3^{ref}\) is the difference between the true integer ambiguity and the arbitrarily set integer one. The reference satellite’s third frequency phase measurement can be written as:

$$\begin{aligned} { \begin{array}{ll} \Phi _{r,3}^{ref} &{} = \rho _r^{ref} + c \overline{\delta t}_r - \gamma _3 {\overline{I}}_1^{ref} + \lambda _3 (N_3^{ref} + B_{r,3} - B^{ref}_3)\\ &{}\quad + \frac{f_2^2 - f_3^2}{f_1^2-f_2^2} (b_{r,1}-b_{r,2}) - \lambda _1 (\delta N_1^{ref} + B_{r,1}) + \epsilon _{\Phi _3}\\ &{}= \rho _r^{ref} + c \overline{\delta t}_r - \gamma _3 {\overline{I}}_1^{ref} + \lambda _3 (N_{03}^{ref} - B^{ref}_3) + \delta t_{13} + \epsilon _{\Phi _3} \end{array}} \end{aligned}$$
(18)

where \(\delta t_{13} = \frac{f_2^2 - f_3^2}{f_1^2-f_2^2} (b_{r,1}-b_{r,2}) - \lambda _1 (\delta N_1^{ref} + B_{r,1}) + \lambda _3 (\delta N_3^{ref} +B_{r,3})\) is equivalent to \(\delta t_{12}\) in the second frequency’s phase measurements, and will be referred to in the rest of this document as the receiver extra-widelane bias.

4.2.2 Non-reference satellites

For any given satellite s, the third frequency carrier-phase can be written as:

$$\begin{aligned} { \begin{array}{ll} \Phi _{r,3}^{s} &{} = \rho _r^s + c \overline{\delta t}_r - \gamma _3 {\overline{I}}_1^{s} + \lambda _3 (N_3^{s} + B_{r,3} - B^{s}_3)\\ &{}\quad + \frac{f_2^2 - f_3^2}{f_1^2-f_2^2} (b_{r,1}-b_{r,2}) - \lambda _1 (\delta N_1^{s} + B_{r,1}) + \epsilon _{\Phi _3}\\ &{} = \rho _r^s + c \overline{\delta t}_r - \gamma _3 {\overline{I}}_1^{s} + \lambda _3 (N_3^{s} + B_{r,3} - B^{s}_3)\\ &{}\quad + \delta t_{13} - \lambda _3 (\delta N_3^{ref} +B_{r,3}) + \epsilon _{\Phi _3}\\ &{} = \rho _r^s + c \overline{\delta t}_r - \gamma _3 {\overline{I}}_1^{s} + \lambda _3 ({\overline{N}}_3^{s} - B^{s}_3) + \delta t_{13} + \epsilon _{\Phi _3}\\ \end{array}} \end{aligned}$$
(19)

where \({\overline{N}}_3^{s} = N_3^s - \delta N_3^{ref}\) is the implicitly single-differenced third frequency integer ambiguity. Therefore, we are able to recover the same equation for all satellites thanks to \(\delta t_{13}\) absorbing the receiver biases and reference satellite ambiguities.

4.3 Complete triple-frequency model

The complete uncombined triple-frequency model can be summarized as follows:

$$\begin{aligned} { \left\{ \begin{array}{ll} P_1^s &{}= \rho _r^s + c ({\overline{dt}}_r -dt^s) + \gamma _1 {\overline{I}}_1 + M_r^s.T_r - b^s_1 + \epsilon _{P_1}\\ P_2^s &{}= \rho _r^s + c ({\overline{dt}}_r -dt^s) + \gamma _2 {\overline{I}}_1 + M_r^s.T_r - b^s_2 + \epsilon _{P_2}\\ P_3^s &{}= \rho _r^s + c ({\overline{dt}}_r -dt^s) + \gamma _3 {\overline{I}}_1 + M_r^s.T_r + IFB_r - b^s_3 + \epsilon _{P_3}\\ \Phi _1^s &{}= \rho _r^s + c (\overline{\delta t}_r -dt^s) - \gamma _1 {\overline{I}}_1 + M_r^s.T_r + \lambda _1 ({\overline{N}}_1^{s} - B^s_1) + \epsilon _{\Phi _1}\\ \Phi _2^{s} &{}= \rho _r^s + c (\overline{\delta t}_r -dt^s) - \gamma _2 {\overline{I}}_1 + M_r^s.T_r + \lambda _2 ({\overline{N}}_2^{s} - B^s_2) + \delta t_{12} + \epsilon _{\Phi _2}\\ \Phi _3^{s} &{}= \rho _r^s + c (\overline{\delta t}_r -dt^s) - \gamma _3 {\overline{I}}_1 + M_r^s.T_r + \lambda _3 ({\overline{N}}_3^{s} - B^s_3) + \delta t_{13} + \epsilon _{\Phi _3}\\ \end{array} \right. } \end{aligned}$$
(20)

with:

$$\begin{aligned} { \left\{ \begin{array}{ll} c {\overline{dt}}_r &{}= c dt_r + \frac{f_1^2}{f_1^2-f_2^2} b_{r,1} - \frac{f_2^2}{f_1^2-f_2^2} b_{r,2}\\ c \overline{\delta t}_r &{}= c \delta t_r + \lambda _1 (\delta N_1^{ref} + B_{r,1}) - \frac{f_2^2}{f_1^2-f_2^2}(b_{r,1} - b_{r,2})\\ {\overline{I}}_1 &{}= I_1 - \frac{f_2^2}{f_1^2-f_2^2} (b_{r,1} - b_{r,2})\\ \delta t_{12} &{}= \lambda _2 (\delta N_2^{ref} + B_{r,2}) - \lambda _1 (\delta N_1^{ref} + B_{r,1}) - (b_{r,1} - b_{r,2})\\ IFB_r &{}= \frac{f_3^2 - f_1^2}{f_1^2-f_2^2} b_{r,1} - \frac{f_3^2 - f_2^2}{f_1^2-f_2^2} b_{r,2} + b_{r,3}\\ \delta t_{13} &{}= \frac{f_2^2 - f_3^2}{f_1^2-f_2^2} (b_{r,1}-b_{r,2}) - \lambda _1 (\delta N_1^{ref} + B_{r,1}) + \lambda _3 (\delta N_3^{ref} +B_{r,3})\\ {\overline{N}}_1^{s} &{}= N_1^{s} -\delta N_1^{ref}\\ {\overline{N}}_2^{s} &{}= N_2^{s} -\delta N_2^{ref}\\ {\overline{N}}_3^{s} &{}= N_3^{s} -\delta N_3^{ref} \end{array} \right. } \end{aligned}$$
(21)

Compared to the dual-frequency model, the triple-frequency model has an additional receiver-dependent term to absorb the pseudorange receiver biases, as well as a carrier-phase-related receiver bias, which absorbs the phase receiver biases. All three estimated ambiguities are free of biases and should, after convergence, reach integer values. Furthermore, the above triple-frequency model can easily be expanded into a quad- of five-frequency model. The additional frequencies’ measurements can be separated for the reference satellite and for non-reference satellites as was done for the expansion of the dual-frequency model with the third frequency.

5 Data and processing

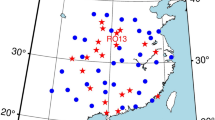
In order to validate the model and assess its performance, a network of 25 worldwide IGS-MGEX stations has been used and their data processed over 7 days between DOY 342 and DOY 348, 2019. The stations are shown in Fig. 1. The 24 h datasets were split into 3 h sessions in order to increase the number of datasets. The total number of processed datasets was 1400, with a sampling interval of 30 s. The purpose from the processing is to validate the proposed model and assess its various parameters. Therefore, we have opted to only process one constellation in order to lower the complexity of the paper by not including inter-constellation biases. Since all Galileo satellites transmit three frequencies, and because the receivers typically track all three frequencies simultaneously, only Galileo satellites were processed in order to keep the same number of satellites between the dual- and triple-frequency modes. The three Galileo frequencies used in the processing are: E1, E5b and E5a. Table 1 highlights the strategies in the estimation and correction of various parameters and errors.

Fig. 1
figure 1

World map of the stations used in the processing

Full size image
Table 1 Processing strategies for the estimated parameters
Full size table

As seen in Sects. 3 and 4 , \(\delta t_{12}\), \(\delta t_{13}\) and \(IFB_r\) all consist of receiver biases. These biases are constant within a few nanoseconds over the course of a day, but we try to avoid such strong assumptions on the biases and instead choose to estimate them as white noise processes without any prior information on the mean or variance. Because the three quantities are common to all satellites, they can be estimated successfully. The satellite Phase Centre Offset (PCO) and Phase Centre Variation (PCV) errors are corrected for using values from the ANTEX file, provided by the IGS.

Phase wind-up, Earth rotation and relativistic effects are corrected for following the IERS conventions. The satellite code and phase biases are corrected for using the CNES products (Laurichesse and Blot 2016). These products are meant to be used together with the GFZ rapid orbit and clock products (Deng et al. 2017) and they provide Observable-specific Signal Biases (OSB). The advantage of using OSB products is that they directly provide the biases on each observable type, eliminating the need for the user to know the model that was used in the estimation of the biases on the network side, nor do they need to know the types of the reference observables. This is a major advantage in moving towards interchangeability of the products. Both code and phase biases are applied at the observable level, similarly to the satellite orbits and clocks, instead of applying the phase biases at the ambiguity level. This approach is believed to be more compatible and in-line with the PPP philosophy and more suitable in a multi-GNSS multi-frequency context as all the corrections are signal-dependent and applied directly to the measurements. Banville et al. (2020), for instance, opted for the OSB format to assess the interoperability of AR products from different analysis centres.

The Least-squares AMBiguity Decorrelation Adjustment (LAMBDA) method introduced in Teunissen (1995) is a widely used method for ambiguity fixing in GNSS. However, it is also known to be one of the slowest methods and is therefore not fit for GNSS applications (Xu et al. 2012). In this work, a modified version of LAMBDA is used: mLAMBDA, introduced in Chang et al. (2005), is a faster and more computationally efficient method. The validation of the ambiguities is done through a combination of the ratio test with a threshold of 0.5, the residuals, and the reference coordinates. In order to fix the ambiguities through mLAMBDA, the uncombined float ambiguities are first estimated based on the uncombined DCM models in Eqs. (13) and (20). These uncombined ambiguities are already single-differenced and free of satellite and receiver biases. They are fed directly to the mLAMBDA method along with their associated float covariances. The mLAMBDA function returns a set of fixed estimates and covariances, which are used to update the state terms. It is possible to form the extra-widelane (EWL), widelane (WL) and narrowlane (NL) combinations for the ambiguities and their covariances prior to calling the mLAMBDA method; however, the results are similar to those without forming the combinations.

6 Results

Results in this section are split into three parts: static dual-frequency results and analysis are showed first. They are followed by a static triple-frequency analysis and a comparison of the dual- and triple-frequency results. Finally, a comparison between static and kinematic processing is done.

6.1 Dual-frequency AR results

Figure 2 illustrates an example of the variations in the parameters that are specific to the DCM for station YELL in northwestern Canada on DOY 344, 2019 over the course of the day. Both the receiver pseudorange and carrier-phase clocks have a similar slow drift. This similarity is due to the fact that they both contain the actual receiver clock, but they are each affected by different biases. The difference between the two receiver clocks contains receiver code and phase biases, as well as \(\delta N_1^{ref}\), which explains the vertical shift between the two graphs. The pseudorange clock is more noisy, as this term is estimated based only on the pseudorange measurements, which are more noisy than their carrier-phase counterparts. To quantify the level of noise in the receiver clocks, a linear polynomial has been fit to them and the RMS between the estimated clocks and the fitted polynomals was calculated. The pseudorange clock has an RMS of 19 dm, compared to 13 dm for the phase clock, proving that pseudorange receiver clocks are more noisy. The receiver biases are also lumped in the receiver widelane bias \(\delta t_{12}\), which is shown in subplot (b) in Fig. 2. \(\delta t_{12}\) is relatively stable over the course of the day with variations up to 2 ns. However, it is preferable not to make assumptions on its stability during the estimation, as Abdelazeem et al. (2016), Zhang et al. (2017) and Zhang et al. (2019) have shown relatively large variations in the receiver biases depending on the receiver’s temperature, location and quality. Estimating those receiver biases as clock-like terms, as was done here, ensures that the ambiguities are stable, integers, and free of residual biases; especially when working with lower-quality/cost receivers. The Integer Recovery Clock (IRC) does not assume the behaviour of the receiver biases either, unlike the Fractional Cycle Biases (FCB) model (Geng et al. 2010). It is worth noting that both the receiver carrier-phase clock and the receiver widelane bias contain the reference satellite’s integer ambiguity. Therefore, these quantities depend on the choice of the reference satellite: a change in the reference satellite results in an integer vertical shift of the receiver carrier-phase clock and receiver widelane bias.

Fig. 2
figure 2

a Receiver code clock \({\overline{dt}}_r\), receiver phase clock \(\overline{\delta t}_r\) and b receiver widelane bias \(\delta t_{12}\) for station YELL on DOY 344, 2019

Full size image

Figures 3 and 4 show the epoch-by-epoch average horizontal and vertical position solutions based on all 1400 datasets, respectively. The plots show the (a) 100th, (b) 95th, (c) 67th and (d) 50th percentiles and highlight the typical performance of the dual-frequency float and fixed solutions. The convergence here and throughout the rest of the paper is defined as the time it takes for the error to settle below 10 cm. The same definition is valid both for the horizontal and vertical errors. The horizontal RMS have been computed between minutes 60 and 180 in order to assess the final level of accuracy that the solutions reach. Tables 2 and 3 provide summary statistics for Figs. 3 and 4. Under these definitions, the 100-percentile dual-frequency float solution converges within 18.5 min for the horizontal component (and 23.5 min for the vertical), while the fixed one converges within 14.5 min horizontally (and 21.5 min vertically). The float solution is able to reach a horizontal RMS of 2.7 cm (and vertical of 2.9 cm), while the fixed one has a value of 1.1 cm for the horizontal (and 2.5 cm for the vertical). Therefore, the benefit of fixing the ambiguities on Galileo is more noticeable for the horizontal component than it is for the vertical one. The 100-percentile horizontal convergence time and RMS see 22\(\%\) and 59\(\%\) decreases, respectively, while the vertical convergence time and RMS see decreases of 9\(\%\) and 14\(\%\), respectively. Shi and Gao (2014b) had also noticed the limited benefit of AR on the vertical component, and they tried to remedy it by constraining the troposphere, as the latter limits the estimation of the vertical component. In this work, lower percentiles have the solution converging faster and with higher accuracies, the convergence times of both float and fixed solutions becoming closer the lower the percentile. This behaviour is due to the solutions already converging fast enough (5.5 min for the horizontal 50th percentile solution), which means that AR’s improvement is limited in this case (5 min for the horizontal 50th percentile solution).

Fig. 3
figure 3

Static dual-frequency average horizontal error based on all datasets at the a 100th, b 95th, c 67th and d 50th percentiles. The horizontal dashed lines represent the convergence threshold

Full size image
Fig. 4
figure 4

Static dual-frequency average vertical error based on all datasets at the a 100th, b 95th, c 67th and d 50th percentiles. The horizontal dashed lines represent the convergence threshold

Full size image
Table 2 Horizontal convergence time and RMS statistics for Fig. 3 results
Full size table
Table 3 Vertical convergence time and RMS statistics for Fig. 4 results
Full size table

Figure 5 is included to highlight the 100-percentile performance of the solutions on each station individually, as opposed to the average from all datasets. Each station’s result contains the average from 56 datasets: 8 3-h datasets per day, for 7 days. The benefit of AR varies depending on the stations, as some see a big improvement, e.g., GANP, while others have relatively the same convergence time, e.g., AREQ. On the other hand, AR significantly improves the accuracy for all stations, as the horizontal RMS see an average centimetre decrease for all stations.

Fig. 5
figure 5

Static dual-frequency average horizontal convergence times and RMS for each station—56 datasets per station

Full size image

6.2 Triple-frequency AR results

Figure 6 illustrates the trends of both the extra-widelane (EWL) and Inter-Frequency Biases (IFB). Similarly to the receiver WL bias in Fig. 2, the receiver EWL bias depends on the receiver biases, as well as the reference satellite’s ambiguities. It is relatively stable but it is best to not make assumptions regarding its stability, and rather estimate it as white noise. Similarly to the receiver WL bias, \(\delta t_{13}\) depends on the reference satellite’s ambiguities and it therefore depends on the choice of reference satellite: a different reference satellite would lead to the same plot shifted vertically by an integer value. On the other hand, the IFB only depends on the receiver biases and not on the reference satellite’s ambiguities. Consequently, it does not depend on the choice of reference satellite. Although the IFB was estimated as a white noise process as well, it is relatively stable. This was expected as \(\delta t_{12}\), \(\delta t_{13}\) and \(IFB_r\) are all made of receiver biases (and additional integer values), which means that they should all follow similar trends, assuming that the receiver biases have similar time-dependence regardless of frequency.

Fig. 6
figure 6

a Receiver EWL bias \(\delta t_{13}\) and b inter-frequency bias \(IFB_r\) for station YELL on DOY 344, 2019

Full size image
Fig. 7
figure 7

Kinematic a dual-frequency and b triple-frequency horizontal error and fixed ambiguities for station YELL on DOY 344, 2019 between 21:00 and 23:00 UTC. The ambiguities jumping from zero to non-zero values mean that a satellite starts being processed. Ambiguities jumping from non-zero values to zero mean that a satellite stops being processed

Full size image

Figure 7 highlights the performance of the float and fixed solutions, as well as the fixed ambiguities for both dual- and triple-frequency solutions for station YELL on DOY 344, 2019 for 2 h in kinematic mode. As stated earlier, the uncombined ambiguities on each frequency are fixed by the LAMBDA function. In order to show that, even in this case, the combination properties are still valid after the fixing, the ambiguities have been combined into NL, WL and EWL after the fixing. Looking at the dual-frequency results, it is clear that the WL ambiguities in red are fixed correctly from the first epoch thanks to their large wavelength, and that the initial variations in the NL ambiguities (which have a much smaller wavelength) are causing the variations in the fixed horizontal solution. Once the NL ambiguities start being fixed correctly, the fixed solution converges and remains at the same level of accuracy, while the float one still has a longer convergence period. These conclusions hold for the triple-frequency solution as well, although it is interesting to notice that the NL ambiguities are fixed correctly faster than in the dual-frequency case thanks to the EWL ambiguities (instantly fixed) helping in the fixing process. Given the correlation between ambiguities from the same satellite, being able to instantaneously fix the EWL ambiguity leads to faster fixing of the WL ambiguity, which in turn leads to faster fixing of the NL ambiguity. A study on the correctness of NL fixing for dual- and triple-frequency data by Geng and Bock (2013) has shown that more NL ambiguities can be fixed in the first tens of seconds of processing with three frequencies than with two frequencies. When it comes to the float solutions, two observations can be made: on one hand, there is a noticeable difference between the float dual- and triple-frequency solutions during the first few epochs. An explanation is that, if the DOP is relatively high during the first few epochs (an average of 2 for this dataset), the third frequency will help improve the positioning solution thanks to its additional measurements. In the case of multi-GNSS processing where the DOP is low, it is expected that both dual- and triple-frequency float solutions will have minimal differences. On the other hand, it can be seen that the dual-frequency solution at 0.4 h is slightly better than the triple-frequency one. This can be explained by the fact that, unlike the dual-frequency case where residual errors can be absorbed by other states, having three frequencies means that the model is not as lenient towards such residual errors, which can have more of an impact on state estimation. Degradations of the position estimates when using three frequencies as opposed to two frequencies have been noticed by Geng et al. (2020) and they were attributed to residual errors.

Figures 8 and 9 expand on Figs. 3 and 4’s respective results by adding the triple-frequency results as well. Comparing all-percentiles dual- and triple-frequency float solutions shows that processing an additional frequency provides a negligible improvement as the 100-percentile triple-frequency float horizontal solution converges in 16.5 min (compared to 18.5 for dual-frequency) and reaches a horizontal RMS of 2.6 cm (compared to 2.7 cm for dual-frequency). Guo et al. (2016) have noticed similar behaviour with BeiDou triple-frequency processing, where they mentioned that the third frequency only helps in certain scenarios, inluding low signal strength for one of the signals, undetected cycle slips with dual-frequency data. Therefore, we believe that this minimal improvement is due to the fact that the additional frequency does not provide any significant additional independent information compared to, e.g., having an additional satellite, which would improve the satellite geometry. For instance, moving from single-frequency processing to dual-frequency processing improves the PPP performance as it helps estimate the ionosphere more accurately (Lou et al. 2016), but moving to triple-frequency processing does not improve the solution as significantly. An example of the improvement for the float solutions was discussed in Fig. 7 in which most of the improvement to the float solution came in the initialization errors, but the convergence time and final accuracies were not affected. On the other hand, there is a larger improvement when it comes to the fixed solution, as the triple-frequency fixed solution converges in 9.5 min and reaches a horizontal RMS of 1.0 cm. Although the accuracy is similar to the dual-frequency fixed solution, there is a noticeable improvement in the convergence time, which sees a 34\(\%\) decrease compared to the dual-frequency fixed solution. These results are relatively better than those presented in Xiao et al. (2019), where the 3D float triple-frequency Galileo solution converged in 64.5 min (compared to 35 min for the 3D convergence in this study) and the fixed solution converged in 56 min (compared to 21.5 min for the 3D convergence here). The authors in Xiao et al. (2019) down-weighted the observations by a factor of 4, which could explain the differences with our results. Li et al. (2020) had average horizontal dual- and triple-frequency AR convergence times of 22.3 and 17.4 min, respectively; although their convergence time definition was different: time taken for the horizontal accuracy to be better than 5 cm and kept within 5 cm during ten consecutive epochs. Though it is important to keep in mind that this manuscript and the cited research use different datasets, which could explain the differences in results. These results mean that the most benefit from triple-frequency processing comes from fixing the ambiguities on three frequencies instead of two. The possible reason behind this result could be that fixing three frequencies adds robustness to the fixing thanks to the EWL ambiguity, which can be fixed instantaneously—meaning that the ambiguities are fixed correctly earlier and more often, leading to the aforementioned improvement.

Fig. 8
figure 8

Static dual- and triple-frequency average horizontal error based on all datasets at the a 100th, b 95th, c 67th and d 50th percentiles. Horizontal dashed lines represent the convergence threshold

Full size image
Fig. 9
figure 9

Static dual- and triple-frequency average vertical error based on all datasets at the a 100th, b 95th, c 67th and d 50th percentiles. Horizontal dashed lines represent the convergence threshold

Full size image

In order to show the improvement of triple-frequency AR over dual-frequency AR at the dataset level, the histograms for the convergence times of all datasets are plotted in Fig. 10. The bin size is 30 s. The figure shows that triple-frequency AR leads to the histogram shifting towards the left compared to dual-frequency AR, as more datasets converge sooner. It also shows that more datasets converge within the first few minutes: 23\(\%\) of the datasets converge within the first 5 min in the triple-frequency case, compared to 12\(\%\) in the dual-frequency case, while 50\(\%\) of the solutions converge within the first 10 min in triple-frequency processing, compared to 36\(\%\) in the dual-frequency counterpart.

Fig. 10
figure 10

Histograms comparing the Galileo horizontal convergence times of the static dual-frequency fixed solutions with the triple-frequency fixed solutions

Full size image

Since the number of visible Galileo satellites is currently relatively limited compared to GPS, the performance of both the float and fixed solutions varies. Some datasets which are subject to a low number of satellites or high Dilution of Precision (DOP) result in poor float and, consequently, poor fixed solutions. Figure 11 paints a picture of the number of Galileo satellites that were processed for all datasets. Sub-figure (a) represents the distribution of the number of satellites based on all epochs from all datasets with a bin size of 1. The histogram shows an average of seven satellites with 15\(\%\) of epochs having five satellites or less and 7\(\%\) of epochs having nine satellites or more. It is expected that epochs with low number of satellites will lead to worse float and fixed solutions due to bad satellite geometry. This is confirmed by the Position Dilution Of Precision (PDOP) distribution shown in sub-figure (b) with a bin size of 0.25. The sub-figure shows an average PDOP of 2.5 with 18\(\%\) of epochs having a PDOP higher than 3. A PDOP of 1 being indicative of a good satellite distribution, the PDOP histogram helps make sense of the improvements that are seen when looking at lower percentiles.

Fig. 11
figure 11

Distribution of a the number of Galileo satellites and b PDOP based on all epochs from all datasets

Full size image

As a summary, Figs. 12 and 13 show the levels of performance of both the dual- and triple-frequency solutions (float and fixed) at different levels of confidence. These statistics correspond to Figs. 8 and 9’s results. Looking at different percentiles helps assess the performance of the solutions without the outliers that are due to the low number of satellites: the lower the percentile, the less outliers are present.

Fig. 12
figure 12

a Average horizontal convergence times and b RMS for both dual- and triple-frequency solutions at different percentiles in static mode

Full size image
Fig. 13
figure 13

a Average vertical convergence times and b RMS for both dual- and triple-frequency solutions at different percentiles in static mode

Full size image

It is interesting to see how much AR improves the horizontal accuracy at all percentiles for both the dual- and triple-frequency cases as AR leads to over 60\(\%\) improvements to the horizontal RMS. On the other hand, the improvements to the vertical accuracy are not as obvious. At all percentiles, dual-frequency AR decreases the horizontal convergence time by 20–30\(\%\) compared to the dual-frequency float solutions, and triple-frequency AR decreases the horizontal convergence time by 40–50\(\%\) compared to the triple-frequency float solutions. The vertical components see improvements, but on a smaller scale. The performance of the float dual- and triple-frequency solutions is very similar at all three levels of confidence, which confirms the earlier assumption that adding a third frequency does not add much new information to the already used two frequencies.

Fig. 14
figure 14

Static a horizontal and b vertical dual- and triple-frequency float and fixed solutions for datasets with an average of over 6 satellites during the first hour. Horizontal dashed lines represent the convergence threshold

Full size image

As mentioned above, compared to GPS, Galileo suffers from a relatively low number of satellites, which would impact the solutions. In order to have an idea on the Galileo performance with a more complete constellation, only the datasets with more than an average of six visible satellites during the first hour of processing were used for the generation of Fig. 14 and Table 4. 73\(\%\) of the datasets fulfill this condition. Both the figure and table show the performances of the float and fixed, dual- and triple-frequency, horizontal and vertical solutions at the 100th percentile. When it comes to the horizontal convergence time, the performance of this solution corresponds roughly to the 95th percentile performance of Fig. 12, while the vertical accuracy is between the 100th and 95th percentiles.

6.3 Kinematic processing

The results shown in previous sections are generated by considering that the receiver is static and by giving a process noise for receiver position states of zero. That zero process noise means that the position coordinates are getting averaged across all epochs. In order to have a better idea on the performance of the proposed DCM model for Galileo satellites without such constraints, the same datasets are processed in kinematic mode and presented in this sub-section. In this case, position coordinate states are given process noise that is equivalent to typical speeds of a car (100 km/h). Since no assumption is made on the dynamics of the receiver, the performance of the kinematic processing is expected to be worse than the static one.

Table 4 Horizontal and vertical convergence time and RMS statistics for Fig. 14 results
Full size table

Figures 15 and 16 highlight the performance of the horizontal and vertical errors, respectively, for the kinematic processing. By visually comparing these two figures with Figs. 8 and 9, it is clear that, as expected, the performance is worse in kinematic processing as solutions take longer to converge and have larger errors. Figure 17 shows the statistics corresponding to the kinematic processing. At all percentiles, the improvements from AR are more significant than in static processing, due to the fact that the solutions are significantly worse in kinematic mode, therefore leaving more room for improvement. At the 100-percentile in kinematic mode, the dual-frequency float solution converges in 61 min compared to 41.5 min for the fixed solution, leading to a 32\(\%\) improvement. These values are bigger than the static case where the float and fixed solutions converged in 18.5 min and 14.5 min, respectively, with an improvement of 22\(\%\). In terms of accuracy, the float and fixed horizontal accuracies in kinematic mode are 7.4 cm and 4.4 cm, respectively, compared to 2.7 cm and 1.1 cm, respectively, for the static processing. With three frequencies, the kinematic float solution converges in 50.5 min, while the fixed one converges in 20 min, as opposed to 16.5 min and 9.5 min in static mode. The reduction of the convergence time to 20 min is a significant improvement, as it is over half the convergence time of the dual-frequency fixed solution, showing the importance of fixing ambiguities on multiple frequencies.

Looking at Fig. 17, one can see that there are big improvements between the different percentiles, especially when comparing the 95-percentile and the 67-percentile. The reason behind this improvement is that the kinematic processing is more sensitive to the PDOP and the number of satellites than the static processing, especially after convergence. Indeed, in static processing, if the number of satellites drops to a low number leading to a high PDOP, the position estimates would not be majorly affected if such scenario happens after convergence, as the position of the receiver would be averaged based on previous epochs. On the other hand, in kinematic processing, a drop in the number of satellites would directly lead to a worse position estimate as the position states are estimated every epoch based on the received measurements. Figure 11 shows that several epochs have high PDOP, which affect the performance of the kinematic processing. Therefore, when looking at lower percentiles, those epochs when the PDOP is high get eliminated, leading to significant performance improvements. This enhancement is even more significant for the 67-percentile, as an additional 28\(\%\) of (bad) data are removed compared to the 95-percentile. Given that this issue is caused by the bad geometry at some epochs, it is expected that processing multiple constellations instead of only Galileo would lead to more consistent performance across datasets, as the epochs would have more satellites to process, and therefore better geometry.

Fig. 15
figure 15

Kinematic dual- and triple-frequency horizontal vertical error based on all datasets at the a 100th, b 95th, c 67th and d 50th percentiles. Horizontal dashed lines represent the convergence threshold

Full size image
Fig. 16
figure 16

Kinematic dual- and triple-frequency average vertical error based on all datasets at the a 100th, b 95th, c 67th and d 50th percentiles. Horizontal dashed lines represent the convergence threshold

Full size image
Fig. 17
figure 17

a Average horizontal convergence times, b horizontal and c vertical RMS for both dual- and triple-frequency solutions at different percentiles in kinematic mode

Full size image

7 Conclusions and future work

The benefit of ambiguity resolution to PPP has been the subject to recent research and it has proved to improve the float PPP solutions in most cases. In this paper, an uncombined multi-frequency AR model is proposed that is based on the combined Decoupled Clock Model. The proposed model has been derived step by step for both the dual-frequency and triple-frequency cases starting from the general PPP equations. It is derived in uncombined mode, which means that it can be easily scaled to four or five frequencies as Galileo broadcasts five frequencies in total. In this model, the code and phase clocks are decoupled similarly to the original DCM. The datum in the phase measurements is then set to the reference satellite’s ambiguities instead of the receiver clock. This datum change is due to the receiver biases being eliminated through implicit differencing, as opposed to explicit diffencing: no assumptions were made regarding the behaviour of receiver biases that get lumped into an additional phase term receiver WL bias \(\delta t_{12}\) and receiver EWL bias \(\delta t_{13}\). Therefore, variations in the receiver biases are estimated in the additional phase terms. The receiver biases are shown to be relatively stable over the course of a day for a sample dataset, with variations of up to 2 ns. The additional WL and EWL receiver biases were shown to be dependent on the choice of reference satellite, unlike the Inter-Frequency Bias, which is absolute and only depends on the receiver code biases.

The advantage of AR is shown for both the dual- and triple-frequency cases. Dual-frequency AR improved the horizontal convergence time of the 100th percentile average result from 18.5 to 14.5 min for the large global IGS dataset assessed, and the 3-h horizontal RMS from 2.7 to 1.1 cm. These improvements are significant and are also valid for individual stations. These results are improved even further by moving to the triple-frequency mode. Although no significant benefit comes from the addition of the float third frequency, performing triple-frequency AR leads to an average solution that converges within 9 min with a horizontal RMS of 1.1 cm. Fixing the additional frequency does not provide major improvements to the final accuracy, but it helps immensely in decreasing the convergence time which is one of the biggest hurdles preventing the wider use of PPP.

Seeing that all the Galileo satellites broadcast all three frequencies that were used in this processing, and wanting to have a fair comparison between the dual- and triple-frequency results, only the Galileo constellation was used in this research. The results presented can be improved by taking into account other constellations. It is expected that adding other constellations will improve the accuracy as well as the convergence time. Indeed, one of the benefits of having additional satellites from other constellations, on top of improving the satellite geometry and increasing the number of measurements, would be to improve the precision of the estimated float ambiguities, therefore leading to a better fixing. Future work also includes expanding the model to more frequencies and processing data using corrections provided through the Galileo High Accuracy Service (HAS), once the service is available.