1 Introduction

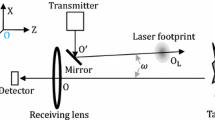
Geometric modeling in airborne LiDAR bathymetry is significantly more complex than in conventional laser scanning since the laser pulse is passing two different optical media, separated by a non-planar instationary interface. Figure 1 shows the LiDAR bathymetry pulse propagation with interactions at water surface, water column, and water bottom.

Fig. 1
figure 1

LiDAR bathymetry pulse propagation adapted from Guenther (1985)

Full size image

At the water surface, a part of the incident laser pulse is reflected back to the sensor. The remaining part passes the air-water interface and propagates through the water column. Due to the different refraction indices, the direction and velocity of the laser pulse propagation changes. The underwater path of the laser pulse is characterized by single and multiple scattering processes at water molecules, small sedimentary particles, and organic materials. Scattering causes a continuous widening (beam spreading) of the laser beam cone, resulting in a curved generating line of the cone (Guenther et al. 2000). Additionally, scattering affects the run-time of the laser pulse (pulse stretching) and influences the distance measurement under water (Guenther 1986). On the one hand, scattering causes detours in the light path and thus an extension of the measured pulse propagation time. On the other hand, it is even possible that reflected photons find a shortcut into the receiver’s field of view (undercutting path, Fig. 1) and thus contribute to a shortening of the measured pulse propagation time. The size of the effect depends on the nadir angle as well as on the water depth and turbidity.

At the water bottom, a portion of the laser pulse is reflected back into the water column. As usual in ALB, a diffuse reflection (Lambertian distribution) is assumed (Guenther 1986). The returning laser pulse is again exposed to scattering processes in the water column and refracted at the water-air interface once more. In contrast to conventional airborne laser scanning, the return path of the pulse echo does not necessarily correspond to the outgoing path. As shown in Fig. 1, diffusely reflected signal components (dashed arrows) can also reach the receiver if they intersect the water–air interface at a location outside the actual field of view with suitable wave inclination. Such beams have usually made a detour. However, it has been shown that beam paths can even take a shortcut (e.g. in the case of diffuse reflection and refraction in a nadir-sided wave trough) (Guenther 1985). All in all, these effects lead to a smearing of the ground pulse echo in the digitized pulse signal, which cannot assumed to be symmetrical and may thus influence the distance measurement.

To achieve an accurate geometric representation of the water bottom, the following effects have to be considered in ALB data processing:

  • refraction and change of propagation speed

  • scattering processes in the water column

  • diffuse reflection at the water bottom

As it is obviously not possible to reconstruct the path of every single photon, a geometric model of the laser bathymetry pulse propagation is required. It comprises models for laser ray, water surface, scattering, and diffuse reflection and provides the basis for geometric corrections, e.g. the refraction correction. Related work on geometric modeling is presented in Sect. 1.1. Section 1.2 highlights the contribution of the paper.

1.1 Related Work

Conventional modeling approaches neglect both scattering and diffuse reflection and use simple models for laser ray and water surface. A common model conception is visualized in Fig. 2. Usually, the laser ray is geometrically modeled as a straight line, thus neglecting effects caused by beam divergence and the finite laser pulse penetrating a curved water surface.

Fig. 2
figure 2

Conventional model conception for laser bathymetry pulse propagation with narrow laser ray refracted at triangulated water surface model and identical outgoing and return path

Full size image

Basically, a water surface model can be derived from the available water surface reflections of the laser pulses. The movement of the water surface during the sequential scanning of a surface area by the laser scanner can be neglected. The consideration as local snapshotFootnote 1 is justified with regard to the high measurement rate of modern airborne laser scanner systems. The measurement rate of common deep water systems is 3–\(40 \hbox { kHz}\) resulting in point densities of \(\le 2\) points/\(\hbox {m}^2\). Topo-bathymetric scanners and the shallow water channels of deep bathymetric scanners allow for high resolution water surface mapping. High measurement rates of up to 700 kHz result in point densities of around 20 points/\(\hbox {m}^2\) (Mandlburger 2020). For water surface modeling, water surface points immediately adjacent in time and points of neighbouring scan circles can be used. The accuracy of the modeled water surface depends on the conditions of data acquisition (scan resolution, complexity of the wave pattern, data gaps, flight mission parameters) as well as on the modeling method. Conventional methods for modeling the water surface are based on a major simplification of the water surface geometry. The simplest assumption is a horizontal planar water surface, at which the laser ray is refracted. More complex modeling methods try to consider the actual geometry of the water surface by connecting the detected water surface points to a triangular mesh (Ullrich and Pfennigbauer 2011).

Laser ray model and water surface model are prerequisites for refraction modeling. The laser pulse is traveling from air with a refractive index \(n_1\) close to 1.0 into the water body with a refractive index \(n_2\). After passing the media interface, the laser pulse is slowed down and refracted towards the surface normal. The changes in propagation direction and run-time are described by Snell’s law:

$$\begin{aligned} \frac{\sin \alpha _1}{\sin \alpha _2}=\frac{v_1}{v_2}=\frac{n_2}{n_1}. \end{aligned}$$
(1)

The sine of the incidence angle \(\alpha _1\) and the refraction angle \(\alpha _2\) correspond to the relation of the velocities \(v_1\) and \(v_2\) in the two media and to the reciprocal relation of the refractive indices. The refractive index \(n_2\) depends on water temperature, depth, and salinity; see e.g. (Höhle 1971). Conventional refraction correction methods assume a constant value of \(n_2=1.33\) for direction and range calculation (Schwarz et al. 2020).

The deviation between actual laser pulse propagation and conventional geometric modeling may cause considerable coordinate errors at the water bottom. The impact of the introduced simplifications on the water bottom point coordinates have been investigated in previous studies (Westfeld et al. 2017; Richter et al. 2018). We developed a laser bathymetry simulation tool to simulate data acquisition for arbitrary wave conditions, recording constellations, and sensors. In the simulation approach, the refraction of finite diameter laser pulses passing the air–water interface is modeled differentially in a strict manner. The simulated measurement data are used to examine different geometric modeling conceptions. The comparison of the reference bottom point coordinates resulting from simulation and the bottom point coordinates resulting from geometric modeling allows the prediction of coordinate errors which have to be expected due to the assumptions made in the geometric modeling approaches. Table 1 (column 2 and 3) provides an overview of the simulations performed in Westfeld et al. (2017) and Richter et al. (2018) and the geometric modeling conceptions studied. In Westfeld et al. (2017), both large footprint systems and small footprint systems are considered, while Richter et al. (2018) focus on small-footprint systems. Westfeld et al. (2017) have shown that, depending on the sea state, beam divergence, and water depth, the effect on lateral bottom point displacement can amount several decimeters, in some cases even meters, in the planimetry coordinates of underwater points. The effect on the height coordinate is in the decimeter range. Even with more complex water surface models, the deviations between the true water surface and the representation by the triangular mesh lead to coordinate errors at the water bottom (Richter et al. 2018).

Table 1 Overview of previous work and current contribution
Full size table

Beam spreading and pulse stretching due to scattering at water molecules, small sedimentary particles and organic materials during the propagation of the laser pulse through the water column are not considered in conventional modeling approaches so far. For modeling the effects, there are basically two different approaches: analytical calculation and numerical simulation.

The analytical calculation is based on the LiDAR equation, which links transmitted and received optical power. There are numerous variants in different levels of complexity, containing different parameters based on different assumptions and simplifications (Kashani et al. 2015). In the conventional LiDAR equation, beam spreading and pulse stretching are not considered. More complex variants also take beam expansion into account (Luchinin 1987; Kondranin and Yurin 1973). Walker and McLean (1999) present a fully analytical LiDAR equation for turbid media, which includes both beam spreading and pulse stretching. The basic idea is to define an analytical function for the beam spreading and the change in laser pulse travel time. Several simplifications are introduced to make the extended LiDAR equation useful for practical applications.

Alternatively, the complex interaction between laser pulse and water can be investigated in a numerical simulation (Monte Carlo simulation, e.g. Guenther (1985) and Harsdorf and Reuter (2000)). Since ray tracing based Monte Carlo simulation considers the propagation of each photon separately, beam spreading and pulse stretching are inherently taken into account. The approach can provide a solution for the propagation of a laser pulse in a turbid medium that is free of any assumptions. The simulation of the outgoing and return path of each photon, however, requires enormous computing power. For this reason, many approaches neglect pulse stretching and introduce the assumption that outgoing and return paths are statistically equal. In a Monte Carlo simulation, the properties of the water column are used as input variables, e.g. the attenuation coefficient, the ratio of scattering and absorption, and the probability that a photon will be scattered in a certain direction. The numerical simulation provides the spatial and temporal distribution of the photons of an emitted laser pulse after the outgoing and return path through the water column. From this, the signal received at the detector as well as information about the extent of the beam spreading can be derived. The comparison with the propagation of a laser pulse in a scattering-free system allows statements on the systematic errors of the bottom point coordinates. The numerical simulation is based on the separate observation of the beam path of each individual photon in the laser pulse and applies to the specific parameters selected as input variables.

Furthermore, Schwarz et al. (2020) present an approach in which the propagation time extension due to scattering effects is considered by using the group velocity instead of the phase velocity for range calculation. The slower group velocity represents the propagation speed of a laser pulse in a dispersive medium and was determined experimentally. In the study, the range dependent bias of the depth measurement was reduced by more than \(1.5\%\). However, recent studies show that systematic depth dependent errors due to multi-path effects within the water column remain in the data set (Mandlburger et al. 2020; Schwarz et al. 2019).

1.2 Contribution

The aim of our study is to develop a refined geometric modeling approach, which allows a better consideration of the true geometry of the laser ray and the water surface as well as the diffuse reflection at the water bottom. For this purpose, we extend the geometric models presented in Westfeld et al. (2017) and Richter et al. (2018) to a divergent laser ray model and a freeform water surface model (Table 1, last column). Furthermore, we consider the return path of the laser pulse. Section 2 presents the developed model conception.

The geometric model is based on partial beams, which combine thousands of photons. Therefore, the modeling of the scattering processes in the water column must be done for sub-beams. This is not possible with methods referring to single photons. Therefore, the findings from analytical calculations and numerical simulations presented in Sect. 1.1 cannot be transferred to the developed model conception. The approach of Schwarz et al. (2020) represents a promising alternative. However, it is not yet implemented in this contribution.

The impact of geometric modeling on the bottom point coordinates is investigated using the LiDAR bathymetry simulation tool developed in previous studies (Westfeld et al. 2017; Richter et al. 2018). Both conventional and refined modeling approaches are examined. For this purpose, the developed model extension was integrated in the existing software (Sect. 3). The software allows the simulation of a LiDAR bathymetry flight with various recording configurations, sensors, and wave conditions. In our study, the focus is on small-footprint systems. As described in Sect. 4, different wave patterns corresponding to wind force 1–5 on the Beaufort scale were considered.

The results of the investigations presented in Sect. 5 show that the complexity of water surface modeling has a direct influence on the accuracy of the water bottom points. The higher the sea swell, the more important is an accurate representation of the true water surface geometry. A better water surface approximation leads to smaller coordinate errors at the water bottom. The coordinate displacement can be further reduced using the enhanced laser ray model, which considers the beam divergence. The results of the diffuse reflection modeling also show a dependence on the sea swell and are the basis for the derivation of correction terms.

2 Geometric Model

The geometric model describes the interaction of the divergent laser pulse with the curved water surface, the water column, and the water bottom. For this purpose, models for laser ray, water surface, refraction, and diffuse reflection at the water bottom are built up. The model conception is shown schematically in Fig. 3 and described in detail in Sects. 2.1–2.4.

Fig. 3
figure 3

Enhanced model conception for laser bathymetry pulse propagation with divergent laser beam refracted at curved water surface model and diffuse reflection at the water bottom

Full size image

2.1 Laser Ray Modeling

The laser beam divergence is considered by dividing the laser ray into a large number of sub-beams, which represent a finite diameter laser footprint at the water surface and the water bottom. The sub-beams are arranged in a regular pattern. The intensity distribution within the incident laser pulse follows a Gaussian intensity profile (Beraldin et al. 2010). The irradiance I is symmetric about the pulse axis and varies with a radial distance r until the outer profile is reached at r=\(r_{max}\):

$$\begin{aligned} I(r)=I_0\cdot e^{-2r^2/r_{\max }^2}, \end{aligned}$$
(2)

With \({I_0}=100\%\) the irradiance is \(100\%\) at the center of the laser pulse (\(I(0)=I_0\cdot e^{0}\)) and \({13.5}{\%}\) at the outer profile (\(I(r_{\max })=I_0\cdot e^{-2}\)).

2.2 Water Surface Modeling

As shown in Fig. 4a and b, conventional modeling methods with horizontal and locally tilted water surface elements simplify the water surface geometry considerably. As a consequence, the information on the local water surface inclination required for refraction correction is not accurate. To overcome this limitation, we use freeform surface modeling to improve the approximation of the true water surface geometry as shown in Fig. 4c. The shape of a freeform surface is defined by control points approximated by piecewise continuous functions, e.g. Hermitian polynomials, Bézier curves, B-Splines, or Non-Uniform Rational B-Splines (NURBS) (Goldman 2009).

Fig. 4
figure 4

Water surface modeling with horizontal water surface elements (a), locally tilted water surface elements (b) and freeform surface (c)

Full size image

In our approach we use B-Splines, which provide a high degree of control flexibility and a fine shape control, to approximate the given water surface points. The freeform surface S(u, v) is described by the following equation with the points \(P_{i,j}\) of the control grid and the B-Spline functions \(N_{i,p}(u)\) and \(N_{j,q}(v)\) (Grimm-Pitzinger and Rudig 2005):

$$\begin{aligned} S(u,v)=\sum \limits _{i=0}^n\sum \limits _{j=0}^m N_{i,p}(u) \cdot N_{j,q}(v) \cdot P_{i,j}. \end{aligned}$$
(3)

The parameters p and q describe the degree of the basic functions and do not have to be identical. The control points \(P_{i,j}\) are determined in a least squares adjustment in such a way that the resulting freeform surface approximates the given water surface points by a double curved surface.

2.3 Refraction Modeling

The refraction is modeled by Snell’s law by considering each sub-beam of the laser ray model separately. The water surface model enables the derivation of information on the local water surface slope and the resulting water surface normal. By intersecting the modeled laser ray with the water surface model, the local incidence angle \(\alpha _1\) between laser ray and water surface normal can be determined. Subsequently, the refraction angle is calculated based on the refractive index \(n_2=1.33\). At the moment, the same refractive index is also used for the speed of light correction.

2.4 Diffuse Bottom Reflection Modeling

After the propagation through the water column the laser pulse hits the water bottom. As stated in Guenther (1986), for coastal waters 4–\({15}{\%}\) of the incident energy is reflected back into the water column, depending on the reflection properties of the water bottom. The reflection occurs in a more or less diffuse way. In our approach, the interaction of the refracted laser ray with the water bottom is described by a diffuse bottom reflection model. The model assumes an ideal diffuse reflection, i.e. the bottom of the water body is considered a Lambertian scatterer. The incident laser pulse is reflected into the hemisphere, resulting in a homogenous distribution of the radiant intensity. For this purpose, a new beam bundle is defined for each sub-beam of the laser ray model (Fig. 5). To cope with the computational effort we limit the opening angle of the beam bundle to \({135}{^{\circ }}\) instead of \({180}{^{\circ }}\). The direction vectors of the reflected laser rays are defined using the elevation angle in the range of \(\pi /8\) to \(\pi /2\) and the azimuth angle in the range of 0–\(2\pi \). The number of elevation angle steps is set to 100 resulting in a step width of \(\frac{3}{8} \pi /100\). The number of azimuth angle steps depends on the elevation angle in order to realize equal distances in azimuth and elevation direction. This results in an even division of the beam bundle cone into reflected beams. For each beam of the bundle, the signal return path is modeled separately including the refraction at the water–air interface. The movement of the water surface between the refraction on the outgoing and return path can be neglected because the time offset between the two interactions is very small (e.g. \({89}\hbox { ns}\) at a water depth of \({10}\hbox { m}\)). As the waves move much slower, the water surface can be assumed to be static. As shown in Fig. 5, the returning beam paths spread out widely in all directions in the water column and are refracted into the entire hemisphere of the air. Only a part is covered by the receiver’s field of view.

Fig. 5
figure 5

Diffuse reflection at the water bottom

Full size image

3 LiDAR Bathymetry Simulation Tool

The numeric simulation of laser bathymetry measurement data includes modeling of the water surface, water bottom, platform movement, scanning mechanism, laser beam divergence, refraction at the water surface, and diffuse reflection at the water bottom. Figure 6 gives an overview of the simulation tool’s processing pipeline.

Fig. 6
figure 6

Overview LiDAR bathymetry simulation tool

Full size image

For water surface modeling we use Tessendorf’s oceanographic statistics based surface wave model for ocean waves (Tessendorf 2001), which is often used for rendering water surfaces in computer graphics. The model treats each wave height as a random variable of its planimetric position at a given time. Based on Tessendorf’s model, a height field is generated by means of Fast Fourier Transform (FFT). The height field represents a realistic ocean surface in form of a dense regular grid and can be modified by different parameters (e.g. grid width of the Fourier transformation, wind speed, wind direction). The bottom surface is assumed horizontal with a roughness defined by the user. The platform movement is modeled as a uniform linear translation with constant course angles. Conical scanning with a circular point pattern on the ground (i.e., Palmer scanner) is commonly used in laser bathymetry and therefore also as basis for this simulation. Scan speed, angular step size, and pulse repetition rate are selected according to the specifications of common LiDAR bathymetry systems. The modeling of beam divergence, refraction, and diffuse reflection is based on the geometric models introduced in Sects. 2.1, 2.3, and 2.4.

The simulation is performed in discrete time steps whose time interval is determined by the pulse repetition rate. Between two simulation steps, water surface waves, scan platform, and scanning mechanism move on. Thus, one simulation step is performed for each emitted laser pulse comprising the following processing steps:

  1. 1.

    set up of laser ray model with current platform position and scan direction

  2. 2.

    extraction of current water surface based on Tessendorf’s model

  3. 3.

    intersection of laser ray model (sub-beams) and water surface

  4. 4.

    calculation of final water surface point represented by the intensity-weighted centroid of all sub-beam intersection points

  5. 5.

    estimation of local water surface inclination

  6. 6.

    refraction modeling for each sub-beam according to Snell’s law

  7. 7.

    intersection of refracted sub-beams with water bottom

  8. 8.

    calculation of final water bottom point represented by the intensity-weighted centroid of all sub-beam intersection points

  9. 9.

    set up of diffuse reflection model for each sub-beam

  10. 10.

    intersection of diffuse reflection model (sub-beams) and water surface

  11. 11.

    refraction modeling for each sub-beam according to Snell’s law

  12. 12.

    analyzing of return path with respect to receiver field of view

The processing steps result in simulated LiDAR bathymetry measurement data with water surface points and water bottom points. In contrast to a real measurement campaign, the local wave-induced water surface is exactly known. Additionally, information on the return path of the signal is available from the diffuse reflection modeling.

4 Experiments

The LiDAR bathymetry simulator presented in Sect. 3 allows the simulation of LiDAR bathymetry flights with various recording configurations, sensors, and wave conditions. In our study we performed 20 simulations with different sea swells and common beam divergence values. Table 2 gives an overview of the considered wave patterns corresponding to wind force 1–5 on the Beaufort scale. The parameters for the water surface modeling according to Tessendorf (2001) were chosen in such a way that the characteristics of the resulting wave pattern approximate the corresponding wave heights and sea conditions. The beam divergence was varied between \({0.5}{\hbox { mrad}}\), \({1}{\hbox { mrad}}\), \({2}{\hbox { mrad}}\), and \({3}{\hbox { mrad}}\), allowing for very small as well as larger laser footprints with elliptic diameters of 0.25–\({1.5}{\hbox { m}}\) at the water surface. The employed beam divergences are representative for shallow bathymetry ALB channels. The aircraft altitude was fixed at \({500}{\hbox { m}}\), which is a common altitude for airborne bathymetry campaigns. The depth of the water was \({1.6}{\hbox { m}}\). The constant off-nadir angle in the circular scanning pattern was \({20}{^{\circ }}\). In each simulation, a \({20}{\hbox { m}} \times {20}{\hbox { m}}\) area was scanned, which corresponds to 2400 laser shots. To keep the computational effort practicable we use 61 subbeams for laser ray modeling. Please note that the number of sub-beams is equal for all beam divergences resulting in a varying resolution of the laser ray models. For diffuse reflection modeling, a bundle of approximately 16,000 beams per sub-beam was used. This results in a total of \(61*16,000\approx {1}\hbox { Mio}.\) reflected beams for each laser shot. Due to this high number the diffuse reflection was only modeled for one laser pulse per type of wave pattern and solely for a beam divergence of \({0.5}{\hbox { mrad}}\). The modeling of the refraction at the water–air surface was done at the simulated water surface.

Table 2 Sea states based on the Beaufort scale (Huler 2007)
Full size table

The simulated LiDAR bathymetry measurement data is used to investigate the effect of water surface modeling, laser ray modeling, and diffuse reflection modeling on the bottom point coordinates. For this purpose, we use the simulated water surface points to model the water surface with the developed enhanced modeling approach. For comparison purposes, the water surface is modeled by conventional modeling approaches with horizontal and locally tilted water surface elements as well. The horizontal water surface elements are realized by defining a locally horizontal water surface element with wave-dependent height at each water surface point. The height of the water surface element is equivalent to the height of the corresponding water surface point. To model the water surface with locally tilted water surface elements, we perform a Delaunay triangulation resulting in a triangle mesh. The triangles represent the locally tilted water surface elements. Since the local water surface inclinations required for refraction correction cannot be determined at the vertices of the triangles, the triangle mesh is resampled in a regular grid at high resolution. The coordinates of the grid points are determined by linear interpolation in the triangle mesh.

To evaluate the modeling approaches, the resulting water surface models are compared with the simulated water surface according to Tessendorf (2001), which serves as a reference. Since the waves continue to move during the scanning process in the simulation, the comparison refers to the local environment around each scanned water surface point at the individual simulation step.

Subsequently, refraction is modeled for the different water surface models and for both narrow and divergent laser rays as described in Sect. 2.3. In case of the narrow laser ray model, the bottom point coordinates are calculated by polar point determination using the intersection point at the water surface, the refraction angle, and the distance covered in the water column, which is known from the simulation. In case of the divergent laser ray model we repeat this procedure for each sub-beam, i.e. the same distance is assumed for each sub-beam. The larger the beam divergence, the less true this assumption is. The discrepancy between assumed distance and individual distance of each sub-beam results in a depth offset. Since the individual distances are unknown, this effect must be accepted. The final bottom point coordinates are represented by the intensity weighted centroid of all determined coordinates. The comparison of the resulting bottom point coordinates with the simulated reference bottom point coordinates allows an analysis of the effect of water surface modeling and laser ray modeling on the coordinate displacements at the water bottom.

Finally, we analyze the return path of the signal. At first we determine all reflected beams of the diffuse reflection model, which are captured by the receiver field of view. For this purpose, the reflected beams are intersected with the detector plane and the distance between the intersection point and the center of the detector is calculated. For the following investigations we consider all signal return paths whose distance to the center of the detector is less than \({2}{\hbox { m}}\). The impact of diffuse reflection on the ground point coordinates can be quantified by the analysis of the covered distances in water and air. In comparison to identical outgoing and return paths, deviating return paths cause parts of the signal to arrive earlier or later at the detector than the main portion of the signal. This influences the shape of the received signal and, in further consequence, the detection of the water bottom echoes in the signal. As a result, the bottom point coordinates contain errors.

5 Results and Discussion

In this section we present the results of the conducted experiments. Section 5.1 examines how well the simulated water surface is approximated by the different water surface models. Subsequently, in Sect. 5.2, we consider the impact of water surface modeling and laser ray modeling on the accuracy of the bottom point coordinates. Finally, the results of the diffuse reflection and return path modeling are presented in Sect. 5.3.

5.1 Evaluation of Water Surface Modeling

Based on the simulated water surface points, the water surface is modeled in different levels of complexity for all 20 simulated measurement data sets (Sect. 4). Figure 7 shows the resulting water surface models (grey) as well as the simulated reference surface (black) at wind force 3 and a laser beam divergence of \({0.5}{\hbox { mrad}}\). Water surface model and simulated reference surface differ both in height and inclination. The height and inclination deviations affect refraction modeling and calculation of the water bottom points, resulting in a coordinate displacement at the water bottom. Subsequently, the height deviations are analyzed. The differences in the local water surface inclination are considered in Sect. 5.2.

Fig. 7
figure 7

Simulated reference surface (black) and modeled water surface (grey) for water surface modeling with horizontal water surface elements (a), locally tilted water surface elements (b), and freeform surface (c)

Full size image

The deviations between simulated water surface according to Tessendorf (2001), which serves as a reference, and water surface model based on simulated scan data can be easily determined by calculating the differences of the respective height fields. However, only those areas are relevant for the comparison, which are used for refraction modeling later. Therefore, the investigation of the deviations is performed only in the area of the laser footprints. As an example, Fig. 8 shows the deviations between reference water surface (i.e. simulated water surface according to Tessendorf (2001)) and freeform water surface model for all five considered wave patterns and a laser beam divergence of \({0.5}{\hbox { mrad}}\). For wind force 1, most of the deviations are within \(\pm {10}\hbox { mm}\). With raising wind force the complexity of the wave patterns increases, resulting in higher deviations between model and reference. For wind force 5, the majority of deviations exceed the range of \({10}{\hbox { mm}}\). The largest deviations occur at the wave crest, which runs from top left to bottom right through the simulated area. Table 3 summarizes the results for all water surface models, wind speeds, and beam divergences. For each wind force the results for horizontal water surface elements (h), locally tilted water surface elements (t), and freeform surface (f) are presented in separate lines. The root mean square (RMS) values are printed in bold.

Fig. 8
figure 8

Deviation between simulated water surface according to Tessendorf (2001) and freeform water surface model in the area of the scanned water surface points, (a)–(e) correspond to wind force 1–5

Full size image
Table 3 Deviations between reference and modeled water surface in mm (h = horizontal water surface elements, t = locally tilted water surface elements, f = freeform water surface)
Full size table

The analysis of the minimum and maximum deviations and the RMS values shows that the characteristics of the waves (size, shape, steepness etc.) have a great influence on the deviations between reference water surface and modeled water surface. Higher undulation of the water surface clearly decrease the accuracy of the modeled water surface. At wind force 1, the RMS values vary between 10.9 and \(12.9\hbox { mm}\). At wind force 5, they an order of magnitude larger with values from 93.5 to 189.8 mm. The beam divergence influences the footprint area in the simulated scanning process as well as the footprint area included in the calculation of the deviations. However, no specific pattern can be recognized in the resulting RMS values. The impact of the water surface modeling approach must be considered in a differentiated way. For wave patterns with a wave height of 0.1–\({0.2}{\hbox { m}}\) (wind force 1 and 2), the simulated water surface is represented equally well by all water surface models independent of the modeling method. The minimum and maximum deviations between reference and model as well as the RMS values have a comparable magnitude. For wave patterns with a wave height of \({0.6}{\hbox { m}}\) and higher (wind force 3–5), the modeling method significantly influences how well the simulated water surface is approximated by the model. The results show that the reference water surface is approximated best by the freeform surface.

5.2 Impact of Water Surface and Laser Ray Modeling

The impact of water surface modeling and laser ray modeling on the coordinate displacements at the water bottom is analyzed by comparing the bottom point coordinates resulting from the geometric modeling with the simulated reference bottom point coordinates. The following cases were considered:

  • water surface model with horizontal water surface elements, laser ray model with narrow laser ray (horizontal case)

  • water surface model with locally tilted water surface elements, laser ray model with narrow laser ray (tilted case)

  • water surface model with freeform surface, laser ray model with narrow laser ray (freeform case)

  • water surface model with freeform surface, laser ray model with divergent laser ray (divergent case)

The coordinate displacements at the water bottom consist of the lateral component dXY and the depth component dZ. The lateral and depth components indicated in the following refer to a horizontal water bottom. In case of changing topography, lateral displacements also result in depth errors. Furthermore, the influence on the Z-component can be significantly higher for inclined water bottom due to beam divergence and terrain representation errors. In addition to the individual components, the 3D displacement dXYZ is reported. Since the coordinate displacements increase linearly with the water depth, all results are expressed in percentage of the water depth.

First of all, we present the results in detail using the example of wind force 3. In the following, special effects at other wind forces are discussed. Figure 9 shows the RMS values of the lateral, depth, and 3D coordinate displacements at the water bottom for all investigated cases (horizontal, tilted, freeform, and divergent) and beam divergences (\({0.5}\hbox { mrad}\), \({1}{\hbox { mrad}}\), \({2}{\hbox { mrad}}\), and \({3}{\hbox { mrad}}\)).

Fig. 9
figure 9

RMS coordinate displacements for wind force 3 in percentage of the water depth (left y-axis) and in meters for a water depth of 5 m (right y-axis)

Full size image

The lateral displacement dXY varies between 4.1 and \({12.4}\,{\%}\) of the water depth depending on the water surface and laser ray model and the beam divergence. For small beam divergences from 0.5 to \({1}{\hbox { mrad}}\), the lateral coordinate displacement decrease with increasing complexity of water surface representation and laser ray modeling. With increasing beam divergence, the tilted and freeform methods sometimes give worse results than the horizontal method. However, the divergent method is always superior to the others. When evaluating the results we have to consider the different resolution of the laser ray models during the simulated scanning process. This also applies to the depth component.

The depth component dZ is generally smaller than the two lateral components. Depending on the modeling method and beam divergence, the RMS value varies between 1.5 and \({7.3}\,{\%}\) of the water depth. Due to the principle of refraction modeling in our experiment (Sect. 4), the divergent laser pulse results in larger depth displacements than the other methods. Since the height component has a high importance in laser bathymetry, the poorer performance of the divergent method in Z-direction is explicitly pointed out here. As the lateral component dXY is dominating, the divergent method still performs best for the 3D displacement presented in Fig. 9c (with exception of beam divergence \({3}{\hbox { mrad}}\)).

The absolute coordinate displacements at the water bottom are visualized in Fig. 10 for a beam divergence of \({1}{\hbox { mrad}}\). The coordinate displacements are displayed separately for the lateral components dXY and the depth component. Each point represents one of the simulated water surface points. The colour coding corresponds to the coordinate displacement at the water bottom. The simulated water surface patch contains smooth areas (left and right) as well as waves (middle) with an amplitude of \({0.6}{\hbox { m}}\). The corresponding wave pattern is shown in Fig. 7. The colour gradient clearly shows the effect of water surface modeling and ray path modeling on the resulting bottom point coordinates with large absolute coordinate displacements for the water surface modeling with horizontal water surface elements and narrow laser ray model, medium displacements for locally tilted water surface elements and freeform water surface model and minimum displacements for freeform water surface and divergent laser ray model. For each modeling method the largest absolute coordinate displacements occur at the wave crest, where the deviations between the water surface models and the simulated water surface are maximal.

Fig. 10
figure 10

Absolute displacements in mm for beam divergence \({1}{\hbox { mrad}}\) and wind force 3

Full size image

After the detailed analysis of the results for wind force 3, the results of the remaining wind forces are discussed now. Figure 11 shows the RMS values of the 3D coordinate displacement at the water bottom for wind force 1, 2, 4, and 5. For ripples and small wavelets with a wave height of 0.1–\({0.2}{\hbox { m}}\) present at wind force 1 and 2, the different geometric models provide very similar results. However, the simplest geometric modeling method with horizontal water surface elements and a narrow laser ray model results in slightly smaller RMS values for the coordinate displacements at the water bottom compared to the other methods. For small and moderate waves with wave heights of 1–\({2}{\hbox { m}}\) at wind force 4 and 5 the previous finding that the freeform water surface model and divergent laser ray model are most suitable for geometric modeling is confirmed. For wind force 5 and a beam divergence of \({0.5}{\hbox { mrad}}\), for example, the RMS value can be reduced from \({23.3}{\%}\) for the horizontal method to \({16.1}{\%}\) for the divergent method. With larger beam divergences, the reduction of the 3D displacements decreases.

Fig. 11
figure 11

RMS of 3D coordinate displacements for wind forces 1, 2, 4, and 5

Full size image

5.3 Results of Diffuse Reflection Modeling

The diffuse reflection modeling (light path from the water bottom through the water column back to the water surface and to the receiver) results in \({1}{\hbox { Mio}}.\) reflected laser beams per simulated laser shot. For each wave pattern one laser shot was modeled for a beam divergence of \({0.5}{\hbox { mrad}}\). As described in Sect. 4, only the signal return paths covered by the receiver field of view are considered in the further analysis. Only a very small portion out of the large number of modeled signal return paths reaches the detector. At lower and middle wind forces (1–3) at least five reflected laser beams are within the receiver field of view. At higher wind forces (4–5) this applies only to one laser beam at a time. The results of diffuse reflection modeling are summarized in Fig. 12.

Fig. 12
figure 12

Results of diffuse reflection modeling for wind force 1–5 with footprint at the water bottom (relevant sub-beams in red, reference water bottom point in blue), histogram distances way back in water and histogram distances way back in air

Full size image

The first column shows the footprint of the laser ray model at the water bottom. The intersection points of the 61 considered sub-beams at the water bottom are visualized in grey. The intensity-weighted centroid of all bottom points representing the simulated bottom reflection is delineated by a blue marker. Intersection points where the diffuse reflection modeling results in a relevant return path to the receiver are shown in red. They are located both near the simulated bottom points as well as at the margin of the footprint. A correlation between the successful return path to the receiver and the position of the sub-beam within the footprint at the water bottom cannot be established.

The last two columns of Fig. 12 show the distances covered in water and air on the return path of the reflected laser beams. For comparison purposes, the distances for the outgoing path of the signal are additionally indicated as dashed red lines. They are derived from the distances between origin of the laser pulse emission, simulated water surface point, and simulated water bottom point. The histograms for the return path in the water body shown in column 3 demonstrate that the reflected laser beams mostly cover a longer distance compared to the outgoing path. The deviation to the outgoing path is 0.02–\({2.85}{\hbox { m}}\) extending the signal run time by 0.1–\({13}{\hbox { ns}}\). The histogram of wind force 5 shows that shorter signal paths can also occur as stated in Guenther (1985). The reflected laser beam travels only \({1.43}{\hbox { m}}\) in the water column instead of \({1.51}{\hbox { m}}\), which results in a run time reduction of \({0.3}{\hbox { ns}}\). On the way back through the air, both longer and shorter distances are covered. At wind force 1 the distances differ between \({-0.29}\) and \({0.60}{\hbox { m}}\) from the comparison distance. At wind force 2, the deviation is between \({-0.70}\) and \({0.92}{\hbox { m}}\). For wind force 3–5 the return path in the air is 0.14–\({1.26}{\hbox { m}}\) longer than the outgoing path.

6 Conclusion

Conventional methods for geometric modeling in airborne LiDAR bathymetry are based on a strong simplification of the water surface geometry, the laser beam geometry, and the reflection processes at the water bottom. Usually, the water surface is modeled with horizontal or locally tilted water surface elements and the laser ray is considered as a straight line. The reflection at the water bottom is modeled as directional reflection assuming an identical signal outgoing and return path. These simplifications limit the coordinate accuracy in airborne LiDAR bathymetry.

In our study we developed enhanced geometric modeling approaches considering the curvature of the water surface, the laser beam divergence, and the diffuse reflection at the water bottom. The influence of geometric modeling on the coordinate accuracy of the water bottom points is investigated using an ALB simulation tool. The numerical simulation of laser bathymetry measurement data for different wave patterns, recording conditions, and sensor specifications enables the prediction of coordinate displacements at the water bottom.

The results of our investigations show that the developed enhanced water surface modeling strategies improve the representation of the water surface geometry. Precise information on the local water surface inclination enables a better refraction correction, increasing the accuracy of the water bottom points. The coordinate displacements at the water bottom are further reduced using the developed divergent laser ray model instead of assuming a narrow laser ray. However, the gain in accuracy depends on the characteristics of the wave pattern and the sensors beam divergence.

The comparison between enhanced and conventional geometric modeling approaches indicates that the presented comprehensive geometric models are able to almost halve the 3D coordinate displacements at the water bottom for wave patterns with small and moderate waves and small to medium beam divergences. Adequate modeling thus theoretically enables the acquisition of LiDAR bathymetry data with a more agitated water surface. However, wave patterns with ripples and small wavelets result in a minor improvement between enhanced and conventional geometric modeling.

After the geometric modeling with the enhanced modeling approaches coordinate displacements of \({1.5}\,{\%}\) (wind force 1, beam divergence \({0.5}{\hbox { mrad}}\)) to \({16}\,{\%}\) (wind force 5, beam divergence \({0.5}{\hbox { mrad}}\)) remain in the data set. At a water depth of \({5}{\hbox { m}}\), this corresponds to 8–\({80}{\hbox { cm}}\) planimetric error. These results have to be put into context with further influences on the coordinate accuracy, which are also included in the error budget. Especially the determination of the water surface points in real-life situations has a great influence on the accuracy of the water bottom points. Most of the modern ALB systems dispense with the near infrared signal and use only the green signal for water surface derivation. Since the green signal penetrates the water column, the water surface points are determined systematically too deep. As shown in Mandlburger et al. (2013), the mean penetration into the water column is in the range of 10–\({25}{\hbox { cm}}\). The underestimation of the water level could be reduced below \({6}{\hbox { cm}}\) by means of statistical analysis of aggregated neighbouring echoes resulting in a water depth error of 1–\({2}{\hbox { cm}}\). Depending on the water depth, the coordinate displacement at the water bottom can be of similar magnitude in calm waters with small waves. In this case, the impact of the geometric modeling is superimposed by coordinate errors resulting from the underestimation of the water level. With increasing wave height and complexity of the wave pattern the geometrical modeling dominates more and more the error budget. While the use of conventional geometric modeling approaches can be justified for inland waters with low swell, small wave heights and shallow water depth, the use of the enhanced geometric modeling methods is strongly recommended for the processing of ALB data in maritime areas.

The results on diffuse reflection modeling indicate that outgoing path and return path of the signal are not identical as assumed in conventional geometric modeling. In most cases deviating return paths are longer than the outgoing path, but shorter return paths do also occur. As a result, the received signal is influenced by photons arriving earlier or later at the receiver than the main portion of the returning photons. An underwater path, which is one meter longer, for instance, causes a temporal offset of approximately \({4}{\hbox { ns}}\) at the receiver. As a consequence, the impaired full-waveform of the received signal affects the detection of the water bottom echo. Therefore, the influence of the signal return path has to be taken into account when assessing the accuracy of the water bottom point coordinates. Our results confirm the findings of a related study, which predict the propagation induced pulse stretching by a Monte Carlo computer simulation (Guenther and Thomas 1984).

It has to be noted that the significance of our investigations is limited by the coarse resolution of laser ray model and diffuse reflection model. Although we considered \({1}{\hbox { Mio}}.\) reflected beams per laser shot, each beam still represents millions of single photons. Due to the distance between the reflected rays in the diffuse reflection model, the outgoing path is not necessarily included in the diffuse reflection beam bundle, otherwise each sub-beam of the laser ray model would have at least one successful return path to the receiver. For more meaningful results, a higher resolution of laser ray model and diffuse reflection model is required. Appropriate investigations will be part of our future work. A larger number of modeled return paths will enable a statistical analysis on the impact of signal portions arriving sooner or later at the receiver. On this basis, refined statements on the accuracy of the water bottom points will be derived. The findings will finally be used to develop correction terms for typical wave patterns which reduce systematic errors in real-world measurement data.

Furthermore, we plan to extend our studies to additional bathymetric sensors. Recently, novel lightweight topo-bathymetric laser scanner systems designed for integration on Unmanned Aerial Vehicles (UAVs) have gained importance. The system VQ-840-G from Riegl, for example, is able to capture river bathymetry in high spatial resolution (Mandlburger et al. 2020). It is operated at a low flying altitude of 50–\({150}{\hbox { m}}\) above ground. The user-selectable beam divergence (\({1}{\hbox { mrad}}\) up to \({6}{\hbox { mrad}}\)) results in a laser footprint of 5–\({30}{\hbox { cm}}\) at a flying altitude of \({50}{\hbox { m}}\) (Riegl 2020). The high pulse repetition rate of up to \({200}{\hbox { kHz}}\) results in a point density on the ground of approximately 20–50 points/m\(^2\). Thus, much more information on the water surface geometry is available for water surface modeling. Our further research will investigate the influence of geometric modeling on the bottom point accuracy for such system specifications. We expect that enhanced geometric models are already be relevant at lower wind speeds.

In addition, the findings of our study are relevant for the further development of our enhanced full-waveform analysis method for the improved detection of water bottom points in maritime applications. The basic idea of the new processing approach is the combination of closely adjacent full-waveform data using full-waveform stacking techniques (Mader et al. 2019, 2021). The geometrically correct tacking of full-waveforms requires exact information on the local water surface inclination, which can be derived from our refined geometric modeling approach.