Abstract
In this paper, we extend existing population growth models and propose a model based on a nonlinear cubic differential equation that reveals itself as a special subclass of Abel differential equations of first kind. We first summarize properties of the time-continuous problem formulation. We state the boundedness, global existence, and uniqueness of solutions for all times. Proofs of these properties are thoroughly given in the Appendix to this paper. Subsequently, we develop an explicit–implicit time-discrete numerical solution algorithm for our time-continuous population growth model and show that many properties of the time-continuous case transfer to our numerical explicit–implicit time-discrete solution scheme. We provide numerical examples to illustrate different behaviors of our proposed model. Furthermore, we compare our explicit–implicit discretization scheme to the classical Eulerian discretization. The latter violates the nonnegativity constraints on population sizes, whereas we prove and illustrate that our explicit–implicit discretization algorithm preserves this constraint. Finally, we describe a parameter estimation approach to apply our algorithm to two different real-world data sets.
Similar content being viewed by others
1 Introduction
1.1 Motivation
Differential equations play a vital role in many sciences. Especially, time development of populations within different time frames is of big interest to fields such as biology [13, 31, 37] and, more specifically, epidemiology [1–4, 9–11, 40, 45, 46] and population dynamics [7, 10, 14–16, 24, 26, 30, 48]. The temporal change of population sizes is not only of scientific interest, but different possibilities of this evolution impact the life of all humans.
Regarding Verhulst’s famous logistic model in 1838 [43], we shortly summarize different models often discussed in the literature [20].
1) Let us begin with a simple linear ordinary differential equation
for the total population size \(N_{1}\) for all \(t \geq 0\). Here \(N_{1}^{\prime } ( t )\) is the first derivative of the population size \(N_{1}\) with respect to time. Separation of variables under the assumption \(A > 0\) leads to the exponentially increasing solution
for all \(t \geq 0\). For \(A > 0\), we obtain
This is why other models should be sought for population dynamics.
2) A quadratic model could be proposed as an alternative. This model reads
for the total population size \(N_{2}\) for all \(t \geq 0\). The solution is given by
for all \(t < \frac{1}{A \cdot N_{2, 0}}\). This model includes one blowup at \(t_{b} = \frac{1}{A \cdot N_{2, 0}}\), that is,
Since it does not seem realistic that population sizes infinitely increase and since there are only limited materials on Earth, we expect that this model needs further modification.
3) Verhulst proposed his logistic model in 1838, which reads
for the total population size \(N_{3}\) for all \(t \geq 0\). Mathematica yields
as the solution which can be also obtained by a partial fraction decomposition. We obtain
for the limiting behavior, where the result corresponds to the carrying capacity. This model has been successfully applied in many situations. However, it does not account for phenomena such as oscillations due to competition between different species [10].
4) Another possibility might be the application of delay-differential equations such as Hutchinson model
with time delay \(\tau > 0\) and its variants as proposed in [49]. Although this model accounts for various different dynamics depending on the time delay, we might have to deal with the time delay \(\tau > 0\) for numerical simulations.
5) Abel differential equations of first kind
have been widely investigated [5, 8, 21]. Even some closed-form solutions for special classes of Abel differential equations of first kind are known [17, 28, 29]. These equations have been used in many different areas of science [41]. However, these types of differential equations are rarely applied to population dynamics of single species.
This explains our motivation for this paper, where we expand Verhulst’s logistic model by two modifications. First, we multiply the quadratic term with a time-dependent tuning function and extend Verhulst’s logistic model by an additional cubic term, which leads us to a specific class of Abel differential equations of first kind. Our model reads
under appropriate conditions to be specified.
1.2 Contributions and outline
Based on the aforementioned disadvantages of the presented models, we propose a nonautonomous nonlinear first-order differential equation, which uses an expansion of Verhulst’s model by a cubic term and introduces multiplication of the quadratic term by a time-dependent tuning function. Our contributions can be summarized as follows:
-
1)
We state our time-continuous problem formulation in Sect. 2.2;
-
2)
Afterward, we analyze this time-continuous problem formulation and show the nonnegativity and boundedness of possible solutions, global uniqueness in time, and global existence in time based on an inductive usage of Banach’s fixed-point theorem in Sect. 2. The proofs can be found in the Appendix;
-
3)
As our last contribution regarding our time-continuous problem formulation, we show a stability bound with respect to initial conditions and data. Hence, we conclude that our problem formulation is well posed on compact time intervals \([ 0, T ]\) for \(T > 0\). The proof of this statement is thoroughly described in the Appendix;
-
4)
As our first major contribution, we introduce an explicit–implicit numerical solution algorithm in Sect. 3 and prove that many properties of the time-continuous case transfer to its time-discrete variant. Additionally, we thoroughly prove that it converges linearly toward the solution of our time-continuous problem;
-
5)
Finally, as our second and final major contribution, we first provide one numerical example to compare the classical explicit Eulerian discretization scheme to our proposed explicit–implicit numerical solution algorithm. In addition, we give further numerical examples for different behaviors of solutions in Sect. 4. Afterward, we describe a parameter estimation approach and conclusively present two examples on real-world data with user-chosen time-dependent functions to illustrate usefulness of our proposed model with respect to real-world applications in Sect. 5.
In Sect. 6, we sum up our results and look out on possible future research directions.
2 Time-continuous problem formulation
In this section, we first sum up some mathematical background material for our analysis. After that, we describe our time-continuous problem formulation for population dynamics in one species. Conclusively, we analyze certain properties of our proposed model in detail. Detailed proofs of these statements can be found in the Appendix.
2.1 Mathematical background material
To especially state the global existence and global uniqueness of the solution of our nonautonomous first-order nonlinear population model, we need to introduce some theoretical background material regarding nonlinear ordinary differential equations. This subsection heavily relies on the structure of [45], which is based on [34, 35, 39]. Let us first recall the Lipschitz continuity of a function on Euclidean spaces.
Definition 2.1
([39, Sect. 3.2])
Let \(m, n \in \mathbb{N}\). If \(S \subset \mathbb{R}^{m}\), a function \(\mathbf{F} : S \longrightarrow \mathbb{R}^{n}\) is called Lipschitz continuous on S if there exists a constant \(L \geq 0\) such that
for all \(\mathbf{x}, \mathbf{y} \in S\). Here, \(\lVert \cdot \rVert \) denotes a suitable norm on the corresponding Euclidean space.
Let \(U \subset \mathbb{R}^{m}\) be open, and let \(\mathbf{F} \colon U \longrightarrow \mathbb{R}^{n}\). We call F locally Lipschitz continuous if for every point \(\mathbf{x_{0}} \in U\), there exists a neighborhood V of \(\mathbf{x_{0}}\) such that the restriction of F to V is Lipschitz continuous on V.
We consider the initial-value problem
where \(\mathbf{z} ( t ) = ( x_{1} ( t ), \ldots , x_{n} ( t ) )\) denotes our solution vector. Our vectorial function is represented by \(\mathbf{G} ( t, \mathbf{z} ( t ) ) = ( g_{1} ( t, \mathbf{z} ( t ) ), \ldots , g_{n} ( t, \mathbf{z} ( t ) ) )\), and \(\mathbf{z_{0}} \in \mathbb{R}^{n}\) are given initial conditions. To conclude the global existence, we can apply the following theorem, which is a consequence of Grönwall’s lemma.
Theorem 2.2
([39, Theorem 4.7.1])
If \(\mathbf{G} \colon [ 0, \infty ) \times \mathbb{R}^{n} \longrightarrow \mathbb{R}^{n}\) is locally Lipschitz continuous in both time and state variables and if there exist nonnegative real functions \(D \colon [ 0, \infty ) \longrightarrow [ 0, \infty )\) and \(K \colon [ 0, \infty ) \longrightarrow [ 0, \infty )\) such that
for all \(\mathbf{z} ( t ) \in \mathbb{R}^{n}\), then the solution of the initial value problem (8) exists for all \(t \in [ 0, \infty )\). Moreover, for every finite \(T \geq 0\), we have
for all \(t \in [ 0, T ]\), where
Additionally, we need Banach’s fixed point theorem to derive the global uniqueness.
Theorem 2.3
([35, Theorem V.18])
Let \(( X, \varrho )\) be a complete metric space with metric \(\varrho \colon X \times X \longrightarrow [ 0, \infty )\). Let \(T \colon X \longrightarrow X\) be a strict contraction, that is, there exists a constant \(K \in [ 0, 1 )\) such that \(\varrho ( Tx, Ty ) \leq K \cdot \varrho ( x, y )\) for all \(x, y \in X\). Then the map T has a unique fixed point.
Finally, we need a modification of Grönwall’s lemma for continuous dependence on perturbations of initial values and data. This might be also known to readers by stability analysis.
Theorem 2.4
([34, Theorem 1.3.1])
Let \(I := [ a, b ]\). Let \(u, f \colon I \longrightarrow [ 0, \infty )\) be continuous nonnegative functions. Let \(g \colon I \longrightarrow ( 0, \infty )\) be a continuous positive nondecreasing function. If
for all \(t \in I\), then
for all \(t \in I\).
2.2 Formulation
First, we state the following assumptions on the model:
-
\(A > 0\), \(B \geq 0\), \(C > 0\);
-
\(f \colon [ 0, \infty ) \longrightarrow ( 0, \infty )\) is a bounded function, that is, there exist positive constants \(m_{f}\) and \(M_{f}\) such that \(m_{f} \leq f ( t ) \leq M_{f}\) for all \(t \geq 0\).
Hence our nonlinear initial value problem for our population model reads
for \(t \geq 0\). In the rest of this section, we want to prove some important properties of our model.
2.3 Boundedness
As one important consequence, we obtain the boundedness and positivity of solutions to the initial value problem (13).
Lemma 2.5
Solutions of our model (13) are bounded, that is, there exist constants \(N_{\min }\) and \(N_{\max}\) such that \(N_{\min } \leq N ( t ) \leq N_{\max}\) for all \(t \geq 0\). In particular, solutions to positive initial values remain positive for all \(t \geq 0\).
2.4 Global existence
In addition to the boundedness, we conclude the existence of solutions to the initial value problem (13) for all \(t \geq 0\).
Theorem 2.6
Solutions to our population growth model (13) exist for all \(t \geq 0\).
2.5 Global uniqueness
As already stated, our proof of global uniqueness in time is heavily based on Banach’s fixed-point theorem, which has proven a valuable tool in different mathematical problem settings [44, 45, 50].
Theorem 2.7
The initial value problem (13) possesses a unique solution for all \(t \geq 0\).
2.6 Continuous dependence on initial conditions and data
Let us first provide a simple stability bound, where only perturbations of initial conditions are considered. In the following, \(\lVert \cdot \rVert _{\infty }\) denotes the maximum norm on a finite-dimensional Euclidean space.
Theorem 2.8
Let \(N_{a} \colon [ 0, T ] \longrightarrow [ 0, \infty )\) be a solution of (13) with initial value \(N_{a} ( 0 ) = N_{a, 0} > 0\), and let \(N_{b} \colon [ 0, T ] \longrightarrow [ 0, \infty )\) be solution of (13) with initial value \(N_{b} ( 0 ) = N_{b, 0} > 0\) with finite time \(T > 0\). We have the stability bound
for all \(t \in [ 0, T ]\), where
and
Now, we want to extend this stability by additionally assuming perturbations with respect to our prescribed data.
Theorem 2.9
Let \(A_{a}, A_{b} > 0\), \(B_{a}, B_{b} \geq 0\), \(C_{a}, C_{b} > 0\), and let \(f_{a}, f_{b} \colon [ 0, T ] \longrightarrow ( 0, \infty )\) be continuous bounded functions, that is, there exist positive constants \(m_{f, a}\), \(m_{f, b}\), \(M_{f, a}\), and \(M_{f, b}\) such that \(m_{f, a} \leq f_{a} ( t ) \leq M_{f, a}\) and \(m_{f, b} \leq f_{b} ( t ) \leq M_{f, b}\) for all \(t \in [ 0, T ]\). Additionally, assume that \(N_{a} \colon [ 0, T ] \longrightarrow [ 0, \infty )\) solves
for all \(t \in [ 0, T ]\) and that \(N_{b} \colon [ 0, T ] \longrightarrow [ 0, \infty )\) solves
for all \(t \in [ 0, T ]\). Then we have the stability bound
for all \(t \in [ 0, T ]\), where
is a time-dependent coefficient, and
3 Explicit–implicit time-discrete problem formulation
In this section, we propose an explicit–implicit time-discrete solution algorithm for (13). We show unique solvability and demonstrate that many properties of the time-continuous case transfer to our time-discrete scheme.
3.1 Time-discrete problem formulation
Let \([ 0, T ]\) be the time interval for model simulations. Let \(\{ t_{j} \} _{j = 1}^{M}\) be a strictly increasing sequence of time points, that is, \(t_{1} = 0 < t_{2} < \cdots < t_{M - 1} < t_{M} = T\). Our time-discrete problem formulation reads
with \(\Delta _{n + 1} = t_{n + 1} - t_{n}\) for all \(n \in \{ 1, \ldots , M - 1 \} \) and given initial population size \(N_{0}\). Here \(f_{n + 1}\) is an abbreviation for \(f_{n + 1} = f ( t_{n + 1} )\). The term of explicit–implicit solution algorithm refers to the right-hand-side of (16). Whereas the first two summands are treated explicitly, the last summand is a mixture of \(N_{n}\) and \(N_{n + 1}\). Hence, the proposed solution algorithm lies somewhere between fully explicit and fully implicit numerical solution schemes. Thus, these algorithms are called explicit–implicit solution algorithms [18, 45].
3.2 Solvability
Now, we can prove that our time-discrete model (16) is uniquely solvable.
Theorem 3.1
The time-discrete explicit–implicit population growth model (16) is uniquely solvable.
Proof
We first observe from (16) that
Rearranging yields
This implies
We conclude unique solvability for all \(n \in \{ 1, \ldots , M - 1 \} \). □
3.3 Boundedness
Theorem 3.2
The unique solution of our time-discrete population growth model (16) is bounded, that is, there exist constants \(N_{\mathrm{num},\min}\) and \(N_{\mathrm{num},\max}\) such that
for all \(n \in \{ 1, \ldots , M \} \).
Proof
1) We first show that \(N_{\mathrm{num},\min} > 0\). By (17), we observe by induction that
for all \(n \in \{ 1, \ldots , M - 1 \} \) because of \(N_{1} = N_{0} > 0\). Hence we obtain \(N_{\mathrm{num},\min} > 0\). This means that our time-discrete solution is nonnegative for all \(n \in \{ 1, \ldots , M \} \).
Additionally, we see that our solution sequence is monotonically decreasing if and only if
This yields
Square addition as in the time-continuous case results in
From (20) and the nonnegativity, we see that our time-discrete solution is monotonically decreasing if and only if
as in the time-continuous case. Since the function f is bounded below by zero, this implies
for our lower bound.
2) Similarly, we can conclude
for our upper bound. This provides both bounds, and the proof is finished. □
The result of Theorem 3.2 implies that our time-discrete population growth model (16) is unconditionally stable and preserves the nonnegativity of population sizes N.
3.4 Convergence
Theorem 3.3
Let us assume that the solution of our time-continuous population growth model (13) is twice continuously differentiable and that the function f is continuously differentiable. Additionally, we assume that \(\Delta _{p} \leq 1\) for all \(p \in \mathbb{N}\) and \(\lim_{p \to \infty } \Delta _{p + 1} = 0\). This implies that the solution of our time-discrete population growth model (16) converges linearly toward the solution of the time-continuous population growth model on a time interval \([ 0, T ]\) for arbitrary \(T > 0\).
Proof
Since this proof is relatively technical, we briefly describe our strategy. We start with consideration of local errors between time-continuous and time-discrete solutions. Afterward, we have to take into account that errors propagate in time. Finally, we need to accumulate these errors.
1) For our investigation of local errors, we assume that \(( t_{p}, N_{p} ) = ( t_{p}, N ( t_{p} ) )\) and consider the time interval \([ t_{p}, t_{p + 1} ]\) for arbitrary \(p \in \{ 1, \ldots , M - 1 \} \). Here, we only consider one time step and denote the time-discrete solution at \(t_{p + 1}\) by \(\widetilde{N_{p + 1}}\). By (17), we have
Application of the triangle inequality yields
after some manipulations. By the mean value theorem of calculus, there are \(\tau _{1}, \xi _{1} \in ( t_{p}, t_{p + 1} )\) such that
These equations yield
where we set
We finally obtain
for local errors.
2) In reality, \(( t_{p}, N_{p} )\) does not lie on the time-continuous solution exactly. For that reason, we must investigate how the procedural error \(N_{p} - N ( t_{p} )\) propagates to the \(( p + 1 )\)th time step. These estimates are carried out in this and the following steps.
We have to consider \(\vert N_{p + 1} - \widetilde{N_{p + 1}} \vert \). We observe that
and
By the triangle inequality, we obtain
Since
and \(\Delta _{p + 1} \leq 1\), we can conclude that
Let us define
This yields
for error propagation in time from the pth time step to the \(( p + 1 )\)th time step.
3) Our proof is based on the inequality \(1 + x \leq \exp ( x )\) for \(x \geq 0\). Note that \(t_{1} = 0 < t_{2} \ldots < t_{M - 1} < t_{M} = T\).
3.1) First, we want to prove inductively that
for all \(p \in \{ 0, \ldots , M - 1 \} \). Let \(p = 0\). Inequality (26) is obviously fulfilled. Let \(p = 1\) to understand the concept. By application of the triangle inequality and inequalities (24) and (25) we observe that
We now assume that
We now want to show (26). We obtain
and this finishes our inductive proof.
3.2) We define \(\Delta := \max_{p \in \mathbb{N}} \Delta _{p}\). We infer that
If the initial conditions of our time-continuous and time-discrete models coincide and \(\Delta \to 0\), then the time-discrete solution converges linearly toward the time-continuous solution of the time-continuous population growth model. Finally, our statement is proven. □
3.5 Algorithmic summary
We summarize our algorithmic approach in Table 1.
4 Numerical examples
Here, we present four examples. In our first example, we compare the classical explicit Eulerian discretization to our proposed explicit–implicit numerical solution algorithm. Three synthetic examples show that different behaviors are possible.
4.1 Example 1: comparison of time discretization algorithms
First, we compare the classical explicit Eulerian time discretization algorithm
to our explicit–implicit numerical solution algorithm
by (16) for all \(n \in \{ 1, 2, \ldots , M - 2, M - 1 \} \). We consider the following inputs:
-
\(A = 1\), \(B = 0.01\), and \(C = 0.00001\);
-
Time step size \(\Delta = 1.0\);
-
Initial population size \(N_{1} = 10\);
-
Simulation time \(T = 6\);
-
Function \(f ( t ) \equiv 1\).
In Fig. 1, we can clearly see that the classical Eulerian time discretization scheme becomes unstable and we obtain negative population sizes, whereas our proposed explicit–implicit numerical solution algorithm remains stable and provides positive population sizes for all times. It is well known in numerical analysis that explicit time-stepping methods are always conditionally stable [22, 23, 25]. Hence, we have to carefully select possible time-discretization schemes with respect to equations we want to solve.
Results of our first example from Sect. 4.1
4.2 Example 2: monotonically increasing solution
We present an example that is monotonically increasing. We consider the following inputs:
-
\(A = 0.1\), \(B = 0.02\), and \(C = 0.00002\);
-
Time step size \(\Delta = 1.0\);
-
Initial population size \(N_{1} = 100\);
-
Simulation time \(T = 1000\);
-
Function \(f ( t ) = 0.05 \cdot \frac{0.001 + \exp ( -0.1 \cdot t )}{0.0009 + \exp ( -0.1 \cdot t )}\);
-
Lower bound \(m_{f} = 0.05\) and upper bound \(M_{f} = \frac{5}{90}\) of f.
In Fig. 2, we see that we can get results that look similar to monotonically increasing solutions from Verhulst’s logistic model.
Results of our second example from Sect. 4.2
4.3 Example 3: solution with changing sign in derivative
We give an example where the derivative of our population model changes its sign in time. For that purpose, we propose the following input parameters:
-
\(A = 0.1\), \(B = 0.04\), and \(C = 0.00002\);
-
Time step size \(\Delta = 1.0\);
-
Initial population size \(N_{1} = 100\);
-
Simulation time \(T = 1000\);
-
Function \(f ( t ) = 0.1 + \frac{ ( 0.01 \cdot t^{2} + 0.1 \cdot t + 1 ) \cdot \exp ( -0.02 \cdot t )}{10 + \exp ( -0.02 \cdot t )}\);
-
Lower bound \(m_{f} = 0.1\) and upper bound \(M_{f} = 1.585\) of f.
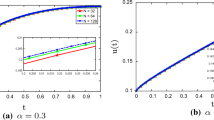
We observe from Fig. 3 that it is possible to obtain solutions that first monotonically increase and later monotonically decrease in time.
Results of our third example from Sect. 4.3
4.4 Example 4: oscillating solution
We want to construct an oscillating example where the following parameters are taken into account:
-
\(A = 0.1\), \(B = 0.02\), and \(C = 0.00002\);
-
Time step size \(\Delta = 1.0\);
-
Initial population size \(N_{1} = 100\);
-
Simulation time \(T = 1000\);
-
Function \(f ( t ) = 0.05 + 0.02 \cdot \sin ( \frac{t}{10} )\);
-
Lower bound \(m_{f} = 0.03\) and upper bound \(M_{f} = 0.07\) for f.
The results for this example with an oscillating solution are shown in Fig. 4.
Results of our fourth example from Sect. 4.4
5 Parameter estimation and real-world applications
For real-world applications, we need to present a parameter estimation approach. We first describe our method and apply it to two real-world data sets from Human World and Japanese populations. From our observations, we especially derive our time-dependent coefficient functions we later apply to both data sets.
5.1 Parameter estimation
We consider the proposed explicit–implicit time discretization method
for all \(n \in \{ 1, 2, \ldots , M - 2, M - 1 \} \), where \(\widetilde{f_{n + 1}} = B \cdot f_{n + 1}\). Here, we assume that time points
are given and, for simplicity and due to real-life data, \(\Delta _{n + 1} \equiv 1\). Finding the nonnegative coefficients
is our main goal. Hence, we want to solve the optimization problem
where we set
with respect to the nonnegativity constraints on the sought parameters, where \(\lVert \cdot \rVert _{2}\) is the Euclidean norm. We apply the function lsqnonneg of GNU Octave to solve this nonnegative linear least-squares problem [19]. For further details on numerical optimization, we refer the interested readers to [33].
5.2 Example 5: human world population
The data are taken from the United Nations [42] for the human total population size including both sexes. We investigate three different settings where parameters and given functions are user-chosen or, in one case, are estimated. For more sophisticated parameter estimation techniques, which are outside the scope of our paper, we refer the interested readers to further works [1, 11, 12, 47], as these techniques might be an interesting extension of this paper.
The following parameters are applied in our first user-chosen setting:
-
\(A_{1} = 0.0225\), \(B_{1} = 0.005\), and \(C_{1} = 0.00025\);
-
Time step size \(\Delta = 1.0\) year;
-
Initial population size \(N_{1} = 2.536431\) billion people;
-
Simulation time \(T_{1} = 500\) years;
-
Function \(f_{1} ( t ) = \frac{0.02 \cdot ( 0.01 + \exp ( -0.02 \cdot t ) )}{0.05 + \exp ( - 0.02 \cdot t )}\);
-
Lower bound \(m_{f_{1}} = 0.004\) and upper bound \(M_{f_{1}} = 0.02\) of f.
We use the following parameters in our second user-chosen setting:
-
\(A_{2} = 0.0180\), \(B_{2} = 0.0009\), and \(C_{2} = 0.0002\);
-
Time step size \(\Delta = 1.0\) year;
-
Initial population size \(N_{1} = 2.536431\) billion people;
-
Simulation time \(T_{2} = 500\) years;
-
Function \(f_{2} ( t ) = \frac{ ( 0.2 \cdot t^{3} + 15.0 \cdot t^{2} + 50.0 \cdot t ) \cdot \exp ( -0.01 \cdot t )}{20.0 \cdot t^{2} + 1.0} + 0.01\);
-
Lower bound \(m_{f_{2}} = 0.01\) and upper bound \(M_{f_{2}} = 5.975\) of f.
In our third setting, we apply the following parameters, where \(A_{3}\) and \(C_{3}\) were estimated by our least-squares approach, and \(B_{3}\) is the arithmetic mean of the depicted data points in Fig. 5:
-
\(A_{3} = 0.018758\), \(B_{3} = 0.000632\), and \(C_{3} = 0.000154\);
-
Time step size \(\Delta = 1.0\) year;
-
Initial population size \(N_{1} = 2.536431\) billion people;
-
Function \(f_{3} ( t ) = 1\).
All chosen functions \(g_{j} ( t ) = B_{j} \cdot f_{j} ( t )\) for \(j \in \{ 1, 2, 3 \} \) are shown in Fig. 5.
The results of all three settings are depicted in Fig. 6. We clearly observe that it is possible to construct fits with different monotonicity assumption regarding future predictions.
The errors between known real-world data and our portrayed settings are portrayed in Fig. 7. All graphs well describe the given data. However, as observed in Fig. 6, all three predictions provide different long-time behaviors.
5.3 Example 6: Japanese population
Data for our last example are again taken from the United Nations [42] for human total population size including both sexes in Japan. The following inputs are considered for this example, where a simplified function f is user-chosen by the results of our least-squares estimation approach as depicted in Fig. 8:
-
\(A = 0.0000001\) (since our approach states \(A \approx 0\), we stay with a small positive chosen number), \(B = 0.0002050\), and \(C = 0.00000019\);
-
Time step size \(\Delta = 1.0\) year;
-
Initial population size \(N_{1} = 82.802\) million people;
-
Simulation time \(T = 200\) years;
-
Function \(f ( t ) = \exp ( -0.03 \cdot t )\).
As already mentioned, our estimation results for our time-dependent coefficient function can be seen in Fig. 8.
The results of this setting are portrayed in Fig. 9, which depicts a rapidly decaying population size in Japan. In contrast to the traditional Verhulst model, which only accounts for monotone behavior, our model is able to capture different intervals of monotonicity in our given data.
6 Conclusion and outlook
In this work, we proposed an extended population growth model based on a nonlinear first-order differential equation with quadratic and cubic terms of population size. At the beginning, we proved the nonnegativity and boundedness globally in time. After that, we established the global existence and uniqueness of the solution of our model in time. Subsequently, we discretized our model and provided an explicit–implicit solution algorithm. We showed that many properties of our time-continuous model transfer to our time-discrete variant. Finally, we applied our results to four synthetic and two real-world examples to demonstrate usefulness and variability of our presented model. As a conclusion, we saw that explicit time-stepping methods suffer from time restrictions and may violate the nonnegativity constraints on populations size, whereas our proposed explicit–implicit numerical solution algorithm preserves the nonnegativity.
Our model seems to be flexible. This flexibility might be extended in future work by multiplication of all terms on the right-hand side by time-dependent tuning functions. Compare, for example, [27, 32, 36, 38]. Additionally, parameter estimation for models in mathematical biology could be regarded as further work because its manual choosing is a delicate task [1, 11, 12, 47]. However, more sophisticated techniques for solving inverse problems are out of the scope of this paper.
As a final extension, our model can be modified by application of fractional differential operators [6].
Availability of data and materials
Data can be found in [42].
References
Akossi, A., Chowell-Puente, G., Smirnova, A.: Numerical study of discretization algorithms for stable estimation of disease parameters and epidemic forecasting. Math. Biosci. Eng. 16, 3674–3693 (2019). https://doi.org/10.3934/mbe.2019182
Ali, M., Shah, S.T.H., Imran, M., Khan, A.: The role of asymptotic class, quarantine and isolation in the transmission of COVID-19. J. Biol. Dyn. 14(1), 398–408 (2020). https://doi.org/10.1080/17513758.2020.1773000
Allen, L.J.S., Burgin, A.: Comparison of deterministic and stochastic SIS and SIR epidemic models in discrete time. Math. Biosci. 163(1), 1–33 (2000). https://doi.org/10.1016/S0025-5564(99)00047-4
Allen, L.J.S., van den Driessche, P.: The basic reproduction number in some discrete-time epidemic models. J. Differ. Equ. Appl. 14, 1127–1147 (2008). https://doi.org/10.1080/10236190802332308
Alwash, M.: Periodic solutions of Abel differential equations. J. Math. Anal. Appl. 329(2), 1161–1169 (2007). https://doi.org/10.1016/j.jmaa.2006.07.039
Atangana, A.: Modelling the spread of COVID-19 with new fractal-fractional operators: can the lockdown save mankind before vaccination? Chaos Solitons Fractals 136, 109860 (2020). https://doi.org/10.1016/j.chaos.2020.109860
Baigent, S., Ching, A.: Balance simplices of 3-species May–Leonard systems. J. Biol. Dyn. 14(1), 187–199 (2020). https://doi.org/10.1080/17513758.2020.1736656
Bohner, M., Streipert, S.: Abel dynamic equations of first and second kind. Georgian Math. J. 22(3), 341–348 (2015). https://doi.org/10.1515/gmj-2015-0026
Bohner, M., Streipert, S., Torres, D.F.M.: Exact solution to a dynamic SIR model. Nonlinear Anal. Hybrid Syst. 32, 228–238 (2019). https://doi.org/10.1016/j.nahs.2018.12.005
Brauer, F., Castillo-Chavez, C.: Mathematical Models in Population Biology and Epidemiology. Springer, New York (2012)
Chen, Y., Cheng, J., Jiang, Y., Lia, K.: A time delay dynamical model for outbreak of 2019-nCov and parameter identification. J. Inverse Ill-Posed Probl. 28, 243–250 (2020). https://doi.org/10.1515/jiip-2020-0010
Clermont, G., Zenker, S.: The inverse problem in mathematical biology. Math. Biosci. 260, 11–15 (2015). https://doi.org/10.1016/j.mbs.2014.09.001
Cuchta, T., Streipert, S.: Dynamic Gompertz model. Appl. Math. Inf. Sci. 14(1), 9–17 (2020). https://doi.org/10.18576/amis/140102
Cushing, J.M.: The evolutionary dynamics of a population model with strong Allee effect. Math. Biosci. Eng. 12(4), 643–660 (2015). https://doi.org/10.3934/mbe.2015.12.643
Cushing, J.M.: Discrete time Darwinian dynamics and semelparity versus iteroparity. Math. Biosci. Eng. 16(4), 1815–1835 (2019). https://doi.org/10.3934/mbe.2019088
Cushing, J.M., Farrell, A.P.: A bifurcation theorem for nonlinear matrix models of population dynamics. J. Differ. Equ. Appl. (2019). https://doi.org/10.1080/10236198.2019.1699916
Dimitrios, T.I.Z., Panayotounakos, E.: Construction of exact parametric or closed form solutions of some unsolvable classes of nonlinear ODEs (Abel’s nonlinear ODEs of the first kind and relative degenerate equations). Int. J. Math. Math. Sci. 2011, 387429 (2011). https://doi.org/10.1155/2011/387429
Du, Y., Zhang, Q., Meyer-Baese, A.: The positive numerical solution for stochastic age-dependent capital system based on explicit-implicit algorithm. Appl. Numer. Math. 165, 198–215 (2021). https://doi.org/10.1016/j.apnum.2021.02.015
Eaton, J.W., Bateman, D., Hauberg, S., Wehbring, R.: GNU Octave Version 5.2.0 Manual: a High-Level Interactive Language for Numerical Computations (2020) https://www.gnu.org/software/octave/doc/v5.2.0/
Eggers, J., Fontelos, M.A.: Singularities: Formation, Structure and Propagation. Cambridge University Press, Cambridge (2015)
Gasull, A., Libre, J.: Limit cycles for a class of Abel equations. SIAM J. Math. Anal. 21(5), 1235–1244 (1990). https://doi.org/10.1137/0521068
Hairer, W., Nørsett, S.P., Wanner, G.: Solving Ordinary Differential Equations I. Springer, Berlin (1993)
Hairer, W., Wanner, G.: Solving Ordinary Differential Equations II. Springer, Berlin (1996)
Huang, M., Hu, L.: Modeling the suppression dynamics of Aedes mosquitoes with mating inhomogeneity. J. Biol. Dyn. 14(1), 656–678 (2020). https://doi.org/10.1080/17513758.2020.1799083
Kress, R.: Numerical Analysis. Springer, New York (1998)
Li, N., Tuljapurkar, S.: The solution of time-dependent population models. Math. Popul. Stud. (2000). https://doi.org/10.1080/08898480009525464.
Ludwig, D., Jones, D.D., Holling, C.S.: Qualitative analysis of insect outbreak systems: the spruce budworm and forest. J. Anim. Ecol. 47(1), 315–332 (1978). https://doi.org/10.2307/3939
Mak, M., Harbo, T.: New method for generating general solution of Abel differential equation. Comput. Math. Appl. 43(1), 91–94 (2002). https://doi.org/10.1016/S0898-1221(01)00274-7
Markakis, M.P.: Closed-form solutions of certain Abel equations of the first kind. Appl. Math. Lett. 22(9), 1401–1405 (2009). https://doi.org/10.1016/j.aml.2009.03.013
Martcheva, M., Milner, F.A.: A two-sex age-structured population model: well-posedness. Math. Popul. Stud. (1999). https://doi.org/10.1080/08898489909525450.
Murray, J.D.: Mathematical Biology I – an Introduction. Springer, New York (2002)
Nkashama, M.N.: Dynamics of logistic equations with non-autonomous bounded coefficients. Electron. J. Differ. Equ. 2000(2), 1 (2000) https://www.emis.de/journals/EJDE/2000/02/nkashama.pdf
Nocedal, J., Wright, S.J.: Numerical Optimization. Springer, New York (2006)
Pachpette, B.G.: Inequalities for Differential and Integral Equations. Academic Press, San Diego (1998)
Reed, M., Simon, B.: Functional Analysis. Academic Press, San Diego (1980)
Rogovchenko, S.P., Rogovchenko, Y.V.: Effect of periodic environmental fluctuations on the Pearl–Verhulst model. Chaos Solitons Fractals 39, 1169–1181 (2009). https://doi.org/10.1016/j.chaos.2007.11.002
Sachs, R.K., Hlatky, L.R., Hahnfeldt, O.: Simple ODE models of tumor growth and anti-angiogenic or radiation treatment. Math. Comput. Model. 33, 1297–1305 (2001)
Safuan, H.M., Jovanoski, Z., Towers, I.N., Sidhu, H.S.: Exact solution of a non-autonomous logistic population model. Ecol. Model. 251, 99–102 (2013). https://doi.org/10.1016/j.ecolmodel.2012.12.016
Schaeffer, D.G., Cain, J.W.: Ordinary Differential Equations: Basics and Beyond. Springer, New York, (2016). https://doi.org/10.1007/978-1-4939-6389-8
Shi, Y., Yu, J.: Wolbachia infection enhancing and decaying domains in mosquito population based on discrete models. J. Biol. Dyn. 14(1), 679–695 (2020). https://doi.org/10.1080/17513758.2020.1805035
Streipert, S.: Abel Dynamic Equations of the First and Second Kind, Master Theses (2012) 6914, https://scholarsmine.mst.edu/masters_theses/6914
United Nations – Department of Economic and Social Affairs, Population Division: world Population Prospects 2019, URL: https://population.un.org/wpp/Download/Standard/Population/, 2019. Last accessed on 25 August, 2020 at 11:41 PM
Verhulst, P.F.: Notice sur la loi que la population poursuit dans son accroissement. Corresp. Math. Phys. 10, 113–121 (1838)
Wacker, B., Kneib, T., Schlüter, J.: Revisiting Maximum Log-Likelihood Parameter Estimation for Two-Parameter Weibull Distributions: Theory and Applications (2020) https://doi.org/10.13140/RG.2.2.15909.73444/2. Preprint
Wacker, B., Schlüter, J.: An age- and sex-structured SIR model: theory and an explicit-implicit solution algorithm. Math. Biosci. Eng. 17(5), 5752–5801 (2020). https://doi.org/10.3934/mbe.2020309
Wacker, B., Schlüter, J.: Time-continuous and time-discrete SIR models revisited: theory and applications. Adv. Differ. Equ. 2020, 556 (2020). https://doi.org/10.1186/s13662-020-02995-1
Wacker, B., Schlüter, J.: Time-discrete parameter identification algorithms for two deterministic epidemiological models applied to the spread of COVID-19 (2020) https://doi.org/10.21203/rs.3.rs-28145/v1. Preprint
Wang, W., Wang, L., Chen, W.: Stochastic Nicholson’s blowflies delayed differential equations. Appl. Math. Lett. 87, 20–26 (2019). https://doi.org/10.1016/j.aml.2018.07.020
Yukalov, V.I., Yukalova, E.P., Sornette, D.: Punctuated evolution due to delayed carrying capacity. Physica D 238, 1752–1767 (2009). https://doi.org/10.1016/j.physd.2009.05.011
Zeidler, E.: Nonlinear Functional Analysis and Its Applications I – Fixed-Point Theorems. Springer, Berlin (1986)
Acknowledgements
Both authors thank all three anonymous reviewers for their helpful and valuable comments, which definitely helped to improve the manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
Benjamin Wacker and Jan Schlüter conceived and designed this study. Benjamin Wacker analyzed time-continuous and time-discrete models. Benjamin Wacker implemented the discretized model. Benjamin Wacker and Jan Schlüter analyzed the data. Benjamin Wacker visualized the results. Benjamin Wacker and Jan Schlüter drafted, edited, and reviewed this manuscript. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Appendix
Appendix
1.1 Proof of Lemma 2.5
First, we see that
for all \(t \geq 0\). Pick arbitrary \(t_{0} \in [ 0, \infty )\) such that
Then
Hence, we choose \(N_{\min } := \min \{ N_{0}, \sqrt{\frac{A}{C}} \} > 0\) as a lower bound for the total population size.
Second, we further notice that
Examining \(N^{\prime } ( t ) = 0\) from (32) yields
for arbitrary \(t \geq 0\) where \(N^{\prime } ( t ) = 0\). Thus we can choose the constant \(N_{\max} := \max \{ N_{0}, \frac{B \cdot M_{f}}{2 \cdot C} + \sqrt{ \frac{4 \cdot A \cdot C + B^{2} \cdot M_{f}^{2}}{4 \cdot C^{2}}} \} \) as an upper bound for the total population size due to the fact that
would hold for an arbitrary \(t_{0} \geq 0\) where \(N ( t_{0} ) \geq N_{\max}\).
Finally, the two previous steps of our proof imply that the solutions of our population growth model (13) stay bounded and positive.
1.2 Proof of Theorem 2.6
We apply Theorem 2.2. Applying the maximum norm and triangle inequality and using the boundedness of the function f and the solution by Lemma 2.5, we obtain
and Theorem 2.2 proves our statement.
1.3 Proof of Theorem 2.7
Let \(t \in [ 0, \tau ]\) be arbitrary for a chosen \(\tau > 0\). Let us assume that both functions \(N \colon [ 0, \infty ) \longrightarrow [ 0, \infty )\) and \(\widetilde{N} \colon [ 0, \infty ) \longrightarrow [ 0, \infty )\) solve our population growth model (13). We see that
which implies
By the boundedness of the solution from Lemma 2.5, we obtain
Choosing \(\tau := \frac{1}{2 \cdot ( A + 2 \cdot B \cdot M_{f} \cdot N_{\max} + 3 \cdot C \cdot N_{\max}^{2} )}\), we observe that
for all \(t \in [ 0, \tau ]\). This yields the uniqueness on the time interval \([ 0, \tau ]\) by Banach’s fixed-point theorem.
Inductively, we can apply a similar argument as in our first step to obtain the uniqueness on time intervals \([ k \cdot \tau , ( k + 1 ) \cdot \tau ]\) for all \(k \in \mathbb{N}_{0}\). Here \(t_{0} = k \cdot \tau \) is our new initial time point. This completes the proof of global uniqueness in time.
1.4 Proof of Theorem 2.8
We first observe that
and
This implies
for all \(t \in [ 0, T ]\). Defining \(\alpha _{1}\) and \(\alpha _{2}\) as stated in our claim of Theorem 2.8, we obtain
and hence, as both \(\alpha _{1}\) and \(\alpha _{2}\) are constant in time, (14) holds after application of Theorem 2.4, which proves our statement.
1.5 Proof of Theorem 2.9
Let us first prove that
for arbitrary \(x_{1}, x_{2}, y_{1}, y_{2} \in \mathbb{R}\). Application of zero addition and the triangle inequality yields
Again, we observe that
and
This implies
We will estimate all terms I, II, and \(III\).
By the inequality of our first step, we conclude that
By multiple application of the inequality of our first step, we infer that
Another application of the inequality of the first step yields
Define the time-dependent coefficient
and the constant
We obtain
Since all assumptions of Theorem 2.4 are fulfilled, our claim is proven.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wacker, B., Schlüter, J.C. A cubic nonlinear population growth model for single species: theory, an explicit–implicit solution algorithm and applications. Adv Differ Equ 2021, 236 (2021). https://doi.org/10.1186/s13662-021-03399-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03399-5