1 Introduction

Modern composites with different polymer, ceramic [6, 12, 16, 26, 31, 37, 40, 43, 44, 46], cement or metal matrix [13, 16, 36, 41, 50] are the most promising kinds of materials used for various branches of innovative industry. The natural composites have disordered internal structures, whereas novel multiphase materials are designed to satisfy specific engineering requirements. It means that various artificial structures with different geometries are produced. In particular, the following internal structures can be distinguish:

  • regular structures build-up of uniformly distributed several phases of the composites including porosity [26, 29, 42, 44] or homogeneously scattered in the matrix nano-particles [16, 19, 50], particles, short fibers, whiskers [16], etc.;

  • irregular internal structures with random distribution of the second phase [6, 31, 37, 40, 46] or reinforcement [16];

  • layered composite (LC) structures manufactured as regular or irregular [16, 24, 25, 34, 38];

  • functional gradation composites (FGC) having: (1) continuous variation of physical and mechanical properties [9, 18, 39, 45, 48, 53] or (2) stepwise shape [24, 34, 35, 38].

It is obvious that the overall performances described by strength, stiffness, ductility, thermal properties, wear resistance, and toughness can be substantially improved by tailoring the three-dimensional distribution of all phases constituting composites, and optimizing the structure parameters. This is important for layered composite structures, where proper arrangements of sequence of layers made of different components play a crucial role for enhancement of elastic and plastic properties, interface bonding, and fracture resistance. The stepwise change of thermo-mechanical properties in the LC can be replaced by FGC with continuous gradation of composite properties, thus removing the technological problem in the fabrication of perfect bonding between layers. Both types of LC and FGC were proposed in order to increase quasi-static and impact toughness at high strains (see, e.g., [13, 27, 28]) by the mechanisms as cracks bridging, crack tip plasticity, and interfacial delamination compared to a homogeneous structures. Both material models play significant roles for manufacturing multi-layered beams [3,4,5, 33], plates [8, 10, 20, 32] and shells.

The sandwich structures can be composed of numerous sets of materials depending on application. In aeronautic constructions, we can find the hi-tech constituents like metallic and polymeric foams, nomex honeycombs. The comprehensive review of sandwich structure for aeronautics from 1930s to present time is presented in [11]. According to present strategy of sustainable development of economy in recent studies, we can observe the attempts to use natural origin materials [47] and fully recyclable thermoplastic [14]. The gained fields of applications and the continuous development of sandwich composites prompt the development of methods of predicting their responses to given mechanical loads. The mathematical tools for sandwiches behavior predictions should be easy to use and deliver the desired results in the shortest possible time. Generalization of the analytical model of sandwich structures was presented in [22], where the authors proposed continuous and symmetrical variation of mechanical properties in thickness direction. They mentioned that further improvement of their theory is to introduce the thin layers binding the faces and core. Besides the mechanical loading, the sandwich structures are frequently subjected to thermal loadings. In this respect, Venkatesan et al. [51] present the methodology to investigate the damage of sandwich structures in cyclic thermal loadings with employing numerical analyses.

In this paper, we investigate the mechanical behavior of multilayered composite beams using a Cosserat-type model for rods, called the theory of directed curves (see [1, 54]). The aim of our work is the determination of the analytical expressions of the effective stiffness coefficients for general composite beams having an arbitrary number of layers. The model of directed curves has been systematically presented for the first time by Zhilin in [54, 55] and has been extended for porous and thermoelastic rods by Bîrsan and Altenbach [2, 3]. Using this approach, we have investigated the mechanical behavior of sandwich composite beams and of functionally graded structural elements in [5, 33]. In the present paper, we generalize the results obtained previously in [5, 33] to the case of orthotropic composite beams made of n layers. The theoretical results are then verified by comparison with numerical simulations of various bending and torsion problems for composite beams.

In Sect. 2, we present the theoretical model of directed curves, which will be used for composite elastic rods. In Sect. 3, we determine the effective stiffness coefficients for orthotropic non-homogeneous rods by comparing the analytical solutions of bending, torsion, and extension problems for directed curves with the corresponding results for three-dimensional rods.

In Sect. 4, we generalize the results to the case of multilayered composite beams made of several orthotropic non-homogeneous materials and establish analytical expressions for the effective stiffness coefficients. The general case of sandwich beams with an arbitrary number of layers is treated in Sect. 5. Then, we illustrate the usefulness and verify the applicability of the obtained formulas by means of several numerical examples, concerning the bending of cantilever sandwich beams or the three-point bending of composite beams.

Section 7 is concerned with circular sandwich columns made of piecewise homogeneous materials. Applying the theoretical results, we obtain closed-form expressions for the effective bending, shear, extensional, and torsion stiffness coefficients. Then, in Sect. 6 we present a parametric study to compare the analytical solutions with numerical results obtained by the finite element method.

Since we obtain in all considered cases a good agreement between the analytical and numerical results, we can infer that the proposed theoretical formulas for effective stiffness coefficients are correct, so they can be successfully applied to characterize the mechanical behavior of general composite beams.

2 The model of directed curves

In this section, we briefly present the model of directed curves, which is a Cosserat-type model for rods and will be used in our paper. For a complete description of this model, we refer to the works [1,2,3, 54, 55].

We denote by \({\mathcal {C}}_0\) be the reference (initial) configuration of the deformable curve and by \(\,s\,\) the material coordinate along \({\mathcal {C}}_0\,\). We choose \(\,s\,\) to be the arclength parameter along \({\mathcal {C}}_0\,\). The reference configuration is determined by the position vector \({\varvec{r}}(s)\) and the attached three directors \({\varvec{d}}_i(s)\). The directors are orthogonal unit vectors, such that the third director \({\varvec{d}}_3(s)\) coincides with the unit tangent \(\,{\varvec{t}}\equiv {\varvec{r}}'(s)\), while \({\varvec{d}}_1\,\) and \({\varvec{d}}_2\) belong to the normal plane to the curve \(\,{\mathcal {C}}_0\,\).

Let \({\mathcal {C}}\,\) be the deformed configuration at time \(\,t\,\). We denote the position vector by \({\varvec{R}}={\varvec{R}}(s,t) \) and the three directors by \({\varvec{D}}_i={\varvec{D}}_i(s,t) \). The third director \({\varvec{D}}_3\) is no longer tangent to the curve \({\mathcal {C}}\) after deformation and the cross sections (determined by \({\varvec{D}}_1\) and \({\varvec{D}}_2\)) are not necessarily normal to the middle curve. This model allows for transverse shear deformation of the rod, but the deformation of the cross sections is not taken into account. We shall employ the direct tensor notation and the summation convention over repeated indices. Greek indices range over the set \(\{1,2\}\,\), while Latin indices take the values \(\{1,2,3\}\,\). We denote the derivative with respect to the line coordinate s by a prime, i.e., \(\,\,(\,\,\,)^{\prime }=\frac{\mathrm {d}}{\mathrm {d}s}\,\,\).

With these notations, we define the rotation tensor by \(\, {\varvec{P}}(s,t)={\varvec{D}}_k(s,t)\otimes {\varvec{d}}_k(s)\) and the displacement vector by \(\,{\varvec{u}}(s,t)={\varvec{R}}(s,t)-{\varvec{r}}(s)\). In the linear theory of rods, we decompose the rotation tensor as \(\,{\varvec{P}}={\varvec{1}}+ \varvec{\psi } \times {\varvec{1}}\,\), where \(\,\varvec{\psi }(s,t)\) is the vector of small rotations. Then, the strain measures for rods are the vector of extension-shear \(\,{\varvec{e}}\,\) and the vector of bending-twisting \(\,\varvec{\kappa }\,\), given by

$$\begin{aligned} {\varvec{e}}={\varvec{u}}^{\,\prime }+ {\varvec{t}}\times \varvec{\psi }\,, \qquad \varvec{\kappa }=\varvec{\psi }^{\,\prime }\,. \end{aligned}$$
(1)

The equilibrium equations for rods have the following form

$$\begin{aligned} {\varvec{N}}^{\prime }+\rho _0\varvec{{\mathcal {F}}}= {\varvec{0}},\qquad {\varvec{M}}^{\prime }+{\varvec{t}}\times {\varvec{N}}+ \rho _0\varvec{{\mathcal {L}}}={\varvec{0}}, \end{aligned}$$
(2)

where \(\,{\varvec{N}}\,\) is the force vector field, \(\,{\varvec{M}}\,\) is the moment vector field, \(\,\rho _0\,\) is the mass density per unit length of \(\,{\mathcal {C}}_0\,\), while \(\,\varvec{{\mathcal {F}}}\,\) and \(\,\varvec{{\mathcal {L}}}\,\) are the external body force and moment per unit mass, respectively. To the system of differential equations (2), we adjoin boundary conditions.

For elastic composite rods, we can write the constitutive equations in the form

$$\begin{aligned} \begin{array}{c} {\varvec{N}}=\dfrac{\partial (\rho _0{\mathcal {U}})}{\partial {\varvec{e}}}\,, \qquad {\varvec{M}}=\dfrac{\partial (\rho _0{\mathcal {U}})}{\partial \varvec{\kappa }}\,, \end{array} \end{aligned}$$
(3)

where

$$\begin{aligned} \begin{array}{c} \rho _0{\mathcal {U}}\big ({\varvec{e}}, \varvec{\kappa }\big )= \dfrac{1}{2}\, {\varvec{e}} \cdot {\varvec{A}}\cdot {\varvec{e}} + {\varvec{e}} \cdot {\varvec{B}}\cdot \varvec{\kappa } +\dfrac{1}{2}\, \varvec{\kappa } \cdot {\varvec{C}}\cdot \varvec{\kappa } \end{array} \end{aligned}$$
(4)

is the internal energy function. Here, the second-order tensors \(\,{\varvec{A}}\,, \,{\varvec{B}}\,\) and \(\,{\varvec{C}}\,\) are constitutive tensors having the following structure [4]

$$\begin{aligned} {\varvec{A}}= & {} A_1{\varvec{d}}_1\otimes {\varvec{d}}_1+ A_2{\varvec{d}}_2\otimes {\varvec{d}}_2+ A_3{\varvec{t}}\otimes {\varvec{t}} + A_{12}({\varvec{d}}_1\otimes {\varvec{d}}_2+ {\varvec{d}}_2\otimes {\varvec{d}}_1), \nonumber \\ {\varvec{B}}= & {} B_{13}{\varvec{d}}_1\otimes {\varvec{t}}+ B_{31}{\varvec{t}}\otimes {\varvec{d}}_1 + B_{23}{\varvec{d}}_2\otimes {\varvec{t}}+ B_{32}{\varvec{t}}\otimes {\varvec{d}}_2\,, \nonumber \\ {\varvec{C}}= & {} C_1{\varvec{d}}_1\otimes {\varvec{d}}_1+ C_2{\varvec{d}}_2\otimes {\varvec{d}}_2+ C_3{\varvec{t}}\otimes {\varvec{t}} + C_{12}({\varvec{d}}_1\otimes {\varvec{d}}_2+ {\varvec{d}}_2\otimes {\varvec{d}}_1). \end{aligned}$$
(5)

The constitutive coefficients \(\,A_i\,,\,C_i\,,\,A_{12}\,,\,C_{12}\,,\,B_{\alpha 3}\,\) and \(\,B_{3\alpha }\,\) describe the effective stiffness properties of thin rods.

2.1 Governing equations for straight rods

In what follows, we restrict our attention to the case of straight composite rods, i.e., the case when the reference curve \(\,{\mathcal {C}}_0\,\) is a straight line. In this case, the governing equations (1)–(5) can be simplified. Thus, let us choose the Cartesian coordinate frame \(\,Ox_1x_2x_3\,\) such that the reference curve \(\,{\mathcal {C}}_0\,\) is situated on the axis \(\,Ox_3\,\) (between the limits \(\,x_3=0,l\)), while the axis \( Ox_1\) and \(Ox_2\) are parallel to the vectors \({\varvec{d}}_1\) and \({\varvec{d}}_2\,\). If we denote by \({\varvec{e}}_i\) the unit vectors along the axes \(Ox_i\,\), then we have \(\,{\varvec{d}}_1={\varvec{e}}_1\) , \({\varvec{d}}_2={\varvec{e}}_2\) , \({\varvec{d}}_3={\varvec{e}}_3={\varvec{t}}\,\) and \(\,s=x_3\,\).

We designate the inertia moments of the cross section by

$$\begin{aligned} I_1= \displaystyle {\int _\varSigma } \,\rho \, x_2^2 \,\mathrm {d}x_1\mathrm {d}x_2\, , \qquad I_2= \displaystyle {\int _\varSigma } \,\rho \, x_1^2 \,\mathrm {d}x_1\mathrm {d}x_2\,, \end{aligned}$$
(6)

where \(\varSigma \) denotes the domain occupied by the cross section of the rod in the \(x_1Ox_2\) plane, while \(\rho \) is the mass density in the three-dimensional rod. Further, we choose the axis \( Ox_1\) and \(Ox_2\) to coincide with the principal axes of inertia of the cross section. Hence, we have

$$\begin{aligned} \langle \,\rho \, x_1 \,\rangle = \langle \,\rho \, x_2 \,\rangle =0\qquad \text{ and }\qquad \langle \,\rho \, x_1 x_2 \,\rangle =0, \end{aligned}$$
(7)

where we employ the notation \(\,\langle \,f\,\rangle =\displaystyle {\int _\varSigma } \,f \,\mathrm {d}x_1\mathrm {d}x_2\,\) for any field \(\,f\,\).

In order to write the component forms of the basic equations for composite straight rods, we decompose the vectors \(\,{\varvec{u}}\,,\,\varvec{\psi }\,,\,{\varvec{N}}\,,\, {\varvec{M}}\,,\,\varvec{{\mathcal {F}}}\,\) and \(\,\varvec{{\mathcal {L}}}\,\) by the axial direction \(\,{\varvec{e}}_3\,\) and the normal plane \(\,({\varvec{e}}_1, {\varvec{e}}_2)\,\) as follows

$$\begin{aligned} {\varvec{u}}= & {} u\,{\varvec{e}}_3+{\varvec{w}},\qquad \varvec{\psi }= \psi \,{\varvec{e}}_3+{\varvec{e}}_3\times \varvec{\vartheta }\,, \qquad {\varvec{N}}=F\,{\varvec{e}}_3+{\varvec{Q}}, \nonumber \\ {\varvec{M}}= & {} H\,{\varvec{e}}_3+{\varvec{e}}_3\times {\varvec{L}},\quad \,\, \varvec{{\mathcal {F}}}={\mathcal {F}}_a\,{\varvec{e}}_3+ \varvec{{\mathcal {F}}}_n, \,\,\quad \varvec{{\mathcal {L}}}= {\mathcal {L}}_a\,{\varvec{e}}_3+\varvec{{\mathcal {L}}}_n\,, \end{aligned}$$
(8)

where the vectors \(\,{\varvec{w}}\,,\,\varvec{\vartheta }\,,\, {\varvec{Q}}\,,\,{\varvec{L}}\,,\,\varvec{{\mathcal {F}}}_n\,\) and \(\,\varvec{{\mathcal {L}}}_n\,\) are parallel to the plane \(\,({\varvec{e}}_1, {\varvec{e}}_2)\). In the relations (8), \(\,u\,\) represents the longitudinal displacement, \(\,{\varvec{w}}=w_\alpha {\varvec{e}}_\alpha \,\) is the vector of transversal displacement, \(\,\,\psi \,\,\) is the torsion, \(\,\varvec{\vartheta }^{\prime }=\vartheta _\alpha ^{\,\prime }{\varvec{e}}_\alpha \,\) is the vector of bending deformation, \(\,F\,\) is the longitudinal force, \(\,{\varvec{Q}}=Q_\alpha {\varvec{e}}_\alpha \,\) is the vector of transversal force, \(\,H\,\) is the torsion moment and \(\,{\varvec{L}}=L_\alpha {\varvec{e}}_\alpha \,\) is the vector of bending moment. With these notations, the relations (3)–(5) yield the following constitutive equations

$$\begin{aligned} Q_1= & {} A_1(w_1'\!-\!\vartheta _1)+A_{12}(w_2'\!-\!\vartheta _2)+B_{13}\psi ',\nonumber \\ Q_2= & {} A_{12}(w_1'\!-\!\vartheta _1)+A_{2}(w_2'\!-\!\vartheta _2)+B_{23}\psi ',\nonumber \\ F= & {} A_3\,u'-B_{31}\,\vartheta ^{\,\prime }_2+B_{32}\,\vartheta ^{\,\prime }_1,\nonumber \\ H= & {} C_3\psi '+B_{13}(w_1'\!-\!\vartheta _1)+B_{23}(w_2'\!-\!\vartheta _2),\nonumber \\ L_1= & {} C_2\,\vartheta ^{\,\prime }_1-C_{12}\,\vartheta ^{\,\prime }_2+B_{32}\,u',\qquad L_2=-C_{12}\,\vartheta ^{\,\prime }_1+C_1\, \vartheta ^{\,\prime }_2-B_{31}\,u'\,. \end{aligned}$$
(9)

From the above relations, we see that the constitutive coefficients \(C_1\) and \(C_2\) represent the bending effective stiffness, \(C_3\) characterizes the torsional rigidity, \(A_1\) and \(A_2\) are the shear effective stiffness coefficients, \(A_3\) expresses the extensional effective stiffness, while \(\,B_{\alpha 3}\,,\,B_{3\alpha }\,\,C_{12}\,,\,A_{12}\,\) are coupling coefficients.

If the material properties of the non-homogeneous rod are independent of the axial coordinate, then the constitutive coefficients \(\,A_i\,,\,C_i\,,\,A_{12}\,,\,C_{12}\,,\,B_{\alpha 3}\,\) and \(\,B_{3\alpha }\,\) are constant. In the following sections, we express these constitutive coefficients in terms of the three-dimensional material constants for composite rods.

3 Non-homogeneous rods: relation to the three-dimensional model

For non-homogeneous rods, let us denote by \(\,{\varvec{u}}^*= u_i^*{\varvec{e}}_i\, \) the displacement vector and by \(\,{\varvec{T}}^*= t_{ij}^* {\varvec{e}}_i\otimes {\varvec{e}}_j\,\) the Cauchy stress tensor in the three-dimensional linear theory. The relationship between these fields and the corresponding quantities defined in the direct approach (see Sect. 2.1) is given by

$$\begin{aligned} \rho _0w_\alpha= & {} \langle \,\rho \,u_\alpha ^*\,\rangle \,,\qquad \rho _0 u=\langle \,\rho \,u_3^*\,\rangle \,,\qquad \rho _0=\langle \,\rho \,\,\rangle \,,\nonumber \\ \vartheta _1= & {} -\dfrac{\langle \,\rho \,x_1u_3^*\,\rangle }{I_2}\,,\qquad \vartheta _2=-\dfrac{\langle \,\rho \,x_2u_3^*\,\rangle }{I_1}\,,\qquad \psi =\dfrac{\langle \,\rho (x_1u_2^*-x_2u_1^*)\,\rangle }{I_1+I_2}\,,\nonumber \\ Q_\alpha= & {} \langle \,t_{3\alpha }^*\,\rangle \,,\quad F=\langle \,t_{33}^*\,\rangle \,,\quad L_\alpha =-\langle \,x_\alpha t_{33}^*\,\rangle \,,\quad H=\langle \,x_1t_{32}^*-x_2t_{31}^*\,\rangle \,. \end{aligned}$$
(10)

To determine the effective stiffness coefficients \(\,A_i\,,\,C_i\,,\,A_{12}\,,\,C_{12}\,,\,B_{\alpha 3}\,\) and \(\,B_{3\alpha }\,\) we compare the solutions of some extension, bending and torsion problems for directed curves with the corresponding results obtained for three-dimensional rods (see, e.g., [17]). The comparison procedure is described in details in [4].

We assume that the three-dimensional rod is made of an orthotropic non-homogeneous material, characterized by the mass density \(\,\rho (x_1,x_2)\,\) and the nine constitutive coefficients \(c_{ij}(x_1,x_2)\). The three-dimensional constitutive equations for orthotropic materials are

$$\begin{aligned} t^*_{11}= & {} c_{11}e_{11}+c_{12}e_{22}+ c_{13}e_{33}\,, \qquad t^*_{22}=c_{12}e_{11}+c_{22}e_{22} +c_{23}e_{33}, \nonumber \\ t^*_{33}= & {} c_{13}e_{11}+c_{23}e_{22} + c_{33}e_{33}\,,\quad t^*_{23}=2c_{44}e_{23}\,,\quad t^*_{31}=2c_{55}e_{31}\,,\quad t^*_{12}=2c_{66}e_{12}\,, \end{aligned}$$
(11)

where \(\,e_{ij}=\frac{1}{2}(u_{i,j}^*+u_{j,i}^*)\,\) is the strain tensor.

The solution of the extension-bending-torsion problem for three-dimensional rods is determined in [17, Sect. 4.1] and is expressed in terms of the solutions to some auxiliary plane strain boundary-value problems. Namely, let us denote by \(\,u_\alpha ^{(k)}(x_1,x_2)\,\) the solutions of the plane strain problems \(\,{\mathcal {Q}}^{(k)}\,\), respectively, (\(k=1,2,3\)), defined by

$$\begin{aligned}&{\mathcal {Q}}^{(\gamma )}:\qquad t_{\beta \alpha ,\beta }+(c_{\alpha 3}\, x_\gamma )_{,\alpha }=0\quad \mathrm {in}\,\,\, \varSigma ,\qquad t_{\beta \alpha }n_\beta =-c_{\alpha 3}\, x_\gamma n_{\alpha } \quad \mathrm {on}\,\,\, \partial \varSigma ,\nonumber \\&{\mathcal {Q}}^{(3)}: \qquad t_{\beta \alpha ,\beta }+c_{\alpha 3,\alpha }=0\quad \quad \mathrm {in}\,\,\, \varSigma ,\qquad \quad t_{\beta \alpha }n_\beta =-c_{\alpha 3}\, n_{\alpha } \quad \mathrm {on}\,\,\, \partial \varSigma \,, \end{aligned}$$
(12)

where the subscript \(\,\alpha =1,2\,\) is not summed, while the subscript \(\,\beta =1,2\,\) is summed. The vector \(\,{\varvec{n}}=n_\alpha {\varvec{e}}_\alpha \,\) is the outward unit normal to \(\,\partial \varSigma \,\). The tensor components \( t_{\beta \alpha } \) which appear in (12) are given by \(\, t_{11}=c_{11}u_{1,1}+c_{12}u_{2,2} \,\), \(\, t_{22}=c_{12}u_{1,1}+c_{22}u_{2,2}\, \), and \(\, t_{12}=c_{66}(u_{1,2}+u_{2,1}) \).

Further, the so-called torsion function \(\varphi (x_1,x_2)\) is determined by the boundary-value problem

$$\begin{aligned}&(c_{55}\,\varphi _{,1})_{,1}+(c_{44}\,\varphi _{,2})_{,2}= c_{55,1}\,x_2-c_{44,2}\,x_1 \qquad \mathrm {in}\quad \varSigma ,\nonumber \\&c_{55}\,\varphi _{,1}\,n_1+c_{44}\,\varphi _{,2}\,n_2= c_{55}\,x_2\,n_1- c_{44}\,x_1\,n_2\qquad \mathrm {on}\quad \partial \varSigma . \end{aligned}$$
(13)

The functions \(\,u_\alpha ^{(k)}\) and \(\varphi \,\), which are defined as the solutions of the boundary-value problems (12) and (13), will be used to write the expressions of the effective stiffness coefficients. If we identify the three-dimensional solution for the extension, bending and torsion of rods presented in [17, Sect. 4.11] with the corresponding solution for directed curves, then we obtain the following expressions of the effective stiffness coefficients

$$\begin{aligned} A_3= & {} \langle \, c_{33}+c_{13} u_{1,1}^{(3)}+c_{23} u_{2,2}^{(3)}\,\rangle \,,\qquad B_{13}=B_{23}=0,\nonumber \\ B_{31}= & {} \langle \, x_2(c_{33}+c_{13} u_{1,1}^{(3)}+c_{23} u_{2,2}^{(3)})\,\rangle \,,\quad B_{32}=- \langle \, x_1(c_{33} +c_{13} u_{1,1}^{(3)}+c_{23} u_{2,2}^{(3)})\,\rangle \,, \nonumber \\ C_1= & {} \langle \, x_2(c_{33}x_2 +c_{13} u_{1,1}^{(2)}+c_{23} u_{2,2}^{(2)})\,\rangle ,\quad C_{12}=- \langle \, x_1(c_{33}x_2 +c_{13} u_{1,1}^{(2)}+c_{23} u_{2,2}^{(2)})\rangle , \nonumber \\ C_2= & {} \langle \, x_1(c_{33}x_1 +c_{13} u_{1,1}^{(1)}+c_{23} u_{2,2}^{(1)})\,\rangle \,, \;\; C_3=\!\langle \,c_{44}x_1(x_1\!+\!\varphi _{,2})+c_{55}x_2(x_2\!-\!\varphi _{,1})\rangle . \end{aligned}$$
(14)

The identification procedure is described in details in [4].

In the next section, we shall generalize the formulas (14) to the case of composite beams made of several orthotropic materials.

4 General composite beams made of orthotropic materials

Let us consider a general composite beam which is made of \(\,n\,\) different non-homogeneous orthotropic materials and occupies in its reference configuration the three-dimensional domain \(\,{\mathcal {B}} = \{(x_1,x_2,x_3)\,|\, (x_1,x_2)\in \varSigma \,,x_3\in (0,l)\}\,\).

The cross section \(\,\varSigma \,\) consists of \(\,n\,\) pairwise disjoint sub-domains \(\,S_1\,,\)...,\(\,S_n\,\), as shown in Fig. 1a. The generic cross section \(\,\varSigma \,\) may include a number of \(\,\,m\,\) ‘layers’ \(\,S_1\,,\dots ,\,S_m\,\) and an arbitrary number of ‘inclusions’ \(\,S_{m+1}\,,\dots ,\,S_n\) (with \(0\le m\le n\)). Thus, the body \(\,{\mathcal {B}} \,\) can be decomposed into \(\,n\,\) domains \(\,{\mathcal {B}}_k= \{(x_1,x_2,x_3)\,|\, (x_1,x_2)\in S_k\,,x_3\in (0,l)\}\,\), such that each body \(\,{\mathcal {B}}_k\) is occupied by a different non-homogeneous orthotropic material having the axes of orthotropy \(Ox_i\,\) and the constitutive coefficients \(\,c_{ij}^{(k)}(x_1,x_2)\), \(\; k=1,\dots ,n \).

Fig. 1
figure 1

a The cross section of a general composite beams; b The separation curve between the domains \(S_l\) and \(S_r\)

Full size image

We designate by \(\,{\mathcal {C}}_k\) the boundary curve of the domain \(S_k\) which does not belong to the cross section boundary \(\partial \varSigma \), i.e., \(\,\,{\mathcal {C}}_k=\partial S_k\setminus \partial \varSigma \,\) (\(k=1,...,n\)). Let \(\,{\varvec{n}}=n_\alpha {\varvec{e}}_\alpha \,\) be the unit normal to the curve \(\,{\mathcal {C}}_k\) (see Fig. 1b). If \(\,{\mathcal {C}}_k\) separates the domains \(S_l\) and \(S_r\,\) (with \( l<r \)), then we denote the jump of any field f across \(\,{\mathcal {C}}_k\) by \(\big [\,f\,\big ]_{-}^{+} \,\,= \,\, f_{\big | S_r}-f_{\big | S_l}\,\).

Assume that the bodies \(\,{\mathcal {B}}_k\) are welded together and there is no separation of material during deformation. The conditions that the displacement and the stress vector fields are continuous in passing from one material to another have to be adjoin to the plane strain boundary-value problems (12), (13), in the case of composite materials. Thus, we consider the extended plane strain boundary-value problems \(\,{\mathcal {R}}^{(1)}\,\), \(\,{\mathcal {R}}^{(2)}\,\) and \(\,{\mathcal {R}}^{(3)}\,\) given by

$$\begin{aligned}&{\mathcal {R}}^{(\gamma )}:\left\{ \begin{array}{l} t_{\beta \alpha ,\,\beta }=-(c_{\alpha 3}\, x_\gamma )_{,\,\alpha }\quad \mathrm {in}\,\,\, \,S_k\,,\qquad \quad (\gamma =1,2)\\ t_{\beta \alpha }n_\beta =-c_{\alpha 3}\, x_\gamma n_{\alpha } \quad \mathrm {on}\,\,\, \partial \varSigma ,\\ \big [u_\alpha \big ]_{-}^{+}=0,\quad n_\beta \big [ t_{\beta \alpha }+c_{\alpha 3}\, x_\gamma \delta _{\alpha \beta } \big ]_{-}^{+}=0\quad \mathrm {on}\,\,\,\, {\mathcal {C}}_k \,\,\,(k=1,...,n), \end{array}\right. \nonumber \\&{\mathcal {R}}^{(3)}:\left\{ \begin{array}{l} t_{\beta \alpha ,\,\beta }=-c_{\alpha 3,\,\alpha }\quad \mathrm {in}\,\,\, \,S_k\,\,\,(k=1,...,n),\\ t_{\beta \alpha }n_\beta =-c_{\alpha 3}\, n_{\alpha } \quad \mathrm {on}\,\,\, \partial \varSigma ,\\ \big [u_\alpha \big ]_{-}^{+}=0,\quad n_\beta \big [ t_{\beta \alpha }+c_{\alpha 3} \,\delta _{\alpha \beta } \big ]_{-}^{+}=0\quad \mathrm {on}\,\,\,\, {\mathcal {C}}_k \,\,\,(k=1,...,n), \end{array}\right. \end{aligned}$$
(15)

where the subscript \(\,\alpha =1,2\,\) is not summed. The solutions of the problems \({\mathcal {R}}^{(s)}\) will be denoted by \(u_\alpha ^{(s)}(x_1,x_2)\), \(s=1,2,3\). The torsion function \(\varphi (x_1,x_2)\) for composite rods is determined from the extended boundary-value problem

$$\begin{aligned}&\left\{ \begin{array}{l} (c_{55}\,\varphi _{,1})_{,1}+(c_{44}\,\varphi _{,2})_{,2}= c_{55,1}\,x_2-c_{44,2}\,x_1 \quad \mathrm {in}\,\,\,\,\, S_k\,\,\,(k=1,...,n),\\ c_{55}\,\varphi _{,1}\,n_1+c_{44}\,\varphi _{,2}\,n_2= c_{55}\,x_2\,n_1- c_{44}\,x_1\,n_2 \quad \mathrm {on}\,\,\, \partial \varSigma ,\\ \big [\varphi \big ]_{-}^{+}=0,\qquad \big [ c_{55}\,\varphi _{,1}\,n_1+c_{44}\,\varphi _{,2}\,n_2- c_{55}\,x_2\,n_1+ c_{44}\,x_1\,n_2 \big ]_{-}^{+}=0 \quad \mathrm {on}\,\,\,\, {\mathcal {C}}_k\,.\end{array}\right. \end{aligned}$$
(16)

If we generalize the analysis made in [4, Sect. 6] to the case of \(\,n\,\) orthotropic materials, then we find the following expressions for the effective stiffness coefficients in terms of the solutions \(u_\alpha ^{(s)} \) and \(\varphi \,\):

$$\begin{aligned} A_3= & {} \!\displaystyle {\sum _{k=1}^{n}\int _{S_k}} \big (c_{33}^{(k)}+c_{13}^{(k)} u_{1,1}^{(3)}+c_{23}^{(k)} u_{2,2}^{(3)}\big )\mathrm {d}x_1\mathrm {d}x_2\,,\qquad A_{12}=0, \nonumber \\ B_{31}= & {} \displaystyle {\sum _{k=1}^{n}\int _{S_k}} x_2\big (c_{33}^{(k)}+c_{13}^{(k)} u_{1,1}^{(3)}+c_{23}^{(k)} u_{2,2}^{(3)}\big )\mathrm {d}x_1\mathrm {d}x_2\,,\qquad B_{13}=0,\nonumber \\ B_{32}= & {} - \displaystyle {\sum _{k=1}^{n}\int _{S_k}} x_1\big (c_{33}^{(k)} +c_{13}^{(k)} u_{1,1}^{(3)}+c_{23}^{(k)} u_{2,2}^{(3)}\big )\mathrm {d}x_1\mathrm {d}x_2\,, \qquad B_{23}=0,\nonumber \\ C_1= & {} \!\!\displaystyle {\sum _{k=1}^{n}\int _{S_k}} x_2\big ( c_{33}^{(k)}x_2 +c_{13}^{(k)} u_{1,1}^{(2)}+c_{23}^{(k)} u_{2,2}^{(2)}\big )\mathrm {d}x_1\mathrm {d}x_2,\nonumber \\ C_2= & {} \displaystyle {\sum _{k=1}^{n}\int _{S_k}} x_1(c_{33}^{(k)}x_1 +c_{13}^{(k)} u_{1,1}^{(1)}+c_{23}^{(k)} u_{2,2}^{(1)})\mathrm {d}x_1\mathrm {d}x_2\,,\nonumber \\ C_{12}= & {} - \displaystyle {\sum _{k=1}^{n}\int _{S_k}} x_1\big ( c_{33}^{(k)}x_2 +c_{13}^{(k)} u_{1,1}^{(2)}+ c_{23}^{(k)} u_{2,2}^{(2)}\big )\mathrm {d}x_1\mathrm {d}x_2\,,\nonumber \\ C_3= & {} \displaystyle {\sum _{k=1}^{n}\int _{S_k}} \big [c_{44}^{(k)}x_1(x_1+\varphi _{,2})+ c_{55}^{(k)}x_2(x_2-\varphi _{,1})\big ]\mathrm {d}x_1\mathrm {d}x_2\,, \end{aligned}$$
(17)

and for the transverse shear stiffness we obtain

$$\begin{aligned} A_1= & {} \dfrac{\kappa \, \mathrm {A}(\varSigma )}{\langle \,x_1^2\,\rangle } \Big ( \displaystyle {\sum _{k=1}^{n}\!\int _{S_k}}\!\! c_{55}^{(k)}\mathrm {d}x_1\mathrm {d}x_2\Big ) \Big (\displaystyle {\sum _{k=1}^{n}\!\int _{S_k}}\!\! \rho ^{(k)}x_1^2\mathrm {d}x_1\mathrm {d}x_2\Big )\Big (\displaystyle { \sum _{k=1}^{n}\! \int _{S_k}}\!\! \rho ^{(k)}\mathrm {d}x_1\mathrm {d}x_2\Big )^{-1}\!,\nonumber \\ A_2= & {} \dfrac{\kappa \, \mathrm {A}(\varSigma )}{\langle \,x_2^2\,\rangle } \Big ( \displaystyle {\sum _{k=1}^{n}\!\int _{S_k}}\!\! c_{44}^{(k)}\mathrm {d}x_1\mathrm {d}x_2\Big ) \Big (\displaystyle {\sum _{k=1}^{n}\!\int _{S_k}}\!\! \rho ^{(k)}x_2^2\mathrm {d}x_1\mathrm {d}x_2\Big )\Big (\displaystyle { \sum _{k=1}^{n}\!\int _{S_k}} \!\!\rho ^{(k)}\mathrm {d}x_1\mathrm {d}x_2\Big )^{-1}\!. \end{aligned}$$
(18)

where \(\,\kappa =\dfrac{\pi ^2}{12}\,\,\) is the shear correction factor and \( \mathrm {A}(\varSigma ) \) denotes the area of \(\varSigma \).

Remark

Notice that the relations (17) represent a generalization of equations (14) for the case of several materials. In the case of piecewise homogeneous composite beams, the formulas (17) for the effective stiffness properties can be simplified, since the constitutive coefficients \(\,c_{ij}\,\) are then piecewise constant in \(\varSigma \).

4.1 Composite beams made of isotropic materials

Let us consider the special case when the composite beams consist of \(\,n\,\) isotropic materials. If we denote by \( \lambda ^{(k)} \) and \( \mu ^{(k)} \) the Lamé moduli of each constituent material (\( k=1,\dots ,n \)), then the constitutive relations (11) hold with

$$\begin{aligned} c_{11}^{(k)}= & {} c_{22}^{(k)} =c^{(k)}_{33}= \lambda ^{(k)}+ 2\mu ^{(k)}, \nonumber \\ c_{12}^{(k)}= & {} c_{13}^{(k)} =c^{(k)}_{23}= \lambda ^{(k)},\qquad c_{44}^{(k)}=c_{55}^{(k)} =c^{(k)}_{66}= \mu ^{(k)}. \end{aligned}$$
(19)

Substituting the relations (19) into the equations (15)-(18), we obtain the corresponding expressions of the effective stiffness coefficients in the isotropic case. For instance, for the torsional rigidity \(C_3\) and shear effective stiffness \(A_1\,,\,A_2\) we find the formulas

$$\begin{aligned} C_3= & {} \displaystyle {\sum _{k=1}^{n}\int _{S_k}} \mu ^{(k)}\big [x_1(x_1+\varphi _{,2})+x_2(x_2-\varphi _{,1})\big ] \mathrm {d}x_1\mathrm {d}x_2\,,\nonumber \\ A_\alpha= & {} \dfrac{\kappa \, \mathrm {A}(\varSigma )}{\langle \,x_\alpha ^2\,\rangle } \Big ( \displaystyle {\sum _{k=1}^{n}\!\int _{S_k}}\!\! \mu ^{(k)}\mathrm {d}x_1\mathrm {d}x_2\Big ) \Big (\displaystyle {\sum _{k=1}^{n}\!\int _{S_k}}\!\! \rho ^{(k)}x_\alpha ^2\mathrm {d}x_1\mathrm {d}x_2\Big )\Big (\displaystyle { \sum _{k=1}^{n}\! \int _{S_k}}\!\! \rho ^{(k)}\mathrm {d}x_1\mathrm {d}x_2\Big )^{-1}\!. \end{aligned}$$
(20)

These results for composite beams made of isotropic materials have been obtained previously in the paper [5].

These formulas for the effective stiffness properties of composite beams made of several non-homogeneous materials are very general and are applicable to a variety of problems. The difficulty resides in finding the solutions to the plane strain boundary-value problems (15) and (16). In some special cases, the boundary-value problems (15), (16) can be solved analytically and the formulas for the effective stiffness coefficients (17), (18) can be simplified.

In the case of composite beams made of isotropic materials with constant Poisson ratio \(\,\nu \,\) (the same constant for all material constituents), the plane strain boundary-value problems \({\mathcal {R}}^{(s)}\) written in (15) admit the following simple solutions

$$\begin{aligned} u_1^{(1)}= & {} -\dfrac{1}{2}\,\nu (x_1^2-x_2^2)\,,\qquad u_2^{(1)}=-\nu \, x_1x_2\,, \qquad u_1^{(2)}=-\nu \, x_1x_2\,, \nonumber \\ u_2^{(2)}= & {} \dfrac{1}{2}\,\nu (x_1^2-x_2^2)\,,\qquad u_1^{(3)}= -\nu \, x_1\,,\qquad u_2^{(3)}=-\nu \, x_2\,. \end{aligned}$$
(21)

We mention that the case of non-homogeneous materials with constant Poisson ratio has been investigated within the classical three-dimensional elasticity theory, e.g., in [21]. Let us denote by \(\,E^{(k)}(x_1,x_2)\) the Young modulus of the non-homogeneous material occupying the domain \({\mathcal {B}}_k\,\). As mentioned above, the Poisson ratio is the same for all materials, i.e., we assume that \(\nu ^{(k)}(x_1,x_2)=\nu \) (constant).

Inserting the relations (19) and (21) into the formulas (17), we obtain in this case the following effective stiffness coefficients [5]

$$\begin{aligned} A_3= & {} \displaystyle {\sum _{k=1}^{n}\int _{S_k}} E^{(k)} \mathrm {d}x_1\mathrm {d}x_2, \qquad A_{12}=0, \qquad B_{31}=\displaystyle {\sum _{k=1}^{n}\int _{S_k}} x_2E^{(k)}\mathrm {d}x_1\mathrm {d}x_2, \nonumber \\ B_{32}= & {} - \displaystyle {\sum _{k=1}^{n}\int _{S_k}} x_1E^{(k)}\mathrm {d}x_1\mathrm {d}x_2 , \qquad B_{\alpha 3}=0, \qquad C_1= \displaystyle {\sum _{k=1}^{n}\int _{S_k}} x_2^2\,E^{(k)}\mathrm {d}x_1\mathrm {d}x_2,\nonumber \\ C_2= & {} \displaystyle {\sum _{k=1}^{n}\int _{S_k}} x_1^2\,E^{(k)}\mathrm {d}x_1\mathrm {d}x_2\,,\qquad C_{12}=- \displaystyle {\sum _{k=1}^{n}\int _{S_k}} x_1x_2\,E^{(k)}\mathrm {d}x_1\mathrm {d}x_2\,. \end{aligned}$$
(22)

The above relations will be employed in the next sections to determine the effective stiffness properties of various sandwich beam structures.

5 Multilayered beams

In this section, we investigate the effective stiffness properties of multilayered beams, which are a type of widely used composite structures.

We consider rectangular beams with \(\,n\,\) layers made of isotropic and homogeneous materials. The pattern of the cross section \(\,\varSigma \,\) for such composite beams is depicted in Fig. 2. Thus, the cross-sectional domain is

$$\begin{aligned} \,\varSigma =\big \{(x_1,x_2)\,\big |\, x_1\in \big (-\frac{b}{2}\,,\frac{b}{2}\,\big ), \; x_2\in (z_n,z_0)\big \}\,\quad \text{ with } \text{ thickness }\;\; a=z_0-z_n\,. \end{aligned}$$

Here, \(\, b\, \) denotes the width of the cross section. The \(\,n\,\) layers \( \,S_i\, \) (\( i=1,\dots ,n \)) occupy the domains

$$\begin{aligned} \,S_i=\big \{(x_1,x_2)\,\big |\, x_1\in \big (-\frac{b}{2}\,,\frac{b}{2}\,\big ), \; x_2\in (z_{i-1},z_i)\big \}\quad \text{ with } \text{ thickness }\;\; t_i=z_i-z_{i-1}\,, \end{aligned}$$

where \(z_0>z_1>...>z_{n-1}>z_n\) are arbitrary real numbers. We denote by \(\,t_i\,\) the thickness, \(\,G_i\,\) the shear modulus, \(\,E_i\,\) the Young modulus, and \(\,\rho _i\,\) the mass density of of the layer \(\,S_i\,\), and by \(\,a=z_0-z_n\,\) the total thickness of the beam.

Fig. 2
figure 2

Cross section of a multilayered beam with n layers

Full size image

5.1 Torsional rigidity for multilayered beams

Let us derive the expression of the torsional rigidity \(\,C_3\,\) for such multilayered beams using the general formula (20)\(_1\,\). The torsion problem (16) reduces to

$$\begin{aligned} \left\{ \begin{array}{l} \varDelta \varphi =0\qquad \text {in}\quad S_1\cup S_2\cup ...\cup S_n\,\,; \\ \dfrac{\partial \varphi }{\partial x_1}=x_2\quad \text {for}\quad x_1=\pm \dfrac{b}{2}\quad ;\quad \dfrac{\partial \varphi }{\partial x_2}=-x_1\quad \text {for}\quad x_2=z_0,z_n\,\,; \\ \big [\varphi \big ]_{-}^{+}=0,\qquad \Big [ \,G\,\big (\,\, \dfrac{\partial \varphi }{\partial x_2}+x_1 \big ) \Big ]_{-}^{+}=0\qquad \mathrm {for}\quad x_2=z_1,\dots ,z_{n-1}\,. \end{array} \right. \end{aligned}$$
(23)

The solution of this problem can be written in the form (series expansion)

$$\begin{aligned} \varphi (x_1,x_2)=x_1x_2 +\sum _{k=0}^{\infty } \big ( A_k^{(i)}\sinh (m\,x_2)+ B_k^{(i)}\cosh (m\,x_2) \big ) \sin (m\,x_1) \quad \text {in}\; S_i\,, \end{aligned}$$
(24)

where \(\,m=\dfrac{(2k+1)\pi }{b}\,\), and \(\,A_k^{(i)}\) and \(\,B_k^{(i)}\) are some constants (\(i=1,...,n\)).

Imposing that the function \(\varphi (x_1,x_2)\) given by (24) satisfies the boundary and continuity conditions on the surfaces \(\,x_2=z_0, z_1,\dots ,z_n\) written in (23)\(_{3,4,5}\), we find the equations

$$\begin{aligned} A_k^{(j)}\sinh (mz_j)+B_k^{(j)}\cosh (mz_j)= & {} A_k^{(j+1)}\sinh (mz_j)+B_k^{(j+1)}\cosh (mz_j), \nonumber \\ G_i\big [A_k^{(i)}\!\cosh (mz_i)+B_k^{(i)}\!\sinh (mz_i)\big ]= & {} G_{i+1}\big [A_k^{(i+1)}\!\cosh (mz_i)+B_k^{(i+1)}\!\sinh (mz_i)\big ] \nonumber \\&+ (G_{i+1}-G_i)\,(-1)^k\,\dfrac{8\,b^2}{\pi ^3(2k+1)^3}\;, \end{aligned}$$
(25)

for any \( i=0,1,\dots ,n \) and \( j=1,...,n-1 \). For each fixed integer \(\,k\,\), the relations (25) represent a system of 2n linear algebraic equations for the 2n unknowns \(\,A_k^{(i)}\) and \(\,B_k^{(i)}\) (\(i=1,...,n\)). Thus, the system (25) allows for the determination of the constants \(\,A_k^{(i)}\) and \(\,B_k^{(i)}\) and the torsion boundary–value problem (23) is solved.

If we introduce now the torsion function (24) into the formula (20)\(_1\,\), then we find the torsional rigidity for multilayered beams in the form

$$\begin{aligned} C_3=\dfrac{b^3}{3}\Big (\!\sum _{i=1}^{n} G_it_i\!\Big )+ 4\!\sum _{i=0}^{n} \Big [\!(G_{i+1}-G_i) \!\! \sum _{k=0}^{\infty } \dfrac{(-1)^k}{m^2}\big (A_k^{(i)}\sinh (mz_i)+B_k^{(i)}\cosh (mz_i)\big )\Big ], \end{aligned}$$
(26)

where \(\,A_k^{(i)}\) and \(\,B_k^{(i)}\) are given by (25). In order to have a compact unified form for the relations (25) and (26), we have introduced above the additional notation conventions \(G_0=0\), \(G_{n+1}=0\), \(A_k^{(0)}=A_k^{(1)}\) and \(B_k^{(0)}=B_k^{(1)}\).

The formula (26) is valid for an arbitrary number of layers \(\,n\). Let us present some special cases and make connections with previously known results.

Remarks

1. :

In the case of beams with 2 layers (\(n=2\)), the system of equations (25) has only 4 equations and it can be solved explicitly to find the constants \(A_k^{(1)}\,,\, A_k^{(2)}\,,\,B_k^{(1)}\) and \(B_k^{(2)}\). Then, inserting these values in the formula (26) we obtain the torsional rigidity

$$\begin{aligned} C_3= & {} \dfrac{b^3}{3}\Big [\big ( G_1t_1+ G_2t_2\big )- \dfrac{192\,b}{\pi ^5}\,\, \displaystyle { \sum _{k=0}^{\infty }} \dfrac{D_{(k)}}{(2k+1)^5}\Big ]\,,\qquad \mathrm {with}\nonumber \\ D_{(k)}= & {} \Big (G_1\sinh (mt_1)\cosh (mt_2)\!+\!G_2\sinh (mt_2)\cosh (mt_1)\Big )^{-1} \times \nonumber \\&\times \Big [(G_1^2\!+\!G_2^2)\cosh (mt_1)\cosh (mt_2) -G_1^2\cosh (mt_2)\!-\!G_2^2\cosh (mt_1)\nonumber \\&+ G_1G_2 \big (\cosh (mt_1)\!+\!\cosh (mt_2)\!-\! \cosh m(t_1\!-\!t_2)\!-\!1\big )\Big ]\,, \end{aligned}$$
(27)

where we denote by \(\,m=\frac{(2k+1)\pi }{b}\,\) and \(t_1\,,\,t_2\) are the thicknesses of the two layers. The expression (27) coincides with the result obtained previously in [17, p. 318].

2. :

In the case of beams with three layers (\(n=3\)), the torsion function \(\,\varphi (x_1,x_2)\,\) is determined by the relation (24) and the system (25), which has 6 equations. We mention that the same torsion function for three-layered beams has been obtained previously in [7, Sect. 81]. This special case can describe sandwich beams with dissimilar faces, see [5, Sect. 6]. Then, from relation (26) with \(n=3\) we get the torsional rigidity expression for non-symmetrical sandwich beams.

3. :

We can generalize the above results concerning the torsional rigidity of multilayered beams to the case of orthotropic materials. Indeed, in this purpose we have to solve the boundary-value problem (16) and use the torsional rigidity formula (17)\(_{10}\) for orthotropic beams. The analysis is similar, except for a greater mathematical complexity.

5.2 Effective bending and extensional stiffnesses

Notice that the middle plane of the layer \(S_k\) is characterized by the equation \(\,x_2=m_k\,\), where we denote \(\,m_k=\frac{z_k+z_{k-1}}{2}\,\) (\(k=1,...,n\)). To compute the effective bending stiffness coefficients, we assume that the Poisson ratio \(\,\nu \,\) is the same for all materials and employ the relations (22). By a simple integration in (22), we find

$$\begin{aligned} A_3= & {} b\,\displaystyle {\sum _{k=1}^n}\, t_kE_k\,,\qquad C_2=\dfrac{b^3}{12}\,\displaystyle {\sum _{k=1}^n }\,t_kE_k\,,\qquad C_{12}=0,\quad B_{32}=0, \nonumber \\ C_1= & {} \dfrac{b}{3}\,\displaystyle {\sum _{k=1}^n} \big (z_{k-1}^3-z_k^3\big )E_k\,,\qquad B_{31}=\dfrac{b}{2}\,\displaystyle {\sum _{k=1}^n} \big (z_{k-1}^2-z_k^2\big )E_k\,. \end{aligned}$$
(28)

Let us denote by \( (EI)_{\mathrm {eq}} \) the equivalent flexural rigidity, which is defined by

$$\begin{aligned} \begin{array}{c} (EI)_{\mathrm {eq}}=C_1-\dfrac{B_{31}^2}{A_3}\,\,. \end{array} \end{aligned}$$
(29)

Inserting (28) into (29) and performing some mathematical calculations, we obtain the expression of the equivalent flexural rigidity for multilayered beams in the form

$$\begin{aligned} (EI)_{\mathrm {eq}}= & {} b\,\Big [\,\displaystyle {\sum _{k=1}^n}\,\dfrac{t_k^3E_k}{12} +\Big (\displaystyle {\sum _{k=1}^n}\, t_kE_k\Big )^{-1}\displaystyle {\sum _{1\le k<l\le n}}\, t_kE_k\cdot t_lE_l\cdot (m_k-m_l)^2\Big ]. \end{aligned}$$
(30)

Notice that the difference \(\,(m_k-m_l)\,\) appearing in (30) is given by

$$\begin{aligned} m_k-m_l= \dfrac{t_k}{2}+t_{k+1}+...+t_{l-1}+\dfrac{t_l}{2}\,\,, \end{aligned}$$

and represents the distance between the middle planes of the layers \(\,S_k\) and \(S_l\,\). We remark that the relation (30) represents a generalization of the formula for flexural rigidity of non-symmetrical sandwich beams given in [52, p. 53].

5.3 Effective shear stiffness of multilayered beams

Let us consider first the case of n-layered beams with a symmetrical arrangement of layers. According to the above notations (see Fig. 2), the separation plane between the layers \(\,S_k\) and \(S_{k+1}\) is characterized by the equation \(\,x_2=z_k\,\). Due to the symmetry, we have \(z_0=-z_n=\frac{a}{2}\,\) and \(\,\rho _k=\rho _{n+1-k}\,,\,\,t_k=t_{n+1-k}\,,\,\,z_k=-z_{n-k}\,\), for any \(k=1,...,n\).

We employ the exact formula for the effective shear stiffness coefficient \(A_2\) for general composite beams, which has been presented in [4, f. (23)]. If we write this formula for the case of multilayered beams, then we obtain the expression

$$\begin{aligned} A_2= & {} k\,\dfrac{ab}{z_0^3-z_n^3}\,\dfrac{\Big (\displaystyle {\sum _{i=1}^n}\, t_iG_i\Big )\cdot \displaystyle {\sum _{i=1}^n} \big (z_{i-1}^3-z_i^3\big )\rho _i}{\Big (\displaystyle {\sum _{i=1}^n}\, t_i\rho _i\Big ) +\displaystyle {\sum _{i=1}^{n-1}}\,(\rho _i-\rho _{i+1})z_i\,F\big (\frac{\pi \, z_i}{a}\big )}\,\,, \end{aligned}$$
(31)

where \(\,F(x)\,\) is the function defined on the interval \(\big (-\frac{\pi }{2}\,,\frac{\pi }{2}\big )\) by

$$\begin{aligned} F(x)=\dfrac{\cos x}{x}\,\ln \Big (\dfrac{1+\sin x}{\cos x}\Big )\quad \mathrm {for}\,\,x\ne 0,\qquad F(0)=1. \end{aligned}$$
(32)

Consider now the general case when the arrangement of the n layers is not necessarily symmetric. According to (7), the position of the axis \(Ox_1\) is determined by the condition \(\,\langle \, \rho \, x_2\,\rangle =0\), which can be written as \(\,\displaystyle {\sum _{k=1}^n}\, \rho _k(z_{k-1}^2-z_k^2)=0\), or equivalently

$$\begin{aligned} \displaystyle {\sum _{k=1}^n}\, \rho _k\,t_k\,(z_{k-1}+z_k)=0, \end{aligned}$$
(33)

since we have

$$\begin{aligned} z_{k-1}-z_k=t_k\,\,,\quad k=1,...,n. \end{aligned}$$
(34)

We can solve the equations (33), (34) as a system of (\(n+1\)) linear algebraic equations for the unknowns \(z_0\), \(z_1\),..., \(z_n\). Thus, we find the values \(z_i\) in terms of the thicknesses of the layers \(t_k\) in the following form

$$\begin{aligned} z_i= \Big (\displaystyle {\sum _{k=1}^n}\, t_k\,\rho _k\,d_{ik}\Big )\cdot \Big (\displaystyle {\sum _{k=1}^n}\, t_k\rho _k\Big )^{-1},\qquad i=0,1,...,n, \end{aligned}$$
(35)

where we have denoted by \( \,d_{ik}\, \) the distances

$$\begin{aligned} d_{ik}=z_i-m_k=-\dfrac{t_k}{2}+(t_1+t_2+...+t_k)-(t_1+t_2+...+t_i). \end{aligned}$$
(36)

We notice that \(\,|d_{ik}|\,\) represents the distance between the middle plane of the layer \(S_k\) and the separation plane of layers \(\,S_i\) and \(S_{i+1}\). We extend the formula (31) also in the case of non-symmetrical beams, with the specification that the coordinates \(\,z_i\) are determined by (35).

To resume, the effective shear stiffness coefficient \(A_2\) for multilayered beams is given by the relations (31) and (35).

Remarks

1. :

In the case of three-layered beams (\(n=3\)), the relations (31), (35) reduce to the formula presented in [5, f. (55)], where the coordinates \(z_0, z_1, z_2\), and \(z_3\) have been explicitly determined.

2. :

If we employ the (approximate) formula (20)\( _2 \) to evaluate the effective shear stiffness \( A_2\, \), then we obtain the simplified version of the relation (31) in the form

$$\begin{aligned} A_2= & {} k\,\dfrac{ab}{z_0^3-z_n^3}\,\Big (\displaystyle {\sum _{i=1}^n}\, t_iG_i\Big )\cdot \Big [\displaystyle {\sum _{i=1}^n} \big (z_{i-1}^3-z_i^3\big )\rho _i\Big ]\cdot \Big (\displaystyle {\sum _{i=1}^n}\, t_i\rho _i\Big )^{-1}, \end{aligned}$$
(37)

where the coordinates \(\,z_i\) are expressed in terms of the thicknesses \(\,t_i\) through equations (35), (36). In the case of sandwich beams with dissimilar faces (\(n=3\)), the relation (37) reduces to the result obtained in [5, f. (57)].

5.4 Bending of cantilever three-layered beam

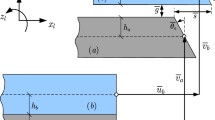
Let us consider the particular case of a three-layered beam (\(n=3\)), i.e., we investigate sandwich beams with dissimilar faces. In this case, we denote by c the thickness of the core layer and by \( E_c \) the Young modulus of the core material. Also, we designate by \( f_1\, \), \( f_2 \) the thicknesses of the two faces and by \( E_{f_1}\, \), \( E_{f_2} \) the Young moduli, respectively. Let \(\,d=c+\frac{f_1+f_2}{2}\,\) be the distance between the middle axis of the faces, see Fig. 3a.

Fig. 3
figure 3

a Cross section of a sandwich beam with dissimilar faces; b Cantilever beam with uniform distributed load q

Full size image

With these notations, the relation (29) for \( n=3 \) reduces to the following formula for the equivalent flexural rigidity of sandwich beams with dissimilar faces

$$\begin{aligned} (EI)_{\mathrm {eq}}= & {} b\Big [ \dfrac{f_1^3E_{f_1}}{12}+\dfrac{f_2^3E_{f_2}}{12}+\dfrac{c^3E_c}{12} \nonumber \\&+ \dfrac{f_1E_{f_1}\cdot f_2E_{f_2} \cdot c E_c}{f_1E_{f_1} + f_2E_{f_2} + cE_c}\Big (\dfrac{d^2}{cE_c}+ \dfrac{(f_1+c)^2}{4f_2E_{f_2}}+ \dfrac{(f_2+c)^2}{4f_1E_{f_1}}\Big )\Big ]. \end{aligned}$$
(38)

The relation (38) is equivalent to the formula for flexural rigidity of non-symmetrical sandwich beams given by Zenkert [52, p. 53]. We mention that the effective stiffness coefficients for sandwich beams with dissimilar faces have been determined previously in [5, Sect. 6].

To apply the above theoretical results, let us consider the bending of a cantilever sandwich beam with dissimilar faces under the action of a uniformly distributed load \(\,q\,\) in the transverse direction \(Ox_2\,\) as shown in Fig. 3b. We solve this bending problem using our model and compare the solution with the results obtained by numerical simulations.

Using the model of directed curves presented in Sect. 2, the relevant equilibrium equations are

$$\begin{aligned} Q_2^{\,\prime }+q=0,\qquad L_2^{\,\prime }+Q_2=0,\qquad F^{\,\prime }=0. \end{aligned}$$
(39)

Then, the constitutive equations (9) reduce to

$$\begin{aligned} Q_2=A_2(w_2^{\,\prime }-\vartheta _2),\qquad L_2=C_1\vartheta _2^{\,\prime }-B_{31}u^{\,\prime },\qquad F=A_3u^{\,\prime }-B_{31}\vartheta _2^{\,\prime }, \end{aligned}$$
(40)

where \(w_2\) is the transverse displacement in \(Ox_2\) direction, \(\vartheta _2\) is the rotation of cross section, and u is the longitudinal displacement. The boundary conditions for the cantilever beam are

$$\begin{aligned}&w_2=0,\qquad \vartheta _2=0,\qquad u=0\qquad \mathrm {for}\quad x_3=0,\nonumber \\&Q_2=0,\qquad L_2=0,\qquad F=0\qquad \mathrm {for}\quad x_3=l, \end{aligned}$$
(41)

Solving the boundary-value problem for ordinary differential equations (39)-(41), we obtain the deflection function

$$\begin{aligned} w_2(x_3)=\dfrac{q}{(EI)_{\mathrm {eq}}}\Big [\dfrac{x_3^4}{24}-l\,\dfrac{x_3^3}{6}\,+\Big (\dfrac{l^2}{2}-\dfrac{(EI)_{\mathrm {eq}}}{A_2}\Big )\dfrac{x_3^2}{2}+ \dfrac{(EI)_{\mathrm {eq}}}{A_2}\,l\,x_3\Big ]. \end{aligned}$$
(42)

Therefore, the maximum deflection \(D=w_2(l)\) has the value

$$\begin{aligned} D= \dfrac{ql^2}{2}\Big (\dfrac{1}{A_2}\,+\,\dfrac{l^2}{4(EI)_{\mathrm {eq}}}\Big ). \end{aligned}$$
(43)

Let us compare the theoretical prediction (43) with the results obtained by a finite element analysis of this problem using the software ABAQUS.

We consider three-layered beams with the following dimensions: length \(l=1\) m, width \(b=50 \) mm, and thicknesses of layers \(f_1=5\) mm, \(f_2=10\) mm, \(c=35\) mm. We analyze three types of such beams, made of the following materials: aluminum–copper–steel, aluminum–foam–steel, and epoxy–foam–polyester, respectively. The material properties \(\{E, \rho \}\) for each layer of these beams are given in Table 1, together with the values of the applied load q.

We denote by \(\,D_{\text {FEM}}\) the maximum deflection of the beam obtained by the finite element method. On the other hand, we designate by \(\,D_{\text {exact}}\) the theoretical value of the maximum deflection (43) when the effective shear stiffness \(A_2\) is expressed by the exact formula (31), while \(\,D_{\text {approx}}\) denotes the maximum deflection (43) when \(A_2\) is given by the approximate expression (37). The relative errors

$$\begin{aligned} \varDelta =\dfrac{D_{\text {FEM}}-D_{\text {exact}}}{\min \big (D_{\text {FEM}}\, ; D_{\text {exact}}\big )}\cdot 100 \end{aligned}$$

are computed for the three types of composite beams considered here and the comparison of numerical and theoretical results is presented in Table 1. Thus, we remark that even the approximate analytical solution \(\,D_{\text {approx}}\) gives accurate results, so that it can be successfully used in many situations.

The good agreement between these solutions represents a validation of our theoretical results concerning the effective stiffness properties of non-symmetrical sandwich beams.

Table 1 Comparison of numerical and analytical results for bending of cantilever three-layered beams
Full size table

5.5 Three-point bending of multilayered beams

Let us consider now the three-point bending of multilayered beams and compare our theoretical results with numerical simulations. The three-point bending problem consists in a beam with simply supported ends, subjected to a central load P, as depicted in Fig. 4a.

Fig. 4
figure 4

a Three-point bending of a beam; b Cantilever beam with concentrated end force P

Full size image

The analytical solution of this three-point bending problem is not difficult to calculate using the direct approach of rods. We find that the maximum deflection D of the beam is given by the well-known formula [15, 52]

$$\begin{aligned} D=\dfrac{P\,l}{4}\,\Big ( \dfrac{l^2}{12\,C_1} \,+\, \dfrac{1}{A_2}\Big ), \end{aligned}$$
(44)

where the effective bending stiffness \(C_1\) is given by (28)\( _5\, \). In the relation (44), the effective shear stiffness \(A_2\) for multilayered beams is calculated either with the exact formula (31), (35), or with the approximate equation (37). This theoretical prediction of the maximum deflection D will be compared with numerical results obtained by finite elements method in the next section.

6 Numerical study and comparison with theoretical results

Let us compare the theoretical results for bending of sandwich beams presented in Sect. 5 with the corresponding numerical solutions obtained by a finite element analysis.

6.1 Methods

In this numerical study, we consider sandwich beams with rectangular cross section. We use the finite element method to compute the deflections of sandwich structures and compare them to identical deflections obtained analytically. All analytical computations were performed by using MathCAD software. The analytical values of deflections \( D_A \) of bended rectangular beams were computed by using formulas (28) and (29) with \( n=5 \) layers, to obtain flexural rigidity. To compute shear rigidity, the formulas (31) and (32) were used. In case of bended sandwiches with rectangular cross sections, the values of shear coefficient factor k were computed by the simplified Voigt method [30]:

$$\begin{aligned} k_v= \dfrac{G_r}{G_V}\;,\qquad \text{ with }\qquad G_r= \left( \sum _{i=1}^5 \dfrac{t_i}{G_ih}\right) ^{-1},\qquad G_V= \dfrac{1}{h} \Big (\sum _{i=1}^5 G_it_i\Big ) . \end{aligned}$$
(45)

The results taken for comparisons were the displacements of beams in the most characteristic points. For instance, in case of cantilever beam we consider its free end, while in three point bending case we take the middle span. The relative error between results obtained by using displacements obtained analytically \( D_A \,\), and numerically \( D_N \) is expressed as follows:

$$\begin{aligned} \varDelta = \dfrac{D_N-D_A}{\min (D_A,D_N)}\cdot 100. \end{aligned}$$

The deflections computed numerically were obtained by using ABAQUS finite element method environment. The beams with rectangular cross section were modeled as two-dimensional by using S4 (4-node doubly curved general-purpose shell, finite membrane strains) elements. Each of considered layers was divided into minimum 4 element in thickness direction. The length of finite elements was adjusted to keep aspect ratio smaller than 4.

The end loading in cantilever beam case was divided into six equal concentrated forces. They are applied along the end edge of beam at points separating individual layers. The boundary conditions in case of cantilever beam were realized by locking all of the available degrees of freedom of the fixed end edge. In case of three-point bending, the boundary conditions were applied in another way. The ending edge has been made rigid by using MPC constraints. The displacements in three directions are locked for MPC control point. The same is true of how the loadings are applied for three-point bending model. The beam was partitioned into two parts. The partition boundary line situated in middle span of the beam was made rigid by MPC constraint, and the applied loading in the concentrated force was applied in MPC control point.

6.2 Materials

In this study, we have considered sandwich beams which consist of the two relatively rigid dissimilar faces and lightweight core between them. The faces are stuck to the core by using some kind of glue. The exemplary sandwich with these structure is presented in Fig. 5.

Fig. 5
figure 5

Structure of sandwich composite

Full size image

The considered sandwich structure can be presented as a 5-layer cross section as shown in Fig. 6. The particular materials are represented by the modulus of elasticity E with index corresponding to the layer number. In most of cases, the set of layers is symmetric. However, in special cases of constructions it is desirable to use different faces thicknesses or make them from different materials. Therefore, in this study we consider the non-symmetrical sandwich cross section in which the top skin is thicker than the bottom skin.

Fig. 6
figure 6

Cross section of considered sandwich beam

Full size image

The adhesive layer in many cases form a separate layer that significantly affects the effective mechanical properties of the composite. In case of core made of cellular materials, i.e., polyurethane foams, some part of the cross section can be penetrated by adhesive agent. The region with filled pores will response to applied loading according to the mixture law. These region is called “interfacial layer” and should be analyzed as a separate material. This fact is frequently omitted in the literature, which leads to mismatch between the predictions of sandwich response to applied mechanical loadings and reality. As mentioned above, the materials are represented by their Young modulus E. The computations are performed in form of parametric studies. The range of parametric studies was assumed from 24 GPa [Fiber Glas Epoxy Composite] to 205 GPa [Steel] for the faces materials. For the core materials, we consider the range from 15 to 1000 MPa, which cover the most frequently used materials from light foams to strong metallic honeycombs. The interfaces were considered from weak materials (15 MPa) to extremely stiff (100 GPa) in order to obtain comprehensive results.

Remark

In many problems dealing with sandwich structures, the zigzag effects are to be taken into account. For instance, in [49] the authors have shown that zigzag effects are important for thick sandwich beams, by calculating examples in which the beam length to thickness ratio equals 5. In our numerical examples, we assume that the cross section of the beam is rigid (no zigzag effects), since we consider slender beams with length to thickness ratio equal to \( \frac{300 \,\text {mm}}{10 \;\text {mm}} = 30 \). Moreover, the bending is performed in conditions of two stiff plates at the ends. Therefore, we neglect zigzag effects and we employ the Timoshenko beam theory in our numerical calculations.

6.3 Results and discussion

In this subsection, we consider that the two faces of the sandwich beam are made of the same material.

6.3.1 Shear correction coefficient impact

In common sandwich beams, the ratio between elastic properties of skin to core exceeds 100. Therefore, shear correction factor suitable for homogenous beams should be corrected. It is easy to show the range of applicability for the relation \( k = \pi ^2/12 \) by a parametric study. Fig. 7 presents dependence of relative error \( \varDelta \) between numerical and analytical results for cantilever beams with different ratios between elastic properties of skin and core \( E_{\mathrm {face}}/E_{\mathrm {core}} \,\). We have denoted by \( \varDelta _{\text {k-num}} \) the difference between the analytical results using constant \( k = \pi ^2/12 \) and numerical results obtained by using ABAQUS finite element method environment. By \( \varDelta _{\text {v-num}} \), we have designated the difference between analytical results with variable k obtained by Voigt method (45). The green line \( \varDelta _{\text {V-K}} \) visualizes in Fig. 7 the difference between results obtained analytically with constant and variable shear coefficient factor k. It is clearly visible that in considered case the value of the relative error \( \varDelta \) increases proportionally to mismatch in elastic properties of sandwich constituents. Assumption of \( k = \pi ^2/12 \) starts to generate high differences between analytical and numerical results when the ratio \( E_{\mathrm {face}}/E_{\mathrm {core}}\) exceeds 200. The value of \( \varDelta \) exceeds 35% when \( E_{\mathrm {face}}/E_{\mathrm {core}}\) is equal to 1024. Thus, the use of the Voigt method (45) is the best choice for our computations.

Fig. 7
figure 7

Dependence of relative error on sandwich non-homogeneity in case constant shear correction factor \( k = \pi ^2/12 \)

Full size image

6.3.2 Interface impact

We assumed the total beam thickness equal to 10 mm, and length 300 mm. Top skin thickness is \( t_1=1 \) mm. Bottom skin thickness \( t_5 \) is equal to 1.5 mm. The interfaces thicknesses \( t_2 \) and \( t_4 \) are various, assumed 0.1 mm, 0.2 mm, and 0.5 mm. Core thickness in all considered cases is the rest of the sandwich thickness. We have considered 3 cases of skin material: 1. Fiber Glas Epoxy Composite [FGEC] \( E_1=E_5 =24 \) GPa; 2. Aluminum \( E_1=E_5=70 \) GPa; and 3. Steel \( E_1=E_5=205 \) GPa. The core was assumed as polyurethane foam with \( E_3 = 15 \) MPa. The interface has various stiffness from 24 GPa to 11 MPa. For simplification, the same Poisson ratio \( \nu = 0.3 \) was assumed for all considered materials. The results of the conducted analyses for cantilever beams are presented in Fig. 8.

Fig. 8
figure 8

Dependence of maximum deflection of cantilever beams on interface thickness, interface stiffness, and sandwich face material

Full size image

As expected, the maximum deflections of considered beams are strongly dependent on face material. Derived results indicate that in case of weak material used as interfacial layer the effective bending stiffness of beam is independent on its thickness. Between \( E_3 \) equal to 15 MPa to approximately 100 MPa deflections of beams are visibly dependent on interface material. This range is very important for sandwich designers, due to the fact that it covers many kinds of adhesive agents used in the industry. The stiffness of sandwiches made of metallic faces is independent on interface properties when its modulus of elasticity exceeds 100 MPa, while this layer has significant impact on effective bending stiffness of sandwich beam. In case of FGEC visible increasing rigidity of beams above 100 000 MPa is obvious, because this effect concerns situation in which the interface material is stiffer than the skin.

The dependence of relative error between results obtained analytically and numerically for cantilever beams with end concentrated load \( P=3 \) N is presented in Fig. 9. The same results for three point bending case with load \( P=3.5 \) N are presented in Fig. 10.

Fig. 9
figure 9

Dependence of relative error \( \varDelta \) on interface and skin elastic properties for cantilever beams

Full size image
Fig. 10
figure 10

Dependence of relative error \( \varDelta \) on interface and skin elastic properties for three-point bending

Full size image

The obtained results for cantilever beams indicate that the convergence of numerical and analytical results mainly depends on the skin stiffness. In case of soft skins made of FGEC, the relative error increases when the interface stiffness exceeds the skin stiffness. For the three-point bending case, the relations are more complicated. The differences smaller than 10 % for all the considered cases, which concern the most popular materials in the industry, show the correctness of the assumptions made.

6.4 Three layer sandwich with dissimilar faces

In the second case, a parametric study was conducted to observe the relative error in case when the top and bottom skins are made of different materials. The study was performed with a constant material [FGEC] for the top skin, while the bottom skin is made of various materials, represented by the modulus of elasticity E. The Young modulus of the bottom skin varies from the value equal to core material up to the highest value common in real beams 205 GPa (Steel). The assumed values are 15 MPa, 2.5 GPa, 5 GPa, 12 GPa, 24 GPa, 50 GPa, 100 GPa, and 205 GPa. The omitting of interface was realized by assuming equal values for \( E_2 \), \( E_3 \), and \( E_4\, \). The calculations were repeated for several core materials, the highest considered values are related to aluminum honeycomb, and the middle value for honeycombs made of nomex. The results derived for cantilever beams are presented in Fig. 11.

The relative error \( \varDelta \) increases as the stiffness of core decreases. The maximal difference between numerical and analytical results are derived for sandwich beams with core made of weak polyurethane foam. The same results for three point bending case are presented in Fig. 12.

Fig. 11
figure 11

The relative error for cantilever beams with dissimilar faces

Full size image
Fig. 12
figure 12

The relative error for beams with dissimilar faces in case of three-point bending

Full size image

The dependence of \( \varDelta \) on the bottom skin rigidity is nonlinear in both considered cases. For faces made of soft materials, the value of \( \varDelta \) is strongly sensitive. The obtained curves become horizontal when the modulus of elasticity for the bottom skin exceeds twice the modulus of elasticity of top skin. It is especially visible in case of cantilever (see. Fig. 11). Above the value of \( E_5=100 \) GPa, the relative error could be treated as independent on bottom skin rigidity. For the three-point bending case, the dependence of \( \varDelta \) on the bottom skin rigidity is more complicated, but the value of relative error does not exceed 9% for all of considered cases. The shear correction factors for particular cases in analytical calculations were obtained by using the simplified Voigt method.

7 Piecewise homogeneous sandwich columns

The piecewise homogeneous circular columns are other sandwich structures which are widely used in practice (see, e.g., [15]). For these types of composite beams, we can compute the effective stiffness coefficients by applying the general relations (17) and (18).

Let us consider a circular sandwich column made of two different homogeneous isotropic materials: the core characterized by the material parameters \(\nu _c\,\), \(E_c\,\), \(\rho _c\,\), \(G_c\,\), and the face with material parameters \(\nu _f\,\), \(E_f\,\), \(\rho _f\,\), \(G_f\,\). We consider the general case in which the Poisson ratios of the face and core materials are not necessarily equal: \(\,\nu _f\ne \nu _c\,\). The cross-sectional domain \(\,\varSigma \,\) of the beam is represented in Fig. 13, where \( R_1 \) is the radius of the core and \( R_2 \) the radius of the whole circular beam.

Fig. 13
figure 13

Cross section of a circular sandwich column

Full size image

The plane strain problems (15) (with coefficients (19)) for piecewise homogeneous materials have been investigated previously using the method of functions of a complex variable in [23], and the solutions \(\,u_\alpha ^{(k)}\,\) for circular domains have been determined (\(k=1,2,3\)). If we insert them into the general formulas (17), we obtain the following effective bending stiffness and extensional stiffness

$$\begin{aligned} C_1=C_2= & {} \dfrac{\pi }{4}\big [E_cR_1^4+E_f(R_2^4-R_1^4)\big ]-\dfrac{\pi (\nu _c-\nu _f)^2(R_2^4-R_1^4)R_1^4}{2\big [\alpha _cR_1^4+\beta _cR_2^4+\alpha _f(R_2^4-R_1^4)\big ]}\,, \nonumber \\ A_3= & {} \pi \big [E_cR_1^2+E_f(R_2^2-R_1^2)\big ]-\dfrac{4\pi (\nu _c-\nu _f)^2(R_2^2-R_1^2)R_1^2}{(\alpha _c-\beta _c)R_1^2+2\beta _cR_2^2+(\alpha _f-\beta _f)(R_2^2-R_1^2)}\,, \end{aligned}$$
(46)

as well as \(B_{3\alpha }=0\,,\,C_{12}=0\). Here, we have introduced the notations

$$\begin{aligned} \alpha _c=\dfrac{3-4\nu _c}{2G_c}\,,\quad \alpha _f=\dfrac{3-4\nu _f}{2G_f}\,,\quad \beta _c=\dfrac{1}{2G_c}\,,\quad \beta _f=\dfrac{1}{2G_f}\,. \end{aligned}$$

To estimate the effective torsional rigidity, we observe that the torsion problem (16) admits in our case the solution \(\varphi =0\), so that the formula (17)\(_{10}\) yields

$$\begin{aligned} C_3= \dfrac{\pi }{2}\big [G_cR_1^4+G_f(R_2^4-R_1^4)\big ]. \end{aligned}$$
(47)

In view of the relations (18), the effective shear stiffness is given by

$$\begin{aligned} A_1=A_2= \kappa \,\pi \,\dfrac{\big [G_cR_1^2+G_f(R_2^2-R_1^2)\big ]\,\big [\rho _cR_1^4+\rho _f(R_2^4-R_1^4)\big ]}{R_2^2\,\big [\rho _cR_1^2+\rho _f(R_2^2-R_1^2)\big ]}\,. \end{aligned}$$
(48)

Thus, the expressions for all the effective stiffness coefficients have been determined for piecewise homogeneous circular sandwich columns.

Using the same method, we can determine the effective stiffness properties for sandwich columns which consists of functionally graded materials, see [5, Sect. 7].

7.1 Bending of cantilever piecewise homogeneous beams by end loads

Consider a cantilever piecewise homogeneous circular column subject to a concentrated end force P acting in the transversal direction, see Fig. 4b. For the maximum deflection \(\,\delta \,\), the analytical solution predicts the following value

$$\begin{aligned} \delta _A =P\,l\,\Big ( \dfrac{l^2}{3C_2}+ \dfrac{1}{A_1}\Big )\,, \end{aligned}$$
(49)

where the effective bending stiffness \(C_2\) and the effective shear stiffness \(A_1\) are given by the relations (46)\(_1\) and (48). This formula will be used for comparison with numerical results in Sect. 7.3.

7.2 Torsion of piecewise homogeneous clamped sandwich columns

Consider a piecewise homogeneous circular sandwich column subjected to torsion by the torque (twisting moment) \(\,M \) acting at one end of the beam, while the other end is clamped.

Denote by \(\,\psi \,\) the angle of twist at the loaded end of the beam. The analytical solution of the problem predicts the following value

$$\begin{aligned} \psi _{A}=\dfrac{M\,l}{C_3}\,\,, \end{aligned}$$
(50)

where the torsional rigidity \(C_3\) is determined by (47).

In order to compare the theoretical solution \(\,\psi _{A}\) with the numerical solution obtained by the finite element analysis, we calculate the angle of twist \(\,\psi _{\mathrm {FEM}}\) in terms of the three-dimensional displacements \(\, u_\alpha ^*\, \) using the relation (10)\(_{6\,}\).

7.3 Comparison with numerical results

Let us compare the above theoretical results for bending and torsion of circular sandwich columns with the corresponding numerical solutions obtained by a finite element analysis.

In case of circular sandwiches, the deflections were computed from equation (49) by means of formulas (46) and (48). Torsional angles and the angle \( \psi \) of circular rods were determined with help of formula (50) with (47). For sandwiches with circular cross sections, the value of k was assumed \( \pi ^2/12 \).

The numerical results were obtained in ABAQUS environment where the sandwich columns with circular cross sections were modeled as three-dimensional by using C3D8 finite elements (8-node linear brick).

7.3.1 Bending

The circular sandwich beam subjected to bending was considered on the example of a cantilever beam with concentrated end load. The dimensions of the cross section were assumed \( R_1 = 14 \) mm and \( R_2= 15 \) mm. The beam length was equal to 300 mm, like in previous cases. In this case, the convergence of the analytical and numerical results was checked for various skin and core materials. The derived results in this parametric study are presented in Figs. 14 and 15.

Fig. 14
figure 14

Relation of relative error to face modulus of elasticity in bending loading conditions, in the case \( \nu _f=\nu _c\, \)

Full size image
Fig. 15
figure 15

Relation of relative error to face modulus of elasticity in bending loading conditions, in the case \( \nu _f\ne \nu _c\, \)

Full size image

The curves presented in Fig. 14 indicate that the differences between numerical and analytical values of beam deflections are smaller than 1.5% in the entire spectrum of considered cases. Regardless of the core material type, the values of relative error depend nonlinearly on the face modulus of elasticity until they reach the point where it stabilizes. This point is dependent on the core material stiffness. When the core material becomes weaker, the stabilization point moves to the left.

7.3.2 Torsion

The sandwich circular beam with the same dimensions like in previous case was subjected to torsional load by a moment equal to 5 Nm. The results of comparisons of analytical and numerical results are presented in Fig. 16.

Fig. 16
figure 16

Dependence of relative error on face modulus of elasticity in torsion loading conditions

Full size image

We remark that the dependence of \( \varDelta \) on \( E_{\mathrm {face}} \) has similar patterns as the one derived for bending, but there is one significant difference: after the stabilization point, the relative error does not dependent on the core material.

8 Conclusions

In order to characterize the mechanical behavior of multilayered beams, we have determined the effective stiffness properties of composite beams with n layers, made of orthotropic or isotropic materials. Thus, the general formulas for the effective stiffness coefficients of orthotropic composite beams are given by the relations (17) and (18).

In the case of multilayered beams made of isotropic materials, we obtain by particularization the analytical expressions of the torsional rigidity (26), effective bending and extensional stiffnesses (28), and shear stiffness (31) or (37). These values have been compared with previously known theoretical results in Sects. 5.1, 5.2, and  5.3. The comparison of analytical solutions with numerical results for some beam bending problems is presented in Sects.  5.4,  6.3, and  6.4.

For circular sandwich columns made of piecewise homogeneous materials, the expressions of the effective stiffness coefficients are given by (46)–(48). Using these values, we have deduced the analytical beam-like solutions the bending and torsion of clamped beams and compared them with numerical results in Sect. 7.3.

The good agreement between the theoretical and numerical results for the considered mechanical problems represents a validation of our analytical formulas for the effective stiffness properties of multilayered composite beams. The range of validity of these formulas is quite large, as it was shown in the numerical study presented in Sect. 6.

In a future work, we intend to continue our approach to describe more complex material behavior, such as micromechanical models with separation of fibers and matrix material. Thus, for a composite beam like in Fig. 1, the inner parts of the cross section can represent fibers of a fiber reinforced beam, which would rotate using the Cosserat model with micro-rotations. To obtain numerical examples in this case, it is necessary to introduce an interface or discontinuity at fiber/matrix contact to make the rotation of fibers with respect to the surrounding matrix possible.