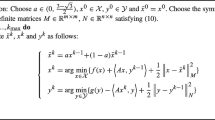A multigrid preconditioner for tensor product spline smoothing

Abstract

Penalized spline smoothing is a well-established, nonparametric regression method that is efficient for one and two covariates. Its extension to more than two covariates is straightforward but suffers from exponentially increasing memory demands and computational complexity, which brings the method to its numerical limit. Penalized spline smoothing with multiple covariates requires solving a large-scale, regularized least-squares problem where the occurring matrices do not fit into storage of common computer systems. To overcome this restriction, we introduce a matrix-free implementation of the conjugate gradient method. We further present a matrix-free implementation of a simple diagonal as well as more advanced geometric multigrid preconditioner to significantly speed up convergence of the conjugate gradient method. All algorithms require a negligible amount of memory and therefore allow for penalized spline smoothing with multiple covariates. Moreover, for arbitrary but fixed covariate dimension, we show grid independent convergence of the multigrid preconditioner which is fundamental to achieve algorithmic scalability.

1 Introduction

Exploring significant patterns in observed data is a fundamental task in many statistical applications. In nonparametric regression the relationship between the covariate variables and the variable of interest is modelled by a smooth but not further specified function of the covariates, that is

$$\begin{aligned} y = s(x^1, \ldots , x^P) + \varepsilon . \end{aligned}$$

The function $s(\cdot )$ attempts to capture the important patterns in the data while leaving out noise and insignificant structures. In this context, penalized spline smoothing methods have become very popular and led to a wide range of applications for one and two covariates (cf. Ruppert et al. 2003; Wand and Ormerod 2008; Fahrmeir et al. 2013). The general process is to represent the smooth unknown function by a high dimensional spline basis and to impose an appropriately chosen roughness penalty to guarantee smoothness. The influence of the penalty is then controlled by a single penalty parameter. The idea of penalized spline smoothing traces back to O’Sullivan (1986) where a rich B-spline basis is combined with a roughness penalty based on integrals of the squared second order derivatives. It was made popular by Eilers and Marx (1996) introducing the P-spline by replacing the integral penalty with higher-order differences of the B-spline coefficients.

The extension of penalized spline smoothing methods to an arbitrary number of covariates is straightforward but suffers from an exponential growth of the number of spline coefficients to be estimated within the number of covariates. This issue is referred to as the curse of dimensionality (cf. Bellman 1957). The computational and especially memory complexity of the related estimation procedure therefore becomes numerically infeasible, even for a moderate number of covariates, such that spline smoothing methods are rarely applied for more than two covariates (cf. Fahrmeir et al. 2013, p. 531).

In the special case that the covariates are located on a regular grid, the spline model can be reformulated in order to exploit the underlying grid structure as proposed by Currie et al. (2006) and Eilers et al. (2006), where the numerical complexity only growth linearly within the number of covariates. A further approach to weaken the curse of dimensionality is by using sparse grids (cf. Zenger 1991; Bungartz and Griebel 2004), where the problem dimension is reduced significantly by taking the hierarchical construction of tensor product B-splines into account. These approaches, however, are designed for gridded covariates and cannot be applied to penalized spline smoothing on scattered data.

For multivariate and scattered covariates penalized spline smoothing is carried out via solving a regularized least-squares problem for the B-spline coefficients. The main challenge is that the underlying tensor product spline basis matrices are large scale, such that their construction and storage becomes numerically infeasible for increasing number of covariates. In this paper, we propose a strategy to circumvent explicit construction and storage of these large matrices by exploiting the underlying tensor product structure. We refer to this approach as matrix-free approach since it only requires the construction of very low-dimensional matrices which are negligible in storage. We apply an iterative solution algorithm, the conjugate gradient (CG) method, to solve for the normal equation of the regularized least-squares problem since it only requires computation of matrix-vector products, but not the matrix explicitly. This finally allows to overcome the bottleneck of memory demands but comes at the price of a possibly long algorithmic runtime since the normal equation is known to be of ill condition. Further, with increasing covariate dimension the condition deteriorates since the number of observations generally remains unchanged.

In order to also significantly speed-up computation time, we present matrix-free preconditioning techniques. We introduce a simple diagonal preconditioner and further we adapt a numerically advanced geometric multigrid technique as preconditioner. Multigrid method are typically applied for the numerical solution of elliptic partial differential equations in two or more dimensions (cf. Brandt 1977; Hackbusch 1978), but the fundamental principal of building a hierarchy of increasingly fine discretization can be adapted to penalized spline smoothing. Finally, we come up with matrix-free preconditioned CG methods for penalized spline smoothing, which significantly reduces memory and computational complexity compared to common estimation methods and therefore allow to carry out penalized spline smoothing with an arbitrary number of covariates. Furthermore, for the geometric multigrid preconditioner, we show grid-independent convergence which is mandatory in order to achieve algorithmic scalability in the sense that simultaneously doubling the degrees of freedom and the number of processors leads to constant algorithmic running times. The presented implementations are available in the R-package mgss (cf. Siebenborn and Wagner 2021).

The remainder of this paper is organized as follows. Section 2 provides the fundamentals of penalized spline smoothing in one and especially multiple dimensions as well as the formulation of the underlying large-scale linear system. In Sect. 3, we show how to perform memory efficient matrix operations on the occurring matrices which results in a matrix-free implementation of the CG-method to solve the large-scale system with comparatively small memory requirements. We further show how to efficiently extract the diagonal of the coefficient matrix to perform a diagonal preconditioned CG-method. In Sect. 4, we develop a matrix-free implementation of a multigrid preconditioned CG-method to drastically reduce the computational complexity. Section 5 gives some practical remarks how the algorithms can be utilized and extended the ideas to further problems within the context of penalized spline smoothing. To show the storage benefits and the numerical performance of the proposed algorithms, they are compared to traditional methods on artificial test data as well as on real data for models of international trade in Sect. 6. Finally, Sect. 7 gives a conclusion of the paper.

2 Penalized spline smoothing

In statistics, smoothing a given data set describes the process of constructing a function that captures the important patterns in the data while leaving out noise and other fine scaled structures. More precisely, for given data $\lbrace (x_i,y_i) \in {\mathbb {R}}^P \times {\mathbb {R}}| i=1,\ldots ,n \rbrace$, where the $y_i \in {\mathbb {R}}$ are observations of a continuous response variable and the $x_i \in {\mathbb {R}}^P$ represent the corresponding values of continuous covariates, we seek a smooth, but not further specified function $s(\cdot ) :\Omega \subset {\mathbb {R}}^P \rightarrow {\mathbb {R}}$ so that

$$\begin{aligned} y_i = s(x_i) + \varepsilon _i, \ i=1,\ldots ,n . \end{aligned}$$

A common assumption is that $\varepsilon _1,\ldots ,\varepsilon _n$ are independent and identically distributed (i.i.d.) random errors with zero mean, common variance $\sigma _{\varepsilon }^2$, and assumed to be independent of the covariates. In penalized spline smoothing methods, initially proposed by O’Sullivan (1986) and made popular by Eilers and Marx (1996) (see also Ruppert et al. 2003 and Fahrmeir et al. 2013), the function $s(\cdot )$ is modelled as a spline function with a rich basis, such that $s(\cdot )$ is flexible enough to capture very complex and highly nonlinear structures. At the same time, in order to prevent overfitting of the observed data, an additional weighted roughness penalty is used. The amount of smoothness is then controlled by a single weight parameter.

2.1 Tensor product splines

We begin by defining a spline basis which forms the underlying linear space for the representation of $s(\cdot )$. Let $\Omega :=[a,b]$ be a bounded and closed interval partitioned by the knots

$$\begin{aligned} {\mathcal {K}}:=\lbrace a=\kappa _0< \cdots < \kappa _{m+1}=b \rbrace . \end{aligned}$$

Let ${\mathcal {C}}^{q}(\Omega )$ denote the space of q-times continuously differentiable functions and let ${\mathcal {P}}_q(\Omega )$ denote the space of polynomials of degree q. We call the function space

$$\begin{aligned} {\mathcal {S}}_{q}({\mathcal {K}}):=\lbrace s \in {\mathcal {C}}^{q-1}(\Omega ) : s|_{\left[ \kappa _{j-1},\kappa _{j} \right] } \in {\mathcal {P}}_q \left( \left[ \kappa _{j-1},\kappa _{j} \right] \right) , \ j=1,\ldots ,m+1 \rbrace \end{aligned}$$

the space of spline functions of degree $q \in {\mathbb {N}}_0$ with knots ${\mathcal {K}}$. It is a finite dimensional linear space of dimension $J :=\mathrm {dim} \left( {\mathcal {S}}_{q}({\mathcal {K}})\right) = m+q+1$. With

$$\begin{aligned} \lbrace \varphi _{j,q} : j=1,\ldots ,J \rbrace \end{aligned}$$

we denote its B-spline basis, proposed in de Boor (1978), which is well suited for numerical applications. To extend the spline concept to P-dimensional covariates, a tensor product approach is common. Let ${\mathcal {S}}_{q_p}({\mathcal {K}}_p)$ be the spline space for the p-th covariate, $p=1,\ldots ,P$, and let

$$\begin{aligned} \lbrace \varphi _{j_p,q_p}^p : j_p=1,\ldots ,J_p \rbrace \end{aligned}$$

denote its B-spline basis. The function

$$\begin{aligned} \varphi _{j,q} :\Omega :=\Omega _1 \times \cdots \times \Omega _P \rightarrow {\mathbb {R}}, \ \varphi _{j,q}(x) = \prod _{p=1}^{P} \varphi ^p_{j_p,q_p}(x^p) , \end{aligned}$$

where $j :=(j_1,\ldots ,j_P)^T$ and $q :=(q_1,\ldots ,q_P)^T$ are multiindices, is called tensor product B-spline. We define the space of tensor product splines as their linear combination

$$\begin{aligned} {\mathcal {S}}_{q}({\mathcal {K}}):=\text {span} \lbrace \varphi _{j,q} : 1 \le j \le J :=(J_1, \ldots , J_P)^T \rbrace , \end{aligned}$$

(2.1)

which is then a $K :=\prod _{p=1}^{P} J_p$ dimensional linear space. Note that we use the same symbol for the univariable and the tensor product spline space as well as for B-splines and tensor product B-splines. The difference is that we make use of the multiindex notation for the tensor products. Every tensor product spline $s \in {\mathcal {S}}_{q}({\mathcal {K}})$ therefore has a unique representation

$$\begin{aligned} s = \sum \limits _{1 \le j \le J} \alpha _j \varphi _{j,q}, \end{aligned}$$

and for computational reasons we uniquely identify the set of multiindices $\lbrace j \in {\mathbb {N}}^P : 1 \le j \le J \rbrace$ in descending lexicographical order as $\lbrace 1,\ldots ,K \rbrace$, such that

$$\begin{aligned} s = \sum \limits _{1 \le j \le J} \alpha _j \varphi _{j,q} = \sum \limits _{k=1}^{K} \alpha _k \varphi _{k,q} \end{aligned}$$

(2.2)

with unique spline coefficients $\alpha _k \in {\mathbb {R}}$.

2.2 Tensor product penalized spline smoothing

Tensor product penalized spline smoothing with a curvature penalty, in analogy to O’Sullivan (1986), is carried out solving the optimization problem

$$\begin{aligned} \min \limits _{s \in {\mathcal {S}}_{q}({\mathcal {K}})} \sum \limits _{i=1}^{n} \left( s(x_i)-y_i \right) ^2 + \lambda \int \limits _{{\mathbb {R}}^P} \sum \limits _{p_1=1}^{P} \sum \limits _{p_2=1}^{P} \left( \dfrac{\partial ^2}{\partial x_{p_1} \partial x_{p_2}} s(x) \right) ^2 \mathrm {d}x . \end{aligned}$$

(2.3)

The objective function consists of three parts. The least squares term

$$\begin{aligned} \mathcal {LS}(s) :=\sum \limits _{i=1}^{n} \left( s(x_i)-y_i \right) ^2 \end{aligned}$$

measures the goodness-of-fit of the spline to the given observations and the regularization or penalty term

$$\begin{aligned} {\mathcal {R}}(s) :=\int \limits _{{\mathbb {R}}^P} \sum \limits _{p_1=1}^{P} \sum \limits _{p_2=1}^{P} \left( \dfrac{\partial ^2}{\partial x_{p_1} \partial x_{p_2}} s(x) \right) ^2 \mathrm {d}x \end{aligned}$$

penalizes the roughness of the spline. The single penalty parameter $\lambda >0$ balances the two competitive terms $\mathcal {LS}(s)$ and ${\mathcal {R}}(s)$. For $\lambda \rightarrow 0$ no roughness penalization is imposed such that the spline function tends to the common least-squares spline of degree q, i.e. the solution of

$$\begin{aligned} \min \limits _{s \in {\mathcal {S}}_{q}({\mathcal {K}})} \mathcal {LS}(s) , \end{aligned}$$

that tries to interpolates the given data. Conversely, for $\lambda \rightarrow \infty$, all impact is given to the regularization term such that the smoothing spline tends to be the least-squares hyperplane. Smoothing parameter selection is an important task in penalized spline smoothing and a variety of data-driven methods exist. A broad overview is given by the monographs of Eubank (1988), Wahba (1990), and Green and Silverman (1993).

Using the unique B-spline representation (2.2), we obtain

$$\begin{aligned} \mathcal {LS}(s) = \Vert \Phi \alpha - y \Vert _2^2 , \end{aligned}$$

where $\Phi \in {\mathbb {R}}^{n \times K}$ is element-wise defined as

$$\begin{aligned} \Phi [i,k] :=\varphi _{k,q}(x_i), \end{aligned}$$

$y \in {\mathbb {R}}^n$ denotes the response vector, $\alpha \in {\mathbb {R}}^K$ denotes the (unknown) spline coefficient vector, and $\Vert \cdot \Vert _2$ denotes the euclidean norm. Further, for the regularization term we obtain

$$\begin{aligned} {\mathcal {R}}(s) = \alpha ^T \left( \sum \limits _{r \in {\mathbb {N}}_0^P ; \vert r \vert = 2} \frac{2}{r!} \Psi _r \right) \alpha = \sum \limits _{r \in {\mathbb {N}}_0^P ; \vert r \vert = 2} \frac{2}{r!} \alpha ^T \Psi _r \alpha , \end{aligned}$$

where each $\Psi _{r} \in {\mathbb {R}}^{K \times K}$ is element-wise defined as

$$\begin{aligned} \Psi _{r}[k,\ell ] = \int \limits _{\Omega } \partial ^{r} \varphi _{k,q}(x) \partial ^{r} \varphi _{\ell ,q}(x) \mathrm {d}x = \left\langle \partial ^{r} \varphi _{k,q} , \partial ^{r} \varphi _{\ell ,q} \right\rangle _{L^2(\Omega )} . \end{aligned}$$

Defining

$$\begin{aligned} \Lambda :=\sum \limits _{r \in {\mathbb {N}}_0^P ; \vert r \vert = 2} \frac{2}{r!} \Psi _r \in {\mathbb {R}}^{K \times K} \end{aligned}$$

the optimization problem (2.3) is equivalently formulated in terms of the B-spline coefficients as

$$\begin{aligned} \min \limits _{\alpha \in {\mathbb {R}}^K} \Vert \Phi \alpha -y\Vert _2^2 + \lambda \alpha ^T\Lambda \alpha . \end{aligned}$$

(2.4)

This is a regularized least squares problem and its solution is equivalent to the solution of the linear equation system

$$\begin{aligned} \left( \Phi ^T \Phi + \lambda \Lambda \right) \alpha = \Phi ^Ty . \end{aligned}$$

(2.5)

Since the coefficient matrix $\Phi ^T \Phi + \lambda \Lambda$ is positive semi-definite, a solution always exists. Under very mild conditions on the covariates the coefficient matrix is positive definite, such that the solution is even unique and analytically given as

$$\begin{aligned} {\widehat{\alpha }} :=\left( \Phi ^T \Phi + \lambda \Lambda \right) ^{-1}\Phi ^Ty. \end{aligned}$$

More information on regularized least squares problems can be found in Björck (1996).

The penalty matrix $\Lambda$ and the related matrices $\Psi _r$, respectively, require the evaluation of several integral terms that might become numerically extensive. For practical applications, a huge simplification is provided by Eilers and Marx (1996) where the knots are equally spaced and the penalty is based on differences of the coefficients of adjacent B-splines. For $P=1$ that is

$$\begin{aligned} \sum \limits _{j=r+1}^{J} \Delta _r(\alpha _j) = \alpha ^T \left( \Delta _r \right) ^T \Delta _r \alpha = \Vert \Delta _r \alpha \Vert _2^2, \end{aligned}$$

where $\Delta _r(\cdot )$ denotes the r-th backwards difference operator and $\Delta _r \in {\mathbb {R}}^{(J-r) \times J}$ denotes the related difference matrix. A common choice is $r=2$. For $P>1$, this penalty is extended to several covariates via

$$\begin{aligned} \Lambda _{\mathrm {diff}} :=\sum \limits _{p=1}^{P} I_{J_1} \otimes \cdots \otimes I_{J_{p-1}} \otimes \left( \Delta _{r_p}^p \right) ^T \Delta _{r_p}^p \otimes I_{J_{p+1}} \otimes \cdots \otimes I_{J_P} \end{aligned}$$

where $\Delta _{r_p}^p \in {\mathbb {R}}^{(J_p-r_p) \times J_p}$ denotes the $r_p$-th order difference matrix for the p-th covariate, $\otimes$ denotes the Kronecker product, and $I_{(\cdot )}$ denotes the identity matrix of the respective dimension (see also Fahrmeir et al. (2013) for further detail). Replacing the curvature penalty matrix $\Lambda$ with the difference penalty matrix $\Lambda _{\mathrm {diff}}$ in problem (2.4) yields the so called P-spline. Note that the difference order $r_p$ of the P-spline is not fixed an can be chosen differently in each direction, which simply allows to take higher order differences into account and can be very useful in practical applications. Conversely, compared to the curvature penalty, it does only penalize roughness in each spatial direction but not on their interactions.

Even though the problem (2.5) looks simple, it becomes numerically infeasible for an increasing number of covariates P, which is shown in the following section. The main focus of this paper is therefore on an efficient solution of (2.5) in terms of both memory requirements and computing time.

2.3 Curse of dimensionality

We now look closer on the regularized least-squares problem (2.4) and the related linear system of equations (2.5), respectively. Since the coefficient matrix $\Phi ^T \Phi + \lambda \Lambda$ is symmetric and positive definite, a variety of efficient solution methods exists. For example, the conjugate gradient (CG) method proposed by Hestenes and Stiefel (1952) and presented in the following section can be applied. Note that it makes no difference for the CG-method if the curvature penalty $\Lambda$ is replaced by the difference penalty $\Lambda _{\mathrm {diff}}$. However, for reasons of simplification, we stick to the curvature penalty in the following.

Unfortunately, penalized spline smoothing is known to suffer from the so called curse of dimensionality (cf. Bellman 1957), i.e. an exponential growth of the number of B-spline coefficients K within the dimension of the covariates P such that

$$\begin{aligned} K = \prod _{p=1}^{P} J_p = {\mathcal {O}}(2^P) . \end{aligned}$$

As a simple example, equally choosing $J_p=35$ B-spline basis functions for each spatial dimension $p=1,\ldots ,P$, the resulting linear equation system (2.5) is of dimension $35^P$. Table 1 gives an overview on the increasing number of degrees of freedom under increasing dimensionality with which we are dealing within this work.

In practice, of course, any other desired choice of the $J_p$ for each spatial dimension $p = 1,\ldots ,P$ is possible. This exponential growth rapidly leads to computational restrictions, such that spline smoothing becomes impracticable for dimensions $P \ge 3$ as already stated by Fahrmeir et al. (2013, p. 531).

Table 1 Number of B-spline coefficients for varying spatial dimension P

To make this more clear, in the above setting of $J_p=35$ for all p and $P=3$ already the storage of the regularization matrix $\Lambda$ requires approximately two gigabyte (GB) of memory, even in a sparse matrix storage format. Since $\Lambda$ is not the only occurring matrix and since all the matrices are not only to be stored but to be manipulated, the method clearly exceeds the internal memory of common computer systems. Therefore, to make tensor product penalized spline smoothing practicable for increasing spatial dimensions P, we need to develop computational and memory efficient methods to solve the large-scale linear system (2.5).

3 Matrix-free conjugate gradient method

As shown in the previous section, penalized spline smoothing with several covariates is boiled down to solving a linear system of equations with a symmetric and positive definite coefficient matrix. The difficulty is hidden in the problem dimension K, since already for a moderate amount of covariates the coefficient matrix cannot be stored on common computer systems. In order to make penalized spline smoothing applicable to multiple covariates, in this section we propose a matrix-free solution strategy that exploits the underlying structure of the tensor product spline and therefore solely requires the negligible storage space of small univariate spline matrices.

3.1 The conjugate gradient method

The conjugate gradient (CG) method, introduced by Hestenes and Stiefel (1952), is the most popular algorithms to solve a linear system $Ax = b$ with a symmetric and positive definite coefficient matrix $A \in {\mathbb {R}}^{K \times K}$ and an arbitrary right-hand side $b \in {\mathbb {R}}^K$. The CG-method is known to be an exact method, i.e. it computes the exact solution $x^* :=A^{-1}b$ in at most K iterations. However, since K might be very large in practice and due to round-off errors, it is generally used as an iterative method. Starting with an initial guess $x_0$, where typically $x_0=0$ or $x_0=b$, the iterative procedure of the CG method is presented in Algorithm 1.

The computational complexity of the CG-method, i.e. the required number of iterations to reach the tolerance, depends on the condition number of the coefficient matrix A, that is

$$\begin{aligned} \mathrm {cond}_2(A) :=\dfrac{ \lambda _{\mathrm {max}}(A) }{ \lambda _{\mathrm {min}}(A) } \ge 1 , \end{aligned}$$

where $\lambda _{\mathrm {max}}(A) >0$ and $\lambda _{\mathrm {min}}(A)>0$ denote the largest and smallest eigenvalue of A, respectively. According to Saad (2003) it holds

$$\begin{aligned} \Vert x_j - x^* \Vert _A \le 2 \left( \dfrac{\sqrt{\mathrm {cond}_2(A)}-1}{\sqrt{\mathrm {cond}_2(A)}+1} \right) ^j \Vert x_0 - x^* \Vert _A \end{aligned}$$

for the j-th iterate of the CG-method. At this, $\Vert \cdot \Vert _A$ denotes the A-induced norm defined by $\Vert x \Vert _A :=x^T Ax$ for all $x \in {\mathbb {R}}^K$. A condition number close to one therefore guarantees a fast convergence of the CG-method.

The memory complexity of the CG-method mainly boils down to the storage of the coefficient matrix A. A major strength of the CG-method is that the matrix A does not have to exist explicitly but only implicitly by its actions on the iterates $x_j$, i.e. it can be implemented matrix-free by efficiently computing the vectors $v_j \leftarrow Ap_j$ in line 4 of Algorithm 1. So, if we know how to compute $v_j$ without explicitly storing the matrix A, the CG-method can be applied with an negligible amount of additional memory.

3.2 Matrix structures

In order to implement a matrix-free version of the CG-method to solve the linear system of penalized smoothing spline problem (2.5), we need to know how to compute matrix vector products with the occurring matrices $\Phi \in {\mathbb {R}}^{n \times K}$, $\Phi ^T \in {\mathbb {R}}^{K \times n}$, and $\Lambda \in {\mathbb {R}}^{K \times K}$ or $\Lambda _{\mathrm {diff}} \in {\mathbb {R}}^{K \times K}$. Therefore, we state some important properties of these matrices that are based on the tensor product nature of the underlying splines.

For each spatial direction $p=1,\ldots ,P$ we define the matrix

$$\begin{aligned} \Phi _p \in {\mathbb {R}}^{n \times J_p} , \ \Phi _p[i,j_p] :=\varphi ^p_{j_p,q_p}(x_i^p) , \end{aligned}$$

which corresponds to the matrix $\Phi$ with one single covariate in direction p. Then, because of the scattered data structure, it holds

$$\begin{aligned} \Phi ^T = \bigodot \limits _{p=1}^P \Phi _p^T , \end{aligned}$$

where $\odot$ denotes the Khatri-Rao product. For each matrix $\Psi _r$, we analogously define a matrix for each spatial direction of the respective derivatives, that is

$$\begin{aligned} \Psi _{r_p}^{p} \in {\mathbb {R}}^{J_p \times J_p} \ ,\Psi _{r_p}^{p}[j_p,\ell _p]= \left\langle \partial ^{r_p} \varphi _{j_p,q_p}^p , \partial ^{r_p} \varphi _{\ell _p,q_p}^p \right\rangle _{L^2(\Omega _p)} . \end{aligned}$$

Then it holds

$$\begin{aligned} \Psi _{r} = \bigotimes \limits _{p=1}^{P} \Psi ^{p}_{r_p} \end{aligned}$$

due to the tensor property.

A further important property of uniform B-splines, i.e. B-splines with equally spaced knots, in one variable is the subdivision formula. Let therefore ${\mathcal {S}}_q({\mathcal {K}}^{2h})$ and ${\mathcal {S}}_q({\mathcal {K}}^{h})$ denote univariable spline spaces with uniform knot set ${\mathcal {K}}^{2h}$ and ${\mathcal {K}}^{h}$ with mesh 2h and h, respectively. As shown in Höllig (2003, p. 32) it holds

$$\begin{aligned} \varphi _{j,q}^{2h} = \frac{1}{2^q} \sum \limits _{i=0}^{q+1} \left( {\begin{array}{c}q+1\\ i\end{array}}\right) \varphi _{2j-(q+1)+i,q}^{h} \end{aligned}$$

(3.1)

and consequently for a spline $s \in {\mathcal {S}}_q({\mathcal {K}}^{2h})$ it follows

$$\begin{aligned} s = \sum \limits _{j=1}^{J^{2h}} \alpha _{j}^{2h} \varphi _{j,q}^{2h} = \sum \limits _{j=1}^{J^{2h}} \alpha _{j}^{2h} \frac{1}{2^q} \sum \limits _{i=0}^{q+1} \left( {\begin{array}{c}q+1\\ i\end{array}}\right) \varphi _{2j-(q+1)+i,q}^{h} . \end{aligned}$$

Since ${\mathcal {S}}_q({\mathcal {K}}^{2h}) \subset {\mathcal {S}}_q({\mathcal {K}}^{h})$, and therefore also $s \in {\mathcal {S}}_q({\mathcal {K}}^{h})$, it holds

$$\begin{aligned} s = \sum \limits _{j=1}^{J^{h}} \alpha _{j}^{h} \varphi _{j,q}^{h} \end{aligned}$$

such that the B-spline coefficients for the different meshes are related through $\alpha ^{(h)} = I_{2h}^{h} \alpha ^{2h}$, where $I_{2h}^{h} \in {\mathbb {R}}^{J^{h} \times J^{2h}}$ is element wise defined as

$$\begin{aligned} I_{2h}^{h} [i,j] :=\frac{1}{2^q} \left( {\begin{array}{c}q+1\\ i-2j+q+1\end{array}}\right) , \quad \ i=1,\ldots ,J^{h}, \quad \ j= 1,\ldots ,J^{2h}. \end{aligned}$$

Because of the tensor property of B-splines, the formula carries over to uniform B-splines with several covariates and the corresponding B-spline coefficients are related through the matrix

$$\begin{aligned} I_{2h}^{h} = \bigotimes _{p=1}^{P} I_{2h_p}^{h_p} \in {\mathbb {R}}^{ K^{h} \times K^{2h} }, \end{aligned}$$

(3.2)

where $h :=(h_1,\ldots ,h_P)^T$ denotes the vector of mesh sizes.

3.3 Matrix operations

By exploiting the presented matrix structures, namely Kronecker and Khatri-Rao products, we now describe how to memory efficiently compute matrix-vector products with those types of matrices.

3.3.1 Kronecker products

Let arbitrary matrices $A_p \in {\mathbb {R}}^{m_p \times n_p}$ be given and let

$$\begin{aligned} A :=\bigotimes \limits _{p=1}^{P} A_p \in {\mathbb {R}}^{m \times n}, \quad \ m :=\prod _{p=1}^{P} m_p , \quad \ n :=\prod _{p=1}^{P} n_p \end{aligned}$$

denote their Kronecker product matrix. We aim for the computation of matrix-vector products with A by only accessing the Kronecker factors $A_1,\ldots ,A_P$. In the case of $m_p=n_p$ for all $p=1,\ldots ,P$, an implementation is provided in Benoit et al. (2001) and we extend their idea to arbitrary factors by Algorithm 2 to form a matrix-vector product with a Kronecker matrix only depending on the Kronecker factors.

3.3.2 Khatri-Rao products

Let arbitrary matrices $A_p \in {\mathbb {R}}^{m_p \times n}$ with the same number of columns be given and let

$$\begin{aligned} A :=\bigodot \limits _{p=1}^{P} A_p \in {\mathbb {R}}^{m \times n}, \ m :=\prod _{p=1}^{P} m_p \end{aligned}$$

denote their Khatri-Rao product matrix. We aim for the computation of matrix-vector products with A and $A^T$ by only accessing the Khatri-Rao factors $A_1,\ldots ,A_P$. By definition of the Khatri-Rao product it holds

$$\begin{aligned} A = \bigodot \limits _{p=1}^{P} A_p = \begin{bmatrix} \bigotimes \limits _{p=1}^{P} A_p[\cdot ,1] , \ldots , \bigotimes \limits _{p=1}^{P} A_p[\cdot ,n] \end{bmatrix} , \end{aligned}$$

where $A_p[\cdot ,j] \in {\mathbb {R}}^{m_p}$ denotes the j-th column of $A_p$, so that

$$\begin{aligned} Ax = \sum \limits _{i=1}^{n}x[i] v_i , \ v_i :=\bigotimes \limits _{p=1}^{P} A_{p}[\cdot ,i] \in {\mathbb {R}}^{m} \end{aligned}$$

for all $x \in {\mathbb {R}}^n$. This yields Algorithm 3 to form a memory-efficient matrix-vector product with a Khatri-Rao matrix only requiring its Khatri-Rao factors. Similarly, it holds

$$\begin{aligned} A^Ty = \begin{pmatrix} v_1^T y \\ \vdots \\ v_n^T y \end{pmatrix} \end{aligned}$$

for all $y \in {\mathbb {R}}^m$. We can thus formulate Algorithm 4 to form a matrix-vector product with a transposed Khatri-Rao matrix by only accessing its Khatri-Rao factors.

Using the Algorithms 2, 3, and 4 we are able to implement a matrix-free CG-method in order to solve the large-scale linear equation system (2.5). But first, we show how to extract the diagonal of a matrix $AA^T \in {\mathbb {R}}^{m \times m}$ without computing the entire matrix, but only accessing the Khatri-Rao factors $A_1,\ldots ,A_P$. This will be useful later on for the implementation matrix-free preconditioners to speed up convergence of the matrix-free CG-method. For $j=1,\ldots ,m$ the j-th diagonal element of $AA^T$ is given by $e_j^T AA^T e_j = \Vert A^T e_j \Vert _2^2$, where $e_j$ denotes the j-th unit vector. It holds

$$\begin{aligned} \Vert A^T e_j \Vert _2^2 = \left\| \begin{pmatrix} v_1^T e_j \\ \vdots \\ v_n^T e_j \end{pmatrix} \right\| _2^2 = \left\| \begin{pmatrix} v_1[j] \\ \vdots \\ v_n[j] \end{pmatrix} \right\| _2^2 = \sum \limits _{i=1}^{n} v_i[j]^2 . \end{aligned}$$

This yields Algorithm 5 to extract the diagonal of $AA^T$ by only accessing the Khatri-Rao factors of A.

3.4 Matrix-free CG-method

After these preparations we come back to the linear equation system (2.5) representing the penalized smoothing spline problem. In order to apply the CG-algorithm 1 with $A :=\Phi ^T\Phi + \lambda \Lambda$ and $b :=\Phi ^Ty$ in a matrix-free approach, we need to compute the right-hand side $\Phi ^Ty$ once as well as multiple matrix-vector products $(\Phi ^T\Phi + \lambda \Lambda )x_j$.

Since $\Phi ^T$ can be written as the Khatri-Rao product matrix

$$\begin{aligned} \Phi ^T = \bigodot \limits _{p=1}^P \Phi _p^T \end{aligned}$$

the right-hand side vector b can be computed matrix-free by applying Algorithm 3.

For a matrix-vector product

$$\begin{aligned} (\Phi ^T\Phi + \lambda \Lambda )x = \Phi ^T(\Phi x) + \lambda (\Lambda x) \end{aligned}$$

with arbitrary $x \in {\mathbb {R}}^K$ we first note that $\Phi = (\Phi ^T)^T$ is the transposed of a Khatri-Rao product matrix such the product $v :=\Phi x$ can be computed matrix-free by applying Algorithm 4. As for the right-hand side, the product $\Phi ^T(\Phi x) = \Phi ^T v$ can be computed matrix-free by applying Algorithm 3. Thus, we can compute the matrix-vector product $\Phi ^T\Phi x$ without explicitly forming and storing the infeasibly large matrix $\Phi ^T\Phi \in {\mathbb {R}}^{K \times K}$ but only storing the comparatively small factor matrices $\Phi _p \in {\mathbb {R}}^{n \times J_p}$. For the product $\Lambda x$ we recall that

$$\begin{aligned} \Lambda = \sum \limits _{r \in {\mathbb {N}}_0^P ; \vert r \vert = 2} \frac{2}{r!} \Psi _r = \sum \limits _{r \in {\mathbb {N}}_0^P ; \vert r \vert = 2} \frac{2}{r!} \left( \bigotimes \limits _{p=1}^{P} \Psi ^{p}_{r_p} \right) \end{aligned}$$

is given as a weighted sum of Kronecker product matrices. Since each of the factor matrices $\Psi ^{p}_{r_p}$ is available and easily fits into storage, the matrix-vector product

$$\begin{aligned} \Lambda x = \sum \limits _{r \in {\mathbb {N}}_0^P ; \vert r \vert = 2} \frac{2}{r!} \left( \bigotimes \limits _{p=1}^{P} \Psi ^{p}_{r_p} \right) x \end{aligned}$$

can be computed matrix-free by applying Algorithm 2 to each addend $\left( \bigotimes _{p=1}^{P} \Psi ^{p}_{r_p} \right) x$. Note that, since

$$\begin{aligned} \Lambda _{\mathrm {diff}} :=\sum \limits _{p=1}^{P} I_{J_1} \otimes \cdots \otimes I_{J_{p-1}} \otimes \left( \Delta _{r_p}^p \right) ^T \Delta _{r_p}^p \otimes I_{J_{p+1}} \otimes \cdots \otimes I_{J_P} \end{aligned}$$

is also give as a sum of Kronecker product matrices, the matrix-free CG-algorithm can be used for the P-spline method as well by simply replacing $\Lambda$ with $\Lambda _{\mathrm {diff}}$.

For a given number P of covariates, the matrix-free CG-method applied to the linear equation system (2.5) solely requires the storage of all occurring Kronecker and Khatri-Rao factors. Its storage demand therefore grows only linearly in P, i.e. it is in ${\mathcal {O}}(P)$, which is a significant improvement compared to ${\mathcal {O}}(2^P)$ required by the naive implementation of the CG-method in the full matrix approach. To put this into rough numbers, as seen in Sect. 2.3, for $P=3$ and $J_p=35$ for all $p=1,2,3$ the storage of the regularization matrix $\Lambda$ requires approximately two GB of RAM. On the contrary, only storing its Kronecker factors comes along with approximately 50, 000 bytes ($=0.00005$ GB). The proposed matrix-free CG-method is implemented within the R-package mgss (cf. Siebenborn and Wagner 2021) as function CG_smooth.

3.5 The preconditioned CG-method

From a memory requirement perspective, the proposed matrix-free CG-method allows to carry out penalized spline smoothing with an arbitrary amount of covariates. A serious issue, however, might be the runtime of the matrix-free CG-method. As mentioned in Sect. 3.1, since the CG-method is exact, the worst-case runtime is bounded above by the the dimension K of the coefficient matrix. But K will become very large while incorporating further covariates. In order to further speed up the computations, we adapt a simple diagonal preconditioner in this section. A numerically more sophisticated geometric multigrid preconditioning technique is presented in Sect. 4.

The main idea of preconditioning techniques is to reformulate a linear equation system $Ax=b$ as $BAx=Bb$ by means of a symmetric and positive definite preconditioner B in such a way that $\mathrm {cond}_2(BA) \ll \mathrm {cond}_2(A)$. Applying the CG-method to the preconditioned linear equation system instead of to the original yields to a much faster convergence, due to the significantly smaller condition number of the coefficient matrix. Of course, the matrix-matrix product BA is never formed in practice, but is applied implicitly within the procedure of the preconditioned CG-method (PCG) as presented in Algorithm 6. As in the CG-method, Algorithm 6 does not need to explicitly know and store the coefficient matrix A or the preconditioner B but only their actions on a vector in form of matrix-vector products are required.

If all diagonal elements $a_{i,i}$ of A are non-zero, the most simplest preconditioner is the diagonal preconditioner

$$\begin{aligned} B :=\mathrm {diag}(1/a_{1,1}, 1/a_{2,2}, \ldots , 1/a_{n,n}) . \end{aligned}$$

The matrix-vector products Br with the preconditioner in Algorithm 6 then reduce to

$$\begin{aligned} Br = ( r_1 / a_{1,1} , r_2 / a_{2,2} , \ldots , r_n / a_{n,n} )^T . \end{aligned}$$

In order to apply the diagonal precondtioner to the linear system (2.5) we need to extract the diagonal of the coefficient matrix $\Phi ^T \Phi + \lambda \Lambda$, which is a vector of length K and therefore easily fits into storage. Since the coefficient is not formed explicitly, we cannot simply extract its diagonal but need a matrix-free approach. It holds

$$\begin{aligned} \mathrm {diag}(\Phi ^T \Phi + \lambda \Lambda )&= \mathrm {diag}(\Phi ^T \Phi ) + \lambda \mathrm {diag}(\Lambda )\\&= \mathrm {diag}(\Phi ^T \Phi ) + \lambda \sum \limits _{r \in {\mathbb {N}}_0^P ; \vert r \vert = 2} \frac{2}{r!} \mathrm {diag}(\Psi _r) . \end{aligned}$$

Due to the construction of $\Phi ^T$ as Khatri-Rao product we can extract the diagonal elements of $\Phi ^T\Phi$ by means of Algorithm 5. For the Kronecker-products $\Psi _{r}$ it holds

$$\begin{aligned} \mathrm {diag}(\Psi _{r}) = \mathrm {diag}\left( \bigotimes \limits _{p=1}^{P} \Psi ^{p}_{r_p}\right) = \bigotimes \limits _{p=1}^{P} \mathrm {diag}(\Psi ^{p}_{r_p}) \end{aligned}$$

which finally yields the diagonal of the coefficient matrix without explicitly knowing the coefficient matrix. If the difference penalty is used instead of the curvature penalty equivalently holds

$$\begin{aligned} \mathrm {diag}(\Lambda _{\mathrm {diff}})= & {} \mathrm {diag} \left( \sum \limits _{p=1}^{P} I_{J_1} \otimes \cdots \otimes I_{J_{p-1}} \otimes \left( \Delta _{r_p}^p \right) ^T \Delta _{r_p}^p \otimes I_{J_{p+1}} \otimes \cdots \otimes I_{J_P} \right) \\= & {} \sum \limits _{p=1}^{P} \mathrm {diag}(I_{J_1}) \otimes \cdots \otimes \mathrm {diag}(I_{J_{p-1}}) \otimes \mathrm {diag}( \left( \Delta _{r_p}^p \right) ^T \Delta _{r_p}^p )\\&\quad \otimes \mathrm {diag}(I_{J_{p+1}}) \otimes \cdots \otimes \mathrm {diag}(I_{J_P}) . \end{aligned}$$

The proposed matrix-free PCG-method with diagonal preconditioner is also implemented within the mgss-package as function PCG_smooth. It is common practice to use a preconditioner when applying a CG-method such that we recommend to use PCG_smooth instead of CG_smooth. Most available preconditioners can be adjusted to significantly reduce the number of required CG iterations. Increasing the number of basis functions while keeping the number of observations constant typically results in larger condition numbers of the system matrix and therefore in an increased number of iterations. An improved preconditioner that overcomes this issue, i.e. resulting in an approximately constant number of CG iterations while increasing the number of basis functions, is presented in the following chapter.

4 A geometric multigrid preconditioner

The diagonal preconditioner for the CG-method is simple to implement but not always effective. In this section, we therefore focus on a more sophisticated preconditioner for the linear equation system (2.5). Since the systems coefficient matrix can not be stored, for the choice of a preconditioner it is again important that only matrix-vector products are involved. This especially cancels out the well-established incomplete Cholesky factorizations as a preconditioner and we thus concentrate on geometric multigrid (MG) methods in this section.

4.1 Multigrid-method

The origins of multigrid methods date back into the late 70th (see for instance Brandt 1977; Hackbusch 1978; Trottenberg et al. 2000 for an overview). Since then, they are successfully applied in the field of partial differential equations. The main idea is to build a hierarchy of—in a geometrical sense—increasingly fine discretizations of the problem. One then uses a splitting iteration like Jacobi or symmetric successive overrelaxation (SSOR) to smooth different frequencies of the error $e = x^*- x$ on different grids, where $x^*$ solves $Ax^*= b$ and x is an approximation. Due to the decreasing computational complexity, the problem can usually be solved explicitly on the coarsest grid, e.g. by a factorization of the system matrix. Between the grids, interpolation and restriction operations are used in order to transport the information back and forth. This works for hierarchical grids, i.e. that all nodes of one grid are also contained in the next finer grid. We achieve this by successively halving the grid spacing from 2h to h. A typical choice for the restriction is the transposed interpolation given by $I_{h}^{2h} = \left( I_{2h}^{h}\right) ^T$.

The outstanding feature of the multigrid method is that under certain circumstances it is possible to solve sparse, linear systems in optimal ${\mathcal {O}}(m)$ complexity, where m is the number of discretization points on the finest grid. Algorithm 7 shows the basic structure of one v-cycle that serves as a preconditioner in the CG method. Here $g \in \lbrace 1, \dots , G \rbrace$ denotes the grid levels from coarse $g=1$ to fine $g=G$, which coincides with the original problem.

The main ingredients of Algorithm 7 are:

• the system matrices $A_g$,

• interpolation matrices $I_{g-1}^{g}$ and restriction matrices $I_{g}^{g-1}$,

• smoothing iteration method,

• the coarse grid solver $A_1^{-1}$.

Note that the smoother (line 5 and 10 in Algorithm 7) does not necessarily have to be convergent on its own. Typical choices are Jacobi or SSOR, for which the convergence depends on the spectral radius of the iteration matrix. Convergence is not necessary for the smoothing property. It is thus recommendable only to apply a small number of pre- and post-smoothing steps $\nu _1$ and $\nu _2$, typically between two to ten, such that a possibly diverging smoother does not affect the overall convergence. This is further addressed in the discussion of Sect. 6.

It might be tempting to apply an algebraic (AMG) instead of a geometric multigrid preconditioner. The attractivity stems from the fact that AMG typically works as a black-box solver on a given matrix without relying a geometric description of grid levels and transfer operators. Yet, common AMG implementations explicitly require access to the matrix, which is prohibitively memory consuming for the tensor-product smoothing splines. In the following, we concentrate on a memory efficient realization of the matrix-vector product in line 6 of Algorithm 7, the interpolation and restriction in lines 7 and 9 as well as the smoothing operation in lines 5 and 10.

4.2 MGCG algorithm for penalized spline smoothing

We aim to apply a matrix-free version of the multigrid v-cycle of Algorithm 7 as a preconditioner in the CG method to solve the linear system (2.5). Therefore, we focus on the different parts of the v-cycle in more detail.

4.2.1 Hierarchy

For the multigrid method, we require hierarchical grids denoted by $g=1,\ldots ,G$, where $g=1$ is the coarsest and $g=G$ the finest grid. Since we do not assume initial knowledge on the data we propose to base the underlying spline space on $m_p = 2^g-1$ equidistant knots in each space dimension $p=1,\ldots ,P$ to achieve best computational performance. From a practical point of view, any other number of equidistant knots will do and the numbers do not have to coincide for the various spatial directions. For $g=1,\ldots ,G$ we define the coefficient matrix

$$\begin{aligned} A_{g} :=\Phi ^T_g \Phi _g + \lambda \Lambda _g. \end{aligned}$$

With

$$\begin{aligned} K_g :=\text {dim}({\mathcal {S}}_q({\mathcal {K}}_{g})) = \prod \limits _{p=1}^{P} (2^g + q_p) = (2^g + 3)^P \end{aligned}$$

we denote the dimension of the spline space ${\mathcal {S}}_q({\mathcal {K}}_{g})$ and hence the size of the coefficient matrix $A_g \in {\mathbb {R}}^{K_g \times K_g}$ on grid level g. Thus, we obtain a hierarchy of linear systems for which we can use the subdivision properties given in Sect. 3.2 for grid transfer.

4.2.2 Grid transfer

For the transfer of a data vector from grid g to grid $g+1$, we require a prolongation matrix $I_{g}^{g+1} \in {\mathbb {R}}^{K_{g+1} \times K_{g}}$. Due to the subdivision formula and the tensor product nature of the splines, we can use (3.2) for this purpose. For the restriction matrix $I_{g+1}^{g} \in {\mathbb {R}}^{K_{g} \times K_{g+1}}$ we choose $I_{g+1}^{g} :=\left( I_{g}^{g+1} \right) ^T$, which yields the Garlerkin property

$$\begin{aligned} A_{g} = I_{g+1}^{g} A_{g+1} I_{g}^{g+1} . \end{aligned}$$

The restriction and prolongation matrices do not fit into storage as well, but to apply the v-cycle Algorithm 7 only matrix-vector products with $I_{g}^{g+1}$ and $I_{g+1}^{g}$ are required. Since

$$\begin{aligned} I_{g}^{g+1} = \bigotimes _{p=1}^{P} I_{g,p}^{g+1,p} \ \text { and } \ I_{g+1}^{g} :=\left( I_{g}^{g+1} \right) ^T = \left( \bigotimes _{p=1}^{P} I_{g,p}^{g+1,p} \right) ^T = \bigotimes _{p=1}^{P} \left( I_{g,p}^{g+1,p} \right) ^T , \end{aligned}$$

these product can be memory efficiently computed by means of Algorithm 2.

4.2.3 Smoothing iteration

To apply the Jacobi method as a smoother, we additionally require the diagonal of the coefficient matrix, which is a vector of length $K_g$. In principle, this is not prohibitively memory consuming, however, since the coefficient matrix is not explicitly accessible, we cannot simply extract its diagonal. However, Algorithm 5 allows the memory efficient computation of the diagonal of $\Phi ^T_g \Phi _g$ for all $g=1,\ldots ,G$, and the diagonal of each matrix $\Psi _{r,g}$ is directly given by the diagonal property of Kronecker matrices. In contrast to the Jacobi smoother, the SSOR method additionally requires explicit access to all elements in one of the triangular parts of the coefficient matrices. It would be possible to compute the desired elements entry-wise within each iteration, but this would be computationally very expensive, since these elements have to be computed repeatedly in each iteration and for each grid level such that these methods are way too expensive. Therefore, we commit to the Jacobi method, implemented in Algorithm 8, as smoothing iteration. However, in Sect. 6 we also test a SSOR smoother in the multigrid algorithm, yet we apply this only to low dimensional tests where we can explicitly assemble and keep the coefficient matrix in memory.

4.2.4 Coarse grid solver

On the coarsest grid $g=1$ the v-cycle algorithm requires the exact solution of a linear system with coefficient matrix $A_{1} \in {\mathbb {R}}^{K_1 \times K_1}$. Since $K_1 \ll K_G$ we assume an explicitly assembled coarse grid coefficient matrix in a sparse matrix format. This allows a factorization of $A_{1}$, that can be precomputed and stored in memory. Keeping the factorization in memory is important, since each call of the multigrid preconditioner requires a solution of a linear system given by $A_{1}$. Due to the symmetry of the matrix we apply a sparse Cholesky factorization. Yet, in higher dimensional spaces even the coarse grid operators might be prohibitively memory consuming. Recall that the number of variables $K_1$ grows exponentially with the space dimension P. We then apply the matrix-free PCG algorithm also as a coarse grid solver. Note that the overall scalability is not affected since the computational costs of the coarse grid solver are fixed, even when the fine grid G is further subdivided as $G \leftarrow G+1$.

4.2.5 MGCG-method

Putting everything together we obtain Algorithm 9, which performs one v-cycle of the multigrid method for the large-scale linear system (2.5) with negligible memory requirement. The v-cycle can be interpreted as linear iteration with iteration matrix

$$\begin{aligned} \begin{aligned} C_{\text {MG},G}&= C_{\text {smooth}}^{\nu _2} \left( I_{n_G} - I_{G-1}^{G} \left( I_{n_{G-1}} - C_{\text {MG},G-1} \right) A_{G-1}^{-1} I_{G}^{G-1} A_G \right) C_{\text {smooth}}^{\nu _1} , \\ C_{\text {MG},1}&= 0 , \end{aligned} \end{aligned}$$

(4.1)

where $C_{\text {smooth}}$ denotes the iteration matrix of the utilized smoothing iteration as stated in Saad (2003, p. 446). Note that the iteration matrix is only for theoretical investigations and is never assembled in practice.

Finally, applying the multigrid v-cycle as preconditioner for the CG method yields Algorithm 10 as memory efficient multigrid preconditioned conjugated gradient (MGCG) method to solve the large-scale linear system (2.5). It is also implemented within the mgss-package as function MGCG_smooth. As we show in chapter 6, compared to the CG- and PCG-algorithm, the MGCG-method for the penalized spline problem (2.5) provides grid independent convergence in the sense that the number of iterations remains constant although the number of spline basis functions is increased. Nevertheless, note that the overall runtime yet increases, since each iteration becomes computationally more expensive due the larger problem dimension.

5 Some practical remarks

In this section we give some information about how to use the proposed algorithms and how to extend the ideas to further problems occurring in the context of penalized spline smoothing.

5.1 Algorithmic remarks

First, it is important to mention that penalized spline smoothing is a well-established and widely used method in statistical modelling and that its properties are well studied. The proposed algorithms in this paper, i.e. CG_smooth, PCG_smooth, and MGCG_smooth, do not change the general method or its modelling process but only the way how the underlying optimization problem is solved. This numerical novelty leads to fast and memory efficient algorithms that in the end allow to carry penalized spline smoothing over to multiple covariates.

Using the CG_smooth or the PCG_smooth method, there are no practical limitations to the modelling process and no numerical setups have to be made. Of course, as in the one and two dimensional case, the user has to think about the underlying model that has to be fitted, i.e. the number of knots, the spline degree, the penalty term, the weight of the penalty, the desired interaction and so on. However, if these decisions are made, they can directly be passed as input parameters. Since the function also returns the R-squared and the Root Mean Square Error (RMSE), different models can be directly compared.

More care on the numerical setup has to be given within the MGCG_smooth method, since it is based on a much more sophisticated preconditioner. Compared to CG_smooth or PCG_smooth that can deal with any introduced type of models, solving with MGCG_smooth is restricted to a special kind models, since it only allows for the curvature penalty and the number of inner knots has to be of the exponential form $2^G$. Further, the weight of the Jacobi-method $\omega$ has to be manually set and this choice can heavily influence the convergence rate. We recommend to start with a smaller value, e.g. $\omega = 0.1$ and to check whether or not the error reduces significantly by around a factor of five to ten in the first iterations. If this is not the case, $\omega$ can be increased. These restrictions on the models and the numerical effort, however, are rewarded with a much faster convergence which will become more clear in Sect. 6.

Typically, a promising strategy for faster convergence is also to combine the methods by performing a few iterations of the MGCG_smooth function (by setting K_max or tolerance) and then switching to the PCG_smooth method using the result of the MGCG-algorithm as initial guess alpha_start.

5.2 Predictions

Let ${\widehat{\alpha }}$ denote the solution of (2.5) such that the fitted spline is given as

$$\begin{aligned} {\widehat{s}}_{\lambda } :=\sum \limits _{k=1}^{K} {\widehat{\alpha }}_k \varphi _{k,q} . \end{aligned}$$

Evaluation of the spline at the original observations $x_i$ leads to the fitted values ${\widehat{y}}_i :={\widehat{s}}_{\lambda }(x_i)$ and evaluating the spline at each observation, i.e. computing all fitted values at once, is efficiently performed via

$$\begin{aligned} {\widehat{y}} :=\Phi {\widehat{\alpha }} \in {\mathbb {R}}^n . \end{aligned}$$

The matrix-vector product $\Phi {\widehat{\alpha }}$ again can be computed by means of Algorithm 4. The spline coefficients, the fitted values as well as the residuals are directly returned from all of the functions CG_smooth, PCG_smooth, and MGCG_smooth.

In practice, the interest is not only in the smoothed values but rather in predicted values at unobserved data points ${\tilde{x}}_j \in {\mathbb {R}}^P$ , i.e. ${\widehat{s}}_{\lambda }({\tilde{x}}_j)$, for $j=1,\ldots ,m$. Defining ${\tilde{\Phi }} \in {\mathbb {R}}^{m \times K}$ element wise as

$$\begin{aligned} {\tilde{\Phi }}[j,k] :=\varphi _{k,q}({\tilde{x}}_j) \end{aligned}$$

the vector of predicts is given by ${\tilde{y}} :={\tilde{\Phi }}{\widehat{\alpha }}$. Since, as before, ${\tilde{\Phi }}$ does not fit into storage, we define the univariate B-spline matrices evaluated at the unobserved data points as

$$\begin{aligned} {\tilde{\Phi }}_p \in {\mathbb {R}}^{n \times J_p} , \ \Phi _p[i,j_p] :=\varphi ^p_{j_p,q_p}(x_i^p) \end{aligned}$$

and conclude that

$$\begin{aligned} {\tilde{\Phi }}^T = \bigodot \limits _{p=1}^{P} {\tilde{\Phi }}_p^T . \end{aligned}$$

Again using Algorithm 4, we obtain the vector of desired predictions ${\tilde{y}}$. The underlying method to obtain those predicts is also implemented within the mgss-package in the predict_smooth function.

5.3 Smoothing parameter selection

As mentioned in Sect. 2, selecting an adequate smoothing parameter $\lambda > 0$ is an important task in penalized spline smoothing. In practice, data-driven methods such as cross-validation techniques are frequently used. Therefore, let again

$$\begin{aligned} {\widehat{\alpha }} :=\left( \Phi ^T \Phi + \lambda \Lambda \right) ^{-1} \Phi ^T y \end{aligned}$$

denote the analytical solution of (2.5) and let

$$\begin{aligned} {\widehat{y}}_{\lambda } :=\Phi {\widehat{\alpha }} = \Phi \left( \Phi ^T \Phi + \lambda \Lambda \right) ^{-1} \Phi ^T y = S_{\lambda } y \end{aligned}$$

be the resulting predicts for a given $\lambda$, where

$$\begin{aligned} S_{\lambda } :=\Phi \left( \Phi ^T \Phi + \lambda \Lambda \right) ^{-1} \Phi ^T \in {\mathbb {R}}^{n \times n} \end{aligned}$$

is refereed to as smoother matrix or hat matrix. In cross-validation (CV) the smoothing parameter is determined as solution of

$$\begin{aligned} \min \limits _{\lambda > 0} \frac{1}{n} \sum \limits _{i=1}^{n} \left( \frac{y_i - {\widehat{y}}_{\lambda }[i] }{1- S_{\lambda }[i,i]} \right) ^2 , \end{aligned}$$

where $[\cdot ]$ and $[\cdot , \cdot ]$ denote the entries of the respective vector and matrix, respectively. Since the calculation of the hat matrix and its diagonal elements can be numerically complex, the diagonal elements $S_{\lambda }[i,i]$ are frequently approximated by their average

$$\begin{aligned} S_{\lambda }[i,i] \approx \frac{1}{n} \sum \limits _{j=1}^{n} S_{\lambda }[j,j] = \frac{1}{n} \mathrm {trace}(S_{\lambda }) , \quad \ i=1,\ldots ,n, \end{aligned}$$

where $\mathrm {trace}(\cdot )$ denotes the trace of a square matrix. This leads to the generalized cross-validation (GCV) method, where the regularization parameter is determined as the solution of

$$\begin{aligned} \min \limits _{\lambda > 0} \frac{1}{n} \sum \limits _{i=1}^{n} \left( \frac{y_i - {\widehat{y}}_{\lambda }[i]}{1- \mathrm {trace}(S_{\lambda })n^{-1}} \right) ^2 . \end{aligned}$$

(5.1)

In order to solve the optimization problem, it is common practice to perform a grid search. That is, a reasonable subset of parameters is specified and the parameter with the smallest objective function value is selected.

To evaluate the objective function of (5.1) for a fixed $\lambda$ we finally need to compute ${\widehat{y}}_{\lambda } = S_{\lambda } y$ and $\mathrm {trace}(S_{\lambda })$. Even if $S_{\lambda }\in {\mathbb {R}}^{n \times n}$ fits into storage it can not be computed since it requires the computation and inversion of $\Phi ^T \Phi + \lambda \Lambda \in {\mathbb {R}}^{K \times K}$. Therefore, we also need a matrix-free approach to compute, or at least estimate, the trace of $S_{\lambda }$ as recently proposed by Wagner et al. (2021). They implemented a matrix-free Hutchinson trace estimator and carried out data-driven smoothing parameter selection via a fixed point iteration based on a mixed-model formulation of the penalized spline smoothing method. For generalized cross validation, however, it suffices to estimate the trace by their matrix-free Hutchinson trace estimator which is implemented within estimae_trace function of the mgss-packages. Further ideas of stochastic trace estimation can be found for example in Avron and Toledo (2011) or Fitzsimons et al. (2016).

The trace of the hat matrix, in this context also referred to as degrees of freedom

$$\begin{aligned} \mathrm {df_{fit}}(\lambda ) :=\mathrm {trace}(S_{\lambda }) \end{aligned}$$

is not only required for smoothing parameter selection but also for model diagnostics and inference such as the Akaike information criterion (AIC)

$$\begin{aligned} \log \left( \sum \limits _{i=1}^{n} (y_i - {\widehat{y}}_i)^2 \right) + 2 \frac{\mathrm {df_{fit}}}{n} \end{aligned}$$

or the corrected Akaike information criterion($\hbox {AIC}_c$)

$$\begin{aligned} \log \left( \sum \limits _{i=1}^{n} (y_i - {\widehat{y}}_i)^2 \right) + 2 \frac{\mathrm {df_{fit}} + 1}{n - \mathrm {df_{fit}} - 2} \end{aligned}$$

as well as for the estimation of confidence and prediction bands. More information is given by Ruppert et al. (2003).

5.4 Interaction models

Beneath the choice of an adequate number of knots, the spline degree, the utilized penalty and its weight there is also the question of the adequate interaction. As already mentioned in Sect. 2.3, increasing the number of covariates in the tensor product penalized spline model requires a data set of adequate size to support the complexity. Further, and much more important, modeling interactions between covariates needs much care and should be done reasonably. Therefore, it is often useful not to model interactions between all covariates but only between suitable subsets. Thus, the user has to choose a suitable model somewhere between the additive approach

$$\begin{aligned} y = \sum \limits _{p=1}^{P} s^p(x^p) + \varepsilon \end{aligned}$$

where the $s^p$ are univariate smooth functions and the full interaction model

$$\begin{aligned} y = s(x^1, \ldots , x^P) + \varepsilon \end{aligned}$$

where s is a smooth function with a P-dimensional input vector. That is, we choose L suitable sets

$$\begin{aligned} U^{\ell } \subset \lbrace 1,\ldots ,P \rbrace , \ \ell =1,\ldots ,L \end{aligned}$$

and consider the model

$$\begin{aligned} y = \sum \limits _{\ell =1}^{L} s^{\ell }(x^{\ell }) + \varepsilon \end{aligned}$$

where $x^{\ell } \in {\mathbb {R}}^{P^{\ell }}$ are the covariate values in $U^{\ell }$. The introduced matrix-free methods can then analogously be applied to compute all the spline functions $s^{\ell }$. The complexity of the model is then determined by $\max (P^\ell )$ instead of P.

6 Numerical results

In this section we apply the presented algorithms to artificial data as well as to real world data on international trades and analyze their performance.

6.1 Numerical performance on test data

First, we demonstrate the numerical performance of the presented algorithms in a selection of synthetic test cases. On the one hand, we consider various spatial dimensions $P=1,\dots , 4$ in order to investigate the computational complexity of the algorithms. On the other hand, we successively apply uniform grid refinements for a maximum grid level of $G=4, \dots , 7$ in each dimension in order to inspect the scalability of the multigrid preconditioner. The algorithmic building blocks, which are critical to computational performance, are accelerated by using the RCPP extension library, introduced in Eddelbuettel (2013) and Eddelbuettel and François (2011), and programmed in C++. These are in particular the matrix-vector products with the coefficient matrix (Algorithm 2, 3, 4), interpolation and restriction (Algorithm 2), and the Jacobi smoother (Algorithm 8). Throughout this section, we consider the following test data set

$$\begin{aligned} \lbrace (x_i,y_i) : i=1,\ldots ,100{,}000 \rbrace , \ P=1,\ldots ,4 , \end{aligned}$$

obtained by uniformly random sampling of the normalized, multivariate sigmoid function

$$\begin{aligned} f_P :[0,1]^P \rightarrow [0,1] , \ x \mapsto \frac{1}{1-\exp \left( -16 \left( \Vert x \Vert _2^2 P^{-1} - 0.5 \right) \right) } \end{aligned}$$

enriched by normally distributed noise $\varepsilon \sim {\mathcal {N}}(0;0.1^2)$, i.e.

$$\begin{aligned} y_i :=f_P(x_i) + \varepsilon _i . \end{aligned}$$

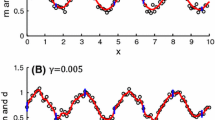
For $P=1$ and $P=2$ the related sigmoid functions are depicted in Fig. 1. We consider these functions since they are irrational functions which exhibit similar behavior for different covariate dimension P. However, since the performance of the solution algorithms is in focus, the exact form of the generating function is of minor importance.

Fig. 1

Plot of the (undisturbed) sigmoid test function for $P=1$ and $P=2$

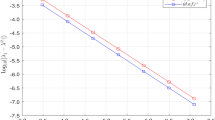
In a first test case, we fix the spatial dimension to $P=2$ and successively refine the B-spline basis on $G=1,\dots ,7$ grids. We then consider four different tests. In each of them, $G \in \lbrace 4,\dots ,7\rbrace$ is chosen to be the maximum grid level for the v-cycle of the multigrid preconditioner. The coarsest grid $g=1$ is used for the coarse grid solver in each case. This leads to problem dimensions of $K_1 = (2^1+3)^2=25$ on the coarse grid and $K_G = (2^G+3)^2$ on the finest grid. Note that the unpreconditioned CG method simply uses the discretization matrix $A_G$ on the G-th grid. The required iterations as well as the computational time of the methods are shown in Fig. 2, where a logarithmic scale is used. We observe that the number of unpreconditioned conjugate gradient iterations significantly increases under grid refinements, i.e. increasing number of basis functions, which is due to the increasing condition number of the system matrix. For both of the multigrid methods, the Jacobi and SSOR preconditioned MGCG algorithms, the number of iterations is almost constant (i.e. 1-2 for SSOR and 4 for Jacobi). This result illustrates that the multigrid preconditioner enables a scalable solver for the regularized least squares problem (2.5) determining the smoothing spline. Clearly, the computational times are increasing since we run only a single core code and each iteration becomes computationally more expensive when increasing K. A standard approach here is to distribute the matrix between an increasing number of processors in a cluster computer and one obtains almost constant running times in the sense of weak scalability. Note that this is not achievable by the plain CG solver due to the increasing number of iterations.

Fig. 2

Number of preconditioned and unpreconditioned conjugate gradient iterations under uniform grid refinements in $P=2$ dimensions

The next test under consideration is the comparison of computational complexity with respect to the spatial dimension. Table 2 shows the number of required iterations of the utilized methods in the dimensions $P=1,\dots ,4$ together with the CPU time in seconds. The underlying hardware is one core of a Xeon W-2155 processor. One can observe that each of the preconditioned iterations is more expensive with respect to computational time. Yet, the MGCG is significantly faster due to the small number of iterations. Note that the computational time of the SSOR multigrid preconditioned iteration is not comparable since it does not rely on the matrix-free approach. This is only for the comparison of MGCG iterations. Since the SSOR smoother needs access to all matrix entries, we explicitly assemble the coefficient matrix $\Phi ^T \Phi + \lambda \Lambda$ in R’s sparse format and use it for the algorithm.

Table 2 Required number of iterations of the considered methods for various dimensions with $G=5$ grids and computational time in seconds

Crucial for the convergence speed of the CG method in the unpreconditioned as well as in the preconditioned case is the condition of the respective coefficient matrix, that is

$$\begin{aligned} \Phi _G^T\Phi _G + \lambda \Lambda _G \end{aligned}$$

for the pure CG method and

$$\begin{aligned} C_{\text {MG},G} \cdot \left( \Phi _G^T\Phi _G + \lambda \Lambda _G \right) \end{aligned}$$

for the MGCG method. An explicit form of the iteration matrix of the multigrid method is given in (4.1), i.e. one call of Algorithm 7 is equivalent to a matrix-vector product with $C_{\text {MG},G}$. Note that for the Jacobi smoother and for the SSOR smoother different preconditioning matrices $C_{\text {MG},G,\text {JAC}}$ and $C_{\text {MG},G,\text {SSOR}}$ arise. Figure 3 visualizes the distribution of the eigenvalues of the respective coefficient matrices for the $P=2$ and $G=5$ case. Additionally, Table 3 shows the condition number of the (un)preconditioned iteration matrix for the CG algorithm. Note that we only compute the eigenvalues in the $P=2$ test case due to the computational complexity, since we have to assemble a matrix representation of the preconditioned system matrix. That is, we have to run the v-cycle on each of the K-dimensional unity vectors to obtain a matrix on which we then perform an eigenvalue decomposition. Here it can be seen that the multigrid preconditioner pushes the eigenvalues towards 1, which explains the significant lower number of required MGCG iterations. Although it seems that the multigrid preconditioner with SSOR smoother outperforms the Jacobi smoother, it is prohibitively expensive with respect to memory requirement. For the SSOR iteration the entire upper triangular part of the system matrix is required, which is not efficiently accessible in our matrix-free approach. In $P=3$ dimensions, the MGCG with SSOR smoother for the considered test problem requires approximately 30 GB of RAM, which is at the limit of the utilized computer systems. By contrast, the matrix-free methods require approximately 16 MB (for CG) and 78 MB (for MGCG_JAC) of RAM.

Fig. 3

Eigenvalues of the (un)preconditioned coefficient matrices for $G=5$ grids and $P=2$ dimensions

Table 3 Condition number of the coefficient matrices for $G=5$ grids and $P=2$ dimensions

6.2 Application to international trade data

To describe bilateral trade flows between countries gravity models are widely used. The basic idea is to model the trade flow as a specific function of the economic sizes and distance between two trading partners and can be extended to further influences on interaction costs. For more detail on gravity models for bilateral trade we refer to Head and Mayer (2014). Even though the basic idea of gravity models is rather simple, they can become very complex when it comes to the choice of models or estimation methods and a variety of approaches exist (cf. Wölwer et al. 2018, for an overview). Instead of restricting the model to a specific form as in the gravity model, we apply a spline model in following that allows for a more flexible fit as well as for the direct incorporation of further covariates. For the presented application the CEPII gravity database is used which is constructed and explained in detail by Head et al. (2010). Note that the goal of the presented application is not to compare different modeling approaches or to analyze the importance of incorporated covariates, but rather to show the applicability of high-dimensional interaction spline models to real world problems.

The traditional gravity model models the trade flow between two countries as a specific function of their distance as well as their respective gross domestic product (GDP). Since the CEPII database contains trade information over several years, the year is also used as covariate in the spline model leading to the $P=4$ dimensional interaction spline model

$$\begin{aligned} t_{o, d} = s(year, dist_{o, d}, GDP_{o}, GDP_{d}) \end{aligned}$$

where o (origin) and d (destination) denote the respective countries, t denotes their trade flow and dist their distance. The CEPII data provides 950, 892 valid data points for this set of covariates from which we sample $n = 750{,}000$ for fitting the model and keep the rest for validation. All variables are scaled by a min-max-normalization to [0, 1].

To fit an adequate spline model to the data we apply the PCG_smooth function with $\mathtt {tolerance} = 10^{-4}$. For the spline model itself we use the curvature penalty, $m = 15$ inner knots and $q=3$ in each direction and a smoothing parameter $\lambda = 0.1$. This setup result in a spline model with $K=130{,}321$ coefficients in total. The PCG-algorithm converged within 4049 iterations and the spline model results in an R-squared of 0.8458 and an RMSE of 0.0026 indicating for a good fit of the spline model to the sampled data. Computing the predictions on the test data using the predict_smooth function shows a mean absolute error (MAE) of 0.0003288 and an RMSE of 0.00315 out of the sample which shows that the model generalizes well. The results are also presented in Table 4.

Table 4 Results of the PCG_smooth algorithm for the trade flow models with $P=4$ covariates

7 Conclusions

In this paper, we presented memory efficient algorithms to solve a large-scale linear system resulting from penalized spline smoothing with multiple covariates and scattered data. The crucial feature is the matrix-free approach that circumvents building and storing huge matrices by exploiting their underlying structure and solely relies on forming matrix-vector products within a conjugate gradient method. This, in contrast to the existing methods for one and two dimensional data or to methods for gridded data, allows to handle penalized spline smoothing in several dimensions and with scattered data from a storage point of view. The proposed implementations CG_smooth and PCG_smooth from the mgss-package can be applied to variety of modeling approaches without in depth numerical knowledge. As the numerical test cases show, the CG-method requires an acceptable running time relative to the problem dimensions, which increases with the number of covariates. The focus of our presentations was on algorithmic studies of a preconditioner based on a matrix-free, geometric multigrid approach within the MGCG_smooth implementation. Using this method is restricted to special types of penalized spline smoothing models but therefore enables almost constant iteration numbers for fixed dimensions even under arbitrary grid refinements, which provides an important building block for algorithmic scalability.