Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-24T05:12:42.001Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigidity of joinings for some measure-preserving systems

Part of: Ergodic theory

Published online by Cambridge University Press:  30 April 2021

CHANGGUANG DONG ,
ADAM KANIGOWSKI  and
DAREN WEI
CHANGGUANG DONG
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD20742, USA (e-mail: dongchg@math.umd.edu, adkanigowski@gmail.com)
ADAM KANIGOWSKI
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD20742, USA (e-mail: dongchg@math.umd.edu, adkanigowski@gmail.com)
DAREN WEI*
Affiliation:
Einstein Institute of Mathematics, Edmond J. Safra Campus, The Hebrew University of Jerusalem, Givat Ram, Jerusalem, 9190401, Israel
*
e-mail: Daren.Wei@mail.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

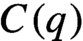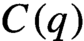We introduce two properties: strong R-property and $C(q)$ -property, describing a special way of divergence of nearby trajectories for an abstract measure-preserving system. We show that systems satisfying the strong R-property are disjoint (in the sense of Furstenberg) with systems satisfying the $C(q)$ -property. 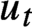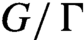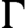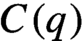Moreover, we show that if $u_t$ is a unipotent flow on $G/\Gamma $ with $\Gamma $ irreducible, then $u_t$ satisfies the $C(q)$ -property provided that 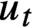$u_t$ is not of the form $h_t\times \operatorname {id}$ , where 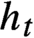$h_t$ is the classical horocycle flow. Finally, we show that the strong R-property holds for all (smooth) time changes of horocycle flows and non-trivial time changes of bounded-type Heisenberg nilflows.

Keywords

rigidity of joiningstime changeshorocycle flowunipotent flowsHeisenberg flows

MSC classification

Primary: 37A35: Entropy and other invariants, isomorphism, classification
Secondary: 37A10: One-parameter continuous families of measure-preserving transformations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 2: Anatole Katok Memorial Issue Part 1: Special Issue of Ergodic Theory and Dynamical Systems , February 2022 , pp. 665 - 690
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A., Forni, G. and Ulcigrai, C.. Mixing for time-changes of Heisenberg nilflows. J. Differential Geom. 89(3) (2011), 369–410.10.4310/jdg/1335207373CrossRefGoogle Scholar
del Junco, A. and Rudolph, D.. On ergodic actions whose self-joinings are graphs. Ergod. Th. & Dynam. Sys. 7(4) (1987), 531–557.CrossRefGoogle Scholar
Fayad, B. and Kanigowski, A.. Multiple mixing for a class of conservative surface flows. Invent. Math. 203(2) (2016), 555–614.CrossRefGoogle Scholar
Feldman, J. and Ornstein, D.. Semirigidity of horocycle flows over compact surfaces of variable negative curvature. Ergod. Th. & Dynam. Sys. 7(1) (1987), 49–72.CrossRefGoogle Scholar
Flaminio, L. and Forni, G.. Invariant distributions and time averages for horocycle flows. Duke Math. J. 119(3) (2003), 465–526 (English summary).CrossRefGoogle Scholar
Forni, G. and Kanigowski, A.. Multiple mixing and disjointness for time changes of bounded-type Heisenberg nilflows. J. Éc. Polytech. Math. 7 (2020), 63–91.CrossRefGoogle Scholar
FraĄczek, K. and Lemańczyk, M.. On mild mixing of special flows over irrational rotations under piecewise smooth functions. Ergod. Th. & Dynam. Sys. 26(3) (2006), 719–738.CrossRefGoogle Scholar
FraĄczek, K. and Lemańczyk, M.. Ratner’s property and mild mixing for special flows over two-dimensional rotations. J. Mod. Dyn. 4(4) (2010), 609–635.CrossRefGoogle Scholar
Gabriel, P., Lemańczyk, M. and Schmidt, K.. Extensions of cocycles for hyperfinite actions and applications. Monatsh. Math. 123 (1997), 209–228.CrossRefGoogle Scholar
Kanigowski, A., Vinhage, K. and Wei, D.. Kakutani equivalence of unipotent flows. Duke Math. J. Advanced Publication 1–67, 2021. https://doi.org/10.1215/00127094-2020-0074.CrossRefGoogle Scholar
Kanigowski, A.. Ratner’s property for special flows over irrational rotations under functions of bounded variation. Ergod. Th. & Dynam. Sys. 35(3) (2015), 915–934.10.1017/etds.2013.74CrossRefGoogle Scholar
Kanigowski, A. and Kułaga-Przymus, J.. Ratner’s property and mild mixing for smooth flows on surfaces. Ergod. Th. & Dynam. Sys. 36(8) (2016), 2512–2537.CrossRefGoogle Scholar
Kanigowski, A., Lemańczyk, M. and Ulcigrai, C.. On disjointness properties of some parabolic flows. Invent. Math. 221(1) (2020), 1–111.CrossRefGoogle Scholar
Kanigowski, A., Vinhage, K. and Wei, D.. Slow entropy of some parabolic flows. Comm. Math. Phys. 370(2) (2019), 449–474.CrossRefGoogle Scholar
Kirillov, A. A.. An Introduction to Lie Groups and Lie Algebras (Cambridge Studies in Advanced Mathematics,113). Cambridge University Press, Cambridge, 2008.CrossRefGoogle Scholar
Marcus, B.. Ergodic properties of horocycle flows for surfaces of negative curvature. Ann. of Math. (2) 105(1) (1977), 81–105.10.2307/1971026CrossRefGoogle Scholar
Margulis, G. A.. Certain measures that are connected with U-flows on compact manifolds. Funktsional. Anal. i Prilozhen. 4(1) 1970, 62–76 (in Russian).CrossRefGoogle Scholar
Ratner, M.. Rigidity of horocycle flows. Ann. of Math. (2) 115(3) (1982), 597–614.CrossRefGoogle Scholar
Ratner, M.. Horocycle flows, joinings and rigidity of products. Ann. of Math. (2) 118(2) (1983), 277–313.CrossRefGoogle Scholar
Ratner, M.. Rigidity of time changes for horocycle flows. Acta Math. 156(1–2) (1986), 1–32.CrossRefGoogle Scholar
Ratner, M.. Rigid reparametrizations and cohomology for horocycle flows. Invent. Math. 88(2) 1987, 341–374.CrossRefGoogle Scholar
Ratner, M.. On measure rigidity of unipotent subgroups of semisimple groups. Acta Math. 165(3–4) (1990), 229–309.CrossRefGoogle Scholar
Thouvenot, J.-P.. Some properties and applications of joinings in ergodic theory. Ergodic Theory and its Connections with Harmonic Analysis (Alexandria, 1993) (London Mathematical Society Lecture Note Series, 205). Cambridge University Press, Cambridge, 1995, pp. 207–235.CrossRefGoogle Scholar
Witte, D.. Rigidity of some translations on homogeneous spaces. Invent. Math. 81(1) (1985), 1–27.CrossRefGoogle Scholar