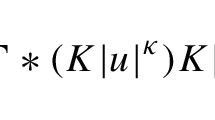Two-term expansion of the ground state one-body density matrix of a mean-field Bose gas

Abstract

We consider the homogeneous Bose gas on a unit torus in the mean-field regime when the interaction strength is proportional to the inverse of the particle number. In the limit when the number of particles becomes large, we derive a two-term expansion of the one-body density matrix of the ground state. The proof is based on a cubic correction to Bogoliubov’s approximation of the ground state energy and the ground state.

1 Introduction

We consider a homogeneous system of N bosons on the unit torus ${{\mathbb {T}}}^d$, for any dimension $d\ge 1$. The system is governed by the mean-field Hamiltonian

$$\begin{aligned} H_{N} = \sum _{j=1}^N -\Delta _{x_j} +\frac{1}{N-1}\sum _{1\le j<k\le N} w(x_j-x_k) \end{aligned}$$

(1)

which acts on the bosonic Hilbert space

$$\begin{aligned} {\mathcal {H}}^N=L^2_{\mathrm{sym}}(({{\mathbb {T}}}^d)^N). \end{aligned}$$

Here the kinetic operator $-\Delta$ is the usual Laplacian (with periodic boundary conditions). The interaction potential w is a real-valued, even function. We assume that its Fourier transform is non–negative and integrable, namely

$$\begin{aligned} w(x)= \sum _{p\in 2\pi {\mathbb {Z}}^d} \widehat{w}(p) e^{ip\cdot x} \quad \text {with}\quad 0\le {\widehat{w}} \in \ell ^1( 2\pi {\mathbb {Z}}^d ). \end{aligned}$$

In particular, w is bounded. Since w is even, $\widehat{w}$ is also even.

Under the above conditions, $H_N$ is well defined on the core domain of smooth functions. Moreover, it is well-known that $H_N$ is bounded from below and can be extended to be a self-adjoint operator by Friedrichs’ method. The self-adjoint extension, still denoted by $H_N$, has a unique ground state $\Psi _N$ (up to a complex phase) which solves the variational problem

$$\begin{aligned} E_N = \inf _{\Vert \Psi \Vert _{{\mathcal {H}}^N}=1} \langle \Psi , H_N \Psi \rangle . \end{aligned}$$

Here $\langle \cdot , \cdot \rangle$ is the inner product in ${\mathcal {H}}^N$.¹

In the present paper, we are interested in the asymptotic behavior of the ground state $\Psi _N \in {\mathcal {H}}^N$ of $H_N$ in the limit when $N\rightarrow \infty$. More precisely, we will focus on the one-body density matrix $\gamma _{\Psi _N}^{(1)}$ which is a trace class operator on $L^2({{\mathbb {T}}}^d)$ with kernel

$$\begin{aligned} \gamma _{\Psi _N}^{(1)}(x,y) = N \int _{{{\mathbb {T}}}^{d(N-1)}} \Psi _N (x, x_1, \ldots , x_N) \overline{\Psi _N (y, x_2, \ldots x_N)}dx_2\ldots dx_N. \end{aligned}$$

Note that $\gamma _{\Psi _N}^{(1)}\ge 0$ and $\mathrm{Tr}\gamma _{\Psi _N}^{(1)}=N$.

1.1 Main result

Our main theorem is

Theorem 1

(Ground state density matrix) Assume that $0\le {\widehat{w}}\in \ell ^1( (2\pi {\mathbb {Z}})^d )$. Then the ground state $\Psi _N$ of the Hamiltonian $H_N$ in (1) satisfies

$$\begin{aligned} \lim _{N\rightarrow \infty } \mathrm{Tr}\Big | \gamma ^{(1)}_{\Psi _N} - \Big (N-\sum _{p\ne 0} \gamma _p^2\Big ) |u_0\rangle \langle u_0| - \sum _{p\ne 0} \gamma _p^2 |u_p\rangle \langle u_p| \Big | =0 \end{aligned}$$

where

$$\begin{aligned} u_p(x)=e^{ip\cdot x},\quad \gamma _{p} = \frac{\alpha _p}{\sqrt{1-\alpha _p^2}}, \quad \alpha _p= \frac{{\widehat{w}}(p)}{p^2+ {\widehat{w}}(p) + \sqrt{p^4+ 2p^2 {\widehat{w}}(p)}} \cdot \end{aligned}$$

Here $|u\rangle \langle u|$ is the orthogonal projection on u. We use the bra-ket notation, where $|u\rangle =u$ is a vector in the Hilbert space ${\mathcal {H}}$ and $\langle u|$ is an element in the dual space of ${\mathcal {H}}$ which maps any vector $v\in {\mathcal {H}}$ to the inner product $\langle u,v\rangle _{{\mathcal {H}}}$.

To the leading order, our result implies Bose–Einstein condensation, namely

$$\begin{aligned} \lim _{N\rightarrow \infty }\frac{1}{N}\gamma _{\Psi _N}^{(1)} = |u_0\rangle \langle u_0| \end{aligned}$$

in the trace norm. This result is well-known and it follows easily from Onsager’s inequality

$$\begin{aligned} \frac{1}{N-1} \sum _{1\le i<j\le N} w(x_i-x_j) \ge \frac{N}{2}{\widehat{w}}(0) - \frac{N}{N-1} w(0) \end{aligned}$$

(2)

(see [18]). The significance of Theorem 1 is that it gives the next order correction to $\gamma ^{(1)}_{\Psi _N}$, thus justifying Bogoliubov’s approximation in a rather strong sense as we will explain.

1.2 Bogoliubov’s approximation

It is convenient to turn to the grand canonical setting. Let us introduce the Fock space

$$\begin{aligned} {\mathcal {F}}= \bigoplus _{n=0}^\infty {\mathcal {H}}^n = {\mathbb {C}} \oplus {\mathcal {H}}\oplus {\mathcal {H}}^2 \oplus \cdots \end{aligned}$$

For any Fock space vector $\Psi =(\Psi _n)_{n=0}^\infty \in {\mathcal {F}}$ with $\Psi _n\in {\mathcal {H}}^n$, we define its norm by

$$\begin{aligned} \Vert \Psi \Vert _{{\mathcal {F}}}^2= \sum _{n=0}^\infty \Vert \Psi _n \Vert _{{\mathcal {H}}^n}^2. \end{aligned}$$

and define the particle number expectation by

$$\begin{aligned} \langle \Psi , {\mathcal {N}}\Psi \rangle = \sum _{n=0}^\infty n \Vert \Psi _n\Vert ^2_{{\mathcal {H}}^n}. \end{aligned}$$

In particular, the vacuum state $|0\rangle = (1,0,0,\ldots )$ is a normalized vector on Fock space which has the particle number expectation $\langle 0| {\mathcal {N}}|0\rangle =0$.

For any $f\in {\mathcal {H}}$, the creation operator $a^*(f)$ on Fock space maps from ${\mathcal {H}}^n$ to ${\mathcal {H}}^{n+1}$ for every $n\ge 0$ and satisfies

$$\begin{aligned}&(a^* (f) \Psi _n )(x_1,\dots ,x_{n+1})\\&\quad = \frac{1}{\sqrt{n+1}} \sum _{j=1}^{n+1} f(x_j)\Psi (x_1,\dots ,x_{j-1},x_{j+1},\dots , x_{n+1}), \quad \forall \Psi _n\in {\mathcal {H}}^n. \end{aligned}$$

Its adjoint is the annihilation operator a(f), which maps from ${\mathcal {H}}^n$ to ${\mathcal {H}}^{n-1}$ for every $n\ge 0$ (with convention ${\mathcal {H}}^{-1}=\{0\}$) and satisfies

$$\begin{aligned} (a(f) \Psi _n )(x_1,\dots ,x_{n-1})&= \sqrt{n} \int _{{\mathbb {R}}^d} \overline{f(x_n)}\Psi (x_1,\dots ,x_n) d x_n, \quad \forall \Psi _n \in {\mathcal {H}}^n. \end{aligned}$$

We will denote by $a_p^*$ and $a_p$ the creation and annihilation operators with momentum $p\in 2\pi {\mathbb {Z}}^d$, namely

$$\begin{aligned} a_p^*=a^*(u_p), \quad a_p=a(u_p), \quad u_p(x)=e^{i p \cdot x}. \end{aligned}$$

They satisfy the canonical commutation relation (CCR)

$$\begin{aligned}{}[a_p,a_q]=0=[a_p^*,a_q^*], \quad [a_p,a_q^*]=\delta _{p,q} \end{aligned}$$

(3)

where $[X,Y]=XY-YX.$

The creation and annihilation operators can be used to express several operators on Fock space. For example, the number operator can be written as

$$\begin{aligned} {\mathcal {N}}= \sum _{n=0}^\infty n {\mathbb {1}}_{{\mathcal {H}}^n} = \sum _{p\in 2\pi {{\mathbb {Z}}}^d} a_p^* a_p. \end{aligned}$$

Similarly, the Hamiltonian $H_N$ in (1) can be rewritten as

$$\begin{aligned} H_N =\sum _{p \in 2\pi {{\mathbb {Z}}}^d} p^2 a_p^* a_p +\frac{1}{2(N-1)} \sum _{p,q,k \in {{\mathbb {Z}}}^d} {\widehat{w}}(k) a^*_{p-k}a^*_{q+k}a_p a_q. \end{aligned}$$

(4)

The right side of (4) is an operator on Fock space, which coincides with (1) when being restricted to ${\mathcal {H}}^N$. In the following we will only use the grand–canonical formula (4).

In 1947, Bogoliubov [4] suggested a heuristic argument to compute the low-lying spectrum of the operator $H_N$ by using a perturbation around the condensation. Roughly speaking, he proposed to first substitute all operators $a_0$ and $a_0^{*}$ in (4) by the scalar number $\sqrt{N}$ (c-number substitution²), and then ignore all interaction terms which are coupled with coefficients of order $o(1)_{N\rightarrow \infty }$. All this leads to the formal expression

$$\begin{aligned} H_N \approx \frac{N}{2}{\widehat{w}}(0) + {\mathbb {H}}_{\mathrm{Bog}} \end{aligned}$$

(5)

where

$$\begin{aligned} {\mathbb {H}}_{\mathrm{Bog}}= \sum _{p\ne 0} \left( \big ( p^2+{\widehat{w}}(p) \big ) a_p^* a_p + \frac{1}{2}{\widehat{w}}(p) \big ( a^*_p a^*_{-p}+ a_p a_{-p}\big )\right) . \end{aligned}$$

(6)

Note that the expression (5) is formal since $H_N$ acts on the N-body Hilbert space ${\mathcal {H}}^N$ while the Bogoliubov Hamiltonian ${\mathbb {H}}_{\mathrm{Bog}}$ acts on the excited Fock space

$$\begin{aligned} {\mathcal {F}}_+ = \bigoplus _{n=0}^\infty {\mathcal {H}}_+^n = {\mathbb {C}} \oplus {\mathcal {H}}_+ \oplus {\mathcal {H}}_+^2 \oplus \cdots , \quad {\mathcal {H}}_+ = Q {\mathcal {H}}\end{aligned}$$

where we have introduced the projections

$$\begin{aligned} Q = \sum _{p\ne 0} |u_p\rangle \langle u_p| = 1- P, \quad P= |u_0\rangle \langle u_0|. \end{aligned}$$

In particular, unlike $H_N$, the quadratic Hamiltonian ${\mathbb {H}}_{\mathrm{Bog}}$ does not preserve the number of particles. Nevertheless, ${\mathbb {H}}_{\mathrm{Bog}}$ can be diagonalized by the following unitary transformation on ${\mathcal {F}}_+$

$$\begin{aligned} U_{\mathrm{B}}= \exp \Big ( \sum _{p\ne 0} \beta _p (a^*_p a^*_{-p}-a_p a_{-p})\Big ) \end{aligned}$$

(7)

where the coefficients $\beta _p>0$ are determined by

$$\begin{aligned} \tanh (2\beta _p)=\alpha _p = \frac{{\widehat{w}}(p)}{p^2+ {\widehat{w}}(p) + \sqrt{p^4+ 2p^2 {\widehat{w}}(p)}} \cdot \end{aligned}$$

In fact, by using the CCR (3) it is straightforward to check that

$$\begin{aligned} U_{\mathrm{B}} a_p U_{\mathrm{B}}^* = \frac{a_p+\alpha _p a_{-p}^*}{\sqrt{1-\alpha _p^2}}=: \sigma _p a_p +\gamma _{p}a_{-p}^*, \qquad \forall p\ne 0 \end{aligned}$$

(8)

where

$$\begin{aligned} \sigma _p := \frac{1}{\sqrt{1-\alpha _p^2}} = \cosh (\beta _p), \quad \gamma _p:= \frac{\alpha _p}{\sqrt{1-\alpha _p^2}} = \sinh (\beta _p). \end{aligned}$$

Consequently,

$$\begin{aligned} U_{\mathrm{B}} {\mathbb {H}}_{\mathrm{Bog}} U_{\mathrm{B}}^* = E_{\mathrm{Bog}} + \sum _{p\ne 0} e(p) a_p^* a_p, \end{aligned}$$

(9)

where

$$\begin{aligned} E_{\mathrm{Bog}} = - \frac{1}{2} \sum _{p\ne 0} \left( |p|^2 + {\widehat{w}}(p) - e(p) \right) , \quad e_p=\sqrt{|p|^4+2 |p|^2 {\widehat{w}}(p)}. \end{aligned}$$

Note that the assumption $0\le \widehat{w} \in \ell ^1(2\pi {{\mathbb {Z}}}^d)$ ensures that $E_{\mathrm{Bog}}$ is finite. Moreover we have the uniform bounds

$$\begin{aligned} \sum _{p \ne 0} \gamma _p \le C,\quad \sup _{p\ne 0} \sigma _p \le C . \end{aligned}$$

(10)

Thus Bogoliubov’s approximation predicts that the ground state energy of $H_N$ is

$$\begin{aligned} E_{ N}= \frac{N}{2} {\widehat{w}}(0) + E_{\mathrm{Bog}} + o(1)_{N\rightarrow \infty }. \end{aligned}$$

(11)

In 2011, Seiringer [18] gave the first rigorous proof of (11). He also proved that the low-lying spectrum of $H_N$ is given approximately by the elementary excitation $e_p$. These results have been extended to inhomogeneous trapped systems in [11], to more general interaction potentials in [12], to a large volume limit in [9], and to situations of multiple-condensation in [14, 17].

Let us recall the approach in [12] which also provides the convergence of the ground state of the mean-field Hamiltonian $H_N$ in (1). Mathematically, the formal expression (5) can be made rigorous using the unitary operator introduced in [12]

$$\begin{aligned} U_N: {\mathcal {H}}^N\rightarrow {\mathcal {F}}_+^{\le N}={\mathbb {1}}^{\le N} {\mathcal {F}}_+, \quad {\mathbb {1}}^{\le N} = {\mathbb {1}}({\mathcal {N}}_+ \le N) \end{aligned}$$

which is defined by

$$\begin{aligned} U_N = \sum _{j=0}^N Q^{\otimes j} \left( \frac{a_0^{N-j}}{\sqrt{(N-j)!}} \right) , \quad U_N^*= \bigoplus _{j=0}^N \left( \frac{(a_0^*)^{N-j}}{\sqrt{(N-j)!}} \right) . \end{aligned}$$

(12)

Recall from [12, Proposition 4.2] that

$$\begin{aligned} U_N a_p^* a_q U_N^*&= a_p^* a_q,\quad U_N a_p^* a_0 U_N^* = a_p^* \sqrt{N-{\mathcal {N}}_+}, \quad \forall p,q \ne 0 \end{aligned}$$

(13)

where ${\mathcal {N}}_+$ is the number operator on the excited Fock space ${\mathcal {F}}_+$,

$$\begin{aligned} {\mathcal {N}}_+ = \sum _{p\ne 0} a_p^* a_p. \end{aligned}$$

Thus $U_N$ implements the c-number substitution in Bogoliubov’s argument because it replaces $a_0$ by $\sqrt{N-{\mathcal {N}}_+}\approx \sqrt{N}$ (we have ${\mathcal {N}}_+\ll N$ due to the condensation). Then the formal expression (5) can be reformulated as

$$\begin{aligned} U_N H_N U_N^* \approx \frac{N}{2}{\widehat{w}}(0) + {\mathbb {H}}_{\mathrm{Bog}} \end{aligned}$$

(14)

which is rigorous since the operators on both sides act on the same excited Fock space. By justifying (14), the authors of [12] recovered the convergence of eigenvalues of $H_N$ first obtained in [18], and also obtained the convergence of eigenfunctions of $H_N$ to those of ${\mathbb {H}}_{\mathrm{Bog}}$. In particular, for the ground state, we have from [12, Theorem 2.2] that

$$\begin{aligned} \lim _{N\rightarrow \infty }U_N \Psi _N = U_B |0\rangle \end{aligned}$$

(15)

where $|0\rangle$ is the vacuum in Fock space. The convergence (15) holds strongly in norm of ${\mathcal {F}}_+$, and also strongly in the norm induced by the quadratic form of ${\mathbb {H}}_{\mathrm{Bog}}$ in ${\mathcal {F}}_+$. In particular, this implies the convergence of one-body density matrix

$$\begin{aligned} \lim _{N\rightarrow \infty } Q \gamma _{\Psi _N}^{(1)} Q = \sum _{p\ne 0} \gamma _p^2 |u_p\rangle \langle u_p| \end{aligned}$$

(16)

in trace class (see (68) for a detailed explanation). Since $\mathrm{Tr}\gamma _{\Psi _N}^{(1)}=N$, (16) is equivalent to

$$\begin{aligned} \lim _{N\rightarrow \infty } \mathrm{Tr}\Big | P \gamma ^{(1)}_{\Psi _N} P + Q \gamma ^{(1)}_{\Psi _N} Q - \Big (N-\sum _{p\ne 0} \gamma _p^2\Big ) |u_0\rangle \langle u_0| - \sum _{p\ne 0} \gamma _p^2 |u_p\rangle \langle u_p| \Big | =0. \end{aligned}$$

(17)

Recall that $P=|u_0\rangle \langle u_0|=1-Q$. The formula (17) looks similar to the result in Theorem 1, except that the cross term $P \gamma _{\Psi _N}^{(1)}Q + Q \gamma _{\Psi _N}^{(1)}P$ is missing. Putting differently, to get the result in Theorem 1 we have to show that

$$\begin{aligned} \lim _{N\rightarrow \infty } \mathrm{Tr}\Big | P \gamma _{\Psi _N}^{(1)}Q + Q \gamma _{\Psi _N}^{(1)}P \Big |=0. \end{aligned}$$

(18)

As explained in [12, Eq. (2.19)], from (16) and the Cauchy–Schwarz inequality one only obtains that the left side of (18) is of order $O(\sqrt{N})$. Moreover, (18) implies that

$$\begin{aligned} \lim _{N\rightarrow \infty } \sqrt{N} \langle U_N \Psi _N, a_p U_N \Psi _N\rangle =0 , \quad \forall p\ne 0, \end{aligned}$$

(19)

thus answering an open question in [13]. As explained in [13, Section 5], (19) would follow if we could replace $U_N \Psi _N$ by $U_B |0\rangle$ (which is a quasi-free state, and thus satisfies Wick’s Theorem [19, Chapter 10]). However, the norm convergence (15) is not strong enough to justify (19).

1.3 Outline of the proof

To prove Theorem 1 we have to extract some information going beyond Bogoliubov’s approximation. Roughly speaking, we will refine (14) by computing exactly the term of order $O(N^{-1})$. Our proof consists of three main steps.

Step 1 (Excitation Hamiltonian). After implementing the c-number substitution, instead of ignoring all terms with coefficients of order $o(1)_{N\rightarrow \infty }$, we will keep all terms of order $O(N^{-1})$. More precisely, in Lemma 7 below we show that

$$\begin{aligned} U_N H_{N} U_N^*= \frac{N}{2} \widehat{w}(0)+ {\mathcal {G}}_N + O(N^{-3/2}) \end{aligned}$$

(20)

in an appropriate sense, where

$$\begin{aligned} {\mathcal {G}}_N&= {\mathbb {H}}_{\mathrm{Bog}} + \frac{{\mathcal {N}}_+(1-{\mathcal {N}}_+)}{2(N-1)} \widehat{w}(0)+ \sum _{p\ne 0} \frac{1-{\mathcal {N}}_+}{N-1} \widehat{w}(p) a^*_p a_p \\&\quad + \left( \frac{1}{2} \sum _{p\ne 0} \widehat{w}(p) a^*_p a^*_{-p} \frac{1-2{\mathcal {N}}_+}{2N}+\,\, \text {h.c.}\right) \\&\quad + \left( \frac{1}{\sqrt{N}} \sum _{\ell ,p\ne 0, \ell +p\ne 0} \widehat{w}(\ell ) a^*_{p+\ell } a^*_{-\ell } a_{p} +\,\, \text {h.c.} \right) \\&\quad + \frac{1}{2(N-1)}\sum _{\begin{array}{c} k,p \ne 0\\ \ell \ne -p,k \end{array}}\widehat{w}(\ell ) a^*_{p+\ell } a^*_{k-\ell } a_p a_k. \end{aligned}$$

The formula (20) is obtained by a direct computation using the actions of $U_N$ as in [12], plus an expansion of $\sqrt{N-{\mathcal {N}}_+}$ and $\sqrt{(N-{\mathcal {N}}_+)(N-{\mathcal {N}}_+-1)}$ in the regime ${\mathcal {N}}_+ \ll N$. The advantage of using ${\mathcal {G}}_N$ is that it is well-defined on the full Fock space ${\mathcal {F}}_+$. This idea has been used to study the norm approximation for the many-body quantum dynamics in [8].

Step 2 (Quadratic transformation). Then we conjugate the operator on the right side of (20) by the Bogoliubov transformation $U_B$ in (7). In Lemma 8 we prove that

$$\begin{aligned} U_B {\mathcal {G}}_N U_B^* = \langle 0| U_B {\mathcal {G}}_N U_B^* |0\rangle + \sum _{p\ne 0} e(p) a_p^* a_p + {\mathcal {C}}_N + R_2 \end{aligned}$$

(21)

where

$$\begin{aligned} {\mathcal {C}}_N= \frac{1}{\sqrt{N}}\sum _{\begin{array}{c} p,q\ne 0\\ p+q\ne 0 \end{array}}\widehat{w}(p) \Big [ (\sigma _{p+q}\sigma _{-p}\gamma _q +\gamma _{p+q}\gamma _{p}\sigma _q ) a^*_{p+q} a^*_{-p} a^*_{-q} +\mathrm {h.c.} \Big ] \end{aligned}$$

and $R_2$ is an error term whose expectation against the ground state is of order $O(N^{-3/2})$.

Note that in ${\mathcal {C}}_N$ we keep only cubic terms with three creation operators or three annihilation operators. These are the most problematic terms. All other cubic terms, as well as all quartic terms, are of lower order and can be estimated by the Cauchy–Schwarz inequality (the quartic terms always come with a factor $N^{-1}$ instead of $N^{-1/2}$ and this helps).

As we will see, the energy contribution of the cubic term ${\mathcal {C}}_N$ is of order $O(N^{-1})$. Thus (21) implies that

$$\begin{aligned} E_N = \frac{N}{2}{\widehat{w}}(0) + \Big \langle 0 \Big | U_B {\mathcal {G}}_N U_B^* \Big | 0 \Big \rangle + O(N^{-1}) \end{aligned}$$

(22)

which improves (11). Moreover, for the ground state we have

$$\begin{aligned} \langle U_B U_N \Psi _N, {\mathcal {N}}_+ U_B U_N \Psi _N \rangle \le CN^{-1} \end{aligned}$$

(23)

which in turn implies the norm approximation (up to an appropriate choice of the phase factor for $\Psi _N$)

$$\begin{aligned} \Vert U_N \Psi _N - U_B^* |0\rangle \Vert _{{\mathcal {F}}_+}^2 \le CN^{-1}. \end{aligned}$$

(24)

and the following bound on the one-body density matrix

$$\begin{aligned} \lim _{N\rightarrow \infty } \mathrm{Tr}\Big | P \gamma _{\Psi _N}^{(1)}Q + Q \gamma _{\Psi _N}^{(1)}P \Big | \le C. \end{aligned}$$

Unfortunately the latter bound is still weaker than (18). Thus the desired result (18) cannot be obtained within Bogoliubov’s theory.

Step 3 (Cubic transformation). To factor out the energy contribution of the cubic term ${\mathcal {C}}_N$ in (21), we will use a cubic transformation. It is given by

$$\begin{aligned} U_S = e^{S}, \quad S= \frac{1}{\sqrt{N}}\sum _{\begin{array}{c} p,q\ne 0\\ p+q\ne 0 \end{array}} \eta _{p,q}\Big (a^*_{p+q}a^*_{-p}a^*_{-q}{\mathbb {1}}^{\le N}-{\mathbb {1}}^{\le N} a_{p+q}a_{-p}a_{-q}\Big ) \end{aligned}$$

(25)

where

$$\begin{aligned} \eta _{p,q}=\frac{\widehat{w}(p)\big (\sigma _{p+q}\sigma _p \gamma _q +\gamma _{p+q}\gamma _p \sigma _q\big )}{e_{p+q}+e_p+e_q}. \end{aligned}$$

(26)

From the assumption ${\widehat{w}} \in \ell ^1(2\pi {{\mathbb {Z}}}^d)$ and the bounds (10) we have the summability

$$\begin{aligned} \sum _{p,q \ne 0} |\eta _{p,q}| \le C. \end{aligned}$$

(27)

Here we insert the cut-off ${\mathbb {1}}^{\le N}$ in the definition of $U_S$ to make sure that it does not change the particle number operator ${\mathcal {N}}_+$ too much; see Lemma 5 for details.

The choice of the cubic transformation above can be deduced on an abstract level. Consider an operator of the form

$$\begin{aligned} A= A_0 + X \end{aligned}$$

where X stands for some perturbation. Then, in principle, we can remove X by conjugating A with $e^{S}$ provided that

$$\begin{aligned} X + [S,A_0]=0 \end{aligned}$$

and that $[S,[S,A_0]]=-[S,X]$ is small in an appropriate sense. This can be seen by the simple expansions

$$\begin{aligned} e^{S} X e^{-S} = X + \int _0^1 e^{sS} [X,S] e^{-sS} ds \end{aligned}$$

and

$$\begin{aligned} e^{S} A_0 e^{-S} = A_0 + [S,A_0] + \int _0^1 \int _0^t e^{sS} [S,[S,A_0]] e^{-sY} ds dt. \end{aligned}$$

In our situation, $A_0= \sum _{p\ne 0} e(p) a_p^* a_p$ and $X={\mathcal {C}}_N$, allowing to find S explicitly in (25).

In Lemma 9 we prove that

$$\begin{aligned} U_S U_B {\mathcal {G}}_N U_B^* U_S^*= \Big \langle 0 \Big | U_S U_B {\mathcal {G}}_N U_B^* U_S^* \Big | 0 \Big \rangle + \sum _{p\ne 0} e(p) a_p^*a_p + R_3 \end{aligned}$$

with an error term $R_3$ whose expectation against the ground state is of order $O(N^{-3/2})$. This allows us to obtain the following improvements of (22), (23) and (24).

Theorem 2

(Refined ground state estimates) Assume that $0\le {\widehat{w}}\in \ell ^1( (2\pi {\mathbb {Z}})^d )$. Then the ground state energy of the Hamiltonian $H_N$ in (1) satisfies

$$\begin{aligned} E_N= \frac{N}{2}{\widehat{w}}(0) + \Big \langle 0 \Big | U_S U_B {\mathcal {G}}_N U_B^* U_S^* \Big | 0 \Big \rangle + O(N^{-3/2}). \end{aligned}$$

Moreover, if $\Psi _N$ is the ground state of $H_N$, then $\Phi = U_S U_B U_N \Psi _N$ satisfies

$$\begin{aligned} \langle \Phi , {\mathcal {N}}_+ \Phi \rangle \le CN^{-3/2}. \end{aligned}$$

Consequently, we have the norm approximation (up to an appropriate choice of the phase factor for $\Psi _N$)

$$\begin{aligned} \Vert U_N \Psi _N - U_B^* U_S^* |0\rangle \Vert _{{\mathcal {F}}_+}^2 \le CN^{-3/2}. \end{aligned}$$

As we will explain, Theorem 2 implies (18) and thus justifies Theorem 1.

The idea of using cubic transformations has been developed to handle dilute Bose gases in [1,2,3, 16, 20], where the interaction potential has a much shorter range but the interaction strength is much larger in its range. In this case, the contribution of the cubic terms is much bigger, and Bogoliubov’s approximation has to be modified appropriately to capture the short-range scattering effect. Results similar to (11) have been proved recently for the Gross-Pitaevskii limit [2] and for the thermodynamic limit [10, 20]. It is unclear to us how to extend Theorem 1 to the dilute regime.

Our work shows that in the mean-field regime, in contrast to the dilute regime, the cubic terms are smaller, and they actually contribute only to the next order correction to Bogoliubov’s approximation (there are also some quadratic and quartic terms which contribute to the same order of the cubic term). On the other hand, it is interesting that the contribution of the cubic terms is not visible in the expansion of the one-body density matrix in Theorem 1; putting differently the approximation in Theorem 1 can be guessed using only Bogoliubov’s theory (although its proof requires more information).

There have been also remarkable works concerning higher order expansions in powers of $N^{-1}$ in the mean-field regime; see [15] for a study of the ground state, [7] for the low-energy spectrum, and [5, 6] for the quantum dynamics. These works are based on perturbative approaches which are very different from ours. Note that the method of Bossmann, Petrat and Seiringer in [7] also gives access to the higher order expansion of the reduced density matrices (see [7, Eq. (3.15)] for a comparison). We hope that our rather explicit strategy complements the previous analysis in [5,6,7, 15] concerning the correction to Bogoliubov’s theory in the mean-field regime.

1.4 Organization of the paper

In Sect. 2 we will derive some useful estimates for the particle number operator ${\mathcal {N}}_+$. Then we analyze the actions of the transformations $U_N$, $U_B$, $U_S$ in Sects. 3, 4 and 5, respectively. Finally, we prove Theorem 2 in Sect. 7 and conclude Theorem 1 in Sect. 7.

2 Moment estimates for the particle number operator

In this section we justify the Bose–Einstein condensation by showing that the ground state has a bounded number of excited particles. As explained in [18], the uniform bound on the expectation of ${\mathcal {N}}_+$ follows easily from Onsager’s inequality (2). For our purpose, we will need uniform bounds for higher moments of ${\mathcal {N}}_+$. The following lemma is an extension of [13, Lemma 5].

Lemma 3

(Number of excited particles) If $\Psi _N$ is the ground state of $H_{N}$, then

$$\begin{aligned} \langle \Psi _N, {\mathcal {N}}_+^s \Psi _N \rangle \le C_s, \qquad \forall s\in {\mathbb {N}}. \end{aligned}$$

Proof

As in [13, Lemma 5], from the operator inequality

$$\begin{aligned} H_{N} \ge (2\pi )^{2} {\mathcal {N}}_+ +\frac{ N^2}{2(N-1)}\hat{w}(0) - \frac{N}{2(N-1)} w(0) \end{aligned}$$

(28)

we obtain

$$\begin{aligned} |E_{N}| \le \frac{N}{2}\hat{w}(0) \quad \text {and} \quad \langle \Psi _N, {\mathcal {N}}_+^{s} \Psi _N \rangle \le C \end{aligned}$$

(29)

for $s=1,2,3$. Let us assume that $s\in {\mathbb {N}}$ is even. We will show that $\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \rangle \le C$.

Since $\Psi _N$ is a ground state of $H_N$, it solves the Schrödinger equation

$$\begin{aligned} H_{N}\Psi _N= E_{N}\Psi _N. \end{aligned}$$

Consequently, we get the identity

$$\begin{aligned} \left\langle \Psi _N, {\mathcal {N}}_+^{\frac{s}{2}} \Big ( H_{N} - E_{N} \Big ) {\mathcal {N}}_+^{\frac{s}{2}} \Psi _N \right\rangle = \Big \langle \Psi _N, {\mathcal {N}}_+^{\frac{s}{2}} [H_{N}, {\mathcal {N}}_+^{\frac{s}{2}}] \Psi _N \Big \rangle . \end{aligned}$$

(30)

The left side of (30) can be estimated using (28) and (29) as

$$\begin{aligned} \left\langle \Psi _N, {\mathcal {N}}_+^{\frac{s}{2}} \Big ( H_{N} - E_{N} \Big ) {\mathcal {N}}_+^{\frac{s}{2}} \Psi _N \right\rangle \ge \left\langle \Psi _N, \Big ( (2\pi )^{2} {\mathcal {N}}_+^{s+1} -C{\mathcal {N}}_+^s \Big ) \Psi _N \right\rangle . \end{aligned}$$

(31)

For the right side of (30), since

$$\begin{aligned}{}[A,B^k]=\sum _{j=0}^{k-1}B^j [A,B] B^{k-j-1}, \end{aligned}$$

using (4) and the CCR (3) we write

$$\begin{aligned}&{\mathcal {N}}_+^{\frac{s}{2}}[H_{N}, {\mathcal {N}}_+^{\frac{s}{2}}] =\frac{1}{2(N-1)} \sum _{j=0}^{\frac{s}{2}-1} \sum _{\ell \ne 0} \sum _{p,q } {\widehat{w}}(\ell ) {\mathcal {N}}_+^{\frac{s}{2}+j}[a^*_{p-\ell }a^*_{q+\ell }a_p a_q, {\mathcal {N}}_+]{\mathcal {N}}_+^{\frac{s}{2}-j-1} \nonumber \\&\quad =\frac{1}{2(N-1)} \sum _{j=0}^{\frac{s}{2}-1}\sum _{\ell \ne 0} {\widehat{w}}(\ell ) {\mathcal {N}}_+^{\frac{s}{2}+j} \Big ( 2 a^*_0 a^*_0 a_{\ell } a_{-\ell } -2 a^*_{-\ell } a^*_{\ell } a_0 a_0 \Big ){\mathcal {N}}_+^{\frac{s}{2}-j-1} \nonumber \\&\qquad + \frac{1}{2(N-1)} \sum _{j=0}^{\frac{s}{2}-1}\sum _{\ell \ne 0 \ne p \ne \ell } {\widehat{w}}(\ell ) {\mathcal {N}}_+^{\frac{s}{2}+j} \Big (a^*_{p-\ell }a^*_{0}a_p a_{-\ell } - a^*_{p-\ell }a^*_{\ell }a_p a_0 \Big ){\mathcal {N}}_+^{\frac{s}{2}-j-1} \nonumber \\&\qquad + \frac{1}{2(N-1)}\sum _{j=0}^{\frac{s}{2}-1} \sum _{\ell \ne 0 \ne q \ne -\ell } {\widehat{w}}(\ell ) {\mathcal {N}}_+^{\frac{s}{2}+j} \Big (a^*_{0}a^*_{q+\ell }a_{\ell } a_{q} - a^*_{-\ell }a^*_{q+\ell }a_0 a_q \Big ){\mathcal {N}}_+^{\frac{s}{2}-j-1}. \end{aligned}$$

(32)

Now we take the expectation against $\Psi _N$ and estimate. For the first term on the right side of (32), by the Cauchy–Schwarz inequality, we get for a given j

$$\begin{aligned}&\left| \left\langle \Psi _N, \sum _{\ell \ne 0} {\widehat{w}}(\ell ) {\mathcal {N}}_+^{\frac{s}{2}+j} a^*_0 a^*_0 a_{\ell } a_{-\ell }{\mathcal {N}}_+^{\frac{s}{2}-j-1} \Psi _N \right\rangle \right| \\&\qquad = \left| \left\langle \Psi _N, \sum _{\ell \ne 0} {\widehat{w}}(\ell ) {\mathcal {N}}_+^{\frac{s}{2}+j} a^*_0 a^*_0 ({\mathcal {N}}_++1)^{-j}({\mathcal {N}}_++1)^{j} a_{\ell } a_{-\ell }{\mathcal {N}}_+^{\frac{s}{2}-j-1} \Psi _N \right\rangle \right| \\&\qquad \le \sum _{\ell \ne 0} \left\| ({\mathcal {N}}_++1)^{-j} a_0 a_0 {\mathcal {N}}_+^{\frac{s}{2}+j} \Psi _N \right\| | {\widehat{w}}(\ell )| \left\| ({\mathcal {N}}_+ +1)^{j} a_{\ell } a_{-\ell } {\mathcal {N}}_+^{\frac{s}{2}-j-1} \Psi _N\right\| \\&\qquad = \sum _{\ell \ne 0} \left\| a_0 a_0 {\mathcal {N}}_+^{\frac{s}{2}} \Psi _N \right\| | {\widehat{w}}(\ell )| \left\| a_{\ell } a_{-\ell } ({\mathcal {N}}_+ -1)^{j} {\mathcal {N}}_+^{\frac{s}{2}-j-1} \Psi _N\right\| \\&\qquad \le \left\| a_0 a_0 {\mathcal {N}}_+^{\frac{s}{2}} \Psi _N \right\| \left( \sum _{\ell \ne 0} |{\widehat{w}}(\ell )|^2 \right) ^{1/2} \left( \sum _{\ell \ne 0} \left\| a_{\ell } a_{-\ell }({\mathcal {N}}_+ -1)^{j} {\mathcal {N}}_+^{\frac{s}{2}-j-1} \Psi _N\right\| ^2 \right) ^{1/2}\\&\qquad \le CN \langle \Psi _N, {\mathcal {N}}_+^{s} \Psi _N\rangle . \end{aligned}$$

Here we have used that $a_0 a_0$ commutes with ${\mathcal {N}}_+$, that $a_0^*a_0 \le N$ on ${\mathcal {H}}^N$ and that $\sum |{\widehat{w}}(\ell )|^2=\Vert w\Vert _{L^2}^2<\infty$. Similarly, for the second term, we have

$$\begin{aligned}&\left| \left\langle \Psi _N, \sum _{\ell \ne 0} {\widehat{w}}(\ell ) {\mathcal {N}}_+^{\frac{s}{2}+j} a^*_{-\ell } a^*_\ell a_0 a_0 {\mathcal {N}}_+^{\frac{s}{2}-j-1} \Psi _N \right\rangle \right| \\&\quad = \left| \left\langle \Psi _N, \sum _{\ell \ne 0} {\widehat{w}}(\ell ) {\mathcal {N}}_+^{\frac{s}{2}+j} a^*_{-\ell } a^*_\ell ({\mathcal {N}}_+ +1)^{-j-1}({\mathcal {N}}_+ +1)^{j+1} a_0 a_0 {\mathcal {N}}_+^{\frac{s}{2}-j-1} \Psi _N \right\rangle \right| \\&\quad \le \sum _{\ell \ne 0} \left\| ({\mathcal {N}}_++1)^{-j-1} a_{-\ell } a_{\ell } {\mathcal {N}}_+^{\frac{s}{2}+j} \Psi _N \right\| | {\widehat{w}}(\ell )| \left\| ({\mathcal {N}}_+ +1)^{j+1} a_{0} a_{0} {\mathcal {N}}_+^{\frac{s}{2}-j-1} \Psi _N\right\| \\&\quad \le CN \langle \Psi _N, ({\mathcal {N}}_++1)^{s} \Psi _N\rangle \end{aligned}$$

as before. For the third term, we can bound

$$\begin{aligned}&\left| \left\langle \Psi _N, \sum _{\ell \ne 0 \ne p \ne \ell } {\widehat{w}}(\ell ) {\mathcal {N}}_+^{\frac{s}{2}+j} a^*_{p-\ell }a^*_{0}a_p a_{-\ell } {\mathcal {N}}_+^{\frac{s}{2}-j-1} \Psi _N \right\rangle \right| \\&\quad \le \sum _{\ell \ne 0 \ne p \ne \ell } |{\widehat{w}}(\ell )| \Vert ({\mathcal {N}}_++1)^{-j} a_{0} a_{p-\ell } {\mathcal {N}}_+^{\frac{s}{2}+j} \Psi _N\Vert \Vert ({\mathcal {N}}_++1)^{j} a_p a_{-\ell }{\mathcal {N}}_+^{\frac{s}{2}-j-1} \Psi _N \Vert \\&\quad \le \left( \sum _{\ell \ne 0 \ne p \ne \ell } |{\widehat{w}}(\ell )|^2 \left\| a_{0} a_{p-\ell } {\mathcal {N}}_+^{\frac{s}{2}} \Psi _N \right\| ^2 \right) ^{1/2} \\&\qquad \left( \sum _{\ell \ne 0 \ne p \ne \ell } \left\| a_p a_{-\ell }({\mathcal {N}}_+-1)^{-j} {\mathcal {N}}_+^{\frac{s}{2}-j-1} \Psi _N \right\| ^2 \right) ^{1/2} \\&\quad \le C N^{1/2}\langle \Psi _N, {\mathcal {N}}_+^s \Psi _N \rangle ^{1/2} \langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N\rangle ^{1/2} \end{aligned}$$

and proceed similarly for other terms. Thus in summary, from (32) we get

$$\begin{aligned} \left| \Big \langle \Psi _N, {\mathcal {N}}_+^{\frac{s}{2}}[H_{N},{\mathcal {N}}_+^{\frac{s}{2}}] \Psi _N \Big \rangle \right|&\le C \langle \Psi _N, ({\mathcal {N}}_+ +1)^s \Psi _N\rangle \nonumber \\&\quad + C N^{-1/2}\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \rangle ^{1/2} \langle \Psi _N, {\mathcal {N}}_+^s \Psi _N\rangle ^{1/2}. \end{aligned}$$

(33)

Inserting (31) and (33) into (30), we obtain

$$\begin{aligned} \left\langle \Psi _N, \Big ( (2\pi )^{2} {\mathcal {N}}_+^{s+1} - C{\mathcal {N}}_+^s \Big ) \Psi _N \right\rangle&\le C \langle \Psi _N, ({\mathcal {N}}_+ +1)^s \Psi _N\rangle \\&\quad + C N^{-1/2}\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \rangle ^{1/2} \langle \Psi _N, {\mathcal {N}}_+^s \Psi _N\rangle ^{1/2}. \end{aligned}$$

By the Cauchy–Schwarz inequality

$$\begin{aligned} \left\langle \Psi _N, {\mathcal {N}}_+^s \Psi _N \right\rangle \le \left\langle \Psi _N, {\mathcal {N}}_+^{s-1} \Psi _N \right\rangle ^{1/2} \left\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \right\rangle ^{1/2} \end{aligned}$$

(34)

we get

$$\begin{aligned} \left\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \right\rangle&\le C \left\langle \Psi _N, {\mathcal {N}}_+^{s-1} \Psi _N \right\rangle ^{1/2} \left\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \right\rangle ^{1/2} \\&\quad + C N^{-1/2}\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \rangle ^{3/4} \langle \Psi _N, {\mathcal {N}}_+^{s-1} \Psi _N\rangle ^{1/4} \end{aligned}$$

which implies

$$\begin{aligned} \left\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \right\rangle ^{1/2}&\le C \left\langle \Psi _N, {\mathcal {N}}_+^{s-1} \Psi _N \right\rangle ^{1/2} \\&\quad + C N^{-1/2}\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \rangle ^{1/4} \langle \Psi _N, {\mathcal {N}}_+^{s-1} \Psi _N\rangle ^{1/4}. \end{aligned}$$

We can now use

$$\begin{aligned} \left\langle \Psi _N, {\mathcal {N}}_+^{s-1} \Psi _N \right\rangle \le \left\langle \Psi _N, {\mathcal {N}}_+^{s-3} \Psi _N \right\rangle ^{1/2} \left\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \right\rangle ^{1/2} \end{aligned}$$

and obtain

$$\begin{aligned} \left\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \right\rangle ^{1/4}&\le C \left\langle \Psi _N, {\mathcal {N}}_+^{s-3} \Psi _N \right\rangle ^{1/4} \\&\quad + C N^{-1/2}\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \rangle ^{1/8}\left\langle \Psi _N, {\mathcal {N}}_+^{s-3} \Psi _N \right\rangle ^{1/8} . \end{aligned}$$

Telescoping this inequality and using [13, Lemma 5] we arrive at a bound on $\left\langle \Psi _N, {\mathcal {N}}_+^{s+1} \Psi _N \right\rangle$ that is uniform in N. This gives the desired result for odd powers of ${\mathcal {N}}_+$. Finally, using (34), we obtain the bound for any $s\in {\mathbb {N}}$ and this ends the proof. $\square$

In order to put Lemma 3 in a good use, we will also need the fact that the moments of ${\mathcal {N}}_+$ are essentially stable under the actions of the Bogoliubov transformation and the cubic transformation.

Lemma 4

Let $U_B$ be given in (7). Then

$$\begin{aligned} U_{\mathrm{B}}{\mathcal {N}}_+^{k}U_{\mathrm{B}}^* \le C_k ({\mathcal {N}}_++1)^{k}, \quad \forall k\in {\mathbb {N}}. \end{aligned}$$

(35)

Lemma 5

Let $U_S=e^S$ be given in (25). Then for all $t\in [-1,1]$ and $k\in {\mathbb {N}}$,

$$\begin{aligned} e^{tS} ({\mathcal {N}}_+ +1)^k e^{-tS} \le C_k ({\mathcal {N}}_+ +1)^k. \end{aligned}$$

(36)

The results in Lemma 4 and Lemma 5 are well-known. For the completeness, let us quickly explain the proof of Lemma 5, following the strategy in [2, Proposition 4.2] (the proof of Lemma 4 is similar and simpler).

Proof of Lemma 5

Take a normalized vector $\Phi \in {\mathcal {F}}_+$ and define

$$\begin{aligned} f(t)=\langle \Phi , e^{tS}({\mathcal {N}}_+ +1)^k e^{-tS}\Phi \rangle , \quad \forall t\in [-1,1]. \end{aligned}$$

Then

$$\begin{aligned} \partial _t f(t)&=\langle \Phi , e^{tS}[S, ({\mathcal {N}}_+ +1)^k] e^{-tS}\Phi \rangle \\&= \frac{2}{\sqrt{N}}{\text {Re}}\Big \langle \Phi , e^{tS} \sum _{\begin{array}{c} p,q\ne 0\\ p+q\ne 0 \end{array}} \eta _{p,q} a^*_{p+q}a^*_{-p}a^*_{-q} {\mathbb {1}}^{\le N}\Theta _k({\mathcal {N}}_+)e^{-tS}\Phi \Big \rangle \end{aligned}$$

with

$$\begin{aligned} \Theta _k({\mathcal {N}}_+)= ({\mathcal {N}}_+ +1)^k-({\mathcal {N}}_+ +4)^k. \end{aligned}$$

Here we have used

$$\begin{aligned}{}[a^*_{p+q}a^*_{-p}a^*_{-q}{\mathbb {1}}^{\le N}, ({\mathcal {N}}_+ +1)^k]=a^*_{p+q}a^*_{-p}a^*_{-q}{\mathbb {1}}^{\le N} \Theta _k({\mathcal {N}}_+). \end{aligned}$$

It is obvious that $|\Theta _k({\mathcal {N}}_+)| \le C_k ({\mathcal {N}}_+ +1)^{k-1}$. Combining with the summability (27) and the Cauchy–Schwarz inequality we obtain

$$\begin{aligned} \Big | \partial _t f(t) \Big |&\le \frac{2}{\sqrt{N}} \left( \sum _{\begin{array}{c} p,q\ne 0\\ p+q\ne 0 \end{array}} \Big \Vert ({\mathcal {N}}_+ +1)^{(k-3)/2} a_{p+q}a_{-p}a_{-q} e^{-tS}\Phi \Vert ^2 \right) ^{1/2} \nonumber \\&\quad \times \left( \sum _{\begin{array}{c} p,q\ne 0\\ p+q\ne 0 \end{array}} |\eta _{p,q}|^2 \Big \Vert {\mathbb {1}}^{\le N} ({\mathcal {N}}_+ +1)^{(3-k)/2} \Theta _k({\mathcal {N}}_+)e^{-tS}\Phi \Big \Vert ^2 \right) ^{1/2}\nonumber \\&\le \frac{C_k}{\sqrt{N}} \Big \Vert {\mathcal {N}}_+^{k/2} e^{-tS} \Phi \Big \Vert \Big \Vert {\mathbb {1}}^{\le N}({\mathcal {N}}_+ +1) ^{(k+1)/2} e^{-tS} \Phi \Big \Vert . \end{aligned}$$

(37)

Thanks to the cut-off, we can bound

$$\begin{aligned} {\mathbb {1}}^{\le N}({\mathcal {N}}_+ +1) ^{(k+1)/2} \le \sqrt{N+1} {\mathcal {N}}_+^{k/2}. \end{aligned}$$

Thus (37) implies that

$$\begin{aligned} \Big | \partial _t f(t) \Big | \le C_k \Big \Vert ({\mathcal {N}}_+ +1 )^{(k+1)/2} e^{-tS} \Phi \Big \Vert ^2 = C_k f(t) \end{aligned}$$

From Grönwall’s lemma, it follows that

$$\begin{aligned} f(t) \le C_k f(0), \quad \forall t\in [-1,1]. \end{aligned}$$

(38)

Since the latter bound is uniform in $\Phi$, we get the desired operator inequality. $\square$

We will also need the following refinement of Lemma 5.

Lemma 6

Let $U_S=e^S$ be given in (25). Then for all $t\in [-1,1]$ and $k\in {\mathbb {N}}$,

$$\begin{aligned} e^{tS} {\mathcal {N}}_+^k e^{-tS} \le C_k \left( {\mathcal {N}}_+^k + \frac{({\mathcal {N}}_+ +1)^{k+1}}{N} \right) . \end{aligned}$$

(39)

Proof

Take a normalized vector $\Phi \in {\mathcal {F}}_+$ and define

$$\begin{aligned} g(t)=\langle \Phi , e^{tS}{\mathcal {N}}_+^k e^{-tS}\Phi \rangle , \quad \forall t\in [-1,1]. \end{aligned}$$

Then proceeding similarly to (37), we have

$$\begin{aligned} \Big | \partial _t g(t) \Big | \le \frac{C_k}{\sqrt{N}} \Big \Vert {\mathcal {N}}_+^{k/2} e^{-tS} \Phi \Big \Vert \Big \Vert {\mathbb {1}}^{\le N}{\mathcal {N}}_+^{(k+1)/2} e^{-tS} \Phi \Big \Vert \le \frac{C_k}{\sqrt{N}} \sqrt{g(t) f(t)} \end{aligned}$$

with f(t) being defined in the proof of Lemma 5. Using (38) and the Cauchy–Schwarz inequality we obtain

$$\begin{aligned} \Big | \partial _t g(t) \Big | \le C_k \left( g(t) + \frac{\langle \Phi , ( {\mathcal {N}}_+ +1 )^{k+1} \Phi \rangle }{N} \right) , \quad \forall t\in [-1,1]. \end{aligned}$$

From Grönwall’s lemma, it follows that

$$\begin{aligned} g(t) \le C_k \left( g(0) + \frac{1}{N}\langle \Phi , ( {\mathcal {N}}_+ +1 )^{k+1} \Phi \rangle \right) , \quad \forall t\in [-1,1]. \end{aligned}$$

The latter bound is uniform in $\Phi$ and it implies the desired conclusion. $\square$

3 Excitation Hamiltonian

In this section, we study the action of the transformation $U_N$ in (12). By conjugating $H_N$ with $U_N$, we can factor out the contribution of the condensation. More precisely, we have

Lemma 7

We have the operator identity on ${\mathcal {F}}_{+}^{\le N}$

$$\begin{aligned} U_N H_{N} U_N^*&= \frac{N}{2} \widehat{w}(0)+ {\mathbb {1}}^{\le N} ({\mathcal {G}}_N + R_1) {\mathbb {1}}^{\le N} \end{aligned}$$

where

$$\begin{aligned} {\mathcal {G}}_N&= {\mathbb {H}}_{\mathrm{Bog}} + \frac{{\mathcal {N}}_+(1-{\mathcal {N}}_+)}{2(N-1)} \widehat{w}(0)+ \sum _{p\ne 0} \frac{1-{\mathcal {N}}_+}{N-1} \widehat{w}(p) a^*_p a_p \\&\quad + \left( \frac{1}{2} \sum _{p\ne 0} \widehat{w}(p) a^*_p a^*_{-p} \frac{1-2{\mathcal {N}}_+}{2N}+\,\, \mathrm{h.c.}\right) \\&\quad + \left( \frac{1}{\sqrt{N}} \sum _{\ell ,p\ne 0, \ell +p\ne 0} \widehat{w}(\ell ) a^*_{p+\ell } a^*_{-\ell } a_{p} +\,\, \mathrm{h.c.} \right) \\&\quad + \frac{1}{2(N-1)}\sum _{\begin{array}{c} k,p \ne 0\\ \ell \ne -p,k \end{array}}\widehat{w}(\ell ) a^*_{p+\ell } a^*_{k-\ell } a_p a_k \end{aligned}$$

and the error term $R_1$ satisfies the quadratic form estimate

$$\begin{aligned}&\pm R_1 \le \frac{C({\mathcal {N}}_++1)^{3}}{N^{3/2}}. \end{aligned}$$

Moreover, we have the operator inequality on ${\mathcal {F}}_{+}$

$$\begin{aligned} {\mathbb {1}}^{\le N} U_N H_{N} U_N^* {\mathbb {1}}^{\le N} \le \frac{N}{2} \widehat{w}(0)+ {\mathcal {G}}_N + \frac{C({\mathcal {N}}_++1)^{3}}{N^{3/2}}. \end{aligned}$$

Proof

A straightforward computation using the relations (12) shows that

$$\begin{aligned} U_N H_{N} U_N^*&= \frac{N}{2} \widehat{w}(0)+\frac{{\mathcal {N}}_+(1-{\mathcal {N}}_+)}{2(N-1)} \widehat{w}(0)+ \sum _{p\ne 0} \Big ( p^2 + \frac{N-{\mathcal {N}}_+}{N-1} \widehat{w}(p) \Big ) a^*_p a_p \\&\quad +\frac{1}{2} \left( \sum _{p\ne 0} \widehat{w}(p) a^*_p a^*_{-p} \frac{\sqrt{(N-{\mathcal {N}}_+)(N-{\mathcal {N}}_+ -1)}}{N-1}+\,\, \text {h.c.}\right) \\&\quad + \left( \sum _{\ell ,p\ne 0, \ell +p\ne 0} \widehat{w}(\ell ) a^*_{p+\ell } a^*_{-\ell } a_{p} \frac{\sqrt{N-{\mathcal {N}}_+}}{N-1}+\,\, \text {h.c.} \right) \\&\quad + \frac{1}{2(N-1)}\sum _{\begin{array}{c} k,p \ne 0\\ \ell \ne -p,k \end{array}}\widehat{w}(\ell ) a^*_{p+\ell } a^*_{k-\ell } a_p a_k. \end{aligned}$$

This operator identity holds on ${\mathcal {F}}_+^{\le N}$. For further analysis, we will expand $\sqrt{N-{\mathcal {N}}_+}$ and $\sqrt{(N-{\mathcal {N}}_+)(N-{\mathcal {N}}_+ -1)}$, making the effective expressions well-defined on the whole Fock space ${\mathcal {F}}_+$. This idea has been used before in [8]. Here it suffices to use

$$\begin{aligned} \Big | \frac{\sqrt{N-{\mathcal {N}}_+}}{N-1} - \frac{1}{N^{1/2}}\Big | \le \frac{C({\mathcal {N}}_++1)}{N^{3/2}} \end{aligned}$$

(40)

and

$$\begin{aligned} \Big | \frac{\sqrt{(N-{\mathcal {N}}_+)(N-{\mathcal {N}}_+-1)}}{N-1} - 1 - \frac{1-2{\mathcal {N}}_+}{2N} \Big | \le \frac{C({\mathcal {N}}_++1)^2}{N^2}. \end{aligned}$$

(41)

The operator inequalities (40) and (41) hold on ${\mathcal {F}}_+^{\le N}$. Thus we can write

$$\begin{aligned} U_N H_{N} U_N^*= \frac{N}{2} \widehat{w}(0)+ {\mathbb {H}}_{\mathrm{Bog}} + {\mathcal {G}}_N + R_1 \end{aligned}$$

with ${\mathcal {G}}_N$ given in the statement of Lemma 7 and with the error term $R_1=R_{1a}+R_{1b}$ where

$$\begin{aligned} R_{1a}&= \frac{1}{2} \sum _{p\ne 0} \widehat{w}(p) a^*_p a^*_{-p} \left( \frac{\sqrt{(N-{\mathcal {N}}_+)(N-{\mathcal {N}}_+-1)}}{N-1} - 1 - \frac{1-2{\mathcal {N}}_+}{2N} \right) \,\,+ \text {h.c.} ,\\ R_{1b}&= \sum _{\ell ,p\ne 0, \ell +p\ne 0} \widehat{w}(\ell ) a^*_{p+\ell } a^*_{-\ell } a_{p} \left( \frac{\sqrt{N-{\mathcal {N}}_+}}{N-1} - \frac{1}{\sqrt{N}} \right) + \,\, \text {h.c.} . \end{aligned}$$

By the Cauchy–Schwarz inequality, we have the quadratic form estimates

$$\begin{aligned} \pm R_{1a}&\le N^{-2} \sum _{p\ne 0} a^*_p a^*_{-p} ({\mathcal {N}}_+ +1) a_{-p}a_p + N^{2} \sum _{p\ne 0} |\widehat{w}(p)|^2 ({\mathcal {N}}_+ +1)^{-1/2}\times \\&\quad \times \left( \frac{\sqrt{(N-{\mathcal {N}}_+)(N-{\mathcal {N}}_+-1)}}{N-1} - 1 - \frac{1-2{\mathcal {N}}_+}{2N} \right) ^2 ({\mathcal {N}}_+ +1)^{-1/2}\\&\le \frac{C({\mathcal {N}}_++1)^3}{N^2} \end{aligned}$$

and

$$\begin{aligned} \pm R_{1b}&\le N^{-3/2} \sum _{\ell ,p\ne 0, \ell +p\ne 0} a^*_{p+\ell } a^*_{-\ell } a_{-\ell } a_{p+\ell } \\&\quad + N^{3/2} \sum _{\ell ,p\ne 0, \ell +p\ne 0} |\widehat{w}(\ell )|^2 \left( \frac{\sqrt{N-{\mathcal {N}}_+}}{N-1} - \frac{1}{\sqrt{N}} \right) a_p^* a_p \left( \frac{\sqrt{N-{\mathcal {N}}_+}}{N-1} - \frac{1}{\sqrt{N}} \right) \\&\le \frac{C({\mathcal {N}}_++1)^3}{N^{3/2}}. \end{aligned}$$

This completes the first part of Lemma 7.

Now let us turn to the operator inequality on the Fock space ${\mathcal {F}}_+$. We have proved that

$$\begin{aligned} {\mathbb {1}}^{\le N} U_N H_N U_N^* {\mathbb {1}}^{\le N} \le {\mathbb {1}}^{\le N} \left( \frac{N}{2}{\widehat{w}}(0) + {\mathcal {G}}_N + \frac{C({\mathcal {N}}_++1)^3}{N^{3/2}} \right) {\mathbb {1}}^{\le N}. \end{aligned}$$

(42)

Let us compare the right side of (42) with the corresponding version without the cut-off ${\mathbb {1}}^{\le N}$. First, consider the terms commuting with ${\mathcal {N}}_+$. Since

$$\begin{aligned} \frac{N}{2}{\widehat{w}}(0) + \sum _{p\ne 0} |p|^2 a_p^* a_p + \frac{1}{2(N-1)}\sum _{\begin{array}{c} k,p \ne 0\\ \ell \ne -p,k \end{array}}\widehat{w}(\ell ) a^*_{p+\ell } a^*_{k-\ell } a_p a_k + \frac{C({\mathcal {N}}_++1)^3}{N^{3/2}} \ge 0, \end{aligned}$$

this operator is not smaller than its product with the cut-off ${\mathbb {1}}^{\le N}$. Moreover, using

$$\begin{aligned} {\mathbb {1}}^{>N}= {\mathbb {1}} - {\mathbb {1}}^{\le N} ={\mathbb {1}}({\mathcal {N}}_+ >N) \le \frac{{\mathcal {N}}_+}{N} \end{aligned}$$

we have

$$\begin{aligned}&\pm {\mathbb {1}}^{>N} \left( \frac{{\mathcal {N}}_+(1-{\mathcal {N}}_+)}{2(N-1)} \widehat{w}(0) + \sum _{p\ne 0} \frac{1-{\mathcal {N}}_+}{N-1} \widehat{w}(p) a^*_p a_p \right) \\&\quad \le {\mathbb {1}}^{>N} \frac{C({\mathcal {N}}_+ +1 )^2}{N} \le \frac{C ({\mathcal {N}}_+ +1 )^3}{N^2}. \end{aligned}$$

Finally, consider

$$\begin{aligned} X:= & {} \left( \frac{1}{2} \sum _{p\ne 0} {\widehat{w}}(p) a_p^* a_{-p}^* \Big (1 + \frac{1-{\mathcal {N}}_+}{N-1} \Big ) + \mathrm{h.c.}\right) \\&+\, \left( \frac{1}{\sqrt{N}} \sum _{\ell ,p\ne 0, \ell +p\ne 0} \widehat{w}(\ell ) a^*_{p+\ell } a^*_{-\ell } a_{p} +\,\, \text {h.c.} \right) . \end{aligned}$$

By the Cauchy–Schwarz inequality $\pm (Y^*Z+ Z^* Y) \le Y^* Y + Z^* Z$ we can bound

$$\begin{aligned} \pm X&\le \sum _{p\ne 0} a_p^* a_{-p}^* ({\mathcal {N}}_+ +1)^{-1} a_{-p} a_p +\sum _{p\ne 0} |{\widehat{w}}(p)|^2 ({\mathcal {N}}_+ +1) \Big (1 + \frac{1-{\mathcal {N}}_+}{N-1} \Big )^2 \\&\quad + \frac{1}{N} \sum _{\ell ,p\ne 0, \ell +p\ne 0} a^*_{p+\ell } a^*_{-\ell } a_{-\ell } a_{p+\ell } + \sum _{\ell ,p\ne 0, \ell +p\ne 0} |\widehat{w}(\ell )|^2 a^*_{p} a_p \\&\le C \left[ ({\mathcal {N}}_+ + 1) + \frac{({\mathcal {N}}_+ + 1)^2}{N} + \frac{({\mathcal {N}}_+ + 1)^3}{N^2} \right] . \end{aligned}$$

Moreover, since X changes the number of particles by at most 2, we have

$$\begin{aligned} X + {\mathbb {1}}^{>N} X {\mathbb {1}}^{>N} - {\mathbb {1}}^{\le N} X {\mathbb {1}}^{\le N} = {\mathbb {1}}^{>N} X + X {\mathbb {1}}^{>N} = 1^{>N} X {\mathbb {1}}^{> N-2}+ {\mathbb {1}}^{> N-2} X {\mathbb {1}}^{>N}. \end{aligned}$$

Hence, combining with the above bound on $\pm X$ we find that

$$\begin{aligned} \pm (X - {\mathbb {1}}^{\le N} X {\mathbb {1}}^{\le N} )&= \pm \Big ( 1^{>N} X {\mathbb {1}}^{> N-2}+ {\mathbb {1}}^{> N-2} X {\mathbb {1}}^{>N} - {\mathbb {1}}^{>N} X {\mathbb {1}}^{>N} \Big )\\&\le C \left[ ({\mathcal {N}}_+ + 1) + \frac{({\mathcal {N}}_+ + 1)^2}{N} + \frac{({\mathcal {N}}_+ + 1)^3}{N^2} \right] {\mathbb {1}}^{ > N-2} \\&\le \frac{C ({\mathcal {N}}_+ +1)^3}{N^2}. \end{aligned}$$

This completes the proof of the operator inequality on ${\mathcal {F}}_+$ in Lemma 7. $\square$

4 Quadratic transformation

Recall that the Bogoliubov transformation $U_B$ in (7) diagonalizes ${\mathbb {H}}_{\mathrm{Bog}}$ as in (9). In this section, we will study the action of $U_N$ on the operator ${\mathcal {G}}_N$. We have

Lemma 8

Let ${\mathcal {G}}_N$ be given in Lemma 7. Then we have the operator identity on ${\mathcal {F}}_{+}$

$$\begin{aligned} U_B {\mathcal {G}}_N U_B^* = \langle 0| U_B {\mathcal {G}}_N U_B^* |0\rangle + \sum _{p\ne 0} e(p) a_p^* a_p + {\mathcal {C}}_N + R_2 \end{aligned}$$

where

$$\begin{aligned} {\mathcal {C}}_N= \frac{1}{\sqrt{N}}\sum _{\begin{array}{c} p,q\ne 0\\ p+q\ne 0 \end{array}}\widehat{w}(p) \Big [ (\sigma _{p+q}\sigma _{-p}\gamma _q +\gamma _{p+q}\gamma _{p}\sigma _q ) a^*_{p+q} a^*_{-p} a^*_{-q} +\mathrm {h.c.} \Big ] \end{aligned}$$

and the error term $R_2$ satisfies

$$\begin{aligned}&\pm R_2 \le \frac{C}{\sqrt{N}} {\mathcal {N}}_+^2 + \frac{C ({\mathcal {N}}_+ +1)^3}{N^{3/2}}. \end{aligned}$$

Proof

Let us decompose

$$\begin{aligned} {\mathcal {G}}_N- {\mathbb {H}}_{\mathrm{Bog}}={\widetilde{{\mathcal {D}}}}_N + {\widetilde{{\mathcal {C}}}}_N \end{aligned}$$

where

$$\begin{aligned} {\widetilde{{\mathcal {C}}}}_N = \frac{1}{\sqrt{N}} \sum _{\ell ,p\ne 0, \ell +p\ne 0} \widehat{w}(\ell ) a^*_{p+\ell } a^*_{-\ell } a_{p} +\,\, \text {h.c.} \end{aligned}$$

Non-cubic terms. Let us prove that $U_B {\widetilde{{\mathcal {D}}}}_N U_B^*- \langle 0| U_B {\widetilde{{\mathcal {D}}}}_N U_B^* |0\rangle$ contains only the terms of the form

$$\begin{aligned} \sum _{m_1, \ldots ,m_s,n_1, \ldots ,n_t \ne 0 } A_{m_1, \ldots ,m_s, n_1, \ldots ,n_t} a_{m_1} ^* \ldots a_{m_s}^* a_{n_1} \ldots a_{n_t} \end{aligned}$$

(43)

with $1\le s+t \le 4$ and the coefficients $A_{m_1, \ldots ,m_s, n_1, \ldots ,n_t}$ satisfy

$$\begin{aligned} \sup _{m_1, \ldots ,m_s\ne 0} \sum _{n_1, \ldots ,n_t \ne 0} |A_{m_1, \ldots ,m_s, n_1, \ldots ,n_t}| \le \frac{C}{N}, \quad \sup _{n_1, \ldots ,n_t \ne 0} \sum _{m_1, \ldots m_s\ne 0} |A_{m_1, \ldots ,m_s, n_1, \ldots ,n_t}| \le \frac{C}{N}. \end{aligned}$$

(44)

Let us start with the quadratic terms involving $a_p^* a_{-p}^*$. Using (8) and the CCR (3) we have

$$\begin{aligned}&U_{\mathrm{B}} \Big ( \frac{1}{4N}\sum _{p\ne 0} \widehat{w}(p) a_p^* a^*_{-p} \Big ) U_{\mathrm{B}}^* = \frac{1}{4N} \sum _{p\ne 0} \widehat{w}(p) (\sigma _p a_p^* + \gamma _p a_{-p}) (\sigma _p a^*_{-p} + \gamma _{p} a_{p}) \nonumber \\&\quad = \frac{1}{4N} \sum _{p\ne 0} \widehat{w}(p) \Big [ \sigma _p^2 a_p^* a^*_{-p} + 2\sigma _p \gamma _{p} a_p^* a_{p} + \gamma _p^2 a_{-p} a_{p}+ \sigma _p \gamma _{p} \Big ]. \end{aligned}$$

(45)

Obviously the constant in (45) satisfies

$$\begin{aligned} \frac{1}{4N} \sum _{p\ne 0} \widehat{w}(p) \sigma _p \gamma _{p} = \Big \langle 0 \Big | U_{\mathrm{B}} \Big ( \frac{1}{4N}\sum _{p\ne 0} \widehat{w}(p) a_p^* a^*_{-p} \Big ) U_{\mathrm{B}}^* \Big | 0 \Big \rangle . \end{aligned}$$

Moreover, the other terms in (45) can be rewritten as

$$\begin{aligned} \frac{1}{4N} \sum _{p\ne 0} \widehat{w}(p) \sigma _p^2 a_p^* a^*_{-p}&= \frac{1}{4N} \sum _{p,q} \widehat{w}(p) \sigma _p^2 \delta _{p=-q}a_p^* a^*_{q}, \end{aligned}$$

(46)

$$\begin{aligned} \frac{1}{2N} \sum _{p\ne 0} \widehat{w}(p) \sigma _p \gamma _{p} a_p^* a_{p}&= \frac{1}{2N} \sum _{p,q} \widehat{w}(p) \sigma _p \gamma _{p} \delta _{q=p} a_p^* a_{q} , \end{aligned}$$

(47)

$$\begin{aligned} \frac{1}{4N} \sum _{p\ne 0} \widehat{w}(p) \gamma _p^2 a_{-p} a_{p}&= \frac{1}{4N} \sum _{p,q} \widehat{w}(p) \gamma _p^2 \delta _{p=-q} a_{p} a_{q} . \end{aligned}$$

(48)

All of the sums in (46), (47), (48) are of the general form (43)–(44), thanks to the uniform bounds (10). The quadratic terms involving $a_p^* a_{p}$ can be treated similarly.

Next, consider

$$\begin{aligned}&U_{\mathrm{B}} \left( \frac{1}{2N}\sum _{p \ne 0 } \widehat{w}(p) a_p^* a^*_{-p} {\mathcal {N}}_+ \right) U_{\mathrm{B}}^* = U_{\mathrm{B}} \left( \frac{1}{2N}\sum _{p,q\ne 0} \widehat{w}(p) a_p^* a^*_{-p} a_q^* a_q \right) U_{\mathrm{B}}^*\nonumber \\&\quad = \frac{1}{2N} \sum _{p,q\ne 0} \widehat{w}(p) (\sigma _p a_p^* + \gamma _p a_{-p}) (\sigma _p a^*_{-p} + \gamma _{p} a_{p}) (\sigma _q a^*_q + \gamma _q a_{-q}) (\sigma _q a_q + \gamma _q a^*_{-q}) \nonumber \\&\quad = \frac{1}{2N} \sum _{p,q\ne 0} \widehat{w}(p) \Big [ \sigma _p^2 a_p^* a^*_{-p} + 2\sigma _p \gamma _{p} a_p^* a_{p} + \gamma _p^2 a_{-p} a_{p}+ \sigma _p \gamma _{p} \Big ]\times \nonumber \\&\qquad \times \Big [ (\sigma _q^2+\gamma _q^2) a_q^* a_q + \sigma _q \gamma _q (a_q^* a^*_{-q} + a_{-q} a_{q}) + \gamma _q^2 \Big ] \nonumber \\&\quad =\frac{1}{2N} \sum _{p,q\ne 0} \widehat{w}(p) \Big [ \sigma _p^2 a_p^* a^*_{-p} + \sigma _p \gamma _{p} \Big ] \Big [ (\sigma _q^2 +\gamma _q^2) a_q^* a_q + \sigma _q \gamma _q (a_q^* a^*_{-q} + a_{-q} a_{q}) + \gamma _q^2 \Big ] \nonumber \\&\qquad + \frac{1}{N} \sum _{p,q} \widehat{w}(p) \sigma _p \gamma _{p} a_p^* \Big [ (\sigma _q^2 +\gamma _q^2) a_q^* a_q + \sigma _q \gamma _q (a_q^* a^*_{-q} + a_{-q} a_{q}) + \gamma _q^2 \Big ] a_p \nonumber \\&\qquad + \frac{1}{N} \sum _{p,q\ne 0} \widehat{w}(p) \sigma _p \gamma _{p} \Big [ (\sigma _q^2 +\gamma _q^2) a_p^* a_p \delta _{p,q} + \sigma _q \gamma _q a_p^* a_{-p}^* (\delta _{p,q} +\delta _{p,-q}) \Big ] \nonumber \\&\qquad +\frac{1}{2N} \sum _{p,q} \widehat{w}(p) \gamma _{p}^2 \Big [ (\sigma _q^2 +\gamma _q^2) a_q^* a_q + \sigma _q \gamma _q (a_q^* a^*_{-q} + a_{-q} a_{q}) + \gamma _q^2 \Big ] a_p a_{-p} \nonumber \\&\qquad + \frac{1}{2N} \sum _{p,q\ne 0} \widehat{w}(p) \gamma _{p}^2 \Big [ (\sigma _q^2 +\gamma _q^2) a_p a_{-p} (\delta _{p,q}+\delta _{p,-q}) \nonumber \\&\qquad + \sigma _q \gamma _q (a_p^* a_p + a_{-p}^* a_{-p} + 1) (\delta _{p,q}+ \delta _{p,-q}) \Big ]. \end{aligned}$$

(49)

It is straightforward to see that, except the constant

$$\begin{aligned}&\frac{1}{2N} \sum _{p,q\ne 0} \widehat{w}(p) \sigma _p \gamma _{p} \gamma _q^2 + \frac{1}{2N} \sum _{p,q\ne 0} \widehat{w}(p) \gamma _{p}^2 \sigma _q \gamma _q (\delta _{p,q}+ \delta _{p,-q}) \\&\quad = \Big \langle 0 \Big | U_{\mathrm{B}} \Big ( \frac{1}{2N}\sum _{p} \widehat{w}(p) a_p^* a^*_{-p} {\mathcal {N}}_+ \Big ) U_{\mathrm{B}}^* \Big | 0 \Big \rangle , \end{aligned}$$

all other terms in (49) can be written as in (43), with the corresponding bound (44) following from (10). By the same argument, we can show that the terms involving $a_p^* a_{p}{\mathcal {N}}_+$, $a^*_{p+\ell } a^*_{q-\ell } a_p a_q$ and ${\mathcal {N}}_+ ({\mathcal {N}}_+-1)$ are of the general form (43) and (44).

Next, let us bound the terms of the general form (43) and (44). We consider the case $s\ge t$ (the other case is treated similarly). By the Cauchy–Schwarz inequality

$$\begin{aligned} Y^*Z+Z^*Y\le Y^* Y + Z^*Z \end{aligned}$$

we have

$$\begin{aligned}&\pm \Big ( \sum _{m_1, \ldots ,m_{s}, n_1, \ldots ,n_{t}} A_{m_1, \ldots ,m_{s}, n_1, \ldots ,n_{t}} a_{m_1}^*\ldots a_{m_{s}}^* a_{n_1}\ldots a_{n_{t}} + \mathrm{h.c.} \Big ) \nonumber \\&\quad \le \varepsilon ^{-1} \sum _{m_1, \ldots ,m_{s}, n_1, \ldots ,n_{t}} |A_{m_1, \ldots ,m_{s}, n_1, \ldots ,n_{t}}| a_{m_1}^*\ldots a_{m_{s}}^* ({\mathcal {N}}_+ +5)^{1-s} a_{m_{s}}\ldots a_{m_1} \nonumber \\&\qquad + \varepsilon \sum _{m_1, \ldots ,m_{s}, n_1, \ldots ,n_{t}} |A_{m_1, \ldots ,m_{s}, n_1, \ldots ,n_{t}}| a_{n_{t}}^* \ldots a_{n_1}^* ({\mathcal {N}}_+ +5)^{s-1} a_{n_1}\ldots a_{n_{t}}\nonumber \\&\quad \le \varepsilon ^{-1} \Big ( \sup _{m_1, \ldots ,m_{s}} \sum _{n_1, \ldots ,n_{t}} |A_{m_1, \ldots ,m_{s}, n_1, \ldots ,n_{t}}| \Big ) \sum _{m_1, \ldots ,m_{s}} a_{m_1}^*\ldots a_{m_{s}}^* ({\mathcal {N}}_+ +5)^{1-s} a_{m_{s}}\ldots a_{m_1} \nonumber \\&\qquad + \varepsilon \Big ( \sup _{n_1, \ldots ,n_{t'}} \sum _{m_1, \ldots ,m_{s}} |A_{m_1, \ldots ,m_{s}, n_1, \ldots ,n_{t}}| \Big ) \sum _{n_1, \ldots ,n_{t'}} a_{n_{t}}^* \ldots a_{n_1}^* ({\mathcal {N}}_+ +5)^{s-1} a_{n_1}\ldots a_{n_{t}} \nonumber \\&\quad \le \varepsilon ^{-1}\frac{C}{N} {\mathcal {N}}_+ + \varepsilon \frac{C}{N} ({\mathcal {N}}_+ + 1) ^{t+s-1} \end{aligned}$$

(50)

for all $\varepsilon >0$. Note that if $\min (t,s) \ge 1$, then on the right side of (50) we can replace $({\mathcal {N}}_++1)^{t+s-1}$ by ${\mathcal {N}}_+^{t+s-1}$.

In particular, for the non-cubic term ${\widetilde{{\mathcal {D}}}}_N$, using (50) with $\varepsilon =N^{-1/2}$ and $t+s\le 4$ we get

$$\begin{aligned} \pm \Big ( U_B {\widetilde{{\mathcal {D}}}}_N U_B^*- \langle 0| U_B {\widetilde{{\mathcal {D}}}}_N U_B^* |0\rangle \Big ) \le \frac{C}{\sqrt{N}} {\mathcal {N}}_+ + \frac{C({\mathcal {N}}_+ +1)^3}{N^{3/2}}. \end{aligned}$$

(51)

Cubic terms. By using (8) we have

$$\begin{aligned}&U_B \left( \frac{1}{\sqrt{N}} \sum _{\ell ,p\ne 0, \ell +p\ne 0} \widehat{w}(\ell ) a^*_{p+\ell } a^*_{-\ell } a_{p} \right) U^*_B \nonumber \\&\quad = \frac{1}{\sqrt{N}} \sum _{\ell ,p\ne 0, \ell +p\ne 0} \widehat{w}(\ell ) (\sigma _{p+\ell }a^*_{p+\ell } + \gamma _{p+\ell } a_{-p-\ell }) (\sigma _{\ell } a^*_{-\ell } + \gamma _{\ell } a_{\ell }) (\sigma _p a_{p} + \gamma _{p} a_{-p}^*)\nonumber \\&\quad = \frac{1}{\sqrt{N}}\sum _{\begin{array}{c} \ell ,p\ne 0\\ \ell +p\ne 0 \end{array}}\widehat{w}(\ell ) \Big ( \sigma _{p+\ell }\sigma _{\ell }\gamma _p a^*_{p+\ell } a^*_{-\ell } a^*_{-p} + \gamma _{p+\ell }\gamma _{\ell }\sigma _p a_{-p-\ell } a_{\ell } a_p\Big ) \nonumber \\&\qquad + \frac{1}{\sqrt{N}}\sum _{\begin{array}{c} \ell ,p\ne 0\\ \ell +p\ne 0 \end{array}} \Big ( \hat{w}(\ell )\sigma _{p+\ell }\sigma _{\ell }\sigma _p+\hat{w}(p+\ell )\sigma _{p+\ell }\gamma _{\ell }\gamma _{-p}+\hat{w}(p)\sigma _{p+\ell }\gamma _p \gamma _\ell \Big ) a^*_{p+\ell } a^*_{-\ell } a_p \nonumber \\&\qquad + \frac{1}{\sqrt{N}}\sum _{\begin{array}{c} \ell ,p\ne 0\\ \ell +p\ne 0 \end{array}} \Big ( \hat{w}(\ell )\sigma _{p+\ell }\gamma _{\ell }\sigma _p+\hat{w}(p+\ell )\sigma _{p+\ell }\sigma _{\ell }\gamma _{p}+\hat{w}(p)\gamma _{-p-\ell } \gamma _p \gamma _\ell \Big ) a_{p+\ell }^* a_p a_\ell . \end{aligned}$$

(52)

By using (10), we can write the last sum of (52) as

$$\begin{aligned} \sum _{p,q,r} \widetilde{A}_{p,q,r} a_p^* a_q a_r \end{aligned}$$

with

$$\begin{aligned} \sup _{p} \sum _{q,r} |\widetilde{A}_{p,q,r}| \le \frac{C}{\sqrt{N}}, \quad \sup _{q,r} \sum _{p} |\widetilde{A}_{p,q,r}| \le \frac{C}{\sqrt{N}}. \end{aligned}$$

Using (50) with $\varepsilon =1$, $t=1,s=2$, we get

$$\begin{aligned}&\pm \Big ( \sum _{p,q,r} \widetilde{A}_{p,q,r} a_p^* a_q a_r + \mathrm{h.c.} \Big ) \le \frac{C}{N} ({\mathcal {N}}_+ + {\mathcal {N}}_+^2)\le \frac{C {\mathcal {N}}_+^2}{N}. \end{aligned}$$

(53)

Here ${\mathcal {N}}_+\le {\mathcal {N}}_+^2$ since the spectrum of ${\mathcal {N}}_+$ is $\{0,1,2, \ldots \}$. The second sum on the right side of (52) can be treated by the same way. Thus from (52) and its adjoint, we have

$$\begin{aligned}&\pm \Big ( U_B {\widetilde{{\mathcal {C}}}}_N U_B^* - \frac{1}{\sqrt{N}}\sum _{\begin{array}{c} \ell ,p\ne 0\\ \ell +p\ne 0 \end{array}}\widehat{w}(\ell ) \Big [ \Big ( \sigma _{p+\ell }\sigma _{\ell }\gamma _p a^*_{p+\ell } a^*_{-\ell } a^*_{-p} \\&\qquad + \gamma _{p+\ell }\gamma _{\ell }\sigma _p a_{-p-\ell } a_{\ell } a_p\Big ) + \mathrm{h.c.}\Big ] \Big ) \\&\quad \le \frac{C{\mathcal {N}}_+^2}{N} \end{aligned}$$

which is equivalent to

$$\begin{aligned}&\pm \Big ( U_B {\widetilde{{\mathcal {C}}}}_N U_B^* - {\mathcal {C}}_N\Big ) \le \frac{C{\mathcal {N}}_+^2}{N} . \end{aligned}$$

(54)

In particular, (54) implies that

$$\begin{aligned} \langle 0| U_B {\widetilde{{\mathcal {C}}}}_N U_B^* |0\rangle =0. \end{aligned}$$

Therefore, from (9), (51) and (54) we obtain the desired conclusion of Lemma 8. $\square$

5 Cubic transformation

To factor out the cubic term ${\mathcal {C}}_N$ in Lemma 8, we will use a cubic renormalization. We will prove

Lemma 9

Let ${\mathcal {C}}_N$ be the cubic term in Lemma 8 and let $U_S$ be given in (25). Then we have the operator identity on Fock spacee ${\mathcal {F}}_+$

$$\begin{aligned} U_S U_B {\mathcal {G}}_N U_B^* U_S^*= \Big \langle 0 \Big | U_S U_B {\mathcal {G}}_N U_B^* U_S^* \Big | 0 \Big \rangle + \sum _{p\ne 0} e(p) a_p^* a_p + R_3 \end{aligned}$$

where

$$\begin{aligned} \pm R_3 \le C\frac{{\mathcal {N}}_+^2}{\sqrt{N}} +\frac{C({\mathcal {N}}_++1)^4}{N^{3/2}} . \end{aligned}$$

Proof

Recall that from Lemma 8 we have

$$\begin{aligned} U_S U_B {\mathcal {G}}_N U_B^* U_S^*= \Big \langle 0 \Big | U_B {\mathcal {G}}_N U_B^* \Big | 0 \Big \rangle + U_S \Big ( \mathrm{d}\Gamma (\xi ) + {\mathcal {C}}_N \Big ) U_S^* + U_S R_2 U_S^* \end{aligned}$$

(55)

with

$$\begin{aligned} \mathrm{d}\Gamma (\xi ) =\sum _{p\ne 0} e(p) a_p^* a_p,\quad \pm R_2 \le \frac{C}{\sqrt{N}} {\mathcal {N}}_+^2 + C\frac{({\mathcal {N}}_+ +1)^3}{N^{3/2}}. \end{aligned}$$

Thanks to Lemmas 5 and 6, we find that

$$\begin{aligned} \pm U_S R_2 U_S^* \le \frac{C}{\sqrt{N}} {\mathcal {N}}_+^2 + C\frac{({\mathcal {N}}_+ +1)^3}{N^{3/2}}. \end{aligned}$$

Thus this error term is part of $R_3$.

For the main term, we use $U_S=e^{S}$ and the Duhamel formula

$$\begin{aligned} e^{X}Y e^{-X}=Y+\int _0^1 e^{tX} [X,Y] e^{-tX}dt \end{aligned}$$

(56)

we can write

$$\begin{aligned}&e^{S} \Big ( \mathrm{d}\Gamma (\xi )+ {\mathcal {C}}_N\Big ) e^{-S}=\mathrm{d}\Gamma (\xi ) + {\mathcal {C}}_N + \int _0^1 e^{tS} \Big ( [S,\mathrm{d}\Gamma (\xi )] + [S,{\mathcal {C}}_N] \Big ) e^{-tS} dt \nonumber \\&\quad = \mathrm{d}\Gamma (\xi ) + \int _0^1 e^{tS} \Big ( {\mathcal {C}}_N + [S,\mathrm{d}\Gamma (\xi )] + [S,{\mathcal {C}}_N] \Big ) e^{-tS} dt - \int _0^1 \int _0^t e^{sS} [S,{\mathcal {C}}_N] e^{-sS} ds dt . \end{aligned}$$

(57)

Controlling ${\mathcal {C}}_N + [S,\mathrm{d}\Gamma (\xi )]$. Since $\mathrm{d}\Gamma (\xi )$ commutes with ${\mathcal {N}}_+$ and

$$\begin{aligned}{}[a_k^* a_k, a_{p+q}^* a^*_{-p} a^*_{-q}] = (\delta _{k,p+q} + \delta _{k,-p} + \delta _{k,-q}) a_{p+q}^* a^*_{-p} a^*_{-q} \end{aligned}$$

we find that

$$\begin{aligned}{}[\mathrm{d}\Gamma (\xi ), S]&= \frac{1}{\sqrt{N}} \sum _{\begin{array}{c} p,q\ne 0\\ p+q\ne 0 \end{array}} \quad \sum _{k\ne 0} e(k) \eta _{p,q} [a_k^* a_k, a_{p+q}^* a^*_{-p} a^*_{-q}] {\mathbb {1}}^{\le N}+\mathrm{h.c.} \nonumber \\&= \frac{1}{\sqrt{N}} \sum _{\begin{array}{c} p,q\ne 0\\ p+q\ne 0 \end{array}} (e(p+q)+e(p) + e(q) ) \eta _{p,q} a_{p+q}^* a^*_{-p} a^*_{-q} {\mathbb {1}}^{\le N}+ \mathrm{h.c.} \nonumber \\&= \frac{1}{\sqrt{N}} \sum _{\begin{array}{c} p,q\ne 0\\ p+q\ne 0 \end{array}} \widehat{w}(p)\big (\sigma _{p+q}\sigma _p \gamma _q +\gamma _{p+q}\gamma _p \sigma _q\big ) a_{p+q}^* a^*_{-p} a^*_{-q} {\mathbb {1}}^{\le N} + \mathrm{h.c.} \end{aligned}$$

which is equivalent to

$$\begin{aligned} {\mathcal {C}}_N + [S,\mathrm{d}\Gamma (\xi )] = \frac{1}{\sqrt{N}} \sum _{\begin{array}{c} p,q\ne 0\\ p+q\ne 0 \end{array}} \widehat{w}(p)\big (\sigma _{p+q}\sigma _p \gamma _q +\gamma _{p+q}\gamma _p \sigma _q\big ) a_{p+q}^* a^*_{-p} a^*_{-q} {\mathbb {1}}^{>N} + \mathrm{h.c.} \end{aligned}$$

where ${\mathbb {1}}^{>N}={\mathbb {1}}-{\mathbb {1}}^{\le N}={\mathbb {1}}({\mathcal {N}}_+ >N)$. Thanks to the summability (10), we can use the Cauchy–Schwarz inequality similarly to (50) (with $\varepsilon =1$) to get

$$\begin{aligned} \pm \Big ( {\mathcal {C}}_N + [S,\mathrm{d}\Gamma (\xi )] \Big ) \le \frac{C}{\sqrt{N}}{\mathcal {N}}_+ + \frac{C({\mathcal {N}}_+ +1)^2}{\sqrt{N}} {\mathbb {1}}^{>N} \le \frac{C}{\sqrt{N}}{\mathcal {N}}_+ + \frac{C({\mathcal {N}}_+ +1)^3}{N^{3/2} } \end{aligned}$$

Combining with Lemmas 5 and 6 we obtain

$$\begin{aligned} e^{tS} \Big ( {\mathcal {C}}_N + [S,\mathrm{d}\Gamma (\xi )] \Big ) e^{-tS} \le \frac{C}{\sqrt{N}}{\mathcal {N}}_+ + \frac{C({\mathcal {N}}_+ +1)^3}{N^{3/2} }, \quad \forall t\in [-1,1]. \end{aligned}$$

(58)

Controlling $[S,{\mathcal {C}}_N]$. Let us decompose $S= {\widetilde{S}} - S^{>}$ where

$$\begin{aligned} {\widetilde{S}}&=\frac{1}{\sqrt{N}}\sum _{\begin{array}{c} p,q\ne 0\\ p+q\ne 0 \end{array}} \eta _{p,q}a^*_{p+q}a^*_{-p}a^*_{-q} - \mathrm{h.c.,}\nonumber \\ S^{>}&= \frac{1}{\sqrt{N}}\sum _{\begin{array}{c} p,q\ne 0\\ p+q\ne 0 \end{array}} \eta _{p,q}a^*_{p+q}a^*_{-p}a^*_{-q} {\mathbb {1}}^{>N}- \mathrm{h.c.} \end{aligned}$$

The main contribution comes from

$$\begin{aligned}{}[{\mathcal {C}}_N,\widetilde{S}]&= \frac{1}{N}\sum _{p,q,r\ne 0} \sum _{p',q',r'\ne 0} \delta _{p+q+r=0} \delta _{p'+q'+r'=0} \eta _{p',q'} \widehat{w}(p) \big (\sigma _{r}\sigma _{p} \gamma _{q} +\gamma _{r}\gamma _{p} \sigma _{q}\big ) \times \\&\quad \times \Big [ a_{r} a_{p} a_{q} , a_{r'}^* a_{p'} ^*a_{q'}^* \Big ] + \mathrm{h.c.} \\&= \frac{1}{N}\sum _{p,q,r\ne 0} \sum _{p',q',r'\ne 0} \delta _{p+q+r=0} \delta _{p'+q'+r'=0} \eta _{p',q'} \widehat{w}(p) \big (\sigma _{r}\sigma _{p} \gamma _{q} +\gamma _{r}\gamma _{p} \sigma _{q}\big ) \times \\&\quad \times \Big ( \delta _{r=r'} a_{p}a_q a_{p'} ^* a_{q'}^* + \delta _{r=p'} a_{p}a_q a_{r'} ^* a_{q'}^* + \delta _{r=q'} a_{p}a_q a_{r'} ^* a_{p'}^* \\&\quad + \delta _{p=r'} a_q a_{p'}^* a_{q'}^* a_r + \delta _{p=p'} a_{q} a_{r'}^* a_{q'}^* a_r + \delta _{p=q'} a_{q} a_{r'}^* a_{p'}^* a_r \\&\quad + \delta _{q=r'} a_{p'}^* a_{q'}^* a_r a_p + \delta _{q=p'} a_{r'}^* a_{q'}^* a_r a_p + \delta _{q=q'} a_{r'}^* a_{p'}^* a_r a_p \Big ) +\mathrm{h.c.} \\ \end{aligned}$$

By using the CCR (3) as in (49), we can write

$$\begin{aligned}{}[\widetilde{S},{\mathcal {C}}_N] = \langle 0 | [\widetilde{S},{\mathcal {C}}_N] | 0\rangle + \sum _{p,q\ne 0}A_{pq} a^*_p a_q+ \sum _{p,q,r,k\ne 0}B_{pqrk}a^*_p a^*_q a_r a_k \end{aligned}$$

where

$$\begin{aligned} \sup _{q\ne 0} \sum _{p\ne 0} |A_{pq} |&\le \frac{C}{N}, \quad \sup _{p\ne 0} \sum _{q\ne 0} |A_{pq} | \le \frac{C}{N}, \\ \sup _{p,q \ne 0} \sum _{r,k \ne 0} |B_{pqrk} |&\le \frac{C}{N}, \quad \sup _{r,k \ne 0} \sum _{p,q \ne 0} |B_{pqrk} | \le \frac{C}{N}. \end{aligned}$$

By the Cauchy–Schwarz inequality as in (50), we get

$$\begin{aligned} \pm \Big ( [\widetilde{S},{\mathcal {C}}_N] - \langle 0 | [\widetilde{S},{\mathcal {C}}_N] |0\rangle \Big ) \le C\frac{{\mathcal {N}}_+}{\sqrt{N}} + \frac{C({\mathcal {N}}_+ +1)^3}{N^{3/2}}. \end{aligned}$$

(59)

It remains to bound $[S^>, {\mathcal {C}}_N]$. From the explicit form of $S^{>}$ and ${\mathcal {C}}_N$, it is straightforward to check that

$$\begin{aligned} \pm \, [S^>, {\mathcal {C}}_N] = \pm \, \Big ( (S^> ) {\mathcal {C}}_N + {\mathcal {C}}_N (S^>)^* \Big ) \le (S^> ) (S^>)^* + {\mathcal {C}}_N^2 \le \frac{C}{N} ({\mathcal {N}}_+ +1)^3. \end{aligned}$$

On the other hand, we observe that

$$\begin{aligned} S^> = {\mathbb {1}}^{>N-4} S^> {\mathbb {1}}^{>N-4} \end{aligned}$$

and that ${\mathcal {C}}_N$ does not change the number of particles more than 3. Therefore,

$$\begin{aligned} \pm [S^>, {\mathcal {C}}_N] = \pm {\mathbb {1}}^{> N-7} [S^>, {\mathcal {C}}_N] {\mathbb {1}}^{> N-7} \le \frac{C}{N} ({\mathcal {N}}_+ +1)^3 {\mathbb {1}}^{> N-7} \le \frac{C}{N^2} ({\mathcal {N}}_+ +1)^4. \end{aligned}$$

(60)

Moreover, it is obvious that

$$\begin{aligned} \langle 0| [S^>,{\mathcal {C}}_N] |0\rangle =0 \end{aligned}$$

for $N\ge 10$. Thus from (59) and (60) we obtain

$$\begin{aligned} \pm \Big ( [S,{\mathcal {C}}_N] - \langle 0 | [S,{\mathcal {C}}_N] |0\rangle \Big ) \le C\frac{{\mathcal {N}}_+}{\sqrt{N}} + \frac{C({\mathcal {N}}_+ +1)^4}{N^{3/2}}. \end{aligned}$$

Combining with Lemma 5 we conclude that

$$\begin{aligned} \pm e^{tS}\Big ( [S,{\mathcal {C}}_N] - \langle 0 | [S,{\mathcal {C}}_N] |0\rangle \Big ) e^{-tS}\le C\frac{{\mathcal {N}}_+}{\sqrt{N}} + \frac{C({\mathcal {N}}_+ +1)^4}{N^{3/2}}, \quad \forall t\in [-1,1]. \end{aligned}$$

(61)

Conclusion. Inserting (58) and (61) in (57) we find that

$$\begin{aligned} \pm \,\Big (e^{S} \Big ( \mathrm{d}\Gamma (\xi )+ {\mathcal {C}}_N\Big ) e^{-S} - \mathrm{d}\Gamma (\xi ) - \frac{1}{2} \langle 0 | [S,{\mathcal {C}}_N] |0\rangle \Big ) \le C\frac{{\mathcal {N}}_+}{\sqrt{N}} + \frac{C({\mathcal {N}}_+ +1)^4}{N^{3/2}}. \end{aligned}$$

Combining with (55) we deduce that

$$\begin{aligned}&\pm \, \Big ( U_SU_B{\mathcal {G}}_N U_B^* U_S^* - \mathrm{d}\Gamma (\xi ) - \Big \langle 0 \Big | U_B {\mathcal {G}}_N U_B^* \Big | 0 \Big \rangle - \frac{1}{2} \langle 0 | [S,{\mathcal {C}}_N] |0\rangle \Big ) \le C\frac{{\mathcal {N}}_+^2}{\sqrt{N}} + \frac{C({\mathcal {N}}_+ +1)^4}{N^{3/2}}. \end{aligned}$$

Taking the expectation of the latter bound again the vacuum, we find that

$$\begin{aligned} \pm \, \Big ( \langle 0 | U_SU_B{\mathcal {G}}_N U_B^* U_S^* |0\rangle - \Big \langle 0 \Big | U_B {\mathcal {G}}_N U_B^* \Big | 0 \Big \rangle - \frac{1}{2} \langle 0 | [S,{\mathcal {C}}_N] |0\rangle \Big ) \le \frac{C}{N^{3/2}}. \end{aligned}$$

Thus we obtain the desired conclusion

$$\begin{aligned} \pm \Big ( U_SU_B{\mathcal {G}}_N U_B^* U_S^* - \mathrm{d}\Gamma (\xi ) - \langle 0 | U_SU_B{\mathcal {G}}_N U_B^* U_S^* |0\rangle \Big ) \le C\frac{{\mathcal {N}}_+^2}{\sqrt{N}} + \frac{C({\mathcal {N}}_+ +1)^4}{N^{3/2}}. \end{aligned}$$

This completes the proof of Lemma 9. $\square$

6 Proof of Theorem 2

Proof

We will prove the ground state energy estimate

$$\begin{aligned} E_N= \frac{N}{2}{\widehat{w}}(0) + \Big \langle 0 \Big | U_S U_B {\mathcal {G}}_N U_B^* U_S^* \Big | 0 \Big \rangle + O\big (N^{-3/2}\big ). \end{aligned}$$

Upper bound. We use the following N-body trial state

$$\begin{aligned} {\widetilde{\Psi }}_N= \frac{1}{\Vert U_N^* {\mathbb {1}}^{\le N} U_{\mathrm{B}}^* U_S^*|0\rangle \Vert } U_N^* {\mathbb {1}}^{\le N} U_{\mathrm{B}}^* U_S^*|0\rangle . \end{aligned}$$

Then by the variational principle and the operator inequality on ${\mathcal {F}}_+$ in Lemma 7 we have

$$\begin{aligned} E_N&\le \langle {\widetilde{\Psi }}_N, H_N {\widetilde{\Psi }}_N\rangle = \frac{1}{\Vert U_N^* {\mathbb {1}}^{\le N} U_{\mathrm{B}}^* U_S^*|0\rangle \Vert ^2} \Big \langle 0\Big | U_S U_{\mathrm{B}} {\mathbb {1}}^{\le N} U_N H_N U_N^* {\mathbb {1}}^{\le N} U_{\mathrm{B}}^*U_S^*\Big |0\Big \rangle \\&\le \frac{1}{\Vert U_N^* {\mathbb {1}}^{\le N} U_{\mathrm{B}}^* U_S^*|0\rangle \Vert ^2} \Big \langle 0\Big |U_S U_{\mathrm{B}} \Big ( \frac{N {\widehat{w}}(0)}{2} + {\mathcal {G}}_N + \frac{C({\mathcal {N}}_+ +1)^3}{N^{3/2}} \Big ) U_{\mathrm{B}}^*U_S^*\Big |0\Big \rangle . \end{aligned}$$

By Lemmas 4 and 5 we know that

$$\begin{aligned} \Big \langle 0\Big |U_S U_{\mathrm{B}} ({\mathcal {N}}_+ +1)^3 U_{\mathrm{B}}^*U_S^*\Big |0\Big \rangle \le C. \end{aligned}$$

Consequently,

$$\begin{aligned} \Vert U_N^* {\mathbb {1}}^{\le N} U_{\mathrm{B}}^* U_S^*|0\rangle \Vert ^2&=1-\langle 0|U_S U_{\mathrm{B}}{\mathbb {1}}^{> N} U_{\mathrm{B}}^* U_S^*|0\rangle \\&\ge 1 - \langle 0|U_S U_{\mathrm{B}} ({\mathcal {N}}_+^3/N^3) U_{\mathrm{B}}^* U_S^*|0\rangle \ge 1-CN^{-3}. \end{aligned}$$

Combining with Lemma 9 we find that

$$\begin{aligned} E_N&\le \frac{1}{\Vert U_N^* {\mathbb {1}}^{\le N} U_{\mathrm{B}}^* U_S^*|0\rangle \Vert ^2} \left( \frac{N {\widehat{w}}(0)}{2} + \Big \langle 0\Big |U_S U_{\mathrm{B}} {\mathcal {G}}_N U_{\mathrm{B}}^*U_S^*\Big |0\Big \rangle + \frac{C}{N^{3/2}} \right) \\&\le \frac{N {\widehat{w}}(0)}{2} + \Big \langle 0\Big |U_S U_{\mathrm{B}} {\mathcal {G}}_N U_{\mathrm{B}}^*U_S^*\Big |0\Big \rangle + \frac{C}{N^{3/2}} . \end{aligned}$$

In the last estimate, we have also used the simple upper bound

$$\begin{aligned} \Big \langle 0\Big |U_S U_{\mathrm{B}} {\mathcal {G}}_N U_{\mathrm{B}}^*U_S^*\Big |0\Big \rangle \le C \end{aligned}$$

(62)

which will be justified below.

Lower bound. Let $\Psi _N$ be the ground state of $H_{N}$ and denote $\Phi := U_S U_B U_N \Psi _N \in {\mathcal {F}}_+.$ By Lemmas 3, 35 and 36, we have

$$\begin{aligned} \langle \Phi , ({\mathcal {N}}_+ +1)^4 \rangle \Phi \rangle \le C. \end{aligned}$$

Then from the operator identity on ${\mathcal {F}}_+^{\le N}$ in Lemma 7 it follows that

$$\begin{aligned} E_N&= \langle \Psi _N, H_N \Psi _N\rangle = \langle U_N \Psi _N, U_N H_N U_N^* U_N\Psi _N\rangle \\&\ge \langle U_N \Psi _N, \left( \frac{N {\widehat{w}}(0)}{2} + {\mathcal {G}}_N - C \frac{({\mathcal {N}}_+ +1)^3 }{N^{3/2}} \right) U_N\Psi _N\rangle \\&\ge \frac{N {\widehat{w}}(0)}{2} + \langle \Phi , U_S U_B {\mathcal {G}}_N U_B^* U_S^* \Phi \rangle - CN^{-3/2}. \end{aligned}$$

Next, using Lemma 9 together with two simple estimates:

$$\begin{aligned} \sum _{p\ne 0} e(p) a_p^* a_p \ge \Big ( \inf _{q\ne 0} e(q) \Big ) \sum _{p\ne 0} a_p^* a_p \ge (2\pi )^2 {\mathcal {N}}_+ \end{aligned}$$

and

$$\begin{aligned} \frac{{\mathcal {N}}_+^2}{\sqrt{N}} \le \varepsilon {\mathcal {N}}_+ + \frac{{\mathcal {N}}_+^2}{\sqrt{N}} {\mathbb {1}}({\mathcal {N}}_+ > \varepsilon \sqrt{N}) \le \varepsilon {\mathcal {N}}_+ + C_\varepsilon \frac{{\mathcal {N}}_+^4}{N^{3/2}} \end{aligned}$$

for $\varepsilon >0$ small (but independent of N), we obtain

$$\begin{aligned} U_S U_B {\mathcal {G}}_N U_B^* U_S^* \ge \langle 0| U_S U_B {\mathcal {G}}_N U_B^* U_S^* |0\rangle + {\mathcal {N}}_+ - C\frac{({\mathcal {N}}_++1)^4}{N^{3/2}}. \end{aligned}$$

Therefore,

$$\begin{aligned} \langle \Phi , U_S U_B {\mathcal {G}}_N U_B^* U_S^* \Phi \rangle \ge \langle 0| U_S U_B {\mathcal {G}}_N U_B^* U_S^* |0 \rangle + \langle \Phi , {\mathcal {N}}_+ \Phi \rangle - CN^{-3/2}. \end{aligned}$$

Thus

$$\begin{aligned} E_N\ge \frac{N {\widehat{w}}(0)}{2} + \langle 0| U_S U_B {\mathcal {G}}_N U_B^* U_S^* |0 \rangle + \Big \langle \Phi , {\mathcal {N}}_+ \Phi \Big \rangle - CN^{-3/2}. \end{aligned}$$

(63)

From (63), since $\Big \langle \Phi , {\mathcal {N}}_+ \Phi \Big \rangle \ge 0$ we obtain the desired energy lower bound

$$\begin{aligned} E_N \ge \frac{N {\widehat{w}}(0)}{2} + \langle 0| U_S U_B {\mathcal {G}}_N U_B^* U_S^* |0 \rangle + O(N^{-3/2}). \end{aligned}$$

This and the obvious upper bound $E_N \le {\widehat{w}}(0) (N/2)$ imply the simple estimate (62). Thus the matching energy upper bound is valid, and hence we conclude that

$$\begin{aligned} E_N = \frac{N {\widehat{w}}(0)}{2} + \langle 0| U_S U_B {\mathcal {G}}_N U_B^* U_S^* |0 \rangle + O(N^{-3/2}). \end{aligned}$$

(64)

Ground state estimates. By comparing the ground state energy expansion (64) with the lower bound (63) we deduce that

$$\begin{aligned} \langle \Phi , {\mathcal {N}}_+ \Phi \rangle \le CN^{-3/2}. \end{aligned}$$

(65)

Let us write $\Phi =(\Phi _j)_{j=0}^\infty$ with $\Phi _j\in {\mathcal {H}}_+^j$. We can choose a phase factor for $\Psi _N$ such that $\Phi _0 \ge 0$. Then

$$\begin{aligned} \Vert \Phi - |0\rangle \Vert ^2 = |\Phi _0 -1|^2 \le 1- |\Phi _0|^2 = \sum _{j\ge 1} |\Phi _j|^2 \le \langle \Phi , {\mathcal {N}}_+ \Phi \rangle \le CN^{-3/2}. \end{aligned}$$

Putting back the definition $\Phi = U_S U_B U_N \Psi _N$ we obtain the norm approximation

$$\begin{aligned} \Vert U_N \Psi _N - U_B^* U_S^* |0\rangle \Vert = \Vert \Phi - |0\rangle \Vert ^2 \le CN^{-3/2}. \end{aligned}$$

This completes the proof of Theorem 2. $\square$

7 Proof of Theorem 1

Proof

Let $\Psi _N$ be the ground state for $H_N$. As explained in the introduction, we will decompose

$$\begin{aligned} \gamma _{\Psi _N}^{(1)} = P \gamma _{\Psi _N}^{(1)} P + Q \gamma _{\Psi _N}^{(1)} Q + P \gamma _{\Psi _N}^{(1)} Q + Q \gamma _{\Psi _N}^{(1)} P. \end{aligned}$$

Diagonal terms. For $Q \gamma _{\Psi _N}^{(1)} Q$, recall from [12, Theorem 2.2 (iii)] that

$$\begin{aligned} U_N \Psi _N \rightarrow U_B^* |0\rangle \end{aligned}$$

strongly in the quadratic form of ${\mathbb {H}}_{\mathrm{Bog}}$ on ${\mathcal {F}}_+$. Moreover, it is easy to see that

$$\begin{aligned} {\mathbb {H}}_{\mathrm{Bog}} \ge \frac{1}{2} \sum _{p\ne 0} |p|^2 a_p^* a_p - C \ge {\mathcal {N}}_+ - C \end{aligned}$$

(see e.g. [13, Proof of Theorem 1]). Therefore, in the limit $N\rightarrow \infty$,

$$\begin{aligned} \mathrm{Tr}Q \gamma _{\Psi _N}^{(1)} Q&= \langle U_N \Psi _N, {\mathcal {N}}_+ U_N \Psi _N\rangle \rightarrow \langle 0| U_B {\mathcal {N}}_+ U_B^* |0\rangle \nonumber \\&= \Big \langle 0 \Big | \sum _{p\ne 0} ( \sigma _p a_p^* + \gamma _p a_{-p}) (\sigma _p a_p + \gamma _p a_{-p}^*) \Big |0 \Big \rangle = \sum _{p\ne 0} \gamma _p^2. \end{aligned}$$

(66)

Here we have used Bogoliubov’s transformation (8). Similarly, for any $p,q\ne 0$ we have

$$\begin{aligned} \langle u_p, Q\gamma _{\Psi _N}^{(1)} Q u_q\rangle&= \langle U_N \Psi _N, a_p^* a_q U_N \Psi _N \rangle \rightarrow \langle 0| U_B (a_p^* a_q) U_B^* |0\rangle \nonumber \\&= \langle 0| ( \sigma _p a_p^* + \gamma _p a_{-p}) (\sigma _q a_q + \gamma _p a_{-q}^*) |0 \rangle = \gamma _p^2 \delta _{p,q}. \end{aligned}$$

(67)

From (66) and (67), we conclude that

$$\begin{aligned} Q\gamma _{\Psi _N}^{(1)} Q \rightarrow \sum _{p\ne 0} \gamma _p^2 |u_p\rangle \langle u_p| \end{aligned}$$

(68)

strongly in trace class. Consequently,

$$\begin{aligned} \mathrm{Tr}(P \gamma _{\Psi _N}^{(1)} P) = N - \mathrm{Tr}Q\gamma _{\Psi _N}^{(1)} Q = N - \sum _{p\ne 0} \gamma _p^2 \end{aligned}$$

and hence

$$\begin{aligned} \mathrm{Tr}\Big | P \gamma _{\Psi _N}^{(1)} P + Q \gamma _{\Psi _N}^{(1)} Q - \Big ( N - \sum _{p\ne 0} \gamma _p^2 \Big ) |u_0\rangle \langle u_0| - \sum _{p\ne 0} \gamma _p^2 |u_p\rangle \langle u_p| \Big | \rightarrow 0. \end{aligned}$$

Off-diagonal terms. Let us prove that

$$\begin{aligned} \mathrm{Tr}\Big | P \gamma _{\Psi _N}^{(1)} Q + Q \gamma _{\Psi _N}^{(1)} P \Big | \le CN^{-1/4}. \end{aligned}$$

(69)

By using $P=|u_0\rangle \langle u_0|$ and the Cauchy–Schwarz inequality, it suffices to show that

$$\begin{aligned} \Vert Q \gamma _{\Psi _N}^{(1)}u_0\Vert ^2 \le CN^{-1/2}. \end{aligned}$$

Since $\{u_p\}_{p\ne 0}$ is an orthonormal basis for ${\mathcal {H}}_+$, we have

$$\begin{aligned} \Vert Q \gamma _{\Psi _N}^{(1)} u_0\Vert ^2 =\sum _{p\ne 0} |\langle u_p, \gamma _{\Psi _N}^{(1)} u_0\rangle |^2 = \sum _{p\ne 0} |\langle \Psi _N, a^*_0 a_p \Psi _N \rangle |^2. \end{aligned}$$

Using the excitation map $U_N$ and the relations (12) we can decompose

$$\begin{aligned}&\langle \Psi _N, a^*_0 a_p \Psi _N \rangle = \langle U_N \Psi _N, \sqrt{N-{\mathcal {N}}_+} a_p U_N \Psi _N \rangle \\&\quad = \sqrt{N} \langle U_N \Psi _N, a_p U_N \Psi _N \rangle + \langle U_N \Psi _N, (\sqrt{N-{\mathcal {N}}_+} -\sqrt{N}) a_p U_N \Psi _N \rangle . \end{aligned}$$

Therefore, by the Cauchy–Schwarz inequality

$$\begin{aligned} \Vert Q \gamma _{\Psi _N}^{(1)} u_0\Vert ^2&\le 2 N \sum _{p\ne 0} |\langle U_N \Psi _N, a_p U_N \Psi _N \rangle |^2 \nonumber \\&\qquad +2 \sum _{p\ne 0} | \langle U_N \Psi _N, (\sqrt{N-{\mathcal {N}}_+} -\sqrt{N}) a_p U_N \Psi _N \rangle |^2. \end{aligned}$$

(70)

For the second sum in (70), using the Cauchy–Schwarz inequality, the simple bound

$$\begin{aligned} \left( \sqrt{N-{\mathcal {N}}_+} -\sqrt{N}\right) ^2 = \Big ( \frac{{\mathcal {N}}_+}{\sqrt{N-{\mathcal {N}}_+}+\sqrt{N}}\Big )^2 \le \frac{{\mathcal {N}}_+^2}{N} \end{aligned}$$

and Lemma 3, we find that

$$\begin{aligned}&\sum _{p\ne 0} | \langle U_N \Psi _N, (\sqrt{N-{\mathcal {N}}_+} -\sqrt{N}) a_p U_N \Psi _N \rangle |^2 \nonumber \\&\quad \le \sum _{p\ne 0} \Vert (\sqrt{N-{\mathcal {N}}_+} -\sqrt{N}) U_N \Psi _N\Vert ^2 \Vert a_p U_N \Psi _N \Vert ^2\nonumber \\&\quad \le N^{-1} \langle U_N \Psi _N, {\mathcal {N}}_+^2 U_N \Psi _N\rangle \langle U_N \Psi _N, {\mathcal {N}}_+ U_N \Psi _N\rangle \nonumber \\&\quad = N^{-1} \langle \Psi _N, {\mathcal {N}}_+^2 \Psi _N\rangle \langle \Psi _N, {\mathcal {N}}_+ \Psi _N\rangle \le CN^{-1}. \end{aligned}$$

(71)

To control the first sum in (70), we will use the bound from Theorem 2:

$$\begin{aligned} \langle \Phi , {\mathcal {N}}_+ \Phi \rangle \le CN^{-3/2}, \quad \text {with}\quad \Phi = U_S U_B U_N \Psi _N. \end{aligned}$$

(72)

Also, from Lemmas 3, 4 and 5 it follows that

$$\begin{aligned} \langle \Phi , ({\mathcal {N}}_+ +1)^4 \Phi \rangle \le C. \end{aligned}$$

(73)

Using the action of Bogoliubov’s transformation in (8) and the uniform bounds (10) we obtain

$$\begin{aligned}&\sum _{p \ne 0}|\langle U_N \Psi _N, a_p U_N \Psi _N \rangle |^2 = \sum _{p \ne 0} |\langle \Phi , U_S U_B a_p U_B^* U_S^* \Phi \rangle |^2 \nonumber \\&\quad = \sum _{p \ne 0} |\langle \Phi , U_S (\sigma _p a_p + \gamma _p a_{-p}^*) U_S^* \Phi \rangle |^2 \le C \sum _{p \ne 0} |\langle \Phi , U_S a_p U_S^* \Phi \rangle |^2. \end{aligned}$$

(74)

To estimate further the right side of (74), we use the Duhamel formula

$$\begin{aligned} U_S a_p U_S^* = a_p + \int _0^1 e^{tS} [S,a_p] e^{-tS} {\mathrm{d}}t \end{aligned}$$

and the Cauchy–Schwarz inequality to get

$$\begin{aligned} \sum _{p \ne 0} |\langle \Phi , U_S a_p U_S^* \Phi \rangle |^2 \le 2 \sum _{p \ne 0} |\langle \Phi , a_p \Phi \rangle |^2 + 2 \sum _{p \ne 0} \int _0^1 |\langle \Phi , e^{tS} [S,a_p] e^{-tS} \Phi \rangle |^2 {\mathrm{d}}t . \end{aligned}$$

(75)

Thanks to (72) we can bound

$$\begin{aligned} \sum _{p \ne 0} |\langle \Phi , a_p \Phi \rangle |^2 \le \sum _{p \ne 0} \Vert a_p \Phi \Vert ^2 = \langle \Phi , {\mathcal {N}}_+ \Phi \rangle \le CN^{-3/2}. \end{aligned}$$

(76)

It remains to handle the term involving the commutator $[S,a_p]$ in (75). Using the CCR (3) and the identity $[a_p, {\mathbb {1}}^{\le N}] = -{\mathbb {1}}({\mathcal {N}}_+=N) a_p$ we can decompose

$$\begin{aligned}{}[a_p, S]&= \frac{1}{\sqrt{N}} \sum _{\begin{array}{c} m,n\ne 0\\ m+n \ne 0 \end{array}} \eta _{m,n} \Big [a_p,a_{m+n}^* a_{-m}^* a_{-n}^* {\mathbb {1}}^{\le N} - {\mathbb {1}}^{\le N} a_{m+n} a_{-m} a_{-n} \Big ] \nonumber \\&= \frac{1}{\sqrt{N}}\sum _{\begin{array}{c} m,n\ne 0\\ m+n \ne 0 \end{array}} \eta _{m,n} (\delta _{p,m+n} a_{-m}^* a_{-n}^* + \delta _{p,-m} a_{m+n}^* a_{-n}^* + \delta _{p,-n} a_{m+n}^* a_n^*) {\mathbb {1}}^{\le N} \nonumber \\&\quad - \frac{1}{\sqrt{N}}\sum _{\begin{array}{c} m,n\ne 0\\ m+n \ne 0 \end{array}} \eta _{m,n} a_{m+n}^* a_{-m}^* a_{-n}^* {\mathbb {1}}({\mathcal {N}}_+=N) a_p\nonumber \\&\quad + \frac{1}{\sqrt{N}}\sum _{\begin{array}{c} m,n\ne 0\\ m+n \ne 0 \end{array}} \eta _{m,n} {\mathbb {1}}({\mathcal {N}}_+=N) a_p a_{m+n} a_{-m} a_{-n} \nonumber \\&=: I_1(p) + I_2(p) + I_3(p). \end{aligned}$$

Hence, by the Cauchy–Schwarz inequality we have for all $t\in [0,1]$,

$$\begin{aligned} \sum _{p\ne 0} |\langle \Phi , e^{tS} [a_p,S] e^{-tS} \Phi \rangle |^2 \le 3\sum _{k=1}^3 \sum _{p\ne 0} |\langle \Phi , e^{tS} I_k(p) e^{-tS} \Phi \rangle |^2. \end{aligned}$$

(77)

The right side of (77) can be bounded using the Cauchy–Schwarz inequality, the summability (27), Lemmas 5, 6, (72) and (73). For the terms involving $I_1(p)$, we have

$$\begin{aligned}&\sum _{p\ne 0} |\langle \Phi , e^{tS} I_1(p) e^{-tS} \Phi \rangle |^2 \\&\quad \le \frac{C}{N} \Big ( \sum _{\begin{array}{c} m,n,p\ne 0\\ m+n \ne 0 \end{array}} |\eta _{m,n}|^2 \delta _{p,m+n} \Big ) \Big ( \sum _{\begin{array}{c} m,n\ne 0\\ m+n \ne 0 \end{array}} \Vert ({\mathcal {N}}_+ +3)^{-1/2} a_{-m} a_{-n} e^{-tS} \Phi \Vert ^2 \Big ) \\&\quad \qquad \Vert ({\mathcal {N}}_+ +3)^{1/2} {\mathbb {1}}^{\le N} e^{ -tS} \Phi \Vert ^2\\&\qquad + \frac{C}{N} \Big ( \sum _{\begin{array}{c} m,n,p\ne 0\\ m+n \ne 0 \end{array}} |\eta _{m,n}|^2 \delta _{p,-m} \Big ) \Big ( \sum _{\begin{array}{c} m,n\ne 0\\ m+n \ne 0 \end{array}} \Vert ({\mathcal {N}}_+ +3)^{-1/2} a_{m+n} a_{-n} e^{-tS} \Phi \Vert ^2 \Big ) \\&\quad \qquad \Vert ({\mathcal {N}}_+ +3)^{1/2} {\mathbb {1}}^{\le N} e^{ -tS} \Phi \Vert ^2 \\&\qquad + \frac{C}{N} \Big ( \sum _{\begin{array}{c} m,n,p\ne 0\\ m+n \ne 0 \end{array}} |\eta _{m,n}|^2 \delta _{p,-n} \Big ) \Big ( \sum _{\begin{array}{c} m,n\ne 0\\ m+n \ne 0 \end{array}} \Vert ({\mathcal {N}}_+ +3)^{-1/2} a_{m+n} a_{-m} e^{-tS} \Phi \Vert ^2 \Big ) \\&\quad \qquad \Vert ({\mathcal {N}}_+ +3)^{1/2} {\mathbb {1}}^{\le N} e^{ -tS} \Phi \Vert ^2\\&\quad \le \frac{C}{N} \Big \langle \Phi , e^{tS} {\mathcal {N}}_+ e^{-tS} \Phi \Big \rangle \Big \langle \Phi , e^{tS} ({\mathcal {N}}_+ +3) e^{ -tS} \Phi \Big \rangle \\&\quad \le \frac{C}{N} \left( \Big \langle \Phi , {\mathcal {N}}_+ \Phi \Big \rangle + \frac{1}{N} \Big \langle \Phi , ({\mathcal {N}}_+ +1)^2 \Phi \Big \rangle \right) \Big \langle \Phi , ({\mathcal {N}}_+ +3) \Phi \Big \rangle \le \frac{C}{N^2}. \end{aligned}$$

Similarly, the terms involving $I_2(p)$ are bounded by

$$\begin{aligned}&\sum _{p\ne 0} |\langle \Phi , e^{tS} I_2(p) e^{-tS} \Phi \rangle |^2 \nonumber \\&\quad \le \frac{C}{N} \Big ( \sum _{\begin{array}{c} m,n\ne 0\\ m+n \ne 0 \end{array}} |\eta _{m,n}|^2 \Big ) \Big ( \sum _{\begin{array}{c} m,n\ne 0\\ m+n \ne 0 \end{array}} \Vert {\mathbb {1}}({\mathcal {N}}_+=N) a_{m+n} a_{-m} a_{-n} e^{-tS} \Phi \Vert ^2 \Big ) \Big ( \sum _{p\ne 0} \Vert a_p e^{ -tS} \Phi \Vert ^2 \Big ) \nonumber \\&\quad \le \frac{C}{N} \Big \langle \Phi , e^{tS} {\mathcal {N}}_+^3 e^{-tS} \Phi \Big \rangle \Big \langle \Phi , e^{tS} {\mathcal {N}}_+ e^{ -tS} \Phi \Big \rangle \nonumber \\&\quad \le \frac{C}{N} \Big \langle \Phi , ({\mathcal {N}}_+ +1)^3 \Phi \Big \rangle \left( \Big \langle \Phi , {\mathcal {N}}_+ \Phi \Big \rangle +\frac{1}{N} \Big \langle \Phi , ({\mathcal {N}}_++1)^2 \Phi \Big \rangle \right) \le \frac{C}{N^{2}}. \end{aligned}$$

Finally for the terms involving $I_3(p)$, using

$$\begin{aligned} {\mathbb {1}}({\mathcal {N}}_+ = N) \le ({\mathcal {N}}_+/N)^4 \end{aligned}$$

we have

$$\begin{aligned}&\sum _{p\ne 0} |\langle \Phi , e^{tS} I_3(p) e^{-tS} \Phi \rangle |^2 \nonumber \\&\quad \le \frac{C}{N} \Big ( \sum _{\begin{array}{c} m,n\ne 0\\ m+n \ne 0 \end{array}} |\eta _{m,n}|^2 \Big ) \Vert {\mathbb {1}}({\mathcal {N}}_+=N) e^{ -tS} \Phi \Vert ^2 \Big ( \sum _{\begin{array}{c} m,n,p\ne 0\\ m+n \ne 0 \end{array}} \Vert a_{m+n} a_{-m} a_{-n} a_p e^{-tS} \Phi \Vert ^2 \Big ) \nonumber \\&\quad \le \frac{C}{N} \Big \langle \Phi , e^{tS} ({\mathcal {N}}_+/N)^4 e^{-tS} \Phi \Big \rangle \Big \langle \Phi , e^{tS} {\mathcal {N}}_+^4 e^{ -tS} \Phi \Big \rangle \nonumber \\&\quad \le \frac{C}{N^5} \Big \langle \Phi , ({\mathcal {N}}_+ +1)^4 \Phi \Big \rangle ^2 \le \frac{C}{N^{5}}. \end{aligned}$$

Thus we conclude from (77) that

$$\begin{aligned} \sum _{p\ne 0} |\langle \Phi , e^{tS} [S,a_p] e^{-tS} \Phi \rangle |^2 \le \frac{C}{N^2}, \quad \forall t\in [0,1]. \end{aligned}$$

(78)

Consequently,

$$\begin{aligned} \sum _{p\ne 0} \int _0^1 |\langle \Phi , e^{tS} [S,a_p] e^{-tS} \Phi \rangle |^2 {\mathrm{d}}t \le \frac{C}{N^2}. \end{aligned}$$

(79)

Inserting (79) and (76) in (75) and (74) we obtain

$$\begin{aligned} \sum _{p \ne 0}|\langle U_N \Psi _N, a_p U_N \Psi _N \rangle |^2 \le C \sum _{p \ne 0} |\langle \Phi , U_S a_p U_S^* \Phi \rangle |^2 \le CN^{-3/2}. \end{aligned}$$

Using the latter bound and (71), we deduce from (70) that

$$\begin{aligned} \Vert Q \gamma _{\Psi _N}^{(1)} u_0\Vert ^2 \le CN^{-1/2}. \end{aligned}$$

This implies (69) and completes the proof of Theorem 1. $\square$