Central Field Motion with Perturbing Acceleration Varying by the Inverse Square Law: Application to the Yarkovsky Effect

Abstract

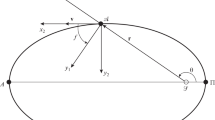
A mean-element differential equation system is solved analytically in the first approximation in a small parameter to investigate the orbital evolution of an asteroid moving under the attraction of the Sun and additional perturbing acceleration ${\mathbf{P}} = {\mathbf{P}}{\kern 1pt}' {\text{/}}{{r}^{2}}$, which arises due to the Yarkovsky effect. Here, $r$ is the heliocentric distance; the modulus of ${\mathbf{P}}{\kern 1pt} '$ is small in comparison with the main acceleration caused by the attraction of the Sun; the vector ${\mathbf{P}}{\kern 1pt} '$ components ($S,\;T,\;W$) are constant in a reference frame with the origin in the central body and axes directed along the radius vector, the transversal (perpendicular to the radius vector in the osculating plane in the direction of motion), and the binormal (directed along the area vector). The values of $S$, $T$, $W$, which are necessary for considering the Yarkovsky effect, can be found either as additional parameters when determining the orbit from observations or by using thermophysical models of the Yarkovsky acceleration. The first approach requires high-precision astrometry for a long period of time; the second one requires knowing the asteroid’s thermophysical characteristics and rotation parameters. In this paper, the semimajor axis drift is calculated for 23 asteroids with transversal acceleration determined by the first approach, taken from different publications. Comparative analysis shows good agreement with the results obtained in other works. Within the second approach, a linear thermophysical model for the Yarkovsky force for spherical asteroids and equations for the force components in a radius-vector-bound reference frame serves as a basis for determining nongravitational parameters for the asteroid 1685 Toro (1948 OA): ${{A}_{1}} = S{\text{/}}r_{0}^{2} = (7.96_{{ - 3.48}}^{{ + 2.72}}) \times {{10}^{{ - 15}}}$ AU/d², ${{A}_{2}} = T{\text{/}}r_{0}^{2} = ( - 3.24_{{ - 0.57}}^{{ + 0.42}}) \times {{10}^{{ - 15}}}$ AU/d², ${{A}_{3}} = W{\text{/}}r_{0}^{2} = 0$ (${{r}_{0}} =$ 1 AU). The next step for 1685 Toro is to find the eccentricity drift, semimajor axis drift, and mean anomaly drift and estimate the asteroid’s displacement from the nonperturbed position over 1000 revolutions around the Sun (1600 yr). Considering the uncertainties for the parameters ${{A}_{1}}$ and ${{A}_{2}}$, the advancement in the mean anomaly is $2.50'$ to $3.28'$, and the displacement is 143 000 to 188 000 km.

APPENDIX

1.1 PROBLEM OF MOTION OF THE ASTEROID 1685 TORO

Using thermal infrared radiation data from the WISE spacecraft, J. Ďurech et al. [20] studied the thermophysical characteristics of the asteroids 1685 Toro (1948 OA), 2100 Ra-Shalom (1978 RA), (3103) Eger, and 161989 Cacus (1978 CA) and estimated the secular changes in their rotation rate due to the YORP effect. Then, based on the available optical and radar astrometry, they drew a conclusion about a drift in the semimajor axis of their orbits due to the Yarkovsky effect.

The most complete data in [20] were obtained for 1685 Toro. For this object, we determined the nongravitational parameters ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$ using a linear thermophysical model of the Yarkovsky force for a spherical asteroid, which is described in detail in [2, 21, 22]. Here, we will only briefly formulate the technique of our calculations.

1.1.1 1. Yarkovsky Acceleration Model

Relying on [2], Xu et al. [19] derived components of the Yarkovsky acceleration (we designate it as ${\mathbf{P}}$) in a projection onto the axes of the system $\mathcal{O}$ [19, relations (12)]:

$$\begin{gathered} {{P}_{r}} = \frac{{4\alpha \Phi }}{{9(1 + \chi )}}\left\{ {{{E}_{{R_{s}^{'}}}}\sin({{\delta }_{{R_{s}^{'}}}} + \lambda )\sin\lambda {{\sin}^{2}}\gamma } \right. \\ \left. {\, + {{E}_{{R_{d}^{'}}}}\cos{{\delta }_{{R_{d}^{'}}}}[{{\cos}^{2}}\lambda + {{\sin}^{2}}\lambda {{\cos}^{2}}\gamma ]} \right\}, \\ \end{gathered} $$

$$\begin{gathered} {{P}_{t}} = \frac{{4\alpha \Phi }}{{9(1 + \chi )}}\left\{ {{{E}_{{R_{s}^{'}}}}\sin({{\delta }_{{R_{s}^{'}}}} + \lambda )\cos\lambda {{\sin}^{2}}\gamma } \right. \\ \left. { - \;{{E}_{{R_{d}^{'}}}}[\cos{{\delta }_{{R_{d}^{'}}}}\sin\lambda \cos\lambda {{\sin}^{2}}\gamma + \sin{{\delta }_{{R_{d}^{'}}}}\cos\gamma ]} \right\}, \\ \end{gathered} $$

(12)

$$\begin{gathered} {{P}_{n}} = \frac{{4\alpha \Phi }}{{9(1 + \chi )}}\left\{ {{{E}_{{R_{s}^{'}}}}\sin({{\delta }_{{R_{s}^{'}}}} + \lambda )\sin\gamma \cos\gamma - {{E}_{{R_{d}^{'}}}}} \right. \\ \times \;\left. {[\cos{{\delta }_{{R_{d}^{'}}}}\sin\lambda \sin\gamma \cos\gamma - \sin{{\delta }_{{R_{d}^{'}}}}\cos\lambda \sin\gamma ]} \right\}, \\ \end{gathered} $$

where the index $s$ refers to the seasonal Yarkosvsky effect, and $d$ refers to the diurnal effect. In (12), $\gamma$ is the obliquity of the asteroid’s spin axis with respect to a normal to its orbital plane; $\lambda = {{\omega }_{{{\text{rev}}}}}(t - {{t}_{0}})$ is the mean longitude; ${{\omega }_{{{\text{rev}}}}}$ is the mean motion; $t$ is time; ${{t}_{0}}$ is the initial time; $\alpha = 1 - A$ is the optical absorption coefficient; and $A$ is the Bond albedo

$$\Phi = \frac{{{{\mathcal{E}}_{ \star }}\pi {{R}^{2}}}}{{mc}},\quad \chi = \frac{{{{\Theta }_{s}}}}{{\sqrt 2 R_{s}^{'}}},$$

$${{\Theta }_{s}} = \frac{{\Gamma \sqrt {{{\omega }_{{{\text{rev}}}}}} }}{{\epsilon \sigma T_{ \star }^{3}}},\quad \Gamma = \sqrt {K\rho C} ,\quad {{T}_{ \star }} = \mathop {\left( {\frac{{\alpha {{\mathcal{E}}_{ \star }}}}{{\epsilon \sigma }}} \right)}\nolimits^{1/4} ,$$

$\Gamma$ is the surface thermal inertia; ${{T}_{ \star }}$ is the temperature at the subsolar point; ${{\mathcal{E}}_{ \star }} = {{L}_{ \odot }}{\text{/}}(4\pi {{a}^{2}})$ is the solar radiation flux at a heliocentric distance of $a$; ${{L}_{ \odot }} = 3.86 \times {{10}^{{26}}}$ W is the Sun’s luminosity; $c = 299{\kern 1pt} {\kern 1pt} 792{\kern 1pt} {\kern 1pt} 458$ m/s is the speed of light [23]; σ = $5.670374419 \times {{10}^{{ - 8}}}$ W m^–2 K^–4 is the Stefan–Boltzmann constant [24]; $m$, $R$, $\rho$, $\epsilon$, $K$, and $C$ are the asteroid’s mass, radius, bulk density, thermal emissivity, thermal conductivity, and specific heat capacity, respectively. Then,

$$R_{s}^{'} = \frac{R}{{{{l}_{s}}}},\quad {{l}_{s}} = \frac{\Gamma }{{\rho C\sqrt {{{\omega }_{{{\text{rev}}}}}} }},$$

$${{\omega }_{{{\text{rev}}}}} = \frac{{2\pi }}{{{{P}_{{{\text{rev}}}}}}},\quad R_{d}^{'} = \frac{R}{{{{l}_{d}}}},$$

$${{l}_{d}} = {{l}_{s}}\sqrt {\frac{{{{\omega }_{{{\text{rev}}}}}}}{{{{\omega }_{{{\text{rot}}}}}}}} ,\quad {{\omega }_{{{\text{rot}}}}} = \frac{{2\pi }}{{{{P}_{{{\text{rot}}}}}}},$$

where ${{P}_{{{\text{rev}}}}}$ is the asteroid’s revolution period around the Sun; ${{P}_{{{\text{rot}}}}}$ is its axial rotation period. Moreover, in (12), the amplitude ${{E}_{{R{\kern 1pt} '}}} = E(\sqrt 2 R{\kern 1pt} ')$ and phase ${{\delta }_{{R{\kern 1pt} '}}} = \delta (\sqrt 2 R{\kern 1pt} ')$ are determined, like in [2], from the relations

$${{E}_{{R{\kern 1pt} '}}}\exp(i{{\delta }_{{R{\kern 1pt} '}}}) = \frac{{A(x) + iB(x)}}{{C(x) + iD(x)}},$$

$${{E}_{{R{\kern 1pt} '}}}\exp( - i{{\delta }_{{R{\kern 1pt} '}}}) = \frac{{A(x) - iB(x)}}{{C(x) - iD(x)}},$$

where $i = \sqrt { - 1}$, $x = \sqrt 2 R{\kern 1pt} '$, and the auxiliary functi-ons are

$$\begin{gathered} A(x) = - (x + 2) - {{e}^{x}}[(x - 2)\cos x - x\sin x], \\ B(x) = - x - {{e}^{x}}[x\cos x + (x - 2)\sin x], \\ \end{gathered} $$

$$\begin{gathered} C(x) = A(x) + \frac{\chi }{{1 + \chi }}(3(x + 2) + {{e}^{x}}[3(x - 2)\cos x \\ \, + x(x - 3)\sin x]), \\ \end{gathered} $$

$$\begin{gathered} D(x) = B(x) + \frac{\chi }{{1 + \chi }}(x(x + 3) - {{e}^{x}}[x(x - 3)\cos x \\ \, - 3(x - 2)\sin x]). \\ \end{gathered} $$

Functions (12) are periodic with respect to $\lambda$; let us now find their average values over an orbital period, assuming that the spin axis orientation and the periods ${{P}_{{{\text{rev}}}}}$ and ${{P}_{{{\text{rot}}}}}$ do not change with time:

$$\overline {{{P}_{r}}} = \frac{{2\alpha \Phi }}{{9(1 + \chi )}}\left( {{{E}_{{R_{s}^{'}}}}\cos{{\delta }_{{R_{s}^{'}}}}{{\sin}^{2}}\gamma } \right.$$

$$\begin{gathered} \, + \left. {{{E}_{{R_{d}^{'}}}}\cos{{\delta }_{{R_{d}^{'}}}}(1 + {{\cos}^{2}}\gamma )} \right), \\ \overline {{{P}_{t}}} = \frac{{2\alpha \Phi }}{{9(1 + \chi )}}{\kern 1pt} \left( {{{E}_{{R_{s}^{'}}}}{\kern 1pt} \sin{{\delta }_{{R_{s}^{'}}}}{\kern 1pt} {{\sin}^{2}}\gamma - 2{{E}_{{R_{d}^{'}}}}{\kern 1pt} \sin{{\delta }_{{R_{d}^{'}}}}{\kern 1pt} \cos\gamma } \right){\kern 1pt} , \\ \end{gathered} $$

(13)

$$\overline {{{P}_{n}}} = 0.$$

In (13), the $\Phi$ coefficient is inversely proportional to the squared heliocentric distance. In order to obtain the parameters ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$, we need to calculate $\Phi$ for a distance of 1 AU [14]. Bearing this in mind and expressing $\cos{{\delta }_{{R'}}}$ and $\sin{{\delta }_{{R'}}}$ through exponential functions, we finally find the nongravitational parameters

$$\begin{gathered} {{A}_{1}} = \frac{{\alpha \Phi (1\;{\text{AU}})}}{{9(1 + \chi )}}\left\{ {[{{E}_{{R_{s}^{'}}}}\exp( - i{{\delta }_{{R_{s}^{'}}}}) + {{E}_{{R_{s}^{'}}}}\exp(i{{\delta }_{{R_{s}^{'}}}})]} \right. \\ \times \;{{\sin}^{2}}\gamma + [{{E}_{{R_{d}^{'}}}}\exp( - i{{\delta }_{{R_{d}^{'}}}}) + {{E}_{{R_{d}^{'}}}}\exp(i{{\delta }_{{R_{d}^{'}}}})] \\ \end{gathered} $$

$$\begin{gathered} \times \;\left. {\mathop {(1 + {{\cos}^{2}}\gamma )}\limits_{} } \right\}, \\ {{A}_{2}} = \frac{{\alpha \Phi (1\;{\text{AU}})}}{{9(1 + \chi )}}\left\{ {i{\kern 1pt} {\kern 1pt} \text{[}{{E}_{{R_{s}^{'}}}}\exp( - i{{\delta }_{{R_{s}^{'}}}}) - {{E}_{{R_{s}^{'}}}}\exp(i{{\delta }_{{R_{s}^{'}}}})]} \right. \\ \end{gathered} $$

(14)

$$\begin{gathered} \times \;{{\sin}^{2}}\gamma - 2i{\kern 1pt} {\kern 1pt} \text{[}{{E}_{{R_{d}^{'}}}}\exp( - i{{\delta }_{{R_{d}^{'}}}}) - \left. {{{E}_{{R_{d}^{'}}}}{\kern 1pt} \exp(i{{\delta }_{{R_{d}^{'}}}})]\cos\gamma } \right\}{\kern 1pt} , \\ {{A}_{3}} = 0. \\ \end{gathered} $$

Remark 1. Relations (12) are valid under the assumption that the asteroid’s orbital plane changes slowly and its spin period is much shorter than the revolution period [19].

Remark 2. The Yarkovsky effect causes a secular change in the mean motion of the asteroid and, therefore, in its period of revolution around the Sun. The YORP effect changes the rotation rate and period of an object around its axis. As a result, the values of the nongravitational parameters will slowly change over time, but in this paper, we consider them to be constant within the framework of the problem posed in the Introduction section.

1.1.2 2. Orbital Evolution of 1685 Toro

For the asteroid 1685 Toro, we now determine the semimajor axis drift over 1 Myr and the displacement of its Yarkovsky-force-perturbed position relative to the unperturbed one over $1000{{P}_{{{\text{rev}}}}}$ (1600 yrs).

Table 5 contains the initial data for Toro with reference to the publication sources. The Bond albedo was calculated by the formula $A = {{p}_{V}}(0.290 + 0.684G)$ [14, 26], where ${{p}_{V}}$ is the geometric albedo and $G$ is the slope parameter.

Table 5.   Orbital elements and thermophysical characteristics of the asteroid 1685 Toro with their uncertainties

Using (14), we found A₁ = $(7.96229_{{ - 3.48}}^{{ + 2.72}})$ × 10^‒15 AU/d² and ${{A}_{2}} = ( - 3.24047_{{ - 0.57}}^{{ + 0.42}}) \times {{10}^{{ - 15}}}$ AU/d² (for comparison, the JPL database [11] gives A₂ = $( - 3.099651371662129 \pm 0.6952) \times {{10}^{{ - 15}}}$ AU/d² and no value for ${{A}_{1}}$). The uncertainties of ${{A}_{1}}$ and ${{A}_{2}}$ were determined by varying thermophysical parameters within their errors.

Then, we used (5) to calculate the eccentricity drift and semimajor axis drift over 1 Myr. Table 6 presents our values and the semimajor axis drifts from [10, 12, 20]. The results are in good agreement.

Table 6.   Eccentricity drifts and semimajor axis drift for the orbit of the asteroid 1685 Toro over 1 Myr and, for comparison, the semimajor axis drifts $da{\text{/}}dt{\kern 1pt} '$ from different publications

The presence of perturbing acceleration also exerts a considerable influence on the mean anomaly. Using the last equation in (5), when over $1000{{P}_{{{\text{rev}}}}}$ (1600 yrs), the mean anomaly deviates from the unperturbed value by $2.50'$ to $3.28'$, considering the uncertainties in  ${{A}_{1}}$, ${{A}_{2}}$. As a result, the asteroid deviates from the   unperturbed position by a distance of 143 000 to     188 000 km. Over this period, de = $( - 1.578327374352_{{ - 0.21}}^{{ + 0.28}})$ × 10^–8 and da = $( - 2.32_{{ - 0.30}}^{{ + 0.41}})$ × 10^–7 AU.