Abstract
In this paper, we study the comparison of fuzzy differential transform method (FDTM), fuzzy Adomian decomposition method (FADM), fuzzy homotopy perturbation method (FHPM), and fuzzy reduced differential transform method (FRDTM) to obtain the solutions of fuzzy \((1 + n)\)-dimensional Burgers’ equation under gH-differentiability. We have investigated many new results to solve the above problem, and the methods have been implemented. The four illustrative numerical examples are presented to demonstrate the effectiveness of the proposed methods and also to demonstrate the efficiency and simplicity of the ways they were developed and derived. The results also show that the methods are powerful mathematical tools for solving fuzzy \((1 + n)\)-dimensional Burgers’ equation.
Similar content being viewed by others
1 Introduction
In 1978, the concept of fuzzy differential equations (FDEs) was originally introduced by Kandel and Byatt [52]. FDEs play an important role within several areas; see [21, 61, 63–66, 69]. First-order linear FDEs or systems according to various interpretations are searched for in many papers [20, 27]. There are only a few works like [56, 59] in which fuzzy, intuitive numbers are used in differential equations. Recently, several authors used numerical and analytical methods for solving fuzzy differential and integral equations; for example, see [3, 6, 18, 22, 24, 25, 35–37, 50, 60, 67, 71].
In the literature, the study of FDEs has several interpretations. First is based on the idea of the Hukuhara derivative [33, 75, 84]. Fractal theory is the theoretical basis for the fractal space-time [26, 47] El Naschieis E-infinity theory [31] and life science [85] also. Lately, various authors have presented the fractal calculus [2, 34, 48, 49].
In 1986, the notion of differential transform method (DTM) was introduced for the first time by Zhou in [89], this method adopts an analytical solution in the form of a polynomial, which is different from the traditional higher-order Taylor formula method. Recently, several researchers used DTM to solve FDEs; see [8, 32, 62, 70, 76].
Keskin and Oturanc in [54] proposed the concept of the reduced differential transform method (RDTM), defining a set of transformation rules to overcome the complicated complex calculations of traditional DTM. Recently, some authors used the method to solve many equations, for example, see [11, 23, 53, 73, 83, 88].
The Adomian decomposition method (ADM), which was primarily introduced by Adomian [1], is a semi-numerical technique for solving linear-nonlinear differential equations by generating a functional series solution in a very efficient manner. Several researchers have already used this method in their work; see [4, 5, 19, 30, 71, 74].
The classical perturbation methods have different limitations and are strongly invalid for nonlinear equations. To overcome the shortcomings, many new technologies have appeared in the open literature; see [10, 16, 40, 42–44, 57]. The homotopy perturbation method (HPM) is a new analytical method that was initially introduced by He [41, 45, 46] to solve linear-nonlinear differential equations. Applications of homotopy theory have recently appeared for different scientists, and the homotopy theory has become a powerful mathematical tool when it is successfully combined with perturbation theory; see [12, 51, 55, 68, 72, 77–79, 81, 82].
This paper is organized as follows. In Sect. 2, some basic definitions, remarks, and theorems that will be used are given. In Sect. 3, we present an analytical solution for the fuzzy \((1 + n)\)-dimensional Burgers’ equation under gH-differentiability by using FDTM, FADM, FHPM, and FRDTM. In Sect. 4, the applied fuzzy \((1 + n)\)-dimensional Burgers’ equation is developed, derived, and illustrated by four numerical examples. Finally, a conclusion is drawn in Sect. 5.
2 Preliminaries
In this section, there are various definitions for the concept of fuzzy numbers, fuzzy-valued functions, and fuzzy derivatives as follows.
Definition 2.1
([28])
Fuzzy numbers are a fuzzy set like \(\tilde{u}:R\rightarrow I=[0,1]\) which satisfies the requirements:
-
(a)
ũ is upper semicontinuous,
-
(b)
\(\tilde{u}(x)=0\) outside some interval [c,d],
-
(c)
there are real numbers \(a,b\) such that \(c\leq a\leq b\leq d\) and
-
\(\tilde{u}(x)\) is monotonic increasing on [c,a],
-
\(\tilde{u}(x)\) is monotonic decreasing on [b,d],
-
\(\tilde{u}(x)=1, a\leq x\leq b\).
-
Definition 2.2
([33])
Let \(\tilde{u}\in E^{1}\) and \([\tilde{u}]_{\alpha }=[\underline{u}_{\alpha },\overline{u}_{\alpha }]\). Then the following conditions are satisfied:
-
(1)
\(\underline{u}_{\alpha }\) is a bounded left continuous nondecreasing function on (0,1].
-
(2)
\(\overline{u}_{\alpha }\) is a bounded left continuous nonincreasing function on (0,1].
-
(3)
\(\underline{u}_{\alpha }\) and \(\overline{u}(\alpha )\) are right continuous at \(\alpha =0\).
-
(4)
\(\underline{u}_{1}\leq \overline{u}_{1}\).
Conversely, if the pair of functions \(a(\alpha )\) and \(b(\alpha )\) satisfy conditions (1)–(4), then there exists unique \(\tilde{u}_{\alpha }\in E^{1}\) such that \([\tilde{u}]_{\alpha }=[a(\alpha ),b(\alpha )] \) for each \(\alpha \in [0,1]\).
Define \(D:E^{1}\times E^{1}\rightarrow R_{+}\cup \{0\}\) by
where \([\tilde{u}]_{\alpha }=[\underline{u}_{\alpha },\overline{u}_{\alpha }]\), \([\tilde{v}]_{\alpha }=[\underline{v}_{\alpha },\overline{v}_{\alpha }]\). \(D(\tilde{u},\tilde{v})\) is called the distance between fuzzy numbers ũ and ṽ. Using the results in [29], we know that
-
(a)
\((E^{1}, D)\) is a complete metric space;
-
(b)
\(D(\tilde{u}+\tilde{w}, \tilde{v}+\tilde{w})=D(\tilde{u},\tilde{v})\);
-
(c)
\(D(k\cdot \tilde{u}, k\cdot \tilde{v})=|k|.D(\tilde{u},\tilde{v}), k \in R\), where \(\tilde{u},\tilde{v},\tilde{w}\in E^{1}\).
Definition 2.3
([15])
As discussed above, fuzzy numbers may be transformed into an interval through an α-level approach. So, for any arbitrary fuzzy number \(\tilde{x}=[\underline{x}(\alpha ), \overline{x}(\alpha )], \tilde{y}=[ \underline{y}(\alpha ), \overline{y}(\alpha )]\) and scalar k, we get the interval-based fuzzy arithmetic as follows:
-
(a)
\(\tilde{x}=\tilde{y}\) if and only if \(\underline{x}(\alpha )=\underline{y}(\alpha )\) and \(\overline{x}(\alpha )=\overline{y}(\alpha )\),
-
(b)
\(\tilde{x}\oplus \tilde{y}=[\underline{x}(\alpha )+\underline{y}( \alpha ), \overline{x}(\alpha )+\overline{y}(\alpha )]\),
-
(c)
\(\tilde{x} \otimes \tilde{y}=[\min (S), \max (S)]\), where \(S=\{\underline{x}(\alpha )\underline{y}(\alpha ), \underline{x}( \alpha ) \overline{y}(\alpha ), \overline{x}(\alpha ) \underline{y}( \alpha ), \overline{x}(\alpha ) \overline{y}(\alpha )\}\),
-
(d)
\(k\odot \tilde{x}= \bigl\{ \scriptsize{ \begin{array}{l@{\quad}l} {[k \overline{x}(\alpha ), k \underline{x}(\alpha )],} & {k<0}, \\ {[k \underline{x}(\alpha ), k \overline{x}(\alpha )],} & {k \geq 0}.\end{array}}\)
Remark 2.4
Let \(\tilde{x},\tilde{y}\) be fuzzy numbers, and \(\tilde{x}\geq 0\) (it means \(\underline{x}(r)\geq 0\) and \(\overline{x}(r)\geq 0\)). Then
Definition 2.5
For arbitrary fuzzy numbers \(\tilde{u},\tilde{v}\in E^{1}, \tilde{u}=[\underline{u}_{\alpha }, \overline{u}_{\alpha }], \tilde{v}=[\underline{v}_{\alpha }, \overline{v}_{\alpha }]\), the quantity \(D(\tilde{u},\tilde{v})=\sup_{\alpha \in [0,1]}\max \{|\underline{u}_{ \alpha }- \underline{v}_{\alpha }|, |\overline{u}_{\alpha }-\overline{v}_{ \alpha }|\}\) is the distance between ũ and ṽ, and also the following properties hold:
-
(a)
\((E^{1},D)\) is a complete metric space,
-
(b)
\(D(\tilde{u}\oplus \tilde{w},\tilde{v}\oplus \tilde{w})=D(\tilde{u}, \tilde{v}), \forall \tilde{u},\tilde{v},\tilde{w}\in E^{1}\),
-
(c)
\(D(\tilde{u}\oplus \tilde{v},\tilde{w}\oplus \tilde{e})\leq D( \tilde{u},\tilde{w})+D(\tilde{v},\tilde{e}),\forall \tilde{u}, \tilde{v},\tilde{w}, \tilde{e}\in E^{1}\),
-
(d)
\(D(\tilde{u}\oplus \tilde{v},\tilde{0})\leq D(\tilde{u},\tilde{0})+D( \tilde{v},\tilde{0}),\forall \tilde{u},\tilde{v}\in E^{1}\),
-
(e)
\(D(k\odot \tilde{u}, k\odot \tilde{v})=|k|D(\tilde{u},\tilde{v}), \forall \tilde{u},\tilde{v}\in E^{1},k\in R\),
-
(f)
\(D(k_{1}\odot \tilde{u}, k_{2}\odot \tilde{u})=|k_{1}-k_{2}|D( \tilde{u},\tilde{0}),\forall \tilde{u}\in E^{1},k_{1},k_{2}\in R\), with \(k_{1}\cdot k_{2}\geq 0\).
Recall the definition of Hukuhara difference in [14]. Let \(\tilde{u},\tilde{v}\in E^{1}\). The Hukuhara difference has been presented as a set w̃ for which \(\tilde{u}\ominus \tilde{v}=\tilde{w}\Leftrightarrow \tilde{u}= \tilde{v}\oplus \tilde{w}\). The H-difference is unique, but it does not always exist (a necessary condition for \(\tilde{u}\ominus \tilde{v}\) to exist is that ũ contains a translate \(\{c\}\oplus \tilde{v} \text{of} \tilde{v}\)).
Definition 2.6
The generalized Hukuhara difference of two fuzzy numbers \(\tilde{u},\tilde{v}\in E^{1}\) is defined as follows:
In terms of the α-levels, we get \([\tilde{u}\ominus _{gH}\tilde{v}]=[\min \{\underline{u}_{\alpha }- \underline{v}_{\alpha },\overline{u}_{\alpha }-\overline{v}_{\alpha }\}, \max \{\underline{u}_{\alpha } -\underline{v}_{\alpha },\overline{u}_{ \alpha }-\overline{v}_{\alpha }\}]\), and if the H-difference exists, then \(\tilde{u}\ominus \tilde{v}=\tilde{u}\ominus _{gH}\tilde{v}\); the conditions for existence of \(\tilde{w}=\tilde{u}\ominus _{gH}\tilde{v}\in E^{1}\) are:
It is easy to show that (i) and (ii) are both valid if and only if w̃ is a crisp number.
Definition 2.7
([13])
Let \(\tilde{u}(x,t): D\rightarrow E^{1}\) and \((x_{0},t)\in D\). We say that ũ is strongly generalized Hukuhara differentiable on \((x_{0},t)\) (gH-differentiable for short) if there exists an element \(\frac{\partial \tilde{u}}{\partial x}|_{(x_{0},t)}\in E^{1}\) such that
-
(i)
for all \(h>0\) sufficiently small, \(\exists \tilde{u}(x_{0}+h,t)\ominus _{gH} \tilde{u}(x_{0},t), \tilde{u}(x_{0},t) \ominus _{gH} \tilde{u}(x_{0}-h,t)\) and the limits (in the metric D)
$$ \lim_{h\rightarrow 0+} \frac{\tilde{u}(x_{0}+h,t)\ominus _{gH} \tilde{u}(x_{0},t)}{h}=\lim_{h \rightarrow 0+}= \frac{ \tilde{u}(x_{0},t) \ominus _{gH} \tilde{u}(x_{0}-h,t)}{h}= \frac{\partial \tilde{u}}{\partial x}_{{gH}}\bigg|_{(x_{0},t)}, $$or
-
(ii)
for all \(h>0\) sufficiently small, \(\exists \tilde{u}(x_{0},t) \ominus _{gH} \tilde{u}(x_{0}+h,t), \tilde{u}(x_{0}-h,t)\ominus _{gH} \tilde{u}(x_{0},t)\) and the limits
$$ \lim_{h\rightarrow 0+} \frac{\tilde{u}(x_{0},t)\ominus _{gH} \tilde{u}(x_{0}+h,t)}{-h} = \lim_{h\rightarrow 0+} \frac{\tilde{u}(x_{0}-h,t)\ominus _{gH} \tilde{u}(x_{0},t)}{-h}= \frac{\partial \tilde{u}}{\partial x}_{gH}\bigg|_{(x_{0},t)}, $$or
-
(iii)
for all \(h>0\) sufficiently small, \(\exists \tilde{u}(x_{0}+h,t)\ominus _{gH} \tilde{u}(x_{0},t), \tilde{u}(x_{0}-h,t)\ominus _{gH} \tilde{u}(x_{0},t)\) and the limits
$$ \lim_{h\rightarrow 0+} \frac{\tilde{u}(x_{0}+h,t)\ominus _{gH} \tilde{u}(x_{0},t)}{h}=\lim_{h \rightarrow 0+} \frac{\tilde{u}(x_{0}-h,t)\ominus _{gH} \tilde{u}(x_{0},t)}{-h}= \frac{\partial \tilde{u}}{\partial x}_{gH}\bigg|_{(x_{0},t)}, $$or
-
(iv)
for all \(h>0\) sufficiently small, \(\exists \tilde{u}(x_{0},t) \ominus _{gH} \tilde{u}(x_{0}+h,t), \tilde{u}(x_{0},t) \ominus _{gH} \tilde{u}(x_{0}-h,t)\) and the limits
$$ \lim_{h\rightarrow 0+} \frac{\tilde{u}(x_{0},t)\ominus _{gH} \tilde{u}(x_{0}+h,t)}{-h}=\lim_{h \rightarrow 0+} \frac{ \tilde{u}(x_{0},t) \ominus _{gH} \tilde{u}(x_{0}-h,t)}{h}= \frac{\partial \tilde{u}}{\partial x}_{gH}\bigg|_{(x_{0},t)}. $$
Definition 2.8
([36])
Let \(\tilde{u}(x,t): D\rightarrow E^{1}\) and \((x_{0},t)\in D\). We define the nth-order derivative of ũ as follows: we say that ũ is strongly generalized Hukuhara differentiable of the nth-order at \((x_{0},t)\) (gH-differentiable for short) if there exist elements \(\frac{\partial ^{s} \tilde{u}}{\partial x^{s}}|_{(x_{0},t)}\in E^{1}\), \(\forall s=1,2,\ldots,n\),
-
(i)
for all \(h>0\) sufficiently small, \(\exists \tilde{u}^{(s-1)}(x_{0}+h,t)\ominus _{gH} \tilde{u}^{(s-1)}(x_{0},t), \tilde{u}^{(s-1)}(x_{0},t) \ominus _{gH} \tilde{u}^{(s-1)}(x_{0}-h,t)\) and the limits (in the metric D)
$$\begin{aligned} &\lim_{h\rightarrow 0+} \frac{\tilde{u}^{(s-1)}(x_{0}+h,t)\ominus _{gH} \tilde{u}^{(s-1)}(x_{0},t)}{h}\\ &\quad = \lim_{h\rightarrow 0+}= \frac{\tilde{u}^{(s-1)}(x_{0},t) \ominus _{gH} \tilde{u}^{(s-1)}(x_{0}-h,t)}{h}= \frac{\partial ^{s} \tilde{u}}{\partial x^{s}}_{gH}\bigg|_{(x_{0},t)}, \end{aligned}$$or
-
(ii)
for all \(h>0\) sufficiently small, \(\exists \tilde{u}^{(s-1)}(x_{0},t) \ominus _{gH} \tilde{u}^{(s-1)}(x_{0}+h,t), \tilde{u}^{(s-1)}(x_{0}-h,t)\ominus _{gH} \tilde{u}^{(s-1)}(x_{0},t)\) and the limits
$$\begin{aligned} &\lim_{h\rightarrow 0+} \frac{\tilde{u}^{(s-1)}(x_{0},t)\ominus _{gH} \tilde{u}^{(s-1)}(x_{0}+h,t)}{-h} \\ &\quad =\lim_{h\rightarrow 0+} \frac{\tilde{u}^{(s-1)}(x_{0}-h,t)\ominus _{gH} \tilde{u}^{(s-1)}(x_{0},t)}{-h}= \frac{\partial ^{s} \tilde{u}}{\partial x^{s}}_{gH}\bigg|_{(x_{0},t)}, \end{aligned}$$or
-
(iii)
for all \(h>0\) sufficiently small, \(\exists \tilde{u}^{(s-1)}(x_{0}+h,t)\ominus _{gH} \tilde{u}^{(s-1)}(x_{0},t), \tilde{u}^{(s-1)}(x_{0}-h,t)\ominus _{gH} \tilde{u}^{(s-1)}(x_{0},t)\) and the limits
$$\begin{aligned} &\lim_{h\rightarrow 0+} \frac{\tilde{u}^{(s-1)}(x_{0}+h,t)\ominus _{gH} \tilde{u}^{(s-1)}(x_{0},t)}{h}\\ &\quad = \lim_{h\rightarrow 0+} \frac{\tilde{u}^{(s-1)}(x_{0}-h,t)\ominus _{gH} \tilde{u}^{(s-1)}(x_{0},t)}{-h}= \frac{\partial ^{s} \tilde{u}}{\partial x^{s}}_{gH}\bigg|_{(x_{0},t)}, \end{aligned}$$or
-
(iv)
for all \(h>0\) sufficiently small, \(\exists \tilde{u}^{(s-1)}(x_{0},t) \ominus _{gH} \tilde{u}^{(s-1)}(x_{0}+h,t), \tilde{u}^{(s-1)}(x_{0},t) \ominus _{gH} \tilde{u}^{(s-1)}(x_{0}-h,t)\) and the limits
$$\begin{aligned} &\lim_{h\rightarrow 0+} \frac{\tilde{u}^{(s-1)}(x_{0},t)\ominus _{gH} \tilde{u}^{(s-1)}(x_{0}+h,t)}{-h}\\ &\quad= \lim_{h\rightarrow 0+} \frac{ \tilde{u}^{(s-1)}(x_{0},t) \ominus _{gH} \tilde{u}^{(s-1)}(x_{0}-h,t)}{h}= \frac{\partial ^{s} \tilde{u}}{\partial x^{s}}_{gH}\bigg|_{(x_{0},t)}. \end{aligned}$$
Definition 2.9
([8])
Let \(\tilde{u}(x,t): D \rightarrow E^{1}\) be a function and set \(\tilde{u}(x,t)=((\underline{u}(x,t)(\alpha ), \overline{u}(x,t)( \alpha ))\) for each \(\alpha \in [0, 1]\). Then
(1) If ũ is gH-differentiable in the first form (i), then \((\underline{u}(x,t)(\alpha )\) and \(\overline{u}(x,t)(\alpha )\) are differentiable functions and
(2) If ũ is gH-differentiable in the second form (ii), then \((\overline{u}(x,t)(\alpha )\) and \(\underline{u}(x,t)(\alpha )\) are differentiable functions and
Assumption 2.10
We only discuss the case of \(\tilde{u}\geq 0\) satisfying \(\frac{\partial \tilde{u}}{\partial t} \ge 0\). In order to simplify our results presentation, we only consider the following case:
Definition 2.11
A fuzzy-number-valued function \(\tilde{f}:[a, b] \rightarrow E^{1}\) is said to be continuous at \(t_{0} \in [a, b]\) if, for each , there is \(\delta >0\) such that whenever \(\vert t-t_{0} \vert <\delta \). If f̃ is continuous for each \(t \in [a, b]\), then we say that f̃ is fuzzy continuous on \([a, b] \).
Definition 2.12
([9])
A fuzzy-valued function \(\tilde{f}:[a, b] \rightarrow E^{1}\) is said to bounded iff there is \(M \geq 0\) such that \(D(\tilde{f}(t), 0)=\|\tilde{f}(u)\| \leq M\) for all \(t \in [a, b] \). Equivalently we get \(\chi _{-M} \leq \tilde{f}(x) \leq \chi _{M}, \forall x \in [a, b]\).
Definition 2.13
([7])
A fuzzy-valued function f̃ of two variables is a rule that assigns to each ordered pair of real numbers \((x,t)\) in a set D a unique fuzzy number denoted by \(\tilde{f}(x,t)\). The set D is the domain of f̃, and its range is the set of values taken by f̃, i.e., \(\{\tilde{f}(x,t)|(x,t)\in D\}\).
The parametric representation of the fuzzy-valued function \(\tilde{f}:D\rightarrow E^{1}\) is expressed by \(\tilde{f}(x,t;\alpha )=[\underline{f}(x,t;\alpha ),\overline{f}(x,t; \alpha )]\) for all \((x,t)\in D\) and \(\alpha \in [0,1]\).
Definition 2.14
([80])
A fuzzy-valued function \(\tilde{f}:[a,b]\rightarrow E^{1}\) is said to satisfy the condition (gH) on \([a,b]\) if, for any \(x_{1}< x_{2}\in [a,b]\), there exists \(\tilde{u}\in E^{1}\) such that \(\tilde{f}(x_{2})=\tilde{f}(x_{1})+\tilde{u}\). We call ũ the gH-difference of \(\tilde{f}(x_{2})\) and \(\tilde{f}(x_{1})\), denoted by \(\tilde{f}(x_{2}) \ominus _{gH}\tilde{f}(x_{1})\).
3 Fuzzy \((1 + n)\)-dimensional Burgers’ equation
In this section, we analyze fuzzy \((1 + n)\)-dimensional Burgers’ equation under gH-differentiability by using some methods. Let us take the following fuzzy \((1 + n)\)-dimensional Burgers equation:
with the initial condition
where \(\alpha ^{\ast }_{i}\), \(i= 1,2,3,4,\ldots,n\), and β are positive constants.
Example 3.1
We consider the following shows that \(\tilde{u}^{2}\) does not always satisfy \(\tilde{u}^{2}\geq \tilde{0}\).
and \(\underline{u}(\alpha )=\alpha -1, \overline{u}(\alpha )=2-2\alpha \) for any \(\alpha \in [0,1]\). Then
\(\underline{[\tilde{u}^{2}]}(\alpha )\leq 0\) for any \(\alpha \in [0,1]\).
3.1 Fuzzy differential transform method
Assume that D denotes a fuzzy DTM operator with \(D^{-1}\) the inverse fuzzy DTM operator.
Definition 3.1
([82])
If \(\tilde{u}(X_{m}, t; \alpha )= [\underline{u}(X_{m}, t; \alpha ), \overline{u}(X_{m}, t; \alpha ) ]\) is analytic in the domain Ψ, then its fuzzy \((n + 1)\)-dimensional DTM can be obtained as follows:
and
where \(\sum^{\infty }_{J_{i}=0} = \sum^{\infty }_{j_{1}=0}\sum^{\infty }_{j_{2}=0} \cdots \sum^{\infty }_{j_{n}=0}, X_{m} = x_{1},x_{2},\ldots,x_{n}\), for \(J_{m} = j_{1},j_{2},\ldots,j_{n}\), then
and
Definition 3.2
([82])
If \(\tilde{u}(X_{m}, t;\alpha ) = D^{-1} [\underline{U}(J_{m}, j_{m+1}; \alpha ), \overline{U}(J_{m}, j_{m+1};\alpha ) ]\), \(\tilde{v}( X_{m}, t;\alpha ) = D^{-1} [\underline{V}(J_{m}, j_{m+1}; \alpha ), \overline{V}(J_{m}, j_{m+1};\alpha ) ]\), and ⊗ denotes convolution, then the basic operations of a fuzzy \((n + 1)\)-dimensional DTM are represented as follows:
-
1.
$$\begin{aligned} &D \bigl[\underline{u}(X_{m}, t; \alpha ) \underline{v}(X_{m}, t; \alpha ) \bigr] \\ &\quad =\underline{U} (J_{m}, j_{m+1};\alpha ) \otimes \underline{V}(J_{m}, j_{m+1};\alpha ) \\ &\quad =\sum_{A_{m}=0}^{J_{m}} \sum _{a_{n+1}=0}^{j_{n+1}} \underline{U}(J_{m}-A_{m}, j_{m+1}-a_{m+1};\alpha ) \underline{V} (A_{m}, a_{m+1};\alpha ), \end{aligned}$$(14)
and
$$\begin{aligned} &D \bigl[\overline{u}(X_{m}, t; \alpha ) \overline{v}(X_{m}, t;\alpha ) \bigr] \\ &\quad =\overline{U} (J_{m}, j_{m+1};\alpha ) \otimes \overline{V}(J_{m}, j_{m+1};\alpha ) \\ &\quad=\sum_{A_{m}=0}^{J_{m}} \sum _{a_{n+1}=0}^{j_{n+1}} \overline{U}(J_{m}-A_{m}, j_{m+1}-a_{m+1};\alpha ) \overline{V} (A_{m}, a_{m+1};\alpha ), \end{aligned}$$(15)where \(A_{m} = a_{1},a_{2},a_{3},\ldots, a_{n}\).
-
2.
$$\begin{aligned} &D\bigl[\alpha ^{\ast } \underline{u}(X_{m}, t;\alpha ) \pm \beta \underline{v}(X_{m}, t;\alpha )\bigr] =\alpha ^{\ast } \underline{U}(J_{m}, j_{n+1};\alpha ) \pm \beta \underline{V}(J_{m}, j_{n+1}; \alpha ), \\ &D\bigl[\alpha ^{\ast } \overline{u}(X_{m}, t;\alpha ) \pm \beta \overline{v}(X_{m}, t;\alpha )\bigr] =\alpha ^{\ast } \overline{U}(J_{m}, j_{n+1} ;\alpha ) \pm \beta \overline{V}(J_{m}, j_{n+1}; \alpha ). \end{aligned}$$
-
3.
$$\begin{aligned} &D \biggl[ \frac{\partial ^{R_{m}+r_{m+1}}}{\partial X_{m}^{R_{m}} \partial t^{r_{n+1}}} \underline{u}(X_{m}, t; \alpha ) \biggr] \\ &\quad= (j_{1}+1 ) (j_{1}+2 ) \cdots (j_{1}+r_{1} ) (j_{2}+1 ) \\ &\qquad{} \times (j_{2}+2 ) \cdots (j_{2}+r_{2} ) \cdots (j_{m+1}+1 ) (j_{m+1}+2 ) \cdots (j_{m+1}+r_{m+1} ) \\ & \qquad{} \times \underline{U} (j_{1}+r_{1}, j_{2}+r_{2}, \ldots, j_{m+1}+r_{m+1} ) ( \alpha ), \end{aligned}$$
and
$$\begin{aligned} &D \biggl[ \frac{\partial ^{R_{m}+r_{m+1}}}{\partial X_{m}^{R_{m}} \partial t^{r_{n+1}}} \overline{u}(X_{m}, t;\alpha ) \biggr] \\ &\quad = (j_{1}+1 ) (j_{1}+2 ) \cdots (j_{1}+r_{1} ) (j_{2}+1 ) \\ & \qquad{} \times (j_{2}+2 ) \cdots (j_{2}+r_{2} ) \cdots (j_{m+1}+1 ) (j_{m+1}+2 ) \cdots (j_{m+1}+r_{m+1} ) \\ & \qquad{} \times \overline{U} (j_{1}+r_{1}, j_{2}+r_{2}, \ldots, j_{m+1}+r_{m+1} ) ( \alpha ), \end{aligned}$$
where \(R_{m} = r_{1},r_{2},\ldots, r_{n}\).
3.2 Fuzzy Adomian decomposition method
We propose the fuzzy linear operators with these inverse operators
Taking these notations, equation (7) becomes
Apply the inverse operators \(\mathcal{L}_{t}^{-1}\) to (16) and (17) with initial condition (8) as follows:
where \(X_{m} = x_{1},x_{2},x_{3},\ldots, x_{n}\) for \(\alpha \in [0,1]\).
A fuzzy ADM consists of demonstrating a solution
using a fuzzy decomposition series as follows:
Fuzzy nonlinear term
where
appeared to use a series of the fuzzy Adomian polynomials as
Component
the solution \(\tilde{u} (X_{m}, t; \alpha )\) is specified in an iterative manner. Substituting the fuzzy decomposition string (20) – (25) for \(\tilde{u} (X_{m}, t; \alpha ) \) in equations (18) and (19), we get
and
Applying the fuzzy ADM to the zeroth component
the surviving components of \(\tilde{u}(X_{m}, t; \alpha ) = [\underline{u}(X_{m}, t; \alpha ), \overline{u}(X_{m}, t; \alpha )]\) are specified in such a frequent way that
and
The fuzzy Adomian polynomials for a fuzzy nonlinear term \(\tilde{u}\odot \frac{\partial \tilde{u}}{\partial x_{1}}=[\min {(S)}, \max {(S)}]\), where \(S= \{ \underline{u}(\alpha ) \frac{\partial \underline{u}(\alpha )}{\partial x_{1}}, \underline{u}( \alpha ) \frac{\partial \overline{u}(\alpha )}{\partial x_{1}}, \overline{u}(\alpha ) \frac{\partial \underline{u}(\alpha )}{\partial x_{1}}, \overline{u}( \alpha ) \frac{\partial \overline{u}(\alpha )}{\partial x_{1}} \} \) is derived from the recursive formula as follows:
The fuzzy Adomian polynomials are defined as follows:
and
Applying (29) and (31) for fuzzy Adomian polynomials \(\tilde{A}_{j}(\alpha )=[\underline{A}_{j}(\alpha ), \overline{A}_{j}( \alpha )]\), we obtain
and
The qth term, \(\tilde{u}_{q}(\alpha )= [\underline{u}_{q}(\alpha ), \overline{u}_{q}(\alpha ) ]\) can be specified from
3.2.1 Convergence analysis of fuzzy ADM
According to [38, 39, 58], we present the convergence analysis of fuzzy ADM for the general fuzzy operator equation given by
where \(\tilde{g}(x,t;\alpha )\) is given in \(\mathcal{H}^{\prime }\). Suppose that \(\mathcal{T}\) is an operator defined by \(\mathcal{T}\tilde{u}(x,t;\alpha ) = -\mathcal{R}\tilde{u}(x,t; \alpha ) -\mathcal{N}\tilde{u}(x,t;\alpha )\).
We consider the Hilbert space \(\mathcal{H} = \mathcal{L}^{2} ((\alpha ^{*},\beta ^{*})\times [0, \mathcal{T}] )\) defined by the set of applications as follows:
with
where \(\tilde{u}(x,t;\alpha ) = [\underline{u}(x,t;\alpha ), \overline{u}(x,t;\alpha ) ]\).
Theorem 3.3
Assume that \(\mathcal{T}\tilde{u}(x,t;\alpha ) = -\mathcal{R}\tilde{u}(x,t; \alpha ) -\mathcal{N}\tilde{u}(x,t;\alpha )\) is semi-continuous (i.e., the restriction of \((-\mathcal{R}-\mathcal{N})\)) to the segments of \(\mathcal{H}\) is continuous, in \(\mathcal{H}^{\prime }\) weak) and satisfies the hypotheses \(\mathcal{H}_{1}, \mathcal{H}_{2}\) as follows:
-
\([\mathcal{H}_{1}]: (\mathcal{T}\tilde{u}(x,t;\alpha )- \mathcal{T}\tilde{v}(x,t;\alpha ), \tilde{u}(x,t;\alpha )- \tilde{v}(x,t; \alpha ) )\geq K\|\tilde{u}(x,t;\alpha )- \tilde{v}(x,t;\alpha ) \|^{2}, \kappa >0, \forall \tilde{u},\tilde{v}\in \mathcal{H}\).
-
\([\mathcal{H}_{2}]: \forall M>0, \exists D(M)>0 \textit{such that, for} \|\tilde{u}\|\leq M, \|\tilde{v}\|\leq M, \tilde{u},\tilde{v}\in \mathcal{H}, \textit{we obtain}\) \(\Rightarrow (\mathcal{T}\tilde{u}(x,t;\alpha )- \tilde{v}(x,t; \alpha ),w(x,t;\alpha ) )\leq D(M)\|\tilde{u}(x,t;\alpha )- \tilde{v}(x,t;\alpha )\|\|\tilde{w}(x,t;\alpha )\|,\forall \tilde{w} \in \mathcal{H}\).
For every \(\tilde{g}(x,t;\alpha ) \in \mathcal{H}^{\prime }\), the fuzzy nonlinear functional equation (46) admits a unique solution \(\tilde{u}(x,t;\alpha ) \in \mathcal{H}\). Furthermore, if the solution \(\tilde{u}(x,t;\alpha )\) can be assimilated as a series \(\tilde{u}(x,t;\alpha ) = \sum^{\infty }_{n=0}\tilde{u}_{n}(x,t; \alpha )\lambda ^{n} \nonumber \), then the fuzzy ADM diagram corresponding to the functional equation under study converges strongly to \(\tilde{u} (x, t; \alpha ) \in \mathcal{H}\), which is the unique solution to the functional equation.
Proof
The operator \(\mathcal{A}\) defined by \(\mathcal{A}\tilde{u}(x,t;\alpha ) = -\mathcal{L}\tilde{u}(x,t; \alpha )-\mathcal{T}\tilde{u}(x,t;\alpha )\), where \(\tilde{u}(x,t;\alpha )\in \mathcal{H}\), satisfies the conditions:
\((\mathcal{H}_{1})\)
According to \((\mathcal{H}_{1})\),
where
\((\mathcal{H}_{2})\)
According to Schwarz’s inequality and \((\mathcal{H}_{2})\), we obtain
and therefore
where
which completes the proof. □
3.3 Fuzzy homotopy perturbation method
We establish the general nonlinear fuzzy differential equation as follows:
where \(\tilde{f}(r;\alpha )=[\underline{f}(r;\alpha ),\overline{f}(r; \alpha )]\in E^{1}\), and we shall define:
-
\(\tilde{A}(\tilde{u})\) is a fuzzy differential operator, which means that \(\underline{A(\tilde{u})}\) and \(\overline{A(\tilde{u})}\) are differential operators,
-
\(\underline{\tilde{A}(\tilde{u})}(\alpha )=\underline{f}(r;\alpha )\) and \(\overline{\tilde{A}(\tilde{u})}(\alpha )=\overline{f}(r;\alpha )\) for any \(\alpha \in [0, 1]\),
with the boundary condition
where B is a boundary operator and ∂Ψ is boundary of the domain Ψ. The fuzzy operator à can be discordant into two parts \(\mathcal{L}\) and \(\mathcal{N}\), where \(\mathcal{L}\) is a fuzzy linear operator, while \(\mathcal{N}\) is a fuzzy nonlinear operator. From equation (50), we obtain
We construct a fuzzy homotopy applying a fuzzy homotopy technique as follows:
or
for \(p\in [0,1]\) is the included parameter, \(\tilde{u}_{0}(\alpha )=[\underline{u}_{0}(\alpha ),\overline{u}_{0}( \alpha )]\) is the initial approximation of equation (50) that satisfies the boundary conditions. Clearly, looking (54) and (55), we obtain
and
The process of changing p from zero to unit is that \(\tilde{v}(r,p;\alpha )=[\underline{v}(r,p;\alpha ),\overline{v}(r,p; \alpha )]\) from \(\tilde{u}_{0}(r;\alpha )=[\underline{u}_{0}(r;\alpha ),\overline{u}_{0}(r; \alpha )]\) to \(\tilde{u}(r;\alpha )=[\underline{u}(r;\alpha ),\overline{u}(r; \alpha )]\). In topology, this is called disfigurement, \(\mathcal{L}(\tilde{v})(\alpha )=[\mathcal{L}(\underline{v})(\alpha ), \mathcal{L}(\overline{v})(\alpha )]\) and \(\underline{A(v)}(\alpha )-\underline{f}(r;\alpha ), \overline{A(v)}(\alpha )-\overline{f}(r;\alpha )\) are called fuzzy homotopy. A fuzzy HPM uses the fuzzy homotopy parameter p as an extending parameter, we get
\(p\rightarrow 1\) produces the approximate solution of equation (50) as follows:
Comparison of p similar powers gives various order solutions. We know that series (60) and (61) represent convergence in most cases. Yet the convergence rate is dependent on the fuzzy nonlinear operator \(\mathcal{N}(\tilde{v})\). We will also look at the same opinions in [46] about \(\mathcal{N}(\tilde{v})\) in a fuzzy environment as follows:
-
A second fuzzy derivative of \(\mathcal{N}(\tilde{v})\) with respect to ṽ should be small as the parameter p may be relatively large.
-
A norm of \(\mathcal{L}^{-1}\frac{\partial \mathcal{N}}{\partial \tilde{v}}\) should be smaller than one so that the series converges.
Applying a fuzzy HPM to (7) and using a fuzzy HPM, we are building a fuzzy simple homotopy as follows:
where \(\frac{\partial ^{2}}{\partial X^{2}_{m}} = \frac{\partial ^{2}}{\partial x_{1}^{2}}, \frac{\partial ^{2}}{\partial x_{2}^{2}},\ldots, \frac{\partial ^{2}}{\partial x_{n}^{2}}\), \(X_{m} = x_{1},x_{2},\ldots, x_{n}\) for \(\vartheta _{m} = \vartheta _{1},\vartheta _{2},\ldots, \vartheta _{n}\).
Subject to
let the solution be as follows:
Taking (65) into (62) with the terms equating and powers comparable to p, we obtain
and
Using (66) into (71), we obtain the fuzzy-valued function \(\tilde{u}_{0},\tilde{u}_{1},\tilde{u}_{2},\tilde{u}_{3},\ldots, \tilde{u}_{n}\). Consequently, keeping (64) and (65) and allowing \(p=1\), we get the approximate solution of (7) as follows:
3.3.1 Convergence analysis of fuzzy HPM
According to [17], we can write equation (55) in the following forms:
where \(\alpha \in [0,1]\).
Applying the inverse operator \(\mathcal{L}^{-1}\) to both sides of (74) and (75), we get
Let
substituting (78) and (79) into the right-hand side of (76) and (77), we obtain
If \(p\rightarrow 1\), the exact solution may be obtained by
and
Theorem 3.4
Let \(\tilde{X}(\alpha ) = [\underline{X}(\alpha ), \overline{X}(\alpha )]\) and \(\tilde{Y}(\alpha ) = [\underline{Y}(\alpha ), \overline{Y}(\alpha )]\) be Banach spaces and \(N: \tilde{X}(\alpha )\rightarrow \tilde{Y}(\alpha )\) be a contractive nonlinear mapping, that is,
According to Banach’s fixed point theorem, \(\mathcal{N}\) has a unique fixed point \(\tilde{u}(\alpha ) = [\underline{u}(\alpha ),\overline{u}(\alpha )]\), that is, \(\mathcal{N}(\underline{u})(\alpha ) = (\underline{u})(\alpha )\) and \(\mathcal{N}(\overline{u})(\alpha ) = (\overline{u})(\alpha )\). Assume that the sequence generated by using fuzzy HPM can be written as follows:
assume that
where
then we obtain
-
(a)
\(\tilde{W}_{n}(x,t;\alpha ) \in B_{r}(\tilde{w}(x,t;\alpha ))\),
-
(b)
\(\lim_{n\rightarrow \infty } \tilde{W}_{n}(x,t;\alpha ) = \tilde{w}(x,t; \alpha )\).
Proof
(a) By inductive approach, for \(n = 1\), where \(\alpha \in [0,1]\), we obtain
Assume that
by induction hypothesis, then
Using (a), we get
(b). Because of
and
that is,
□
3.4 Fuzzy reduced differential transform method
We present a fuzzy-valued function \(\tilde{u}(X_{m}, t; \alpha ) = [\underline{u}(X_{m}, t; \alpha ), \overline{u}(X_{m}, t; \alpha ) ]\) of \((n+1)\)-variables and assume that it can be represented as a product of \((n+1)\) single-variable fuzzy-valued function
where
Based on the one-dimensional fuzzy DTM properties, a fuzzy-valued function \(\tilde{u}(X_{m}, t; \alpha )\) as
and
where \(\sum^{\infty }_{J_{m}=0} = \sum^{\infty }_{j_{1}=0}\sum^{\infty }_{j_{2}=0} \cdots \sum^{\infty }_{j_{n}=0}\) and
for
recalled spectrum \(\tilde{u}(X_{m}, t; \alpha )\).
Suppose that \(R_{D}, R_{D}^{-1}\) denote a fuzzy RDTM operator and an inverse operator, respectively.
Definition 3.5
([11])
If \(\tilde{u}(X_{m}, t; \alpha ) \) is continuously differentiable with respect to space with time in the domain of interest, then it is a fuzzy-valued function of the spectrum
A fuzzy reduced differential function of \(\tilde{u}(X_{m}, t; \alpha )\). The lowercase \(\tilde{u}(X_{m}, t; \alpha )\) assimilates the original fuzzy-valued function, while the uppercase \(\tilde{U}_{j}(X_{m}; \alpha )\) stands for the fuzzy RDTM fuzzy-valued function.
Note that the relation shown in (84) and (85) is the Poisson series form of the input term \(\tilde{u}(X_{m}, t; \alpha )\) with respect to the variables \(X_{m}, t\), to request N, using variable weights \(\tilde{U}_{j}(X_{m}; \alpha )\).
The fuzzy differential inverse reduced transform of
is given as follows:
Taking (87) into (84), we obtain
Definition 3.6
([11])
If \(\tilde{u}(X_{m}, t; \alpha ) = R_{D}^{-1}[\tilde{U}_{j}(X_{m}; \alpha )]\), \(\tilde{v}(X_{m}, t; \alpha ) = R_{D}^{-1}[\tilde{V}_{j}(X_{m}; \alpha )]\) and the convolution ⊗ denotes the fuzzy \((n + 1)\)-dimensional RDTM version of multiplication, then the basic operations of the fuzzy \((n + 1)\)-dimensional RDTM are:
-
1.
$$\begin{aligned} &R_{D} \bigl[\underline{u}(X_{m}, t; \alpha )\underline{v} (X_{m}, t; \alpha ) \bigr] \\ &\quad = \underline{U}_{j}(X_{m}; \alpha )\otimes \underline{V}_{j}(X_{m}; \alpha ) \\ &\quad =\sum^{j}_{r=0}\underline{U}_{j}(X_{m}; \alpha ) \underline{V}_{j-r}(X_{m}; \alpha ), \end{aligned}$$(90)$$\begin{aligned} &R_{D} \bigl[\overline{u}(X_{m}, t; \alpha ) \overline{v}(X_{m}; \alpha ) \bigr] \\ &\quad = \overline{U}_{j}(X_{m}, t; \alpha )\otimes \overline{V}_{j}(X_{m}; \alpha ) \\ & \quad=\sum^{j}_{r=0}\overline{U}_{j}(X_{m}; \alpha ) \overline{V}_{j-r}(X_{m}; \alpha ). \end{aligned}$$(91)
-
2.
$$\begin{aligned} &R_{D} \bigl[\alpha ^{*} \underline{u}(X_{m}, t; \alpha )\pm \beta \underline{v} (X_{m}, t; \alpha ) \bigr] \\ & \quad= \alpha ^{*} \underline{U}_{j}(X_{m}; \alpha )\pm \beta \underline{V}_{j}(X_{m}; \alpha ), \end{aligned}$$(92)$$\begin{aligned} &R_{D} \bigl[\alpha ^{*} \overline{u}(X_{m}; \alpha )\pm \beta \overline{v} (X_{m}, t; \alpha ) \bigr] \\ & \quad=\alpha ^{*} \overline{U}_{j}(X_{m}; \alpha ) \pm \beta \overline{V}_{j}(X_{m}; \alpha ). \end{aligned}$$(93)
-
3.
$$\begin{aligned} &R_{D} \biggl(\frac{\partial ^{r}}{\partial x_{i}^{r}}\underline{u}(X_{m}, t; \alpha ) \biggr) \\ &\quad = \frac{\partial ^{r}}{\partial x_{i}^{r}}\underline{U}_{j}(X_{m}; \alpha ),\quad i=1,2,3,\ldots,n; r = 1,2,3,4,\ldots \end{aligned}$$(94)$$\begin{aligned} &R_{D} \biggl(\frac{\partial ^{r}}{\partial x_{i}^{r}}\overline{u}(X_{m}, t; \alpha ) \biggr) \\ &\quad = \frac{\partial ^{r}}{\partial x_{i}^{r}}\overline{U}_{j}(X_{m}; \alpha ),\quad i=1,2,3,\ldots,n; r=1,2,3,4,\ldots \end{aligned}$$(95)
-
4.
$$\begin{aligned} R_{D} \biggl(\frac{\partial ^{r}}{\partial t^{r}}\underline{u}(X_{m}, t ; \alpha ) \biggr) &=(j+1) (j+2) (j+3)\cdots (j+r)\underline{U}_{j+r}(X_{m}; \alpha ) \\ &=\frac{(j+r)!}{j!}\underline{U}_{j+r}(X_{m}; \alpha ),\quad r=1,2,3,4,\ldots \end{aligned}$$(96)$$\begin{aligned} R_{D} \biggl(\frac{\partial ^{r}}{\partial t^{r}}\overline{u}(X_{m}, t ; \alpha ) \biggr)& =(j+1) (j+2) (j+3)\cdots (j+r)\overline{U}_{j+r}(X_{m}; \alpha ) \\ &=\frac{(j+r)!}{j!}\overline{U}_{j+r}(X_{m}; \alpha ),\quad r=1,2,3,4,\ldots \end{aligned}$$(97)
-
5.
$$\begin{aligned} &RD \biggl[ \frac{\partial ^{\mathcal{R}^{*}_{m}+r_{m+1}}}{\partial X_{m}^{\mathcal{R}^{*}_{m}} \partial t^{r_{m+1}}} \underline{u}(X_{m}, t;\alpha ) \biggr] \\ &\quad=\frac{(j+r_{m+1})!}{j!} \frac{\partial ^{\mathcal{R}^{*}_{m}+r_{m+1}}}{\partial X_{m}^{\mathcal{R}^{*}_{m}} } \underline{U}_{j+r_{m+1}}(X_{m}; \alpha ), \end{aligned}$$(98)$$\begin{aligned} &RD \biggl[ \frac{\partial ^{\mathcal{R}^{*}_{m}+r_{m+1}}}{\partial X_{m}^{R_{m}} \partial t^{r_{m+1}}} \underline{u}(X_{m}, t;\alpha ) \biggr] \\ &\quad =\frac{(j+r_{m+1})!}{j!} \frac{\partial ^{\mathcal{R}^{*}_{m}+r_{m+1}}}{\partial X_{m}^{\mathcal{R}^{*}_{m}} } \underline{U}_{j+r_{m+1}}(X_{m}; \alpha ). \end{aligned}$$(99)
-
6.
$$\begin{aligned} R_{D} \bigl(X^{a_{m}}_{m}t^{am} \bigr) &=X^{a_{m}}_{m} \delta (j_{m}-a_{m}) \\ &=\textstyle\begin{cases} X_{m}^{a_{m}}, & j_{m}=a_{m}, \\ 0 & \text{otherwise}, \end{cases}\displaystyle \end{aligned}$$(100)
where \(X_{m}^{a_{m}} = x^{a_{1}}_{1}x^{a_{2}}_{2}x^{a_{3}}_{3}\cdots x^{a_{n}}_{n}\), for \(\mathcal{R}^{*}_{m} = r_{1},r_{2},\ldots, r_{n}\).
4 Numerical examples
In this section, we applying some numerical techniques for solving the fuzzy \((1 + n)\)-dimensional Burgers’equation under gH-differentiability. In the ending, Four examples are provided.
Example 4.1
We consider the following fuzzy \((1 + 1)\)-dimensional Burgers’ equation:
with the initial condition
where \(\tilde{u} = \tilde{u}(x,t)\) is a fuzzy-valued function satisfying \(\tilde{u}(x,t)\geq \tilde{0}\). Above \(\tilde{k}^{n}\in E^{1}\), \(n= 1,2,3,\ldots\) , a fuzzy number is defined by
and \([\underline{\tilde{k}^{n}}](\alpha )=(0.2+0.2\alpha )^{n}, [ \overline{\tilde{k}^{n}}](\alpha )=(0.6-0.2\alpha )^{n}\).
The parametric form of (101) is
for \(\alpha \in [0,1]\), where \(\underline{u}\) stands for \(\underline{u}(x,t;\alpha )\), similar to u̅.
Case [A]. Fuzzy differential transform method:
Applying the FDTM to equations (104) and (105) yields
and
Using initial condition (102), we have
where
Taking (110) and (111) into equations (106) and (107), we have a fuzzy-valued function of
as follows:
and
The exact solution is given as follows:
Case [B]. Fuzzy Adomian decomposition method:
Applying (32) into (35), we obtain
and
Using the fuzzy decomposition series, we have
The exact solution is given in a closed form as follows:
Case [D]. Fuzzy homotopy perturbation method:
Applying the FHPM to equations (104) and (105), we get
Applying the fuzzy homotopy parameter to extend a solution, we have
Using \(p = 1\) in (120) and (121), we get
Using (121) into (118), with the terminology equating and powers similar to p, we obtain a series of fuzzy linear equations:
and
According to initial condition (102) and the solution of (124) and (127), we obtain
Substituting \(\underline{u}_{0}, \overline{u}_{0}\) from (130) and (131) in equations (125) and (128), we obtain the solution to (125) and (128) as follows:
From \(\underline{u}_{0}, \overline{u}_{0}\) and \(\underline{u}_{1}, \overline{u}_{1}\) in (126) and (129), we obtain the solution to (126) and (129) as follows:
Applying (122) and (123), the approximate solution of (104) and (105), we get
The exact solution can be obtained as follows:
Case [D]. Fuzzy reduced differential transform method:
Applying the fuzzy RDTM to equations (104) and (105), we get
Using initial condition (102), we obtain
Taking (140) into (137), we obtain \(\tilde{U}_{j}(\alpha ) = [\underline{U}_{j}(\alpha ),\overline{U}_{j}( \alpha )]\) fuzzy-valued function respectively:
According to the fuzzy differential inverse transformation, we have
The exact solution is obtained as follows:
Example 4.2
We consider the following fuzzy \((1+ 2)\)-dimensional Burgers’ equation:
subject to the initial condition
where \(\tilde{u} = \tilde{u}(x,y,t)\) is a fuzzy-valued function satisfying \(\tilde{u}(x,y,t)\geq \tilde{0}\). Above \(\tilde{k}^{n}\in E^{1}\), \(n= 1,2,3,\ldots\) , a fuzzy number is
and \([\underline{\tilde{k}^{n}}](\alpha )=(0.1+0.1\alpha )^{n}, [ \overline{\tilde{k}^{n}}](\alpha )=(0.3-0.1\alpha )^{n}\).
The parametric form of (144) is
for \(\alpha \in [0,1]\), where \(\underline{u}\) stands for \(\underline{u}(x, y, t)(\alpha )\), similar to u̅.
Case [A]. Fuzzy differential transform method
Applying the FDTM to (147) and (148), we obtain
and
Using initial condition (145), we get
where
From (154) into (149), we get a fuzzy-valued function
as follows:
and
The exact solution can be obtained as follows:
Case [B]. Fuzzy Adomian decomposition method
Applying equations (32) into (35), we obtain
and
Using the fuzzy decomposition series, we obtain
The exact solution is obtained as follows:
Case [C]. Fuzzy homotopy perturbation method
Applying the fuzzy HPM, we structure the simple homotopy as follows:
Let the solution have the following form:
According to \(p=1\) in equations (163) and (164), we get the approximate solution as follows:
Taking (163) and (164) into (161) and (162), and the terminology equating with powers similar to p, we get
and
Taking (145) and a solution of (167) and (170), we get
From the solution of (168) and (171), we have
We obtain the solution of (169) and (172) as follows:
and
Using (165) and (166), the approximate solution of (147) and (148), we obtain
The exact solution is obtained as follows:
Case [D]. Fuzzy reduced differential transform method
Applying the fuzzy RDTM to equations (147) and (148) yields
Using initial condition (145), we get
Taking (183) into (180), we get \(\tilde{U}_{0}(\alpha ) = [\underline{U}_{0}(\alpha ), \overline{U}_{0}( \alpha )]\) fuzzy-valued function, respectively:
Applying the differential inverse transformation, we have
The exact solution can be obtained as follows:
Example 4.3
We consider the following fuzzy \((1+ 3)\)-dimensional Burgers’ equation:
subject to the initial condition
where \(\tilde{u} = \tilde{u}(x,y,z,t)\) is a fuzzy-valued function satisfying \(\tilde{u}(x,y,z,t)\geq \tilde{0}\). Above \(\tilde{k}^{n}\in E^{1}\), \(n= 1,2,3,\ldots\) , a fuzzy number is defined by
and \([\underline{\tilde{k}^{n}}](\alpha )=(0.4+0.1\alpha )^{n}, [ \overline{\tilde{k}^{n}}](\alpha )=(0.6-0.1\alpha )^{n}\).
The parametric form of (187) is
for \(\alpha \in [0,1]\), where \(\underline{u}\) stands for \(\underline{u}(x, y, z, t)(\alpha )\), similar to u̅.
Case (A). Fuzzy differential transform method:
Applying the FDTM to equations (190) and (191), we get
and
Using initial condition (188), we obtain
where
Taking (196) and (197) into equations (192) and (193), we get
as follows:
and
Using (12) and (13), we obtain
The exact solution can be obtained as follows:
Case (B). Fuzzy Adomian decomposition method:
Applying equations (32) into (35), we obtain
and
Taking the fuzzy decomposition series, we have
The exact solution can be obtained as follows:
Case (C). Fuzzy homotopy perturbation method:
Applying a fuzzy HPM, construct a simple homotopy as follows:
Assume that the solution contains the following:
Using \(p = 1\) in equations (202) and (203), we obtain
Using (203) into (200) and the terminology equating with powers similar to p, we obtain
and
Taking initial condition (188) and the solution of (206) and (209), we get
From the solution of (207) and (210), we get
We obtain the solution of (208) and (211) as follows:
and
Using (204) and (205), the approximate solution of (190) and (191) is
The exact solution can be obtained as follows:
Case [D]. Fuzzy reduced differential transform method
Taking a fuzzy RDTM to (190) and (191) yields
Using initial condition (188), we obtain
According to (222) into (219), we have \(\tilde{U}_{j}(\alpha )\) fuzzy-valued function, respectively:
Applying the fuzzy differential inverse transformation, we have
The exact solution is obtained as follows:
Example 4.4
We consider the following fuzzy \((1 + n)\)-dimensional Burgers’ equation:
with the initial condition
for \(\tilde{u} = \tilde{u}(x_{1},x_{2},x_{3},\ldots,x_{n},t)\) is a fuzzy-valued function satisfying \(\tilde{u}(x_{1},x_{2},x_{3},\ldots,x_{n},t)\geq \tilde{0}\). Above \(\tilde{k}^{n}\in E^{1}\), \(n= 1,2,3,\ldots\) , a fuzzy number is
and \([\underline{\tilde{k}^{n}}](\alpha )=(0.4+0.1\alpha )^{n}, [ \overline{\tilde{k}^{n}}](\alpha )=(0.6-0.1\alpha )^{n}\).
The parametric form of (226) is
for \(\alpha \in [0,1]\), where \(\underline{u}\) stands for \(\underline{u}(x_{1},x_{2},x_{3},\ldots,x_{n},t)(\alpha )\), similar to u̅.
Case (A). Fuzzy differential transform method:
Applying the FDTM to (229) and (230), we get
and
Using initial condition (227), we get
and
where
Taking (235) into (236), we get
as follows:
and
According to (12) and (13), we obtain
and
The exact solution can be obtained as follows:
Case (B). Fuzzy Adomian decomposition method:
Applying (32) into (35), we obtain
and
Using the fuzzy decomposition series, we have
and
The exact solution is obtained as follows:
Case (C). Fuzzy homotopy perturbation method:
According to the fuzzy HPM equations (229) and (230), we get
Taking a fuzzy HPM with the fuzzy homotopy parameter p extends the solution as follows:
Applying \(p=1\) in equations (241) and (242) with the approximate solution as follows:
Taking (242) into (239), with the terminology equating and powers similar to p, we get
and
Applying the solution to (245) and (248) with initial condition (227) gives
The solution to (246) and (249) is as follows:
We obtain the solution to (247) and (250) as
and
Applying (243) and (244), the approximate solution of (229) and (230), we have
and
The exact solution is obtained as follows:
Case [D]. Fuzzy reduced differential transform method
Applying the fuzzy RDTM to (229) and (230) yields
Using initial condition (227), we get
According to (262) into (259), we can get \(\tilde{U}_{j}(\alpha )\) fuzzy-valued function, respectively:
and
Taking the fuzzy differential inverse transformation, we have
The exact solutions can be obtained as follows:
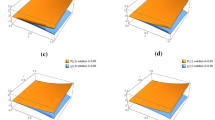
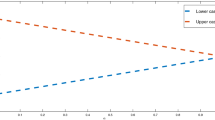
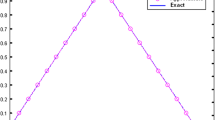
(a) Example 4.1, Case (A), (B), (C), and (D) \(x = 0.1, t = 1, n = 1\), (b) Example 4.2, Case (A), (B), (C), and (D) \(x = 0.001, y = 1, t = 0, n = 2\), (c) Example 4.3, Case (A), (B), (C), and (D) \(x = 0.02, y = 0, z = 0, t = 0.7, n = 3\), (d) Example 4.4, Case (A), (B), (C), and (D) (Let \(x_{1} = 0\), \(x_{2} = 0.1\), \(x_{3} = 0.2\), \(x_{4} = 0.3\), \(x_{5} = 0.4, x_{6} = 0.5, x_{7} = 0.6, x_{8} = 0.7, x_{9} = 0.8, x_{10} = 0.9, x_{11} = 1\)), \(t = 0.0002\), \(n = 4\)
5 Conclusions
In this paper, we studied the comparison of fuzzy differential transform method (FDTM), fuzzy Adomian decomposition method (FADM), fuzzy homotopy perturbation method (FHPM), and fuzzy reduced differential transform method (FRDTM), which have been successfully applied to the solutions of fuzzy \((1 + n)\)-dimensional Burgers’ equation under gH-differentiability. We have investigated many new results to solve the mentioned problem and applied the methods. The results obtained show that the methods are powerful mathematical tools for solving fuzzy \((1 + n)\)-dimensional Burgers’ equation. Finally, we presented some numerical examples and figures to illustrate the results of this work.
Availability of data and materials
Not applicable.
References
Adomian, G.: A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 135, 501–544 (1988)
Ain, Q.T., He, J.H.: On two-scale dimension and its applications. Therm. Sci. 23(3), 1707–1712 (2019)
Akin, O., Khaniyev, T., Oruc, O., Torksen, I.B.: An algorithm for the solution of second order fuzzy initial value problems. Expert Syst. Appl. 40, 953–957 (2013)
Allahviranloo, T.: The Adomian decomposition method for fuzzy system of linear equations. Appl. Math. Comput. 163, 553–563 (2005)
Allahviranloo, T.: An analytic approximation to the solution of fuzzy heat equation by Adomian decomposition method. Int. J. Contemp. Math. Sci. 4(3), 105–114 (2009)
Allahviranloo, T., Abbasbandy, S., Behzadi, S.S.: Solving nonlinear fuzzy differential equations by using fuzzy variational iteration method. Soft Comput. 18, 2191–2200 (2014)
Allahviranloo, T., Gouyandeha, Z., Armanda, A., Hasanoglub, A.: On fuzzy solutions for heat equation based on generalized Hukuhara differentiability. Fuzzy Sets Syst. 265, 1–23 (2015)
Allahviranloo, T., Kiani, N.A., Motamedi, N.: Solving fuzzy differential equations by differential transform method. Inf. Sci. 179, 956–966 (2009)
Anastassiou, G.A.: Fuzzy Mathematics: Approximation Theory. Springer, Berlin (2010)
Andrianov, I., Awrejcewicz, J.: Construction of periodic solution to partial differential equations with nonlinear boundary conditions. Int. J. Nonlinear Sci. Numer. Simul. 1(4), 327–332 (2000)
Arshad, M., Lu, D., Wang, J.: \((N+ 1)\)-dimensional fractional reduced differential transform method for fractional order partial differential equations. Commun. Nonlinear Sci. Numer. Simul. 48, 509–519 (2017)
Ate, I., Zegeling, P.A.: A homotopy perturbation method for fractional-order advection-diffusion-reaction boundary-value problems. Appl. Math. Model. 47, 425–441 (2017)
Bede, B., Gal, S.G.: Generalizations of the differentiable fuzzy number valued functions with applications to fuzzy differential equations. Fuzzy Sets Syst. 151(3), 581–599 (2005)
Bede, B., Stefanini, L.: Generalized differentiability of fuzzy-valued functions. Fuzzy Sets Syst. 230, 119–141 (2013)
Behera, D., Chakraverty, S.: Solving fuzzy complex system of linear equations. Inf. Sci. 277, 154–162 (2014)
Bender, C.M., Pinsky, K.S., Simmons, L.M.: A new perturbative approach to nonlinear problems. J. Math. Phys. 30(7), 1447–1455 (1989)
Biazar, J., Aminikhah, H.: Study of convergence of homotopy perturbation method for systems of partial differential equations. Comput. Math. Appl. 58, 2221–2230 (2009)
Bica, A.M., Ziari, S.: Open fuzzy cubature rule with application to nonlinear fuzzy Volterra integral equations in two dimensions. Fuzzy Sets Syst. 358, 108–131 (2019)
Biswas, S., Roy, T.K.: Adomian decomposition method for fuzzy differential equations with linear differential operator. J. Comput. Inf. Sci. Eng. 11(4), 243–250 (2016)
Buckley, J.J., Feuring, T.: Fuzzy differential equations. Fuzzy Sets Syst. 110, 43–54 (2000)
Buckley, J.J., Feuring, T., Hayashi, Y.: Linear systems of first order ordinary differential equations: fuzzy initial conditions. Soft Comput. 6, 415–421 (2002)
Cabral, V.M., Barros, L.C.: Fuzzy differential equations with completely correlated parameters. Fuzzy Sets Syst. 265, 86–98 (2015)
Cenesiz, Y., Keskin, Y., Kurnaz, A.: The solution of the nonlinear dispersive equations by RDT method. Int. J. Nonlinear Sci. 9(4), 461–467 (2010)
Chen, M.H., Han, C.S.: Some topological properties of solutions to fuzzy differential systems. Inf. Sci. 197, 207–214 (2012)
Chen, M.H., Li, D.H., Xue, X.P.: Periodic problems of first order uncertain dynamical systems. Fuzzy Sets Syst. 162, 67–78 (2011)
Cheng, H.: The Casimir effect for parallel plates in the spacetime with a fractal extra compactified dimension. Int. J. Theor. Phys. 52, 3229–3237 (2013)
Diamond, P., Kloeden, P.: Metric Spaces of Fuzzy Sets. World Scientific, Singapore (1994)
Dubois, D., Prade, H.: Operations on fuzzy numbers. Int. J. Syst. Sci. 9, 613–626 (1978)
Dubois, D., Prade, H.: Fuzzy Sets and Systems: Theory and Applications. Academic Press, New York (1980)
Ebaid, A., Rach, R., El-Zahar, E.: A new analytical solution of the hyperbolic Kepler equation using the Adomian decomposition method. Acta Astronaut. 138, 1–9 (2017)
El Naschie, M.S.: A review of E infinity theory and the mass spectrum of high energy particle physics. Chaos Solitons Fractals 19, 209–236 (2004)
Ghazanfari, B., Ebrahimi, P.: Differential transformation method for solving fuzzy fractional heat equations. Int. J. Math. Model. Comput. 5, 81–89 (2015)
Goetschel, R., Voxman, W.: Elementary fuzzy calculus. Fuzzy Sets Syst. 18, 31–43 (1986)
Golmankhaneh, K., Tuncb, C.: Sumudu transform in fractal calculus Alireza. Appl. Math. Comput. 350, 386–401 (2019)
Gong, Z.T., Hao, Y.D.: Global existence and uniqueness of solutions for fuzzy differential equations under dissipative-type conditions. Comput. Math. Appl. 56, 2716–2723 (2008)
Gong, Z.T., Hao, Y.D.: Fuzzy Laplace transform based on the Henstock integral and its applications in discontinuous fuzzy systems. Fuzzy Sets Syst. 283, 1–28 (2018)
Gouyandeh, Z., Allahviranloo, T., Abbasbandy, S., Armand, A.: A fuzzy solution of heat equation under generalized Hukuhara differentiability by fuzzy Fourier transform. Fuzzy Sets Syst. 309, 81–97 (2017)
Hamoud, A., Ghadle, K.: Modified Adomian decomposition method for solving fuzzy Volterra–Fredholm integral equations. J. Indian Math. Soc. 85, 52–69 (2018)
Hamoud, A.A., Azeez, A., Ghadle, K.: A study of some iterative methods for solving fuzzy Volterra–Fredholm integral equations. Indones. J. Elec. Eng. Comp. Sci. 11(3), 1228–1235 (2018)
He, J.H.: Variational iteration method: a kind of nonlinear analytical technique: some examples. Int. J. Non-Linear Mech. 34(4), 699–708 (1999)
He, J.H.: Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 178, 257–262 (1999)
He, J.H.: Bookkeeping parameter in perturbation methods. Int. J. Nonlinear Sci. Numer. Simul. 2(3), 257–264 (2001)
He, J.H.: A note on delta-perturbation expansion method. Appl. Math. Mech. 23(6), 634–638 (2002)
He, J.H.: Comparison of homotopy perturbation method and homotopy analysis method. In: International Congress of Mathematicians, Beijing, pp. 20–28 (2002)
He, J.H.: Homotopy perturbation method: a new nonlinear analytical technique. Appl. Math. Comput. 13(2–3), 73–79 (2003)
He, J.H.: A simple perturbation method to Blasius equation. Appl. Math. Comput. 2–3, 217–222 (2003)
He, J.H.: A tutorial review on fractal spacetime and fractional calculus. Int. J. Theor. Phys. 53, 3698–3718 (2014)
He, J.H.: Fractal calculus and its geometrical explanation. Results Phys. 10, 272–276 (2018)
He, J.H., Ain, Q.T.: New promises and future challenges of fractal calculus from two-scale thermodynamics to fractal variational principle. Therm. Sci. 24(2), 659–681 (2020)
He, S., Sun, K., Wang, H.: Dynamics and synchronization of conformable fractional-order hyperchaotic systems using the homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 73(15), 146–164 (2019)
Jameel, A.F., Saaban, A., Ahadkulov, H., Alipiah, F.M.: Approximate solution fuzzy pantograph equation by using homotopy perturbation method. J. Phys. Conf. Ser. 890, 1–8 (2017)
Kandel, A., Byatt, W.J.: Fuzzy differential equations. In: Proceedings of International Conference Cybernetics and Society, pp. 1213–1216 (1978)
Keskin, Y., Oturanc, G.: Reduced differential transform method for partial differential equation. Int. J. Nonlinear Sci. Numer. Simul. 10(6), 741–749 (2009)
Keskin, Y., Servi, S., Oturance, G.: Reduced differential transform method for solving Klein Gordon equations. In: Proceeding of the World Congress on Engineering, vol. 1, London, U.K. (2011)
Kumar, D., Singh, J., Kumar, S.: Numerical computation of fractional multidimensional diffusion equations by using a modified homotopy perturbation method. J. Assoc. Arab Univ. Basic Appl. Sci. 17, 20–26 (2015)
Lata, S., Kumar, A.: A new method to solve time-dependent intuitionistic fuzzy differential equations and its application to analyze the intuitionistic fuzzy reliability systems, SAGA. Concurrent Engineering published online, July (2012)
Liao, S.J.: Homotopy analysis method: a new analytic method for nonlinear problems. Appl. Math. Mech. 19(10), 957–962 (1998)
Meher, R., Meher, S.K.: Analytical treatment and convergence of the Adomian decomposition method for instability phenomena arising during oil recovery process. Int. J. Eng. Math. 2013, 752561 (2013)
Melliani, S., Chadli, L.S.: Introduction to intuitionistic fuzzy partial differential equations. Notes IFS 7(3), 39–42 (2001)
Mirzaee, F., Yari, M.K., Paripour, M.: Solving linear and nonlinear Abel fuzzy integral equations by homotopy analysis method. J. Taibah Univ. Sci. 9, 104–115 (2015)
Moghaddam, R.G., Allahviranloo, T.: On the fuzzy Poisson equation. Fuzzy Sets Syst. 347, 105–128 (2018)
Mohammed, O.H., Ahmed, S.A.: Solving fuzzy fractional boundary value problems using fractional differential transform method. J. Al-Nahrain Univ. 16, 225–232 (2013)
Mondal, S.P., Banerjee, S., Roy, T.K.: First order linear homogeneous ordinary differential equation in fuzzy environment. Int. J. Pure Appl. Sci. Technol. 14(1), 16–26 (2013)
Mondal, S.P., Roy, T.K.: First order linear non homogeneous ordinary differential equation in fuzzy environment. Math. Theory Model. 3(1), 85–95 (2013)
Mondal, S.P., Roy, T.K.: First order linear homogeneous ordinary differential equation in fuzzy environment based on Laplace transform. J. Fuzzy Set Valued Anal. 2013, 1–18 (2013)
Mondal, S.P., Roy, T.K.: First order linear homogeneous fuzzy ordinary differential equation based on Lagrange multiplier method. J. Soft Comput. Appl. 2013, 1–17 (2013)
Mustafa, A.M., Gong, Z.T., Osman, M.: The solution of fuzzy variational problem and fuzzy optimal control problem under granular differentiability concept. Int. J. Comput. Math. (2020). https://doi.org/10.1080/00207160.2020.1823974
Narayanamoorthy, S., Sathiyapriya, S.P.: Homotopy perturbation method: a versatile tool to evaluate linear and nonlinear fuzzy Volterra integral equations of the second kind. SpringerPlus 387, 1–16 (2016)
Oberguggenberger, M., Pittschmann, S.: Differential equations with fuzzy parameters. Math. Comput. Model. Dyn. Syst. 5, 181–202 (1999)
Osman, M., Gong, Z.T., Mohammed, A.: Differential transform method for solving fuzzy fractional wave equation. J. Comput. Anal. Appl. 29(3), 431–453 (2021)
Osman, M., Gong, Z.T., Mustafa, A.M.: Comparison of fuzzy Adomian decomposition method with fuzzy VIM for solving fuzzy heat-like and wave-like equations with variable coefficients. Adv. Differ. Equ. 2020(327), 1 (2020)
Osman, M., Gong, Z.T., Mustafa, A.M.: Application to the fuzzy fractional diffusion equation by using fuzzy fractional variational homotopy perturbation iteration method. Adv. Res. J. Mult. Disco. 51(3), 15–26 (2020)
Osman, M., Gong, Z.T., Mustafa, A.M.: A fuzzy solution of nonlinear partial differential equations. Open J. Math. Anal. 5(1), 51–63 (2021)
Pirzada, U.M., Vakaskar, D.C.: Solution of fuzzy heat equations using Adomian decomposition method. Int. J. Adv. Appl. Math. Mech. 3(1), 87–91 (2015)
Puri, M.L., Ralescu, D.A.: Differentials of fuzzy functions. J. Math. Anal. Appl. 91, 552–558 (1983)
Rivaz, A., Fard, O.S., Bidgoli, T.A.: Solving fuzzy fractional differential equations by generalized differential transform method. SeMA J. 73, 149–170 (2016)
Sakar, M.G., Uludag, F., Erdogan, F.: Numerical solution of time-fractional nonlinear PDEs with proportional delays by homotopy perturbation method. Appl. Math. Model. 40, 6639–6649 (2016)
Sarmad, A.A., Jameel, F.A., Saaban, A.: Homotopy perturbation method approximate analytical solution of fuzzy partial differential. IAENG Int. J. Appl. Math. 49(1), 22–28 (2019)
Sekar, S., Sakthivel, A.: Numerical investigation of linear first order fuzzy differential equations using He-s homotopy perturbation method. IOSR J. Math. 5, 33–38 (2015)
Shao, Y., Mou, Q., Gong, Z.T.: On retarded fuzzy functional differential equations and nonabsolute fuzzy integrals. Fuzzy Sets Syst. 275, 121–140 (2019)
Singh, J., Swroop, R., Kumar, D.: A computational approach for fractional convection-diffusion equation via integral transforms. Ain Shams Eng. J. 9, 1019–1028 (2018)
Srivastava, K.V., Awasthi, K.M.: \((1 + n)\)-dimensional Burgers’ equation and its analytical solution: a comparative study of HPM, ADM and DTM. Ain Shams Eng. J. 5(2), 533–541 (2014)
Taha, B.A.: The use of reduced differential transform for solving partial differential equations with variable coefficients. J. Basrah Res. (Sci.) 37(4), 226–273 (2011)
Vorobiev, D., Seikkala, S.: Towards the theory of fuzzy differential equations. Fuzzy Sets Syst. 125, 231–237 (2002)
West, G.B., Brown, J.H., Enquist, B.J.: The fourth dimension of life: fractal geometry and allometric scaling of organisms. Science 284, 1677–1679 (1999)
Wu, C., Gong, Z.: On Henstock integral of fuzzy-number-valued functions (1). Fuzzy Sets Syst. 120, 523–532 (2001)
Yang, H., Gong, Z.: I11-posedness for fuzzy Fredholm integral equations of the first kind and regularization methods. Fuzzy Sets Syst. 358, 132–149 (2019)
Yu, J., Jing, J., Sun, Y., Wu, S.: \((n + 1)\)-Dimensional reduced differential transform method for solving partial differential equations. Appl. Math. Comput. 273, 697–705 (2016)
Zhou, J.K.: Differential Transformation and Its Applications for Electrical Circuits. Huazhong University Press, Wuhan (1986) (in Chinese)
Acknowledgements
The authors would like to express their sincere appreciation to the editors and anonymous reviewers for their helpful and detailed comments and suggestions, which led to improving the presentation and quality of the work. M. Osman and A.M. Mustafa, we would like to express our gratitude to Prof. Zengtai Gong, not just for introducing us to such an interesting area of research, but also for guiding us through the present work and supporting us during the difficult times we experienced. We would also like to thanks and gratituded to all the professors in the College of Mathematics and Statistics, Northwest Normal University, Lanzhou, Gansu, China.
Funding
This work is supported by National Natural Science Foundation of China (61763044).
Author information
Authors and Affiliations
Contributions
In this paper, all authors contributed equally. The authors read and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Osman, M., Gong, Z., Mustafa, A.M. et al. Solving fuzzy \((1+ n)\)-dimensional Burgers’ equation. Adv Differ Equ 2021, 219 (2021). https://doi.org/10.1186/s13662-021-03376-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03376-y