On the regularity of curvature fields in stress-driven nonlocal elastic beams

Abstract

Elastostatic problems of Bernoulli–Euler nanobeams, involving internal kinematic constraints and discontinuous and/or concentrated force systems, are investigated by the stress-driven nonlocal elasticity model. The field of elastic curvature is output by the convolution integral with a special averaging kernel and a piecewise smooth source field of elastic curvature, pointwise generated by the bending interaction. The total curvature is got by adding nonelastic curvatures due to thermal and/or electromagnetic effects and similar ones. It is shown that fields of elastic curvature, associated with piecewise smooth source fields and bi-exponential kernel, are continuously differentiable in the whole domain. The nonlocal elastic stress-driven integral law is then equivalent to a constitutive differential problem equipped with boundary and interface constitutive conditions expressing continuity of elastic curvature and its derivative. Effectiveness of the interface conditions is evidenced by the solution of an exemplar assemblage of beams subjected to discontinuous and concentrated loadings and to thermal curvatures, nonlocally associated with discontinuous thermal gradients. Analytical solutions of structural problems and their nonlocal-to-local limits are evaluated and commented upon.

1 Introduction

In the last few years, there has been a huge increase in technological applications characterized by smaller and smaller structures whose design and optimization require assessing technically significant scale phenomena [8]. In parallel, a flowering of proposals for the theoretical modelling of nonlocal behaviour has appeared in the literature. Nonlocal continuum models can be conveniently used to capture in an effective way size effects at micro- and nanoscales [5, 7, 13], when compared with computationally expensive atomistic strategies [6]. In the framework of nonlocal theories [3, 4, 9, 10], the stress-driven integral formulation of elasticity provides a consistent methodology to examine the size-dependent behaviour of nanocontinua. Serious issues intrinsic to Eringen’s strain-driven integral convolution law are thus overcome [11, 12].

The present analysis is developed in the simplest case of the geometrically linear Bernoulli–Euler theory of plane straight beams. Denoting by $\,x\,$ the abscissa along the axis, the total curvature field $\,\chi \,$ associated with a piecewise regular transversal displacement field $\,v\,$ is pointwise described in each regularity domain by¹

$$\begin{aligned} \chi (x):=\partial _x^2v\,. \end{aligned}$$

(1)

The natural constitutive assumption is that the total curvature $\,\chi \,$ is the sum of elastic curvature $\,{\chi ^\mathrm{el}}\,$ and of nonelastic curvature fields $\,{\chi ^\mathrm{nel}}\,$ due to any other effect, such as thermal, electromagnetic and similar one, so that

$$\begin{aligned} \chi ={\chi ^\mathrm{el}}+{\chi ^\mathrm{nel}}\,. \end{aligned}$$

(2)

According to the stress-driven nonlocal elasticity model [11], the elastic curvature is the convolution integral between a source field of local elastic curvature $\frac{M}{K}$ (possibly nonsmooth) and an averaging kernel $\,\phi \,$:

$$\begin{aligned} \begin{aligned} {\chi ^\mathrm{el}}(x)&\,=\Bigl (\phi *\frac{M}{K}\Bigr )(x) :=\int _{0}^{L} \phi (x-\xi ,c)\cdot \frac{M}{K}(\xi )\,\mathrm {d}\xi \,, \end{aligned} \end{aligned}$$

(3)

with $\,c>0\,$ characteristic length, $\,M\,$ bending interaction², and $\,K\,$ local elastic bending stiffness given by the second moment of Euler–Young modulus $\,E\,$ on the beam cross sections.

The special properties of Helmholtz’s averaging kernel:

$$\begin{aligned} \phi (x,c):=\frac{1}{2\,c}\,\exp \Big (-\frac{|x|}{c}\Big )\,, \end{aligned}$$

(4)

will play a key role in the subsequent regularity analysis.

By this special choice, the convolution integral equation (3) can be inverted [11] by expressing the source field $\,\frac{M}{K}\,$ in terms of the output field $\,{\chi ^\mathrm{el}}\,$.

Specifically, for smooth source fields $\,\frac{M}{K}\,$ in the domain $\,[0,\text {L}]\,$, the elastic curvature $\,{\chi ^\mathrm{el}}\,$ expressed by Eq. (3) results to be the unique solution of the differential equation [11, Eq. (57)],

$$\begin{aligned} \frac{1}{c^2}{\chi ^\mathrm{el}}(x)-\partial _x^2{\chi ^\mathrm{el}}(x) =\frac{1}{c^2} \frac{M}{K}(x)\,, \qquad x\in [0,\text {L}]\,, \end{aligned}$$

(5)

with the constitutive boundary conditions [11, Eq. (58)]

$$\begin{aligned} \left\{ \begin{aligned}&\,\partial _x{\chi ^\mathrm{el}}(0)=\frac{1}{c}\,{\chi ^\mathrm{el}}(0)\,, \\&\,\partial _x{\chi ^\mathrm{el}}(L)=-\frac{1}{c}\,{\chi ^\mathrm{el}}(L)\,. \end{aligned} \right. \end{aligned}$$

(6)

The motivation of the present paper consists in extending the constitutive differential formulation Eqs. (5) and (6) to piecewise smooth source fields $\,\frac{M}{K}\,$ in order to solve assemblages of nanobeams involving internal kinematic constraints and nonsmoothly distributed and/or concentrated force systems.

The problem is tackled by detecting the regularity properties of the elastic curvature fields expressed by the convolution integral with the special averaging kernel Eq. (4).

For simplicity sake, the assemblage domain is partitioned into two parts $[0,L]=[0,x_d]\cup [x_d,L],$ and we set

$$\begin{aligned} {\chi ^\mathrm{el}}(x)=\Bigl (\phi *\frac{M}{K}\Bigr )(x) = \left\{ \begin{aligned}&{\chi _1^\mathrm{el}}(x)\,, \qquad x\in [0,x_d]\,, \\&{\chi _2^\mathrm{el}}(x)\,, \qquad x\in [x_d,L]\,. \end{aligned} \right. \end{aligned}$$

(7)

The plan is the following.

In Sect. 2, regularity properties of elastic curvature fields $\,{\chi ^\mathrm{el}}\,$ given by Eq. (7) are discussed in terms of the source field $\,\frac{M}{K}\,$ and of its derivative. As an implication, equivalent integral and differential laws of stress-driven nonlocal elasticity for nanobeams, supplemented with the proper constitutive boundary and interface conditions, are presented.

The new approach is applied in Sect. 3 to a case-problem involving both elastic and thermal nonlocal effects.

Closing remarks are outlined in Sect. 4.

2 Differential formulation of nonlocal elasticity

The next two propositions are prodromic in formulating a constitutive differential problem equivalent to the stress-driven integral model of nonlocal elasticity Eq. (7) equipped with the special averaging kernel Eq. (4).

Proposition 1

Elastic curvatures generated by the stress-driven convolution integral Eq. (7) with the special kernel Eq. (4) are continuously differentiable fields ${\chi ^\mathrm{el}}\in \mathrm {C}^1([0,L];\mathfrak {R})$ in the whole domain, for any piecewise smooth source field of local elastic curvature.

Proof

Applying the definition of the convolution integral Eq. (3) and using the special kernel Eq. (4), the elastic curvature $\,{\chi ^\mathrm{el}}\,$ in Eq. (7) writes as

$$\begin{aligned} \begin{aligned} {\chi ^\mathrm{el}}(x)&= \left\{ \begin{aligned}&{\chi _1^\mathrm{el}}(x)\,, \qquad x\in [0,x_d] \\&{\chi _2^\mathrm{el}}(x)\,, \qquad x\in [x_d,L] \end{aligned}, \right.&\\&=\left\{ \begin{aligned}&\frac{1}{2c}\int _0^x \mathrm{exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm{d}t +\frac{1}{2c} \int _x^{x_d} \mathrm{exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm{d}t \, \\&+ \frac{1}{2c}\int _{x_d}^L \mathrm{exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm{d}t, \qquad x\in [0,x_d]\,,\\&\frac{1}{2c}\int _0^{x_d} \mathrm{exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm{d}t +\frac{1}{2c} \int _{x_d}^x \mathrm{exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm{d}t \, \\&+\frac{1}{2c} \int _{x}^L \mathrm{exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm{d}t, \qquad x\in [x_d, L]\,. \end{aligned} \right. \end{aligned} \end{aligned}$$

(8)

By known results of calculus, the elastic curvature field Eq. (8) is continuously differentiable in the whole domain, with the derivative given by

$$\begin{aligned} \partial _x{\chi ^\mathrm{el}}(x) = \left\{ \begin{aligned}&\frac{1}{2c^2} \bigg (- \int _0^x \mathrm{exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm{d}t + \int _x^{x_d} \mathrm{exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm{d}t \, \\&+\int _{x_d}^L \mathrm{exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm{d}t\bigg ), \qquad x\in [0,x_d]\,, \\&\frac{1}{2c^2} \bigg (- \int _0^{x_d} \mathrm{exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm{d}t - \int _{x_d}^x \mathrm{exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm{d}t \, \\&+\int _x^L \mathrm{exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm{d}t\bigg ), \qquad x\in [x_d, L]\,. \end{aligned} \right. \end{aligned}$$

(9)

$\square$

Combining Eq. (8) with Eq. (9), several equivalent expressions of the elastic curvature derivative can be given. For instance, the expression:

$$\begin{aligned} \begin{aligned} \partial _x{\chi ^\mathrm {el}}(x) = \left\{ \begin{aligned}&\frac{1}{c} \bigg ({\chi ^\mathrm {el}}(x) - \frac{1}{c}\int _0^x \mathrm {exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm {d}t\bigg )\,,&x\in [0,x_d]\,, \\ {}&\frac{1}{c} \bigg (- {\chi ^\mathrm {el}}(x) + \frac{1}{c}\int _x^L \mathrm {exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm {d}t\bigg )\,,&x\in [x_d, L]\,, \end{aligned} \right. \end{aligned} \end{aligned}$$

(10)

evaluated at the point $x_d$, provides the interface conditions in ([2, Eqs. (13)$_2$, (14)$_1$]).

Proposition 2

Second and higher-order derivatives of elastic curvatures, expressed according to the convolution Eq. (7) and kernel Eq. (4), are given by

$$\begin{aligned} \begin{aligned} \partial _x^2{\chi ^\mathrm {el}}(x) = \left\{ \begin{aligned}&\frac{1}{c^2} \bigg (\int _0^x \mathrm {exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm {d}t -\int _{x_d}^x \mathrm {exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm {d}t \, \\ {}&+\int _{x_d}^L \mathrm {exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm {d}t - \frac{M_1}{K_1}(x) \bigg ), \qquad x\in [0,x_d[\,, \\ {}&\frac{1}{c^2} \bigg (\int _0^{x_d} \mathrm {exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm {d}t + \int _{x_d}^x \mathrm {exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm {d}t \, \\ {}&-\int _L^x \mathrm {exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm {d}t - \frac{M_2}{K_2}(x) \bigg ), \qquad x\in ]x_d, L]\,\end{aligned} \right. \end{aligned} \end{aligned}$$

(11)

with $\, n \in \{0, 1, 2, ...\}\,$ and $\,\partial _x^{0}\,$ the identity operator.

Proof

The second derivative of the elastic curvature $\,{\chi ^\mathrm{el}}\,$ in Eq. (8) is given by

$$\begin{aligned} \partial _x^2{\chi ^\mathrm {el}}(x) = \left\{ \begin{aligned}&\frac{1}{2c^3} \bigg (\int _0^x \mathrm {exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm {d}t -\int _{x_d}^x \mathrm {exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm {d}t \, \\ {}&+\int _{x_d}^L \mathrm {exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm {d}t\bigg ) - \frac{1}{c^2}\frac{M_1}{K_1}(x) , \qquad x\in [0,x_d[\,, \\ {}&\frac{1}{2c^3} \bigg (\int _0^{x_d} \mathrm {exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_1}{K_1}(t) \mathrm {d}t + \int _{x_d}^x \mathrm {exp}\bigg (\frac{t-x}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm {d}t \, \\ {}&-\int _L^x \mathrm {exp}\bigg (\frac{x-t}{c}\bigg )\frac{M_2}{K_2}(t) \mathrm {d}t\bigg ) - \frac{1}{c^2}\frac{M_2}{K_2}(x), \qquad x\in ]x_d, L]\,. \end{aligned} \right. \end{aligned}$$

(12)

Using Eq. (8) in Eq. (12), we infer Eq. (11) for $\,n=0\,$. For $\,n\ge 1\,$ the proof of Eq. (11) is got by $\,n$-times differentiating Eq. (12). $\square$

Some noteworthy regularity properties of the elastic curvature field can be inferred from Propositions 1 and 2, as summarized in Table 1.

Table 1 Regularity properties of the elastic curvature field

Consequent to the analysis above, for piecewise smooth source fields $\,\frac{M}{K}\,$ in the domain $\,[0,\text {L}]\,$, the elastic curvature $\,{\chi ^\mathrm{el}}\,$ expressed by Eq. (7) results to be the unique solution of a constitutive differential problem with boundary and interface conditions. Specifically, setting $\,n=0\,$ in Eq. (11), the constitutive problem is described by the system of second-order differential equations:

$$\begin{aligned} \left\{ \begin{aligned}&\, \frac{1}{c^2}{\chi _1^\mathrm{el}}(x)-\partial _x^2{\chi _1^\mathrm{el}}(x) =\frac{1}{c^2}\frac{M_1}{K_1}(x)\,, \qquad x\in [0,x_d]\,, \\&\quad \frac{1}{c^2}{\chi _2^\mathrm{el}}(x)-\partial _x^2{\chi _2^\mathrm{el}}(x) =\frac{1}{c^2}\frac{M_2}{K_2}(x)\,, \qquad x\in [x_d,L] \,, \end{aligned} \right. \end{aligned}$$

(13)

each one pertaining to a regularity domain for the source field $\,\frac{M}{K}\,$.

The relevant boundary and interface conditions are, respectively, given by

$$\begin{aligned} \left\{ \begin{aligned}&\,\partial _x{\chi _1^\mathrm{el}}(0)=\frac{1}{c}\,{\chi _1^\mathrm{el}}(0)\,, \\&\,\partial _x{\chi _2^\mathrm{el}}(L)=-\frac{1}{c}\,{\chi _2^\mathrm{el}}(L)\,, \end{aligned} \right. \end{aligned}$$

(14)

and

$$\begin{aligned} \left\{ \begin{aligned}&\,{\chi _1^\mathrm{el}}(x_d)={\chi _2^\mathrm{el}}(x_d)\,, \\&\,\partial _x{\chi _1^\mathrm{el}}(x_d)=\partial _x{\chi _2^\mathrm{el}}(x_d)\,. \end{aligned} \right. \end{aligned}$$

(15)

Note that Eq. (14) is got by evaluating and comparing the expressions in Eqs. (8), (9) at the domain boundary $\,\partial [0,\text {L}]\,$. According to Prop.1, Eq. (15) collects the continuity conditions of elastic curvature and of its derivative. Equivalently, as illustrated in the synoptic Table 1, alternative constitutive interface conditions can be chosen, depending on regularity properties of the source field $\,\frac{M}{K}\,$ considered in the stress-driven law of nonlocal elasticity Eq. (7).

2.1 Asymptotic elastic curvatures

The stress-driven integral elasticity formulation Eq. (7) is well defined for any value of the scale-length parameter $\,c>0\,$. It is interesting to examine limit behaviours as $\,c\rightarrow 0^+\,$ of elastic curvatures at regularity internal points $\,x\in \,]0,x_d[\,\cup \,]x_d,L[\,$, at beam ends $\,x\in \{\,0,L\,\}$, and at the interface point $\,x=x_d\,$.

To this end, let us recall from [12] that the nonlocal-to-local limit ($\,c\rightarrow 0^+\,$) of the averaging kernel $\,\phi \,$ depends on the location of the evaluation point and precisely is given by

• Dirac impulse $\,\varvec{\delta }\,$ at regularity internal points;

• halved Dirac impulse $\,\frac{\varvec{\delta }}{2}\,$ at beam ends, due to elimination of the part of the kernel which falls out of the domain of integration.

Regarding the limit elastic curvature at interface point $\,x=x_d\,$, it is convenient to split the convolution integral Eq. (7) into two parts,

$$\begin{aligned} \begin{aligned} {\chi ^\mathrm {el}}(x_d)&\,=\Big (\phi *(M/K)\Big )(x_d) =\int _{0}^{L} \phi (x_d-\xi ,c)\cdot \frac{M}{K}(\xi )\,\mathrm {d}\xi \\ {}&\,=\int _{0}^{x_d} \phi (x_d-\xi ,c)\cdot \frac{M_1}{K_1}(\xi )\,\mathrm {d}\xi +\int _{x_d}^{L} \phi (x_d-\xi ,c)\cdot \frac{M_2}{K_2}(\xi )\,\mathrm {d}\xi \,, \end{aligned} \end{aligned}$$

(16)

and to observe that $\,x_d\,$ is boundary point of both the integration domains. Thus, the limit nonlocal curvature at point $\,x=x_d\,$ is the average value of local elastic curvatures $\,\frac{M_1}{K_1}(x_d)\,$ and $\,\frac{M_2}{K_2}(x_d)\,$.

In sum, the limit behaviour of the nonlocal elastic curvature is given by

$$\begin{aligned} \begin{aligned} \chi {}_{{\scriptstyle 0^+}}^{el}(x):=\lim _{c\rightarrow {0^+}}{\chi ^\mathrm {el}}(x)= \left\{ \begin{aligned}&\frac{M_1}{2K_1}(0) \,, \qquad&x=0\,, \\ {}&\frac{M_1}{K_1}(x) \,, \qquad&x\in \,]0,x_d[\,, \\ {}&\frac{1}{2}\Bigl ( \frac{M_1}{K_1}(x_d) +\frac{M_2}{K_2}(x_d) \Bigr ) \,, \qquad&x=x_d\,, \\ {}&\frac{M_2}{K_2}(x) \,, \qquad&x\in \,]x_d,L[\,, \\ {}&\frac{M_2}{2K_2}(L) \,, \qquad&x=L\,. \end{aligned} \right. \end{aligned} \end{aligned}$$

(17)

Remark 1

As got in Eq. (17), except for null measure sets, the limit nonlocal elastic curvature coincides with the one obtained by the local elasticity model. Accordingly, asymptotic displacement solutions for $\,c\rightarrow {0^+}\,$ of nonlocal beam problems are coincident with local solutions in the whole structural domain. The theoretical prediction is confirmed by numerical evidence in Sect. 3.

3 Structural problem

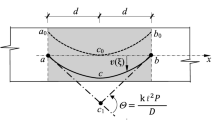
Let us consider the articulated assemblage of Bernoulli–Euler beams in Fig. 1 formulated by the stress-driven nonlocal model of elasticity.

Fig. 1

Geometric sketch of an assemblage of beams under concentrated couple, piecewise smooth distributed loading, and thermal distortion

The elastostatic problem is expressed in terms of transverse displacements $\,v=\{\,v_1,v_2,v_3\,\}\,$ by partitioning the beam domain $\,[0,L]\,$, differentiating twice the elasticity laws (13) (rewritten in the three intervals), enforcing equilibrium $\,\partial _x^2M=\partial _x^2\{\,M_1,M_2,M_3\,\} =\{\,q,0,0\,\}$, and using the formulae Eqs. (1) and (2).

The resulting differential problem of elastic equilibrium to be integrated is

$$\begin{aligned} \left\{ \begin{aligned}&\, \frac{1}{c^2}\partial _x^4v_1(x) -\partial _x^6v_1(x) =\frac{1}{c^2}\,\Bigl (\frac{q}{K_1} +\partial _x^2{\chi ^\mathrm{nel}}(x)\Bigr ) -\partial _x^4{\chi ^\mathrm{nel}}(x)\,,&\,x\in \Bigl [0,\frac{L}{3}\Bigr ]\,, \\&\,\frac{1}{c^2}\partial _x^4v_2(x) -\partial _x^6v_2(x) =\frac{1}{c^2}\,\partial _x^2{\chi ^\mathrm{nel}}(x) -\partial _x^4{\chi ^\mathrm{nel}}(x)\,,&\,x\in \Bigl [\frac{L}{3},\frac{2L}{3}\Bigr ]\,, \\&\,\frac{1}{c^2}\partial _x^4v_3(x) -\partial _x^6v_3(x) =\frac{1}{c^2}\,\partial _x^2{\chi ^\mathrm{nel}}(x) -\partial _x^4{\chi ^\mathrm{nel}}(x)\,,&\,x\in \Bigl [\frac{2L}{3},L\Bigr ] \,. \end{aligned} \right. \end{aligned}$$

(18)

The set $\,\{\,v_1,v_2,v_3\,\}\,$ of displacement functions is evaluated by integrating the differential problem Eq. (18) and enforcing standard (essential) kinematic and (natural) static boundary conditions, nonstandard (constitutive) boundary Eq. (14) and continuity Eq. (15) boundary conditions. Using still Eqs. (1), (2) and (14), (15) are, respectively, expressed in terms of displacements by

$$\begin{aligned} \left\{ \begin{aligned}&\,\partial _x^3v_1(0)-\partial _x{\chi ^\mathrm{nel}}(0) =\frac{1}{c}\, (\partial _x^2v_1(0)-{\chi ^\mathrm{nel}}(0))\,, \\&\,\partial _x^3v_3(L)-\partial _x{\chi ^\mathrm{nel}}(L) =-\frac{1}{c}\, (\partial _x^2v_3(L)-{\chi ^\mathrm{nel}}(L))\,, \end{aligned} \right. \end{aligned}$$

(19)

and

$$\begin{aligned} \left\{ \begin{aligned}&\,\partial _x^2v_1(L/3)=\partial _x^2v_2(L/3)\,, \\&\,\partial _x^3v_1(L/3) =\partial _x^3v_2(L/3)\,, \\&\,\partial _x^2v_2(2L/3)=\partial _x^2v_3(2L/3)\,, \\&\,\partial _x^3v_2(2L/3) =\partial _x^3v_3(2L/3). \end{aligned} \right. \end{aligned}$$

(20)

The butterfly-shaped thermal distortion with gradient $\,g{}_{{\scriptstyle \varDelta T}}:=\frac{\varDelta T}{h}\,$ leads to nonlocal nonelastic effects captured by the convolution integral

$$\begin{aligned} {\chi ^\mathrm{nel}}(x) =\chi ^\mathrm{th}(x):=\int _{\frac{2\,L}{3}}^L \phi (x-\xi ,c)\, \alpha \,g{}_{{\scriptstyle \varDelta T}} \, d\xi \,, \qquad x\in [0,L]\,, \end{aligned}$$

(21)

with $\,\alpha \,$ the coefficient of linear isotropic thermal expansion.

The elastostatic problem is solved using the Mathematica software due to Stephen Wolfram [14]. In order to provide numerical values to the solver, we set $\,K=K_1=K_2=K_3$, $\,L=1$, and

$$\begin{aligned} \frac{qL^3}{ K} =\frac{\mathcal {M}L}{ K} =\displaystyle {\frac{\alpha \varDelta T}{h}L= 1}\,. \end{aligned}$$

(22)

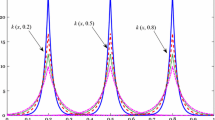
The prescribed thermal curvature Eq. (21) is depicted in Fig. 2 for increasing length-scale parameter $\,\lambda = \frac{c}{L}\,$ which regulates entities of nonlocal effects.

Fig. 2

Thermal curvature $\,\chi ^\mathrm{th}\,$ versus $\,x\,$ for $\,\lambda \in \{0^+, 0.05, 0.1, 0.2, 0.3, 0.4\}\,$

Note that the local thermal curvature, vanishing in the interval $\,[0,\frac{2L}{3}]\,$ and equal to $\,\alpha g_{\varDelta T}\,$ in the interval $\,[\frac{2L}{3},L]\,$, is recovered as the nonlocal parameter tends to zero, $\,\lambda \rightarrow 0^+\,$.

Figure 3 represents the elastic curvature field $\,\chi ^\mathrm {el}\,$ for increasing values of $\,\lambda \,$, a smooth function for strictly positive values of $\,\lambda \,$ as predicted in Sect. 2.

Fig. 3

Elastic curvature $\,\chi ^\mathrm {el}\,$ versus $\,x\,$ for $\,\lambda \in \{0^+, 0.05, 0.1, 0.2, 0.3, 0.4\}\,$

For $\,\lambda = 0^+\,$ the local elastic curvature is recovered except for the beam ends $\,\{\,0,L\,\}\,$ and for the interface $\,\{\,\frac{2L}{3}\,\}\,$ where the asymptotic values theoretically predicted in Eq. (17) are obtained. Total curvatures $\,\chi \,$ depicted in Fig. 4 become lower and uniform as the nonlocal parameter increases, and, at limit, the local total curvature is recovered $\,\forall x \in ]0, L[\,$.

Fig. 4

Total curvature $\,\chi \,$ versus $\,x\,$ for $\,\lambda \in \{0^+, 0.05, 0.1, 0.2, 0.3, 0.4\}\,$

Finally, a plot of transverse displacement $\,v\,$ as function of $\,\lambda \,$ (Fig. 5) shows a stiffening behaviour for increasing nonlocal parameter, in agreement with the smaller-is-stiffer phenomenon [1].

Fig. 5

Displacement $\,v\,$ versus $\,x\,$ for $\,\lambda \in \{0^+, 0.05, 0.1, 0.2, 0.3, 0.4\}\,$

4 Closing remarks

Outcomes of the research may be summarized as follows.

• (i) The size-dependent behaviour of Bernoulli–Euler nanobeams has been investigated by the stress-driven nonlocal integral theory of elasticity, with the bi-exponential averaging kernel.

• (ii) Regularity properties of the curvature fields generated by the nonlocal elastic law have been investigated and detected. This result does indeed play a key role in formulating the constitutive system of second-order differential equations equivalent to the stress-driven convolution integral of nonlocal elasticity. The relevant nonstandard boundary and interface conditions are shown to stem directly from the continuity property of the elastic curvature and its derivative in the whole domain.

• (iii) The proposed nonlocal approach has been exploited to solve the elastostatic problem of an assemblage of beams subjected to complex loading conditions including discontinuous and concentrated forces and impressed distortions.

• (iv) The integration strategy pertaining to the deflection curve of local elastic beams has been so extended to stress-driven nonlocal elasticity. An effective modelling is thus available to assess size effects in nanobeams.