Skip to main content
SpringerLink
Log in

Smart control of laminated plates using Murakami zig-zag functions

  • Published:
International Journal of Mechanics and Materials in Design Aims and scope Submit manuscript

Abstract

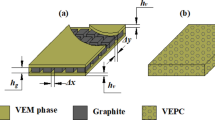
The study aims at vibration control of laminated plates by the active constraining layer damping (ACLD) treatment incorporating the Murakami zig-zag function (MZZF) while deriving the displacement fields. The control is achieved by activating the ACLD patches by supplying the control voltage. The ACLD patch has two component layers, namely 1–3 piezoelectric composite (PZC) constraining material layer and the viscoelastic constrained material layer. The complete ACLD plate system is modelled as a three layered structure using a MZZF in the displacement fields of the individual layers, and the FE model is obtained by the virtual work principle. A MATLAB FE code has been developed considering the closed loop feedback system for the control of the input parameters. The present method of modelling the ACLD system has proven to be accurate and cost effective for damping the vibrations of the composite plates. Also, the change in piezo fiber orientation angle on the control and performance of the ACLD patches has been effectively studied in detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  • Bailey, T., Ubbard, J.E.: Distributed piezoelectric-polymer active vibration control of a cantilever beam. J. Guid. Control Dyn. 8, 605–611 (1985)

    Article  Google Scholar 

  • Baz, A., Ro, J.: Performance characteristics of active constrained layer damping. Shock Vib. 2, 33–42 (1995)

    Article  Google Scholar 

  • Brischetto, S., Carrera, E., Demasi, L.: Improved response of unsymmetrically laminated sandwich plates by using zig-zag functions. J. Sandw. Struct. Mater. 11, 257–267 (2009a)

    Article  Google Scholar 

  • Brischetto, S., Carrera, E., Demasi, L.: Improved bending analysis of sandwich plates using a zig-zag function. Compos. Struct. 89, 408–415 (2009b)

    Article  Google Scholar 

  • Carrera, E.: C0 Reissner–Mindlin multilayered plate elements including zig-zag and interlaminar stress continuity. Int. J. Numer. Methods Eng. 39, 1797–1820 (1996)

    Article  Google Scholar 

  • Carrera, E.: C0z requirements-models for the two dimensional analysis of multilayered structures. Compos. Struct. 37, 373–383 (1997)

    Article  Google Scholar 

  • Carrera, E.: An assessment of mixed and classical theories on global and local response of multilayered orthotropic plates. Compos. Struct. 50, 183–198 (2000)

    Article  Google Scholar 

  • Carrera, E.: On the use of the Murakami’s zig-zag function in the modeling of layered plates and shells. Comput. Struct. 82, 541–554 (2004)

    Article  Google Scholar 

  • Carrera, E., Ciuffreda, A.: A unified formulation to assess theories of multilayered plates for various bending problems. Compos. Struct. 69, 271–293 (2005)

    Article  Google Scholar 

  • Dunn, M.L., Taya, M.: Micromechanics predictions of the effective electroelastic moduli of piezoelectric composites. Int. J. Solids Struct. 30, 161–175 (1993)

    Article  Google Scholar 

  • Kumar, R.S., Ray, M.C.: Smart damping of geometrically nonlinear vibrations of functionally graded sandwich plates using 1–3 piezoelectric composites. Mech. Adv. Mater. Struct. 23, 652–669 (2016)

    Article  Google Scholar 

  • Lo, K.H., Christensen, R.M., Wu, E.M.: A high-order theory of plate deformation part 2: laminated plates. J. Appl. Mech. 44, 669–676 (1977)

    Article  Google Scholar 

  • Murakami, H.: Laminated composite plate theory with improved in-plane responses. J. Appl. Mech. 53, 661–666 (1986)

    Article  Google Scholar 

  • Pagano, N.J., Hatfield, S.J.: Elastic behavior of multilayered bidirectional composites. AIAA J. 10, 931–933 (1972)

    Article  Google Scholar 

  • Panda, S., Ray, M.C.: Nonlinear finite element analysis of functionally graded plates integrated with patches of piezoelectric fiber reinforced composite. Finite Elem. Anal. Des. 44, 493–504 (2008)

    Article  Google Scholar 

  • Piezocomposites, Materials Systems Inc., 543 Great Road, Littleton, MA 01460

  • Ray, M.C.: Micromechanics of piezoelectric composites with improved effective piezoelectric constant. Int. J. Mech. Mater. Des. 3, 361–371 (2006)

    Article  Google Scholar 

  • Ray, M.C., Baz, A.: Optimization of energy dissipation of active constrained layer damping treatments of plates. J. Sound Vib. 208, 391–406 (1997)

    Article  Google Scholar 

  • Ray, M.C., Bhattacharya, R.: Static analysis of an intelligent structure. Comput. Struct. 52, 617–631 (1994)

    Article  Google Scholar 

  • Ray, M.C., Faye, A.: Active structural-acoustic control of laminated composite plates using vertically/obliquely reinforced 1–3 piezoelectric composite patch. Int. J. Mech. Mater. Des. 5, 123–141 (2009)

    Article  Google Scholar 

  • Ray, M.C., Mallik, N.: Active control of laminated composite beams using a piezoelectric fiber reinforced composite layer. Smart Mater. Struct. 13, 146–152 (2004)

    Article  Google Scholar 

  • Ray, M.C., Pradhan, A.K.: The performance of vertically reinforced 1–3 piezoelectric composites in active damping of smart structures. Smart Mater. Struct. 15, 631–641 (2006)

    Article  Google Scholar 

  • Ray, M.C., Pradhan, A.K.: On the use of vertically reinforced 1–3 piezoelectric composites for hybrid damping of laminated composite plates. Mech. Adv. Mater. Struct. 14, 245–261 (2007)

    Article  Google Scholar 

  • Ray, M.C., Rao, K.M.: Exact analysis of coupled electroelastic. Comput. Struct. 45, 667–677 (1992)

    Article  Google Scholar 

  • Ray, M.C., Reddy, J.N.: Active control of laminated cylindrical shells using piezoelectric fiber reinforced composites. Compos. Sci. Technol. 65, 1226–1236 (2005)

    Article  Google Scholar 

  • Ray, M.C., Rao, K.M., Samanta, B.: Exact solution for static analysis of an intelligent structure under cylindrical bending. Comput. Struct. 47, 1031–1042 (1993)

    Article  Google Scholar 

  • Ray, M.C., Bhattacharya, R., Samanta, B.: Exact solutions for dynamic analysis of composite plates with distributed piezoelectric layers. Comput. Struct. 66, 737–743 (1998)

    Article  Google Scholar 

  • Reddy, J.N.: A simple higher-order theory for laminated composite plates. J. Appl. Mech. 51, 745 (1984)

    Article  Google Scholar 

  • Reddy, J.N.: Mechanics of Laminated Composite Plates, Theory and Analysis. CRC Press, Boca Raton (1997)

    MATH  Google Scholar 

  • Reddy, J.N.: On laminated composite plates with integrated sensors and actuators. Eng. Struct. 21, 568–593 (1999)

    Article  Google Scholar 

  • Reddy, B.A., Ray, M.C.: Optimal control of smart functionally graded plates using piezoelectric fiber reinforced composites. J. Vib. Control 13, 795–814 (2007)

    Article  Google Scholar 

  • Sahoo, S.R., Ray, M.C.: Analysis of smart damping of laminated composite beams using mesh free method. Int. J. Mech. Mater. Des. 14, 359–374 (2017)

    Article  Google Scholar 

  • Sarangi, S.K., Ray, M.C.: Active damping of geometrically nonlinear vibrations of laminated composite shallow shells using vertically/obliquely reinforced 1–3 piezoelectric composites. Int. J. Mech. Mater. Des. 7, 29–44 (2011a)

    Article  Google Scholar 

  • Sarangi, S.K., Ray, M.C.: Active damping of geometrically nonlinear vibrations of laminated composite plates using vertically reinforced 1–3 piezoelectric composites. Acta Mech. 222, 363–380 (2011b)

    Article  Google Scholar 

  • Smith, W.A., Auld, B.A.: Modeling 1–3 composite piezoelectrics: thickness-mode oscillations. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 38, 40–47 (1991)

    Article  Google Scholar 

  • Suresh Kumar, R., Ray, M.C.: Active constrained layer damping of smart laminated composite sandwich plates using 1–3 piezoelectric composites. Int. J. Mech. Mater. Des. 8, 197–218 (2012)

    Article  Google Scholar 

  • Whitney, J.M., Pagano, N.J.: Shear deformation in heterogeneous anisotropic plates. J. Appl. Mech. 37, 1031–1036 (1970)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, National Institute of Technology Raipur, Raipur, Chhattisgarh, 492010, India

    N. Mehadi Khan & Rajana Suresh Kumar

Authors
  1. N. Mehadi Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rajana Suresh Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rajana Suresh Kumar.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The matrices \(\left[{Z}_{1}\right], \left[{Z}_{2}\right], \left[{Z}_{3}\right], \left[{Z}_{4}\right], \left[{Z}_{5}\right],\mathrm{and} \left[{Z}_{6}\right]\) found in Eqs. (7) and (8) are given by

$$\left[ {Z_{1} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {\overline{Z}_{1} } \right]} & {\left[ {\overline{M}_{Z1} } \right]} \\ \end{array} } \right], \left[ {Z_{2} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {\overline{Z}_{2} } \right]} & {\left[ {\overline{M}_{Z2} } \right]} \\ \end{array} } \right], \left[ {Z_{3} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {\overline{Z}_{3} } \right]} & {\left[ {\overline{M}_{Z3} } \right]} \\ \end{array} } \right]$$
$$\left[ {Z_{4} } \right] = \left[ {\begin{array}{*{20}c} {\overline{I}} & {\left[ {\overline{M}_{Z4}^{{\prime }} } \right]} & {\left[ {\overline{Z}_{4} } \right]} \\ \end{array} \left[ {\overline{M}_{Z4} } \right]} \right], \left[ {Z_{5} } \right] = \left[ {\begin{array}{*{20}c} {\overline{I}} & {\left[ {\overline{M}_{Z5}^{{\prime }} } \right]} & {\left[ {\overline{Z}_{5} } \right]} \\ \end{array} \left[ {\overline{M}_{Z5} } \right]} \right],$$
$$\left[ {Z_{6} } \right] = \left[ {\begin{array}{*{20}c} {\overline{I}} & {\left[ {\overline{M}z_{Z6}^{{\prime }} } \right]} & {\left[ {\overline{Z}_{6} } \right]} \\ \end{array} \left[ {\overline{M}_{Z6} } \right]} \right]$$

where \(\left[ {\overline{Z}_{1} } \right]_{k = 1 to N} = \left[ {\overline{Z}_{2} } \right]_{k = N + 1} = \left[ {\overline{Z}_{1} } \right]_{k = N + 2} = \left[ {\begin{array}{*{20}c} z & 0 & 0 & 0 \\ 0 & z & 0 & 0 \\ 0 & 0 & z & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\).

$$\left[ {\overline{M}_{Z1} } \right]_{k = 1 to N} = \left[ {\overline{M}_{Z1} } \right]_{k = N + 1} = \left[ {\overline{M}_{Z1} } \right]_{k = N + 2} = \left[ {\begin{array}{*{20}c} {\left( { - 1} \right)^{k} \zeta_{k} } & 0 & 0 & 0 \\ 0 & {\left( { - 1} \right)^{k} \zeta_{k} } & 0 & 0 \\ 0 & 0 & {\left( { - 1} \right)^{k} \zeta_{k} } & 0 \\ 0 & 0 & 0 & {2z} \\ \end{array} } \right]_{ }$$
$$\left[ {\overline{I}} \right] = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right],\left[ {\overline{Z}_{4} } \right]_{k = 1 to N} = \left[ {\overline{Z}_{5} } \right]_{k = N + 1} = \left[ {\overline{Z}_{6} } \right]_{k = N + 2} = \left[ {\begin{array}{*{20}c} z & 0 \\ 0 & z \\ \end{array} } \right]$$
$$\left[ {\overline{M}_{Z4} } \right]_{{k = 1{\text{ to}} N}} = \left[ {\overline{M}_{Z5} } \right]_{k = N + 1} = \left[ {\overline{M}_{Z6} } \right]_{k = N + 2} = \left[ {\begin{array}{*{20}c} {z^{2} } & 0 \\ 0 & {z^{2} } \\ \end{array} } \right]_{{}}$$
$$\left[ {\overline{M}_{Z4}^{{\prime }} } \right]_{k = 1 to N} = \left[ {\overline{M}_{Z4}^{{\prime }} } \right]_{k = N + 1} = \left[ {\overline{M}_{Z4}^{{\prime }} } \right]_{k = N + 2} = \left[ {\begin{array}{*{20}c} {\left( { - 1} \right)^{k} \frac{2}{{h^{k} }}} & 0 \\ 0 & {\left( { - 1} \right)^{k} \frac{2}{{h^{k} }}} \\ \end{array} } \right]_{{}}$$
$$\left[{B}_{tb}\right]=\left[{B}_{tb1 } {B}_{tb2 } \, \ldots \, {B}_{tb8 }\right], \, \left[{B}_{rb}\right]=\left[{B}_{rb1 } {B}_{rb2 } \, \ldots \, {B}_{rb8 }\right], \left[{B}_{ts}\right]=\left[{B}_{ts1 } {B}_{ts2 } \, \ldots \, {B}_{ts8 }\right] \mathrm{and} \, \left[{B}_{rs}\right]=\left[{B}_{rs1 } {B}_{rs2 } \, \ldots \, {B}_{rs8}\right]$$

The submatrices \(\left[{B}_{tbj}\right]\), \(\left[{B}_{rbj}\right]\), \(\left[{B}_{tsj}\right]\) and \(\left[{B}_{rsj}\right]\) found in Eq. (22) are as follows:

$$\left[{B}_{tbj}\right]=\left[\begin{array}{ccc}\frac{\partial {n}_{j}}{\partial x}& 0& 0\\ 0& \frac{\partial {n}_{j}}{\partial y}& 0\\ \frac{\partial {n}_{j}}{\partial x}& \frac{\partial {n}_{j}}{\partial x}& 0\\ 0& 0& 0\end{array}\right], \left[{B}_{tsj}\right]=\left[\begin{array}{ccc}0& 0& \frac{\partial {n}_{j}}{\partial x}\\ 0& 0& \frac{\partial {n}_{j}}{\partial y}\end{array}\right], {\left[{B}_{tbj}\right]}^{*}=\left[\begin{array}{ccc}\frac{\partial {n}_{j}}{\partial x}& 0& 0\\ 0& \frac{\partial {n}_{j}}{\partial y}& 0\\ \frac{\partial {n}_{j}}{\partial x}& \frac{\partial {n}_{j}}{\partial x}& 0\\ 0& 0& 1\end{array}\right],$$
$$\left[{B}_{rbj}\right]=\left[\begin{array}{cc}{\left[{B}_{tbj}\right]}^{*}& {0}^{1*}\\ {0}^{1*}& {\left[{B}_{tbj}\right]}^{*}\end{array}\right], \left[{B}_{rsj}\right]=\left[\begin{array}{c}\begin{array}{cc}{\mathrm{I}}^{2}& {0}^{2*}\\ {0}^{2*}& {\mathrm{I}}^{2}\\ \left[{B}_{tsj}\right]& {0}^{2*}\end{array}\\ \begin{array}{cc}{0}^{2*}& \left[{B}_{tsj}\right]\end{array}\end{array}\right]$$

While, the rigidity matrices, coupling electro-elastic rigidity vectors pertaining to 1–3 PZC material found in Eq. (29) are explicitly given as

$$\left[ {D_{tb} } \right] = \mathop \sum \limits_{k = 1}^{N} \mathop \int \nolimits_{{h_{k} }}^{{h_{k + 1} }} \left[ {\overline{C}_{b}^{k} } \right] dz, \left[ {D_{trb} } \right] = \mathop \sum \limits_{k = 1}^{N} \mathop \int \nolimits_{{h_{k} }}^{{h_{k + 1} }} \left[ {\overline{C}_{b}^{k} } \right] \left[ {Z_{1} } \right] dz,$$
$$\left[ {D_{rrb} } \right] = \mathop \sum \limits_{k = 1}^{N} \mathop \int \nolimits_{{h_{k} }}^{{h_{k + 1} }} \left[ {Z_{1} } \right]^{T} \left[ {\overline{C}_{b}^{k} } \right]\left[ {Z_{1} } \right] dz, \left[ {D_{ts} } \right] = \mathop \sum \limits_{k = 1}^{N} \mathop \int \nolimits_{{h_{k} }}^{{h_{k + 1} }} \left[ {\overline{C}_{s}^{k} } \right] dz$$
$$\left[ {D_{trs} } \right] = \mathop \sum \limits_{k = 1}^{N} \mathop \int \nolimits_{{h_{k} }}^{{h_{k + 1} }} \left[ {\overline{C}_{b}^{k} } \right] \left[ {Z_{4} } \right] dz, \left[ {D_{rrs} } \right] = \mathop \sum \limits_{k = 1}^{N} \mathop \int \nolimits_{{h_{k} }}^{{h_{k + 1} }} \left[ {Z_{4} } \right]^{T} \left[ {\overline{C}_{b}^{k} } \right]\left[ {Z_{4} } \right] dz$$
$$\left[ {D_{tb} } \right]_{v} = h_{v} \left[ {\overline{C}_{b}^{N + 1} } \right],\left[ {D_{trb} } \right]_{v} = \mathop \int \nolimits_{{h_{N + 1} }}^{{h_{N + 2} }} \left[ {\overline{C}_{b}^{N + 1} } \right] \left[ {Z_{2} } \right]{\text{ dz}}$$
$$\left[ {D_{rrb} } \right]_{v} = \mathop \int \nolimits_{{h_{N + 1} }}^{{h_{N + 2} }} \left[ {Z_{2} } \right]^{T} \left[ {\overline{C}_{b}^{N + 1} } \right] \left[ {Z_{2} } \right]{\text{ dz, }}\left[ {D_{ts} } \right]_{v} = h_{v} \left[ {\overline{C}_{s}^{N + 1} } \right]$$
$$\left[ {D_{trs} } \right]_{v} = \mathop \int \nolimits_{{h_{N + 1} }}^{{h_{N + 2} }} \left[ {\overline{C}_{s}^{N + 1} } \right] \left[ {Z_{5} } \right]{\text{ dz}},\left[ {D_{rrs} } \right]_{v} = \mathop \int \nolimits_{{h_{N + 1} }}^{{h_{N + 2} }} \left[ {Z_{5} } \right]^{T} \left[ {\overline{C}_{b}^{N + 1} } \right] \left[ {Z_{5} } \right]{\text{ dz}}$$
$$\left[ {D_{tb} } \right]_{p} = h_{p} \left[ {\overline{C}_{b}^{N + 2} } \right],\left[ {D_{trb} } \right]_{p} = \mathop \int \nolimits_{{h_{N + 2} }}^{{h_{N + 3} }} \left[ {\overline{C}_{b}^{N + 2} } \right] \left[ {Z_{3} } \right]{\text{ dz}}$$
$$\left[ {D_{rrb} } \right]_{p} = \mathop \int \nolimits_{{h_{N + 2} }}^{{h_{N + 3} }} \left[ {Z_{3} } \right]^{T} \left[ {\overline{C}_{b}^{N + 2} } \right] \left[ {Z_{3} } \right]{\text{ dz, }}\left[ {D_{ts} } \right]_{p} = h_{p} \left[ {\overline{C}_{s}^{N + 2} } \right]$$
$$\left[ {D_{trs} } \right]_{p} = \mathop \int \nolimits_{{h_{N + 2} }}^{{h_{N + 3} }} \left[ {\overline{C}_{s}^{N + 2} } \right] \left[ {Z_{6} } \right]{\text{ dz, }}\left[ {D_{rrs} } \right]_{p} = \mathop \int \nolimits_{{h_{N + 2} }}^{{h_{N + 3} }} \left[ {Z_{6} } \right]^{T} \left[ {\overline{C}_{b}^{N + 2} } \right] \left[ {Z_{6} } \right]{\text{ dz}}$$
$$\left[ {D_{tbs} } \right]_{p} = \mathop \int \nolimits_{{h_{N + 2} }}^{{h_{N + 3} }} \left[ {\overline{C}_{bs}^{N + 2} } \right]{\text{ dz, }}\left[ {D_{trbs} } \right]_{p} = \mathop \int \nolimits_{{h_{N + 2} }}^{{h_{N + 3} }} \left[ {\overline{C}_{bs}^{N + 2} } \right] \left[ {Z_{6} } \right]{\text{ dz}}$$
$$\left[ {D_{rtbs} } \right]_{p} = \mathop \int \nolimits_{{h_{N + 2} }}^{{h_{N + 3} }} \left[ {Z_{3} } \right]^{T} \left[ {\overline{C}_{bs}^{N + 2} } \right]{\text{ dz, }}\left[ {D_{rrbs} } \right]_{p} = \mathop \int \nolimits_{{h_{N + 2} }}^{{h_{N + 3} }} \left[ {Z_{3} } \right]^{T} \left[ {\overline{C}_{bs}^{N + 3} } \right]\left[ {Z_{6} } \right]{\text{ dz}}$$
$$\left\{ {D_{tb} } \right\}_{p} = \mathop \int \nolimits_{{h_{N + 2} }}^{{h_{N + 3} }} - \frac{{\left\{ {\overline{e}_{b} } \right\}}}{{h_{p} }}{\text{ dz}}, \left\{ {D_{rb} } \right\}_{p} = \mathop \int \nolimits_{{h_{N + 2} }}^{{h_{N + 3} }} - \left[ {Z_{3} } \right]^{T} \frac{{\left\{ {\overline{e}_{b} } \right\}}}{{h_{p} }}{\text{ dz}}$$
$$\left\{ {D_{ts} } \right\}_{p} = \mathop \int \nolimits_{{h_{N + 2} }}^{{h_{N + 3} }} - \frac{{\left\{ {\overline{e}_{s} } \right\}}}{{h_{p} }}{\text{ dz, }}\left\{ {D_{rs} } \right\}_{p} = \mathop \int \nolimits_{{h_{N + 2} }}^{{h_{N + 3} }} - \left[ {Z_{6} } \right]^{T} \frac{{\left\{ {\overline{e}_{s} } \right\}}}{{h_{p} }}{\text{ dz}}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khan, N.M., Suresh Kumar, R. Smart control of laminated plates using Murakami zig-zag functions. Int J Mech Mater Des 17, 463–487 (2021). https://doi.org/10.1007/s10999-021-09542-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10999-021-09542-0

Keywords

Search

Navigation