Numerical Solution of Fractional Order Advection Reaction Diffusion Equation with Fibonacci Neural Network

Abstract

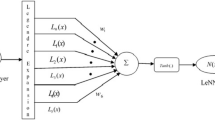
The authors have developed an efficient method with the Fibonacci neural network’s help to solve the fractional-order reaction-diffusion equation in the present article. The Fibonacci neural network consists of an input layer with one perceptron, a hidden layer with $n\times m$ perceptions, and an output layer with one perceptron. The authors have used various degrees of the Fibonacci polynomial as an activation function to the input in the hidden layer. The authors then convert the fractional order diffusion equation with initial and boundary conditions into a non-constrained optimization problem, which is then called the cost function. Marquardt’s method is used to update the values of weights to minimize the cost function. After that, the authors used the discussed method on four examples with an exact solution and showed that our method works more accurately than previously existing methods through comparison. In the last, authors have used the discussed method to solve the unsolved diffusion equation and observe the change in solute concentration for different fractional-order at different times.