Abstract
The high-order harmonic generation (HHG) in xenon is studied by using the time-dependent density-functional theory. The dynamics of all electrons on the outer 4th and 5th atomic shells is considered with subsequent separation of contributions of different atomic orbitals to the HHG amplitude. It is shown that giant enhancement of HHG yield in a spectral region near 100 eV is caused by perturbation of the electron–electron interaction potential induced by recolliding photoelectron wavepacket originated from the 5p0 orbital. This perturbation leads to the collective oscillations of all orbitals on the 4th shell closely localized in space and strongly interacting with each other. The resulting HHG yield is enhanced by more than an order of magnitude compared with the response of the single 5p0 orbital. The high accuracy of the numerical results is confirmed by comparing the calculated HHG spectra and photoionization cross-sections with experimental results and an analytical parameterization of the HHG yield.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
High-order harmonic generation (HHG) is one of the most well-known phenomena of strong-field physics, which is of interest for numerous applications [1, 2]. HHG serves as a unique tool for producing subfemtosecond and attosecond highly coherent light pulses in the extreme ultraviolet (XUV) range. The high intensity of generated XUV pulses and their precise synchronization with the laser field allows pump-probe studies of ultrafast phenomena in quantum systems from atoms and molecules to periodic solid structures (see [3, 4] and references therein). Moreover, XUV pulses obtained within HHG can be used for far-field imaging with nanometer resolution [5], frequency-stabilized seeding for free-electron lasers [6] and controlling magnetic dynamics [7].
The physical mechanism of HHG is qualitatively explained in the framework of a three-step scenario [8]. At the first step, atom or molecule is ionized by an intense field, at the second step, liberated electron is accelerated, and at the third step, electron returns back and recombines with the emission of high-energy photon in a wide energy range. While at the second step, the decisive factor is the interaction of moving electron with the laser field, the type and state of the target affect the ionization probability and the recombination cross section [9–20]. Thus, the multielectron dynamics associated with the motion of various electrons in an atom or molecule can significantly affect both the form of HHG spectra and the optimal generation regimes [12, 14, 21–29].
A typical example of the large influence of multielectron effects at the recombination stage is the giant enhancement of HHG yield in xenon, associated with the interaction of the photoelectron, originating from the external 5p0 orbital, with the inner electrons of the atom [14, 23–26, 30, 31]. This enhancement was first predicted in [30] based on the analytical parametrization of the HHG spectra within the so-called electron wave packet (EWP), which describes the ionization and propagation of photoelectron in the continuum, and a differential photorecombination cross section (PRCS), which is related to a differential photoionization cross section (PICS) according to the principle of the detailed balance [32]. PICS from the outer 5p subshell of Xe atom has a broad maximum near photon energy of 100 eV due to the giant resonance in the PICS from the inner 4d subshell and interchannel coupling via electron–electron interaction [33, 34]. Experimental measurements of HHG spectra in Xe using near-IR driving wavelengths confirm the existence of a giant (more than an order of magnitude) harmonic yield enhancement near 100 eV, which qualitatively agrees with the result of analytical parameterization [10, 14, 26, 30, 31]. The giant enhancement in the HHG spectrum of Xe atom was numerically studied in references [24, 26] by applying time-dependent configuration-interaction singles approach and in reference [25] by using time-dependent R-matrix theory. In these studies, the dynamical interaction between orbitals on the outer 5th shell and 4d subshell was taken into account, while the other orbitals were freezed. Although the calculated HHG spectra's coincidence with results of analytical parametrization and experiment is not perfect, obtained HHG spectra contain a broad maximum in the vicinity of 100 eV, which disappears if the interaction between the orbitals is excluded from calculations. Moreover, all five 4dm orbitals (m = 0, ±1, ±2) on 4d subshell contribute to the HHG, and it is not sufficient to take into account only the 4d0 orbital aligned in the direction of the laser polarization [24]. However, due to the rapid increase in the required computational resources with the number of active orbitals, the role of other orbitals on the 4th shell in HHG has not been studied previously.
An alternative approach that may be applicable to investigate the enhancement of HHG yield in Xe is the time-dependent density-functional theory (TDDFT) [35, 36]. The heart of the TDDFT are the time-dependent Kohn–Sham (TDKS) equations for atomic orbitals, which include the interaction of electrons with the laser pulse, nucleus, and electron–electron exchange–correlation interaction. This approach describes with high accuracy giant resonance in the PICSs of various Xe and Xe-like ions [37–40]. However, this approach has not been used previously to study HHG in Xe due to the high complexity of calculations. The main difficulties are caused by a high probability of recolliding electron to move over long distances and acquire high energies, the very sharp increase of the potential energy in the vicinity of the ion, the divergences arising at partial freezing of individual shells of an atom.
Recently, we developed the numerical code for TDKS equations solution in a spherical coordinate system that is based on the careful discretization of the numerical grid, careful selection of calculation region size, and parallelization between the nodes of a computing cluster [20]. This code allowed to simulate HHG in argon taking into account all electrons and demonstrate that a significant multielectron effect in HHG at high laser-pulse intensity is the laser-induced polarization of the atom itself [20]. In this work, we use this numerical code to carry out numerical simulation of the HHG in Xe, taking into account the dynamics of all subshells on the 4th and 5th atomic shells. We show that at the enhancement region and at higher frequencies HHG is influenced not only by the 4d subshell, but also the other, 4p and 4s subshells on the 4th shell. The results are explained based on the dynamics of electron–electron potential induced by the recombining 5p0 wave packet and the interaction between electrons on the 4th shell. We also perform the analysis of the Xe atom interaction with monochromatic XUV field and demonstrate a high linear response of 4p and 4s subshells.
The paper is organized as follows. In section 2, we discuss the TDKS equations and details of the numerical method. Section 3 is devoted to study the dynamics of orbitals of Xe atom in monochromatic XUV field. In section 4 we calculate HHG spectrum in the infrared field and compare it with the results of experiment and the analytical parametrization of the HHG spectrum, which provides high accuracy of EWP calculation at frequencies below the cutoff frequency [41]. Contributions of different orbitals and subshells to the total dipole acceleration are studied in section 4.1. Our main results are summarized in section 5. In the appendix we present the details of the analytical parametrization of the HHG spectrum. Atomic units (a.u.) are used throughout the paper unless specified otherwise.
2. General formulation
2.1. Initial electronic structure of xenon atom
The initial condition for the TDKS equations corresponds to the unperturbed Xe atom in the ground state. It is found within stationary density functional theory, which expresses the state of a multielectron atom in terms of stationary Kohn–Sham (KS) orbitals, 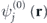 . The unperturbed KS orbitals satisfy the system of stationary KS equations:
. The unperturbed KS orbitals satisfy the system of stationary KS equations:
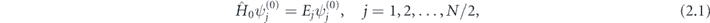
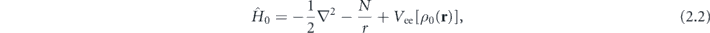
where N is the total number of electrons in an atom (for Xe, N = 54), Vee[ρ0] = VH[ρ0] + Vxc[ρ0] is the electron–electron interaction potential, which is the functional of the electron density 5
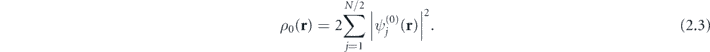
The electron–electron interaction potential is presented by a sum of Hartree potential describing the electron repulsion in the mean-field approximation,
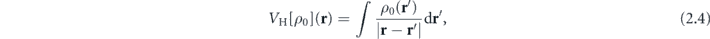
and the exchange–correlation potential Vxc[ρ0], which is considered in the spin-unpolarized LB94 approximation [42]. Since all shells of Xe atom are fully occupied, both ρ0(r) and Vee[ρ0] are spherically symmetric, so that a particular solution of the equation (2.1) can be characterized by the principal quantum number (n), angular momentum (l) and its magnetic projection (m) on the quantization axis z:
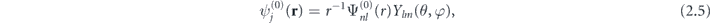
where 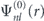 is the radial part of KS orbital, Ylm
(θ, φ) is the spherical harmonic, angles θ and φ are polar and azimuthal angles of the spherical coordinate system. Principal quantum number
is the radial part of KS orbital, Ylm
(θ, φ) is the spherical harmonic, angles θ and φ are polar and azimuthal angles of the spherical coordinate system. Principal quantum number 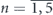 corresponds to the number of electron shell; l corresponds to different subshells and
corresponds to the number of electron shell; l corresponds to different subshells and 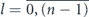 for n ⩽ 3, l = {0, 1, 2} for n = 4, and l = {0, 1} for n = 5; m changes from −l to l for any subshell. The energy levels are degenerate in m, so that the orbital wavefunctions
for n ⩽ 3, l = {0, 1, 2} for n = 4, and l = {0, 1} for n = 5; m changes from −l to l for any subshell. The energy levels are degenerate in m, so that the orbital wavefunctions 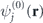 for fixed subshell (n, l) correspond to the same binding energy. For the definiteness we assume that KS orbital index j increases with n, l and m, i.e.
for fixed subshell (n, l) correspond to the same binding energy. For the definiteness we assume that KS orbital index j increases with n, l and m, i.e.
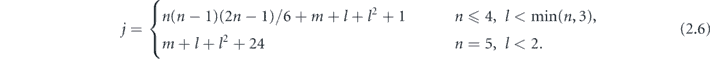
The corresponding ground state configuration, taking into account the presence of two electrons with different spins in each state (n, l, m), is written as [Ar]3d104s24p64d105s25p6, where [Ar] = 1s22s22p63s23p6 is the electronic configuration of Ar atom.
The radial parts of KS orbitals Ψnl(0) (r) are found within the imaginary time propagation method [43] (see the numerical scheme of time propagation in section 2.2). In order to resolve oscillations of wave functions with the scale ∼1/N near the nucleus, we use a nonuniform spatial grid, which has a higher density of nodes near the nucleus. The radial nodes of the spatial grid are specified as
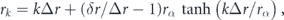
where k is an integer, δr = 10−4 a.u. is tiny step of the radial grid, which is realized near the nucleus; Δr = 0.1 a.u. is the radial step for large distances; rα = 20 a.u. is the scale for changing spatial step from δr to Δr. The size of radial grid was limited by 200 a.u.
The binding energies of KS orbitals are derived from (2.1). They are listed in table 1 along with experimental binding energies, which resolve spin–orbit splitting of p and d energy levels [44, 45]. The deviation of the numerical and experimental binding energies do not exceed 11%. In particular, for the outer 5p subshell, the accuracy of agreement with the experiment is 5%, for 5s, 4p, and 4d subshells, it is 1%, and for the 4s orbital, it is 11%. Thus, the used LB94 exchange–correlation approximation is generally well suited for describing the electronic configuration of the Xe atom.
Table 1. Absolute values of orbital binding energies of Xe. (A) Our DFT calculation with LB94 exchange–correlation potential [42]. (B) Experiment [44, 45].
| Orbital | Energy (eV) | |
|---|---|---|
| (A) DFT | (B) Experiment | |
| 1s | 33 068.8 | 34 561 |
| 2s | 5032.4 | 5453 |
| 2p | 4741.3 | 5107 (3p1/2), 4786 (3p3/2) |
| 3s | 1039.8 | 1148.7 |
| 3p | 915.2 | 1002.1 (3p1/2), 940.6 (3p3/2) |
| 3d | 682.6 | 689 (3d3/2), 676.4 (3d5/2) |
| 4s | 189.4 | 213.2 |
| 4p | 145.5 | 146.7 (4p1/2), 145.5 (4p3/2) |
| 4d | 69.9 | 69.5 (4d3/2), 67.5 (4d5/2) |
| 5s | 23 | 23.3 |
| 5p | 12.8 | 13.4 (5p1/2), 12.1 (5p3/2) |
2.2. Time-dependent Kohn–Sham equations
We consider the interaction of a linearly polarized laser pulse with an atomic target in the dipole approximation. For this case, TDKS equations are
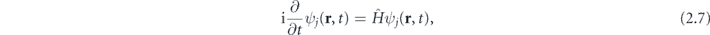
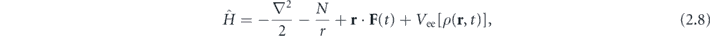
where 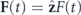 is the electric field of a short laser pulse, ψj
(r, t) is the wave function of the TDKS orbital determining the time-dependent electron density
is the electric field of a short laser pulse, ψj
(r, t) is the wave function of the TDKS orbital determining the time-dependent electron density
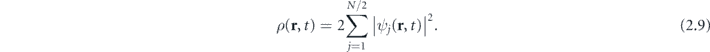
The TDKS equations are solved with initial condition
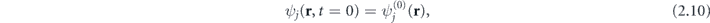
which we have discussed in the previous subsection.
Interaction of an intense laser pulse with an atomic target induces a time-dependent dipole moment D(t). For linearly polarized field, the dipole moment is directed along z axis, 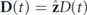 and is expressed in terms of density distribution:
and is expressed in terms of density distribution:

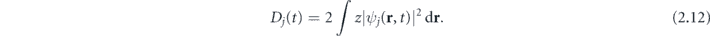
The properties of the radiation generated by atom subjected into intense laser field are determined by the dipole acceleration a(t):
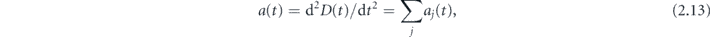
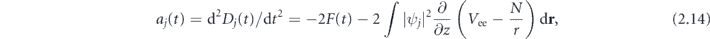
where aj (t) is the partial dipole acceleration of the KS orbital having index j. The spectral density of the dipole acceleration is given by squared Fourier transform of a(t),
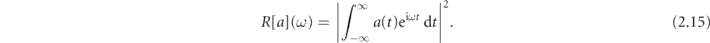
The general formulation of the density functional method allows one to study the contributions of different KS orbitals, subshells, and whole shells of an atom to the total dipole acceleration; thereby, TDKS equations provide access to the inner details of the atomic response in the external field. Corresponding contributions from shell or subshell, respectively, are given by proper summation in j:

where the range of j determines the contribution for whole shell n or either subshell (n, l). The spectral density of partial contributions of KS orbitals, subshells, and shells are calculated using equation (2.15) as R[aj
](ω), ![$R\left[{\bar{a}}_{nl}\right]\left(\omega \right)$](https://content.cld.iop.org/journals/1367-2630/23/4/043014/revision3/njpabe8a9ieqn8.gif) , and
, and ![$R\left[{\hat{a}}_{n}\right]\left(\omega \right)$](https://content.cld.iop.org/journals/1367-2630/23/4/043014/revision3/njpabe8a9ieqn9.gif) , respectively.
, respectively.
The algorithm for the numerical solution of TDKS equation (2.7) is the same as that used by us in reference [20]. Taking into account that for linearly polarized laser pulse the magnetic quantum number is conserved for each KS orbital, the KS orbitals are expanded in spherical harmonics [43, 46]:
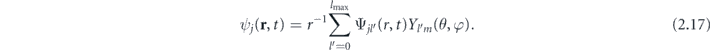
Each term corresponds to the orbital momentum l', and Ψjl'(r, t) is the radial part satisfying the initial condition 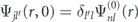 . Here, δl'l
is the Kronecker symbol, and n, l, m are quantum numbers that define KS orbital number j by (2.6). Since |ψj
(r, t)|2 does not depend on the azimuthal angle, the electron–electron interaction potential can be expanded in the Legendre polynomial, Pk
(cos θ), series. For considered laser pulse parameters, this expansion may be limited by the first three terms:
. Here, δl'l
is the Kronecker symbol, and n, l, m are quantum numbers that define KS orbital number j by (2.6). Since |ψj
(r, t)|2 does not depend on the azimuthal angle, the electron–electron interaction potential can be expanded in the Legendre polynomial, Pk
(cos θ), series. For considered laser pulse parameters, this expansion may be limited by the first three terms:
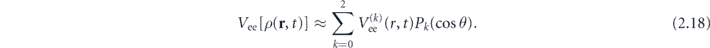
Using expansion (2.17) and approximation (2.18) we reduce equation (2.7) to the system of coupled equations:
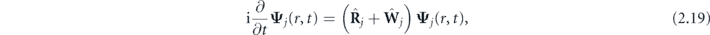
where Ψj
is the column-vector whose l'th element is Ψjl'(r, t). Elements of the diagonal matrix 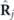 are
are
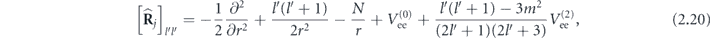
and elements of the pentadiagonal matrix 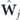 are determined by
are determined by
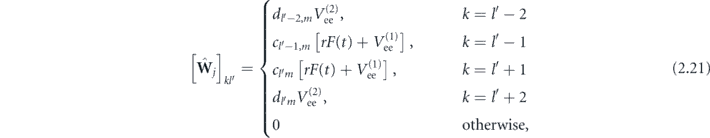
where
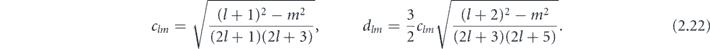
The propagation of Ψj (r, t) over time step Δt is performed using three-split-operator symmetric decomposition [47]:
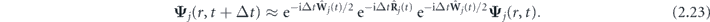
First and third exponential operators are applied through the diagonalization of matrix  within unitary transformation
within unitary transformation 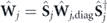 , where
, where 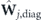 is the diagonal matrix and unitary matrix
is the diagonal matrix and unitary matrix 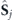 is known analytically:
is known analytically:
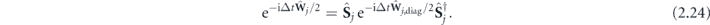
The second exponential operator is approximated by Crank–Nicolson method:

The second derivative in 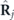 is calculated by using the Numerov approximation [46].
is calculated by using the Numerov approximation [46].
The maximum orbital momentum in expansion of wave functions in spherical harmonics is lmax = 64 for calculations in section 3 and lmax = 512 for calculations in section 4. The orbitals on 1–3 shells are frozen, i.e. 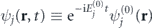 for j ⩽ 14. Freezing of internal orbitals makes it possible to use a relatively large time step Δt = 0.02 a.u. without losing accuracy in numerical calculations. The absorbing layer is modeled by multi-hump imaginary potentials [48] with total absorption layer width rabs = 50 a.u., providing a wide range of effectively absorbed de Broglie wavelengths.
for j ⩽ 14. Freezing of internal orbitals makes it possible to use a relatively large time step Δt = 0.02 a.u. without losing accuracy in numerical calculations. The absorbing layer is modeled by multi-hump imaginary potentials [48] with total absorption layer width rabs = 50 a.u., providing a wide range of effectively absorbed de Broglie wavelengths.
3. Interaction with monochromatic XUV field
In this section, we consider the interaction of Xe atom with a perturbative monochromatic XUV field. Within the numerical solution of TDKS equation (2.7), we calculate the total (angle-integrated) PICS and study the response of individual subshells from the 4th and 5th shells.
The XUV field F(t) is parameterized as F(t) = F0 f(t)cos(ω0 t), where ω0 is the carrier frequency, and f(t) is trapezoidal envelope with duration τp = 5 fs for flat top part and τ0 = 0.5 fs for tuning on/off part. The intensity of the XUV pulse is fixed, I = 2 × 1012 W cm−2, while frequency ω0 is considered in the range 20–220 eV. For such parameters we can neglect the contribution from the two-photon ionization.
The PICS  is found based on the sum of the averaged ionization probabilities per unit time from individual KS orbitals:
is found based on the sum of the averaged ionization probabilities per unit time from individual KS orbitals:
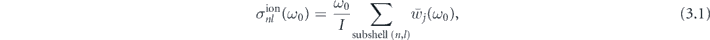
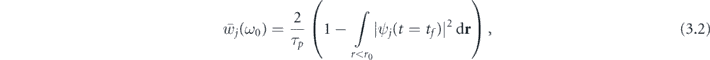
where, tf
= τp
+ 2τ0 is the ending time of the XUV pulse, r0 = 10 a.u. determines the radius of the sphere, whose edge separates bounded (r < r0) and free electrons (r > r0). The used value of r0 was chosen based on the stability of  when changing r0 near 10 a.u. for all considered n, l in a wide range of ω0. Figure 1(a) shows PICS
when changing r0 near 10 a.u. for all considered n, l in a wide range of ω0. Figure 1(a) shows PICS  for all subshells on 4th and 5th shells. PICSs for 5p, 5s, and 4d subshells contain wide maxima near ω0 ≈ 100 eV. The corresponding maximum in 4d PICS is more than an order of magnitude higher than that for 5p and 5s subshells. Note that the calculated PICSs are in excellent agreement with the experimental PICS from reference [49], which confirms the high accuracy of the TDKS equation (2.7) with used electron–electron interaction potential for studying phenomena caused by electron–electron interactions in Xe atom. PICSs for 4s and 4p subshells are negligible in the region of the giant resonance 60 eV < ω < 130 eV due to insufficient photon energy for ionization (the threshold of the photoelectric effect for 4p subshell is |E4p
| = 145.5 eV, for 4s, |E4s
| = 189.4 eV, see table 1).
for all subshells on 4th and 5th shells. PICSs for 5p, 5s, and 4d subshells contain wide maxima near ω0 ≈ 100 eV. The corresponding maximum in 4d PICS is more than an order of magnitude higher than that for 5p and 5s subshells. Note that the calculated PICSs are in excellent agreement with the experimental PICS from reference [49], which confirms the high accuracy of the TDKS equation (2.7) with used electron–electron interaction potential for studying phenomena caused by electron–electron interactions in Xe atom. PICSs for 4s and 4p subshells are negligible in the region of the giant resonance 60 eV < ω < 130 eV due to insufficient photon energy for ionization (the threshold of the photoelectric effect for 4p subshell is |E4p
| = 145.5 eV, for 4s, |E4s
| = 189.4 eV, see table 1).
Figure 1. (a) Angle-integrated partial PICSs  of Xe for 5p, 5s, 4d, 4p and 4s subshells. Solid lines are TDDFT results, dashed lines are TDDFT results with frozen electron–electron potential, and black crosses are experimental data for 4d, 5s, and 5p subshells from reference [49]. (b) and (c) Linear response of individual subshells at the 4th shell (thin lines) and the whole 4th shell (thick line) calculated as
of Xe for 5p, 5s, 4d, 4p and 4s subshells. Solid lines are TDDFT results, dashed lines are TDDFT results with frozen electron–electron potential, and black crosses are experimental data for 4d, 5s, and 5p subshells from reference [49]. (b) and (c) Linear response of individual subshells at the 4th shell (thin lines) and the whole 4th shell (thick line) calculated as ![$R\left[{\bar{a}}_{nl}\right]\left({\omega }_{0}\right)$](https://content.cld.iop.org/journals/1367-2630/23/4/043014/revision3/njpabe8a9ieqn23.gif) and
and ![$R\left[{\hat{a}}_{n}\right]\left({\omega }_{0}\right)$](https://content.cld.iop.org/journals/1367-2630/23/4/043014/revision3/njpabe8a9ieqn24.gif) for n = 4, respectively, in monochromatic XUV field with frequency ω0 and intensity I = 2 × 1012 W cm−2. The panels (b) and (c) corresponds to the TDDFT result with time-dependent and frozen electron–electron potential, respectively. The dashed vertical lines in panels (b) and (c) denote the transition energies between subshells with orbital angular momentum l differing by one.
for n = 4, respectively, in monochromatic XUV field with frequency ω0 and intensity I = 2 × 1012 W cm−2. The panels (b) and (c) corresponds to the TDDFT result with time-dependent and frozen electron–electron potential, respectively. The dashed vertical lines in panels (b) and (c) denote the transition energies between subshells with orbital angular momentum l differing by one.
Download figure:
Standard image High-resolution imageIn the central mean-field model, the shape resonance in the 4d PICS originates from a sharp resonance-like increase in the matrix element of the transition from the 4d state to the continuum ɛf state. This results from the double-well structure of the effective potential created by the ion field and centrifugal force. The barrier between these two wells suppresses the overlapping of continuum ɛf and 4d bound state wave functions. This overlapping gradually increases with increasing ɛ and is maximized for those energies, which are located near the maximum of this barrier [50–54]. As a result, the matrix element of the 4d → ɛf transition increases sharply. The further increasing photoelectron energy in f-channel leads to a decreasing transition matrix element due to the nodal structure of 4d orbital, thereby forming the shape of the giant resonance in the 4d PICS.
Our TDKS calculations of PICSs with the frozen potential for electron–electron interaction (Vee(r, t) ≡ Vee[ρ0(r)]) show: (i) the maximum of PICS for 4d subshell is located at ω0 ≈ 80 eV; (ii) PICSs for 5p and 5s subshells do not show up maxima (see dashed lines in figure 1(a)). The account of the time-dependent dynamics into potential Vee(r, t) shifts the maximum of the 4d PICS and makes the shape of resonance wider. Moreover, due to the energy exchange with the external shell, PICSs for 5p and 5s subshells also get a strong maximum around 90 eV (see solid lines in figure 1(a)). All these issues are found in agreement with previous results in reference [40].
The broadening and shift of the giant resonance in 4d PICS is primarily the consequence of the 'collectivization' of ten 4d electrons via the interchannel coupling [33, 40, 51, 53, 54]. However, when the Xe atom is exposed to an external field at the frequency ω0 ≳ 100 eV, a linear response (i.e. induced dipole moment) is observed not only for 4d but also for 4p and 4s subshells. This can be seen from the calculation of spectral densities at the carrier frequency ω0 of the dipole acceleration for individual subshells, ![$R\left[{\bar{a}}_{nl}\right]\left({\omega }_{0}\right)$](https://content.cld.iop.org/journals/1367-2630/23/4/043014/revision3/njpabe8a9ieqn25.gif) , and for the 4th shell,
, and for the 4th shell, ![$R\left[{\hat{a}}_{n}\right]\left({\omega }_{0}\right)$](https://content.cld.iop.org/journals/1367-2630/23/4/043014/revision3/njpabe8a9ieqn26.gif) , where n = 4. Freezing of the electron–electron potential leads to a decrease in the 4p and 4s orbitals response in the range ω0 = 100–130 eV by an order of magnitude or even higher (see figure 1(c)). Thus, the electron–electron interaction with the 4d subshell causes the enhancement of the response of 4p and 4s subshells. This strong interchannel coupling is realized due to similar spatial distribution of all orbitals on the 4th shell (see figure 2). Indeed, according to the perturbation theory for the TDKS equations [37, 55], the coupling matrix element between different KS orbitals is maximized for similar spatial distributions of their wavefunctions. Figure 2 shows that the wide maxima of the radial probability distributions of KS orbitals |Ψnl(0)
|2(r) for 4d, 4p and 4s subshells are located at r ∼ 0.68–0.75 a.u., and the characteristic scales of the decreasing from the maximum for 4d, 4p and 4s wave functions are approximately the same. This promotes a laser photon energy transfer from the 4d subshell to orbitals on 4p and 4s subshells through the electron–electron interaction. This physical channel, along with the interaction between electrons on the 4d subshell, can also be one of the reasons for the shift and expansion of the giant resonance in the PICS for the 4d subshell.
, where n = 4. Freezing of the electron–electron potential leads to a decrease in the 4p and 4s orbitals response in the range ω0 = 100–130 eV by an order of magnitude or even higher (see figure 1(c)). Thus, the electron–electron interaction with the 4d subshell causes the enhancement of the response of 4p and 4s subshells. This strong interchannel coupling is realized due to similar spatial distribution of all orbitals on the 4th shell (see figure 2). Indeed, according to the perturbation theory for the TDKS equations [37, 55], the coupling matrix element between different KS orbitals is maximized for similar spatial distributions of their wavefunctions. Figure 2 shows that the wide maxima of the radial probability distributions of KS orbitals |Ψnl(0)
|2(r) for 4d, 4p and 4s subshells are located at r ∼ 0.68–0.75 a.u., and the characteristic scales of the decreasing from the maximum for 4d, 4p and 4s wave functions are approximately the same. This promotes a laser photon energy transfer from the 4d subshell to orbitals on 4p and 4s subshells through the electron–electron interaction. This physical channel, along with the interaction between electrons on the 4d subshell, can also be one of the reasons for the shift and expansion of the giant resonance in the PICS for the 4d subshell.
Figure 2. Radial probability distribution |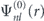 |2 for stationary KS orbitals on 4th and 5th shells.
|2 for stationary KS orbitals on 4th and 5th shells.
Download figure:
Standard image High-resolution imageIt should be noted that the calculated responses of individual subshells of the Xe atom in the XUV field contain narrow resonance maxima seen in figure 1(b). The corresponding frequencies equal to the difference in the binding energies of the given subshell and the other subshells having angular momentum differing by one. This resonance maxima originate from the transition between the initial state (n, l, m) of each KS orbital ψj to the state (n', l', m) of unperturbed Hamiltonian under the action of external XUV field with a resonant frequency ω0 = |Ej' − Ej |, where Ej' is the energy of the (n', l', m) level and l' = l ± 1. 6 As a result, the dipole moment of jth KS orbital, Dj (t), contains a cross-term that oscillates with this frequency. However, the dipole moment of j'th KS orbital, Dj'(t), also contain oscillations at the same resonant frequency and the same amplitude but the opposite sign, which is due to the back transition (n', l', m) → (n, l, m) in the j'th KS orbital ψj'. As a result, all the 'artificial' resonances of KS orbitals cancel each other in the total dipole moment. Indeed, as is seen from figure 1(b), the responses of 4d and 4p subshells have narrow resonance maxima at ω0 = |E4d − E4p | ≈ 75.6 eV, but there is no any enhancement in the total response of the 4th shell at this resonance frequency.
4. HHG in xenon
The nonlinear response of the xenon atom appears at high harmonics of the IR frequency when the atom is subjected into an intense IR field. This section considers the HHG in Xe subjected to the two-cycle IR-field having intensity I = 1.9 × 1014 W cm−2 and wavelength λ = 1.8 μm. The selected parameters correspond to the experiment [14]. In the numerical calculations, we parameterize the electric component of the laser pulse in terms of vector potential:
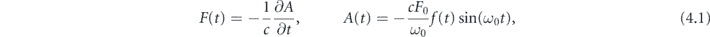
where ω0 = 2πc/λ is the carrier frequency, c is the speed of light, F0 is the strength of a laser pulse, whose magnitude determines the intensity of a laser pulse as 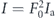 , where F0 is normalized to the atomic electric-field unit and Ia = 3.51 × 1016 W cm−2. The envelope of the vector potential is f(t) = sin2(πt/τ) for 0 < t < τ and f(t) = 0 otherwise. The intensity full-width at half maximum duration τp
= τ[2 arccos(2−1/4)/π] = 12 fs corresponds to two field periods at the carrier frequency.
, where F0 is normalized to the atomic electric-field unit and Ia = 3.51 × 1016 W cm−2. The envelope of the vector potential is f(t) = sin2(πt/τ) for 0 < t < τ and f(t) = 0 otherwise. The intensity full-width at half maximum duration τp
= τ[2 arccos(2−1/4)/π] = 12 fs corresponds to two field periods at the carrier frequency.
In figure 3(a) we show a comparison of HHG spectra R[a](ω) calculated within TDDFT (blue solid line), analytical parameterization (red solid line) suggested in references [10, 56, 57], and experimental result [14] (black line). 7 The analytical parameterization of HHG yield consists in the separation of the atomic and laser parts (EWP):
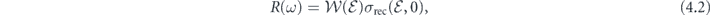
where 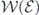 is the EWP,
is the EWP, 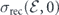 is the differential PRCS of electron with kinetic energy
is the differential PRCS of electron with kinetic energy 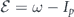 , where Ip
is the ionization potential (see more details in appendix
, where Ip
is the ionization potential (see more details in appendix
Figure 3. (a) HHG spectra for Xe atom subjected to the two-cycle linearly polarized laser pulse with peak intensity I = 1.9 × 1014 W cm−2 and central wavelength λ = 1.8 μm. The blue dotted line is the TDDFT result, blue solid line is the smoothed TDDFT result, the red line is the (smoothed) analytical result for HHG yield (4.2) utilizing experimental PRCS [49, 62], black line denotes normalized experimental HHG spectrum from reference [14]. (b) Time-frequency spectrogram |S(ω, t)|2 (in arbitrary units) of the dipole acceleration a(t) calculated using TDDFT. Black lines denote the classical dependences of the emitted photon energy on the return time moment for first return (dotted lines) and higher-order returns (dashed lines).
Download figure:
Standard image High-resolution imageTo ensure that the high harmonic generation in Xe is provided within the standard three-step scenario (and impact ionization does not play an important role), we calculate the Gabor transform of the dipole acceleration found from TDDFT:
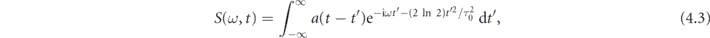
where τ0 = 0.2 fs. Figure 3(b) shows the time-frequency distribution |S(ω, t)|2 and the classical dependences of the generation frequency for the trajectories with one and higher-order returns [63] (dotted and dashed lines, respectively) on the return time moment. The generation frequency was found as ωc
= Ekin + Ip
, where Ip
= 12.1 eV is the ionization potential of Xe atom, Ekin is the gained kinetic energy calculated using classical Newton equation (see appendix
4.1. Individual response of orbitals on two active shells
The TDDFT formalism allows one to separate the contributions of different KS orbitals to the total dipole acceleration, thereby providing a detailed study of their collective contribution to the enhancement of the HHG yield. In figure 4 we present the Fourier spectra of contributions aj
(t) for individual orbitals, of contributions 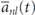 for subshells 4d, 4p, and 4s, and contribution for 4th shell determined by
for subshells 4d, 4p, and 4s, and contribution for 4th shell determined by 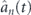 for n = 4.
for n = 4.
Figure 4. Fourier spectra of the partial contributions of different KS orbitals aj
(t), subshells 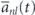 , and 4th shell
, and 4th shell 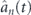 for n = 4 to the total dipole acceleration given by equation (2.13) for the same parameters, as in figure 3. (a) Results for the 5p0, 5p±1 and 5s orbitals (orange, gray, and light blue lines, respectively). (b) Results for 4d, 4p, and 4s subshells and the entire 4th shell (red, green, brown, and black lines, respectively). (c) Results for 4d orbitals with m = 0, 1, 2 (thin black, gray, and thick red lines, respectively). (d) Results for 4p0, 4p1 and 4s orbitals (black, green, and brown lines, respectively). The blue lines in (a) and (b) show the total smoothed HHG yield; the black line in (a) is the total smoothed HHG yield calculated with frozen electron–electron potential.
for n = 4 to the total dipole acceleration given by equation (2.13) for the same parameters, as in figure 3. (a) Results for the 5p0, 5p±1 and 5s orbitals (orange, gray, and light blue lines, respectively). (b) Results for 4d, 4p, and 4s subshells and the entire 4th shell (red, green, brown, and black lines, respectively). (c) Results for 4d orbitals with m = 0, 1, 2 (thin black, gray, and thick red lines, respectively). (d) Results for 4p0, 4p1 and 4s orbitals (black, green, and brown lines, respectively). The blue lines in (a) and (b) show the total smoothed HHG yield; the black line in (a) is the total smoothed HHG yield calculated with frozen electron–electron potential.
Download figure:
Standard image High-resolution image4.1.1. 5p0 orbital
Let us consider the response of the outer-valence 5p0 orbital, which is oriented in space along the electric field and interacts most actively with the linearly-polarized IR laser pulse. As seen from figure 4(a), the partial dipole acceleration spectrum of 5p0 KS orbital contains a high-frequency flat plateau with the same cutoff as the full HHG spectrum. At low frequencies, ω ∼ 15–30 eV, the response of 5p0 orbital contains a near-threshold enhancement associated with a sharp increasing of the transition matrix element from the continuum state to the 5p0 state with decreasing frequency of emitted photons [11, 51, 53, 67, 68]. The response of the 5p0 KS orbital is well described by the three-step scenario for the HHG [1, 8], i.e. the electron from the 5p0 KS orbital is ionized by a laser pulse, then it is accelerated by a laser field in the continuum and, finally, electron recombines to the initial state with the emission of a photon with energy equal to the sum of gained kinetic energy and ionization potential. The only peculiarity is that response of 5p0 KS orbital contains a narrow peak at ω = E5p − E4d ≈ 57.1 eV caused by the transition between 5p0 and 4d0 levels led by the electron–electron interaction. In the full HHG spectrum, this resonant peak is compensated by the corresponding resonance term in the response of 4d0 KS orbital (see section 3). It should be emphasized that the spectrum of the dipole acceleration of 5p0 KS orbital is similar to the HHG spectrum obtained with frozen electron–electron interaction approximation shown by the black line in figure 4(a). This explicitly shows that giant enhancement near 100 eV results from the strong interchannel coupling between different subshells.
4.1.2. Other orbitals from 5th and 4th shells
The tunneling rate in the infrared laser field of intensity 1.9 × 1014 W cm−2 for orbitals others than 5p0 is negligibly small. In the case of orbitals on the 4th shell and the 5s orbital, this is due to large binding energy (see table 1). In the case of 5p±1 orbitals having the same binding energy as 5p0, this is due to suppressing of the tunneling ionization for m ≠ 0 [69]. In addition, an important effect that reduces the probability of tunneling ionization for all KS orbitals, including 5p0, is the polarization of the atom in an external field [20, 70, 71].
8
As our calculations show, the final ionization probability of 5p±1 orbitals is ≈0.6%; for other lower-lying orbitals, it is even less. Smallness in the tunneling rates suppresses the three-step scenario for all orbitals others than 5p0. However, as our numerical calculation show (see figure 4(b)), 4d and 4p subshells also contribute to the total HHG yield. This non-three-step contribution can be explained by strong coupling of these subshells to the 5p0 KS orbital and each other caused by electron–electron potential. Indeed, the time-dependent wave function of the 5p0 KS orbital,  , where
, where  , can presented as a sum of two terms [72–74]:
, can presented as a sum of two terms [72–74]:
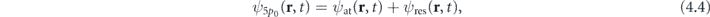
where ψat(r, t) is so-called adiabatic part, which can be well approximated by the field-free wave function, 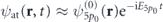 , and ψres(r, t) is the rescattering part of the wave function. Although this rescattering part is exponential small, it induces both the time-dependent moment given by the 5p0 orbital,
, and ψres(r, t) is the rescattering part of the wave function. Although this rescattering part is exponential small, it induces both the time-dependent moment given by the 5p0 orbital, 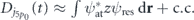 , and variation in the electron density ρ(r, t) from the corresponding field-free distribution,
, and variation in the electron density ρ(r, t) from the corresponding field-free distribution,
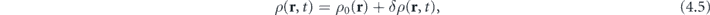
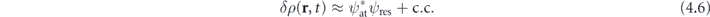
The small changes in the density ρ(r, t) lead a variation of electron–electron interaction, δVee:
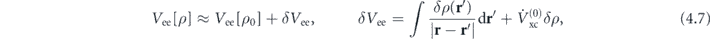
where 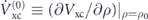 . The term δVee can be considered as a perturbation which acts as a broadband excitation source inducing the time-dependent moment Dj
(t) of KS orbitals. Moreover, the rescattering part of 5p0 KS orbital can affect on all orbitals including those with m ≠ 0. The account of δVee within perturbation theory leads to variation ψj
(r, t) of the KS orbitals with index
. The term δVee can be considered as a perturbation which acts as a broadband excitation source inducing the time-dependent moment Dj
(t) of KS orbitals. Moreover, the rescattering part of 5p0 KS orbital can affect on all orbitals including those with m ≠ 0. The account of δVee within perturbation theory leads to variation ψj
(r, t) of the KS orbitals with index 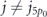 :
:
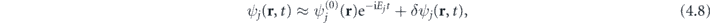
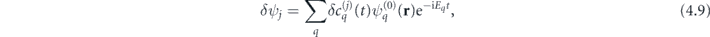
where the sum is carried out over all possible states q of the unperturbed Hamiltonian (2.1) forming a complete orthogonal system of wavefunctions 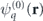 , and
, and
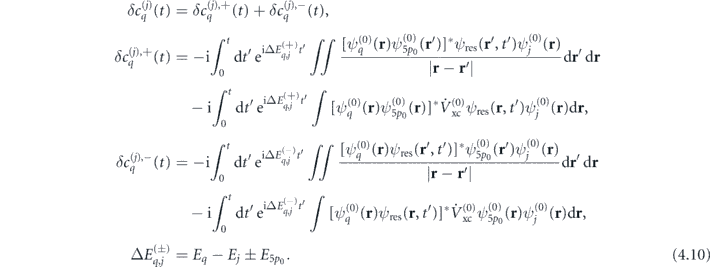
Using the variation in ψj , the time-dependent dipole moment of jth KS orbital (2.12) can be written as
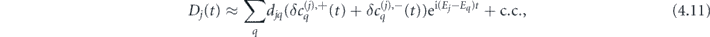
where ![${d}_{jq}=\int {\left[{\psi }_{j}^{\left(0\right)}\left(\mathbf{r}\right)\right]}^{{\ast}}z{\psi }_{q}^{\left(0\right)}\left(\mathbf{r}\right)\mathrm{d}\mathbf{r}$](https://content.cld.iop.org/journals/1367-2630/23/4/043014/revision3/njpabe8a9ieqn43.gif) is the transition dipole matrix element. Among all possible intermediate states q, only those with the same quantum numbers m and differing by one orbital angular momentum l compared to the jth state contribute to the sum (4.11).
is the transition dipole matrix element. Among all possible intermediate states q, only those with the same quantum numbers m and differing by one orbital angular momentum l compared to the jth state contribute to the sum (4.11).
The high response of KS orbitals for j ≠ 5p0 can be interpreted as a collective dynamics of the valence 5p0 electron and a core electrons (see also references [14, 24, 31]). Indeed, in the first step, the valence electron (5p0 electron) tunnels through the barrier and gets some extra kinetic energy Ek
into the laser-perturbed continuum, which shares with a core electron on jth orbital. The correlation between these two electrons induces changing in electron–electron interaction and leads to the 'relaxation' of these two electrons into 5p0 orbital and intermediate qth state with a hole in jth state. The subsequent transition from qth state to jth state returns the atom to the initial ground state with a harmonic emission of frequency 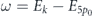 in agreement with the energy conservation law.
in agreement with the energy conservation law.
Excitation of oscillations of the 4th shell due to the recolliding photoelectron leads to the formation of a giant HHG yield in the frequency range ω = 60–130 eV, which at ω = 100 eV is more than one order of magnitude higher compared to the contribution of 5p0 KS orbital. In this frequency range, the 4d subshell contains a giant resonance in PICS, so that 4d orbitals have large coupling matrix elements with the rescattering continuum wavepacket, 5p0 state and intermediate  f states in the continuum, and also high dipole matrix elements of transition
f states in the continuum, and also high dipole matrix elements of transition  f → 4d. Different orbitals from 4d subshell near the giant enhancement have the same high response (see figure 4(c) and reference [24]), which is due to the interaction of laser-perturbed 5p0 KS orbital with all m orbitals and with the 'collectivization' of electrons in the 4d subshell [33, 40, 54]. However, as seen from figure 4(b), a large response in the region of giant HHG enhancement is also observed for deeper-lying 4p and 4s subshells. We note that it was previously accepted that only 4d subshell participates in HHG enhancement. Moreover, as can be seen from figures 4(c) and (d), the responses of individual KS orbitals in the 4th shell have a comparable response at ω > 100 eV. Coherent summation of responses from different subshells on 4th shell leads to a noticeable (more than two times) increase in HHG yield compared to the contribution of only 4d subshell in the frequency range ω ∼ 80–140 eV. Above the giant enhancement region, at ω > 170 eV, the response of the 4p subshell exceeds the response of the 4d subshell despite fewer electrons on the 4p subshell. The reason for the broadband high-frequency response of 4p and 4s orbitals is related, from the one hand, to the action of the Vee perturbation induced by the rescattering wavepacket from 5p0 orbital. From the other hand, as shown in section 3, 4p and 4s subshells can oscillate due to the coupling with the 4d orbital. In the case of HHG, this means that the recollision-induced perturbations δψj
(4.9) in the wavefunctions of 4d KS orbitals induce a secondary perturbation in the electron–electron potential, which acts on all other KS orbitals, including 4p and 4s orbitals. Note that the effect of this secondary disturbance is also noticeable in the response of orbitals from 5th shell at ω = 70–130 eV (see figure 4(a)). In this frequency range signal amplification is observed for 5p±1 orbitals. In general, the contribution of the 5p±1 and 5s orbitals to HHG is significantly lower than that for the 4th shell and 5p0 orbital because of the small matrix element of the transition to the high-energy continuum states. At the same time, induced time-dependent electron–electron potential δVee leads to a broadband response of the 5s and 5p±1 KS orbitals on the outer shell for the frequency range ω ∼ 15–30 eV. A large low-frequency response of orbitals on the outer shell also exists in other noble-gas atoms, e.g. for Ar atom see references [20, 22]. The responses of orbitals on the outer shell are in phase and provide visible contribution (comparable with that for of 5p0 KS orbital) to the total HHG yield for ω ∼ 15–30 eV.
f → 4d. Different orbitals from 4d subshell near the giant enhancement have the same high response (see figure 4(c) and reference [24]), which is due to the interaction of laser-perturbed 5p0 KS orbital with all m orbitals and with the 'collectivization' of electrons in the 4d subshell [33, 40, 54]. However, as seen from figure 4(b), a large response in the region of giant HHG enhancement is also observed for deeper-lying 4p and 4s subshells. We note that it was previously accepted that only 4d subshell participates in HHG enhancement. Moreover, as can be seen from figures 4(c) and (d), the responses of individual KS orbitals in the 4th shell have a comparable response at ω > 100 eV. Coherent summation of responses from different subshells on 4th shell leads to a noticeable (more than two times) increase in HHG yield compared to the contribution of only 4d subshell in the frequency range ω ∼ 80–140 eV. Above the giant enhancement region, at ω > 170 eV, the response of the 4p subshell exceeds the response of the 4d subshell despite fewer electrons on the 4p subshell. The reason for the broadband high-frequency response of 4p and 4s orbitals is related, from the one hand, to the action of the Vee perturbation induced by the rescattering wavepacket from 5p0 orbital. From the other hand, as shown in section 3, 4p and 4s subshells can oscillate due to the coupling with the 4d orbital. In the case of HHG, this means that the recollision-induced perturbations δψj
(4.9) in the wavefunctions of 4d KS orbitals induce a secondary perturbation in the electron–electron potential, which acts on all other KS orbitals, including 4p and 4s orbitals. Note that the effect of this secondary disturbance is also noticeable in the response of orbitals from 5th shell at ω = 70–130 eV (see figure 4(a)). In this frequency range signal amplification is observed for 5p±1 orbitals. In general, the contribution of the 5p±1 and 5s orbitals to HHG is significantly lower than that for the 4th shell and 5p0 orbital because of the small matrix element of the transition to the high-energy continuum states. At the same time, induced time-dependent electron–electron potential δVee leads to a broadband response of the 5s and 5p±1 KS orbitals on the outer shell for the frequency range ω ∼ 15–30 eV. A large low-frequency response of orbitals on the outer shell also exists in other noble-gas atoms, e.g. for Ar atom see references [20, 22]. The responses of orbitals on the outer shell are in phase and provide visible contribution (comparable with that for of 5p0 KS orbital) to the total HHG yield for ω ∼ 15–30 eV.
5. Summary and conclusions
To conclude, in this work, we have used the time-dependent density functional theory to study the HHG by Xe atom in an intense infrared pulse. In contrast to the previous numerical studies of this phenomenon, the dynamics of the whole 4th and 5th shells of the Xe atom is taken into account, leading to a good agreement with the experiment and the analytical parameterization of HHG yield in terms of the EWP and exact (experimental) PRCS to the 5p0 state. It was demonstrated that as for argon atom [20], in the low-frequency range of generated spectral harmonics (ω ∼ 15–30 eV), a comparable contribution to HHG is given by all orbitals from the outer shell. The origin of such unusual collective contribution is the broadband component in electron–electron potential induced by the recolliding 5p0 wave packet, which collisionally disturbs outer shell orbitals, thereby induces the time-dependent dynamics in these orbitals. In the giant enhancement region (ω ∼ 60–130 eV), the 5th shell's response is much smaller than that of the 4th shell, which is easily excited by the electron–electron potential due to the giant resonance in 4d transition to the continuum. Moreover, in addition to 4d subshell, deeper-lying 4p and 4s subshells also participate in the HHG, giving substantial contribution at higher frequencies. The reason for the substantial response of the 4p and 4s subshells at the giant resonance is the dynamic interaction between the orbitals on the 4th shell, associated with the close localization of their wave functions in space. The results of numerical simulations demonstrate that a similar response of 4p and 4s subshells is presented by interaction of Xe atom with an external linearly-polarized XUV field. Therefore, correlation interaction between all orbitals on the 4th shell can contribute to both the formation of the HHG spectra by infrared field and PICSs from 4d, 5p, and 5s subshells of Xe atom.
Acknowledgement
Numerical simulations were supported by the Russian Science Foundation (Grant No. 20-11-20289). This work was also supported by the Russian Foundation for Basic Research (Grant No. 20-32-70213), Grants Council of the President of the Russian Federation (Grant No. MK-1849.2020.2), and the Foundation for the Advancement of Theoretical Physics and Mathematics 'BASIS' (Grant No. 19-1-2-52-1).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Appendix A.: Analytical factorization of HHG yield
The HHG yield in an intense low-frequency linearly-polarized laser field can be factorized into two factors [30, 56, 57, 66, 75]. The first universal factor,  , known as EWP, describes tunneling and propagation of an active electron in a laser field along closed classical trajectories with returning energy
, known as EWP, describes tunneling and propagation of an active electron in a laser field along closed classical trajectories with returning energy 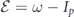 , where ω is harmonic frequency. The second factor is field-free differential PRCS for the zero angle between returning electron momentum and polarization vector of emitted photon,
, where ω is harmonic frequency. The second factor is field-free differential PRCS for the zero angle between returning electron momentum and polarization vector of emitted photon, 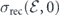 ,
,
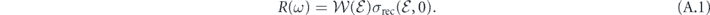
Differential PRCS 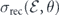 is related to the differential PICS, σion(ω, θ), by the principle of detailed balance [32]:
is related to the differential PICS, σion(ω, θ), by the principle of detailed balance [32]:
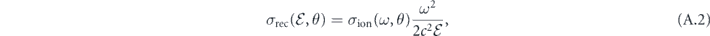
where θ is an angle between photon polarization vector and electron momentum.
Although factorization (A.1) was theoretically justified within the single-active electron approximation (SAEA) [56, 66, 75], it provides a qualitative agreement with HHG experimental results [11, 12, 14–16]. For practical calculations, the form of EWP can be found numerically within SAEA calculation for a reference atom [56, 57], or either within analytical expressions [41, 76]. In this work, EWP was calculated analytically within adiabatic approximation for HHG [41]. Within adiabatic approximation, the EWP is determined by the set of real times { }, corresponding to the moments of ionization (
}, corresponding to the moments of ionization ( ) and recombination (
) and recombination (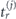 ). These times obey a system of transcendental equations:
). These times obey a system of transcendental equations:
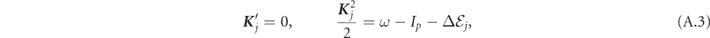
where K 'j and K j are instantaneous electron momenta at the moment of ionization and recombination

and 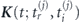 is instantaneous (at the moment t) momentum of an electron moving along a closed trajectory in the time interval
is instantaneous (at the moment t) momentum of an electron moving along a closed trajectory in the time interval 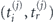 in the laser field with vector potential
in the laser field with vector potential 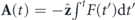 ,
,
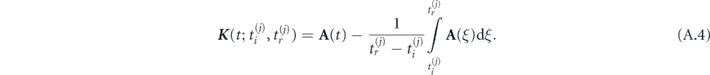
The term 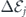 is the quantum correction [72]
is the quantum correction [72]
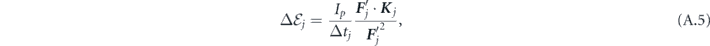
where 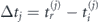 and
and 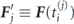 . Detailed analysis of the system (A.3) for the case of linearly-polarized laser field can be found in [77].
. Detailed analysis of the system (A.3) for the case of linearly-polarized laser field can be found in [77].
The EWP  is proportional to the square of a sum over the partial amplitudes, corresponding to closed electron trajectories,
is proportional to the square of a sum over the partial amplitudes, corresponding to closed electron trajectories,
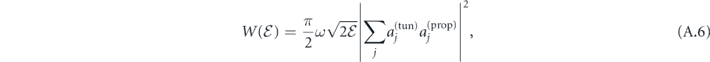
where each partial amplitude can be factorized in terms of tunneling,  , and propagation,
, and propagation, 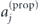 , factors. The tunneling factor,
, factors. The tunneling factor, 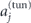 , is given by
, is given by
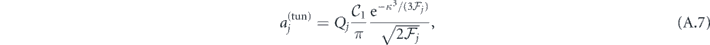
where 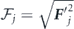 ,
, 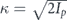 and
and 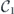 is dimensionless asymptotic coefficient of the initial bound state for the neutral atom,
is dimensionless asymptotic coefficient of the initial bound state for the neutral atom,
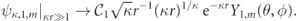
The Coulomb factor, Qj , in equation (A.7) for the case of linearly polarized laser field reduces to a 'static' factor [78],
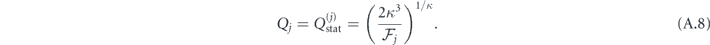
The propagation factor, 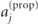 , is given by
, is given by
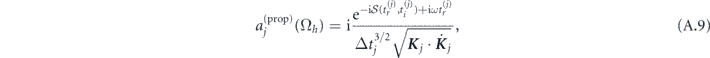
where  , and
, and 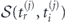 is the classical action of an electron
is the classical action of an electron
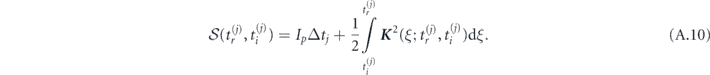
The angular distribution of PICS follows from parametrization
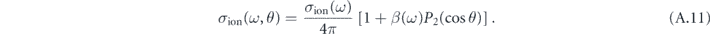
Here, σion(ω) is the angle-integrated partial cross section for 5p subshell, β(ω) is the photoelectron asymmetry parameter, P2(cos θ) = (3 cos2 θ − 1)/2 is a Legendre polynomial and θ is the angle between the photoelectron momentum direction and the photon polarization direction, ω is the photon energy. The values of σion(ω) and β(ω) are taken from the results of experimental measurements in references [49, 62].
Footnotes
- 5
In this work, we do not take into account spin–orbit interaction and other relativistic effects.
- 6
Since the ionization is weak, the potential −N/r + Vee[ρ(r, t)] has the same stationary bound energies as the unperturbed potential.
- 7
- 8
For 5p0 KS orbital, survival probability is 88.4%, while in frozen-core model, i.e. excluding polarizability, just 19.3%.








