Feature selection using self-information and entropy-based uncertainty measure for fuzzy neighborhood rough set

Abstract

Feature selection based on the fuzzy neighborhood rough set model (FNRS) is highly popular in data mining. However, the dependent function of FNRS only considers the information present in the lower approximation of the decision while ignoring the information present in the upper approximation of the decision. This construction method may lead to the loss of some information. To solve this problem, this paper proposes a fuzzy neighborhood joint entropy model based on fuzzy neighborhood self-information measure (FNSIJE) and applies it to feature selection. First, to construct four uncertain fuzzy neighborhood self-information measures of decision variables, the concept of self-information is introduced into the upper and lower approximations of FNRS from the algebra view. The relationships between these measures and their properties are discussed in detail. It is found that the fourth measure, named tolerance fuzzy neighborhood self-information, has better classification performance. Second, an uncertainty measure based on the fuzzy neighborhood joint entropy has been proposed from the information view. Inspired by both algebra and information views, the FNSIJE is proposed. Third, the K–S test is used to delete features with weak distinguishing performance, which reduces the dimensionality of high-dimensional gene datasets, thereby reducing the complexity of high-dimensional gene datasets, and then, a forward feature selection algorithm is provided. Experimental results show that compared with related methods, the presented model can select less important features and have a higher classification accuracy.

Introduction

Feature selection is an important data preprocess in the fields of granular computing and artificial intelligence [1,2,3,4,5,6]. Its main goal is to reduce redundant features and simplify the complexity of the classification model, thereby improving the generalization ability of classification model [7,8,9,10,11,12]. So far, feature selection has been widely used in the fields of pattern recognition, data mining, machine learning, and so on [13,14,15,16,17].

Related work

Pawlak proposed the classic rough set model in 1982 [18], which was successfully applied in the field of feature selection [19,20,21,22,23,24,25,26,27]. However, the Pawlak proposed that rough set is based on the general binary relationship and is only suitable for discrete data [28]. Some information may be lost, while the discretization method is used for continuous data [29]. To solve this problem, many scholars expanded the rough set model. Dubois et al. introduced the concept of fuzzy rough set via combining rough set and fuzzy set, which overcomes the discrete problem and can directly reduce continuous data [30]. Hu et al. [31] proposed a new method of neighborhood granulation and neighborhood rough set for sensitive feature selection. Wang et al. [32] constructed FNRS to use parameterized fuzzy relations to describe fuzzy information granularity, which reduced the possibility of samples being misclassified. Qian et al. [33] studied the pessimistic multi-granularity rough set decision model of attribute reduction, which overcomes the shortcomings of most models that limit their application due to a single binary relationship.

As one of the most important rough set models, FNRS received extensive attention in the fields of machine learning and data mining. Shreevastava et al. proposed a new intuitionistic fuzzy neighborhood rough set model via combination of intuitionistic fuzzy set and neighborhood rough set, and applied it to heterogeneous datasets [34]. Yue et al. [35] developed fuzzy neighborhoods to be applied to cover data classification. Sun et al. [36] proposed a new fuzzy neighborhood multi-granularity rough set model by combining FNRS with multi-granularity rough set model, which expanded the type of rough set model. Xu et al. [37] redefined the fuzzy neighborhood relationship in FNRS and introduced it into conditional entropy, and proposed a new model—fuzzy neighborhood conditional entropy—which improved the measurement mechanism. In fact, the classification information is not only related to the lower approximation of the decision classification consistency, but also the upper approximation of the decision classification divergence. Wang et al. [38] introduced the concept of self-information into neighborhood rough set, and constructed neighborhood self-information measure using the upper and lower approximations of decision, which is helpful to the select optimal feature subset.

In the past few decades, uncertainty measures for feature selection from the algebra view and information view had been vigorously developed [37, 39]. From algebra view, Wang et al. introduced distance measure into fuzzy rough set model and proposed a new attribute reduction method [40]. Liu et al. designed a hash-based algorithm to calculate the positive region of neighborhood rough set, which was applied in attribute reduction [41]. Hu et al. [42] developed a matrix-based dynamic method to calculate the positive, boundary, and negative regions of neighborhood multi-granularity rough set. Fan et al. [43] focused on boundary samples using the largest decision neighborhood rough set model. Liu et al. [58,59,60] solved some practical problems from the algebra view. The importance of features based on algebra view can only express the influence of features present in feature subsets [40,41,42,43]. From information view, information entropy and some of its deformations had been widely used in feature selection in recent years. Xu et al. [37] studied the fuzzy neighborhood conditional entropy to evaluate the feature meaning in FNRS. Zhang et al. [17] proposed information entropy based on fuzzy rough set and applied it in fuzzy information system. The importance of features based on the information view only explains the impact of uncertainty classification on features [17, 37, 44, 45]. If combining the two views for feature selection, it helps to improve the quality of uncertainty measurement in decision system. Wang [45] simultaneously studied rough reduction and relative reduction from two views. Sun et al. [46] constructed an attribute reduction method based on neighborhood multi-granularity rough set, which can handle mixed incomplete datasets from two views at the same time.

Our work

To solve the problem that most feature evaluation functions only consider the information contained in the lower approximation of the decision, which may cause part of the information to be lost, this article focus on studying the feature selection method based on FNSIJE. The main content of this paper is as follows:

• Analysis shows the shortcoming of the evaluation function based on the dependency of FNRS.

• We propose three types of uncertainty indices using upper and lower approximations: decision index, optimistic decision index, and pessimistic decision index. Three definitions of precision and roughness are given based on this basis, and then combined with the concept of self-information, four fuzzy neighborhood self-information measures are proposed, and related properties are studied. Through theoretical analysis, we find the most suitable fuzzy neighborhood self-information for feature selection and apply it in practice.

• To better discuss feature selection methods based on algebra and information views, this paper studies the uncertainty measure method based on fuzzy neighborhood joint entropy. Then, we combine measure and information entropy to propose a fuzzy neighborhood self-information-based fuzzy neighborhood joint entropy (FNSIJE) method for feature selection. FNSIJE not only considers the classification information provided by the upper and lower approximations of the neighborhood decision system at the same time, but also can simultaneously select features from the algebra and information views.

The article is organized as follows: The section “Preliminaries” is the concepts of self-information and FNRS. The section “Insufficiency of neighborhood correlation functions and uncertainty measurement based on FNSIJE” points out the shortcoming of the neighborhood correlation functions; in view of this shortcoming, we propose four fuzzy neighborhood self-information measures, and study their related properties. Then, the feature selection model based on FNSIJE is constructed by combining tolerance decision self-information measure and fuzzy neighborhood joint entropy. In the section “Feature selection method based on FNSIJE model”, we design a heuristic feature subset selection method. In the section “Experimental analysis”, six UCI datasets and four microarray gene expression profile datasets are used for experimental verification. The section “Conclusion” is the conclusion of this article and the outlook for future work.

Preliminaries

In this section, it mainly deals with relevant concepts of self-information and FNRS.

Self-information

Definition 1

[47] The measure I(x) was proposed by Shannon to express the uncertainty of signal x. x is called the self-information if it as the following properties:

• (1) Non-negative: $I(x) \ge 0$.

• (2) If $p(x) \rightarrow 0$, then $I(x) \rightarrow \infty$.

• (3) If $p(x)=0$, then $I(x) = 1$.

• (4) Monotonic: if $p(x) < p(y)$, then $I(x) < I(y)$.

Here, p(x) is the probability of x.

Fuzzy neighborhood rough set

Let $\text {NDS}=\langle U,A,D,V,f,\delta \rangle$ be a neighborhood decision system. $U=\{ {{x_1},{x_2}, \ldots , {x_m}}\}$ is the set of samples. A is the set of conditional attributes and D is the set of decision classes. $V = \bigcup _{a \in A} {{V_a}}$. $f:U \times \{ A \cup D\} \rightarrow V$ is the map function, which f(a, x) is the attribute value of x on attribute a. $\delta$ is the parameter of the neighborhood radius, which $0 \le \delta \le 1$. The neighborhood decision system is simplified to $\text {NDS} = \langle U,A,D\rangle$.

Definition 2

[32, 48] Let $B \subseteq A$ be a attribute subset on the universe U, and then, B can induce a fuzzy relation $R_B$ on U; $R_B$ is a fuzzy similarity relation if the following conditions are satisfied:

• (1) Reflexivity: ${R_B}(x,x) = 1$.

• (2) Symmetry: ${R_B}(x,y) = {R_B}(y,x)$, $\forall x,y \in U$.

Definition 3

Given $\text {NDS} = \langle U,A,D\rangle$, fuzzy neighborhood radius parameter $\lambda (0< \lambda < 1)$ is used to describe the similarity of samples. For any $x,y \in U$, the fuzzy neighborhood similarity relationship between two samples x and y with regard to a is expressed as:

$$\begin{aligned} {R_a} =\left\{ \begin{array}{ll} 0,&{}\quad \left| {f(a,x)\!-\!f(a,y)} \right| > \lambda \\ 1-\left| {f(a,x)\!-\!f(a,y)} \right| ,&{}\quad \left| {f(a,x)\!-\!f(a,y)} \right| \le \lambda . \end{array} \right. \end{aligned}$$

(1)

The fuzzy neighborhood similarity matrix is ${[x]_a}(y) = {R_a}(x,y)$, for any $B \subseteq A$, ${[x]_a}(y) = {\min _{a \in B}}({[x]_a}y))$ [37].

Definition 4

Given $\text {NDS} = \langle U,A,D\rangle$, $B \subseteq A$, for any $x,y \in U$, the parameterized fuzzy neighborhood information granule of x associated with B is expressed as:

$$\begin{aligned} {\alpha _B}(x) = {[x]_a}(y) = \left\{ \begin{array}{ll} 0,&{}\quad {R_B}(x,y) < 1 - \lambda \\ {R_B}(x,y),&{}\quad {R_B}(x,y) \ge 1 - \lambda . \end{array} \right. \end{aligned}$$

(2)

Definition 5

Given $\text {NDS} = \langle U,A,D\rangle$, $U =\{ {x_1},{x_2}, \ldots , {x_m} \}$, $\text {AT} = \{ {\text {AT}_{1},\text {AT}_{2}, \ldots , \text {AT}_{n}} \}$ and $U/D = \{ {D_1},{D_2},\ldots ,{D_t} \}$, then the fuzzy decision of the sample derived from D is expressed as:

$$\begin{aligned} \text {FD} = \{ {\text {FD}_1^{\mathrm{T}},\text {FD}_2^{\mathrm{T}}, \ldots , \text {FD}_t^{\mathrm{T}}} \}. \end{aligned}$$

(3)

Here, $\text {FD}_{j} = \{ \text {FD}_{j}({x_1}),\text {FD}_{j}({x_2}), \ldots , \text {FD}_{j}({x_m})\}$ is the fuzzy rough set of sample decision equivalence class, and $j = 1,2, \ldots ,t$. When $l = 1,2, \ldots , m$, $\text {FD}_{j}({x_l})$ is recorded as the degree of membership of ${x_l} \in U$ on $\text {FD}_j$ and denoted [36] by:

$$\begin{aligned} \text {FD}_{j}({x_l}) = \frac{{\left| {{{[{x_l}]}_A}(y) \cap {D_j}} \right| }}{{\left| {{{[{x_l}]}_A}(y)} \right| }}, \end{aligned}$$

(4)

where ${[{x_l}]_A}(y)$ is fuzzy neighborhood similarity degree.

Definition 6

Given $\text {NDS} = \langle U,A,D\rangle$, $B \subseteq A$, for any $X \subseteq U$, ${\alpha _B}(x)$ is the parametric fuzzy neighborhood information granule of $x \in U$. Then, the fuzzy neighborhood upper and lower approximations of X with respect to B are, respectively, expressed as:

$$\begin{aligned} \overline{R_B^\lambda } (X)= & {} \left\{ {x \in U\left| {{\alpha _B}(x) \cap X \ne \emptyset } \right. } \right\} \end{aligned}$$

(5)

$$\begin{aligned} \underline{R_B^\lambda } (X)= & {} \left\{ {x \in U\left| {{\alpha _B}(x) \subseteq X} \right. } \right\} . \end{aligned}$$

(6)

Definition 7

Given $\text {NDS} = \langle U,A,D \rangle$, suppose any ${D_j} \in U/D = \{ {{D_1},{D_2}, \ldots ,{D_t}} \}$, then the fuzzy neighborhood positive region and its dependency degree of D in relation to B are expressed, respectively, by:

$$\begin{aligned} \text {POS}_B^\lambda (D)= & {} \mathop \cup \limits _{j = 1}^{\mathrm{t}} \underline{R_B^\lambda } ({D_j}) \end{aligned}$$

(7)

$$\begin{aligned} d_B^\lambda (D)= & {} \frac{{\left| {\text {POS}_B^\lambda (D)} \right| }}{{\left| U \right| }}. \end{aligned}$$

(8)

Insufficiency of neighborhood correlation functions and uncertainty measurement based on FNSIJE

In the first subsection of this section, we will analyze the shortcoming of the evaluation function based on the classical dependency function. To avoid this deficiency, in the second subsection of this section, first, we construct three indices with different meanings using the upper and lower approximations of decision: decision index, optimistic decision index, and pessimistic decision index. Second, we redefine three types of precision and roughness on the basis of the three indices; combining with the concept of self-information, four fuzzy neighborhood self-information measures are proposed and elaborate their properties in detail. Finally, through theoretical analysis, we find that the most suitable measure for feature selection and information entropy is combined to form a new mixed uncertainty measure for feature selection to reduce the noise in the neighborhood decision system.

Insufficiency of neighborhood related functions

Formula (8) is employed as the evaluation function for feature selection in classical FNRS, and a variety of feature selection methods based on formula (8) are proposed and applied. However, this construction method only considers positive samples; in other words, only consistent samples in the lower approximation of the decision are involved, while ignoring the upper approximation that diverges from the decision classification. However, the upper approximation also contains some classification information that cannot be ignored. Therefore, an ideal evaluation function should be a function containing both upper and lower approximations of decision. In the section “Uncertainty measurement based on FNSIJE”, we construct the uncertainty measure based on FNSIJE as the evaluation function of feature selection, making the feature selection mechanism more reasonable.

Uncertainty measurement based on FNSIJE

Definition 8

Let $\text {NDS} = \langle U,A,D \rangle$, $U/D = \{ {D_1},{D_2}, \ldots , {D_t} \}$, and $B \subseteq A$. The decision index $\text {dec}({D_r})$, the optimistic decision index $\text {op}{t_B}({D_r})$, and the pessimistic decision index $\text {pes}{s_B}({D_r})$ of $D_r$ are defined, respectively, as:

$$\begin{aligned} \text {dec}({D_r})= & {} \left| {{D_r}} \right| \end{aligned}$$

(9)

$$\begin{aligned} \text {op}{t_B}({D_r})= & {} \left| {\underline{R} _B^\lambda ({D_r})} \right| \end{aligned}$$

(10)

$$\begin{aligned} \text {pes}{s_B}({D_r})= & {} \left| {{\overline{R}} _B^\lambda ({D_r})} \right| . \end{aligned}$$

(11)

Here, ${\overline{R}} _B^\lambda ({D_r})$ and $\underline{R} _B^\lambda ({D_r})$ are the fuzzy neighborhood upper and lower approximations, respectively. The optimistic decision index $\text {op}{t_B}({D_r})$ is represented by the cardinal number of its lower approximation, which denotes the number of samples with consistent classification. The pessimistic decision index $\text {pes}{s_B}({D_r})$ is represented by the cardinal number of its upper approximation, which represents the number of samples that may belong to the decision class. $\left| \cdot \right|$ denotes the cardinality of a set:

Property 1

${\mathrm{op}}{t_B}({D_r}) \le {\mathrm{dec}}({D_r}) \le {\mathrm{pes}}{s_B}({D_r})$.

Proof

It can be directly inferred from Definition 8.

Property 2

Let ${B_1} \subseteq {B_2} \subseteq A$ and ${D_r} \in U/D,$ and then

• (1) ${\mathrm{op}}{t_{{B_1}}}({D_r}) \le {\mathrm{op}}{t_{{B_2}}}({D_r})$.

• (2) ${\mathrm{pes}}{s_{{B_1}}}({D_r}) \ge {\mathrm{pes}}{s_{{B_2}}}({D_r})$.

Proof

• (1) Because ${B_1} \subseteq {B_2} \subseteq A$, thus $R_{{B_2}}^\lambda ({D_r}) \subseteq R_{{B_1}}^\lambda ({D_r})$. It follows from Definition 8 that $\text {op}{t_{{B_1}}}({D_r}) \le \text {op}{t_{{B_2}}}({D_r})$.

• (2) It is similar to (1).

Property 2 shows that both optimistic and pessimistic decision indices are monotonous. With the increase of the number of features, the optimistic decision index increases and the decision consistency is enhanced. For pessimistic decision index, attribute reduction is produced with the reduction of decision uncertainty.

Next, we define the precision and roughness of the optimistic decision index to depict the classification ability of a feature subset.

Definition 9

Let $B \subseteq A$, $D_r \in U/D$, and the precision and roughness of the optimistic decision index are, respectively, defined as:

$$\begin{aligned} \rho _B^{(1)}({D_r})= & {} \frac{{\text {op}{t_B}({D_r})}}{{\text {dec}({D_r})}} \end{aligned}$$

(12)

$$\begin{aligned} \omega _B^{(1)}({D_r})= & {} 1 - \frac{{\text {op}{t_B}({D_r})}}{{\text {dec}({D_r})}} = 1 - \rho _B^{(1)}({D_r}). \end{aligned}$$

(13)

Apparently, $0 \le \rho _B^{(1)}({D_r}),\omega _B^{(1)}({D_r}) \le 1$. $\rho _B^{(1)}({D_r})$ indicates the degree to which the sample is completely divided into $D_r$. $\omega _B^{(1)}({D_r})$ indicates the degree to which a sample may belong to $D_r$. Both $\rho _B^{(1)}({D_r})$ and $\omega _B^{(1)}({D_r})$ reflect the classification ability of feature subset B.

When $\rho _B^{(1)}({D_r}) = 1$, $\omega _B^{(1)}({D_r}) = 0$, then, $\text {dec}({D_r}) = \text {op}{t_B}({D_r})$. In this case, all samples are correctly classified into the corresponding decision, and the feature subset B has the strongest classification ability. When $\rho _B^{(1)}({D_r}) = 0$, $\omega _B^{(1)}({D_r}) = 1$, then $\text {op}{t_B}({D_r}) = 0$. In this case, all samples have not been assigned to the correct decision. This moment, B, has the weakest classification ability.

Property 3

Let ${B_1} \subseteq {B_2} \subseteq A$ and ${D_r} \in U/D,$ and then

• (1) $\rho _{{B_1}}^{(1)}({D_r}) \le \rho _{{B_2}}^{(1)}({D_r})$.

• (2) $\omega _{{B_1}}^{(1)}({D_r}) \ge \omega _{{B_2}}^{(1)}({D_r})$.

Proof

• (1) Because ${B_1} \subseteq {B_2}$, it follows from Property 2(1) that $\text {op}{t_{{B_1}}}({D_r}) \le \text {op}{t_{{B_2}}}({D_r})$. Thus, we can have $\frac{{\text {op}{t_{{B_1}}}({D_r})}}{{\text {dec}({D_r})}}$ $\le \frac{{\text {op}{t_{{B_2}}}({D_r})}}{{\text {dec}({D_r})}}$. By Definition 9, we have $\rho _{{B_1}}^{(1)}({D_r}) \le \rho _{{B_2}}^{(1)}({D_r})$.

• (2) By Property 3(1), we can obtain that $\rho _{{B_1}}^{(1)}({D_r}) \le \rho _{{B_2}}^{(1)}({D_r})$ for ${B_1} \subseteq {B_2}$. Thus, we can have that $1 - \rho _{{B_1}}^{(1)}({D_r}) \ge 1 - \rho _{{B_2}}^{(1)}({D_r})$. From Definition 9, we can obtain $\omega _{{B_1}}^{(1)}({D_r}) \ge \omega _{{B_2}}^{(1)}({D_r})$.

Property 3 shows that the precision and roughness of optimistic decision index are monotonous. With the increase of the number of new features, the precision of optimistic decision index gradually increases, while the roughness decreases.

Definition 10

Let $B \subseteq A$, ${D_r} \in U/D$, and the optimistic decision self-information of $D_r$ can be defined as:

$$\begin{aligned} I_B^1({D_r}) = - \omega _B^{(1)}({D_r})\log \rho _B^{(1)}({D_r}). \end{aligned}$$

(14)

Apparently, Definition 10 satisfies the properties (1), (2), and (3) of Definition 1. Then, Property (4) can be confirmed according to Property 4.

Property 4

Let ${B_1} \subseteq {B_2} \subseteq A$ and ${D_r} \in U/D,$ and then, $I_{{B_1}}^1({D_r}) \ge I_{{B_2}}^1({D_r})$.

Proof

Because ${B_1} \subseteq {B_2} \subseteq A$, it follows from Property 3 that $\rho _{{B_1}}^{(1)}({D_r}) \le \rho _{{B_2}}^{(1)}({D_r})$. Thus, we can see that $0 \le - \log \rho _{{B_2}}^{(1)}({D_r}) \le - \log \rho _{{B_1}}^{(1)}({D_r})$ and $0 \le \omega _{{B_2}}^{(1)}({D_r}) \le \omega _{{B_1}}^{(1)}({D_r})$. Then, we can obtain $I_{{B_1}}^1({D_r}) \ge I_{{B_2}}^1({D_r})$.

Definition 11

Let $\text {NDS} = \langle U,A,D \rangle$, $U/D = \{ {D_1},{D_2},$ $\ldots , {D_t} \}$, $B \subseteq A$, and the optimistic decision self-information of $N\!D\!S$ is defined as:

$$\begin{aligned} I_B^1(D) = \sum \limits _{r = 1}^t {I_B^1({D_r})}. \end{aligned}$$

(15)

Self-information was originally used to describe the instability of signal output. Applying self-information to decision system can describe the uncertainty of decision, which is an effective means to evaluate decision ability.

$I_B^1(D)$ describes the classification information of feature subset B. The smaller $I_B^1(D)$ is, the stronger the classification ability of feature subset B is. $I_B^1(D) = 0$ indicates that all samples in U can be completely classified into their respective classes by feature subset B.

The selected feature subset based on optimistic decision self-information only pays attention to the consistency of the classification objects, ignoring the information contained in the uncertain classification samples. However, these uncertain informations are often not negligible. Therefore, it is necessary to analyze the information contained in uncertain classification objects.

Next, we define the precision and roughness of pessimistic decision to depict the uncertainty of feature subset B.

Definition 12

Let $\text {NDS} = \langle U,A,D \rangle$, $U/D = \{ {D_1},{D_2},$ $\ldots , {D_t} \}$, and $B \subseteq A$, and the precision and roughness of the pessimistic decision index are defined as follows:

$$\begin{aligned} \rho _B^{(2)}({D_r})= & {} \frac{{\text {dec}({D_r})}}{{\text {pes}{s_B}({D_r})}} \end{aligned}$$

(16)

$$\begin{aligned} \omega _B^{(2)}({D_r})= & {} 1 - \frac{{\text {dec}({D_r})}}{{\text {pes}{s_B}({D_r})}} = 1 - \rho _B^{(2)}({D_r}). \end{aligned}$$

(17)

It is obviously that $0 \le \rho _B^{(2)}({D_r}),\omega _B^{(2)}({D_r}) \le 1$. $\rho _B^{(2)}({D_r})$ can be regarded as the uncertainty degree of the decision equivalence class ${D_r}$. $\omega _B^{(2)}({D_r})$ indicates the degree which the sample cannot be correctly classified into decision class.

When $\rho _B^{(2)}({D_r}) = 1$, $\omega _B^{(2)}({D_r}) = 0$, then $\text {dec}({D_r}) = \text {pes}{s_B}({D_r})$. That means all objects which belong to${D_r}$ are completely sorted into ${D_r}$ by B. In this case, feature subset B has the strongest classification ability.

Property 5

Let ${B_1} \subseteq {B_2} \subseteq A$ and $D_r\in U/D,$ and then

• (1) $\rho _{{B_1}}^{(2)}({D_r}) \le \rho _{{B_2}}^{(2)}({D_r})$.

• (2) $\omega _{{B_1}}^{(2)}({D_r}) \ge \omega _{{B_2}}^{(2)}({D_r})$.

Proof

• (1) Because ${B_1} \subseteq {B_2}$, it follows from Property 2(2) that $\text {pes}{s_{{B_1}}}({D_r}) \ge \text {pes}{s_{{B_2}}}({D_r})$. Thus, we can have $\frac{{\text {dec}({D_r})}}{{\text {pes}{s_{{B_1}}}({D_r})}} \le \frac{{\text {dec}({D_r})}}{{\text {pes}{s_{{B_2}}}({D_r})}}$. By Definition 12, we have $\rho _{{B_1}}^{(2)}({D_r}) \le \rho _{{B_2}}^{(2)}({D_r})$.

• (2) By Property 5(1), we can obtain that $\rho _{{B_1}}^{(2)}({D_r}) \le \rho _{{B_2}}^{(2)}({D_r})$ for ${B_1} \subseteq {B_2}$. Thus, we can have that $1 - \rho _{{B_1}}^{(2)}({D_r}) \ge 1 - \rho _{{B_2}}^{(2)}({D_r})$. From Definition 12, we can obtain $\omega _{{B_1}}^{(2)}({D_r}) \ge \omega _{{B_2}}^{(2)}({D_r})$.

Property 5 shows that the precision and roughness of the pessimistic decision index are monotonous. As the number of new features increases, the precision of the pessimistic decision index gradually increases and the roughness gradually decreases.

Definition 13

Let $B \subseteq A$ and $D_r\in U/D$, and the pessimistic decision self-information of $D_r$ can be denoted as:

$$\begin{aligned} I_B^2({D_r}) = - \omega _B^{(2)}({D_r})\log \rho _B^{(2)}({D_r}). \end{aligned}$$

(18)

Apparently, Definition 13 satisfies the properties (1), (2), and (3) of Definition 1. Then, Property (4) can be confirmed according to Property 6.

Property 6

Let ${B_1} \subseteq {B_2} \subseteq A$ and $D_r \in U/D,$ and then, $I_{{B_1}}^2({D_r})\ge I_{{B_2}}^2({D_r})$.

Proof

Because ${B_1} \subseteq {B_2}$, it follows from Property 5(1) that $\rho _{{B_1}}^{(2)}({D_r}) \le \rho _{{B_2}}^{(2)}({D_r})$. Thus, we can see that $0 \le - \log \rho _{{B_2}}^{(2)}({D_r}) \le - \log \rho _{{B_1}}^{(2)}({D_r})$ and $0 \le \omega _{{B_2}}^{(2)}({D_r}) \le \omega _{{B_1}}^{(2)}({D_r}) \le 1$. By Definition 13, we can obtain $I_{{B_1}}^2({D_r}) \ge I_{{B_2}}^2({D_r})$.

Definition 14

Let $\text {NDS} = \langle U,A,D \rangle$, $U/D = \{ {D_1},{D_2},$ $\ldots , {D_t} \}$, and $B \subseteq A$, and the pessimistic decision self-information of $N\!D\!S$ is defined as:

$$\begin{aligned} I_B^2(D) = \sum \limits _{r = 1}^t {I_B^2({D_r})}. \end{aligned}$$

(19)

Through the above analysis, the optimistic decision self-information $I_B^1(D)$ focuses on the ability to completely divide the sample into correct decision $D_r$ through feature subset B. Although the pessimistic decision self-information $I_B^2(D)$ can obtain samples that may belong to decision $D_r$, it cannot ensure that all classification information is consistent. Hence, both $I_B^1(D)$ and $I_B^2(D)$ describe the classification ability of feature subset B from one-sided perspective, which cannot reflect the comprehensive information included in the decision. Therefore, we will propose two other self-information to measure the uncertainty of classification information. They can not only avoid considering the uncertainty of decision information from a one-sided perspective to a greater extent, but they are also more in line with actual decision in theory.

Definition 15

Let $B \subseteq A$ and ${D_r} \in U/D$, and the optimistic-pessimistic decision self-information of $D_r$ is defined as:

$$\begin{aligned} I_B^3({D_r}) = I_B^1({D_r}) + I_B^2({D_r}). \end{aligned}$$

(20)

Property 7

Let ${B_1} \subseteq {B_2} \subseteq A$ and ${D_r} \in U/D,$ and then, $I_{{B_1}}^3({D_r}) \ge I_{{B_2}}^3({D_r})$.

Proof

From Properties 4 and 6, we can know that $I_{{B_1}}^1({D_r}) \ge I_{{B_2}}^1({D_r})$ and $I_{{B_1}}^2({D_r}) \ge I_{{B_2}}^2({D_r})$ for ${B_1} \subseteq {B_2}$. Thus, we can obtain that $I_{{B_1}}^1({D_r}) + I_{{B_1}}^2({D_r}) \ge I_{{B_2}}^1({D_r}) + I_{{B_2}}^2({D_r})$. By Definition 15, we have $I_{{B_1}}^3({D_r}) \ge I_{{B_2}}^3({D_r})$.

Definition 16

Let $\text {NDS} = \langle U,A,D \rangle$, $U/D = \{ {D_1},{D_2},$ $\ldots , {D_t} \}$ and $B \subseteq A$, the optimistic-pessimistic decision self-information of $N\!D\!S$:

$$\begin{aligned} I_B^3(D) = \sum \limits _{r = 1}^t {I_B^3({D_r})}. \end{aligned}$$

(21)

Definition 17

Let $B \subseteq A$ and ${D_r} \in U/D$, and the precision and roughness of the tolerance decision index are defined as follows:

$$\begin{aligned} \rho _B^{(3)}({D_r})= & {} \frac{{\text {op}{t_B}({D_r})}}{{\text {pes}{s_B}({D_r})}} \end{aligned}$$

(22)

$$\begin{aligned} \omega _B^{(3)}({D_r})= & {} 1 - \frac{{\text {op}{t_B}({D_r})}}{{\text {pes}{s_B}({D_r})}} = 1 - \rho _B^{(3)}({D_r}). \end{aligned}$$

(23)

Apparently, $0 \le \rho _B^{(3)}({D_r}),\omega _B^{(3)}({D_r}) \le 1$. $\rho _B^{(3)}({D_r})$ depicts the ratio of optimistic decision and pessimistic decision samples, which characterizes the classification ability of feature subset B. When $\rho _B^{(3)}({D_r}) = 1$, $\omega _B^{(3)}({D_r})$ $= 0$, it is the ideal state of the feature subset B, and the feature subset B has the optimal classification ability at this time. On the contrary, when $\rho _B^{(3)}({D_r}) = 0$, the feature subset B has no effect on classification and has the weakest classification ability.

Property 8

Let ${B_1} \subseteq {B_2} \subseteq A,$ ${D_r} \in U/D$ and $B \subseteq A,$ and then:

• (1) $\rho _{{B_1}}^{(3)}({D_r}) \le \rho _{{B_2}}^{(3)}({D_r}),$ $\omega _{{B_1}}^{(3)}({D_r}) \ge \omega _{{B_2}}^{(3)}({D_r})$.

• (2) $\rho _B^{(3)}({D_r}) = \rho _B^{(1)}({D_r}) \cdot \rho _B^{(2)}({D_r})$.

• (3) $\omega _B^{(3)}({D_r})\! =\! \omega _B^{(1)}({D_r}) \!+\! \omega _B^{(2)}({D_r})\! - \!\omega _B^{(1)}({D_r}) \cdot \omega _B^{(2)}({D_r})$.

Proof

• (1) Because ${B_1} \subseteq {B_2}$, it follows from Property 2 that $\text {op}{t_{{B_1}}}({D_r}) \le \text {op}{t_{{B_2}}}({D_r})$ and $\text {pes}{s_{{B_1}}}({D_r}) \ge \text {pes}{s_{{B_2}}}({D_r})$. Then, we can have $\frac{{\text {op}{t_{{B_1}}}({D_r})}}{{\text {pes}{s_{{B_1}}}({D_r})}} \le \frac{{\text {op}{t_{{B_2}}}({D_r})}}{{\text {pes}{s_{{B_2}}}({D_r})}}$. By Definition 17, we have $\rho _{{B_1}}^{(3)}({D_r}) \le \rho _{{B_2}}^{(3)}({D_r})$. Thus, we can have that $1 - \rho _{{B_1}}^{(3)}({D_r}) \ge 1 - \rho _{{B_2}}^{(3)}({D_r})$. Therefore, we can obtain $\omega _{{B_1}}^{(3)}({D_r}) \ge \omega _{{B_2}}^{(3)}({D_r})$.

• (2) From Definitions 9 and 12, we have $\rho _B^{(1)}({D_r})$ $= \frac{{\text {op}{t_B}({D_r})}}{{\text {dec}({D_r})}}$ and $\rho _B^{(2)}({D_r}) = \frac{{\text {dec}({D_r})}}{{\text {pes}{s_B}({D_r})}}$, then $\rho _{{B_{}}}^{(1)}({D_r}) \cdot \rho _{{B_{}}}^{(2)}({D_r}) \!=\! \frac{{\text {op}{t_B}(Dr)}}{{\text {dec}_{B}(Dr)}} \! \cdot \! \frac{{\text {dec}_{B}(Dr)}}{{\text {pes}{s_B}(Dr)}}\!= \! \frac{{\text {op}{t_B}(Dr)}}{{\text {pes}{s_B}(Dr)}}$. From Definition 17, we can obtain $\rho _B^{(3)}({D_r}) = \frac{{\text {op}{t_B}({D_r})}}{{\text {pes}{s_B}({D_r})}}$, and thus, $\rho _B^{(3)}({D_r}) = \rho _B^{(1)}({D_r}) \cdot \rho _B^{(2)}({D_r})$.

• (3) From Definition 17 and Property 8(2), we have:

  $$\begin{aligned} \begin{aligned} \omega _B^{(3)}({D_r})&= 1 - \rho _B^{(3)}({D_r})\\&= 1 - \rho _B^{(1)}({D_r}) \cdot \rho _B^{(2)}({D_r})\\&= 1 \!- \!\left[ {1\! - \!\omega _B^{(1)}({D_r})} \right] \cdot \left[ {1\! - \omega _B^{(2)}({D_r})} \right] \\&= \omega _B^{(1)}({D_r}) + \omega _B^{(2)}({D_r}) - \omega _B^{(1)}({D_r}) \cdot \omega _B^{(2)}({D_r}). \end{aligned} \end{aligned}$$

Definition 18

Let $B \subseteq A$ and ${D_r} \in U/D$, and the tolerance decision self-information of $D_r$ is defined as:

$$\begin{aligned} I_B^4({D_r}) = - \omega _B^{(3)}({D_r})\log \rho _B^{(3)}({D_r}). \end{aligned}$$

(24)

Clearly, Definition 18 satisfies (1), (2), and (3) of Definition 1. Property (4) is verified by Property 9.

Property 9

Let ${B_1} \subseteq {B_2} \subseteq A$ and ${D_r} \in U/D,$ and then, $I_{{B_1}}^4({D_r}) \ge I_{{B_2}}^4({D_r})$.

Proof

Because ${B_1} \subseteq {B_2}$, it follows from Property 8(1) that $\rho _{{B_1}}^{(3)}({D_r}) \le \rho _{{B_2}}^{(3)}({D_r})$. Thus, we can see that $0 \le - \log \rho _{{B_2}}^{(3)}({D_r}) \le - \log \rho _{{B_1}}^{(3)}({D_r})$ and $0 \le \omega _{{B_2}}^{(3)}({D_r}) \le \omega _{{B_1}}^{(3)}({D_r}) \le 1$. Then, from Definition 18, we can obtain $I_{{B_1}}^4({D_r}) \ge I_{{B_2}}^4({D_r})$.

Property 10

$I_B^4({D_r}) \ge I_B^3({D_r})$.

Proof

$$\begin{aligned}&I_B^{(4)}({D_r}) = - \omega _B^{(3)}({D_r})\log \rho _B^{(3)}({D_r})\\&\quad = - \left[ {\omega _B^{(1)}({D_r}) + \omega _B^{(2)}({D_r}) - \omega _B^{(1)}({D_r}) \cdot \omega _B^{(2)}({D_r})} \right] \\&\qquad \cdot \log \left[ {\rho _B^{(1)}({D_r}) + \rho _B^{(2)}({D_r})} \right] \\&\quad = - \left[ {\omega _B^{(1)}({D_r}) + \omega _B^{(2)}({D_r}) - \omega _B^{(1)}({D_r}) \cdot \omega _B^{(2)}({D_r})} \right] \\&\qquad \cdot \left[ {\log \rho _B^{(1)}({D_r}) + \log \rho _B^{(2)}({D_r})} \right] \\&\quad = - \omega _B^{(1)}({D_r}) \cdot \log \rho _B^{(1)}({D_r}) - \omega _B^{(2)}({D_r}) \cdot \log \rho _B^{(2)}({D_r})\\&\qquad + \left[ {\omega _B^{(1)}({D_r}) - 1} \right] \cdot \omega _B^{(2)}({D_r}) \cdot \log \rho _B^{(1)}({D_r})\\&\qquad + \left[ {\omega _B^{(2)}({D_r}) - 1} \right] \cdot \omega _B^{(1)}({D_r}) \cdot \log \rho _B^{(2)}({D_r})\\&\quad = I_B^1({D_r}) + I_B^2({D_r}) + \left[ {\omega _B^{(1)}({D_r}) - 1} \right] \cdot \omega _B^{(2)}({D_r})\\&\qquad \cdot \log \rho _B^{(1)}({D_r}) + \left[ {\omega _B^{(2)}({D_r}) - 1} \right] \cdot \omega _B^{(1)}({D_r}) \cdot \log \rho _B^{(2)}({D_r}). \end{aligned}$$

It is clear that $0 \le \rho _B^{(1)}({D_r}) \le 1$, $0 \le \omega _B^{(1)}({D_r}) \le 1$ from Definition 9, and we have $\log \rho _B^{(1)}({D_r}) \le 0$, $\omega _B^{(1)}({D_r}) - 1 \le 0$. Similarly, we can see $0 \le \rho _B^{(2)}({D_r}) \le 1$, $0 \le \omega _B^{(2)}({D_r}) \le 1$ from Definition 12, and we have $\log \rho _B^{(1)}({D_r}) \le 0$, $\omega _B^{(2)}({D_r}) - 1 \le 0$. It can be proved that:

$$\begin{aligned} \left\{ \begin{array}{l} \left[ {\omega _B^{(1)}({D_r}) - 1} \right] \cdot \omega _B^{(2)}({D_r}) \cdot \log \rho _B^{(1)}({D_r}) \ge 0 \quad \textcircled {1}\\ \left[ {\omega _B^{(2)}({D_r}) - 1} \right] \cdot \omega _B^{(1)}({D_r}) \cdot \log \rho _B^{(2)}({D_r}) \ge 0\quad \textcircled {2}. \end{array} \right. \end{aligned}$$

Thus, $\Delta \mathrm{{ =\textcircled {1} + \textcircled {2}}} \ge 0$:

$$\begin{aligned} \begin{aligned} I_B^4({D_r})&= I_B^1({D_r}) + I_B^2({D_r}) + \Delta \\&= I_B^3({D_r}) + \Delta \\&\ge I_B^3({D_r}). \end{aligned} \end{aligned}$$

Definition 19

Let $\text {NDS} = \langle U,A,D \rangle$, $U/D = \{ {D_1},{D_2},$ $\ldots , {D_t} \}$, and $B \subseteq A$, and the tolerance decision self-information of $N\!D\!S$ is defines as:

$$\begin{aligned} I_B^4(D) = \sum \limits _{r = 1}^t {I_B^4({D_r})}. \end{aligned}$$

(25)

Property 11

Let ${B_1} \subseteq {B_2} \subseteq A,$ and then, $I_{{B_1}}^4(D) \ge I_{{B_2}}^4(D)$.

Proof

It is straightforward from Property 9.

Remark 1

According to the above theoretical analysis, tolerance fuzzy neighborhood decision self-information (FNSI) can not only consider the decision uncertainty from a more comprehensive perspective, but also is sensitive to the change of feature subset size, and thus, it is more suitable for feature selection.

Definition 20

[36] Let $\text {NDS} = \langle U,A,D \rangle$ and $U = \left\{ {{x_1},{x_2}, \ldots , {x_m}} \right\}$, and then, the fuzzy neighborhood entropy of A is denoted by:

$$\begin{aligned} \text {FNE}_{\alpha }(A) = - \sum \limits _{l = 1}^m {\frac{{\left| {{\alpha _A}({x_l})} \right| }}{{\left| U \right| }}{{\log }_2}} \frac{{\left| {{\alpha _A}({x_l})} \right| }}{{\left| U \right| }}. \end{aligned}$$

(26)

Here, ${\alpha _A}({x_l})$ is the parameterized fuzzy neighborhood granule, ${x_l} \in U$ and $l = 1,2, \ldots , m$.

Definition 21

Let $\text {NDS} = \langle U,A,D \rangle$, $U/D = \{ {D_1},{D_2},$ $\ldots , {D_t} \}$ and $\text {AT} \subseteq A$, and the fuzzy neighborhood joint entropy of $\text {AT}$ and D is defined as:

$$\begin{aligned} \begin{aligned} \text {FNE}_{\alpha }\!(\text {AT}\!,\!D\!)\! = \!&- \frac{1}{{\left| U \right| }}\sum \limits _{l = 1}^m {\sum \limits _{j = 1}^t {\frac{{\left| {{\alpha _A}({x_t}) \cap \text {FD}_{j}} \right| }}{{\left| U \right| }} } } \\&\times {\log _2}\frac{{\left| {{\alpha _A}({x_l}) \cap \text {FD}_{j}} \right| }}{{\left| U \right| }}. \end{aligned} \end{aligned}$$

(27)

Here, ${x_l} \in U$, $l = 1,2, \ldots , m$, and $j = 1,2, \ldots ,t$, and $\left| {{\alpha _A}({x_l}) \cap \text {FD}_{j}} \right|$ indicates that the degree of membership of ${\alpha _A}({x_l})$ is not greater than the number of non-zero values of the samples of $\text {FD}_{j}$ [37].

Definition 22

Let $\text {NDS} = \langle U,A,D \rangle$, $U/D = \{ {D_1},{D_2},$ $\ldots , {D_t} \}$, and $\text {AT} \subseteq A$, and then, the FNSI-based fuzzy neighborhood joint entropy (FNSIJE) of $\text {AT}$ and D is defined as:

$$\begin{aligned}&\text {FNSIJE}_{\alpha }(\text {AT}_{i},D) = - I_B^4(D) \nonumber \\&\quad \times \frac{1}{{\left| U \right| }}\sum \limits _{l = 1}^m {\sum \limits _{j = 1}^t {\frac{{\left| {{\alpha _{{A_i}}}({x_l}) \cap \!\text {FD}_{j}} \right| }}{{\left| U \right| }}{{\log }_2}} \frac{{\left| {{\alpha _{{A_i}}}({x_l}) \cap \!\text {FD}_{j}} \right| }}{{\left| U \right| }}}.\nonumber \\ \end{aligned}$$

(28)

Here, $I_B^4(D)$ is the tolerance decision self-information of $\text {NDS}$, ${\alpha _A}({x_l})$ is the parameterized fuzzy neighborhood granule, $x_l \in U$ and $l = 1,2, \ldots , m$, $\left| {{\alpha _A}({x_l}) \cap \text {FD}_{j}} \right|$ indicates that the degree of membership of ${\alpha _A}({x_l})$ is not greater than the number of non-zero values of the samples of $\text {FD}_{j}$, $j = 1,2, \ldots ,t$.

Property 12

Let $\text {NDS} = \langle U,A,D \rangle ,$ $U/D = \{ {D_1},{D_2}, \ldots , {D_t} \},$ $\text {AT} \subseteq A,$ $\text {AT} = \left\{ {\text {AT}_{1},\text {AT}_{2}, \ldots , \text {AT}_{n}} \right\}$ and $U = \left\{ {{x_1},{x_2}, \ldots , {x_m}} \right\} ,$ and then:

$$\begin{aligned} \text {FNSIJE}_{\alpha }(\text {AT}_{i},D)= I_B^4(D) \times \text {FNE}_{\alpha }(\text {AT}_{i},D) \ge 0. \end{aligned}$$

Remark 2

From Definition 22 and Property 12, $I_B^4(D)$ is the fuzzy neighborhood self-information measure from algebra view, and $\text {FNE}_{\alpha }(\text {AT}_{i},D)$ denotes the fuzzy neighborhood joint entropy from the information view. Therefore, FNSIJE can simultaneously measure the uncertainty of neighborhood decision from both the algebra and information views.

Feature selection method based on FNSIJE model

In this section, we will propose a feature selection method based on the FNSIJE model and apply it to the neighborhood decision system.

FNSIJE-based feature selection

Definition 23

Let $\text {NDS} = \langle U,A,D \rangle$, $\text {AT}' \subseteq \text {AT} \subseteq A$, $\text {AT} = \left\{ {\text {AT}_{1},\text {AT}_{2}, \ldots , \text {AT}_{n}} \right\}$, $\text {AT}'$ is the reduction of $\text {AT}$ with regard to D, if it is satisfied:

• (1) $\text {FNSIJE}_{\alpha }(\text {AT}',D) = \text {FNSIJE}_{\alpha }(\text {AT},D)$.

• (2) $\text {FNSIJE}_{\alpha }(\text {AT}',D) > \text {FNSIJE}_{\alpha }(\text {AT}' - \text {AT}_{i},D)$, for any $\text {AT}_{i} \subseteq \text {AT}'$.

Equation (1) shows that the reduced subset has the same classification ability as the entire dataset, and Eq. (2) ensures that the reduced subset has no redundant feature.

Definition 24

Let $\text {NDS} = \langle U,A,D \rangle$, $\text {AT}' \subseteq \text {AT} \subseteq A$, $\text {AT} = \{\text {AT}_1, \text {AT}_2, \ldots , \text {AT}_n\}$, $\text {AT}_i \subseteq \text {AT}'$ and $i = 1,2,\ldots ,n,$ and then, the attribute significance of subset $\text {AT}_i$ with respect to D is defined as:

$$\begin{aligned} \text {SIG}(\!\text {AT}_{i}\!,\!\text {AT}'\!,\!D)= & {} \text {FNSIJE}_{\alpha }\!(\!\text {AT}' \!- \!\text {AT}_{i}\!,\!D\!)\nonumber \\&-\text {FNSIJE}_{\alpha }\!(\text {AT}\!'\!,\!D\!). \end{aligned}$$

(29)

Feature selection algorithm

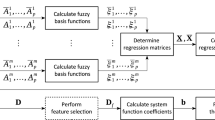
According to the above definition, a FNSIJE-based feature selection (FNSIJE-KS) method is demonstrated in Algorithm 1.

For this FNSIJE-KS method, the most significant impact on complexity is the calculation of parameterized fuzzy neighborhood granule. The time complexity is about O(mn), where m is the size of objects and n is the size of features. This method is a loop in steps 9–15, and its time complexity is $O({n^3}m)$ at worst. Suppose the size of the selected feature subset is r, the time complexity of fuzzy neighborhood granule is about O(rm). As n is much greater than r for the most part. Thus, the total time complexity is close to O(mn).

Experimental analysis

In this section, we conduct a series of experiments to test the feasibility and stability of FNSIJE-KS. The experiment is divided into five parts: the section “Datasets and experimental design” is the datasets and experimental environment used in the experiments; the section “Performance on different fuzzy neighborhood para-meters” is the impact of different fuzzy neighborhood parameters on the classification performance of our method; the section “Classification results of the UCI datasets” is the classification results of the UCI datasets; the section “Classification results of gene datasets” is the classification results of the gene datasets; the section “Statistical analysis” is the statistical analysis.

Datasets and experimental design

The experiment performs feature selection on ten public datasets including six low-dimensional UCI datasets and four high-dimensional microarray gene expression profile datasets (hereinafter referred to as gene datasets). The six UCI datasets can be downloaded at http://archive.ics.uci.edu/ml/datasets.php, and the four gene datasets can be downloaded at http://portals.broadinstitute.org/cgi-bin/cancer/datasets.cgi.

Table 1 lists all datasets.

Table 1 Ten datasets in experiments

All experiments are implemented using MATLAB R2016a under Windows 10 with an Intel Core i5-3470 CPU at 3.20 GHz and 4.0 GB RAM. The classification accuracy is verified under the three classifiers KNN, CART and C4.5 in WEKA 3.8, and all parameters under the three classifiers are set to default values. To ensure the consistency of experiments, we use tenfold cross-validation in the following subsections.

Performance on different fuzzy neighborhood para-meters

This subsection analyzes the influence of different fuzzy neighborhood parameters on the classification performance of our method, and finds the most appropriate parameter for each dataset.

To reduce the time complexity originate from the four gene datasets with high dimensions, we use the Kolmogorov–Smirnov test (K–S test) for preliminary dimensionality reduction.

K–S test is a common non-parametric method used to compare whether two types of samples belong to the same distribution. It is extremely sensitive in identifying the difference of distribution morphology of two types of samples [49]. It has made development and breakthrough in the fields of cancer gene data analysis [50], emotional recognition, etc. [51]. Not only that, it also has many advantages: high calculation speed and strong operability, which can effectively reduce time complexity.

Assume that the original dataset covers two types of independent samples, denoted as positive (A) and negative (B). The total number of samples in the gene dataset is recorded as n, take a gene X in the original gene dataset as an example, the observed value of gene X is ${x_{(1)}},{x_{(2)}}, \ldots ,{x_{(n)}}$, refer to its eigenvalues to sort in descending order, and the corresponding order observation value can be obtained as ${x_{(1)}} \le {x_{(2)}} \le \cdots \le {x_{(n)}}$. Therefore, the cumulative distribution function of the gene is [52]:

$$\begin{aligned} \begin{aligned} F(x) = \left\{ \begin{array}{ll} 0,&{}\quad x \!< \!{x_{(1)}}\\ \frac{k}{n},x(k) \le x \le x(k + 1);&{}\quad k = 1,2, \ldots ,n - 1\\ n,&{}\quad x \le x(n). \end{array} \right. \end{aligned}\nonumber \\ \end{aligned}$$

(30)

On the basis of formula (30), the cumulative distribution functions ${F_{A(x)}}$ and ${F_{B(x)}}$ of the two types of samples are calculated, respectively, and then, the K–S test statistic TS is recorded as:

$$\begin{aligned} T\!S = \max \left| {{F_{A(x)}} - {F_{B(x)}}} \right| . \end{aligned}$$

(31)

According to the K–S test principle, under the significance level $\beta$, if $\text {TS} < \text {TS}_{{{\mathrm{crit}}}}$ ($\text {TS}_{{{\mathrm{crit}}}}$ is the critical value under the significance level $\beta$), it is believed that the gene is not significantly different between the positive sample and the negative sample. If $\text {TS} \ge \text {TS}_{{{\mathrm{crit}}}}$, it is believed that there is a significant difference between the positive sample and the negative sample of the gene at the significance level of $1 - \beta$ [53]. $\beta$ and the corresponding critical value $\text {TS}_{{{\mathrm{crit}}}}$ (here, $s(n) = \sqrt{\frac{{{n_1} + {n_2}}}{{{n_1}{n_2}}}}$, ${n_1}$ and ${n_2}$ are the number of positive and negative genes, respectively) are shown in Table 2 [54].

Table 2 Significance level of K–S test and corresponding critical value

Fig. 1

Examples of K–S test statistics

It can be seen from formula (31) that the larger the value $\text {TS}$, the greater the difference between the positive and negative of the gene, which means that the gene has a stronger ability to distinguish between the positive and negative samples. Taking the gene dataset Prostate as an example, which contains 77 normal samples and 59 tumor samples, and each sample contains 12,600 genes. As shown in Fig. 1a, b, comparing the cumulative distribution probability and K–S test statistics $\text {TS}$ of the 78th gene and the 3474th gene (the abscissa x represents the gene value, the ordinate F(x) represents the cumulative probability corresponding to x), we can see the difference of the 3474th gene in the two types of samples is significantly greater than that of the 78th gene, so 3474th gene has better distinguishing ability.

To reduce the time complexity of gene datasets, this paper uses K–S test method to preprocess the data, to reduce the dimensionality reduction. The algorithm description of K–S test method is shown in Algorithm 2.

Table 3 The number of genes in the four gene datasets after dimensionality reduction with K–S test under different significance levels

Since the K–S test can sensitively detect the difference in the distribution shape of different gene samples, it is helpful to eliminate irrelevant genes and achieve the purpose of reducing the dimensionality of the dataset. Table 3 shows the number of genes in the four gene datasets under different significance levels (0.10, 0.005, 0.01, 0.05, and 0.001) after dimension reduction by K–S test. Classification accuracy changes with the size of gene subsets in most cases. Figure 2 illustrates the change trend of the accuracy via the gene selected feature subsets under different significance levels for four gene datasets under the classifier KNN. Here, the abscissa represents five different significance levels, and the ordinate represents classification accuracy.

Adhering to the principle that the gene selected feature subset has a smaller dimension and higher classification accuracy, combined with Table 3 and Fig. 2, it can be seen that significance level $\beta$ sets to 0.005 is more suitable for dataset Colon, $\beta$ sets to 0.001 is more suitable for dataset DLBCL and Leukemia, and $\beta$ sets to 0.1 is more suitable for dataset Prostate.

Fig. 2

Classification accuracy of gene subsets under different significance levels

In the following portion, we will discuss the impact of the fuzzy neighborhood parameters $\lambda$ on FNSIJE-KS. The change curve of classification accuracy on different $\lambda$ for 10 datasets is shown in Fig. 3 (abscissa represents parameters $\lambda$ and ordinate represents classification accuracy). We design the value of $\lambda$ to vary from 0 to 1, with a step size of 0.05. The classification accuracy of the six UCI datasets under the classifiers KNN and CART is shown in Fig. 3a–f; the accuracy of the four gene datasets under the classifiers KNN, CART, and C4.5 is shown in Fig. 3g–j.

Fig. 3

Classification accuracy under different fuzzy neighborhood parameter values on ten datasets

It can be seen from Fig. 3 that the change of $\lambda$ does have a certain impact on the classification performance of FNSIJE-KS, but all datasets can achieve a high classification accuracy in a wider range of $\lambda$. Tables 4 and 5 list the optimal fuzzy neighborhood parameters selected for each UCI dataset and gene dataset under different classifiers, respectively.

Table 4 Optimal fuzzy neighborhood parameters for six UCI datasets

Table 5 Optimal fuzzy neighborhood parameters for four gene datasets

Classification results of the UCI datasets

In this subsection, to verify the classification effectiveness of the FNSIJE-KS method on UCI datasets, we compare the size and classification accuracy of selected feature subsets by FNSIJE-KS and three existing methods. The three methods include FNRS (method based on fuzzy neighborhood rough set) [32], FNCE (method based on fuzzy neighborhood conditional entropy) [37], and FNPME-FS (method based on fuzzy neighborhood pessimistic multigranulation entropy) [36].

In the first portion of the subsection, we use the obtained fuzzy neighborhood parameters $\lambda$, let the four feature selection methods use ten-fold cross-validation on six UCI datasets, and the average size of the original datasets and the selected feature subsets by different methods are exhibited in Table 6. The optimal selected feature subsets by FNSIJE-KS for the six UCI datasets under the classifiers KNN and CART are shown in Table 7.

Table 6 Number of selected features with four feature selection methods

Table 7 Optimal subset with FNSIJE-KS for six UCI datasets

Table 6 describes the average size of the selected feature subsets by the four methods. In Table 6, the bolded numbers show that the size of the reduced datasets is the least with respect to other methods. The selected feature subsets by FNSIJE-KS on the datasets Glass, Ionosphere, and Wine reach the minimum size, which are 2.1, 2.2, and 4.75, respectively. In short, comparing with FNRS, FNCE, and FNPME-FS, the mean size of selected feature subsets using FNSIJE-KS is the least for six UCI datasets.

The second portion pays attention to the effectiveness of classification for FNSIJE-KS. Tables 8 and 9 list classification accuracy of selected feature subsets by FNSIJE-KS and other three feature selection methods (FNRS [32], FNCE [37], and FNPME-FS [36]) under classifiers KNN and CART, respectively. In Tables 8 and 9, the bolded numbers indicate that the classification accuracy of the selected feature subsets is the best with respect to other methods.

Table 8 Classification accuracy with four methods on classifier KNN

Table 9 Classification accuracy with four methods on classifier CATR

No method always outperforms other methods under different classifiers and learning tasks. As observed from the results of four methods demonstrate in Tables 6, 8, and 9 illustrate the differences among the four methods. From Tables 6 and 8, it can be seen that FNSIJE-KS has the highest classification accuracy of the selected feature subsets on datasets Glass and Wpbc, 99.07 and 77.27$\%$, respectively, under the classifier KNN. Furthermore, the average size of the selected feature subset by FNSIJE-KS is the 2.8, 10.2, and 3.6 smaller than those by FNRS, FNCE, and FNPME-FS on Glass dataset, respectively. The selected feature subsets by FNSIJE-KS and FNPME-FS have the same classification accuracy of 90.31$\%$ on dataset Ionosphere, and the selected feature subset by FNSIJE-KS is 9.4 less than those selected by FNPME-FS.

Similarly, from Tables 6 and 9, it is clear that the average classification accuracy of FNSIJE-KS is larger than FNRS, FNCE, and FNPME-FS on almost UCI datasets under classifier CART , except only one dataset Wine. In addition, FNPME-FS selects fewer features than FNRS and FNPME-FS when its classification accuracy is equal to FNRS and FNPME-FS on dataset Glass. According to Tables 8 and 9, comparing FNSIJE-KS with FNRS, FNCE, and FNPME-FS, the mean classification accuracy of FNSIJE-KS has been improved under two classifiers KNN and CART on the UCI datasets.

In summary, the FNSIJE-KS method is easy to eliminate redundant features as a whole and displays better classification performance than other compared methods on UCI datasets.

Classification results of gene datasets

This subsection is dealing with the classification effectiveness of the FNSIJE-KS method on gene datasets.

In the first portion of this subsection, we compare the size of selected gene subsets by the FNSIJE-KS method and three existing methods (FNRS [32], FNCE [37], and FNPME-FS [36]).

We use the obtained $\lambda$, let the four feature selection methods use tenfold cross-validation on four gene datasets, and the average size of the original datasets and the selected gene subsets by different methods are described in Table 10. In Table 10, the bolded numbers show that the size of the reduced gene datasets is the least with respect to other methods. Then, the optimal selected gene subsets by FNSIJE-KS for the four gene datasets under three classifiers KNN, C4.5, and CART are demonstrated in Table 11.

Table 10 Number of selected genes with four feature selection methods

Table 11 Gene subset with FNSIJE-KS for four gene datasets

As is clearly shown from Table 10, for three gene datasets Colon, DLBCL, and Leukemia, FNSIJE-KS is significantly superior to the other three methods. Moreover, the mean size of the selected gene subset by FNSIJE-KS is less than those by FNRS, FNCE, and FNPME-FS. Briefly, FNSIJE-KS can select less genes for gene datasets.

In the second portion of this subsection, we discuss the classification performance of the selected gene subsets by FNSIJE-KS and other four feature selection methods under classifiers KNN and C4.5. Among them, four feature selection methods include FNRS [32], FNCE [37], FNPME-FS [36], and EGGS (entropy gain-based gene selection method) [55].

Let five feature selection methods use tenfold cross-validation on four gene datasets, and the classification accuracy of selected gene subsets under the classifiers KNN and C4.5 are illustrated in Tables 12 and 13, respectively. In Tables 12 and 13, the bolded numbers indicate that the classification accuracy of the selected gene subsets is the best with respect to other four methods.

Table 12 Classification accuracy with five methods on classifier KNN

Table 13 Classification accuracy with five methods on classifier C4.5

From Tables 10 and 12, the classification accuracy of selected gene subsets by FNSIJE-KS is 13.23, 6.75, 2.88, and 27.97$\%$, respectively, which is higher than those selected by FNRS, FNCE, FNPME-FS, and EGGS under classifier KNN on dataset Prostate. Both FNSIJE-KS and FNPME-FS have the highest classification accuracy of selected gene subsets on dataset Leukemia, which is 94.44$\%$; furthermore, the selected gene subset by FNSIJE-KS is less than those of FNPME-FS. However, FNSIJE-KS selects 2.5 and 2.8 fewer genes than FNCE and FNPME-FS on datasets Colon and DLBCL, respectively, although its classification accuracy is slightly lower than FNCE and FNPME-FS.

In the same way, from Tables 10 and 13, the classification accuracy of selected gene subset by FNSIJE-KS achieves highest value of 85.48$\%$ under classifier C4.5 on dataset Colon, which is 3.22, 11.29, 4.83, and 20.84$\%$ higher than those by the other four methods, respectively. The classification accuracy of selected gene subsets by FNSIJE-KS and FNPME-FS reaches the highest value at the same time on dataset Prostate, which is 88.23$\%$, and the selected gene subset by FNSIJE-KS is 4.45 fewer than those by FNPME-FS.

In short, from Tables 12 and 13, comparing with FNRS, FNCE, FNPME-FS, and EGGS, the mean classification accuracy of selected gene subsets by the FNSIJE-KS method has been improved under classifiers KNN and C4.5, both reaching the highest level.

This final portion is verify the classification performance of the FNSIJE-KS method under the classifier CART for four gene datasets. Three feature selection methods compared with FNSIJE-KS include FNRS [32], FNCE [37], and FNPME-FS [36].

Let the four feature selection methods use the tenfold cross-validation method on four gene datasets, and classification accuracy of selected gene subsets under the classifier CART is shown in Table 14. In Table 14, the bolded numbers indicate that the classification accuracy of the selected gene subsets is the best with respect to other three methods.

Table 14 Classification accuracy with four methods on classifier CART

As seen from the average classification result illustrated in Table 14, and combining Table 10, our method FNSIJE-KS achieves the largest value for the gene dataset Colon under the classifier CART. Meanwhile FNSIJE-KS selects fewest genes than three other feature selection methods. FNSIJE-KS and FNRS have the highest classification performance on selected gene subset of dataset Prostate, which is 86.03$\%$. Comparing FNSIJE-KS with FNRS, FNCE, and FNPME-FS, the mean classification accuracy of the selected gene subset by FNSIJE-KS reached the highest level under the classifier CART.

In summary, the FNSIJE-KS method can eliminate redundant features in the mass and exhibits better classification performance than other compared methods on the gene datasets.

Statistical analysis

To systematically study the statistical performance on classification accuracy of all compared methods in this paper, Friedman test and corresponding post hoc will be carried out in this subsection. Friedman statistic [56] is conveyed as:

$$\begin{aligned}&{\chi ^2} = \frac{{12n}}{{k(k + 1)}}\left( \sum \limits _{i = 1}^k {r_i^2} - \frac{{k{{(k + 1)}^2}}}{4}\right) \end{aligned}$$

(32)

$$\begin{aligned}&F = \frac{{(n - 1){\chi ^2}}}{{n(k - 1) - {\chi ^2}}}, \end{aligned}$$

(33)

where $r_{i}$ is the mean ranking of method on all datasets, n and k represent the number of datasets and methods, respectively, and F is a F-distribution under $\left( {k - 1} \right)$ and $\left( {k - 1} \right) \left( {n - 1} \right)$ freedom degrees.

In this first portion, the classification accuracy of the four feature selection methods in Tables 8 and 9 under the classifiers KNN and CART is statistically analyzed.

First, for the classification accuracy on six UCI datasets in Tables 8 and 9, the Friedman tests are achieved by the comparison of FNSIJE-KS with FNRS, FNCE, and FNPME-FS. Tables 15 and 16 list the mean rankings of the four methods under the classifiers KNN and CART, respectively. Calling icdf in MATLAB 2016a calculates critical value $F(3,15)=2.4898,$ when $\alpha =0.1$.

Assuming that the four methods are equivalent in classification performance, the value of Friedman statistics should not exceed the critical value F(3, 15). On the contrary, the four methods differ significantly in feature selection performance.

Table 15 Rank of four methods with classifier KNN on UCI datasets

Table 16 Rank of four methods with classifier CART on UCI datasets

According to Friedman statistics, we can get that $F=1.8431$ under the classifier KNN and $F= 11.0948$ under the classifier CART. Obviously, the value under the classifier CART is greater than the critical value F(3, 15). This phenomenon indicates that the FNRS, FNCE, FNPME-FS, and FNSIJE-KS are significantly different.

Second, we need to do a post hoc test for the difference between the four methods. The post hoc test used here is Nemenyi test [57]. The statistics first needs to determine the critical value of the distance between the mean ranking values, which is denoted as:

$$\begin{aligned} \text {CD}_{\alpha } = {q_a}\sqrt{\frac{{k\left( {k + 1} \right) }}{{6n}}}. \end{aligned}$$

(34)

Here, $q_{a}$ represents the critical tabulated value of this test. It can be obtained that $q_{0.1}=2.291$ when $\alpha =0.1$ and the number of methods is 4. Thus, $\text {CD}_{0.1}=1.7076$.

If the distance of the corresponding mean rankings between the two methods is larger than the critical distance $\text {CD}_{0.1}$, the two methods are considered to be significantly different. From Table 15, the distance between mean rankings of FNSIJE-KS to FNCE is 1.95, which is greater than 1.7076 under the classifier KNN. Therefore, the Nemenyi tests show that FNSIJE-KS is significantly greater than FNCE at $\alpha =0.1$. However, the distances between mean rankings of FNSIJE-KS to FNRS and FNPME-FS are less than 1.7076. This phenomenon repeals that there is no significant difference between FNSIJE-KS to FNRS and FNPME-FS. For the classifier CART, the distance between mean rankings of FNSIJE-KS to FNCE is 2.5, which is greater than 1.7076; it is obviously obtained that FNSIJE-KS is significantly greater than FNCE at $\alpha =0.1$. However, the distances between mean rankings of FNSIJE-KS to FNRS and FNPME-FS are less than 1.7076. This reveals that there is no significant difference between FNSIJE-KS to FNRS and FNPME-FS.

The following portion is executed on five different methods FNRS, FNCE, FNPME-FS, and FNSIJE-KS for four gene datasets from Tables 12 and 13 under two classifiers KNN and C4.5. Tables 17 and 18 list the mean rankings of the five methods under the classifiers KNN and C4.5, respectively.

Table 17 Rank of five methods with classifier KNN on gene datasets

Table 18 Rank of five methods with classifier C4.5 on gene datasets

After calculation, $F(4,12)=2.4801$ when $\alpha = 0.1$, and then, we can compute that $F=8.5221$ for Classifier KNN and $F=10.0225$ for Classifier C4.5. It is apparent to obtain that the two values are greater than the critical value F(4, 12). This result exhibits that five methods are significantly different.

Then, we perform Nemenyi tests on the five feature selection methods in Tables 12 and 13 under the classifiers KNN and C4.5. It is easily obtained that ${q_{0.1}} = 2.459$ when the number of methods is 5 and $\alpha =0.1$. Thus, it can calculate that $\text {CD}_{0.1} = 2.7492$ $(k=5, n=4)$ according to formula (34). For classifier KNN, the distances between mean rankings of FNSIJE-KS to other four methods are less than 2.7492, and this result shows that five methods are no significant difference. For classifier C4.5, the distance between mean rankings of FNSIJE-KS to EGGS is greater than 2.7492. Thus, the Nemenyi tests show that FNSIJE-KS is significantly better than EGGS at $\alpha =0.1$.

In the final portion of this subsection, we discuss the statistical results of the four compared methods for four gene datasets from Table 14 under the classifier CART. The mean rankings of four methods under classifier CART are computed and demonstrated in Table 19.

Table 19 Rank of five methods with classifier CART on gene datasets

It is apparently obtained that $F(3,9)=2.8129$ when $\alpha = 0.1$, and then, we can compute that 5.00 for classifier CART. This exhibits that the values is greater than the critical value F(3, 9). Thus, four methods are significantly different under classifier CART.

Then, we perform Nemenyi test on the four feature selection methods in Table 14 under the classifier CART. It is easily obtained that $q_{0.1}=2.291$ when the number of methods is 4 and $\alpha =0.1$. Thus, it can calculate that 2.0914 $(k=4, n=4)$ according to formula (34). For the classifier CART, the distance between mean rankings of FNSIJE-KS to FNCE is greater than 2.0914. Thus, the Nemenyi test shows that FNSIJE-KS is significantly better than FNCE at $\alpha =0.1$.

To sum up, FNSIJE-KS is better than the other compared methods in the Friedman statistic test.

Conclusion

In neighborhood decision system, the traditional dependency function based on FNRS only considers the classification information contained in the lower approximation while ignoring the classification information contained in the upper approximation. This construction method may lead to the loss of some information. To solve this problem, we propose an improved model based on self-information and information entropy. First, from the algebra view, the four types of fuzzy neighborhood self-information measures are defined using the upper and lower approximations in FNRS and combining with the concept of self-information, and the related properties are discussed in detail. It is proved that the fourth measure changes more with the change of feature subset, which is helpful to select the optimal feature subset. The significance of features based on algebra view can interpret the influence of the features included in feature subset. Second, the fuzzy neighborhood joint entropy is given from the information view. Information view-based feature significance can illustrate the importance on features from uncertainty classification. Then, from both algebra and information views, a model based on FNSIJE is proposed to analyze the noise, uncertainty, and ambiguity of the neighborhood decision system. Third, a new forward search method for feature selection is designed, which makes that the selected feature subsets have higher classification performance. All the designed experiments demonstrate that our FNSIJE-KS method can select fewer features for some low-dimensional UCI datasets and high-dimensional gene datasets, which has the optimal classification performance. In the future work, we will further study more effective search strategies based on FNSIJE to balance the size of selected feature subsets and classification accuracy as much as possible, and explore on incomplete information systems.