1 Introduction

As already predicted in the late 1970s [1], space debris become a major issue for the use of satellites [2, 3]. In particular, the amount of space debris in low earth orbit (LEO) is increasing rapidly [3]. To detect and map space debris, high performance radar sensors can be used [3, 4]. Due to the enormous progress in the field of high-power microwave technology [5, 6], corresponding radar sensors can also be operated in high frequency bands such as the W-band [7, 8]. Due to the high bandwidth available there, very high resolutions can be achieved [7,8,9]. In near future, even W-band transmission powers in the range of 100 kW may be achieved [10]. To realize a W-band radar sensor with such a high transmission power, a suitable high-power amplifier as well as an appropriate transmission line is required. The transmission line connects the output of the high-power amplifier with the antenna feed. Due to the high power, oversized transmission lines are required. A suitable transmission mode is the HE11 hybrid mode in a corrugated circular waveguide [11,12,13]. Low ohmic loss, small mode conversion, and low-sidelobe radiation patterns can be achieved [11,12,13]. Important components of an overmoded transmission line are miter bends [14, 15], polarizers [16, 17], rotary joints [18], and waveguide diameter tapers [19, 20]. For design verification of such components, low power measurements are required. Here, the fundamental TE10 mode within a rectangular waveguide, provided by a microwave extension module [21] of a Network Analyzer (NWA), has to be converted into the HE11 hybrid mode within a highly oversized corrugated circular waveguide. In a simple way, this may be realized by a corrugated horn antenna [22, 23], illuminating the aperture of a highly overmoded circular waveguide [24, 25]. However, since the component behavior under test may be sensitive in respect to the mode content [14, 15], a mode purity as best as possible is required, within the considered frequency range. A concept based on a corrugated horn is limited in respect of the mode purity [24, 25]. Therefore, a waveguide mode converter is preferred here, which may attain a significant better mode purity [24]. Such a mode converter may consist of (1) commercial rectangular TE10 ↦ circular TE11 transition and (2) customized TE11 ↦ HE11 mode converter, based on tapered variation of the corrugation depth [26, 27], integrated within a waveguide diameter up-taper.

For the numerical synthesis of such an advanced mode converter with broadband frequency behavior, coupled mode theory [28,29,30] may be applied. However, in calculations on a perturbed corrugated waveguide, varying eigenvalues are of particular importance to consider. The present paper addresses fast numerical calculations on eigenvalues of a corrugated waveguide with varying diameter and corrugation depth. To the best knowledge of the authors, similar calculations along an arbitrary perturbation were not published yet.

The paper is organized as follows: Section 2 introduced the coupled mode formalism, able to calculate mode conversion within multimode waveguides. In Section 3, fundamentals of corrugated waveguides and their eigenvalues are discussed. Section 4 addresses numerical calculations on the eigenvalues of a corrugated waveguide with varying diameter and corrugation depth. Section 5 closes with the conclusion and an outlook for future research activities.

2 Coupled Mode Theory

The principle concept of the coupled mode theory is to expand an electromagnetic field within a perturbed waveguide as superposition of eigenmodes of a uniform reference waveguide, with the same cross section [28,29,30]. Neglecting ohmic wall losses and backward travelling waves due to reflections (highly oversized waveguide) as well as restricting to adiabatically varying waveguide parameters (characteristic length of variation large compared to the wavelength), the corresponding mode amplitudes satisfy the first-order differential equation [28,29,30]:

$$ \frac{\mathrm{d}}{\mathrm{d}z}{I}_n(z)=-j{\beta}_n\cdotp {I}_n(z)+\sum \limits_m^{n\ne m}{\mathrm{K}}_{nm}\cdotp {I}_m(z) $$
(1)

with In(z) as complex mode amplitude at the position z, βn as corresponding phase constant, and Κnm as coupling coefficient [30,31,32] between the nth and mth eigenmode of the uniform reference waveguide. To eliminate fast varying phase terms, the substitution In(z) = An(z) · exp[−jβn · z] is introduced with An(z) as slowly varying complex mode amplitude. Using the Runge-Kutta integration method [33], such a substitution reduces the required step width and therefore the required computational effort. It follows:

$$ \frac{\mathrm{d}}{\mathrm{d}z}{\mathrm{A}}_n(z)=\sum \limits_m^{n\ne m}{\mathrm{K}}_{nm}\cdotp \exp \left[- j\varDelta \beta \cdotp z\right]\cdotp {A}_m(z) $$
(2)

with

$$ \Delta \beta ={\beta}_n-{\beta}_m $$
(3)

In general, the exponent in Eq. (2) has to be substituted by [11, 34]:

$$ -j{\int}_0^L\Delta \beta\ \mathrm{d}z $$
(4)

with L as the perturbation length. This allows consideration of varying phase constants, for example, caused by a varying waveguide diameter.

In matrix representation, Eq. (2) reads:

$$ \frac{\mathrm{d}}{\mathrm{d}z}\mathbf{Y} (z)=\mathbf{H}\cdotp \mathbf{Y} (z) $$
(5)

with

$$ \mathbf{Y} (z)=\left(\begin{array}{c}{A}_1(z)\\ {}{A}_2(z)\\ {}\vdots \\ {}{A}_N(z)\end{array}\right) $$
(6)

and

$$ {h}_{ij}=\left\{\begin{array}{cc}0& \mathrm{for}\ i=j\\ {}{\mathrm{K}}_{nm}\cdotp \exp \left[-j{\int}_0^L\left({\beta}_i-{\beta}_j\right)\ \mathrm{d}z\right]& \mathrm{for}\ i\ne j\end{array}\right. $$
(7)

as the coefficients of the coupling matrix H.

Equations (5)–(7) show that knowledge about varying phase constants is of particular importance to control mode conversion within a perturbed waveguide. This results in the particular importance of varying mode eigenvalues since the phase constant depends on the waveguide diameter as well as on the mode eigenvalue [11]:

$$ \beta =k\cdotp \sqrt{\ 1-{\left(\ \frac{X}{ka}\ \right)}^2\kern0.5em } $$
(8)

with a as the waveguide diameter, k = 2π/λ as the free-space wavenumber, and X as the mode eigenvalue.

3 Corrugated Waveguide

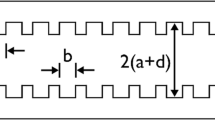
Figure 1 shows a simplified sketch of a corrugated waveguide with the radius a, the corrugation period c, the slot width b, and the corrugation depth d.

Fig. 1
figure 1

Corrugated waveguide with the waveguide radius a, the corrugation period c, the slot width b, and the corrugation depth d

Full size image

Typically, hybrid modes of a corrugated waveguide are referred according to the balanced hybrid mode condition [22]:

$$ {\vartheta}_m(X)=\pm m $$
(9)

with

$$ {\vartheta}_m(X)=X\cdotp \frac{J{\prime}_m(X)}{J_m(X)} $$
(10)

The function Jm(x) is the Bessel function of the first kind and the order m. The function \( {J}_m^{\prime }(x) \) is its first derivation in respect of x. For the nth root and +/−, HEmn / EHmn modes occur [22, 35]. Equation (9) is valid for a highly oversized waveguide (ka = 2π · a/λ ↦ ∞) having a longitudinal wall surface impedance Zs =  − Ez/Hφ ≠ 0. For ka ≠ ∞, the surface-impedance model [11, 22, 31, 32], which assumes a uniform surface impedance, is widely used. Corresponding calculations lead to [35]:

$$ {\vartheta}_m(X)-\frac{{\left(m\overset{\sim }{\beta}\right)}^2}{\vartheta_m(X)}={\left(\frac{X}{ka}\right)}^2\cdotp {S}_m\left( ka,k\left(a+d\right)\right) $$
(11)

with

$$ {\displaystyle \begin{array}{c}\overset{\sim }{\beta }=\beta /k=\sqrt{\ 1-{\left(\frac{X}{ka}\right)}^2\kern0.5em }\\ {}{S}_m\left(x,y\right)=x\cdotp \frac{J_m^{\prime }(x)\ {Y}_m(y)-{J}_m(y)\ {Y}_m^{\prime }(x)}{J_m(x)\ {Y}_m(y)-{J}_m(y)\ {Y}_m(x)}\end{array}} $$
(12)

The function Ym(x) is the Bessel function of the second kind and the order m, and \( {Y}_m^{\prime }(x) \) is its first derivation in respect of x.

In principle, Eq. (11) is derived as [35,36,37,38,39] (1) calculation of the field components for r ≤ a as superposition of transversal electric (TE) and transversal magnetic (TM) field components, (2) calculation of the field components for a < r < (a + d) as a pure TM mode with Ez = const., and (3) matching the field components at r = a.

A pure TM mode within the corrugation requires b <  λ/2. In this way, a radial TE mode cannot be supported, and no Bragg reflection [40, 41] occurs [42, 43]. The longitudinal surface impedance Zs at r = a can be represented as [35, 44]:

$$ {Z}_s=-j{Z}_0\cdotp \frac{ka}{S_m\left( ka,k\left(a+d\right)\right)}\approx j{Z}_0\ \tan (kd) $$
(13)

For ka ↦ ∞ and Zs ≠ 0, Eq. (11) merges into Eq. (9).

Note that the surface-impedance model neglects space harmonics [45, 46] and therefore is restricted to c ≈ b (thin corrugation ridges) and b ≪ λ/2 (large number of corrugation slots per wavelength) [22, 23, 35,36,37,38,39]. In more general calculations, space harmonics within r ≤ a as well as a < r ≤ (a + d) have to be considered. Corresponding calculations lead to rather elaborate equations [22] which are out of scope of the present paper. Simplified equations result for the restriction to K space harmonics within r ≤ a. Corresponding calculations lead to [22]:

$$ \frac{b}{c}\cdotp \sum \limits_{N=-K}^K{\left(\frac{1}{\eta}\right)}^2\cdotp \left[\kern0.5em {\vartheta}_m\left(\eta \right)-\frac{{\left(m{\overset{\sim }{\beta}}_N\right)}^2}{\vartheta_m\left(\eta \right)}\kern0.5em \right]\cdotp \frac{\sin \left({\beta}_N\cdotp \frac{b}{2}\right)}{\left({\beta}_N\cdotp \frac{b}{2}\right)}=\frac{S_m\left( ka,k\left(a+d\right)\right)}{(ka)^2}\kern0.5em $$
(14)

In principle, the derivation of Eq. (14) is identical to the mode matched procedure introduced for the surface-impedance model. But now, for r ≤ a, space harmonics are considered with βN = β + N · 2π/c, \( {\overset{\sim }{\beta}}_N={\beta}_N/k \), and \( \eta =a\cdotp \sqrt{\ {k}^2-{\beta}_N^2\kern0.5em } \) [22, 45, 46]. For K = 0 (fundamental space harmonic), c ≈ b, and b ≪ λ/2, Eq. (14) merges into Eq. (11).

Figure 2 compares calculated eigenvalues for m = 1 (HE1n / EH1n modes) and X ∈ [0, 7], based on Eq. (14) with K = 1 (first spatial harmonic) and the surface-impedance model, given in Eq. (11). The blue data points are calculated using the surface impedance model. The yellow data points are calculated with ka = 10, b = 0.1 · λ/2, and c = 1.1 · b, fulfilling the terms and conditions of the surface-impedance model (c ≈ b, b ≪ λ/2), whereas the brown data points are calculated with ka = 10, b = 0.4 · λ/2, and c = 2 · b, violating the terms and conditions of the surface-impedance model. Figure 2 shows good agreement of the surface-impedance model and Eq. (14), as long as those terms and conditions are fulfilled. Otherwise, significant deviations occur.

Fig. 2
figure 2

Calculated eigenvalues for m = 1 (HE1n / EH1n modes), X ∈ [0, 7], and ka = 10 for varying corrugation depth d, considering the first space harmonic (K = 1, yellow and brown curves) and the surface-impedance model (blue curve)

Full size image

The curves in Fig. 2 were calculated using the Newton-Raphson method, addressed in Section 4.1. Calculations with K = 1 and K = 2 revealed that the consideration of an increasing number of space harmonics leads just to small variations compared with the calculations based on the first space harmonic.

In the following, the consideration is restricted to the surface-impedance model. The explicit corrugation geometry is omitted here which leads to a more descriptive representation of the principle procedure. However, this requires that the terms and conditions of the surface-impedance model (c ≈ b, b ≪ λ/2) are fulfilled (see Fig. 2). In the case, that they cannot be fulfilled; only Eq. (11) must be replaced by Eq. (14).

4 Numerical Calculations

To calculate the variation of the eigenvalues along an arbitrary perturbation, Eq. (11) is solved numerically. In Subsection 4.1, the Newton-Raphson method is introduced, which here is used for numerical calculations. Subsection 4.2 addresses corresponding results.

4.1 Newton-Raphson Method

The principle concept of the Newton-Raphson method is to linearize the considered function f(x) at a starting point x0 and use those roots as improved starting point of a second iteration [47, 48]. It follows:

$$ {x}_{n+1}={x}_n+\Delta x $$
(15)

with

$$ \Delta x=-\frac{f\left({x}_n\right)}{f^{\prime}\left({x}_n\right)} $$
(16)

The iteration is aborted when the rate of change of the approximated solution falls below a specified value.

For numerical calculations, the central difference quotient can be used [49]:

$$ {f}^{\prime }(x)\approx \frac{f\left(x+h\right)-f\left(x-h\right)}{2h} $$
(17)

To avoid tripping due to a too small h and a not sufficient accuracy through a too large h, \( h=\sqrt{\mathrm{eps}\ } \) is used here, with eps as floating point relative accuracy (for double precision: eps = 2−52) [50].

To find all solutions of interest, the Newton-Raphson method is calculated multiple times with random initialization within the range of interest.

4.2 Results

Figure 3 shows the calculated eigenvalues for m = 1 (HE1n / EH1n modes), X ∈ [0, 7], and very large ka = 1000 (\( \hat{=}\infty \), blue curves), as well as for  ka = 10 (brown curves) in dependence of the corrugation depth d ∈ [0, λ/2]. For ka ↦ ∞, the eigenvalues are close to constant. For moderate ka, the eigenvalues depend strongly on the corrugation depth. However, for d ≈ λ/4, in each case, broadband frequency behavior is shown, with a relative bandwidth far beyond 10%. For d ↦ 0 or λ/2, Eq. (13) gives Zs = 0, and the HEmn / EHmn modes merge into ordinary TEmn / TMmn modes [51, 52]. As shown in Fig. 3, this transition is abrupt at large ka. For a TE11 ↦ HE11 mode converter, discussed in Section 1, this is critical in respect of parasitic mode conversion [27, 51, 52].

Fig. 3
figure 3

Eigenvalues for ka ↦ ∞ and ka = 10 in dependence of the normalized corrugation depth d

Full size image

To ensure a high mode purity, a customized variation as well on the corrugation depth [26, 27, 51, 52] as the waveguide diameter may be used. However, this requires the ability to calculate the variation of the eigenvalues along an arbitrary perturbation with low computational effort. This is possible with the presented procedure here. As example, Fig. 4 shows numerical calculations for m = 1 (HE1n / EH1n modes), X ∈ [0, 7], and ka = 50 (blue color) along a tapered variation of the corrugation depth (brown color), with:

$$ \frac{\mathrm{d}}{\mathrm{d}z}d(z)\propto {\sin}^2\left(\ \frac{\pi }{L}z\ \right) $$
(18)

Figure 4 shows that due to the tapered variation of the corrugation depth, the strong variation at d ↦ 0 or λ/2 could be smoothened. The eigenvalues change slowly along the perturbation, which leads to low parasitic mode conversion. For a TE11 ↦ HE11 mode converter, discussed in Section 1, this is essential [26, 27, 51, 52]. For a numerical synthesis, an even more optimized tapering of the corrugation depth may be applied. However, this is out of scope of the present paper. For comparison, Fig. 5 shows the eigenvalues along a perturbation with ka = 50 and a constant rate of change (linear progression).

Fig. 4
figure 4

Eigenvalues for ka = 50 and a tapered rate of change of the varying corrugation depth d

Full size image
Fig. 5
figure 5

Eigenvalues for ka = 50 and a constant rate of change of the varying corrugation depth d

Full size image

5 Conclusion

The present paper addresses fast numerical calculations on the eigenvalues of hybrid modes in corrugated circular waveguides with arbitrary perturbation of the waveguide diameter and the corrugation depth, in case that the surface-impedance model is valid. Such calculations are essential for the synthesis of optimized mode converters and diameter tapers within corrugated waveguides.

Future research activities will address the embedding of the outlined procedure into the numerical synthesis of broadband corrugated waveguide mode converters and diameter tapers. Such passive microwave components will be essential for future broadband high-power microwave applications.