Skip to main content
SpringerLink
Log in

In-plane stiffness of imperfect thin rectangular plates subjected to biaxial loads in elastic post-buckling region

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

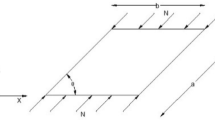
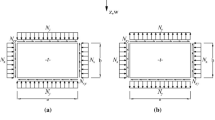
The elastic post-buckling behavior of thin plates covers a relatively vast region in which geometry nonlinearity (large deflection) and material linearity (Hooke's low) are realized. In this region, a thin rectangular plate has constant stiffnesses in both orthogonal directions. Few simplified analysis guidelines have been analytically represented for in-plane stiffnesses of an elastic post-buckled thin plate subjected to biaxial loads. In this study, Marguerre's equations (the generalized form of von Karman equations), which describe the elastic post-buckling behavior of imperfect thin plates, are solved. Galerkin's method is used to solve these equations in a semi-analytical procedure. Simply supported imperfect thin rectangular plates are considered, and the stresses and displacements functions are obtained in two orthogonal directions to determine corresponding in-plane stiffnesses of the plate. Also, the maximum applicable load is obtained so that the material's linear behavior is maintained. The semi-analytical procedure has accuracy enough to predict the in-plane stiffness of post-buckled plates and can be easily used for practical purposes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Abbreviations

a :

Length of the plate

\(b\) :

Width of the plate

\(h\) :

Thickness of the plate

\(f\) :

Amplitude of the deflection function

\({f}_{0}\) :

Amplitude of the initial imperfection function

\({f}_{\mathrm{cr}}\) :

Amplitude of the deflection function at the beginning of the elastic post-buckling region

\({f}_{\mathrm{max}}\) :

Amplitude of the deflection function at the end of the elastic post-buckling region

\({f}_{\mathrm{T}}\) :

Total amplitude of the deflection function

\({k}_{x}\) :

Elastic buckling coefficient of the plate

\({\bar{k}}_{x}\) :

In-plane stiffness of the plate in the x-direction

\({\bar{k}}_{y}\) :

In-plane stiffness of the plate in the y-direction

\(m\) :

Number of half-waves in the x-direction

\(n\) :

Number of half-waves in the y-direction

\(u\) :

Displacement function in the x-direction

\(v\) :

Displacement function in the y-direction

\(w\) :

Displacement function in the z-direction

\({w}_{0}\) :

Initial imperfection function in the z-direction

\({w}_{\mathrm{T}}\) :

Total displacement function in the z-function

\(D\) :

Flexural rigidity of the plate

\(E\) :

Modulus of elasticity

\(F\) :

Airy's stress function

\({N}_{x}\) :

Applied load in the x-direction

\({N}_{y}\) :

Applied load in the y-direction

\({N}_{xy}\) :

Applied load in the xy-direction

\(\beta \) :

Loads' ratio

\(\lambda \) :

Slenderness ratio of the plate

\(\mu \) :

Poisson's ratio

\({\sigma }_{\rm e}\) :

Stress intensity

\({\sigma }_{p}\) :

Proportional limit stress

\({\sigma }_{x}\) :

Normal stress in the x-direction

\({\sigma }_{xa}\) :

Average stress in the x-direction

\({\sigma }_{xa,\mathrm{max}}\) :

Average stress in the x-direction at the end of the elastic post-buckling region

\({\sigma }_{x,\mathrm{cr}}\) :

Elastic buckling stress in the x-direction

\({\sigma }_{y}\) :

Normal stress in the y-direction

\({\sigma }_{ya}\) :

Average stress in the y-direction

\({\sigma }_{\mathrm{yeild}}\) :

Yield stress of the plate material

\(\phi \) :

Aspect ratio of the plate

6. References

  1. Hosseini-Hashemi, S., Khorshidi, K., Amabili, M.: Exact solution for linear buckling of rectangular Mindlin plates. J. Sound Vib. 315(1), 318–342 (2008). https://doi.org/10.1016/j.jsv.2008.01.059

    Article  Google Scholar 

  2. Mittelstedt, C., Erdmann, H., Schröder, K.-U.: Postbuckling of imperfect rectangular composite plates under inplane shear closed-form approximate solutions. Arch. Appl. Mech. 81(10), 1409–1426 (2011). https://doi.org/10.1007/s00419-010-0491-y

    Article  MATH  Google Scholar 

  3. Khorshidi, K., Fallah, A.: Buckling analysis of functionally graded rectangular nano-plate based on nonlocal exponential shear deformation theory. Int. J. Mech. Sci. 113, 94–104 (2016). https://doi.org/10.1016/j.ijmecsci.2016.04.014

    Article  Google Scholar 

  4. Khorshidi, K., Fallah, A.: Effect of exponential stress resultant on buckling response of functionally graded rectangular plates. J. Stress Anal. 2(1), 27–33 (2017). https://doi.org/10.22084/jrstan.2017.12894.1019

    Article  Google Scholar 

  5. Van Do, V.N., Chang, K.-H., Lee, C.-H.: Post-buckling analysis of FGM plates under in-plane mechanical compressive loading by using a mesh-free approximation. Arch. Appl. Mech. 89(7), 1421–1446 (2019). https://doi.org/10.1007/s00419-019-01512-5

    Article  Google Scholar 

  6. Ma, P., He, B., Fang, Y., Jiao, Y., Qi, H.: An efficient finite strip procedure for initial post-buckling analysis of thin-walled members. Arch. Appl. Mech. 90(3), 585–601 (2020). https://doi.org/10.1007/s00419-019-01627-9

    Article  Google Scholar 

  7. Chajes, A.: Principles of structural stability theory. Prentice Hall, Englewood Cliffs (1974)

    Google Scholar 

  8. Marguerre, K.: Zur Theorie der gekrümmter Platte grosser Formänderung. In: The Fifth International Congress for Applied Mechanics, Cambridge, UK, pp. 93–101 (1938)

  9. Jayachandran, S.A., Vaidyanathan, C.V.: Post critical behaviour of biaxially compressed plates on elastic foundation. Comput. Struct. 54(2), 239–246 (1995). https://doi.org/10.1016/0045-7949(94)00317-V

    Article  MATH  Google Scholar 

  10. Elgaaly, M.: Post-buckling behavior of thin steel plates using computational models. Adv. Eng. Softw. 31(8), 511–517 (2000). https://doi.org/10.1016/S0965-9978(00)00037-5

    Article  MATH  Google Scholar 

  11. Mateus, A.F., Witz, J.A.: A parametric study of the post-buckling behaviour of steel plates. Eng. Struct. 23(2), 172–185 (2001). https://doi.org/10.1016/S0141-0296(00)00005-5

    Article  Google Scholar 

  12. Abodi, J.T.: Effect of patch length ratio of in-plane loading on the post-buckling behavior of rectangular thin plates. Int. J. Civ. Eng. Struct. 3(2), 53–66 (2014)

    Google Scholar 

  13. Katsikadelis, J.T., Babouskos, N.G.: Post-buckling analysis of viscoelastic plates with fractional derivative models. Eng. Anal. Boundary Elem. 34(12), 1038–1048 (2010). https://doi.org/10.1016/j.enganabound.2010.07.003

    Article  MathSciNet  MATH  Google Scholar 

  14. Stamatelos, D.G., Labeas, G.N., Tserpes, K.I.: Analytical calculation of local buckling and post-buckling behavior of isotropic and orthotropic stiffened panels. Thin-Walled Struct. 49(3), 422–430 (2011). https://doi.org/10.1016/j.tws.2010.11.008

    Article  Google Scholar 

  15. Bakker, M.C.M., Rosmanit, M., Hofmeyer, H.: Approximate large-deflection analysis of simply supported rectangular plates under transverse loading using plate post-buckling solutions. Thin-Walled Struct. 46(11), 1224–1235 (2008). https://doi.org/10.1016/j.tws.2008.02.003

    Article  Google Scholar 

  16. Byklum, E., Steen, E., Amdahl, J.: A semi-analytical model for global buckling and postbuckling analysis of stiffened panels. Thin-Walled Struct. 42(5), 701–717 (2004). https://doi.org/10.1016/j.tws.2003.12.006

    Article  Google Scholar 

  17. He, J.-H.: A Lagrangian for von Karman equations of large deflection problem of thin circular plate. Appl. Math. Comput. 143(2), 543–549 (2003). https://doi.org/10.1016/S0096-3003(02)00383-1

    Article  MathSciNet  MATH  Google Scholar 

  18. Grądzki, R., Kowal-Michalska, K.: Post-buckling analysis of elastic–plastic plates basing on the Tsai-Wu criterion. J. Theor. Appl. Mech. 37(4), 893–908 (1999)

    MATH  Google Scholar 

  19. Steen, E.: Elastic buckling and postbuckling of eccentrically stiffened plates. Int. J. Solids Struct. 25(7), 751–768 (1989). https://doi.org/10.1016/0020-7683(89)90011-5

    Article  MATH  Google Scholar 

  20. Rhodes, J., Harvey, J.M.: The post-buckling behaviour of thin flat plates in compression with the unloaded edges elastically restrained against rotation. J. Mech. Eng. Sci. 13(2), 82–91 (1971). https://doi.org/10.1243/JMES_JOUR_1971_013_014_02

    Article  MATH  Google Scholar 

  21. Dombourian, E.M., Smith, C.V., Carlson, R.L.: A perturbation solution to a plate postbuckling problem. Int. J. Non-Linear Mech. 11(1), 49–58 (1976). https://doi.org/10.1016/0020-7462(76)90038-X

    Article  MATH  Google Scholar 

  22. Shen, H.-S.: Postbuckling of orthotropic plates on two-parameter elastic foundation. J. Eng. Mech. 121(1), 50–56 (1995). https://doi.org/10.1061/(ASCE)0733-9399(1995)121:1(50)

    Article  Google Scholar 

  23. Zhang, J.W., Shen, H.S.: Postbuckling of orthotropic rectangular Plates in Biaxial Compression. J. Eng. Mech. 117(5), 1158–1170 (1991). https://doi.org/10.1061/(ASCE)0733-9399(1991)117:5(1158)

    Article  Google Scholar 

  24. Wang, H., Ou, M., Wang, T.: Post-buckling behaviour of orthotropic rectangular plates. Comput. Struct. 41(1), 1–5 (1991). https://doi.org/10.1016/0045-7949(91)90151-B

    Article  MATH  Google Scholar 

  25. Hui-shen, S.: Postbuckling behaviour of rectangular plates under combined loading. Thin-Walled Struct. 8(3), 203–216 (1989). https://doi.org/10.1016/0263-8231(89)90003-7

    Article  Google Scholar 

  26. Hui-shen, S.: Perturbation analysis for the postbuckling of rectangular orthotropic plates. Appl. Math. Mech. 10(4), 373–384 (1989). https://doi.org/10.1007/BF02017778

    Article  MathSciNet  MATH  Google Scholar 

  27. Hui-shen, S., Jian-wu, Z.: Perturbation analyses for the postbuckling of simply supported rectangular plates under uniaxial compression. Appl. Math. Mech. 9(8), 793–804 (1988). https://doi.org/10.1007/BF02465403

    Article  MATH  Google Scholar 

  28. Zheng, X., Lee, J.S.: On the convergence of the Chien’s perturbation method for von Karman plate equations. Int. J. Eng. Sci. 33(8), 1085–1094 (1995). https://doi.org/10.1016/0020-7225(94)00121-Y

    Article  MATH  Google Scholar 

  29. Casciaro, R., Garcea, G., Attanasio, G., Giordano, F.: Perturbation approach to elastic post-buckling analysis. Comput. Struct. 66(5), 585–595 (1998). https://doi.org/10.1016/S0045-7949(97)00112-0

    Article  MATH  Google Scholar 

  30. Koiter, W.T.: On the stability of elastic equilibrium, vol. 833. National Aeronautics and Space Administration (1967)

  31. Sun, G., Kennedy, D., Williams, F.W.: A post-buckling analysis for isotropic prismatic plate assemblies under axial compression. Int. J. Mech. Sci. 42(9), 1783–1803 (2000). https://doi.org/10.1016/S0020-7403(99)00055-7

    Article  MATH  Google Scholar 

  32. Byklum, E., Amdahl, J.: A simplified method for elastic large deflection analysis of plates and stiffened panels due to local buckling. Thin-Walled Struct. 40(11), 925–953 (2002). https://doi.org/10.1016/S0263-8231(02)00042-3

    Article  Google Scholar 

  33. Steen, E., Byklum, E., Hellesland, J.: Elastic postbuckling stiffness of biaxially compressed rectangular plates. Eng. Struct. 30(10), 2631–2643 (2008). https://doi.org/10.1016/j.engstruct.2008.02.006

    Article  Google Scholar 

  34. Yamaki, N.: Postbuckling behavior of rectangular plates with small initial curvature loaded in edge compression. J. Appl. Mech. 26, 407–417 (1959)

    MathSciNet  MATH  Google Scholar 

  35. Yamaki, N.: Postbuckling behavior of rectangular plates with small initial curvature loaded in edge compression—(continued). J. Appl. Mech. 27(2), 335–342 (1960). https://doi.org/10.1115/1.3643962

    Article  MATH  Google Scholar 

  36. Ueda, Y., Rashed, S.M.H., Paik, J.K.: An incremental Galerkin method for plates and stiffened plates. Comput. Struct. 27(1), 147–156 (1987). https://doi.org/10.1016/0045-7949(87)90189-1

    Article  MATH  Google Scholar 

  37. Ilanko, S.: Vibration and post-buckling of in-plane loaded rectangular plates using a multiterm Galerkin’s method. J. Appl. Mech. 69(5), 589–592 (2002). https://doi.org/10.1115/1.1489449

    Article  MathSciNet  MATH  Google Scholar 

  38. Paik, J.K., Lee, M.S.: A semi-analytical method for the elastic–plastic large deflection analysis of stiffened panels under combined biaxial compression/tension, biaxial in-plane bending, edge shear, and lateral pressure loads. Thin-Walled Struct. 43(3), 375–410 (2005). https://doi.org/10.1016/j.tws.2004.07.022

    Article  Google Scholar 

  39. Paik, J.K., Thayamballi, A.K., Lee, S.K., Kang, S.J.: A semi-analytical method for the elastic–plastic large deflection analysis of welded steel or aluminum plating under combined in-plane and lateral pressure loads. Thin-Walled Struct. 39(2), 125–152 (2001). https://doi.org/10.1016/S0263-8231(00)00058-6

    Article  Google Scholar 

  40. Salvado Ferreira, P., Virtuoso, F.B.E.: Semi-analytical models for the post-buckling analysis and ultimate strength prediction of isotropic and orthotropic plates under uniaxial compression with the unloaded edges free from stresses. Thin-Walled Struct. 82, 82–94 (2014). https://doi.org/10.1016/j.tws.2014.04.003

    Article  Google Scholar 

  41. Coan, J., Urbana, I.: Large-deflection theory for plates with small initial curvature loaded in edge compression. J. Appl. Mech. 18, 143–151 (1951)

    Article  MathSciNet  Google Scholar 

  42. Pagani, A., Daneshkhah, E., Xu, X., Carrera, E.: Evaluation of geometrically nonlinear terms in the large-deflection and post-buckling analysis of isotropic rectangular plates. Int. J. Non-Linear Mech. 121, 103461 (2020). https://doi.org/10.1016/j.ijnonlinmec.2020.103461

    Article  Google Scholar 

  43. Wu, B., Pagani, A., Filippi, M., Chen, W.Q., Carrera, E.: Large-deflection and post-buckling analyses of isotropic rectangular plates by Carrera Unified Formulation. Int. J. Non-Linear Mech. 116, 18–31 (2019). https://doi.org/10.1016/j.ijnonlinmec.2019.05.004

    Article  Google Scholar 

  44. Libove, C.: Buckle pattern of biaxially compressed simply supported orthotropic rectangular plates. J. Compos. Mater. 17(1), 45–48 (1983). https://doi.org/10.1177/002199838301700104

    Article  Google Scholar 

  45. Jahanpour, A., Roozbahani, F.: An applicable formula for elastic buckling of rectangular plates under biaxial and shear loads. Aerosp. Sci. Technol. 56, 100–111 (2016). https://doi.org/10.1016/j.ast.2016.07.005

    Article  Google Scholar 

  46. Boresi, A.P., Schmidt, R.J.: Advanced mechanics of materials, 6th edn. Wiley, New York (2003)

    Google Scholar 

  47. Mathematica, Trial version 8. 2010, Wolfram Research, Inc.: Champaign, IL

Download references

Funding

Not applicable.

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Malayer University, Malayer, Iran

    Alireza Jahanpour & Farideh Ahmadvand-Shahverdi

Authors
  1. Alireza Jahanpour
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Farideh Ahmadvand-Shahverdi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alireza Jahanpour.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jahanpour, A., Ahmadvand-Shahverdi, F. In-plane stiffness of imperfect thin rectangular plates subjected to biaxial loads in elastic post-buckling region. Arch Appl Mech 91, 2973–2989 (2021). https://doi.org/10.1007/s00419-021-01943-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-021-01943-z

Keywords

Search

Navigation