Abstract
For a parameter dimension \(d\in {\mathbb {N}}\), we consider the approximation of many-parametric maps \(u: [-\,1,1]^d\rightarrow {\mathbb R}\) by deep ReLU neural networks. The input dimension d may possibly be large, and we assume quantitative control of the domain of holomorphy of u: i.e., u admits a holomorphic extension to a Bernstein polyellipse \({{\mathcal {E}}}_{\rho _1}\times \cdots \times {{\mathcal {E}}}_{\rho _d} \subset {\mathbb {C}}^d\) of semiaxis sums \(\rho _i>1\) containing \([-\,1,1]^{d}\). We establish the exponential rate \(O(\exp (-\,bN^{1/(d+1)}))\) of expressive power in terms of the total NN size N and of the input dimension d of the ReLU NN in \(W^{1,\infty }([-\,1,1]^d)\). The constant \(b>0\) depends on \((\rho _j)_{j=1}^d\) which characterizes the coordinate-wise sizes of the Bernstein-ellipses for u. We also prove exponential convergence in stronger norms for the approximation by DNNs with more regular, so-called “rectified power unit” activations. Finally, we extend DNN expression rate bounds also to two classes of non-holomorphic functions, in particular to d-variate, Gevrey-regular functions, and, by composition, to certain multivariate probability distribution functions with Lipschitz marginals.
Similar content being viewed by others
1 Introduction
In recent years, so-called deep artificial neural networks (“DNNs” for short) have seen dramatic development in applications from data science and machine learning.
Accordingly, after early results in the 1990s on genericity and universality of DNNs (see [27] for a survey and references), in recent years the refined mathematical analysis of their approximation properties, viz. “expressive power,” has received increasing attention. A particular class of many-parametric maps whose DNN approximation needs to be considered in many applications are real-analytic and holomorphic maps. Accordingly, the question of DNN expression rate bounds for such maps has received some attention in the approximation theory literature [21, 22, 36].
It is well known that multi-variate, holomorphic maps admit exponential expression rates by multivariate polynomials. In particular, countably parametric maps \(u: [-\,1,1]^\infty \rightarrow {\mathbb R}\) can be represented under certain conditions by so-called generalized polynomial chaos expansions with quantified sparsity in coefficient sequences. This, in turn, implies N-term truncations with controlled approximation rate bounds in terms of N, with approximation rates which do not depend on the dimension of the active parameters in the truncated approximation [6, 7]. The polynomials which appear in such expansions can, in turn, be represented by DNNs, either exactly for certain activation functions, or approximately for example for the so-called rectified linear unit (“ReLU”) activation with exponentially small representation error [18, 37].
The purpose of the present paper is to establish corresponding DNN expression rate bounds in Lipschitz-norm (i.e., \(W^{1,\infty }\)-norm) for high-dimensional, analytic maps \(u:[-\,1,1]^d\rightarrow {\mathbb R}\). We focus on ReLU DNNs, but comment in passing also on versions of our results for other DNN activation functions. Next, we briefly discuss the relation of previous results to the present work and also outline the structure of this paper.
1.1 Recent Mathematical Results on Expressive Power of DNNs
The survey [27] presented succinct proofs of genericity of shallow NNs in various function classes, as shown originally, e.g., in [15, 16, 20] and reviewed the state of mathematical theory of DNNs up to that point. Moreover, exponential expression rate bounds for analytic functions by neural networks had already been achieved in the 1990s. We mention in particular [22] where smooth, nonpolynomial activation functions were considered.
More closely related to the present work are the references [21, 36]. In [21], approximation rates for deep NN approximations of multivariate functions which are analytic have been investigated. Exponential rate bounds in terms of the total size of the NN have been obtained, for sigmoidal activation functions. In [37], it was observed that the multiplication of two real numbers, and consequently polynomials, can efficiently be approximated by deep ReLU NNs. This was used in [36] to prove bounds on the DNN approximation of certain functions \(u:[-\,1,1]^d \rightarrow {\mathbb R}\) which admit holomorphic extensions to some open subset of \(\mathbb {C}^d\) by deep ReLU NNs. In particular, it was assumed that u admits a Taylor expansion about the origin of \(\mathbb {C}^d\) which converges absolutely and uniformly on \([-\,1,1]^d\). It is well known that not every u which is real-analytic in \([-\,1,1]^d\) admits such an expansion. In the present paper, we prove sharper expression rate bounds for both, the ReLU activation \(\sigma _1\) and RePU activations \(\sigma _r\), for functions which merely are assumed to be real-analytic in \([-\,1,1]^d\), in \(L^\infty ([-\,1,1]^d)\) and in stronger norms, thereby generalizing both [21, 36].
1.2 Contributions of the Present Paper
We prove exponential expression rate bounds of DNNs for d-variate, real-valued functions which depend analytically on their d inputs. Specifically, for holomorphic mappings \(u: [-\,1,1]^d\rightarrow {\mathbb R}\), we prove expression error bounds in \(L^\infty ([-\,1,1]^d)\) and in \(W^{k,\infty }([-\,1,1]^d)\), for \(k\in {\mathbb {N}}\) (the precise range of k depending on properties of the NN activation \(\sigma \)). We consider both, ReLU activation \(\sigma _1:{\mathbb R}\rightarrow {\mathbb R}_+: x\mapsto x_+\) and RePU activations \(\sigma _r:{\mathbb R}\rightarrow {\mathbb R}_+: x\mapsto (x_+)^r\) for some integer \(r\ge 2\). Here, \(x_+ = \max \{x,0\}\). The expression error bounds in our main result, Theorem 3.6, with ReLU activation \(\sigma _1\) are in \(W^{1,\infty }([-\,1,1]^d)\) and of the general type \(O(\exp (-b N^{1/(d+1)}))\) in terms of the NN size N, with a constant \(b>0\) depending on the domain of analyticity, but independent of N (however, with the constant implied in the Landau symbol \(O(\cdot )\) depending exponentially on d, in general). With activation \(\sigma _r\) for \(r\ge 2\), Theorem 3.10 has corresponding expression error bounds in \(W^{k,\infty }([-\,1,1]^d)\) for arbitrary fixed \(k\in {\mathbb N}\) and of the type \(O(\exp (-b N^{1/d}))\) in terms of the NN size N. For all \(r\in \mathbb {N}\), the parameters of the \(\sigma _r\)-neural networks approximating u (so-called “weights” and “biases”) are continuous functions of u in appropriate norms. All of our proofs are constructive, i.e., they demonstrate how to build sparsely connected DNNs achieving the claimed convergence rates. We comment in Remarks 3.7 and 3.11 how these statements imply results for (the simpler architecture of) fully connected neural networks.
The main results, Theorems 3.6 and 3.10, are expression rate bounds for holomorphic functions. Similar bounds for Gevrey-regular functions are given in Sect. 4.3.4. In Sect. 4.3.5, we conclude the same bounds also for certain classes of nonholomorphic, merely Lipschitz-continuous functions, by leveraging the compositional nature of DNN approximation and Theorems 3.6 and 3.10.
1.3 Outline
The structure of the paper is as follows. In Sect. 2, we present the definition of the DNN architectures and fix notation and terminology. We also review in Sect. 2.2 a “ReLU DNN calculus,” from recent work [10, 26], which will facilitate the ensuing DNN expression rate analysis. A first set of key results are ReLU DNN expression rates in \(W^{1,\infty }([-\,1,1]^d)\) for multivariate Legendre polynomials, which are proved in Sect. 2.3. These novel expression rate bounds are explicit in the \(W^{1,\infty }\)-accuracy and in the polynomial degree. They are of independent interest and remarkable in that the ReLU DNNs which emulate the polynomials at exponential rates, as we prove, realize continuous, piecewise affine functions. They are based on [18, 37]. The proofs, being constructive, shed a rather precise light on the architecture, in particular depth and width of the ReLU DNNs, that is sufficient for polynomial emulation. In Sect. 2.4, we briefly comment on corresponding results for RePU activations; as a rule, the same exponential rates are achieved for slightly smaller NNs and in norms which are stronger than \(W^{1,\infty }\).
Section 3 then contains the main results of this note: exponential ReLU DNN expression rate bounds for d-variate, holomorphic maps. They are based on a) polynomial approximation of these maps and on b) ReLU DNN reapproximation of the approximating polynomials. These are presented in Sects. 3.1 and 3.2. Again we comment in Sect. 3.3 on modifications in the results for RePU activations. Section 4 contains a brief indication of further directions and open problems.
1.4 Notation
We adopt standard notation consistent with our previous works [40, 41]: \(\mathbb {N}=\{1,2,\ldots \}\) and \(\mathbb {N}_0:=\mathbb {N}\cup \{0\}\). We write \(\mathbb {R}_+ := \{x \in \mathbb {R}: x\ge 0\}\). The symbol C will stand for a generic, positive constant independent of any asymptotic quantities in an estimate, which may change its value even within the same equation.
In statements about polynomial expansions we require multi-indices \({\varvec{\nu }}=(\nu _j)_{j=1,\ldots ,d}\in \mathbb {N}_0^d\) for \(d\in \mathbb {N}\). The total order of a multi-index \({\varvec{\nu }}\) is denoted by \(|{\varvec{\nu }}|_1:=\sum _{j=1}^d \nu _j\). The notation \({{\,\mathrm{supp}\,}}{\varvec{\nu }}\) stands for the support of the multi-index, i.e., \({{\,\mathrm{supp}\,}}{\varvec{\nu }}= \{j\in \{1,\ldots ,d\}\,:\,\nu _j\ne 0\}\). The size of the support of \({\varvec{\nu }}\in \mathbb {N}_0^d\) is \(|{{\,\mathrm{supp}\,}}{\varvec{\nu }}|\); it will, subsequently, indicate the number of active coordinates in the multivariate monomial term \({{\varvec{y}}}^{\varvec{\nu }}:=\prod _{j=1}^d y_j^{\nu _j}\).
A subset \(\varLambda \subseteq \mathbb {N}_0^d\) is called downward closedFootnote 1, if \({\varvec{\nu }}=(\nu _j)_{j=1}^d\in \varLambda \) implies \({\varvec{\mu }}=(\mu )_{j=1}^d\in \varLambda \) for all \({\varvec{\mu }}\le {\varvec{\nu }}\). Here, the ordering “\(\le \)” on \(\mathbb {N}_0^d\) is defined as \(\mu _j\le \nu _j\), for all \(j=1,\ldots ,d\). We write \(|\varLambda |\) to denote the finite cardinality of a set \(\varLambda \).
We write \(B_\varepsilon ^{{\mathbb C}}:=\{z\in \mathbb {C}\,:\,|z|<\varepsilon \}\). Elements of \(\mathbb {C}^{d}\) will be denoted by boldface characters such as \({{\varvec{y}}}=(y_j)_{j=1}^d \in [-\,1,1]^{d}\subset \mathbb {C}^{d}\). For \({\varvec{\nu }}\in \mathbb {N}_0^d\), standard notations \({{\varvec{y}}}^{{\varvec{\nu }}}:=\prod _{j=1}^d y_j^{\nu _j}\) and \({\varvec{\nu }}!=\prod _{j=1}^d\nu _j!\) will be employed (with the conventions \(0! := 1\) and \(0^0 := 1\)). For \(n\in {\mathbb N}_0\) we let \(\mathbb {P}_n:={\text {span}} \{y^j\,:\,0\le j\le n\}\) be the space of polynomials of degree at most n, and for a finite index set \(\varLambda \subset \mathbb {N}_0^d\) we denote \(\mathbb {P}_\varLambda := {\text {span}} \{{{\varvec{y}}}^{\varvec{\nu }}\,:\,{\varvec{\nu }}\in \varLambda \}\).
2 Deep Neural Network Approximations
2.1 DNN Architecture
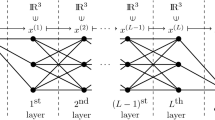
We consider deep neural networks (DNNs for short) of feed forward type. Such a NN f can mathematically be described as a repeated composition of affine transformations with a nonlinear activation function.
More precisely: For an activation function \(\sigma :\mathbb {R}\rightarrow \mathbb {R}\), a fixed number of hidden layers \(L\in {\mathbb N}_0\), numbers \(N_\ell \in {\mathbb N}\) of computation nodes in layer \(\ell \in \{1,\ldots ,L+1\}\), \(f:{\mathbb R}^{N_0}\rightarrow {\mathbb R}^{N_{L+1}}\) is realized by a feedforward neural network, if for certain weights \(w_{i,j}^\ell \in {\mathbb R}\), and biases \(b_j^\ell \in {\mathbb R}\) it holds for all \({{\varvec{x}}}=(x_i)_{i=1}^{N_0}\)
and
and finally
In this case, \(N_0\) is the dimension of the input, and \(N_{L+1}\) is the dimension of the output. Furthermore, \(z_j^\ell \) denotes the output of unit j in layer \(\ell \). The weight \(w_{i,j}^{\ell }\) has the interpretation of connecting the ith unit in layer \(\ell -1\) with the jth unit in layer \(\ell \).
If \(L=0\), then (2.1c) holds with \(Z_i^0 := X_i\) for \(i=1,\ldots , N_0\). Except when explicitly stated, we will not distinguish between the network (which is defined through \(\sigma \), the \(w_{i,j}^\ell \) and \(b_j^\ell \)) and the function \(f:{\mathbb R}^{N_0}\rightarrow {\mathbb R}^{N_{L+1}}\) it realizes. We note in passing that this relation is typically not one to one, i.e., different NNs may realize the same function as their output. Let us also emphasize that we allow the weights \(w_{i,j}^{\ell }\) and biases \(b^\ell _j\) for \(\ell \in \{1,\ldots ,L+1\}\), \(i\in \{1,\ldots ,N_{\ell -1}\}\) and \(j\in \{1,\ldots ,N_\ell \}\) to take any value in \({\mathbb R}\), i.e., we do not consider quantization as, e.g., in [1, 26].
As is customary in the theory of NNs, the number of hidden layers L of a NN is referred to as depthFootnote 2 and the total number of nonzero weights and biases as the size of the NN. Hence, for a DNN f as in (2.1), we define
In addition, \({{\,\mathrm{size}\,}}_{{\text {in}}}({f}):=|\{(i,j):w^1_{i,j}\ne 0\}| +|\{j\,:\,b_{j}^{1} \ne 0\}|\) and \({{\,\mathrm{size}\,}}_{{\text {out}}}({f}):=|\{(i,j):w^{L+1}_{i,j}\ne 0\}| +|\{j\,:\,b_{j}^{L+1} \ne 0\}|\), which are the number of nonzero weights and biases in the input layer of f and in the output layer, respectively.
The proofs of our main results Theorems 3.6 and 3.10 are constructive, in the sense that we will explicitly construct NNs with the desired properties. We construct these NNs by assembling smaller networks, using the operations of concatenation and parallelization, as well as so-called “identity-networks” which realize the identity mapping. Below, we recall the definitions. For these operations, we also provide bounds on the number of nonzero weights in the input layer and the output layer of the corresponding network, which can be derived from the definitions in [26].
2.2 DNN Calculus
Throughout, as activation function \(\sigma \) we consider either the ReLU activation function
or, as suggested in [17, 19, 21], for \(r\in {\mathbb N}\), \(r\ge 2\), the RePU activation function
If a NN uses \(\sigma _r\) as activation function, we refer to it as \(\sigma _r\)-NN. ReLU NNs are referred to as \(\sigma _1\)-NNs. We assume throughout that all activations in a DNN are of equal type.
Remark 2.1
(Historical note on rectified power units) “Rectified power unit” (RePU) activation functions are particular cases of so-called sigmoidal functions of order \(k\in \mathbb {N}\) for \(k\ge 2\), i.e., \(\lim _{x\rightarrow \infty } \frac{\sigma (x)}{x^k}=1\), \(\lim _{x\rightarrow -\infty } \frac{\sigma (x)}{x^k}=0\) and \(\left| \sigma (x) \right| _{}\le K(1+\left| x \right| _{})^k\) for \(x\in \mathbb {R}\). The use of NNs with such activation functions for function approximation dates back to the early 1990s, cf. e.g., [19, 21]. Proofs in [21, Sect. 3] proceed in three steps. First, a given function f was approximated by a polynomial, then this polynomial was expressed as a linear combination of powers of a RePU, and finally, it was shown that for \(r\ge 2\) and arbitrary \(A>0\) the RePU \(\sigma _r\) can be approximated on \([-A,A]\) with arbitrarily small \(L^\infty ([-A,A])\)-error \(\varepsilon \) by a NN with a continuous, sigmoidal activation function of order \(k = r\), which has depth 1 and fixed network size independent of A and \(\varepsilon \) [21, Lemma 3.6]. As remarked directly below [21, Lemma 3.6], this result remains true for the \(L^\infty ({\mathbb R})\)-norm (instead of \(L^\infty ([-A,A])\)) if, additionally, \(\sigma \) is uniformly continuous on \({\mathbb R}\). As also remarked below [21, Lemma 3.6], a similar statement holds for the approximation of the ReLU \(\sigma _1\) by a NN with sigmoidal activation function of the order \(k=1\).
For any \(r\in {\mathbb N}\), in the proof of [21, Lemma 3.6] it was observed that for continuous, sigmoidal \(\sigma \) of order \(k=r\), the \(\sigma \)-NN that approximates \(\sigma _r\) is uniformly continuous on \([-A,A]\). From this, it follows that \(\sigma _r\)-NNs can be approximated up to arbitrarily small \(L^\infty ([-A,A])\)-error by \(\sigma \)-NNs with NN size independent of A and \(\varepsilon \). Again, uniform continuity of \(\sigma \) on \({\mathbb R}\) implies the same result w.r.t. the \(L^\infty ({\mathbb R})\)-norm.
The exact realization of polynomials by \(\sigma _r\)-networks for \(r\ge 2\) was observed in the proof of [21, Theorem 3.3], based on ideas in the proof of [5, Theorem 3.1]. The same result was recently rediscovered in [17, Theorem 3.1], whose authors were apparently not aware of [5, 21].
We now indicate several fundamental operations on NNs which will be used in the following. These operations have been frequently used in recent works [10, 25, 26].
2.2.1 Parallelization
We now recall the parallelization of two networks f and g, which in parallel emulates f and g. We first describe the parallelization of networks with the same inputs as in [26, Definition 2.7], the parallelization of networks with different inputs is similar and introduced directly afterward.
Let f and g be two NNs with the same depth \(L\in \mathbb {N}_0\) and the same input dimension \(n\in \mathbb {N}\). Denote by \(m_f\) the output dimension of f and by \(m_g\) the output dimension of g. Then there exists a neural network \(\left( f,g\right) \), called parallelization of f and g, which in parallel emulates f and g, i.e.,
It holds that \({{\,\mathrm{depth}\,}}(\left( f,g\right) )=L\) and that \({{\,\mathrm{size}\,}}(\left( f,g\right) )={{\,\mathrm{size}\,}}(f)+{{\,\mathrm{size}\,}}(g)\), \({{\,\mathrm{size}\,}}_{{\text {in}}}(\left( f,g\right) )={{\,\mathrm{size}\,}}_{{\text {in}}}(f)+{{\,\mathrm{size}\,}}_{{\text {in}}}(g)\) and \({{\,\mathrm{size}\,}}_{{\text {out}}}(\left( f,g\right) )={{\,\mathrm{size}\,}}_{{\text {out}}}(f)+{{\,\mathrm{size}\,}}_{{\text {out}}}(g)\).
We next recall the parallelization of networks with inputs of possibly different dimension as in [10, Setting 5.2]. To this end, we let f and g be two NNs with the same depth \(L\in \mathbb {N}_0\) whose input dimensions \(n_f\) and \(n_g\) may be different, and whose output dimensions we will denote by \(m_f\) and \(m_g\), respectively.
Then there exists a neural network \(\left( f,g\right) _{\mathrm {d}}\), called full parallelization of networks with distinct inputs of f and g, which in parallel emulates f and g, i.e.,
It holds that \({{\,\mathrm{depth}\,}}(\left( f,g\right) _{\mathrm {d}})=L\) and that \({{\,\mathrm{size}\,}}(\left( f,g\right) _{\mathrm {d}})={{\,\mathrm{size}\,}}(f)+{{\,\mathrm{size}\,}}(g)\), \({{\,\mathrm{size}\,}}_{{\text {in}}}(\left( f,g\right) _{\mathrm {d}})={{\,\mathrm{size}\,}}_{{\text {in}}}(f)+{{\,\mathrm{size}\,}}_{{\text {in}}}(g)\) and \({{\,\mathrm{size}\,}}_{{\text {out}}}(\left( f,g\right) _{\mathrm {d}})={{\,\mathrm{size}\,}}_{{\text {out}}}(f)+{{\,\mathrm{size}\,}}_{{\text {out}}}(g)\).
Parallelizations of networks with possibly different inputs can be used consecutively to emulate multiple networks in parallel.
2.2.2 Identity Networks
We now recall identity networks [26, Lemma 2.3], which emulate the identity map.
For all \(n\in \mathbb {N}\) and \(L\in \mathbb {N}_0\) there exists a \(\sigma _1\)-identity network \({{\,\mathrm{Id}\,}}_{\mathbb {R}^n}\) of depth L which emulates the identity map \({{\,\mathrm{Id}\,}}_{\mathbb {R}^n}:\mathbb {R}^n\rightarrow \mathbb {R}^n:{{\varvec{x}}}\mapsto {{\varvec{x}}}\). It holds that
Analogously, for \(r\ge 2\) there exist \(\sigma _r\)-identity networks. To construct them, we use the concatenation \(f\bullet g\) of two NNs f and g as introduced in [26, Definition 2.2]. As we shall make use of it subsequently in Propositions 2.3 and 2.4, we recall its definition here for convenience of the reader.
Definition 2.2
[26, Definition 2.2] Let f, g be such that the output dimension of g equals the input dimension of f, which we denote by k. Denote the weights and biases of f by \(\{u^{\ell }_{i,j}\}_{i,j,\ell }\) and \(\{a^{\ell }_j\}_{j,\ell }\) and those of g by \(\{v^{\ell }_{i,j}\}_{i,j,\ell }\) and \(\{c^{\ell }_j\}_{j,\ell }\). Then, we denote by \(f\bullet g\) be the NN with weights and biases
for \(\ell =1,\ldots ,{{\,\mathrm{depth}\,}}(f)+{{\,\mathrm{depth}\,}}(g)+1\).
It is easy to check, that the network \(f\bullet g\) emulates the composition \({{\varvec{x}}}\mapsto f(g({{\varvec{x}}}))\) and satisfies \({{\,\mathrm{depth}\,}}(f\bullet g) = {{\,\mathrm{depth}\,}}(f)+{{\,\mathrm{depth}\,}}(g)\).
The concatenation of Definition 2.2 will only be used in the proof of Propositions 2.3 and 2.4. Throughout the remainder of this work, we use sparse concatenations \(f\circ g\) introduced in Sect. 2.2.3, whose network size can be estimated by \(C({{\,\mathrm{size}\,}}(f) + {{\,\mathrm{size}\,}}(g))\) for an absolute constant C. The reason for introducing \(\circ \) in addition to \(\bullet \), is that the size of \(f\bullet g\) cannot be bounded by \(C({{\,\mathrm{size}\,}}(f) + {{\,\mathrm{size}\,}}(g))\) for an absolute constant C. This can be seen by considering the number of nonzero weights in layer \(\ell ={{\,\mathrm{depth}\,}}(g)+1\), e.g., for \(k=1\), and arbitrary layer sizes \(N_{{{\,\mathrm{depth}\,}}(g)}\) of g and \(N_1\) of f.
Proposition 2.3
For all \(r\ge 2\), \(n\in \mathbb {N}\) and \(L\in \mathbb {N}_0\) there exists a \(\sigma _r\)-NN \({{\,\mathrm{Id}\,}}_{\mathbb {R}^n}\) of depth L which emulates the identity function \({{\,\mathrm{Id}\,}}_{\mathbb {R}^n}:\mathbb {R}^n\rightarrow \mathbb {R}^n:{{\varvec{x}}}\mapsto {{\varvec{x}}}\). It holds that
Proof
First we consider \(n=1\) and proceed in two steps: We discuss \(L=0,1\) in Step 1 and \(L>1\) in Step 2.
Step 1. For \(L=0\), let \({{\,\mathrm{Id}\,}}_{{\mathbb R}^n}\) be the network with weights \(w^1_{i,j}=\delta _{i,j}\), \(b^1_j=0\), \(i,j=1,\ldots ,n\). We next consider \(L=1\). It was shown in [17, Theorem 2.5] that there exist \((a_k)_{k=0}^r\in {\mathbb R}^{r+1}\) and \((b_k)_{k=1}^r\in {\mathbb R}^r\) such that for all \(x\in {\mathbb R}\)
This shows the existence of a network \(\mathrm{Id}_{{\mathbb R}^1}:{\mathbb R}\rightarrow {\mathbb R}\) of depth 1 realizing the identity on \({\mathbb R}\). The network employs 2r weights and 2r biases in the first layer, and 2r weights and one bias (namely \(a_0\)) in the output layer. Its size is thus \(6r+1\).
Step 2. For \(L>1\), we consider the L-fold concatenation \({{\,\mathrm{Id}\,}}_{\mathbb {R}^1} \bullet \cdots \bullet {{\,\mathrm{Id}\,}}_{\mathbb {R}^1}\) of the identity network \({{\,\mathrm{Id}\,}}_{\mathbb {R}^1}\) from Step 1. The resulting network has depth L, input dimension 1 and output dimension 1. The number of weights and the number of biases in the first layer both equal 2r, the number of weights in the output layer equals 2r, and the number of biases 1. In each of the \(L-1\) other hidden layers, the number of weights is \(4r^2\), and the number of biases 2r. In total, the network has size at most \(4r + (L-1)(4r^2+2r) + 2r+1 \le L(4r^2+2r)\), where we used that \(r\ge 2\).
Identity networks with input size \(n\in \mathbb {N}\) are obtained as the full parallelization with distinct inputs of n identity networks with input size 1. \(\square \)
2.2.3 Sparse Concatenation
The sparse concatenation of two \(\sigma _1\)-NNs f and g was introduced in [26, Definition 2.5].
Let f and g be \(\sigma _1\)-NNs, such that the number of nodes in the output layer of g equals the number of nodes in the input layer of f. Denote by n the number of nodes in the input layer of g, and by m the number of nodes in the output layer of f. Then, with “\(\bullet \)” as in Definition 2.2, the sparse concatenation of the NNs f and g is defined as the network
where \({{\,\mathrm{Id}\,}}_{{\mathbb R}^k}\) is the \(\sigma _1\)-identity network of depth 1. The network \(f\circ g\) realizes the function
i.e., by abuse of notation, the symbol “\(\circ \)” has two meanings here, depending on whether we interpret \(f\circ g\) as a function or as a network. This will not be the cause of confusion however. It holds \({{\,\mathrm{depth}\,}}(f\circ g)={{\,\mathrm{depth}\,}}(f)+1+{{\,\mathrm{depth}\,}}(g)\),
and
For a proof, we refer to [26, Remark 2.6].
A similar result holds for \(\sigma _r\)-NNs. In this case we define the sparse concatenation \(f\circ g\) as in (2.3), but with \({{\,\mathrm{Id}\,}}_{{\mathbb R}^k}\) now denoting the \(\sigma _r\)-identity network of depth 1 from Proposition 2.3.
Proposition 2.4
For \(r\ge 2\) let f, g be two \(\sigma _r\)-NNs such that the output dimension of g, which we denote by \(k\in {\mathbb N}\), equals the input dimension of f, and suppose that \({{\,\mathrm{size}\,}}_{{\text {in}}}(f),{{\,\mathrm{size}\,}}_{{\text {out}}}(g)\ge k\). Denote by \(f\circ g\) the \(\sigma _r\)-network obtained by the \(\sigma _r\)-sparse concatenation. Then \({{\,\mathrm{depth}\,}}(f\circ g)={{\,\mathrm{depth}\,}}(f)+1+{{\,\mathrm{depth}\,}}(g)\) and
Furthermore,
Proof
It follows directly from Definition 2.2 and Proposition 2.3 that \({{\,\mathrm{depth}\,}}(f\circ g)={{\,\mathrm{depth}\,}}(f)+1+{{\,\mathrm{depth}\,}}(g)\). To bound the size of the network, note that the weights in layers \(\ell =1,\ldots ,{{\,\mathrm{depth}\,}}(g)\) equal those in the first \({{\,\mathrm{depth}\,}}(g)\) layers of g. Those in layers \(\ell ={{\,\mathrm{depth}\,}}(g)+3,\ldots ,{{\,\mathrm{depth}\,}}(g)+2+{{\,\mathrm{depth}\,}}(f)\) equal those in the last \({{\,\mathrm{depth}\,}}(f)\) layers of f. Layer \(\ell ={{\,\mathrm{depth}\,}}(g)+1\) has at most \(2r{{\,\mathrm{size}\,}}_{{\text {out}}}(g)\) weights and 2rk biases, whereas layer \(\ell ={{\,\mathrm{depth}\,}}(g)+2\) has at most \(2r{{\,\mathrm{size}\,}}_{{\text {in}}}(f)\) weights and k biases. This shows Eq. (2.5) and the bound on \({{\,\mathrm{size}\,}}_{{\text {in}}}(f\circ g)\) and \({{\,\mathrm{size}\,}}_{{\text {out}}}(f\circ g)\). \(\square \)
Identity networks are often used in combination with parallelizations. In order to parallelize two networks f and g with \({{\,\mathrm{depth}\,}}(f)<{{\,\mathrm{depth}\,}}(g)\), the network f can be concatenated with an identity network, resulting in a network whose depth equals \({{\,\mathrm{depth}\,}}(g)\) and which emulates the same function as f.
2.3 ReLU DNN Approximation of Polynomials
2.3.1 Basic Results
In [18], it was shown that deep networks employing both ReL and BiS (“binary step”) units are capable of approximating the product of two numbers with a network whose size and depth increase merely logarithmically in the accuracy. In other words, certain neural networks achieve uniform exponential convergence of the operation of multiplication (of two numbers in a bounded interval) w.r.t. the network size. Independently, a similar result for ReLU networks was obtained in [37]. Here, we shall use the latter result in the following slightly more general form shown in [32]. Contrary to [37], it provides a bound of the error in the \(W^{1,\infty }([-\,1,1])\)-norm (instead of the \(L^\infty ([-\,1,1])\)-norm).
Proposition 2.5
[32, Proposition 3.1] For any \(\delta \in (0,1)\) and \(M\ge 1\) there exists a \(\sigma _1\)-NN \({{\tilde{\times }}}_{\delta ,M}:[-M,M]^2\rightarrow {\mathbb R}\) such that
where \(\frac{\partial }{\partial a}{{\tilde{\times }}}_{\delta ,M} (a,b)\) and \(\frac{\partial }{\partial b}{{\tilde{\times }}}_{\delta ,M} (a,b)\) denote weak derivatives. There exists a constant \(C>0\) independent of \(\delta \in (0,1)\) and \(M\ge 1\) such that \({{\,\mathrm{size}\,}}_{{\text {in}}}({{\tilde{\times }}}_{\delta ,M})\le C\), \({{\,\mathrm{size}\,}}_{{\text {out}}}({{\tilde{\times }}}_{\delta ,M}) \le C\),
Moreover, for every \(a\in [-M,M]\), there exists a finite set \(\mathcal {N}_a\subseteq [-M,M]\) such that \(b\mapsto {{\tilde{\times }}}_{\delta ,M} (a,b)\) is strongly differentiable at all \(b\in (-M,M)\backslash \mathcal {N}_a\).
It is immediate that Proposition 2.5 implies the existence of networks approximating the multiplication of n different numbers. We now show such a result, generalizing [32, Proposition 3.3] in that we consider the error again in the \(W^{1,\infty }([-1, 1])\)-norm (instead of the \(L^\infty ([-1, 1])\)-norm).
Proposition 2.6
For any \(\delta \in (0,1)\), \(n\in {\mathbb N}\) and \(M\ge 1\), there exists a \(\sigma _1\)-NN \({{\tilde{\prod }}}_{\delta ,M}:[-M,M]^n\rightarrow {\mathbb R}\) such that
where \(\frac{\partial }{\partial x_i}\) denotes a weak derivative.
There exists a constant C independent of \(\delta \in (0,1)\), \(n\in {\mathbb N}\) and \(M\ge 1\) such that
Proof
We proceed analogously to the proof of [32, Proposition 3.3], and construct \({{\tilde{\prod }}}_{\delta ,1}\) as a binary tree of \({{\tilde{\times }}}_{\cdot ,\cdot }\)-networks from Proposition 2.5 with appropriately chosen parameters for the accuracy and the maximum input size.
We define \({\tilde{n}} := \min \{2^k:k\in \mathbb {N}, 2^k\ge n\}\), and consider the product of \({\tilde{n}}\) numbers \(x_1,\ldots ,x_{{\tilde{n}}}\in [-M,M]\). In case \(n<{\tilde{n}}\), we define \(x_{n+1},\ldots ,x_{{\tilde{n}}} := 1\), which can be implemented by a bias in the first layer. Because \({\tilde{n}}<2n\), the bounds on network size and depth in terms of \({\tilde{n}}\) also hold in terms of n, possibly with a larger constant.
It suffices to show the result for \(M=1\), since for \(M>1\), the network defined through \({{\tilde{\prod }}}_{\delta ,M}(x_1,\ldots ,x_n):=M^n{{\tilde{\prod }}}_{\delta /M^n,1}(x_1/M,\ldots ,x_n/M)\) for all \((x_i)_{i=1}^n\in [-M,M]^n\) achieves the desired bounds as is easily verified. Therefore, w.l.o.g. \(M=1\) throughout the rest of this proof.
Equation (2.6a) follows by the argument given in the proof of [32, Proposition 3.3], we recall it here for completeness. By abuse of notation, for every even \(k\in \mathbb {N}\) let a (k-dependent) mapping \(R=R^1\) be defined via
For \(\ell \ge 2\) set \(R^\ell :=R\circ R^{\ell -1}\). That is, for each product network \({{\tilde{\times }}}_{\delta /{{\tilde{n}}}^2,2}\) as in Proposition 2.5 we choose maximum input size “\(M=2\)” and accuracy “\(\delta /{\tilde{n}}^2\).” Hence, \(R^\ell \) can be interpreted as a mapping from \({\mathbb R}^{2^\ell }\rightarrow {\mathbb R}\). We now define \({{\tilde{\prod }}}_{\delta ,1}:[-\,1,1]^{n}\rightarrow {\mathbb R}\) via
and next show the error bounds in (2.6) (recall that by definition \(x_{n+1}=\cdots =x_{{{\tilde{n}}}}=1\) in case \({{\tilde{n}}}>n\)).
First, by induction we show that for \(\ell \in \{1,\ldots ,\log _2({\tilde{n}})\}\) and for all \(x_1,\ldots ,x_{2^\ell }\in [-\,1,1]\)
For \(\ell =1\) it holds that \(R(x_1,x_2)={{\tilde{\times }}}_{\delta /{{\tilde{n}}}^2,2}(x_1,x_2)\), hence (2.9) follows directly from the choice for the accuracy of \({{\tilde{\times }}}_{\delta /{{\tilde{n}}}^2,2}\), which is \(\delta /{\tilde{n}}^2\). For \(\ell \in \{2,\ldots ,\log _2({\tilde{n}})\}\), we assume that Eq. (2.9) holds for \(\ell -1\). With \(| \prod _{j=1}^{2^{(\ell -1)}} x_j |_{} \le 1\)and \(\frac{2^{2(\ell -1)}}{{\tilde{n}}^2}\delta <1\), it follows that \(\left| R^{\ell -1}(x_1,\ldots ,x_{2^{(\ell -1)}}) \right| _{}<2\), hence \(R^{\ell -1}(x_1,\ldots ,x_{2^{(\ell -1)}})\) may be used as input of \({{\tilde{\times }}}_{\delta /{\tilde{n}}^2,2}\). We find
where we used \((1+\delta 2^{2(\ell -1)}/{{\tilde{n}}}^2)\le 2\). This shows (2.9) for \(\ell \). Inserting \(\ell =\log _2({\tilde{n}})\) into (2.9) gives (2.6a).
We next show (2.6b). Without loss of generality, we only consider the derivative with respect to \(x_1\), because each \({{\tilde{\times }}}_{\delta /{{\tilde{n}}}^2,2}\)-network is symmetric under permutations of its arguments. For \(\ell \in \{1,\ldots ,\log _2({\tilde{n}})\}\) we show by induction that for almost every \((x_i)_{i=1}^{2^\ell }\in [-\,1,1]^{2^\ell }\)
Again, \(R(x_1,x_2)={{\tilde{\times }}}_{\delta /{{\tilde{n}}}^2,2}(x_1,x_2)\) and for \(\ell =1\) Eq. (2.10) follows from Proposition 2.5 and the choice for the accuracy of \({{\tilde{\times }}}_{\delta /{{\tilde{n}}}^2,2}\), which is \(\delta /{\tilde{n}}^2\).
For \(\ell >1\), under the assumption that (2.10) holds for \(\ell -1\), we find
where \(\frac{\partial }{\partial a}{{\tilde{\times }}}_{\delta /{{\tilde{n}}}^2,2}\) denotes the (weak) derivative of \({{\tilde{\times }}}_{\delta /{{\tilde{n}}}^2,2}:[-2,2]\times [-2,2]\rightarrow {\mathbb R}\) w.r.t. its first argument as in Proposition 2.5. This shows (2.10) for \(\ell >1\), as desired. Filling in \(\ell =\log _2({\tilde{n}})\) gives (2.6b).
The number of binary tree layers (each denoted by R) is bounded by \(O(\log _2({\tilde{n}}))\). With the bound on the network depth from Proposition 2.5, for \(M=1\) the second part of (2.7) follows.
To estimate the network size, we cannot use the estimate \({{\,\mathrm{size}\,}}(f\circ g)\le 2{{\,\mathrm{size}\,}}(f)+2{{\,\mathrm{size}\,}}(g)\) from Eq. (2.4), because the number of concatenations \(\log _2({{\tilde{n}}})-1\) depends on n, hence the factors 2 would give an extra n-dependent factor in the estimate on the network size. Instead, from Eq. (2.4) we use \({{\,\mathrm{size}\,}}(f\circ g)\le {{\,\mathrm{size}\,}}(f)+{{\,\mathrm{size}\,}}_{{\text {in}}}(f)+{{\,\mathrm{size}\,}}_{{\text {out}}}(g)+{{\,\mathrm{size}\,}}(g)\) and the bounds from Proposition 2.5. We find (\(2^{\log _2({\tilde{n}})-\ell }\) being the number of product networks in binary tree layer \(\ell \))
which finishes the proof of (2.7) for \(M=1\). \(\square \)
The previous two propositions can be used to deduce bounds on the approximation of univariate polynomials on compact intervals w.r.t. the norm \(W^{1,\infty }\). One such result was already proven in [25, Proposition 4.2], which we present in Proposition 2.9 in a slightly modified form, allowing for the simultaneous approximation of multiple polynomials reusing the same approximate monomial basis. This yields a smaller network and thus gives a slight improvement over using the parallelization of networks obtained by applying [25, Proposition 4.2] to each polynomial separately. To prove the result, we first recall the following lemma:
Lemma 2.7
[25, Lemma 4.5] For all \(\ell \in {\mathbb N}\) and \(\delta \in (0,1)\) there exists a \(\sigma _1\)-NN \({{\tilde{{\varvec{\varPsi }}}}}^\ell _\delta \) with input dimension one and output dimension \(2^{\ell -1}+1\) such that
where C is independent of \(\ell \) and \(\delta \).
Corollary 2.8
Let \(n\in {\mathbb N}\) and \(\delta \in (0,1)\). There exists a NN \({\varvec{\varPsi }}_\delta ^n\) with input dimension one and output dimension \(n+1\) such that \(({\varvec{\varPsi }}_\delta ^n(x))_{1}=1\) and \(({\varvec{\varPsi }}_\delta ^n(x))_{2}=x\) for all \(x\in {\mathbb R}\), and
and
where C is independent of n and \(\delta \).
Proof
Define \(k:=\lceil \log _2(n)\rceil \) and for \(\ell \in \{1,\ldots ,k\}\) let \(\phi _\ell :{\mathbb R}\rightarrow {\mathbb R}\) be an identity network with \({{\,\mathrm{depth}\,}}(\phi _\ell )=\max _{i\in \{1,\ldots ,k\}}{{\,\mathrm{depth}\,}}({{\tilde{{\varvec{\varPsi }}}}}^i_\delta )-{{\,\mathrm{depth}\,}}({{\tilde{{\varvec{\varPsi }}}}}^\ell _\delta )\) as in (2.2). Set
Then by Lemma 2.7, \({\hat{{\varvec{\varPsi }}}}^n_\delta (x)\) is an approximation to
where the braces indicate which part of the network approximates these outputs. Adding one layer to eliminate the double entries and (in case \(2^k>n\)) the approximations \(x^k\) with \(k>n\), and adding the first entry which always equals \(1=x^0\), we obtain a network \({\varvec{\varPsi }}^n:{\mathbb R}\rightarrow {\mathbb R}^{n+1}\) satisfying (2.12). The depth bound is an immediate consequence of \({{\,\mathrm{depth}\,}}({\varvec{\varPsi }}^n_\delta ) \le C+ \max _{i\in \{1,\ldots ,k\}}{{\,\mathrm{depth}\,}}({{\tilde{{\varvec{\varPsi }}}}}^i_\delta )\), (2.11) and \(k\le C\log (n)\). To bound the size, first note that by (2.2) and (2.11) holds \({{\,\mathrm{size}\,}}(\phi _\ell )\le C (k^3+k\log (1/\delta ))\) for a constant \(C>0\) independent of n and \(\delta \). Thus,
where we used \(k\le C\log (n)\) and \(n\ge 1\). This shows (2.13). \(\square \)
Proposition 2.9
There exists a constant \(C>0\) such that the following holds: For every \(\delta >0\), \(n\in {\mathbb N}_0\), \(N\in {\mathbb N}\) and N polynomials \(p_i=\sum _{j=0}^nc^i_j y^j\in \mathbb {P}_n\), \(i=1,\ldots ,N\) there exists a \(\sigma _1\)-NN \({{\tilde{{{\varvec{p}}}}}}_\delta :[-\,1,1]\rightarrow {\mathbb R}^{{N}}\) such that
and, with \(C_0:=\max \{{\max _{i=1,\ldots ,N}}\sum _{j=2}^n|{c^i_j}|,\delta \}\),
Proof
We apply a linear transformation to the network in Corollary 2.8. Specifically, let \(\varPhi :{\mathbb R}^n\rightarrow {\mathbb R}^N\) be the network expressing the linear function with ith component \((\varPhi ({{\varvec{x}}}))_i=\sum _{j=0}^ic_j^ix_{j+1}\), where \({{\varvec{x}}}=(x_i)_{i=1}^{n+1}\). In other words, with \(W\in {\mathbb R}^{N\times (n+1)}\) given by \(W_{i\ell }=c_{\ell -1}^i\), \(\varPhi \) is the depth 0 ReLU NN \(\varPhi ({{\varvec{x}}})=W{{\varvec{x}}}\) of size at most \(N(n+1)\). Then by (2.12),
satisfies for each \(i\in \{1,\ldots ,N\}\)
By (2.13)
and finally
\(\square \)
Remark 2.10
If \(y_0\in {\mathbb R}\) and \(p_i(y)=\sum _{j=0}^n c^i_j (y-y_0)^j\), \(i=1,\ldots ,N\), then Proposition 2.9 can still be applied for the approximation of \(p_i(y)\) for \(y\in [y_0-1,y_0+1]\), since the substitution \(z= y-y_0\) corresponds to a shift, which can be realized exactly in the first layer of a NN, cp. (2.1a). Thus, if \(q_i(z):=\sum _{j=0}^n c^i_j z^j\) and if \(\left\| q_i-({\tilde{{{\varvec{q}}}}}_\delta )_i \right\| _{W^{1,\infty }([-\,1,1])}\le \delta \) as in Proposition 2.9, then \(y\mapsto {\tilde{{{\varvec{p}}}}}_\delta (y):={\tilde{{{\varvec{q}}}}}_\delta (y-y_0)\) is a NN satisfying the accuracy and size bounds of Proposition 2.9 w.r.t. the \([W^{1,\infty }([y_0-1,y_0+1])]^N\)-norm.
2.3.2 ReLU DNN Approximation of Univariate Legendre Polynomials
For \(j\in {\mathbb N}_0\) we denote by \(L_j\) the jth Legendre polynomial, normalized in \(L^2([-\,1,1],\lambda /2)\), where \(\lambda /2\) denotes the uniform probability measure on \([-\,1,1]\). For \(j\in \mathbb {N}_0\) it holds that \(L_j(x)=\sum _{\ell =0}^j c^j_\ell x^\ell \), where, with \(m(\ell ):=(j-\ell )/2\),
see, e.g., [11, Sect. 10.10 Equation (16)], (the factor \(\sqrt{2j+1}\) is needed to obtain the desired normalization). We define \(c^j_\ell :=0\) for \(\ell >j\).
Analogous to [25, Equation (4.13)] it holds that \(\sum _{\ell =0}^j |c^j_\ell |\le 4^j\) for all \(j\in \mathbb {N}\) (we use that \(\sqrt{2j+1} \le \sqrt{\pi j}\)). Inserting this into Proposition 2.9 with \(N = n\) and \(p_i = L_i\) for \(i=1,\ldots ,N\), we find the following result on the approximation of univariate Legendre polynomials by \(\sigma _1\)-NNs (similar to [23, Proposition 2.5] for the approximation of Chebyšev polynomials).
Proposition 2.11
[25, Proposition 4.2 and Equation (4.13)] For every \(n\in {\mathbb N}\) and for every \(\delta \in (0,1)\) there exists a \(\sigma _1\)-NN \({\tilde{{{\varvec{L}}}}}_{n,\delta }\) with input dimension one and with output dimension n such that for a positive constant C independent of n and \(\delta \) there holds
Remark 2.12
Alternatively, the \(\sigma _1\)-NN approximation of Legendre polynomials of degree n could be based on the three term recursion formula for Legendre polynomials or the Horner scheme for polynomials in general, by concatenating n product networks from Proposition 2.5 (and affine transformations). Because, depending on the scaling of the Legendre polynomials, either the accuracy \(\delta \) of the product networks or the maximum input size M needs to grow exponentially with n, both the network depth and the network size of the resulting NN approximation of univariate Legendre polynomials would be bounded by \(C n (n+\log (1/\delta ))\). That network size is of the same order as in Proposition 2.11, but the network depth has a worse dependence on the polynomial degree n. For more details, see [23, Proposition 2.5], where this construction is used to approximate truncated Chebyšev expansions based on the three term recursion for Chebyšev polynomials, which is very similar to that for Legendre polynomials.
For future reference, we note that by (2.14) and Eq. (2.16), for all \(n\in {\mathbb N}\), \(j=1,\ldots ,n\), \(\delta \in (0,1)\) and \(k\in \{0,1\}\)
2.3.3 ReLU DNN Approximation of Tensor Product Legendre Polynomials
Let \(d\in \mathbb {N}\). Denote the uniform probability measure on \([-\,1,1]^d\) by \(\mu _d\), i.e., \(\mu _d := 2^{-d}\lambda \) where \(\lambda \) is the Lebesgue measure on \([-\,1,1]^d\). Then, for all \({\varvec{\nu }}\in {\mathbb N}_0^d\) the tensorized Legendre polynomials \(L_{\varvec{\nu }}({{\varvec{y}}}):=\prod _{j=1}^d L_{\nu _j}(y_j)\) form a \(\mu _d\)-orthonormal basis of \(L^2([-\,1,1]^d,\mu _d)\). We shall require the following bound on the norm of the tensorized Legendre polynomials which itself is a consequence of the Markoff inequality, and our normalization of the Legendre polynomials: for any \(k\in {\mathbb N}_{0}\)
To provide bounds on the size of the networks approximating the tensor product Legendre polynomials, for finite subsets \(\varLambda \subset \mathbb {N}_0^d\) we will make use of the quantity
Proposition 2.13
For every finite subset \(\varLambda \subset \mathbb {N}_0^d\) and every \(\delta \in (0,1)\) there exists a \(\sigma _1\)-NN \({{\varvec{f}}}_{\varLambda ,\delta }\) with input dimension d and output dimension \(|\varLambda |\), such that the outputs \(\{ {\tilde{L}}_{{\varvec{\nu }},\delta } \}_{{\varvec{\nu }}\in \varLambda }\) of \({{\varvec{f}}}_{\varLambda ,\delta }\) satisfy
and for a constant \(C>0\) that is independent of d, \(\varLambda \) and \(\delta \) it holds
Proof
Let \(\delta \in (0,1)\) and a finite subset \(\varLambda \subset \mathbb {N}_0^d\) be given.
The proof is divided into three steps. In the first step, we define ReLU NN approximations of tensor product Legendre polynomials \(\{{\tilde{L}}_{{\varvec{\nu }},\delta }\}_{{\varvec{\nu }}\in \varLambda }\) and fix the parameters used in the NN approximation. In the second step, we estimate the error of the approximation, and the \(L^\infty ([-\,1,1]^d)\)-norm of the \({\tilde{L}}_{{\varvec{\nu }},\delta }\), \({\varvec{\nu }}\in \varLambda \). In the third step, we describe the network \({{\varvec{f}}}_{\varLambda ,\delta }\) and estimate its depth and size.
Step 1. For all \({\varvec{\nu }}\in \mathbb {N}_0^d\), we define \(n_{{\varvec{\nu }}} := |{{\,\mathrm{supp}\,}}{\varvec{\nu }}|\) and \(M_{{\varvec{\nu }}} := 2|{\varvec{\nu }}|_1 +2\). We can now define
where \({{\tilde{\prod }}}_{M_{{\varvec{\nu }}}^{-3}\delta /2,M_{\varvec{\nu }}}:[-M_{\varvec{\nu }},M_{\varvec{\nu }}]^{|{{\,\mathrm{supp}\,}}{\varvec{\nu }}|}\rightarrow {\mathbb R}\) is as in Proposition 2.6. For the network approximating univariate Legendre polynomials \({\tilde{{{\varvec{L}}}}}_{m(\varLambda ),\delta '}\) from Proposition 2.11, we set the accuracy parameter as \(\delta ' := \tfrac{1}{2}d^{-1} (2m(\varLambda )+2)^{-d-1} \delta <1\). Let us point out that by (2.15) for all \({\varvec{\nu }}\in \mathbb {N}_0^d\) and all \(j\in {{\,\mathrm{supp}\,}}{\varvec{\nu }}\)
so that, as required by Proposition 2.6, the absolute values of the arguments of \({{\tilde{\prod }}}_{M_{{\varvec{\nu }}}^{-3}\delta /2,M_{\varvec{\nu }}}\) in (2.18) are all bounded by \(M_{\varvec{\nu }}\).
Step 2. For the \(L^\infty ([-\,1,1])\)-error of \({{\tilde{L}}}_{{\varvec{\nu }},\delta }\) we find
Using Proposition 2.13, (2.15), (2.16) and \(M_{\varvec{\nu }}=2|{\varvec{\nu }}|_1+2\le 2m(\varLambda )+2\), the last term can be bounded by
It follows that for all \({\varvec{\nu }}\in \varLambda \)
To determine the error of the gradient, without loss of generality we only consider the derivative with respect to \(y_1\). In the case \(1\notin {{\,\mathrm{supp}\,}}{\varvec{\nu }}\), we trivially have \(\frac{\partial }{\partial {y_1}}(L_{\varvec{\nu }}({{\varvec{y}}})-\tilde{L}_{{\varvec{\nu }},\delta }({{\varvec{y}}}))=0\) for all \({{\varvec{y}}}\in [-\,1,1]^d\). Thus, let \(\nu _1\ne 0\) in the following. Then, with \(\delta ' = \tfrac{1}{2}d^{-1} (2m(\varLambda )+2)^{-d-1} \delta \)
where \(\frac{\partial }{\partial x_1} {{\tilde{\prod }}}_{M_{{\varvec{\nu }}}^{-3}\delta /2,M_{\varvec{\nu }}}\) denotes the (weak) derivative of
with respect to its first argument, cf. Proposition 2.6.
Using (2.16) and Proposition 2.11 for the first term, Proposition 2.11, (2.15) and (2.16) for the second term and Proposition 2.6 and (2.16) for the third term, we further bound the NN approximation error by
Step 3. We now describe the network \({{\varvec{f}}}_{\varLambda ,\delta }\), which in parallel emulates \(\{{\tilde{L}}_{{\varvec{\nu }},\delta }\}_{{\varvec{\nu }}\in \varLambda }\). The network is constructed as the concatenation of two subnetworks, i.e.,
The subnetwork \({{\varvec{f}}}_{\varLambda ,\delta }^{(2)}\) evaluates, in parallel, approximate univariate Legendre polynomials in the input variables \((y_j)_{j\le d}\). It is defined as
where the pair of round brackets denotes a parallelization.
The subnetwork \({{\varvec{f}}}_{\varLambda ,\delta }^{(1)}\) takes the output of \({{\varvec{f}}}_{\varLambda ,\delta }^{(2)}\) as input and computes
where in the last two lines the outer pair of round brackets denotes a parallelization. The depth of the identity networks is such that all components of the parallelization have equal depth.
We have the following expression for the network depth:
Definition here and in the remainder of this proof by \(C>0\) constants independent of d, \(\varLambda \) and \(\delta \in (0,1)\),
where we used that \(2m(\varLambda )+2\le 4m(\varLambda )\) when \(\varLambda \ne \{{\varvec{0}}\}\).
Similarly, due to \(M_{\varvec{\nu }}=2|{\varvec{\nu }}|_1+2\le 4m(\varLambda )\) (if \(\varLambda \ne \{{\varvec{0}}\}\)), we can choose the identity networks in the definition of \({{\varvec{f}}}_{\varLambda ,\delta }^{(1)}\) such that
where we used that \(n_{{\varvec{\nu }}}\le d\). Finally, we find the following bound on the network depth:
For the network size, we find that
With Proposition 2.11, we estimate the size of \({{\varvec{f}}}_{\varLambda ,\delta }^{(2)}\) as
The depth of each of the identity networks in the definition of \({{\varvec{f}}}_{\varLambda ,\delta }^{(1)}\) is bounded by \({{\,\mathrm{depth}\,}}({{\varvec{f}}}_{\varLambda ,\delta }^{(1)}) \le C(1+d\log d)\big (1+ \log _2 m(\varLambda ) + \log _2(1/\delta ) \big )\).
It follows that
Hence, we arrive at
\(\square \)
2.4 RePU DNN Emulation of Polynomials
The approximation of polynomials by neural networks can be significantly simplified if instead of the ReLU activation \(\sigma _1\) we consider as activation function the so-called rectified power unit (“RePU” for short): recall that for \(r\in {\mathbb N}\), \(r\ge 2\), the RePU activation is defined by \(\sigma _r(x)=\max \{0,x\}^r\), \(x\in {\mathbb R}\). In contrast to \(\sigma _1\)-NNs, as shown in [17], for every \(r\in {\mathbb N}\), \(r\ge 2\) there exist RePU networks of depth 1 realizing the multiplication of two real numbers without error. This yields the following result proven in [17, Theorem 4.1] for \(r=2\). With [17, Theorem 2.5] this extends to all \(r\ge 2\). To render the presentation self-contained, an alternative proof is provided in Appendix A, based on ideas in [25]. Unlike in [17], it is shown that the constant C is independent of d. This is relevant in particular when considering RePU emulations of truncated polynomial chaos expansions of countably parametric maps \(u:[-\,1,1]^{\mathbb N}\rightarrow {\mathbb R}\), shortly discussed in Sect. 4.3.3. Polynomial approximations of such maps depend on a finite number \(d(\varepsilon )\in {\mathbb N}\) of parameters only, but with \(d(\varepsilon )\rightarrow \infty \) as \(\varepsilon \downarrow 0\).
Proposition 2.14
Fix \(d\in {\mathbb N}\) and \(r\in {\mathbb N}\), \(r\ge 2\). Then there exists a constant \(C>0\) independent of d but depending on r such that for any finite downward closed \(\varLambda \subseteq {\mathbb N}_0^d\) and any \(p\in \mathbb {P}_\varLambda \) there is a \(\sigma _r\)-network \({{\tilde{p}}}:{\mathbb R}^d\rightarrow {\mathbb R}\) which realizes p exactly and such that \({{\,\mathrm{size}\,}}({{\tilde{p}}})\le C{|\varLambda |}\) and \({{\,\mathrm{depth}\,}}({{\tilde{p}}})\le C\log _2(|\varLambda |)\).
Remark 2.15
Let \(\psi :{\mathbb R}\rightarrow {\mathbb R}\) be an arbitrary \(C^2\) function that is not linear, i.e., it does not hold \(\psi ''(x)=0\) for all \(x\in {\mathbb R}\). In [29, Theorem 3.4] it is shown that \(\psi \)-networks can approximate the multiplication of two numbers a, b in a fixed bounded interval up to arbitrary accuracy with a fixed number of units. We also refer to [32, Sect. 3.3] where we explain this observation from [29] in more detail. From this, one can obtain a version of Proposition 2.14 for arbitrary \(C^2\) activation functions. To state it, we fix \(d\in {\mathbb N}\). Then there exists \(C>0\) (independent of d) such that for every \(\delta >0\), for every downward closed \(\varLambda \subseteq {\mathbb N}_0^d\) and every \(p\in \mathbb {P}_\varLambda \), there exists a \(\psi \)-neural network \(q:[-M,M]^d\rightarrow {\mathbb R}\) such that \(\sup _{x\in [-M,M]^d}|p(x)-q(x)|\le \delta \), \({{\,\mathrm{size}\,}}(q)\le C|\varLambda |\) and \({{\,\mathrm{depth}\,}}(q)\le C\log _2(|\varLambda |)\).
As discussed in Remark 2.1, the same also holds, e.g., for NNs with continuous, sigmoidal activation \(\sigma \) of order \(k\ge 2\).
Recently, there has been some interest in the approximation of ReLU NNs by rational functions and NNs with rational activation functions and vice versa, e.g., in [3, 34]. In the latter, \(\sigma = p/q\) is used as activation for polynomials p, q of prescribed degree, but within each computational node trainable coefficients of p and q. For all prescribed \(\deg (p)\ge 2\) and \(\deg (q)\in {\mathbb N}_0\), each node in such a network can emulate the multiplication of two numbers exactly ([3, Proposition 10] and its proof), hence Proposition 2.14 also holds for such NNs (the proof in Appendix A applies, using that also the identity map can be emulated by networks with such activations).
As a result, Theorem 3.10 also holds for all activation functions discussed in this remark.
3 Exponential Expression Rate Bounds
We now proceed to the statement and proof of the main result of the present note, namely the exponential rate bounds for the DNN expression of d-variate holomorphic maps. First, in Sect. 3.1 we recall (classical) polynomial approximation results for analytic functions, similar to those in [35]. Subsequently, these are used to deduce DNN approximation results for ReLU and RePU networks.
3.1 Polynomial Approximation
Fix \(d\in \mathbb {N}\). For \(\rho >1\) define the open Bernstein ellipse
and for the poly-radius \({\varvec{\rho }}=(\rho _j)_{j=1}^d \in (1,\infty )^d\) define the poly-ellipse

Let \(u:[-\,1,1]^d\rightarrow {\mathbb R}\) admit a complex holomorphic extension to the polyellipse \({{\mathcal {E}}}_{\varvec{\rho }}\). Such a function can be approximated on \([-\,1,1]^d\) by multivariate Legendre expansions, with the error decaying uniformly like \(\exp (-\beta N^{1/d})\) for some \(\beta >0\) and in terms of the dimension N of the approximation space. This statement is made precise in Theorem 3.5.
Remark 3.1
Suppose that \(u:[-\,1,1]^d\rightarrow {\mathbb R}\) is (real) analytic. Then it allows a complex holomorphic extension to some open set \(O\subseteq {\mathbb C}^d\) containing \([-\,1,1]^d\). Since for \(\rho >1\) close to 1, the maximal distance of a point in \({{\mathcal {E}}}_\rho \) to the interval \([-\,1,1]\) becomes arbitrarily small, there always exists \(\rho >1\) such that u allows a holomorphic extension to  .
.
For the proof of the theorem, we shall use the following result mentioned in [38, Equation (1.5)].
Lemma 3.2
Let \((a_j)_{j=1}^d\in (0,\infty )^d\). Then, with \(a:=\sum _{j=1}^d 1/a_j\)
The lemma is proved by computing (as an upper bound of the left-hand side in (3.2)) the volume of the set \(\{(x_j)_{j=1}^d\in {\mathbb R}_+^d\,:\,\sum _{j=1}^d \frac{(x_j-1)}{a_j}\le 1\}\), which equals the right-hand side in (3.2). The significance of this result is, that it provides an upper bound for the size of multi-index sets of the type
To see this, note that due to \(\log ({\varvec{\rho }}^{-{\varvec{\nu }}})=-\sum _{j=1}^d \nu _j\log (\rho _j)\), for any \(\varepsilon \in (0,1)\) we have
Applying Lemma 3.2 with \(a_j=\log (1/\varepsilon )/\log (\rho _j)\) we thus get (see also [2, Lemma 4.4]):
Lemma 3.3
It holds
Remark 3.4
Note that
This implies the existence of a constant C (depending on \({\varvec{\rho }}\) but independent of d) such that for all \(\varepsilon \in (0,1)\) with \(\rho _{\mathrm{min}}:=\min _{j=1,\ldots ,d}\rho _j\) and \(\rho _{\mathrm{max}}:=\max _{j=1,\ldots ,d}\rho _j\) [cp. (2.17)]
We are now in position to prove the following theorem, variations of which can be considered as classical.
Theorem 3.5
Let \(d\in {\mathbb N}\) and \({\varvec{\rho }}=(\rho _j)_{j=1}^d\in (1,\infty )^d\). Let \(u:\mathcal {E}_{\varvec{\rho }}\rightarrow {\mathbb C}\) be holomorphic. Then, for all \(k\in \mathbb {N}_0\) and for any \(\beta >0\) such that
there exists \(C>0\) (depending on d, \({\varvec{\rho }}\), k, \(\beta \) and u) such that with
and \(\varLambda _\varepsilon \) in (3.3) it holds for all \(\varepsilon \in (0,1)\)
Proof
Due to the holomorphy of u on \({{\mathcal {E}}}_{\varvec{\rho }}\), for a constant \(C>0\) depending on d and \({\varvec{\rho }}\), \(l_{\varvec{\nu }}\in {\mathbb R}\) satisfies the bound
For \(d=1\) a proof can be found in [9, Chapter 12]. For general \(d\in {\mathbb N}\) the bound follows by application of the one dimensional result in each variable. For more details we refer for instance to [6, Eqs. (2.14) and (2.16)] or [39, Corollary B.2.7].
Since \((L_{\varvec{\nu }})_{{\varvec{\nu }}\in \mathbb {N}_0^d}\) forms an orthonormal basis of (the Hilbert space) \(L^2([-\,1,1]^d,\mu _d)\) we have
converging in \(L^2([-\,1,1]^d,\mu _d)\). Furthermore, with (3.9) and (2.16), for \(k\in {\mathbb {N}}_0\) and every \({\varvec{\nu }}\in {\mathbb {N}}_0^d\)
Using [41, Lemma 3.10] (which is a variation of [7, Lemma 7.1])
and thus, (3.10) also converges in \(W^{k,\infty }([-\,1,1]^d)\).
Next, for \(j\in \{1,\ldots ,d\}\) let \({\varvec{{\mathbf {e}}}}_j:=(\delta _{ij})_{i=1}^d\) and introduce
Note that for \(\varepsilon \in (0,1)\)
Furthermore, since for every \({\varvec{\nu }}\in A_\varepsilon \) there exists \(j\in {{\,\mathrm{supp}\,}}{\varvec{\nu }}\subseteq \{1,\ldots ,d\}\) such that \({\varvec{\rho }}^{-({\varvec{\nu }}-{\varvec{{\mathbf {e}}}}_j)}\ge \varepsilon \) and therefore \({\varvec{\nu }}-{\varvec{{\mathbf {e}}}}_j\in \varLambda _\varepsilon \), we find with (3.4) that there exists a constant C depending on d and \({\varvec{\rho }}\) but independent of \(\varepsilon \in (0,1)\) such that for all \(\varepsilon \in (0,1)\)
Furthermore, for such \({\varvec{\nu }}\in A_\varepsilon \) and \(j\in {{\,\mathrm{supp}\,}}{\varvec{\nu }}\subseteq \{1,\ldots ,d\}\) with \(\rho _{\mathrm{min}}:=\min _{i\in \{1,\ldots ,d\}}\rho _i\) we get
and therefore
Using (3.11), there is \(C>0\) depending on d, \({\varvec{\rho }}\), k but independent of \(\varepsilon \in (0,1)\), with
The sum in the second brackets is finite independent of \(\varepsilon \) by [41, Lemma 3.10]. The sum in the first brackets can be bounded using (3.12) and (3.13) to obtain a constant \(C>0\) depending on u, d, \({\varvec{\rho }}\) and k such that for all \(\varepsilon \in (0,1)\)
To finish the proof, note that our above calculation shows that for any \(\tau \in (0,1)\) there exists \(C_\tau >0\) depending on u, d, \({\varvec{\rho }}\) and k such that
for all \(\varepsilon \in (0,1)\). Moreover, (3.4) implies
Hence for all \(\varepsilon \in (0,1)\)
where \(C:=C_\tau \exp (\tau \sum _{j=1}^d\log (\rho _j))\), \(\beta :=\tau (d!\prod _{j=1}^d\log (\rho _j))^{1/d}\) and where \(\tau \in (0,1)\) can be arbitrarily close to 1. \(\square \)
For later use, we note that the right-hand side of (3.7) can be estimated by Stirling’s inequality, with \(\rho _{\min } = \min _{j=1}^d \rho _j\) and \(\rho _{\max } = \max _{j=1}^d \rho _j\):
3.2 ReLU DNN Approximation
We now come to the main result, concerning the approximation of holomorphic functions on bounded intervals by ReLU networks.
Theorem 3.6
Fix \(d\in \mathbb {N}\) and let \({\varvec{\rho }}=(\rho _j)_{j=1}^d\in (1,\infty )^d\). Assume that \(u:[-\,1,1]^d\rightarrow {\mathbb R}\) admits a holomorphic extension to \({{\mathcal {E}}}_{\varvec{\rho }}\).
Then, there exist constants \(\beta '=\beta '({\varvec{\rho }},d)>0\) and \(C=C(u,{\varvec{\rho }},d)>0\), and for every \({{\mathcal {N}}}\in {\mathbb N}\) there exists a \(\sigma _1\)-NN \({{\tilde{u}}}_{{\mathcal {N}}}:[-\,1,1]^d\rightarrow {\mathbb R}\) satisfying
and the error bound
Proof
Throughout this proof, let \(\beta >0\) be fixed such that (3.7) holds. We proceed in three steps: In Step 1, we introduce a NN approximation of u, whose error, network depth and size we estimate in Step 2. Based on these estimates, we show Equations (3.15)–(3.16) in Step 3.
Step 1. Let \(d\in {\mathbb N}\). In this step, for any \(\varepsilon \in (0,1)\) we introduce a network \({\hat{u}}_\varepsilon \) approximating u (with increasing accuracy as \(\varepsilon \rightarrow 0\)).
Fix \(\varepsilon \in (0,1)\) arbitrary, let \(\varLambda _\varepsilon \subseteq {\mathbb N}_0^d\) be as in (3.3) and set \(u_\varepsilon :=\sum _{{\varvec{\nu }}\in \varLambda _\varepsilon }l_{\varvec{\nu }}L_{\varvec{\nu }}\) with the Legendre coefficients \(l_{\varvec{\nu }}\) of u as in (3.8).
Let \({\text {Affine}}_{u}\) be a NN of depth 0, with input dimension \(|\varLambda _\varepsilon |\), output dimension 1 and size at most \(|\varLambda _\varepsilon |\) which implements the affine transformation \(\mathbb {R}^{|\varLambda _\varepsilon |}\rightarrow \mathbb {R}: (z_{\varvec{\nu }})_{{\varvec{\nu }}\in \varLambda } \mapsto \sum _{{\varvec{\nu }}\in \varLambda _\varepsilon } l_{{\varvec{\nu }}}z_{{\varvec{\nu }}}\). Furthermore, let \({{\varvec{f}}}_{\varLambda _\varepsilon ,\delta }\) be the network from Proposition 2.13, emulating approximations to all multivariate Legendre polynomials \((L_{\varvec{\nu }})_{{\varvec{\nu }}\in \varLambda _\varepsilon }\). We define a NN
Then
where (with \(\beta >0\) as in (3.7)) the accuracy \(\delta >0\) of the \(\sigma _1\)-NN approximations of the tensor product Legendre polynomials is chosen as
Step 2. For the NN \({\hat{u}}_\varepsilon \) we obtain the error estimate
With Theorem 3.5 this yields the existence of a constant \(C>0\) (depending on d, \({\varvec{\rho }}\), \(\beta \) and u) such that
We now bound the depth and the size of \({\hat{u}}_\varepsilon \). Using Proposition 2.13 and (3.6), we obtain
for \(C>0\) depending on \({\varvec{\rho }}\). To bound the NN size, Proposition 2.13 and (3.6) give
for a constant \(C_2 > 0\) which depends on \({\varvec{\rho }}\), but is independent of d, \(\beta \), u and of \(\varepsilon \in (0,1)\).
Step 3. Finally, we define \({{\tilde{u}}}_{{\mathcal {N}}}\). Fix \(\beta >0\) satisfying (3.7) and \({{\mathcal {N}}}\in {\mathbb N}\) such that \({{\mathcal {N}}}> {{\mathcal {N}}}_0:=C_2(1+\beta )d^{4}\), with the constant \(C_2\) as in (3.19). Set
Next, let \(\varepsilon \in (0,1)\) be such that
which is possible since \({\widehat{{{\mathcal {N}}}}}>1\) due to the assumption \({{\mathcal {N}}}>{{\mathcal {N}}}_0= C_2(1+\beta )d^{4}\). Define \({{\tilde{u}}}_{{\mathcal {N}}}:= {\hat{u}}_\varepsilon \).
First let us estimate the size of \({{\tilde{u}}}_{{\mathcal {N}}}\). By (3.5)
Hence (3.19) and the definition of \({\widehat{{{\mathcal {N}}}}}\) imply
Similarly one obtains the bound on the depth of \({{\tilde{u}}}_{{\mathcal {N}}}\) by using (3.18). This shows (3.15).
Next we estimate the error \(\left\| u-{{\tilde{u}}}_{{\mathcal {N}}} \right\| _{W^{1,\infty }([-\,1,1]^d)}\). By (3.5)
Thus, (3.17) gives
By (3.20) this is (3.16) for any \({{\mathcal {N}}}> {{\mathcal {N}}}_0\) and with
for \(C_2\) as in (3.19) (independent of d, \(\beta \) and u). With \({{\tilde{u}}}_{{\mathcal {N}}}:=0\) (i.e., a trivial NN giving the constant value 0) for all (finitely many) \({{\mathcal {N}}}\le {{\mathcal {N}}}_0\), we conclude that (3.16) holds for all \({{\mathcal {N}}}\in {\mathbb N}\) (by increasing \(C>0\) in (3.16) if necessary). \(\square \)
Remark 3.7
(Fully connected networks) In the proof of Theorem 3.6 we explicitly constructed a sparsely connected DNN to approximate u. In practice, it might be tedious to implement this type of architecture. Instead one can set up a fully connected network, containing our sparse architecture. We shortly discuss the implications of Theorem 3.6 in this case.
The width \(w\in {\mathbb N}\) of a neural network \(\phi \) (i.e., the maximum number of nodes in one of its layers) is trivially bounded by \(\mathrm{size}(\phi )\). For a fully connected network of width w, the weight matrix connecting two layers may have \(w^2\) nonzero weights. Denote now by \({\hat{u}}_{{\mathcal {N}}}\) a fully connected \(\sigma _1\)-NN of width \(w={{\mathcal {N}}}\) and depth \(\mathrm{depth}({\hat{u}}_{{\mathcal {N}}})\le C {{\mathcal {N}}}^{1/(d+1)}\log _2({{\mathcal {N}}})\) (with C as in (3.15)) realizing the function \({{\tilde{u}}}_{{\mathcal {N}}}\) from Theorem 3.6. The existence of \({\hat{u}}_{{\mathcal {N}}}\) is an immediate consequence of the depth and size bounds given in Theorem 3.6. Then by (3.15), denoting its total number of weights, also counting vanishing weights, by \({{\,\mathrm{\#weights}\,}}({\hat{u}}_{{{\mathcal {N}}}})\),
and by (3.16)
This yields the error bound
for fully connected networks, and where \({\hat{\beta }}>0\) is some constant independent of \({{\mathcal {N}}}\). Hence, the exponent in the error estimate has (up to logarithmic terms) decreased from \(\frac{1}{d+1}\) for the sparsely connected network in Theorem 3.6 to \(\frac{1}{2d+3}\) for the fully connected network.
Remark 3.8
Note that in Step 2 of the proof, the network \({\hat{u}}_\varepsilon \) depends on u only via the Legendre coefficients \(\{l_{{\varvec{\nu }}}\}_{{\varvec{\nu }}\in \varLambda _\varepsilon }\), appearing only as weights in the output layer. In particular, the weights and biases of \({\hat{u}}_\varepsilon \) continuously depend on u with respect to the \(L^2([-\,1,1]^d,\mu _d)\)-norm, because the Legendre coefficients do so. Finally, the \(L^2([-\,1,1]^d,\mu _d)\)-norm is bounded by the \(L^\infty ([-\,1,1]^d)\)-norm.
Remark 3.9
The same result does not follow if we approximate the basis of multivariate polynomials by applying Proposition 2.6 to approximate the product of \(m(\varLambda _\varepsilon )\) linear factors. With \(\delta := \exp (-\beta |\varLambda _\varepsilon |^{1/d})\), each basis polynomial would have a network size of the order \(O(m(\varLambda _\varepsilon )\log (1/\delta )) = O(m(\varLambda _\varepsilon )^2) = O(|\varLambda _\varepsilon |^{2/d})\), hence the total network size would be of the order \(O(|\varLambda _\varepsilon |^{1+2/d})\), corresponding to \(C \exp (- \beta ' {{\mathcal {N}}}^{1/(d+2)})\) in the right-hand side of (3.16).
3.3 RePU DNN Approximation
For RePU approximations, with activation \(\sigma _r(x)\) for integer \(r\ge 2\), we may combine Proposition 2.14 (which is almost identical to [17, Theorem 4.1]) and Theorem 3.5 to infer the following result. Note that the decay of the provided upper bound of the error in (3.23) in terms of the network size \({{\mathcal {N}}}\) is slightly faster than the one we obtained for ReLU approximations in (3.16).
Theorem 3.10
Fix \(d\in \mathbb {N}\), \(k\in {\mathbb N}_0\) and \(r\in {\mathbb N}\), \(r\ge 2\). Let \({\varvec{\rho }}=(\rho _j)_{j=1}^d\in (1,\infty )^d\). Assume that \(u:[-\,1,1]^d\rightarrow {\mathbb R}\) admits a holomorphic extension to \({{\mathcal {E}}}_{\varvec{\rho }}\).
Then, there exists \(C>0\) and a constant \(C_1>0\) which only depends on r such that with \(\beta \) as in (3.7), for every \({{\mathcal {N}}}\in {\mathbb N}\), there exists a \(\sigma _r\)-NN \({\tilde{u}}_{{{\mathcal {N}}}}:[-\,1,1]^d\rightarrow {\mathbb R}\) satisfying
and, with \(\beta ' := \beta /(d+1)\),
Here, we can consider the \(W^{k,\infty }([-\,1,1]^d)\)-norm of \((u-{\tilde{u}}_{{\mathcal {N}}})\) for \(k\in {\mathbb N}\) independent of r, because u is holomorphic on \([-\,1,1]^d\), and \({\tilde{u}}_{{\mathcal {N}}}\) is a polynomial by construction. Also, we note with (3.14) that \(\beta ' = \log (\rho _{\min })/(2e)\) is attainable for all \(d\in {\mathbb N}\).
Proof
For \(\varepsilon \in (0,1)\) let \(\varLambda _\varepsilon \) be as in (3.3). This set is finite and downward closed. Hence, by Proposition 2.14 there exists a \(\sigma _r\)-NN \({\hat{u}}_\varepsilon \) such that \({\hat{u}}_\varepsilon ({{\varvec{y}}}) = \sum _{{\varvec{\nu }}\in \varLambda _\varepsilon }l_{\varvec{\nu }}L_{\varvec{\nu }}({{\varvec{y}}})\) for all \({{\varvec{y}}}\in [-\,1,1]^d\). According to this proposition, the NN \({\hat{u}}_\varepsilon \) satisfies \({{\,\mathrm{size}\,}}({\hat{u}}_\varepsilon ) \le C_1|\varLambda _\varepsilon |\) and \({{\,\mathrm{depth}\,}}({\hat{u}}_\varepsilon ) \le C_1\log |\varLambda _\varepsilon |\). This is (3.22) for \({{\mathcal {N}}}:=|\varLambda _\varepsilon |\). By Theorem 3.5, it holds (3.23) for such \({{\mathcal {N}}}\), with \(\beta '=\beta \).
For general \({{\mathcal {N}}}>1\), it follows as in Step 3 of the proof of Theorem 3.6 (with \({{\mathcal {N}}}\) taking the role of \({\widehat{{{\mathcal {N}}}}}\) in (3.21)) that there exists \(\varepsilon \in (0,1)\) such that \((d+1)^{-d}{{\mathcal {N}}}\le |\varLambda _\varepsilon | \le {{\mathcal {N}}}\). This implies that (3.23) holds for any \({{\mathcal {N}}}\in {\mathbb N}\) with \(\beta ' := \beta /(d+1)\) and a constant C depending on d. \(\square \)
Remark 3.11
(Fully connected networks) A similar statement as in Remark 3.7 also holds for \(\sigma _r\)-NNs with \(r\ge 2\). By the same arguments, we obtain an error bound of the type
for a fully connected \(\sigma _r\)-NN \({\hat{u}}_{{\mathcal {N}}}\), whose total number of weights, also counting vanishing weights, we denote by \({{\,\mathrm{\#weights}\,}}({\hat{u}}_{{{\mathcal {N}}}})\). Here \(k\in {\mathbb N}\) is arbitrary but fixed, and \({\hat{\beta }}>0\) is a constant independent of \({{\mathcal {N}}}\).
Remark 3.12
It follows from the proof of Proposition 2.14 that the weights of \({\tilde{u}}_{{{\mathcal {N}}}}\) depend continuously on the Legendre coefficients of u, which themselves depend continuously on u w.r.t. the \(L^2([-\,1,1]^d,\mu _d)\)-norm, which is bounded by the \(L^\infty ([-\,1,1]^d)\)-norm.
Remark 3.13
A similar result as in Theorem 3.10 was obtained in [21, Theorem 3.3]. It assumed a different class of activation functions, termed “sigmoidal functions of order \(k\ge 2\)” (see Remark 2.1). The \(L^\infty ([-\,1,1]^d)\) error bound provided in [21, Theorem 3.3] is, in our notation, of the type \(\exp (- b{{\mathcal {N}}}^{1/d})\) for a suitable constant \(b>0\) and a DNN of size \({{\mathcal {N}}}\log ({{\mathcal {N}}})\). This is slightly worse than Theorem 3.10. Also note that in [21] the number of neurons is used as measure for the NN size, which may be smaller but not larger than the number of nonzero weights if all neurons have at least one nonzero weight.
4 Conclusion
We review in Sect. 4.1 the main results obtained in the previous sections. In Sect. 4.2, we relate these results to results which appeared in the literature. In Sect. 4.3, we discuss several novel implications of the main results, which could be of interest in various applications. We point out that although the present analysis is developed in detail for DNNs with ReLU activation, as explained in Remarks 2.1 and 2.15, all DNN expression error bounds proved up to this point, and also in the ensuing remarks remain valid (possibly even with slightly better estimates for the DNN sizes) for smoother activation functions, such as sigmoidal, tanh, or softmax activations.
4.1 Main Results
We have established for analytic maps \(u:[-\,1,1]^d\rightarrow {\mathbb R}\) exponential expression rate bounds in \(W^{k,\infty }([-\,1,1]^d)\) in terms of the DNN size for the ReLU activation (for \(k=0,1\)) and for the RePU activations \(\sigma _r\), \(r\ge 2\) (for \(k\in {\mathbb N}_0\)). The present analysis improves earlier results in that the NN sizes are slightly reduced and we obtain exponential convergence of ReLU and RePU DNNs for general d-variate analytic functions, without assuming the Taylor expansion of u around \(0\in {\mathbb R}^d\) to converge on \([-\,1,1]^d\). We also point out that by a simple scaling argument our main results in Theorems 3.6 and 3.10 imply corresponding expression rate results for analytic functions defined on an arbitrary cartesian product of finite intervals \(\times _{j=1}^d [a_j,b_j]\), where \(-\infty< a_j<b_j<\infty \) for all \(j\in \{1,\ldots ,d\}\).
4.2 Related Results
We already commented on [36] where ReLU NN expression rates for multivariate, holomorphic functions u were obtained. Assumptions in [36, Theorem 2.6] included absolute convergence of Taylor expansions of u about the origin with convergence radius sufficiently large to contain the unit cube \([-\,1,1]^d\), implying existence of a complex holomorphic extension to \((B_1^{\mathbb C})^d\). Under those assumptions \(L^\infty ({[-(1-\delta ),(1-\delta )]^d})\)-error bounds were obtained for any \(\delta \in (0,1)\). With a linear coordinate transformation, error bounds on \([-\,1,1]^d\) follow under the assumption that the Taylor expansion converges absolutely on \([-(1-\delta )^{-1},(1-\delta )^{-1}]^d\). The presently proposed argument being based on (classical) Bernstein ellipses is admissible for functions u which are real analytic merely in \([-\,1,1]^d\) (cp. Remark 3.1). Our proofs are constructive, with constructions being based on ReLU NN emulations of Legendre polynomials, drawing on [25]. In [33], alternative constructions of so-called RePU NNs are proposed which are based on NN emulation of univariate Chebyšev polynomials. It is argued in [33] (and verified in numerical experiments) that the numerical size of NN weights scales more favorably than the weights in the presently proposed emulations. “Chebyšev” versions of the present proofs could also be facilitated, resulting in the same scalings of NN sizes and depths, however, as are obtained here.
4.3 Applications and Generalizations
4.3.1 Solution Manifolds of PDEs
One possible application of our results concerns the approximation of (quantities of interest of) solution manifolds of parametric PDEs depending on a d-dimensional parameter \({{\varvec{y}}}\in [-\,1,1]^d\). Such a situation arises in particular in Uncertainty Quantification (UQ). There, a mathematical model is described by a PDE depending on the parameters \({{\varvec{y}}}\), which in turn can for instance determine boundary conditions, forcing terms or diffusion coefficients. It is known for a wide range of linear and nonlinear PDE models (see, e.g., [6]), that parametric PDE solutions depend analytically on the parameters. In addition, for these models usually one has precise knowledge on the domain of holomorphic extension of the objective function u, i.e., knowledge of the constants \((\rho _j)_{j=1}^d\) in Theorem 3.5. These constants determine the sets of multi-indices \(\varLambda _\varepsilon \) in (3.3). As our proofs are constructive and based on the sets \(\varLambda _\varepsilon \), such information can be leveraged to a priori guide the identification of suitable network architectures.
4.3.2 ReLU DNN Expression of Data-to-QoI Maps for Bayesian PDE Inversion
The exponential \(\sigma _1\)-DNN expression rate bound, Theorem 3.6, implies exponential expressivity of data-to-quantity of interest maps in Bayesian PDE inversion, as is shown in [14]. Here, the assumption of centered, additive Gaussian observation noise in the data model underlying the Bayesian inverse theory implies holomorphy of the data to prediction map in the Bayesian theory as we show [14]. This, combined with the present results in Theorems 3.6 and 3.10 implies exponential expressivity of \(\sigma _r\) DNNs for this map, for all \(r\ge 1\).
4.3.3 Infinite-Dimensional (\(d=\infty \)) Case
The expression rate analysis becomes more involved, if the objective function u depends on an infinite dimensional parameter (i.e., a parameter sequence) \({{\varvec{y}}}\in [-\,1,1]^{\mathbb N}\). Such functions occur in UQ for instance if the uncertainty is described by a Karhunen–Loeve expansion. Under certain circumstances, u can be expressed by a so-called generalized polynomial chaos (gpc) expansion. Reapproximating truncated gpc expansions by NNs leads to expression rate results for the approximation of infinite dimensional functions, as we showed in [32]. One drawback of [32] is however, that the proofs crucially relied on the assumption that u is holomorphic on certain polydiscs containing \([-\,1,1]^{\mathbb N}\). This criterion is not always met in practice [6]. To overcome this restriction, we will generalize the expression rate results of [32] in a forthcoming paper, by basing the analysis on the present results for the approximation of d-variate functions which are merely assumed to be analytic in some (possibly small) neighborhood of \([-\,1,1]^d\).
4.3.4 Gevrey Functions
DNN approximations of tensor product Legendre polynomials constructed in Sect. 2 can be used more generally than for the approximation of holomorphic functions by truncated Legendre expansions. We consider as an example, for \(d\in {\mathbb N}\), the approximation of non-holomorphic, Gevrey-regular functions (see, e.g., [28] and the references there for definitions and properties of such functions). Gevrey-regular functions appear as natural solution classes for certain PDEs (e.g., [13] and [4, Chapter 8]). Here, for some \(\delta \ge 1\) we consider maps \(u:[-\,1,1]^d\rightarrow {\mathbb R}\) that satisfy, for constants \(C,A>0\) depending on u, the bound
We write \(u\in {{\mathcal {G}}}^\delta ([-\,1,1]^d,C,A)\) for u satisfying (4.1). Evidently, \({{\mathcal {G}}}^\delta ([-\,1,1]^d,C,A) \subset C^\infty ([-\,1,1]^d)\). These maps are analytic when \(\delta =1\), but possibly non-analytic when \(\delta >1\).
Proposition 4.1
For dimension \(d\in {\mathbb {N}}\), and for constants \(C,A>0\), for \(u\in {{\mathcal {G}}}^\delta ([-\,1,1]^d,C,A)\) exist \(C'(d,\delta ,u)>0\) and \(\beta '(d,\delta ,u)>0\), and for every \({{\mathcal {N}}}\in {\mathbb N}\) there exists a ReLU DNN \({\tilde{u}}_{{\mathcal {N}}}\) such that
In the proof, which is provided in Appendix B, we furthermore show that there exist constants \(C',\beta '>0\) such that for every \(p\in {\mathbb N}\) and every \(u\in {{\mathcal {G}}}^\delta ([-\,1,1]^d,C,A)\) holds
Here, \(N = \mathrm{dim}(\otimes _{j=1}^d{\mathbb P}_p([-\,1,1])) = (p+1)^d\) denotes the dimension of the space of all d-variate polynomials of degree at most p in each variable.
4.3.5 ReLU Expression of Non-smooth Maps by Composition
The results were based on the quantified holomorphy of the map \(u:[-\,1,1]^d\rightarrow {\mathbb C}\). While this could be perceived as a strong requirement (and, consequently, limitation) of the present results, by composition the present deep ReLU NN emulation rate bounds cover considerably more general situations. The key observation is that deep ReLU NNs are closed under concatenation (or under composition of realizations) as we explained in Sect. 2.2.3.
Let us give a specific example from high-dimensional integration, where the task is to evaluate the integral
Here, \(u: [-\,1,1]^d \rightarrow {\mathbb R}\) is a function which is holomorphic in a polyellipse \({{\mathcal {E}}}_{\varvec{\rho }}\) as in (3.1) and \(\pi \) denotes an a-priori given probability density on the coordinates \(y_1,\ldots ,y_d\) w.r.t. the measure \(\mu _d\) (i.e., \(\pi :[-\,1,1]^d\rightarrow [0,\infty )\) is measurable and satisfies \(\int _{[-\,1,1]^d}\pi ({{\varvec{x}}})\mathrm {d}\mu _d({{\varvec{x}}})=1\)). Assuming that the coordinates are independent, the density \(\pi \) factors, i.e., \( \pi = \bigotimes _{j=1}^d \pi _j \) with certain marginal probability densities \(\pi _j\) which we assume to be absolutely continuous w.r. to the Lebesgue measure, i.e., \(\int _{-1}^1 \pi _j(\xi ) \mathrm {d}\xi = 2\). In the case that the marginals \(\pi _j>0\) are simple functions for example on finite partitions \({{\mathcal {T}}}_j\) of \([-\,1,1]\) (as, e.g., if \(\pi _j\) is a histogram for the law of \(y_j\) estimated from empirical data), the changes of coordinates in (4.3)
are bijective. Furthermore, in this case each component map \(T_j:[-\,1,1]\rightarrow [-\,1,1]\) is bijective, continuous and piecewise affine, and can therefore be exactly represented by a \(\sigma _1\)-NN of depth 1 and width proportional to \(\#({{\mathcal {T}}}_j)\).
Denote by \(T = (T_1,\ldots ,T_d)^\top \) the d-variate diagonal transformation, and let \(T^{-1}:[-\,1,1]^d\rightarrow [-\,1,1]^d\) denote its inverse (which is also continuous, piecewise linear). Denoting by \(dT^{-1}({{\varvec{x}}})\) the Jacobian matrix of \(T^{-1}\) at \({{\varvec{x}}}\in [-\,1,1]^d\) we may then rewrite (4.3) as
where \(g = u\circ T^{-1}\) is not continuously differentiable. Here we have used that \(dT^{-1}(T({{\varvec{y}}}))=(dT({{\varvec{y}}}))^{-1}\) and \(\det (dT({{\varvec{y}}}))=\pi ({{\varvec{y}}})\), i.e., \(\det dT^{-1}({{\varvec{x}}}) = \pi (T^{-1}({{\varvec{x}}}))^{-1}\).
Now, the function \({\tilde{g}}_{{{\mathcal {N}}}} := {\tilde{u}}_{{{\mathcal {N}}}}\circ T^{-1}\) with the \(\sigma _1\)-NN \({\tilde{u}}_{{{\mathcal {N}}}}\) constructed in Theorem 3.6 is a \(\sigma _1\)-NN which still affords the error bound (3.16): Denote for \(n\in {\mathbb N}_0 \) and \(f\in W^{1,\infty }([-\,1,1]^d,\mathbb {R}^n)\)
where \(\left\| \cdot \right\| _{}\) is the Euclidean norm on \({\mathbb R}^n\) resp. on \({\mathbb R}^d\). As usual, for \(n=1\) we write \(|f|_{W^{1,\infty }([-\,1,1]^d)}:= |f|_{W^{1,\infty }([-\,1,1]^d,{\mathbb R})}\) instead. With these conventions, it holds
for a constant C which now additionally depends on \(|T^{-1}(\cdot )|_{W^{1,\infty }([-\,1,1]^d,\mathbb {R}^d)}\). The approximation of the integral (4.3) can thus be reduced to the problem of approximating the integral of the surrogate \({{\tilde{g}}}_{{\mathcal {N}}}\), which can be efficiently represented by a \(\sigma _1\)-NN. In the case that u is merely assumed Gevrey-regular as in Sec. 4.3.4, a similar calculation leads to a bound of the type (4.5), but with \(\exp (-\beta ' {{\mathcal {N}}}^{\frac{1}{d+1}})\) replaced by \(\exp \Big (-\beta '{{\mathcal {N}}}^{\min \left\{ \tfrac{1}{2\delta },\tfrac{1}{d\delta +1}\right\} }\Big )\).
More generally, if \(\pi :[-\,1,1]^d\rightarrow (0,\infty )\) is, for example, a continuous density function (not necessarily a product of its marginals), there exists a bijective transport \(T:[-\,1,1]^d\rightarrow [-\,1,1]^d\) such that analogous to (4.4) it holds \(\int _{[-\,1,1]^d} u({{\varvec{y}}})\pi ({{\varvec{y}}})\mathrm {d}{{\varvec{y}}}= \int _{[-\,1,1]^d} u(T^{-1}({{\varvec{x}}}))\mathrm {d}{{\varvec{x}}}\) (contrary to the situation above, this transformation T is not diagonal in general). One explicit representation of such a transport is provided by the Knothe–Rosenblatt transport, see, e.g., [30, Sect. 2.3]. It has the property that T inherits the smoothness of \(\pi \), cp. [30, Remark 2.19]. In case \(T^{-1}\) can be realized without error by a \(\sigma _1\) (or \(\sigma _r\)) network, we find again an estimate of the type (3.16). If \(T^{-1}\) does not allow an explicit representation by a NN, however, we may still approximate \(T^{-1}\) by a NN \({{\tilde{S}}}_{{\mathcal {N}}}\) to obtain a NN \({{\tilde{g}}}_{{\mathcal {N}}}:={{\tilde{u}}}_{{\mathcal {N}}}\circ {{\tilde{S}}}_{{\mathcal {N}}}\) approximating \(g=u\circ T^{-1}\). This will introduce an additional error in (4.5) due to the approximation of \(T^{-1}\).
Notes
Index sets with the ”downward closed” property are also referred to in the literature [24] as lower sets.
In other recent references (e.g., [25]), slightly different terminology for the number L of layers in the DNN differing from the convention in the present paper by a constant factor, is used. This difference will be inconsequential for all results that follow.
References
Bölcskei, H., Grohs, P., Kutyniok, G., Petersen, P.: Optimal approximation with sparsely connected deep neural networks. SIAM J. Math. Data Sci. 1(1), 8–45 (2019). https://doi.org/10.1137/18M118709X
Bonito, A., DeVore, R., Guignard, D., Jantsch, P., Petrova, G.: Polynomial approximation of anisotropic analytic functions of several variables. Constr. Approx. (2020). https://doi.org/10.1007/s00365-020-09511-4
Boullé, N., Nakatsukasa, Y., Townsend, A.: Rational neural networks. Accepted for Publication in 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, Canada (2020). https://proceedings.neurips.cc/paper/2020/hash/a3f390d88e4c41f2747bfa2f1b5f87db-Abstract.html
Chemin, J.Y.: Fluides parfaits incompressibles. Astérisque 230, 177 (1995). http://www.numdam.org/item/AST_1995_230_1_0
Chui, C.K., Li, X.: Approximation by ridge functions and neural networks with one hidden layer. J. Approx. Theory 70(2), 131–141 (1992). https://doi.org/10.1016/0021-9045(92)90081-X
Cohen, A., Chkifa, A., Schwab, C.: Breaking the curse of dimensionality in sparse polynomial approximation of parametric PDEs. J. Math. Pures Appl. 103(2), 400–428 (2015). https://doi.org/10.1016/j.matpur.2014.04.009
Cohen, A., DeVore, R., Schwab, C.: Convergence rates of best \(N\)-term Galerkin approximations for a class of elliptic sPDEs. Found. Comput. Math. 10(6), 615–646 (2010). https://doi.org/10.1007/s10208-010-9072-2
Costabel, M., Dauge, M., Schwab, C.: Exponential convergence of \(hp\)-FEM for Maxwell equations with weighted regularization in polygonal domains. Math. Models Methods Appl. Sci. 15(4), 575–622 (2005). https://doi.org/10.1142/S0218202505000480
Davis, P.: Interpolation and Approximation. Dover Books on Mathematics. Dover Publications, New York (1975)
Elbrächter, D., Grohs, P., Jentzen, A., Schwab, C.: DNN expression rate analysis of high-dimensional PDEs: application to option pricing. Constr. Approx. (2020) (accepted for publication). arXiv:1809.07669
Erdélyi, A., Magnus, W., Oberhettinger, F., Tricomi, F.G.: Higher Transcendental Functions, vol. 2. McGraw-Hill, New York (1953) (Based on notes left by Harry Bateman)
Feischl, M., Schwab, C.: Exponential convergence in \(H^1\) of \(hp\)-FEM for Gevrey regularity with isotropic singularities. Numer. Math. 144(2), 323–346 (2020). https://doi.org/10.1007/s00211-019-01085-z
Foias, C., Temam, R.: Gevrey class regularity for the solutions of the Navier–Stokes equations. J. Funct. Anal. 87(2), 359–369 (1989). https://doi.org/10.1016/0022-1236(89)90015-3
Herrmann, L., Schwab, C., Zech, J.: Deep neural network expression of posterior expectations in Bayesian PDE inversion. Inver. Probl. (2020). https://doi.org/10.1088/1361-6420/abaf64
Hornik, K.: Approximation capabilities of multilayer feedforward networks. Neural Netw. 4(2), 251–257 (1991). https://doi.org/10.1016/0893-6080(91)90009-T
Hornik, K., Stinchcombe, M., White, H.: Multilayer feedforward networks are universal approximators. Neural Netw. 2(5), 359–366 (1989). https://doi.org/10.1016/0893-6080(89)90020-8
Li, B., Tang, S., Yu, H.: Better approximations of high dimensional smooth functions by deep neural networks with rectified power units. Commun. Comput. Phys. 27(2), 379–411 (2019). https://doi.org/10.4208/cicp.OA-2019-0168
Liang, S., Srikant, R.: Why deep neural networks for function approximation? In: 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24–26, 2017, Conference Track Proceedings. OpenReview.net (2017). https://openreview.net/forum?id=SkpSlKIel
Mhaskar, H.: Neural networks for localized approximation of real functions. In: Neural Networks for Signal Processing III—Proceedings of the 1993 IEEE-SP Workshop, pp. 190–196. IEEE (1993). https://doi.org/10.1109/NNSP.1993.471870
Mhaskar, H., Micchelli, C.: Approximation by superposition of sigmoidal and radial basis functions. Adv. Appl. Math. 13(3), 350–373 (1992). https://doi.org/10.1016/0196-8858(92)90016-P
Mhaskar, H.N.: Approximation properties of a multilayered feedforward artificial neural network. Adv. Comput. Math. 1(1), 61–80 (1993). https://doi.org/10.1007/BF02070821
Mhaskar, H.N.: Neural networks for optimal approximation of smooth and analytic functions. Neural Comput. 8, 164–177 (1996). https://doi.org/10.1162/neco.1996.8.1.164
Montanelli, H., Yang, H., Du, Q.: Deep ReLU networks overcome the curse of dimensionality for bandlimited functions. J. Comput. Math. (2021) (to appear). arXiv:1903.00735
Nobile, F., Tempone, R., Webster, C.G.: An anisotropic sparse grid stochastic collocation method for partial differential equations with random input data. SIAM J. Numer. Anal. 46(5), 2411–2442 (2008). https://doi.org/10.1137/070680540
Opschoor, J.A.A., Petersen, P.C., Schwab, C.: Deep ReLU networks and high-order finite element methods. Anal. Appl. 18(05), 715–770 (2020). https://doi.org/10.1142/S0219530519410136
Petersen, P., Voigtlaender, F.: Optimal approximation of piecewise smooth functions using deep ReLU neural networks. Neural Netw. 108, 296–330 (2018). https://doi.org/10.1016/j.neunet.2018.08.019
Pinkus, A.: Approximation theory of the MLP model in neural networks. In: Acta Numerica, vol. 8, pp. 143–195. Cambridge University Press, Cambridge (1999). https://doi.org/10.1017/S0962492900002919
Rodino, L.: Linear Partial Differential Operators in Gevrey Spaces. World Scientific Publishing Co., Inc., River Edge (1993). https://doi.org/10.1142/9789814360036
Rolnick, D., Tegmark, M.: The power of deeper networks for expressing natural functions. In: International Conference on Learning Representations (2018). https://openreview.net/forum?id=SyProzZAW
Santambrogio, F.: Optimal transport for applied mathematicians. In: Progress in Nonlinear Differential Equations and their Applications, vol. 87. Calculus of Variations, PDEs, and Modeling. Birkhäuser, Cham (2015). https://doi.org/10.1007/978-3-319-20828-2
Schötzau, D., Schwab, C., Wihler, T.P.: \(hp\)-DGFEM for second order elliptic problems in polyhedra II: exponential convergence. SIAM J. Numer. Anal. 51(4), 2005–2035 (2013). https://doi.org/10.1137/090774276
Schwab, C., Zech, J.: Deep learning in high dimension: neural network expression rates for generalized polynomial chaos expansions in UQ. Anal. Appl. (Singap.) 17(1), 19–55 (2019). https://doi.org/10.1142/S0219530518500203
Tang, S., Li, B., Yu, H.: ChebNet: efficient and stable constructions of deep neural networks with rectified power units using Chebyshev approximations (2019). arXiv:1911.05467
Telgarsky, M.: Neural networks and rational functions, pp. 3387–3393. PMLR, International Convention Centre, Sydney, Australia (2017). http://proceedings.mlr.press/v70/telgarsky17a.html
Tran, H., Webster, C.G., Zhang, G.: Analysis of quasi-optimal polynomial approximations for parameterized PDEs with deterministic and stochastic coefficients. Numer. Math. 137(2), 451–493 (2017). https://doi.org/10.1007/s00211-017-0878-6
Weinan, E., Wang, Q.: Exponential convergence of the deep neural network approximation for analytic functions. Sci. China Math. 61(10), 1733–1740 (2018). https://doi.org/10.1007/s11425-018-9387-x
Yarotsky, D.: Error bounds for approximations with deep ReLU networks. Neural Netw. 94, 103–114 (2017). https://doi.org/10.1016/j.neunet.2017.07.002
Yau, S.T., Zhang, L.: An upper estimate of integral points in real simplices with an application to singularity theory. Math. Res. Lett. 13(5–6), 911–921 (2006). https://doi.org/10.4310/MRL.2006.v13.n6.a6
Zech, J.: Sparse-grid approximation of high-dimensional parametric PDEs. Ph.D. Thesis, Dissertation 25683, ETH Zurich, Zurich (2018). https://doi.org/10.3929/ethz-b-000340651
Zech, J., Dung, D., Schwab, C.: Multilevel approximation of parametric and stochastic PDEs. M3AS 29(9), 1753–1817 (2019). https://doi.org/10.1142/S0218202519500349
Zech, J., Schwab, C.: Convergence rates of high dimensional Smolyak quadrature. ESAIM: M2AN 54(4), 1259–1307 (2020). https://doi.org/10.1051/m2an/2020003
Acknowledgements
Research performed in part during a visit to the CRM Montreal, Canada, of CS and JZ in May 2019.
Funding
Open Access funding provided by ETH Zurich.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by Wolfgang Dahmen, Ronald A. DeVore, and Philipp Grohs.
Dedicated to Professor Ron De Vore on the occasion of his 80th anniversary.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported in part under an SNSF Early Postdoc.Mobility Fellowship 184530 to JZ.
Appendices
Proof of Proposition 2.14
Proof
The proof consists of 2 steps. In Step 1, we define subnetworks, similar to those in [25, Lemma 4.5], to emulate all monomials \({{\varvec{x}}}^{\varvec{\nu }}\) for \({\varvec{\nu }}\in \varLambda \) of order \(2^{k-1} \le |{\varvec{\nu }}|_1 \le 2^k\). In Step 2, we use them to construct \({\tilde{p}}\).
Step 1. Throughout this proof, we denote the NN input by \({{\varvec{x}}}\in {\mathbb R}^d\).
For \(k\in {\mathbb N}_0\), we define the index sets \(\varLambda _k := \{{\varvec{\nu }}\in \varLambda : |{\varvec{\nu }}|_1 = k \}\) and \(\Delta _k := \{{\varvec{\nu }}\in \varLambda : 2^{k-1} < |{\varvec{\nu }}|_1 \le 2^k \}\).
In this first step of the proof, we define subnetworks to emulate \({{\varvec{x}}}^{\varvec{\nu }}\) for \({\varvec{\nu }}\in \varLambda _{2^{k-1}}\cup \Delta _k\).
We will use that there exists a \(\sigma _r\)-NN \({{\tilde{\times }}}_r\) of depth 1, with input dimension 2 and output dimension 1, which exactly emulates the product operator \({\mathbb R}^2\rightarrow {\mathbb R}:(x,y)\mapsto xy\).
For \(r=2\), this was shown in [17, Lemma 2.1]; for \(r>2\) it follows from [17, Theorem 2.5] and the polarization identity \(xy = \tfrac{1}{4} (x+y)^2 - \tfrac{1}{4} (x-y)^2\), which was used in the proof of [17, Lemma 2.1].
We note that the size of \({{\tilde{\times }}}_r\) depends on r.
Next, for all \(k\in {\mathbb N}\) such that \(\Delta _k\ne \emptyset \) we define the \(\sigma _r\)-NN \(\varPsi _k\) as
where the identity networks have depth 1.
With the convention that \(\varLambda _{1/2}:=\emptyset \), we define \(\varPsi _k\) such that applied to the inputs \(\{{{\varvec{x}}}^{\varvec{\nu }}:{\varvec{\nu }}\in \varLambda _{2^{k-2}}\cup \Delta _{k-1}\}\) the identity networks compute the input values \({{\varvec{x}}}^{\varvec{\nu }}:{\varvec{\nu }}\in \varLambda _{2^{k-1}}\subset \Delta _{k-1}\) and the product networks compute \({{\varvec{x}}}^{\varvec{\nu }}:{\varvec{\nu }}\in \Delta _k\).
This is possible, because \(\varLambda \) is downward closed: for all \({\varvec{\nu }}\in \Delta _k\) and all \({\varvec{\mu }}\le {\varvec{\nu }}\) such that \(2^{k-2}\le |{\varvec{\mu }}|_1\le 2^{k-1}\), we assumed that \({{\varvec{x}}}^{\varvec{\mu }}\) is part of the input of \(\varPsi _k\) (\({\varvec{\nu }}\in \varLambda \) implies \({\varvec{\mu }}\in \varLambda \), hence \({\varvec{\mu }}\in \varLambda _{2^{k-1}}\bigcup \Delta _{k-1}\)).
In particular, there exists \({\varvec{\mu }}\in \Delta _{k-1}\) such that \(|{\varvec{\mu }}|_1 = \left\lceil |{\varvec{\nu }}|_1/2 \right\rceil \). This implies that \(|{\varvec{\nu }}-{\varvec{\mu }}|_1 = \left\lfloor |{\varvec{\nu }}|_1/2 \right\rfloor \) and thus \({\varvec{\nu }}-{\varvec{\mu }}\in \varLambda _{2^{k-2}}\cup \Delta _{k-1}\).
As a result, \({{\varvec{x}}}^{\varvec{\nu }}\) can be computed as \({{\varvec{x}}}^{\varvec{\nu }}= {{\tilde{\times }}}_r({{\varvec{x}}}^{\varvec{\mu }},{{\varvec{x}}}^{{\varvec{\nu }}-{\varvec{\mu }}})\).
Next, we estimate the NN depth and size of \(\varPsi _k\). It holds that \({{\,\mathrm{depth}\,}}(\varPsi _k) = 1\),
Step 2. In this step, we construct \({\tilde{p}}\).
Let \(m := m(\varLambda )\) as defined in Eq. (2.17) and \(k := \min \{k\in {\mathbb N}: 2^k\ge m\}\). In addition, we will write \(p({{\varvec{x}}}) =: \sum _{{\varvec{\nu }}\in \varLambda } t_{{\varvec{\nu }}}{{\varvec{x}}}^{\varvec{\nu }}\).
We define \({\tilde{p}}\) as
where for \(j=1,\ldots ,k\)
where the \(\sigma _r\)-identity network has depth 1.
In addition, denote by \({\varvec{\nu }}^{(i)}\), \(i=1,\ldots ,|\Delta _k|\) an enumeration of \(\Delta _k\) whose order corresponds to the output of \(\varPsi _k\). Then, \({\text {Affine}}\) is a NN of depth 0, input dimension \(|\varLambda _{2^{k-1}}| + |\Delta _k|+1\), output dimension 1, computing the affine transformation
where the constant \(t_{{\varvec{0}}}\) is a NN bias. Thus, \({\text {Affine}}\) ignores the first \(|\varLambda _{2^{k-1}}|\) inputs, takes an affine combination of the then following \(|\Delta _k|\) inputs, and adds the last input.
As a result, \({\tilde{p}}({{\varvec{x}}}) = p({{\varvec{x}}})\) for all \({{\varvec{x}}}\in {\mathbb R}^d\).
To bound the network depth and size, we note that for \(j=1,\ldots ,k\)
We obtain the following bounds on the depth and size of \({\tilde{p}}\): In case \(|\varLambda |=1\), the constant polynomial p can be emulated exactly by a \(\sigma _r\)-NN \({\tilde{p}}\) of depth 0 and size 1.
In case \(|\varLambda |\ge 2\), it holds by Proposition 2.4:

where C, C(r) are independent of d. \(\square \)
Proof of Proposition 4.1
Proof
As in the holomorphic case, to approximate functions \(u\in {{\mathcal {G}}}^\delta ([-\,1,1]^d,C,A)\), we first build a tensor product polynomial approximation by \(H^2\)-projection to the space \(\mathbb {Q}_p\) of polynomials in d variables with coordinatewise degree at most \(p\in {\mathbb N}\). Evidently, \(\mathrm{dim}(\mathbb {Q}_p) = (p+1)^d\).
For \(d=1\), we denote by \(I_3:H^2([-\,1,1],\mu _1) \rightarrow \mathbb {P}_3\) the Hermite interpolation operator defined by \(I_3u(\pm 1) = u(\pm 1)\) and \((I_3u)'(\pm 1) = u'(\pm 1)\) for all \(u\in H^2([-\,1,1],\mu _1)\). For \(p\in {\mathbb N}\), \(p\ge 3\), denote by \(\pi _{p-2,0}: L^2([-\,1,1],\mu _1) \rightarrow \mathbb {P}_{p-2}\) the \(L^2([-\,1,1],\mu _1)\)-orthogonal projection to \(\mathbb {P}_{p-2}\). For all \(v\in L^2([-\,1,1],\mu _1)\) it holds that \(v = \sum _{j=0}^\infty l_j L_j \mapsto \sum _{j=0}^{p-2} l_j L_j =: \pi _{p-2,0}v\), where analogous to (3.8) it holds \(l_j = \int _{[-\,1,1]} v L_j \mathrm {d}\mu _1\). Bounds on Legendre coefficients required in DNN emulation expression rate bounds from Sect. 2.3.3 are implied by stability of \(\pi _{p-2,0}\) in \(L^2([-\,1,1],\mu _1)\):
Based on this projector, we define the \(H^2([-\,1,1],\mu _1)\)-projector \(\pi _{p,2}: H^2([-\,1,1],\mu _1) \rightarrow \mathbb {P}_p\) by \(\pi _{p,2}u (x) = I_3u(x) + \int _{-1}^x\int _{-1}^{y_1}\pi _{p-2,0}((u-I_3u)'')(y_2) \mathrm {d}y_2 \mathrm {d}y_1\) for all \(u\in H^2([-\,1,1],\mu _1)\), as in [8, Sect. A.1], where it is shown that \(\pi _{p,2}u\) satisfies \(\pi _{p,2}u(\pm 1)=u(\pm 1)\) and \((\pi _{p,2}u)'(\pm 1)=u'(\pm 1)\).
For general \(d\in {\mathbb N}\), for all \(p\in {\mathbb N}\), \(p\ge 3\) we consider the tensor product projector \(\varPi ^d_{p,2} := \pi _{p,2}^{(1)}\otimes \cdots \otimes \pi _{p,2}^{(d)}\), where \(\pi _{p,2}^{(i)}\) denotes the coordinate-wise projection with respect to \(x_j\), \(j=1,\ldots ,d\). We recall stability and error bounds in terms of the \(H^2_{{{\,\mathrm{mix}\,}}}([-\,1,1]^d,\mu _d)\)-norm, which is defined as
By the continuous embedding \(H^2_{{{\,\mathrm{mix}\,}}}([-\,1,1]^d,\mu _d) \hookrightarrow W^{1,\infty }([-\,1,1]^d)\), the bounds below imply error bounds w.r.t. the \(W^{1,\infty }([-\,1,1]^d)\)-norm. By [31, Propositions 5.2 and 5.3], the former of which is [8, Theorem A.1 and Proposition A.1], for all \(u\in {{\mathcal {G}}}^\delta ([-\,1,1]^d,C,A)\) it holds for all \(p\in {\mathbb N}\), \(p\ge 3\) and for all \(s\in \{2,\ldots ,p-1\}\)
We fix \(\alpha = (4\max \{A,1\})^{-1/\delta } \in (0,1)\) and similar to [12, Proposition 4, Equation (40)] substitute \(s = \max \{2,\left\lfloor \alpha p^{1/\delta } \right\rfloor \}\). For sufficiently large \(p\in {\mathbb N}\) it holds that \(2\le \alpha p^{1/\delta }\) and thus \(s \le \alpha p^{1/\delta } \le s+1\). The estimates that follow are derived under this assumption, but hold for all \(p\ge 3\) after possibly increasing multiplicative constants. With Stirling’s inequality, \(\sqrt{2\pi } \sqrt{n} (n/e)^n \le n! \le e \sqrt{n} (n/e)^n\) for \(n\in {\mathbb N}\), we estimate the square of the right-hand side of (B.1):
where we used \(((s+2)!)^{2\delta } \le (s+2)^{4\delta } (s!)^{2\delta }\). Now, since \(1-\delta \le 0\) and \(p-1-s+\frac{1}{2}\ge 0\) for \(s<p\),
due to \(s\le \alpha p^{1/\delta }\). Using that there exists \(C>0\) depending on \(\delta \) such that \(s^\delta (s+2)^{4\delta } \le C 2^{2s}\) for all \(s\ge 2\), we arrive at
Substituting into (B.1) shows that
Now, \(\varPi ^d_{p,2}u\) can be approximated by ReLU DNNs from Proposition 2.13. We set \(\varLambda _p := \{{\varvec{\nu }}: | {\varvec{\nu }} |_{\infty }\le p\}\), and express \(\varPi ^d_{p,2}u\) in the basis of tensor product Legendre polynomials. The size of the Legendre coefficients \((c_{{\varvec{\nu }}})_{{\varvec{\nu }}\in \varLambda _p}\) of \(\varPi ^d_{p,2}u\) can be estimated crudely by \(|c_{{\varvec{\nu }}}|^2 \le \sum _{{\varvec{\nu }}\in \varLambda _p} |c_{{\varvec{\nu }}}|^2 = \left\| \varPi ^d_{p,2}u \right\| _{L^2({[-\,1,1]^d},\mu _d)}^2 \le C(d) \left\| u \right\| _{H^2_{{{\,\mathrm{mix}\,}}}({[-\,1,1]^d},\mu _d)}^2 = C(d,u)^2\) for all \({\varvec{\nu }}\in \varLambda _p\), and their sum by \(\sum _{{\varvec{\nu }}\in \varLambda _p} |c_{{\varvec{\nu }}}| \le C(d,u) (p+1)^d\).
As in Step 1 in the proof of Theorem 3.6, we reapproximate the polynomial \(\varPi ^d_{p,2}u\) by \(\hat{u}_p := {\text {Affine}}_u\circ {{\varvec{f}}}_{\varLambda _p,\epsilon }\), for \({{\varvec{f}}}_{\varLambda _p,\epsilon }\) from Proposition 2.13 and \({\text {Affine}}_u:{\mathbb R}^{|\varLambda _p|}\rightarrow {\mathbb R}: (z_{{\varvec{\nu }}})_{{\varvec{\nu }}\in \varLambda _p}\mapsto \sum _{{\varvec{\nu }}\in \varLambda _p} c_{{\varvec{\nu }}}z_{{\varvec{\nu }}}\). We take \(\epsilon = (p+1)^{-d} \exp (-\log (2)\alpha p^{1/\delta })\) as the accuracy parameter of \({{\varvec{f}}}_{\varLambda _p,\epsilon }\), so that we obtain
Together with the estimate of the polynomial interpolation error, it holds that
We finally estimate the NN depth and size, using that \(|\varLambda _p|=(p+1)^d\) and \(m(\varLambda _p) = dp\):
for some \(C_1(\alpha )>0\). For all \({{\mathcal {N}}}\in {\mathbb N}\) satisfying \({{\mathcal {N}}}\ge C_1(\alpha )d^4(4^2+4^{d+1/\delta })\), we choose \(p := \max \{p\in {\mathbb N}: C_1(\alpha )d^4 ((p+1)^2+(p+1)^{d+1/\delta }) \le {{\mathcal {N}}}\}\), so that \(p\ge 3\) and
and define \({\tilde{u}}_{{{\mathcal {N}}}} := \hat{u}_p\), which shows the proposition for such \({{\mathcal {N}}}\). For the finitely many \({{\mathcal {N}}}\in {\mathbb N}\) satisfying \({{\mathcal {N}}}< C_1(\alpha )d^4(4^2+4^{d+1/\delta })\), we define \({\tilde{u}}_{{\mathcal {N}}}:= 0\), for which the proposition holds after increasing the constants, if necessary. This completes the proof of Proposition 4.1. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Opschoor, J.A.A., Schwab, C. & Zech, J. Exponential ReLU DNN Expression of Holomorphic Maps in High Dimension. Constr Approx 55, 537–582 (2022). https://doi.org/10.1007/s00365-021-09542-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00365-021-09542-5