Introduction

Engineering components are typically designed to operate under nominally elastic loading conditions. However, localized plasticity can occur in the vicinity of stress concentrations at unintentional internal defects—particularly in metallic materials, developing into larger scale damage under repeated loading or over long service lifetimes [4, 23]. Under these conditions, the details of the polycrystalline microstructure, i.e., the presence of texture, annealing twins, or clusters of elastically stiff or compliant grains, can influence macroscopic mechanical properties [5, 22, 25]. It has been known for decades that microstructure plays a central role in determining the local onset of yielding and the eventual failure of components, but quantifying cause and effect has been slow due to limitations in experimental and computational capabilities. In recent years, however, the advances in 3D materials science instrumentation [14, 27] have enabled researchers to generate \(\hbox {mm}^3\)-scaled multimodal microstructural datasets that in conjunction with finite element methods, link microstructure to properties.

The microstructural datasets are one part of a comprehensive methodology that continues with building virtual samples, simulating their loading and ultimately parsing correlations from the collective results. Software tools like Dream.3D [21] and Neper [36, 37] are available to construct virtual samples directly from the characterization data. Using crystal-scale finite element formulations, the mechanical behavior of polycrystalline virtual samples can be explored to better understand the role of microstructure on localized plasticity and failure. For example, the finite element code FEpX has been previously used to evaluate the bounds of strength, elastic modulus, and ductility in \(\alpha +\beta \) titanium by screening a range of instantiated samples with different microstructures [7, 8, 15]. Progress at-large is facilitated by improvements made across the experimental and computational workflows that support endeavors such as Integrated Computational Materials Engineering (ICME) [10] and the Materials Genome Initiative (MGI) [13].

In the context of expanding the toolsets available to researchers in the ICME arena, this paper presents the description and implementation of MechMet. MechMet is an open-source finite element code for computing the elastic strains and stresses within a virtual sample for the convenient calculation of mechanical metrics in the elastic regime. The term ’metric’ is employed here to indicate a standardized measure of a response or behavior for making quantitative comparisons within or among samples of a material. One well-known metric, for example, is the Schmid factor for individual crystals that facilitates comparing the relative strengths of crystals across a polycrystal for prescribed loading conditions. This is one of many metrics for polycrystalline materials; others are possible that also incorporate a crystal’s mechanical environment.

MechMet supplements more complete elasto-plastic polycrystal finite element codes, such as FEpX [11], by computing useful metrics based on elastic analyses together with knowledge of the slip system strengths. Virtual samples for use with these finite element codes are often reconstructed from 3D maps of lattice orientations generated using EBSD-based TriBeam tomography [18] or X-ray-based high-energy diffraction microscopy (HEDM) [29, 35]. Rather than limiting the examination of these characterization data to microstructural metrics alone (such as grain geometry and topology), estimates of mechanical properties such as stiffness and strength can also be obtained using virtual, finite element specimens that are based on the grain maps themselves or on novel structural deviations in microstructure. Using open-source software such as Neper or Dream.3D, virtual samples derived from a 3D dataset can be loaded and the full stress tensor computed for each crystal. With the stress tensor projected onto the slip systems, it is possible to estimate the crystal-scale yield strength. Similarly, the anisotropic single crystal elastic moduli can be estimated using a comparison of the response of a loaded virtual sample created from a near-field HEDM dataset to the lattice strains from the far-field HEDM experiment.Footnote 1 Within the context of ICME and component design, MechMet could also be used for the fast assessment of the variability in properties (especially for properties driven by the early elastic loading condition, such as fatigue) or in the evaluation of the sensitivity of components with a limited number of grains (including MEMS devices, protective coatings, additively manufactured ligaments and thin-walled structures) and their deviation from “bulk” mechanical response [7, 8, 15, 16].

MechMet is a stand-alone MATLAB-based finite element package that works with two other resources: (1) virtual polycrystal instantiation and meshing tools for preparing the input data (in particular, Neper) and (2) visualization/interpretation tools (in particular, Paraview [1] or VisIt [9]) for examination of the output data. The code executes on commonly-available laptop or desktop computers, but scales well for use on a high performance computing cluster, which will be discussed in more detail. First, the underlying mechanics employed by MechMet is presented. This is followed with several applications that are intended to provide an overview of its capabilities and to demonstrate its use on targeted polycrystalline materials applications.

Theory and Implementation

The MechMet implementation solves field equations for elasticity using the finite element method. One of several basic loading modes may be applied to a virtual sample to generate a continuous displacement field over the sample. From the computed displacement field, strain and stress fields are determined, which serve as the input data required to determine a number of mechanical metrics. The metrics are organized into two groups: ones based solely on the (elastic) stiffness and ones based on a combination of stiffness and strength. The results (displacement, strain, stress and mechanical metrics) are written to a file that may be used for visualization or additional analyses. Outlined in the following subsections are: the governing equations that are solved to determine the displacement fields, a range of mechanical metrics that distill the field data into useful materials parameters, and the finite element formulation used.

Governing Equations

MechMet solves the field equations for the elastic motion of a polycrystalline body. The motion is defined by the displacement field, \(\varvec{u}(\varvec{x})\), which is assumed to be continuous and is limited to linear kinematics. The displacement field arises as a consequence of the application of loads and varies over the domain of the body as a function of position, \(\varvec{x}\). The displacements are sufficiently small that the deformed configuration of the body is sufficiently close to the undeformed configuration. The two may be used interchangeably without introducing significant error, and there is no need to distinguish between them further. Under these restrictions, the strains and rotations derived from the displacement field must be small. Further, there cannot exist discontinuities in the motion such as might occur around a crack.

The strain tensor, \(\varvec{\epsilon }\), is derived from the displacement field:

$$\begin{aligned} \varvec{\epsilon }= {{\,\mathrm{symm}\,}}( {\mathrm{grad }}\varvec{u}) \end{aligned}$$
(1)

and used in Hooke’s law to determine the stress, \({\varvec{\sigma }}\):

$$\begin{aligned} {\varvec{\sigma }}= \varvec{{{\mathcal {C}}}}(\varvec{r})\varvec{\epsilon }\end{aligned}$$
(2)

where \(\varvec{{{\mathcal {C}}}}(\varvec{r})\) is the anisotropic elasticity tensor, which depends on the orientation of the crystallographic lattice with respect to a sample frame. The orientation is parameterized by the Rodrigues vector, \(\varvec{r}\):

$$\begin{aligned} \varvec{r} = \varvec{n} \tan \frac{\phi }{2} \end{aligned}$$
(3)

where \(\varvec{n}\) is the (unit) axis of rotation and \(\phi \) is the angle of rotation from the sample axes to the crystal axes. The linear, anisotropic behaviors represented by \(\varvec{{{\mathcal {C}}}}(\varvec{r})\) presently are limited to two crystal classes: cubic and hexagonal. Generally, the materials this code was designed and optimized for will exhibit high stiffness to strength (on the order of 100-1000) so that the strains are always small within the elastic regime. No attempt is made to determine if a computed stress state violates the yield condition. Rather, the body remains elastic regardless of the level of stress computed.

The computed motion is required to satisfy equilibrium over the body’s volume, V:

$$\begin{aligned} {\mathrm{div}}{{\varvec{\sigma }}}^T + {\varvec{\iota }} = 0 \end{aligned}$$
(4)

where \(\varvec{\iota }\) is the body force vector. No dynamic effects are included. MechMet assumes that the body forces are negligible in comparison with loads applied to the surface, S, through imposed tractions or displacements. Respectively, these are specified as natural and essential conditions:

  • Natural boundary conditions (applied on \(S_T\)):

    $$\begin{aligned} \varvec{T}= \varvec{{{\bar{T}}}} \end{aligned}$$
    (5)

  • Essential boundary conditions (applied on \(S_u\)):

    $$\begin{aligned} \varvec{u}= \varvec{{{\bar{u}}}} \end{aligned}$$
    (6)

Mechanical Metrics

The solution of the field equations for prescribed boundary conditions gives the displacement field over the body. From spatial gradients of this field, the strain tensor is computed over the body. Using Hooke’s law, the stress tensor is computed from the strain, again over the body’s volume. The stress and strain fields provide the necessary quantities to evaluate several mechanical metrics. The metrics reflect two attributes of polycrystalline solids: (1) the single-crystal mechanical properties of stiffness and strength and (2) the local responses within individual grains (crystals) that are dependent on the grain interactions that occur during loading. The single-crystal mechanical properties are already known and are inputs to the MechMet analyses. The local responses are drawn from the solution and thus reflect the heterogeneity of stress and strain due to anisotropy of the single crystal mechanical properties.

Two categories for mechanical metrics are determined: ones based on stiffness alone and ones based on a combination of stiffness and strength. Stiffness describes the incremental increase is stress (load) associated with an incremental increase in strain (displacement). As MechMet computes only the elastic response, the stiffnesses are likewise elastic. In contrast, the strength represents a bound on the purely elastic regime. Given information about the yield surface of constituent crystals in the form of slip system strengths, it is possible to estimate the onset of yielding, or equivalently the limit of a purely elastic response, at points within a polycrystal. The second category of metrics, which combine slip system strength information with stiffness information, provide insight into the onset of yielding. The following subsections are devoted to these categories, respectively.

Stiffness-based Metrics

The single-crystal stiffness is the anisotropic elasticity tensor, \(\varvec{{{\mathcal {C}}}}(\varvec{r})\), appearing in Eq. 2. In matrix form, Hooke’s law for cubic symmetry takes the form:

$$\begin{aligned} \left\{ \begin{array}{c} \sigma _{11} \\ \sigma _{22} \\ \sigma _{33} \\ \sigma _{23} \\ \sigma _{13} \\ \sigma _{12} \end{array} \right\}= & {} \left[ \begin{array}{c c c c c c} C_{11} &{} C_{12} &{} C_{12} &{} &{} &{} \\ C_{12} &{} C_{11} &{} C_{12} &{} &{} &{} \\ C_{12} &{} C_{12} &{} C_{11} &{} &{} &{} \\ &{} &{} &{} C_{44} &{} &{} \\ &{} &{} &{} &{} C_{44} &{} \\ &{} &{} &{} &{} &{} C_{44} \end{array} \right] \left\{ \begin{array}{c} \epsilon _{11} \\ \epsilon _{22} \\ \epsilon _{33} \\ \gamma _{23} \\ \gamma _{13} \\ \gamma _{12} \end{array} \right\} \nonumber \\&\quad {\mathrm{Cubic \, Symmetry}} \end{aligned}$$
(7)

when written in bases tied to the crystallographic axes. Here Voigt notation is used, strength-of-materials convention for shears (\(\gamma _{12}=2 \epsilon _{12}\), etc.), and blank entries are zeros. A similar matrix exists for hexagonal crystals that takes into account the hexagonal symmetries [30].

For the stiffness metrics, the focus is on directional stiffness—or directional Young’s modulus, which relates the axial stress to the axial strain under presumption of uniaxial stress. To extract this from the elasticity tensor, it is convenient to invert the stiffness matrix in Eq. 7 to obtain the compliance matrix:

$$\begin{aligned} \left\{ \begin{array}{c} \epsilon _{11} \\ \epsilon _{22} \\ \epsilon _{33} \\ \gamma _{23} \\ \gamma _{13} \\ \gamma _{12} \end{array} \right\}= & {} \left[ \begin{array}{c c c c c c} S_{11} &{} S_{12} &{} S_{13} &{} &{} &{} \\ S_{12} &{} S_{22} &{} S_{12} &{} &{} &{} \\ S_{13} &{} S_{12} &{} S_{33} &{} &{} &{} \\ &{} &{} &{} S_{44} &{} &{} \\ &{} &{} &{} &{} S_{44} &{} \\ &{} &{} &{} &{} &{} S_{44} \end{array} \right] \left\{ \begin{array}{c} \sigma _{11} \\ \sigma _{22} \\ \sigma _{33} \\ \sigma _{23} \\ \sigma _{13} \\ \sigma _{12} \end{array} \right\} \nonumber \\&\quad {\mathrm{Cubic \, Symmetry}} \end{aligned}$$
(8)

The directional stiffness is readily obtained as the reciprocal of the appropriate diagonal of the compliance. For instance, the directional Young’s modulus in the \(x_1\) direction is simply: \(1/S_{11}\). Typically, it is the directional modulus in a sample direction that is of interest, so the stiffness matrix is transformed from the crystal basis to the sample basis.

In anisotropic polycrystals, the stress and deformation are heterogeneous, implying that the local stress and strain do not equal the nominal (average) stress and strain everywhere. MechMet characterizes these local variations with a metric called the embedded directional stiffness. This metric is calculated by dividing the average stress by the local (FEM) strain in each element. For tensile loading in the \(x_1\) direction, for example, the embedded directional stiffness, \({{\hat{E}}}\), is defined by:

$$\begin{aligned} {{\hat{E}}} =\frac {{{\bar{\sigma }}}_{11}} {\epsilon _{11}} \end{aligned}$$
(9)

where \({{\bar{\sigma }}}_{11}\) is the average value of \(\sigma _{11}\) over the polycrystal. The adjective “embedded” is employed here to emphasize that the metric applies to individual crystals within a polycrystal and thus includes the effect of grain interactions. This is in contrast to the single-crystal (S-X) directional stiffness, which is the reciprocal of a diagonal component of the compliance matrix, so therefore the S-X stiffness does not depend on any local variables beyond the crystal orientation of each element.

The embedded stiffness is analogous to the experimentally determined diffraction modulus (or diffraction elastic moduli), which is the nominal stress divided by the lattice strain (usually for all crystals on the same crystallographic fiber). Neutron and X-ray diffraction methods exploit diffraction moduli for applications like residual stress determination. There exists an extensive literature in this regard; here we cite a few articles that are helpful for seeing the similarity of the embedded stiffness to the diffraction modulus [2, 20, 43].

For comparison purposes, another metric is calculated in MechMet. This metric is the ratio of the embedded stiffness to the single-crystal directional stiffness, and is labeled with its acronym: RE2SX (Ratio of Embedded stiffness To S-X stiffness). For tensile loading in the \(x_1\) direction,

$$\begin{aligned} {\mathrm{RE2SX}} =\frac{{{\hat{E}}}}{1/S_{11}} \end{aligned}$$
(10)

This metric indicates how the apparent stiffness of a crystal embedded within a polycrystal is responding to load in comparison with a crystal of like orientation under the same load but loaded in isolation.

Strength+Stiffness-based Metrics

Metrics that embody both stiffness and strength are useful for assessing the onset of plastic yielding in polycrystals. There are several traditional metrics for strength alone—the Schmid and Taylor factors, for example. The Schmid factor expresses the ratio of the resolved shear stress on a slip system to the applied stress, typically under conditions of uniaxial stress [24].

$$\begin{aligned} \kappa = \tau ^k/ \sigma _{applied} \end{aligned}$$
(11)

where the resolved shear stress, \(\tau ^k\), is computed from the local stress and the symmetric portion of the Schmid tensor, \(p^k\), as:

$$\begin{aligned} \tau ^k = {\text{tr}} (p^k \sigma) \end{aligned}$$
(12)

\(\sigma _{applied}\) is the dominant component of the stress, such as the axial component in a uniaxial stress state. In evaluating the Schmid factor, MechMet currently invokes one family (octahedral) of slip systems for FCC crystals, three families (basal, prismatic, and pyramidal) for HCP crystals, and either one family of \(\{110\} <111>\) or four families of \(\{110\} <111>\), \(\{112\} <111>\), \(\{123\} <111>\), \(\{134\} <111>\) for BCC crystals—with varying slip system strengths. If the Schmid factor is high for a slip system, then that system is heavily loaded and is more likely to experience slip (yielding) than other slip systems with lower Schmid factors. For crystals with a single value of slip system strength for all slip systems, if the minimum value of the Schmid factor taken over all the slip systems is high in comparison with other crystals within the polycrystal, then that crystal can be thought of as having low strength. Conversely, a crystal with high relative strength is one with low Schmid factor. Thus, the reciprocal Schmid factor is a metric of strength. If the slip systems possess different strengths, then rescaling of the Schmid factor by the relative strength must occur before ranking the relative strengths of the crystals. The rescaled Schmid factors are referred to as relative Schmid factors in MechMet.

As with the S-X stiffness, the Schmid factor is a local quantity (or requires the assumption that the local stress is the same as the nominal stress). Thus it lacks information regarding spatial heterogeneity of stress that arises from grain interactions in anisotropic polycrystals. This is important for yielding because the onset of yielding is dictated by the ratio of the active stress to the strength. Namely, yielding initiates when the stress reaches the strength. To account for this, the level of stress within a crystal must be considered along with the strength. As has been demonstrated for polycrystalline and polyphase solids, the ratio of the directional strength-to-stiffness provides a useful metric for static and cyclic loading (Wong and Dawson 2011).

An effective approach for computing the directional strength-to-stiffness is to use the apparent stiffness, as it directly accounts for a specific arrangement of grains and thus offers an explicit quantification of the crystallographic neighborhoods within a polycrystal. The approach developed by Wong et al [45] for uniaxial loading was extended to multiaxial stress states in Poshadel et al [33, 34] and forms the basis for the metrics computed in MechMet.

Based on the preceding discussion, MechMet offers two metrics for analyzing the onset of yielding. First, the Schmid factor is provided. This is modified from the definition above to account for different strength being associated with the slip system families. The relative Schmid factor is computed as the ratio of the resolved shear stress for unit stress to the relative slip system strength. This is equivalent to the ratio of the Schmid factor to the relative slip system strength. Second, the directional strength-to-stiffness ratio (\({\mathrm{Y2E}}\)) is computed as the product of the nominal strain and the slip system strength, divided by the actual resolved shear stress:

$$\begin{aligned} {\mathrm{Y2E}} = \frac{{{\bar{\epsilon }}} {{\hat{\tau }}}^k}{\tau ^k} \end{aligned}$$
(13)

Here \({{\bar{\epsilon }}}\) is the nominal (average) strain and \({{\hat{\tau }}}\) is the slip system strength of the most relevant slip system. This formula is rigorously shown to give the directional strength-to-stiffness ratio for multiaxial stress states in [33].

Together the two metrics offered by MechMet provide the capability to analyze microstructures in terms of either a single-crystal measure of strength or a combination of stiffness and strength. The latter \({\mathrm{Y2E}}\) metric has the advantage of including the influence of local neighborhood, which is critical in anisotropic media exhibiting heterogeneous responses under mechanical loading.

Finite Element Implementation

MechMet employs a standard finite element formulation to solve the elasticity field equations. A residual, \(R_u\), is formed over the volume from the local form of equilibrium given in Eq. 4:

$$\begin{aligned} R_u = \int _{V} \varvec{\psi } \cdot \left( {\mathrm{div}}{{\varvec{\sigma }}}^T + {\varvec{\iota }}\right) {\mathrm {d}}{V} \end{aligned}$$
(14)

where \(\varvec{\psi }\) are the weights. The body forces are shown here but are presently neglected. Equation 14 is transformed to the weak form by integration by parts and application of the divergence theorem to give:

$$\begin{aligned} R_u= & {} - \int _V \; {\mathrm{tr}}\left( {{\varvec{\sigma }}}^{\mathrm{T}}\,{\mathrm{grad }}\varvec{\psi } \right) {\mathrm {d}}{V} +\int _{S_T} \varvec{t} \cdot \varvec{\psi }\, {\mathrm {d}}{S} \nonumber \\&+\int _{V} \varvec{\iota } \cdot \varvec{\psi }\, {\mathrm {d}}{V} \end{aligned}$$
(15)

The finite element matrix equation for the displacement field is generated from the weak form of the residual by introduction of the interpolation (trial) functions for the displacement field and the weights. MechMet utilizes isoparametric elements for this purpose. The mapping of the coordinates of points is specified by interpolation functions, \(\Big [ \,{\mathsf {N}}(\xi , \eta , \zeta ) \,\Big ]\), and the coordinates of the nodal points, \(\left\{ X \right\} \):

$$\begin{aligned} \left\{ x \right\} = \Big [ \,{\mathsf {N}}(\xi , \eta , \zeta ) \,\Big ]\left\{ X \right\} \end{aligned}$$
(16)

where \((\xi , \eta , \zeta )\) are local coordinates within an element. The same mapping functions are used for the solution (trial) functions and the weights:

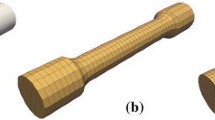
$$\begin{aligned} \Big \{ u \Big \} = \Big [ \,{\mathsf {N}}(\xi , \eta , \zeta ) \,\Big ]\Big \{ {\mathsf {U}} \Big \}\quad {\mathrm{and}} \quad \Big \{ \psi \Big \} = \Big [ \,{\mathsf {N}}(\xi , \eta , \zeta ) \,\Big ]\Big \{ { \Psi } \Big \} \end{aligned}$$
(17)

MechMet uses a 10-node, tetrahedral, serendipity element, as shown in Fig. 1. This \(C^0\) element provides pure quadratic interpolation of the displacement field.

Fig. 1
figure 1

10-node tetrahedral element with quadratic interpolation of the velocity, shown in the parent configuration and bounded by a unit cube

Full size image

The strain is written using the spatial derivatives (derivatives with respect to \(\varvec{x}\)) of the mapping functions and the nodal displacements as:

$$\begin{aligned} \Big \{ \mathsf {\epsilon } \Big \} = \Big [ \,{\mathsf {B}} \,\Big ]\Big \{ {\mathsf {U}} \Big \}\end{aligned}$$
(18)

Following standard procedures for isoparametric elements [41], \(\Big [ \,{\mathsf {B}} \,\Big ]\) is computed using the derivatives of \(\Big [ \,{\mathsf {N}}(\xi , \eta , \zeta ) \,\Big ]\) with respect to local coordinates, \((\xi , \eta , \zeta )\), together with the Jacobian of the mapping specified by Eq. 16. The same procedure is used to evaluate spatial gradients of the weights. Substitution of the trial and weight functions into Eq. 15 delivers a matrix equation for the nodal displacements:

$$\begin{aligned} \Big [ \,{\mathsf {K}}\,\Big ]\Big \{ {\mathsf {U}} \Big \}= {\mathsf {F}} \end{aligned}$$
(19)

where \(\Big [ \,{\mathsf {K}}\,\Big ]\) and \({\mathsf {F}}\) are the assembled versions of the elemental stiffness and force matrices:

$$\begin{aligned} \Big [ \,{\mathsf {k}}^{ e}\,\Big ]= & {} \int _{V^{ e}} \Big [ \,{\mathsf {B}} \,\Big ]^{\mathrm{T}}\Big [ \,{\mathsf {C}} \,\Big ]\Big [ \,{\mathsf {B}} \,\Big ]{\mathrm {d}}{V}\end{aligned}$$
(20)
$$\begin{aligned} \Big \{ {\mathsf {f}}^{ e}\Big \}= & {} \int _{S^{ e}_T} \Big [ \,{\mathsf {N}} \,\Big ]^{\mathrm{T}}\Big \{ T \Big \} \, {\mathrm {d}}{S} \end{aligned}$$
(21)

where, again, the body forces have been neglected.

Stress Recovery Procedure

The solution of Eq. 19 gives the nodal point displacements for the finite element representation of the displacement field over the entire body. The elements used in MechMet have \(C^0\) continuity, meaning that the displacement is continuous across (and within) elements, but the spatial derivatives of displacement are not continuous across element boundaries. The strain is defined in terms of the spatial derivatives according to Eq. 18, and thus is not smooth across element boundaries. Likewise, the stress is not smooth across element boundaries as it is linearly related to the strain and shares the same representation attributes. It is common in finite element analyses to perform post-solution operations, often called stress recovery, on derivative quantities both to estimate the potential error in a solution and to improve the quality of the derivative quantities [48].

In MechMet, stress recovery is performed using a methodology that is adapted for polycrystalline samples. Polycrystalline samples are comprised of subdomains of the entire body that correspond to the separate grains. The grains have anisotropic mechanical properties that are inherited from the crystal structure. In the absence of crack-like discontinuities of the motion, the displacements are continuous at grain boundaries. However, mechanics principles allow for the presence of stress discontinuities that do not influence the tractions at the grain boundaries (for equilibrium tractions will be continuous across interfaces). The smoothing of the stress begins with the representation of stress with smooth functions. A convenient choice is the finite element interpolation functions used for the displacement field which, as mentioned before, exhibit \(C^0\) continuity. Each component of the stress is treated as a scalar field, \(a(\varvec{x})\), represented over an element according to:

$$\begin{aligned} a(\varvec{x}) = [N(\varvec{x})] \{ A \} \end{aligned}$$
(22)

Like the displacement field, the scalar field is continuous within and between elements. The nodal point values, \(\{ A \}\), are determined from a weighted residual cast over the element:

$$\begin{aligned} R_i = \int _{V^{ e}} {{\tilde{\psi }}}(\varvec{x}) \left[ \{a(\varvec{x}) - [N(\varvec{x})] \{ A\}\}\right] \, {\mathrm {d}}{V} \end{aligned}$$
(23)

where \({{\tilde{\psi }}}(\varvec{x})\) is the weighting function. Standard finite element procedures are followed to develop a matrix equation for the nodal point stresses from Eq. 23:

$$\begin{aligned} \left[ L \right] \{ A \}= & {} \{ J \}\end{aligned}$$
(24)
$$\begin{aligned} \left[ L^e \right]= & {} \int _{V^{ e}} \ [ N(\varvec{x})]^T [ N(\varvec{x})] {\mathrm {d}}{V} \end{aligned}$$
(25)

and

$$\begin{aligned} \{ J^e \} = \int _{V^{ e}} [ N(\varvec{x})]^T a(\varvec{x}) {\mathrm {d}}{V} \end{aligned}$$
(26)

The data necessary to evaluate the \(J^e\) matrix is available at the element’s quadrature points using the computed displacement field. The solution to this equation gives the nodal values that provide an optimal fit to the spatial distribution embodied in the raw (quadrature point) stress values independently for each element. If the range in values over any element is deemed too large, a penalty is applied to suppress high gradients within the element. This is done by appending a penalty term to \(\left[ L^e \right] \):

$$\begin{aligned} \left[ P^e \right] \,=\, \int _{V^{ e}} \alpha _d [ N^{\prime }(\varvec{x})]^T [N^{\prime }(\varvec{x})]{\mathrm {d}}{V} \end{aligned}$$
(27)

The damping factor, \(\alpha _d\), is increased until the nodal point variations are less than the quadrature point variations. The stress has six independent components, which dictates that there are six stress degrees-of-freedom at each nodal point of the mesh over a grain.

For nodal points shared by multiple elements, the values from contributing elements are simply averaged to determine the nodal point value for the complete mesh. This provides a unique value for each nodal point and thereby restores continuity of the field across elements. However, as the intent is to smooth the stress components independently for each grain, a modification of the original mesh is necessary so that elements from different grains do not share nodal points. This modification to the mesh involves duplicating nodes at the grain boundaries and recomputing the connectivity arrays. These changes are made after the displacement field is determined using a mesh with continuity of displacement across grain boundaries.

Code Access and Execution

The MechMet source code is available at the GitHub repository: https://github.com/dplab/MechMet.

In addition to the source code, example files and input instructions are provided. Executing MechMet requires the following information in the form of input files:

  1. 1.

    tessellation data for the virtual polycrystal that provides phase and grain identification and lattice orientations of the grains (typically generated with Neper);

  2. 2.

    an associated mesh of the virtual polycrystal sample (also generated with Neper);

  3. 3.

    the single-crystal properties (elastic moduli and slip system strengths) for all phases (compiled by the user). Currently, users may designate cubic or hexagonal crystal symmetry.

Users may choose from a menu of loading options that include:

  1. 1.

    uniaxial extension or compression in any of the coordinate directions (with traction-free lateral surfaces) or

  2. 2.

    biaxial extension or compression in two coordinate directions (with a traction-free condition on the remaining surfaces).

MechMet automatically determines the surface displacement needed to impose a nominal strain of 0.001. Users are prompted for an output file name for recording data in a format handled by the visualization packages (namely, a VTK file).

Onset of Yielding in Ti-7Al with MechMet: A Generic Application

Often a goal of a material-focused investigation is to correlate microstructural features with the intensity of stress and deformation under load. Grain boundaries and the lattice misorientations across grain boundaries are features that are frequently examined as the mismatch of properties that accompany these features can contribute to zones of elevated stresses in their vicinity. However, the particular spatial locations in the microstructure that present elevated stresses depend on the type of loading. Specific grain boundaries where stresses are high under tensile loading in one sample direction, for example, may well be quite unremarkable under tensile loading in a perpendicular direction. The mechanical metrics computed in MechMet do depend on the loading mode and direction and thus provide guidance for interpreting observed mechanical responses and for hypothesizing how a sample might respond under different loading. This Ti-7Al example demonstrates various capabilities of MechMet for quantifying the onset and progression of yielding. Stress distributions are provided along with mechanical metrics both for stiffness and for the combination of stiffness and strength. Together these are used to better understand the differences in predicted responses for the same sample subjected to two different loading modes.

A single-phase (hexagonal) Ti-7Al alloy was characterized in 3D with synchrotron high energy X-ray diffraction microscopy (HEDM) [31] at the Cornell High Energy Synchrotron Source (CHESS) and reconstructed using new methods that couple with lattice strain measurements collected with synchrotron high-energy X-ray diffraction (far-field HEDM) [29]. Figure 2a shows the HEDM 3D voxelized grain data. Figure 2b shows the Neper tessellated mesh of the voxel map, together with the finite element discretization. This tessellation has a total of 442 grains. Planar grain boundaries are evident along with the lattice orientations. An associated finite element mesh was also generated with Neper with 309,622 2nd-order tetrahedral elements and 430,376 nodal points. This mesh was used both for the computation of mechanical metrics with MechMet and for the simulation of plastic deformation patterns with an elasto-viscoplastic finite element model presented later. The grains were assigned elastic moduli and relative slip system strengths that had previously been evaluated for the hexagonal close-packed phase of a similar alloy of titanium (Ti-6Al-4V) [12, 32, 44]. The S-X elastic moduli and slip system strengths are summarized in Table 1 and Table 2.

Table 1 Single-crystal elastic constants used for Ti-7Al.
Full size table
Table 2 Initial slip system strengths used for Ti-7Al, including relative ratios normalized by each set’s basal strength. \(g_{0,b}\), \(g_{0,p}\) and \(g_{0,\pi }\) are the initial slip system strengths of the basal, prismatic, and pyramidal slip systems, respectively.
Full size table

The mechanical attributes of the sample were compared with MechMet for two loading conditions: axial extension in the x-direction and in the z-direction. The loading is applied in the simulation by displacing one boundary of the sample in the direction of its normal by the amount needed to impose an average axial strain of 0.1%. The sample’s lateral surfaces are traction-free. Plots of the grain-by-grain single-crystal directional stiffness (Young’s modulus in the extension direction) for the two loading conditions are presented in Fig. 2c, d. The presence of the elastic anisotropy is evident from the substantial color changes in many grains. A crystal is comparatively more or less compliant under different loading modes because the orientation of the loading axis with respect to the crystallographic axes changes with the loading mode.

Fig. 2
figure 2

MechMet simulations are performed on a mesh generated from an HEDM 3D reconstruction of a Ti-7Al sample, shown in a with inverse pole figure (IPF) coloring of the grain orientations, referenced to the y-direction. b Neper tessellation showing the generated finite element mesh with arbitrary grain coloring. Grain-by-grain single-crystal directional stiffness c for x-direction extension and d for z-direction extension as shown in the figure legend

Full size image

Figure 3a,b depicts the distributions of the axial stress component associated with the two loading conditions. The spatial heterogeneity of the stress distributions (and elastic strain distributions, as well) under nominally homogeneous deformations are a direct consequence of the anisotropic elastic properties at the crystal scale. The directional single-crystal stiffness distributions were presented for the two loading cases in Fig. 2 and offer a possible explanation that grains with higher directional stiffness should exhibit higher stress. However, this does not adequately explain the observed heterogeneity of the stress. First, unlike the single-crystal stiffness, the stress is not uniform within the grains and, second, the stresses do not exhibit the same grain-to-grain proportionality as the stiffness. These are a consequence of the neighborhood effects—namely that the traction applied to a grain across the boundary with its neighbor depends on the relative stiffness of grains in the vicinity, or neighborhood, of that boundary.

A simple rule for quantifying neighborhood effects is not known, although the effects can be examined with a stiffness-based metric for the sample such as the embedded stiffness described in Sect. 2.2 and shown in Fig. 3c,d. As discussed in Sect. 2.2, the embedded stiffness differs qualitatively from the single-crystal directional stiffness distribution in that it is based on the local strain and the nominal stress. It gives a measure of the apparent stiffness of a volume of material within a grain embedded within the sample. It is evident from comparing the plots of single-crystal and embedded stiffness that the neighboring grains alter each grain’s loading from the nominal state with the result that high stresses do not spatially correlate strongly with high directional stiffness alone. An interesting difference in the stress distributions between the two loading modes is that x-direction extension shows greater regions of more highly stressed material than does z-direction extension, an attribute that is expressed in the plastic straining distributions as presented later. Figure 3e,f presents frequency distributions for the embedded stiffness. Note that the distribution for x-direction extension loading has a lower average and greater spread than the z-direction extension distribution. Greater spread implies that the sample is more heterogeneous under x-direction extension loading, consistent with the less homogeneous spatial mapping of stress.

Fig. 3
figure 3

Stress distributions at 0.1% nominal strain for a \(\sigma _{xx}\) for x-direction extension and b \(\sigma _{zz}\) for z-direction extension. Spatial distributions for the embedded stiffness defined in Eq. 9c for x-direction extension and d for z-direction extension. Frequency distributions and cumulative frequency distributions for the embedded stiffness for e for x-direction extension and f for z-direction extension. The mean of the values in e, f is 127.1 and 118.2 GPa, with standard deviations of 9.7 and 5.9 and maximum values of 198.3 and 171.3 GPa

Full size image

Recall from Sect. 2.2, MechMet provides two metrics that are related to yielding. The first is simply the relative Schmid factor, which quantifies whether or not a crystal is favorably oriented for slip to occur under an assumed nominal loading. The second is the \({\mathrm{Y2E}}\) metric that is based on a ratio of strength and stiffness. \({\mathrm{Y2E}}\) quantifies a combination of the propensity for slip and the intensity of loading. MechMet uses the embedded stiffness in its computation of the directional strength-to-stiffness ratio, thereby taking into account the influence of neighborhood on the intensity of loading. This approach has been found to be more effective than the Schmid factor for predicting initial yield [33]. Figure 4a,b displays the distributions of the reciprocal of the directional strength-to-stiffness ratio for the two loading modes. For ease of visualization, the reciprocal of the ratio is plotted instead of the value itself so that elevated values indicate a greater rather than lesser likelihood of plastic flow. A noticeable difference between x-direction extension and z-direction extension is the greater volume of material for which the metric indicates a higher likelihood for yielding. Figure 4c,d shows frequency distributions for the directional strength-to-stiffness. The distribution for extension in the x-direction has a lower mean value than the distribution for extension in the z-direction, confirming the tendency for grains to yield at lower stresses under x-direction extension.

Fig. 4
figure 4

Distributions for the natural logarithm of the reciprocal of the directional strength-to-stiffness ratio. a for x-direction extension and b for z-direction extension. Frequency distributions and cumulative frequency distributions of the strength-to-stiffness ratio for c x-direction extension and d z-direction extension. The mean of the values in c, d is \(4.6\times 10^{-3}\) and \(5.1\times 10^{-3}\), with standard deviations of \(8.0\times 10^{-4}\) and \(9.5\times 10^{-4}\) and maximum values of \(9.5\times 10^{-3}\) and \(1.1\times 10^{-2}\)

Full size image

In addition to the MechMet analyses, the virtual sample was deformed to \(\approx 1\%\) strain by extension in either the x-direction or z-direction at a nominal strain rate of 1 \(s^{-1}\) using the elastoplastic finite element code FEpX [11]. The boundary conditions were specified to match the MechMet analyses: on the extending surfaces, imposed normal motion together with zero tangential tractions, and on the lateral surfaces, symmetry planes on the coordinate surfaces (zero normal motion and zero tangential tractions) and zero tractions on the opposing surfaces. The progression of yielding within the sample is shown for the two loading modes and is correlated with the elemental directional strength-to-stiffness ratio. First, the computed macroscopic stress–strain responses are shown in Fig. 5. Note that the stress levels initially increase more rapidly under x-direction extension than under z-direction extension, which is consistent with the higher average stiffness.

Fig. 5
figure 5

Stress–strain curves computed in FEpX  simulations for x-direction (red with x markers) and z-direction (blue with o markers) extension. The sample nominal strains are 0.0038 at Point A, 0.0046 at Point B, and 0.0053 at Point C

Full size image

The distributions of plastic straining (effective plastic deformation rate calculated by FEpX) at Points A, B and C are shown in Fig. 6 on an element-by-element basis. Plastic straining initiates earlier in the loading for x-extension as is evident from the spatial plots for Point A of the loading given in Fig. 6a,b, as well as the histograms. Under both loading modes, the plastic activity expands over the sample volume and intensifies with increasing extension. At Points B and C, there are peaks of the frequency distribution at a strain rate equal to the nominal strains of 1 \(s^{-1}\). At Point C, the mean plastic strain rate is approaching the nominal value and a large majority of the elements exhibit nonzero plastic strain rate (\(\approx 80\%\) for x-extension and \(\approx 82\%\) for z-extension)

Fig. 6
figure 6

Visualizations of the plastic deformation rate, frequency distribution, and cumulative frequency distribution of the elemental plastic deformation rate, all computed in FEpX for Ti-7Al. a, c, e x-direction axial extension and b, d, f z-direction axial extension. a, b Load Point A, c, d Load Point B, and e, f Load Point C from Fig. 5. At axial stress of 328 MPa: For all plots, the first bin is truncated at 0.1. Actual values are: a 0.74, b 0.90, c 0.38, d 0.50, e 0.20, and f 0.18. The mean, standard deviation and maximum values for the binned frequency distributions are for x-extension: a 0.16, 0.34, 4.91, c 0.69, 0.71, 5.60, e 0.94, 0.72, 6.35, and for z-extension: b 0.04, 0.13, 2.44, d 0.49, 0.59, 5.46, f 0.87, 0.64, 5.61

Full size image

These trends in the initiation of plastic activity corroborate the mechanical metrics associated with strength. Subplots of Fig. 7 show correlations between the directional strength-to-stiffness and the plastic deformation rate. At Point A of the loading, a small fraction of the elements exhibit plastic flow and these tend to be at the low end of the directional strength-to-stiffness range. As the deformation proceeds to Points B and C, elements with higher values of the directional strength-to-stiffness participate in the plastic deformation, shifting the center of the distribution. Simultaneously, the deformation makes the transition from elastic to plastic, so that by Point C, the mean plastic deformation rate is approaching the sample nominal rate. These quantitative metrics confirm what the eye perceives in the spatial distributions.

Fig. 7
figure 7

Frequency distribution for combinations of elements with non-zero plastic deformation rate and the strength-to-stiffness ratio with local cubic spline surface. a x-direction extension and b z-direction extension for Load Point A. c x-direction extension and d z-direction extension for Load Point B. e x-direction extension and f z-direction extension for Load Point C. The contour lines in all the plots are at 100 count intervals. Beneath the insets at upper right, no elements are observed to deform plastically

Full size image

As stated earlier, the total number of grains in this sample is 442, which limits drawing definitive conclusions about how the loading mode influences the initiation and propagation of plastic flow in Ti-7Al. Instead, the example is used to illustrate the possibilities to extract mechanical metrics from HEDM characterization and to relate these to the onset of yielding, here for extensional loading along two different sample directions. Stress distributions within the elastic regime are shown, and the associated distributions of embedded (apparent) stiffness, a metric that takes into account the local neighbor of each grain. Differences in the average stiffness are apparent, along with differences in the structural homogeneity of the sample. Next, the implication of the elastic stiffness on the local strength is demonstrated by the directional strength-to-stiffness metric. Again, the sample exhibits distinct differences in its responses to loading in x-extension versus z-extension. Overall, under x-extension loading, the sample is weaker in that the average value of the strength-to-stiffness metric is lower. The mechanical metric distributions computed with MechMet were then examined in light of simulation data generated with FEpX for the same two extensional loading cases. Overall, the sample is observed to be stiffer and begins yielding at lower strain under x-extension than under z-extension. Further, grains with lower values of directional strength-to-stiffness in general are sites of the initiation of plastic flow. Thus, by examining the mechanical metrics it is possible to hypothesize how individual samples that have been characterized by 3D methods will respond under mechanical loading of different types and directions.

The MechMet code is efficient enough to run on an average workstation computer or laptop, but the mesh size will likely be limited by memory. The MechMet code utilizes the MATLAB in-line sparse solver [28], facilitating meshes with 100-200K elements. For example, a 150K element mesh for the Ti-7Al sample was executed on a laptop using 6 cores and 16 GB of memory and approximately 45–60 min compute time. An advantage to MechMet being built on the MATLAB platform is that it can scale to high-performance computing resources with no user input required. A single 20-core (40 thread) Xeon processor HPC node at UC Santa Barbara was used to run the Ti-7Al dataset with 150,000 and 300,000 element meshes, which required roughly 5 and 30 min, respectively.

Two Focused MechMet Applications

As stated in the Introduction, the target potential user base for MechMet is experimentally focused research groups who wish to supplement their interpretations of experimental data with basic finite element analyses. In particular, elastic analyses of experimental loading can provide valuable insight into the stress states of grains in the sample and, importantly, into the influence of neighboring crystals on the stress. Further, examining these responses in light of the crystal properties, presented in MechMet as mechanical metrics, can be quite helpful. In the following subsections, two such examples are presented.

Using MechMet to Identify Life Limiting Grains in Ti-6Al-4V

Ti-6Al-4V forms bands of similarly oriented grains when forged through certain thermomechanical pathways. These bands, known as microtextured regions (MTRs), reduce the fatigue and dwell fatigue life of the material [19]. Although this effect is empirically well quantified, the mechanisms behind this reduction are poorly understood. MechMet is a useful tool for identifying specific detrimental features in a microstructure that lead to stress or elastic strain concentrations, and it can be used to predict the location(s) where local stresses first rise above the critical resolved shear stress under monotonic loading. These early yielding locations are likely associated with fatigue crack initiation sites due to the buildup of localized plasticity on every stress cycle, even when the stress amplitude is within the macroscopically elastic regime.

A 3D Electron Back Scatter Diffraction (EBSD) dataset of equiaxed Ti-6Al-4V containing several MTRs was collected [22] via femtosecond laser serial sectioning with the TriBeam microscope [18]. The dimensions of this dataset are \(200\upmu \hbox {m} \times 500\upmu \hbox {m} \times 800\upmu \hbox {m}\), which is large enough to include over 50,000 grains. A subvolume of this dataset containing portions of 3 MTRs was selected for analysis in MechMet. The central MTR primarily consists of grains with c-axes aligned parallel to the load (vertical), while the two MTRs on either side primarily contain grains with c-axes aligned perpendicular to the load (horizontal) (Fig. 8b). Due to the anisotropic elastic and plastic properties of Ti-6Al-4V, the central MTR is both elastically stiffer and plastically stronger than the two MTRs on the sides [22], so henceforth the central MTR will be referred to as the “strong MTR,” while the other two are “weak MTRs.” Additionally, all 3 MTRs contain a few grains that are misoriented from the average orientation of the MTR.

The 917 grains in this subvolume were tessellated and meshed with Neper, the output of which is shown in Fig. 8c, d. The tessellation process simplifies the grains into polyhedra with flat faces that can be meshed using relatively few elements compared to the as-collected voxel based data. This simplification enables the analysis of larger volumes of data by reducing the total number of mesh elements. This particular mesh contains 284,217 10-node tetrahedral elements. The single crystal elastic constants and the initial slip system strengths are detailed in Table 3 and Table 4. MechMet took approximately 1 hr to run on a workstation with 128 GB of RAM, with utilization peaking around 80-90 GB. Therefore, a workstation with more memory or additional microstructure simplifications, such as small grain removal, mesh decimation, or fewer elements per grain will be necessary to solve a mesh constructed from a significantly larger volume of the original dataset.

Table 3 Single-crystal elastic constants used for Ti-6Al-4V. The same values were used in prior FFT-based crystal plasticity simulations [22]
Full size table
Table 4 Initial slip system strengths used for Ti-6Al-4V, including relative ratios normalized by each set’s basal strength. \(g_{0,b}\), \(g_{0,p}\) and \(g_{0,\pi }\) are the initial slip system strengths of the basal, prismatic and pyramidal slip systems, respectively. The same values were used in prior FFT-based crystal plasticity simulations [22]
Full size table
Fig. 8
figure 8

Visualization from the workflow to produce a MechMet input mesh from experimental 3D EBSD data. a As-collected 3D EBSD data with the locations of subvolumes indicated. b Cropped subvolume of (a) containing 917 grains and three microtextured regions. c Grain tessellation produced in Neper. d Meshed dataset produced in Neper. a and b use IPF coloring while c and d are colored by single crystal stiffness in the assigned loading direction

Full size image

The microstructure was extended in the vertical direction, meaning that the MTRs act similarly to a fiber composite loaded in the fiber direction. The same extension was applied across the entire sample, resulting in the three MTRs experiencing the same overall strain. The higher elastic stiffness of the strong MTR therefore resulted in higher local stresses throughout the strong MTR. Additionally, the stiffness of grains within the strong MTR was much more heterogeneous, resulting in much higher local stress and strain variations within the strong MTR than the neighboring weak MTRs (see Fig. 9a, b). The ratio of embedded to isolated stiffness (RE2SX) is an effective metric for quantifying the effect of grain neighborhoods. Grains in the strong MTR at the center of the dataset display a ratio lower than unity, indicating that the constraint imposed by the stiff grain neighborhood is causing grains to strain more than would be expected of a similarly oriented single-crystal where the local stress would be lower (i.e., equal to the macroscopic applied stress). Grains in the two weak MTRs on the left and right sides of the dataset display ratios above unity due to the more compliant grain neighborhoods and corresponding lower local stress (see Fig, 9c).

Fig. 9
figure 9

MechMet output from dataset in Fig. 8. a Axial stress component (MPa). b Axial strain component. c Ratio of embedded stiffness to isolated (i.e., single-crystal) stiffness (RE2SX), as defined in Eq. 10. d Directional strength-to-stiffness ratio (\({\mathrm{Y2E}}\)), as defined in Eq. 13. White arrow marks a misoriented grain within the strong MTR that is predicted to yield early

Full size image

Low strength-to-stiffness (\({\mathrm{Y2E}}\)) ratios indicate where plasticity will first occur in a theoretical tensile test, which may help to identify detrimental microstructural features related to fatigue crack initiation. The grains with the lowest \({\mathrm{Y2E}}\) ratio are misoriented grains that are well oriented for basal slip within the otherwise hard oriented strong MTR (see Fig. 9d). This result agrees with previous results using FFT-based crystal plasticity models [22]. There are several other misoriented grains within the strong MTR that have higher \({\mathrm{Y2E}}\) than the basal oriented grains; grains oriented for prismatic slip experience lower local stress due to being more compliant than grains oriented for basal slip, while other grains are oriented poorly for both basal and prismatic slip. In both cases, the resolved shear stress on the most active slip system is much lower in these grains than in the basal oriented grains, so the basal oriented grains are expected to yield first.

Fig. 10
figure 10

Another subvolume from the same Ti-6Al-4V dataset in Fig. 8. a IPF map of the EBSD data referenced to the loading direction (vertical) . b Surface strain measured by DIC. c Grains with relative Schmid factors over 0.48, colored by strength to embedded stiffness ratio. d Earliest yielding grain (highlighted in black) as predicted by MechMet is directly below the most intense slip band as measured by DIC. e and f are side views of c and d, respectively

Full size image

Surface strain measurements from high resolution digital image correlation (DIC) on this Ti-6Al-4V dataset revealed several slip bands forming well below the nominal macroscopic yield stress for this material [17]. A second subvolume containing the most intense slip band was cropped, tessellated, and meshed via the same procedure as in Fig. 8. DIC data was merged to the 3D volume using the method described in [6]. MechMet analysis found that the grain with the lowest \({\mathrm{Y2E}}\) was directly below this intense slip band. This grain is highlighted in black in Fig. 10d. Although there are 23 grains in this subvolume with a higher relative Schmid factor (see Fig. 10c), the lower Y2E indicates that the black highlighted grain should yield first and could potentially be linked to the nucleation of this intense slip band.

Microplasticity in Pure Niobium with MechMet

The tailored performance of structural metals exposed to extreme environments, such as enhanced high temperature strength of rocket and turbine engine components, requires a fundamental understanding of the plastic deformation mechanisms. BCC refractory multi-principal element alloys (MPEAs) [38] are currently of interest due to their exceptional high temperature properties. In general BCC metals and alloys exhibit complex plastic deformation behaviors due to an abundance of slip planes that are available for dislocation motion [42]. MechMet is ideally suited to study differences in dislocation glide on unique slip systems over large volumes in polycrystals. This approach complements experimental high-resolution DIC techniques used to quantify dislocation slip traces resulting from localized plastic deformation and identify active slip systems [3, 39, 40]. DIC imaging at lower stresses than the macroscopic yield strength reveals incipient plasticity (i.e., microplasticity) within the nominally elastic regime [17], shown in Fig. 11b. MechMet provides an opportunity to explore the microplastic behavior of polycrystalline BCC Nb via input of either a single slip system strength corresponding to the family of \(\{110\}\) planes with \(<111>\) directions or four slip system strengths corresponding to the families of \(\{110\}\), \(\{112\}\), \(\{123\}\) and \(\{123\}\) and \(\{134\}\) planes, all with \(<111>\) directions. The former was input for the following results.

Fig. 11
figure 11

Local strain evolution in Nb obtained experimentally by high-resolution DIC. a Maximum Schmid factor for the {110}\(<{\bar{1}}11>\) family mapped in the y-loading direction for a grain pair of interest, identified by the dashed arrow. b, c Surface strain measured by DIC within the macroscale elastic and plastic deformation regimes, respectively

Full size image

MechMet loading inputs were chosen to be representative of the experimental DIC loading conditions. Uniaxial loading in the y-direction by MechMet corresponded to monotonic loading of DIC samples along the [010] direction. The 0.1% average strain applied in MechMet was chosen due to DIC imaging in the macroscopic elastic regime at 0.12% nominal strain as shown in Fig. 11b. EBSD was used to identify grain orientations for the Nb sample studied by DIC, shown in Fig. 12a and indexed by the EMSphInx algorithm [26]. Pole figures obtained using EDAX OIM analysis 8 software enabled identification of the Nb crystallographic texture in Fig. 12b. Specifically in the loading direction, the sample had a minimally textured grain orientation distribution, shown in Fig. 12c, given the maximum 1.79 multiples of a random distribution (MRD) scaling. The microstructure also exhibited equiaxed grain structure with an average size of \(76\,\upmu \hbox {m}\).

A virtual sample was generated using Neper to create grain structure from a Voronoi tessellation with grain orientations assigned directly from the Nb EBSD measurements. The nearest-neighbor interactions, however, were not maintained. Neper was used to tessellate 175 grains, Fig. 12d, and mesh the 135,694 2nd-order tetrahedral elements, Fig. 12e. The virtual Nb microstructure was generated, and metrics were obtained using MechMet within 45 min on a laptop with 32 GB of RAM, intermittently using a maximum of 26 GB RAM.

Fig. 12
figure 12

Workflow to produce MechMet input mesh from experimental 2D EBSD data. a As-collected 2D EBSD data in inverse pole figure (IPF) coloring in the loading direction. b Pole figures of the experimental crystallographic texture c IPF triangle in the loading direction d 175 grains tessellated in Neper. e Dataset meshed in Neper to maintain the experimental texture. d, e are colored based on the single crystal stiffness in the loading direction

Full size image

MechMet requires several input parameters, including elastic constants and slip system strength. The elastic constants used for Nb are provided in Table 5. For initial analysis, a single slip system strength of 16 MPa was used based on molecular statics predictions for the glide of edge dislocations in Nb [42].

Table 5 Single-crystal elastic constants used for Nb [47]
Full size table

MechMet is a valuable tool for conducting sensitivity studies of these input material properties, which may not have been measured with sufficient precision. For instance, there is a significant discrepancy in the \(C_{44}\) elastic constant for Nb determined by experiment (\(C_{44}=28.4\,\hbox {GPa}\)) compared to prediction by density functional theory (\(C_{44}=18.1\,\hbox {GPa}\)) or molecular statics (\(C_{44}=35.03\,\hbox {GPa}\)) [46]. Figure 13 shows the MechMet output of strain, the embedded to single-crystal stiffness (RE2SX) ratio, and the directional strength-to-stiffness (\({\mathrm{Y2E}}\)) ratio with respect to these three different \(C_{44}\) values. With decreasing \(C_{44}\) values, the elastic strain and RE2SX parameters both partition more favorably on a grain-by-grain basis toward their maximum and minimum values. Partitioning in such a manner represents a less uniform response of the polycrystal, for instance in the strain accumulated in Fig. 13c. This is in comparison with the directional \({\mathrm{Y2E}}\), which exhibits lower intensity for all grains with increasing \(C_{44}\), indicating a higher propensity for yielding of all grains in the polycrystal with increasing \(C_{44}\).

The white arrow in Fig. 13a points toward banding of higher intensity grains, corresponding to a region of prominent elastic strain accumulation. In examining the directional \({\mathrm{Y2E}}\) of grains associated with this band in Fig. 13g, there is one grain of noticeably higher intensity, identified with the lower white arrow, indicating that yielding of this grain is highly improbable compared to grain neighbors in the band. The upper white arrow in Fig. 13g points to a grain of similarly high intensity located outside of this band. Comparing the elastic strain to the calculated metrics, such as directional \({\mathrm{Y2E}}\), emphasizes the value of MechMet in evaluating complex grain neighbor interactions, in this case qualitatively, to better understand the local mechanical behaviors that likely result in yielding.

Fig. 13
figure 13

The sensitivity of elastic strain and two mechanical metrics to changes in the elastic constant input, \(C_{44}\). a–c Axial elastic strain component. d–f Ratio of embedded stiffness to single crystal stiffness (i.e., RE2SX) g–i Strength to embedded stiffness ratio (i.e., directional \({\mathrm{Y2E}}\)). Coloring is scaled according to each parameter in the y-loading direction. A white arrow highlights (a) banding of elastic strain and (g) two grains of interest due to their high directional \({\mathrm{Y2E}}\) intensities

Full size image

In Fig. 11b, the dashed arrow points toward a grain that exhibited microplasticity (visible slip traces) during the DIC experiment at 0.12% nominal strain and Fig. 11c shows the local evolution of strain accumulation during macroscopic loading into the plastic regime at 0.82% nominal strain. A large discrepancy in Schmid factor is observed across the grain boundary in Fig. 11a indicating a plastically strong and weak grain pair. Slip traces of high intensity that were observed throughout the rest of the strong grain did not persist all the way to this boundary identified by the dashed arrow in Fig. 11b, c. A representative grain neighborhood will be examined in the simulated microstructure, Fig. 14, by focusing on a grain pair that exhibits a large discrepancy in relative Schmid factor.

Fig. 14
figure 14

MechMet output from the dataset in Fig. 12, all loaded in the y-direction. a relative Schmid factor mapped for each grain in the simulated 3D MechMet microstructure. b Axial elastic stress component. c Axial elastic strain component. d Strength-to-stiffness (\({\mathrm{Y2E}}\)) ratio. b–d Dashed arrows highlight a grain pair and boundary of interest. Note that the MechMet microstructure has been rotated from the axes identified in Figs. 12 and 13

Full size image

The Neper and MechMet input values are representative of Nb even if direct comparisons cannot be made (in this particular study) between the simulated and real microstructures because the grain nearest-neighbors are not maintained. As opposed to the experimentally mapped Schmid factors in Fig. 11a, the simulated relative Schmid factor within each grain is normalized by the slip system strength that was an input in MechMet for the \(\{110\}\) slip systems. The output mechanical response at this grain boundary is provided in Fig. 14b, c. The elastic strain within each grain on either side of this boundary is certainly high (0.14%) compared to that at the boundary (0.065%) in Fig. 14c. This is similar behavior to the DIC boundary selected in Fig. 11b. The local elastic strain response may be explored both by DIC and MechMet, however, MechMet additionally can map the local elastic stress as shown in Fig. 14b for the simulated microstructure. The strength-to-stiffness ratio in Fig. 14d is used to identify, by the dashed arrow, the grain in this pair that is most likely to yield at the grain scale. By definition of the directional \({\mathrm{Y2E}}\) metric, a resolved shear stress may be extracted. Comparison of the resolved shear stress for each \(\{110\}\) system to the input slip system strength within a given grain indicates the likelihood of yield even more locally, at the scale of unique slip systems.

This workflow affords the opportunity to gauge a material’s propensity for incipient plasticity as a result of both Schmid factor and local grain compatibility effects due to realistic inputs. The easily obtained outputs allow rapid comparison of materials with a wide range of mechanical properties. The MechMet code may be further customized to include more slip systems and corresponding slip system strengths to better represent the multiplicity of slip systems experimentally observed in BCC refractory MPEAs. As previously mentioned, an alternate form of the MechMet code for BCC materials is available at the GitHub repository that solves the field equations and calculates metrics for 72 unique slip systems and requires the input of 4 different slip system strengths.

Conclusions

MechMet is demonstrated to be a useful tool for the fast and efficient computation of elastic loading of virtual polycrystals using an easy to implement formulation of the finite element method. Using MechMet, the displacement field over the entire sample is computed and the local, three-dimensional, multiaxial elastic strain and stress tensors with sub-crystal resolution are evaluated. Using these tensor fields, metrics for the elastic stiffness can be estimated that explicitly account for the sample microstructure and mode of loading. Further, with a knowledge of the slip system strengths, an estimate of the yield strength within each element can be computed by projecting the stress onto the known slip system. The mechanical metrics calculated with MechMet capture the mechanical response due to the uniquely imposed loading conditions that result from the microstructure (grain topology, lattice orientations, elastic anisotropy). These metrics are much more informative than the global Schmid factor, which relies on slip system strengths alone. Specifically, the following useful mechanical metrics can be generated using MechMet:

  • Embedded (apparent) directional stiffness

  • Directional strength-to-stiffness ratio

  • Isolated (single-crystal) directional stiffness

  • Relative Schmid factor

The first two metrics incorporate information that is specific to the sample and the loading applied to it, as well as single-crystal properties. In contrast, the last two reflect only the single-crystal properties without regard to the mechanical environment.

Examples of MechMet applied to a Ti-7Al alloy, a Ti-6Al-4V, and a pure Nb sample show that realistic metrics and fields are generated. In the Ti-6Al-4V simulations, the mechanical metric of strength-to-stiffness is used to determine grains and grain neighborhoods that are likely to experience elevated stresses and could become initiation sites in fatigue. Furthermore, the aggregate mechanical response of MTRs is also captured in the MechMet simulation through comparison of the embedded to isolated stiffness. This example demonstrates the additional insight gained using the metrics that incorporate the mechanical environment. In the Nb samples, MechMet is demonstrated as a useful tool in screening for grain regions where localization will occur during mechanical testing (and DIC measurements). The sensitivity of elastic constant variability on mechanical metrics was also investigated with MechMet. This is important because estimates of elastic constants can be difficult to obtain and/or be highly variable between researchers. Visualization of the metric fields, as well as the underlying finite element solution, is straightforward via formatted output files that can be readily imported and processed with Paraview or VisIt.