Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-23T07:22:26.872Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIFORM LOWER BOUND AND LIOUVILLE TYPE THEOREM FOR FRACTIONAL LICHNEROWICZ EQUATIONS

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  21 April 2021

ANH TUAN DUONG Open the ORCID record for ANH TUAN DUONG [Opens in a new window] ,
VAN HOANG NGUYEN Open the ORCID record for VAN HOANG NGUYEN [Opens in a new window]  and
THI QUYNH NGUYEN Open the ORCID record for THI QUYNH NGUYEN [Opens in a new window]
ANH TUAN DUONG*
Affiliation:
Department of Mathematics, Hanoi National University of Education, 136 Xuan Thuy Street, Cau Giay District, Ha Noi, Viet Nam and Thang Long Institute of Mathematics and Applied Sciences, Nghiem Xuan Yem, Hoang Mai, Ha Noi, Viet Nam
VAN HOANG NGUYEN
Affiliation:
Department of Mathematics, FPT University, Ha Noi, Viet Nam e-mail: vanhoang0610@yahoo.com; hoangnv47@fe.edu.vn
THI QUYNH NGUYEN
Affiliation:
Faculty of Fundamental Science, Hanoi University of Industry, Ha Noi, Viet Nam e-mail: nguyen.quynh@haui.edu.vn
*
e-mail: tuanda@hnue.edu.vn
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the fractional parabolic Lichnerowicz equation

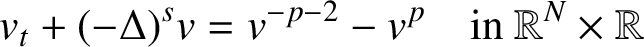
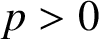$$ \begin{align*} v_t+(-\Delta)^s v=v^{-p-2}-v^p \quad\mbox{in } \mathbb R^N\times\mathbb R \end{align*} $$
where $p>0$ and 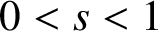$ 0<s<1 $ . We establish a Liouville-type theorem for positive solutions in the case 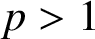$p>1$ and give a uniform lower bound of positive solutions when 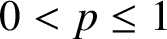$0<p\leq 1$ . In particular, when v is independent of the time variable, we obtain a similar result for the fractional elliptic Lichnerowicz equation
$$ \begin{align*} (-\Delta)^s u=u^{-p-2}-u^p \quad\mbox{in }\mathbb R^N \end{align*} $$
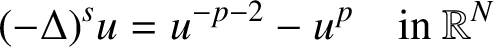
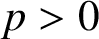with $p>0$ and 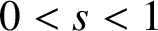$0<s<1$ . This extends the result of Brézis [‘Comments on two notes by L. Ma and X. Xu’, C. R. Math. Acad. Sci. Paris349(5–6) (2011), 269–271] to the fractional Laplacian.

Keywords

fractional elliptic equationfractional Lichnerowicz equationfractional parabolic equationLiouville type theoremuniform lower bound of solutions

MSC classification

Primary: 35B53: Liouville theorems, Phragmén-Lindelöf theorems
Secondary: 35B35: Stability 35J60: Nonlinear elliptic equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 3 , December 2021 , pp. 484 - 492
Check for updates
Copyright
©2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of A. T. Duong is funded by the Vietnam Ministry of Education and Training under grant number B2021-SPH-15.

References

Brezis, H., ‘Comments on two notes by L. Ma and X. Xu’, C. R. Math. Acad. Sci. Paris 349(5–6) (2011), 269–271.10.1016/j.crma.2011.01.024CrossRefGoogle Scholar
Chen, H. and Véron, L., ‘Initial trace of positive solutions to fractional diffusion equations with absorption’, J. Funct. Anal. 276(4) (2019), 1145–1200.10.1016/j.jfa.2018.10.013CrossRefGoogle Scholar
Choquet-Bruhat, Y., Isenberg, J. and Pollack, D., ‘The Einstein-scalar field constraints on asymptotically Euclidean manifolds’, Chinese Ann. Math. Ser. B 27(1) (2006), 31–52.10.1007/s11401-005-0280-zCrossRefGoogle Scholar
Choquet-Bruhat, Y., Isenberg, J. and Pollack, D., ‘The constraint equations for the Einstein-scalar field system on compact manifolds’, Classical Quantum Gravity 24(4) (2007), 809–828.10.1088/0264-9381/24/4/004CrossRefGoogle Scholar
Dung, N. T., Khanh, N. N. and Ngô, Q. A., ‘Gradient estimates for some $f$ -heat equations driven by Lichnerowicz’s equation on complete smooth metric measure spaces’, Manuscripta Math. 155(3–4) (2018), 471–501.10.1007/s00229-017-0946-3CrossRefGoogle Scholar
Duong, A. T. and Nguyen, V. H., ‘A Liouville type theorem for fractional elliptic equation with exponential nonlinearity’, Preprint, arXiv:1911.05966, 2019.Google Scholar
Ferrari, F. and Verbitsky, I. E., ‘Radial fractional Laplace operators and Hessian inequalities’, J. Differential Equations 253(1) (2012), 244–272.CrossRefGoogle Scholar
Frank, R. L., Lenzmann, E. and Silvestre, L., ‘Uniqueness of radial solutions for the fractional Laplacian’, Comm. Pure Appl. Math. 69(9) (2016), 1671–1726.10.1002/cpa.21591CrossRefGoogle Scholar
Hebey, E., Pacard, F. and Pollack, D., ‘A variational analysis of Einstein-scalar field Lichnerowicz equations on compact Riemannian manifolds’, Comm. Math. Phys. 278(1) (2008), 117–132.CrossRefGoogle Scholar
Ma, L., ‘Liouville type theorem and uniform bound for the Lichnerowicz equation and the Ginzburg–Landau equation’, C. R. Math. Acad. Sci. Paris 348(17–18) (2010), 993–996.10.1016/j.crma.2010.07.031CrossRefGoogle Scholar
Ma, L., ‘Boundedness of solutions to Ginzburg–Landau fractional Laplacian equation’, Internat. J. Math. 27(5) (2016), 1650048, 6 pages.10.1142/S0129167X16500488CrossRefGoogle Scholar
Ma, L. and Xu, X., ‘Uniform bound and a non-existence result for Lichnerowicz equation in the whole $n$ -space’, C. R. Math. Acad. Sci. Paris 347(13–14) (2009), 805–808.10.1016/j.crma.2009.04.017CrossRefGoogle Scholar
Molica Bisci, G., V. Radulescu, D. and Servadei, R., Variational Methods for Nonlocal Fractional Problems, Encyclopedia of Mathematics and its Applications, 162 (Cambridge University Press, Cambridge, 2016).CrossRefGoogle Scholar
Zhao, L., ‘Harnack inequality for parabolic Lichnerowicz equations on complete noncompact Riemannian manifolds’, Bound. Value Probl. 2013 (2013), 190.CrossRefGoogle Scholar
Zhao, L., ‘Gradient estimates for a simple parabolic Lichnerowicz equation’, Osaka J. Math. 51(1) (2014), 245–256.Google Scholar